
Возможности Мастера MQL5, которые вам нужно знать (Часть 15): Метод опорных векторов с полиномом Ньютона
Введение
Метод опорных векторов (Support Vector Machines, SVM) — это алгоритм классификации на основе машинного обучения. Классификация отличается от кластеризации, которую мы рассматривали в предыдущих статьях здесь и здесь. Основное различие между ними заключается в том, что классификация разделяет данные на предопределенные наборы с учителем, в то время как кластеризация стремится определить, какие именно наборы существуют и сколько их, без учителя.
Вкратце, SVM классифицирует данные, учитывая взаимосвязь, которую каждая точка данных будет иметь со всеми остальными, если к данным будет добавлено измерение. Классификация достигается, если мы можем определить гиперплоскость, которая позволяет чисто анализировать предопределенные наборы данных.
Часто рассматриваемые наборы данных имеют несколько измерений, и именно это свойство делает SVM очень мощным инструментом для классификации таких наборов данных, особенно если числа в каждом наборе невелики или относительная пропорция наборов данных искажена. Исходный код реализации SVM, имеющих более двух измерений очень сложен. Часто в сценариях использования на Python или C# используются библиотеки, минимизируя необходимость вводить код вручную.
Данные с высокой размерностью имеют тенденцию подгонять кривые под обучающие данные, что делает их менее надежными в данных вне выборки, и это один из главных недостатков SVM. С другой стороны, данные с меньшей размерностью гораздо лучше проходят перекрестную проверку и имеют больше вариантов использования.
В этой статье мы рассмотрим очень простой вариант SVM, который обрабатывает двумерные данные (также известный как линейный SVM), поскольку полный исходный код реализации, поскольку полный исходный код не должен содержать ссылок на сторонние библиотеки. Обычно разделяющая гиперплоскость выводится одним из двух методов: полиномиальное ядро (polynomial kernel) или радиальное ядро (radial kernel). Последнее является более сложным и не будет здесь обсуждаться.
Обычно полиномиальное ядро формально определяется следующим уравнением:
![]()
Определение идеальных значений c и d, которые задают уравнение гиперплоскости, представляет собой итерационный процесс, целью которого является расположить опорные векторы как можно дальше друг от друга, поскольку они измеряют разрыв между двумя наборами данных.
Однако в этой статье, как указано в названии, мы будем использовать полином Ньютона для вывода уравнения гиперплоскости на двумерных наборах данных. В недавней статье мы рассмотрели полином Ньютона, поэтому часть его реализации будет пропущена.
Мы реализуем полином Ньютона в трех сценариях. Сначала мы интерполируем средние точки между двумя предопределенными наборами данных, чтобы получить граничный набор точек, и эти точки используются для вывода уравнения линии/кривой, которое определяет нашу гиперплоскость. Определив эту гиперплоскость, мы рассматриваем ее как классификатор при принятии торговых решений для тестового экспертного класса сигналов, который будет использоваться. Во втором сценарии мы добавляем функцию регрессии, так что класс экспертного сигнала выводит не только значения 0 или 100 (как в первом сценарии), но также предоставляет значения между этими диапазонами. Мы вычисляем значение регрессии, исходя из того, насколько близко неклассифицированный вектор находится к известным векторным точкам. В-третьих, мы развиваем второй сценарий, интерполируя лишь небольшое количество точек при определении гиперплоскости. Небольшое количество точек, или опорных векторов, находится ближе к другому набору данных, тем самым "уточняя" уравнение гиперплоскости и принимая при этом всё остальное.
О полиномиальном ядре
В этой части мы рассматриваем линейные SVM, учитывая, что полная реализация исходного кода должна быть предоставлена в общий доступ и мы хотим избежать использования библиотек, предлагая полную прозрачность всего исходного кода. При практическом применении SVM нелинейные типы используются очень часто, учитывая сложность и многомерность многих наборов данных. Решение этих проблем в SVM оказалось возможным благодаря "трюку с ядром" (kernel trick). Это метод, позволяющий изучать набор данных на более высоком уровне измерения, сохраняя при этом его исходную структуру. Трюк с ядром использует скалярное произведение векторов для сохранения значений векторов меньшей размерности. При указании набора данных в более высоких измерениях разделение наборов данных достигается легко и с меньшими вычислительными ресурсами.
Как указано выше, наша функция ядра формально определена так:
![]()
где x и y служат точками данных для любых двух сравниваемых точек данных в каждом наборе, c — константа (значение которой часто изначально устанавливается равным 1), а d — степень полинома. По мере увеличения d можно определить более точное уравнение гиперплоскости, однако это может привести к чрезмерной подгонке, поэтому необходимо установить баланс. Точки данных x и y во многих случаях представлены в векторном или даже матричном формате, поэтому степень T представляет собой транспонирование x.
В иллюстративных целях реализация полиномиального ядра в MQL5 может иметь следующую форму.
//+------------------------------------------------------------------+ //| Define a data point structure | //+------------------------------------------------------------------+ struct Sdatapoint { double features[2]; int label; Sdatapoint() { ArrayInitialize(features, 0.0); label = 0; }; ~Sdatapoint() {}; }; //+------------------------------------------------------------------+ //| Function to calculate the polynomial kernel value | //+------------------------------------------------------------------+ double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree) { double _kernel_sum = 0.0; for (int i = 0; i < 2; i++) { _kernel_sum += (A.features[i] * B.features[i]); } _kernel_sum += Constant; // Add constant term return(pow(_kernel_sum, Degree)); }
Весовые коэффициенты взаимосвязи между точками данных, находящимися в отдельных наборах, вычисляются и сохраняются в матрице ядра. Она количественно определяет расстояние между точками данных и, следовательно, отфильтровывает точки данных на краю каждого набора данных, которые находятся ближе к соседнему набору.
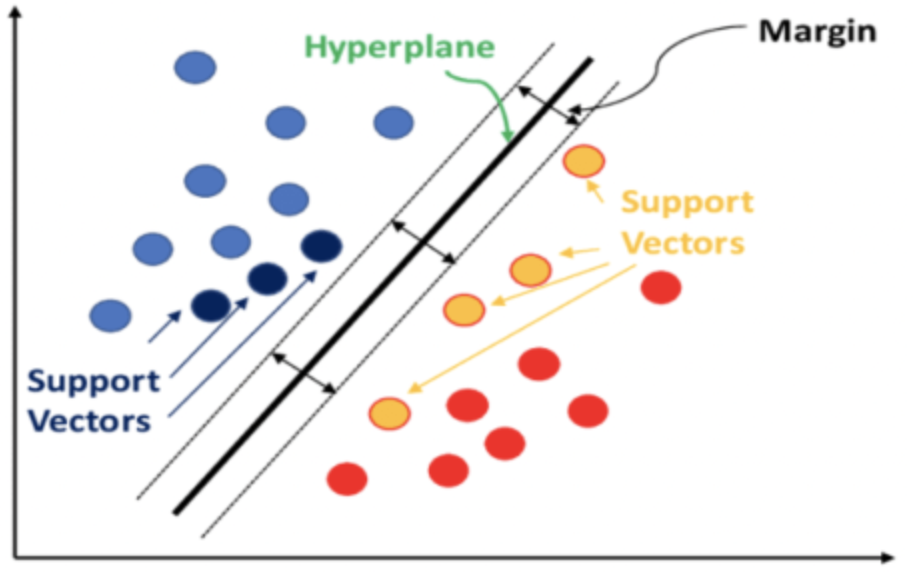
Эти опорные векторы затем служат входными данными для вычисления уравнения гиперплоскости. Все это обрабатывается в библиотечных функциях, таких как PyLIBSVM или Shogun для Python, Kernlab или SVMlight в R. Именно такие библиотечные функции, учитывая сложную природу вывода уравнения гиперплоскости, вычисляют и выводят гиперплоскость.
При определении матрицы ядра можно учитывать различные значения констант и полиномиальных степеней для нахождения оптимального решения. Поскольку это делает и без того сложный процесс получения гиперплоскости из одной матрицы еще более сложным из-за необходимости работы с несколькими матрицами, будет разумно всегда выбирать окончательную ("неоптимальную") константу и степень полинома один раз в начале и использовать ее для получения гиперплоскости. С этой целью константу часто также принимают равной 1. Как и следовало ожидать, чем выше степень полинома, тем лучше классификация, но это сопряжено с риском переобучения, о котором уже упоминалось выше.
Кроме того, более высокие степени полиномов, как правило, требуют больших вычислительных затрат, поэтому с самого начала необходимо установить интуитивно понятное значение, которое не будет слишком большим.
Полиномиальные ядра, которые здесь рассматриваются, относительно просты для понимания, но они не являются наиболее используемыми или предпочтительными ядрами во многих реализациях SVM. Более популярным является ядро радиально-базисной функции.
Ядро радиально-базисной функции (radial basis function, RBF) выбирается чаще, поскольку преимущество SVM заключается в обработке многомерных данных, а ядро RBF справляется с этой задачей лучше, чем полиномиальное ядро. После выбора ядра будет решена задача двойной оптимизации, в которой, как упоминалось выше, наборы данных отображаются в пространстве более высокой размерности, и благодаря правилам скалярного произведения, которые заложены в трюке с ядром, эта оптимизация (back and forth, вперед и назад) может быть выполнена более эффективно и выражена более просто. Сложная природа уравнений гиперплоскости для наборов данных с более чем двумя измерениями делает это свойство незаменимым. В конечном итоге уравнение гиперплоскости принимает следующий вид:
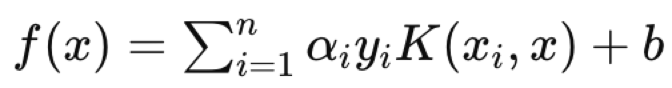
где:
- f(x) — функция решения.
- αi — коэффициенты, полученные в результате оптимизации.
- yi — метки классов.
- K(xi,x) — функция ядра.
- b — постоянное смещение.
Уравнение гиперплоскости определяет, как два набора данных разделяются функцией решения, назначающей метку класса, которая определяет, к какой стороне принадлежит любая точка запроса. Таким образом, точкой данных запроса будет x в уравнении, где xi и yi — данные поезда и его классификаторы соответственно.
Сфера применения SVM обширна и включает в себя такие разноплановые задачи, как фильтрация спама (если есть возможность встроить заголовки и содержимое электронных писем в структурированный формат), проверку заемщиков на надежность и т. д. SVM выгодно отличается от других вариантов машинного обучения надежностью при разработке моделей на основе небольших или очень неравномерных наборов данных.
Реализация средствами MQL5
Структура модели, которую мы используем для хранения значений x и y, очень похожа на наши недавние реализации, с той разницей, что здесь добавлен счетчик для каждого типа классификатора. SVM по своей сути является классификатором, и мы рассмотрим примеры его применения, где эти счетчики окажутся полезными.
Итак, значения вектора x равны 2 в каждом индексе, поскольку мы ограничиваем многомерность наших наборов данных до 2, чтобы иметь возможность использовать полином Ньютона. Увеличение размерности также создает риск чрезмерной подгонки. Первое измерение или значение x — это изменения в буфере высоких цен, тогда как второе измерение, как и следовало ожидать, будет представлять собой изменения в буфере низких цен. Выбор входных данных теперь является важнейшим аспектом машинного обучения. Хотя преобразователи, сверточные и рекуррентные нейронные сети весьма ресурсоемки, решение относительно входных данных и того, как вы их внедряете или нормализуете, может оказаться более важным.
Мы выбрали очень простой набор данных, но читатель должен знать, что его выбор входных данных не ограничивается необработанными ценовыми данными или даже значениями индикаторов, но может включать в себя значения новостных экономических индикаторов. Опять же, то, как вы решите проводить нормализацию, может иметь решающее значение.
//+------------------------------------------------------------------+ //| Function to get and prepare data. | //+------------------------------------------------------------------+ double CSignalSVM::GetOutput(int Index) { double _get = 0.0; .... .... int _x = StartIndex() + Index; for(int i = 0; i < m_length; i++) { for(int ii = 0; ii < Dimensions(); ii++) { if(ii == 0) //dim-1 { m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1); } else if(ii == 1) //dim-2 { m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1); } } if(i > 0) //assign classifier { if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0) { m_model.y[i - 1] = 1; m_model.y1s++; } else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0) { m_model.y[i - 1] = 0; m_model.y0s++; } } } // _get = SetOutput(); return(_get); }
Наш набор данных y будет представлять собой запаздывающие изменения цены закрытия, как это было ранее. Мы вводим счетчики для двух классов, обозначенных как y0 и y1. Они просто регистрируют для каждого обработанного бара, для которого установлены два значения x, было ли последующее изменение цены закрытия бычьим (в этом случае регистрируется 0) или медвежьим (в этом случае регистрируется 1).
Поскольку y является вектором, мы могли бы, попутно, извлечь эти значения 0 и 1, сравнив их текущие значения с векторами, заполненными нулями, и векторами, заполненными единицами, поскольку возвращаемые значения фактически представляли бы собой количество нулей и единиц в векторе y соответственно.
Функция set-output — еще одно дополнение к функциям, которые у нас были при обработке данных нашей модели. Она берет значения вектора x для каждого класса и интерполирует среднюю точку между двумя наборами, которая может служить гиперплоскостью двух наборов. Это не подход SVM, как уже упоминалось, но поскольку мы хотим определить гиперплоскость с помощью полинома Ньютона, он дает нам набор точек, с которыми мы можем работать для вывода уравнения гиперплоскости.
//+------------------------------------------------------------------+ //| Function to set and train data | //+------------------------------------------------------------------+ double CSignalSVM::SetOutput(void) { double _set = 0.0; matrix _a,_b; Classifier(_a,_b); if(_a.Rows() * _b.Rows() > 0) { matrix _interpolate; _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions()); for(int i = 0; i < int(_a.Rows()); i++) { for(int ii = 0; ii < int(_b.Rows()); ii++) { _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]); _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]); } } vector _w; vector _x = _interpolate.Col(0); vector _y = _interpolate.Col(1); _w.Init(m_model.y0s * m_model.y1s); _w[0] = _y[0]; m_newton.Set(_w, _x, _y); double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0; m_newton.Get(_w, _xx, _zz); if(_yy < _zz) { _set = 100.0; } else if(_yy > _zz) { _set = -100.0; } _set *= Regressor(_x, _y, _xx, _yy); } return(_set); }
Мы рассматриваем три подхода к получению гиперплоскости в рамках этого метода. Самый первый подход рассматривает все точки в каждом наборе при построении точек гиперплоскости путем интерполяции среднего значения каждой точки в наборе в каждую точку в альтернативном наборе. Очевидно, что здесь не рассматриваются опорные векторы, но они представлены здесь в целях изучения и сравнения с другими подходами.
Второй метод аналогичен первому, с той лишь разницей, что прогнозируемое значение y регрессируется, то есть вместо того, чтобы иметь его равным 0 или 1, мы используем функцию "регулятора" для преобразования или нормализации выходных прогнозов в виде значения с плавающей точкой в диапазоне от 0,0 до 1,0. Это фактически создает систему, которая в принципе еще дальше от SVM, но все еще использует гиперплоскость для дифференциации двумерных точек данных.
//+------------------------------------------------------------------+ //| Regressor for the model | //+------------------------------------------------------------------+ double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY) { double _x_max = fmax(X.Max(), XX); double _x_min = fmin(X.Min(), XX); double _y_max = fmax(Y.Max(), YY); double _y_min = fmin(Y.Min(), YY); return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min))))); }
Мы можем получить прокси-регрессивное значение, сравнивая прогнозируемое значение с максимальным и минимальным значением в его наборе таким образом, что если оно соответствует минимуму, возвращается 0, а не 1, которая была бы возвращена, если бы оно соответствовало максимальному значению.
В-третьих, мы улучшаем метод в части 2, добавляя функцию "классификатора", которая фильтрует точки в каждом из множеств, используемых при выводе гиперплоскости. Рассматривая точки, которые находятся дальше всего от центроида своего множества, но ближе всего к центроиду противоположного множества, мы получаем два подмножества точек, по одному из каждого класса, которые можно использовать для интерполяции границы гиперплоскости между двумя множествами.
//+------------------------------------------------------------------+ //| 'Classifier' for the model that identifies Support Vector points | //| for each set. | //+------------------------------------------------------------------+ void CSignalSVM::Classifier(matrix &A, matrix &B) { if(m_model.y0s * m_model.y1s > 0) { matrix _a_centroid, _b_centroid; _a_centroid.Init(1, Dimensions()); _b_centroid.Init(1, Dimensions()); for(int i = 0; i < m_length; i++) { if(m_model.y[i] == 0) { _a_centroid[0][0] += m_model.x[i][0]; _a_centroid[0][1] += m_model.x[i][1]; } else if(m_model.y[i] == 1) { _b_centroid[0][0] += m_model.x[i][0]; _b_centroid[0][1] += m_model.x[i][1]; } } _a_centroid[0][0] /= m_model.y0s; _a_centroid[0][1] /= m_model.y0s; _b_centroid[0][0] /= m_model.y1s; _b_centroid[0][1] /= m_model.y1s; double _a_sd = 0.0, _b_sd = 0.0; double _ab_sd = 0.0, _ba_sd = 0.0; for(int i = 0; i < m_length; i++) { if(m_model.y[i] == 0) { double _0 = 0.0; _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0); _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0); _a_sd += sqrt(_0); double _1 = 0.0; _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0); _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0); _ab_sd += sqrt(_1); } else if(m_model.y[i] == 1) { double _1 = 0.0; _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0); _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0); _b_sd += sqrt(_1); double _0 = 0.0; _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0); _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0); _ba_sd += sqrt(_0); } } _a_sd /= m_model.y0s; _ab_sd /= m_model.y0s; _b_sd /= m_model.y1s; _ba_sd /= m_model.y1s; for(int i = 0; i < m_length; i++) { if(m_model.y[i] == 0) { double _0 = 0.0; _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0); _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0); double _1 = 0.0; _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0); _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0); if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1)) { A.Resize(A.Rows()+1,Dimensions()); A[A.Rows()-1][0] = m_model.x[i][0]; A[A.Rows()-1][1] = m_model.x[i][1]; } } else if(m_model.y[i] == 1) { double _1 = 0.0; _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0); _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0); double _0 = 0.0; _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0); _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0); if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0)) { B.Resize(B.Rows()+1,Dimensions()); B[B.Rows()-1][0] = m_model.x[i][0]; B[B.Rows()-1][1] = m_model.x[i][1]; } } } } }
Приведенный выше код, который это делает, немного длинный, и я уверен, что можно реализовать его более эффективно, особенно если задействовать встроенные функции векторных и матричных типов данных, которые недавно были введены в MQL5. Но сначала мы находим центроид (или среднее значение) каждого набора данных. После этого мы приступаем к вычислению стандартного отклонения каждого набора данных, и оно получается с помощью переменных, имеющих суффикс _sd. Вооружившись координатами центроида и величиной стандартного отклонения, мы можем измерить и сравнить для каждой точки, насколько она удалена от своего центроида, а также насколько она удалена от центроида противоположного набора данных, при этом вычисленные стандартные отклонения служат пороговым значением для слишком большого или слишком малого расстояния.
Интерполированные точки — это все, что нам нужно для определения уравнения с полиномом Ньютона. Как мы уже видели, чем больше точек предоставлено, тем выше показатель степени уравнения. Максимальное количество интерполированных точек, которые мы можем использовать с полиномом Ньютона, контролируется размером наборов данных и прямо пропорционально параметру m_length — переменной, которая устанавливает, сколько точек данных в истории нам нужно просмотреть при определении двух наборов данных в модели.
Из трех методов, используемых для получения гиперплоскости, только последний имеет некоторое сходство с типичными методами SVM. Мы определяем опорные векторы путем отбора точек внутри каждого набора, которые находятся ближе всего к границе набора и, следовательно, более соответствуют гиперплоскости. Эти опорные векторные точки затем служат входными данными для нашего класса полиномов Ньютона при выводе уравнения гиперплоскости. Напротив, если бы мы применили строгий метод опорных векторов (SVM), мы бы добавили дополнительное измерение к нашим точкам данных для дополнительной дифференциации, одновременно перебирая константы в уравнении полиномиального ядра, что позволяет это сделать. Даже при наличии только двумерных данных это явно на порядок сложнее, не говоря уже о задействованных вычислительных ресурсах. На самом деле, для простоты и практичности одна из этих констант (c) всегда предполагается равной 1, в то время как оптимизируется только переменная степени полинома (d в уравнениях выше). Как вы, наверно, уже поняли, для наборов данных, имеющих более 2 измерений, это явно потребует сторонней библиотеки, потому что, если нет ничего иного, то искомое уравнение степени 4, 5 или n будет на несколько порядков сложнее.
Реализация полинома Ньютона очень похожа на ту, что мы рассмотрели в предыдущей статье, за исключением некоторой отладки функции Get, которая запускает построенное уравнение для определения следующего значения y. Код прилагается ниже.
Результаты тестера
Каждый из трех файлов классов сигналов, прикрепленных в конце статьи, можно собрать в советника с помощью мастера MQL5. Примеры того, как это делается, доступны здесь издесь.
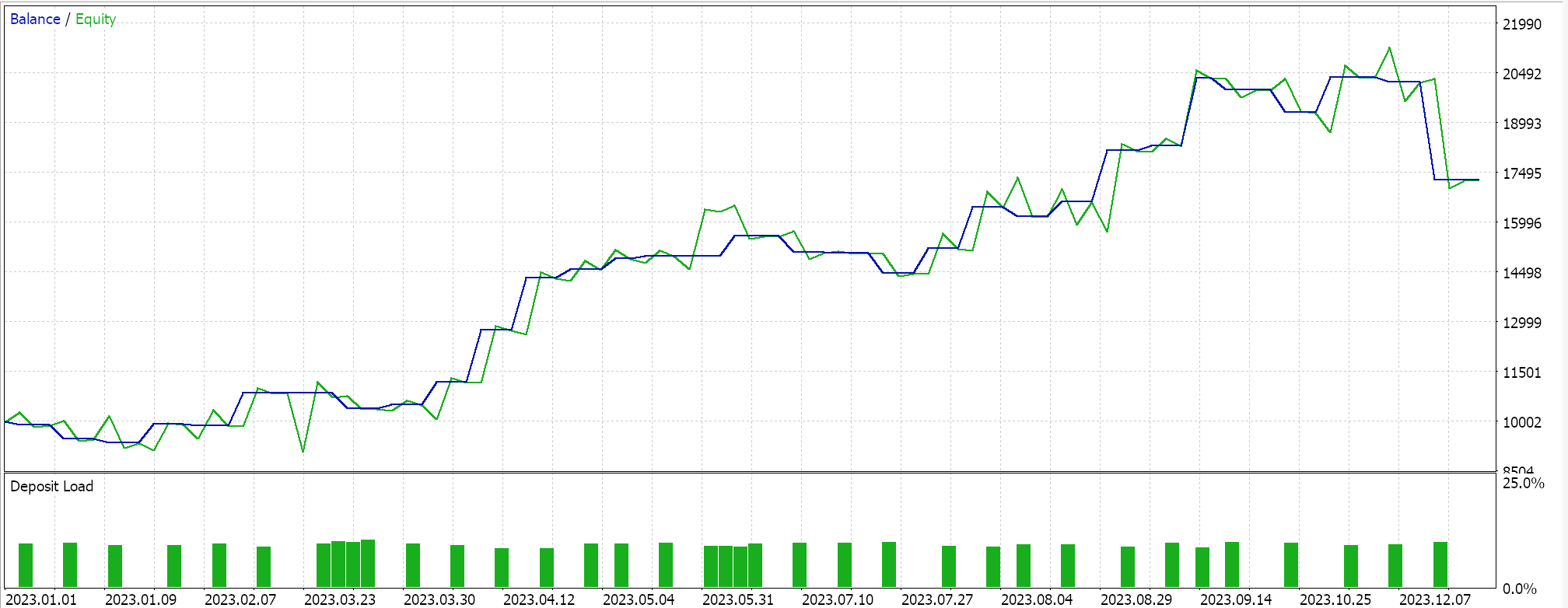
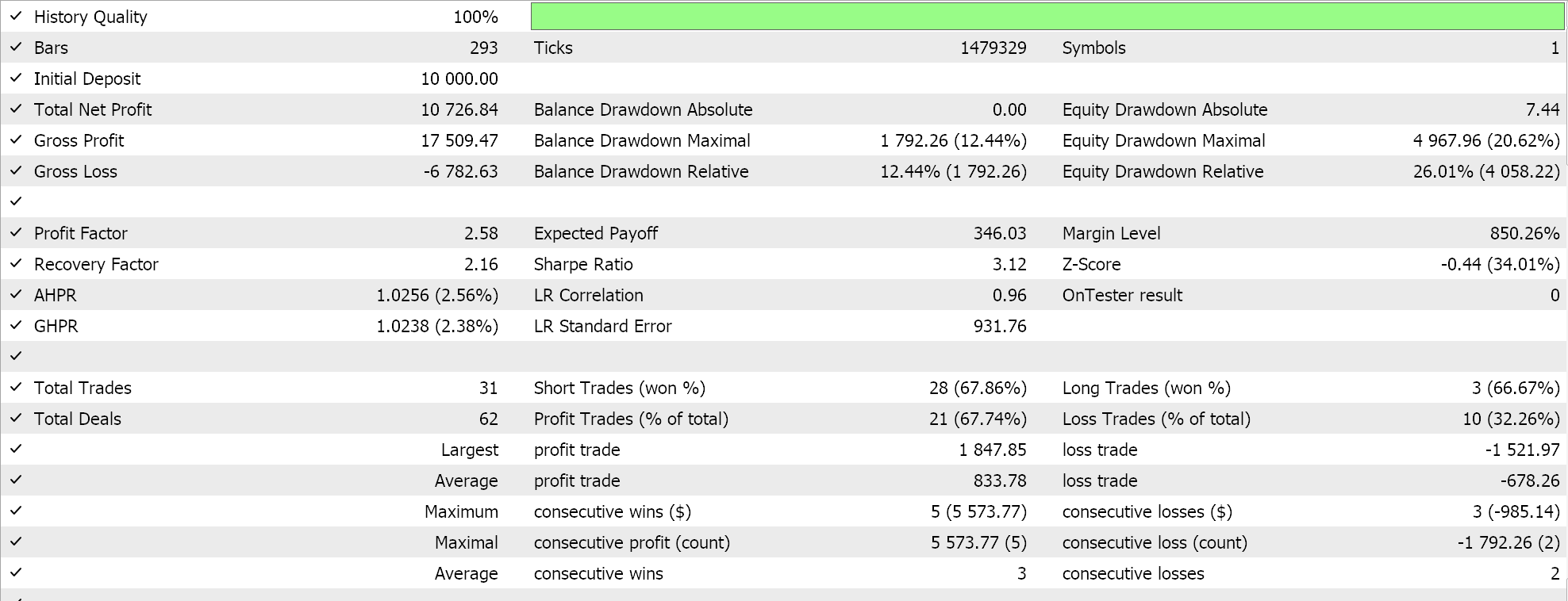
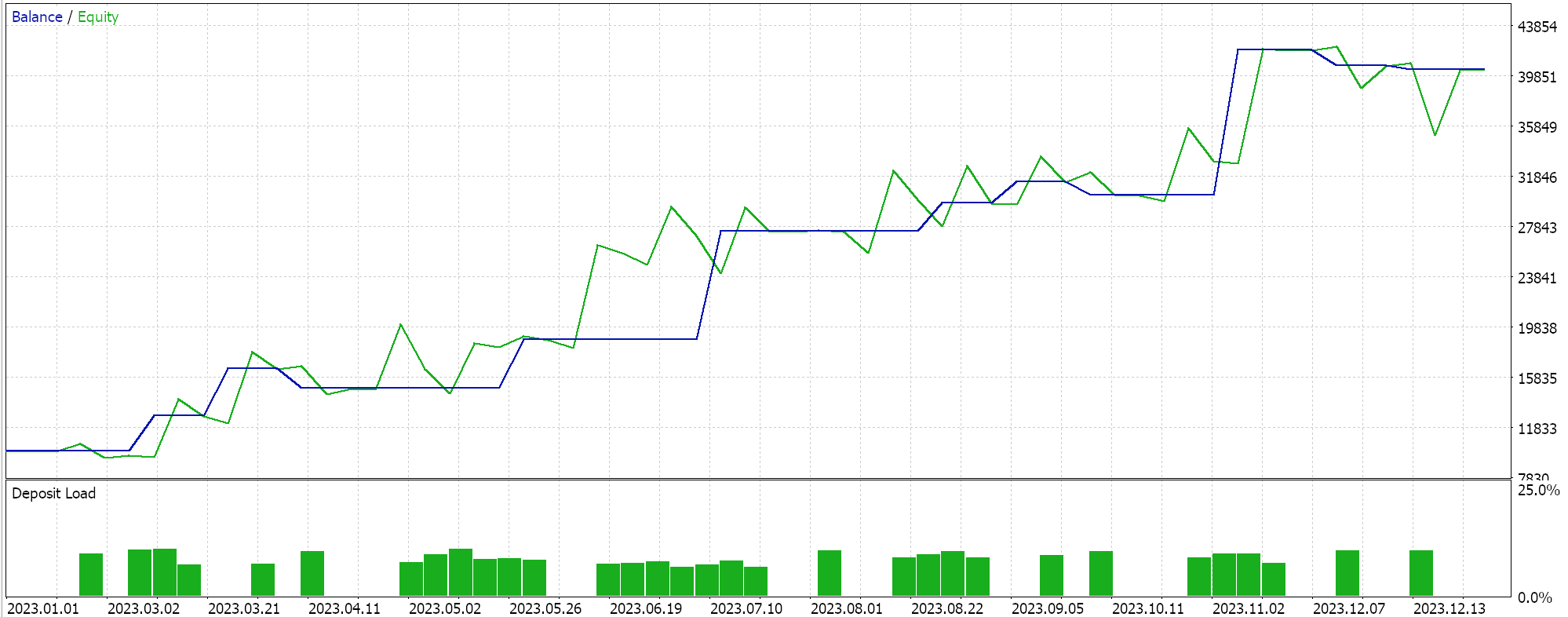
Итак, при запуске тестов для самой первой реализации, где гиперплоскость получена путем интерполяции по всем точкам в любом наборе без проверки на наличие опорных векторов, мы получили следующие результаты:
Если мы выполним аналогичные тестовые прогоны, как указано выше, где нашим тестовым символом будет EURJPY на дневном таймфрейме за 2023 год, для второго метода, который только добавляет регрессию к методу выше, мы получим следующее:
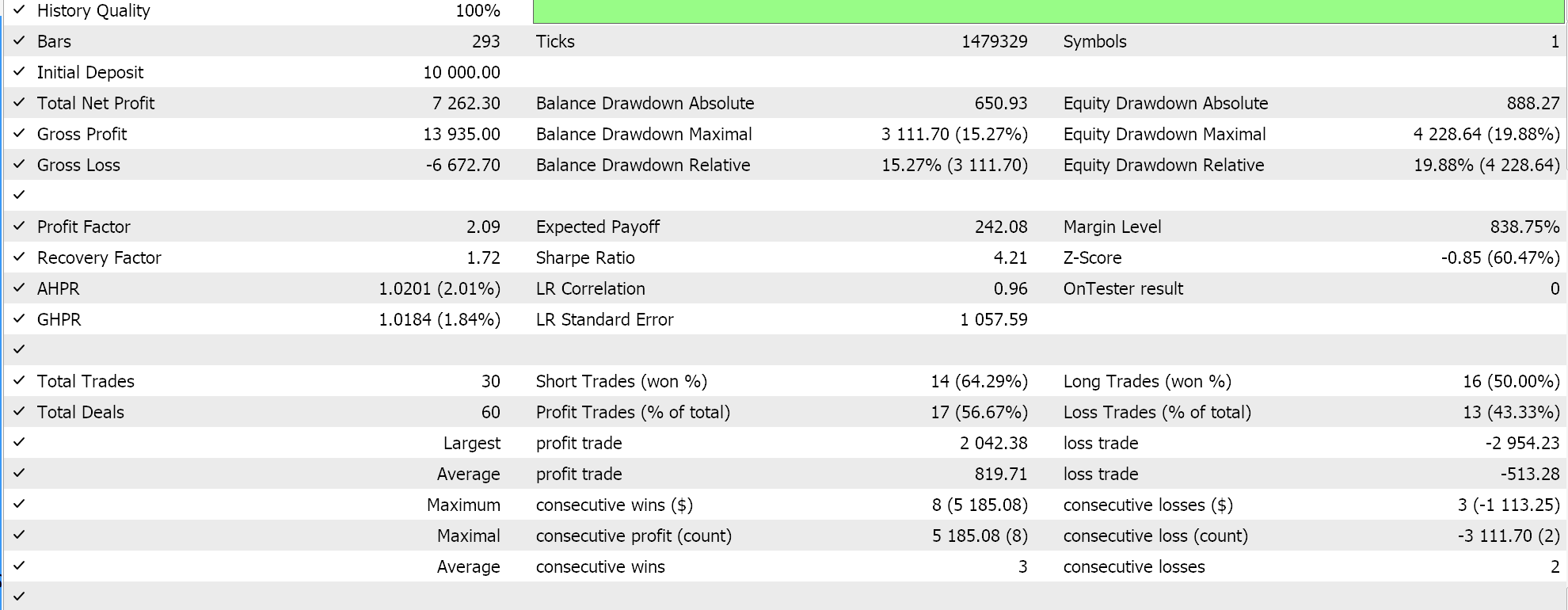
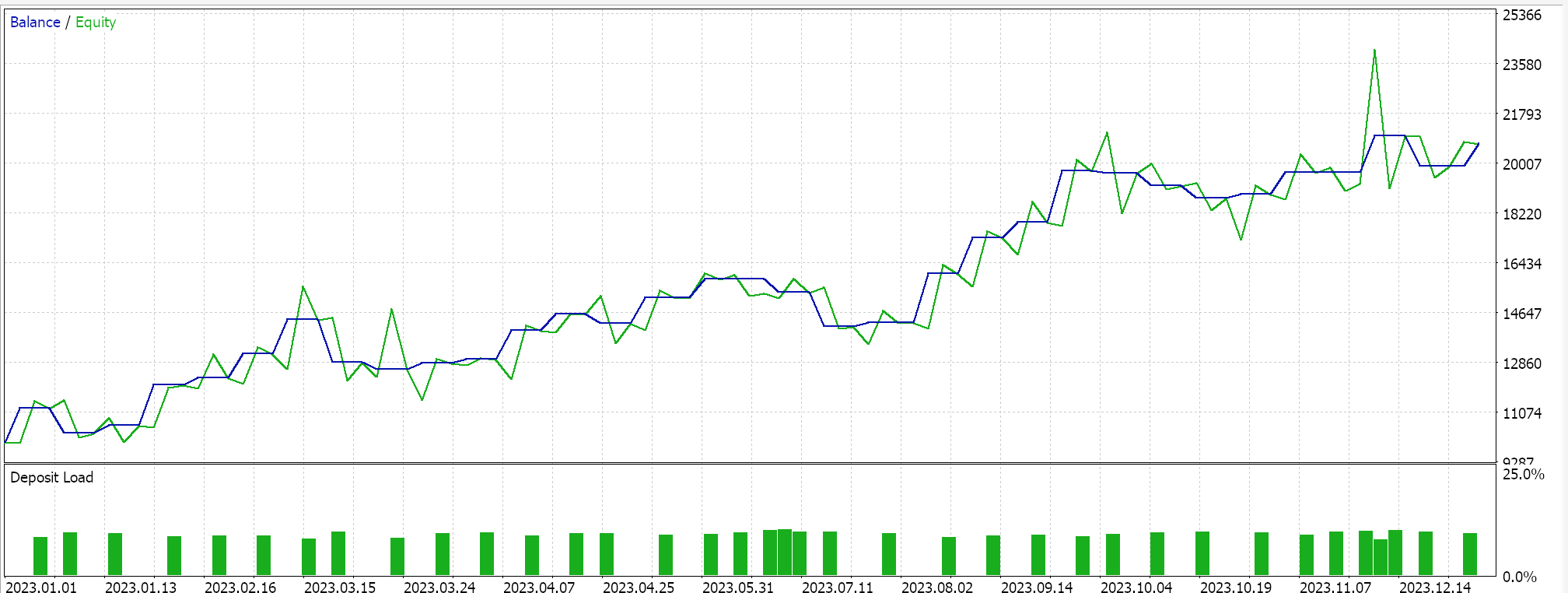
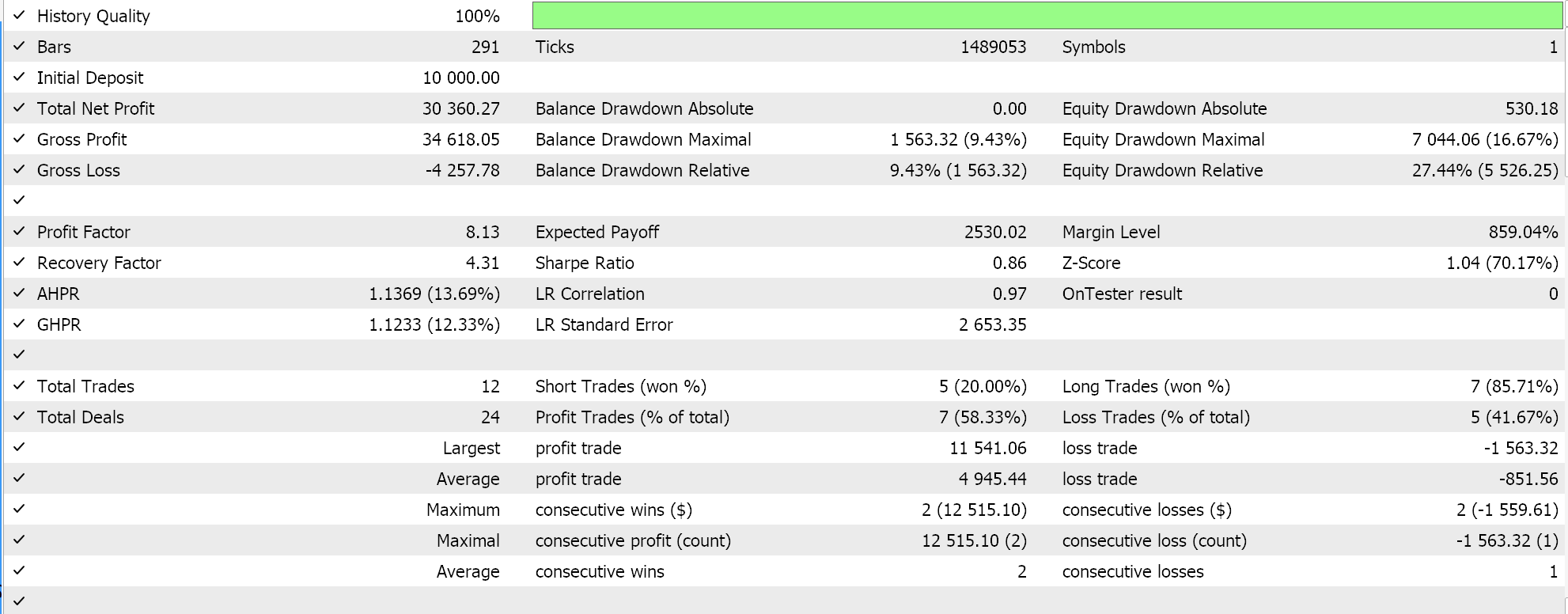
Наконец, подход, наиболее похожий на SVM, который проверяет любой набор данных на наличие опорных векторных точек перед выводом его гиперплоскости, при тестировании дает следующие результаты:
При беглом изучении отчетов выше можно сделать вывод, что метод, использующий опорные векторы, является наиболее перспективным, и это, вероятно, не должно вызывать удивления, учитывая необходимость дополнительной тонкой настройки (даже несмотря на то, что количество параметров во всех трех методах одинаково).
Кстати, тестирование проводится на реальных тиках с лимитными ордерами, целевой уровень прибыли и стоп-лоссы не используются. Как всегда, необходимо провести больше испытаний, прежде чем делать более значимые выводы. Однако интересно отметить, что при том же количестве входных параметров метод опорных векторов работает лучше. Он заключал меньше сделок, и это дало значительно лучшую производительность, чем два других подхода.
Как видно из результатов, добавление регрессии во втором подходе лишь незначительно улучшило производительность. Количество сделок также почти не изменилось, однако предварительная проверка точек набора данных на предмет опорных векторов перед определением гиперплоскости явно изменила ситуацию. Отчеты MetaTrader очень субъективны, и многие спорят о том, какой показатель наиболее важен. У меня также нет однозначного ответа на этот вопрос. Однако я думаю, что сравнение средней прибыли и среднего убытка (за сделку), а также соотношение среднего количества последовательных выигрышей к среднему количеству последовательных убытков может быть полезным. Все эти значения часто объединяются при расчете соотношения, называемого ожиданием. Это сильно отличается от ожидаемого выигрыша, который представляет собой просто прибыль, поделенную на все сделки. Если сравнить ожидаемую продолжительность всех отчетов, то метод, использующий опорные векторы, почти в десять раз лучше по сравнению с двумя другими подходами.
Заключение
Мы рассмотрели еще один пример быстрой разработки и тестирования возможной торговой идеи, чтобы оценить, является ли она улучшением или соответствует существующей стратегии.
SVM — довольно сложный алгоритм, который редко, если вообще когда-либо, реализуется без помощи сторонней библиотеки, будь то PyLIBSVM для Python или SVMlight для R. Более того, один из оптимизируемых параметров часто принимается равным 1, чтобы упростить этот процесс. Подводя итог, можно сказать, что в этом процессе размерность копии изучаемого набора данных увеличивается с помощью специальной обратимой формулы, называемой полиномиальным ядром. Относительная простота и обратимость этого полиномиального ядра позволили ему получить название "трюк с ядром". Эта простота и обратимость, которые возможны благодаря скалярным произведениям, крайне необходимы в случаях, когда набор данных имеет более двух измерений, поскольку, как можно себе представить, в случаях наборов данных с очень высокой размерностью уравнение гиперплоскости, которое должным образом классифицирует такие наборы данных, неизбежно будет очень сложным.
Таким образом, представив альтернативный способ вывода гиперплоскости с помощью полинома Ньютона, который, во-первых, не требует столь больших вычислительных затрат, а также гораздо лучше понятен и представим, можно не только протестировать различные реализации SVM, но и рассматривать их либо как альтернативы существующей стратегии, либо как дополнительные. Среда MQL5 IDE допускает оба сценария. В первом случае нам придется разрабатывать совершенно новую торговую систему на основе кода класса сигнала, представленного здесь. Но не следует упускать из виду огромный потенциал мастера MQL5, который позволяет собирать и тестировать несколько стратегий одновременно. Это также можно сделать быстро и с минимальным кодированием при отборе идей и стратегий на предварительном этапе. Как всегда, помимо рассмотрения класса сигнала собранных мастером классов, можно также изучить класс трейлинга и классы управления капиталом.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/14681
 Разрабатываем мультивалютный советник (Часть 17): Дальнейшая подготовка к реальной торговле
Разрабатываем мультивалютный советник (Часть 17): Дальнейшая подготовка к реальной торговле
 Нейронная сеть на практике: Секущая прямая
Нейронная сеть на практике: Секущая прямая
 Нейросети в трейдинге: Иерархический векторный Transformer (HiVT)
Нейросети в трейдинге: Иерархический векторный Transformer (HiVT)
 Циклы и Forex
Циклы и Forex
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
заинтересовала статья, но при компиляции у меня возникла проблема:
файл 'C:\Users\sxxxxx\AppData\Roaming\MetaQuotes\Terminal\4B1CE69F57770545xxxxxxxx2C\MQL5\Include\my\Cnewton.mqh' не найден.
заинтересовала статья, но при компиляции у меня возникла проблема:
файл 'C:\Users\sxxxxx\AppData\Roaming\MetaQuotes\Terminal\4B1CE69F57770545xxxxxxxx2C\MQL5\Include\my\Cnewton.mqh' не найден.
Я не нашел Cnewton.mqh.
Класс с таким именем есть (в предыдущих статьях), но он не подходит для этого примера, не может быть использован и скомпилирован.
Автор статьи должен включить эту библиотеку, чтобы мы могли ее использовать.
Существует класс с таким именем (в предыдущих статьях), но он не подходит для данного примера, не может быть использован и скомпилирован.
Автор статьи должен включить эту библиотеку, чтобы мы могли ее использовать.
Здравствуйте,
Вложение было добавлено, статья отправлена на публикацию и скоро будет обновлена.