Популяционные алгоритмы оптимизации: Алгоритм оптимизации китов (Whale Optimization Algorithm, WOA)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Горбатые киты, эти величественные морские гиганты, действительно являются хозяевами океана. Когда горбатые киты вступают в танец охоты, время словно замирает, а каждое движение наполнено грацией и точностью. Мастера "пузырьковой сети" создают водную завесу из пузырьков, чтобы ограничить и собрать свою добычу в центре кольца. Этот уникальный метод кормления подчеркивает их интеллект и стратегическое мышление в процессе охоты.

Синхронизация их действий с другими особями, даже незнакомыми, говорит о глубоком взаимопонимании и единении, демонстрирует способность к коллективной работе и координации вне зависимости от обстоятельств.

Их способность поглощать до 1.4 метрических тонн пищи в день подчеркивает их роль в морской экосистеме как одних из самых мощных "потребителей" океана. Их жизненный ритм, сменяющийся от периодов обильной охоты до времен покоя и поста, говорит нам о величии и непредсказуемости океана, в котором они царствуют. Время зимовки, когда горбатые киты почти не питаются, свидетельствуют об их удивительной способности к выживанию. Они полагаются на запасы жира, которые накапливают во время богатых уловов, чтобы пережить времена, когда пища становится редкостью. Это напоминает нам о том, как природа учит животных быть экономными и мудрыми в расходовании ресурсов.

Горбатые киты — это живые хроники выживания и приспособляемости, символы мудрости, воплощение силы и красоты океана, неисчерпаемого источника вдохновения для нас.

Алгоритм WOA (Whale Optimization Algorithm) — это метаэвристический алгоритм оптимизации, который был предложен Мирджалили и Льюисом в 2016 году. Они были вдохновлены поведением китов при охоте.

Киты используют различные стратегии охоты, включая "пузырьковую сеть" и "спиральное проникновение". В "пузырьковой сети" киты окружают свою добычу, создавая "сеть" из пузырей, чтобы запутать и напугать добычу. В "спиральном проникновении" киты поднимаются из глубин океана в спиральном движении, чтобы захватить добычу.

Эти стратегии охоты были абстрактно моделированы в алгоритме WOA. В алгоритме WOA "киты" представляют собой решения проблемы оптимизации, а "охота" представляет собой процесс поиска оптимального решения.

2. Описание алгоритма

Алгоритм WOA начинается с инициализации популяции китов со случайными позициями. Затем выбирается лидер - кит с наилучшим значением целевой функции (по факту - лучшее глобальное решение). Позиции остальных китов обновляются с учетом позиции лидера. Это происходит в двух режимах: в режиме исследования и в режиме эксплуатации. В режиме исследования киты обновляют свои позиции, используя случайный поиск в окрестности текущего глобального лучшего решения. В режиме эксплуатации киты обновляют свои позиции, приближаясь к текущему своему лучшему решению.

Алгоритм WOA был успешно применен для решения многих задач оптимизации и показал хорошие результаты. Однако, как и любой алгоритм оптимизации, он имеет свои преимущества и недостатки. Например, он может быть склонен к попаданию в локальные оптимумы и иметь относительно медленную скорость сходимости.

Вот как можно связать интересные факты о горбатых китах с принципами алгоритма WOA:

• Сотрудничество и координация. Горбатые киты часто охотятся в группах, сотрудничая друг с другом для общего успеха. Это напоминает принципы алгоритма WOA, где индивидуальные агенты (как киты) работают вместе, обмениваясь информацией и координируя свои действия для достижения оптимального решения.

• Интеллектуальные стратегии. Горбатые киты используют разнообразные интеллектуальные стратегии охоты, такие как создание "пузырьковой сети" и координация действий в группе. Алгоритм WOA также основан на интеллектуальных стратегиях оптимизации, включая поиск оптимальных решений и адаптацию к изменяющимся условиям.

• Адаптивность и эффективность. Горбатые киты демонстрируют адаптивность и эффективность в процессе охоты, изменяя свои методы в зависимости от ситуации. Алгоритм WOA также стремится к адаптивности и эффективности, применяя различные стратегии оптимизации и модифицируя свое поведение для достижения лучших результатов.

Таким образом, алгоритм WOA черпает вдохновение из уникальных стратегий и поведения горбатых китов в процессе охоты, что помогает ему эффективно и интеллектуально решать задачи оптимизации в различных областях.

Модифицированный алгоритм оптимизации WOAm (Whale Optimization Algorithm) включает в себя несколько основных этапов:

1. Движение относительно глобального решения:
    - На начальном этапе алгоритма каждая "китовая" особь (решение) движется в направлении глобального оптимального решения. Это помогает исследовать пространство решений и находить общее направление к оптимуму.

2. Улучшение своего положения:
    - Каждая особь (кит) пытается улучшить своё текущее положение, приближаясь к лучшему решению. Особи могут менять свои параметры или стратегии, чтобы достичь лучшей производительности.

3. Движение по спирали:
    - Этот этап представляет собой важный механизм алгоритма WOA. Особи могут перемещаться по спирали вокруг лучшего решения, что помогает им более эффективно исследовать пространство поиска и приближаться к оптимальному решению.

4. Миграция:
    - Этот этап включает в себя случайное изменение позиций особей, чтобы обеспечить разнообразие и предотвратить застревание в локальных оптимумах. Миграция помогает алгоритму избегать преждевременной сходимости к недостаточно хорошему решению.

Эти этапы в совокупности обеспечивают эффективный поиск оптимального решения в пространстве задачи оптимизации. Я внёс изменения, добавив четвертый этап, чтобы улучшить устойчивость алгоритма к застреванию. Моделирование миграции китов в живой природе на новые территории в поисках пищи необходимо, когда предыдущие источники истощены. Это дополнение придает алгоритму дополнительную гибкость и помогает более эффективно исследовать пространство решений, отражая стратегии выживания и адаптации в природе.

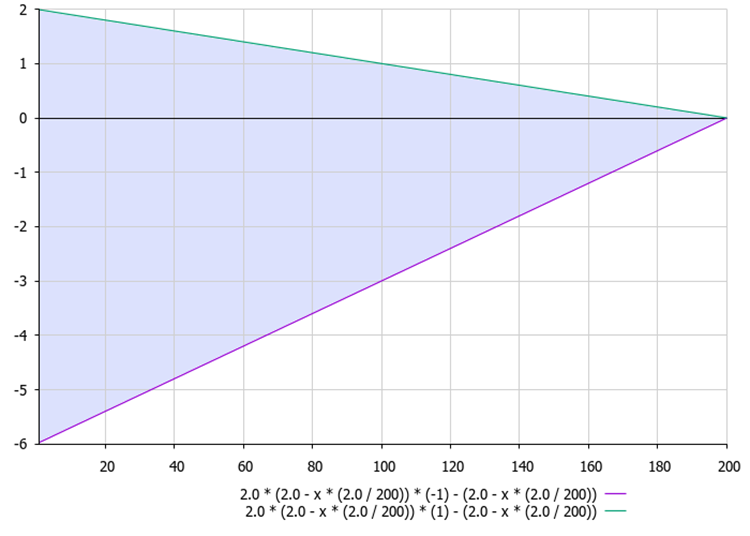
Рисунок 1. Область значений коэффициента "A" в формуле A = 2.0 * aKo * r - aKo в зависимости от текущей эпохи.

Псевдокод для алгоритма оптимизации китового поиска (WOAm):

1. Инициализировать популяцию случайным положением.
2. Вычислить приспособленность.
3. Вычислить коэффициент aKo: aKo = 2.0 - epochNow * (2.0 / epochs).
4. Генерируем случайное число "r" из равномерного распределения в интервале от -1 до 1.
5. Вычислить переменные "A" и "C":
   - A = 2.0 * aKo * r - aKo (рисунок 1)
   - C = 2.0 * r
6. Устанавливаем значения для "spiralCoeff", случайного числа "l" из равномерного распределения и случайной вероятности "p".
7. Если "p" меньше, чем "refProb", то:
   - Если абсолютное значение "A" больше 1.0, то: X = Xbest - A * |Xbest - Xprev|
   - Иначе, выбираем случайный индекс "leaderInd" от 0 до "popSize" и: X = Xlead - A * |Xlead - Xprev|
8. Иначе, если случайная вероятность меньше чем spiralProb, то: X = Xprev + | Xprev - X| * exp (b * l) * cos (2 * M_PI * l)
9. В противном случае: X = PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30)
10. Вычислить приспособленность.
11. Обновить глобальное решение.
12. Повторять с п.3 до выполнения критерия останова.

Рисунок 2. "Пузырьковая" охота китов, которая инспирировала написание алгоритма оптимизации WOA.

Переходим к написанию кода алгоритма WOAm.

Для описания каждого кита определим структуру "S_WOA_Agent". Давайте разберем, что здесь происходит:

1. Структура содержит следующие поля:
    - cPrev[] - массив для хранения предыдущих координат агента.
    - fPrev - переменная для хранения предыдущей оценки (фитнеса) агента.

2. Init - метод структуры "S_WOA_Agent", который инициализирует поля структуры. Он принимает целочисленный аргумент "coords", который используется для изменения размера массива "cPrev" с помощью функции "ArrayResize".

3. fPrev = -DBL_MAX - устанавливает начальное значение переменной "fPrev" равным минимально возможной величине числа типа double.

Этот код представляет собой базовую структуру данных для агентов в алгоритме оптимизации WOAm и инициализирует их поля при создании нового агента.

//——————————————————————————————————————————————————————————————————————————————
struct S_WOA_Agent
{
    double cPrev []; //previous coordinates
    double fPrev;    //previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Определим класс "C_AO_WOAm" алгоритма WOAm, который является наследником базового класса популяционных алгоритмов "C_AO" и содержит следующие поля и методы:

1. Публичные поля:

• ao_name - имя алгоритма оптимизации.
• ao_desc - описание алгоритма оптимизации.
• popSize - размер популяции.
• params - массив параметров алгоритма.
• refProb - вероятность уточнения.
• spiralCoeff - коэффициент спирали.
• spiralProb - вероятность спирали.
• agent - вектор агентов.

2. Методы:

• C_AO_WOAm - конструктор класса, инициализирующий поля класса.
• SetParams - метод для установки параметров алгоритма.
• Init - метод для инициализации алгоритма. Принимает минимальный и максимальный диапазоны поиска, шаг поиска и количество эпох.
• Moving - метод для перемещения агентов.
• Revision - метод для ревизии агентов.

3. Приватные поля:

• epochs - количество эпох.
• epochNow - текущая эпоха.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_WOAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_WOAm () { }
  C_AO_WOAm ()
  {
    ao_name = "WOAm";
    ao_desc = "Whale Optimization Algorithm M";

    popSize = 100;   //population size


    ArrayResize (params, 4);

    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "refProb";     params [1].val = refProb;
    params [2].name = "spiralCoeff"; params [2].val = spiralCoeff;
    params [3].name = "spiralProb";  params [3].val = spiralProb;
  }

  void SetParams ()
  {
    popSize     = (int)params [0].val;
    refProb     = params      [1].val;
    spiralCoeff = params      [2].val;
    spiralProb  = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double refProb;     //refinement probability
  double spiralCoeff; //spiral coefficient
  double spiralProb;  //spiral probability


  S_WOA_Agent agent []; //vector

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
};
//——————————————————————————————————————————————————————————————————————————————

Метод "Init" класса "C_AO_WOAm" используется для инициализации переменных класса на основе переданных параметров. Этот метод выполняет стандартную инициализацию с использованием метода "StandardInit", который принимает минимальный и максимальный диапазоны поиска, а также шаг поиска.

Если стандартная инициализация прошла успешно, метод продолжает инициализацию переменных "epochs" и "epochNow". Значение "epochs" устанавливается равным переданному параметру "epochsP", а "epochNow" инициализируется значением 0.

Затем метод изменяет размер массива "agent" до размера "popSize". Для каждого элемента в "agent" вызывается метод "Init" с параметром "coords".

Метод возвращает "true", если инициализация прошла успешно, и "false" в противном случае.

Этот метод выполняет начальную настройку алгоритма оптимизации WOAm с заданными параметрами и готовит его к выполнению оптимизации на заданное количество эпох.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_WOAm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Moving" класса "C_AO_WOAm" используется для перемещения агентов в процессе оптимизации. Метод выполняет следующие действия:

"epochNow++;" - увеличивается значение текущей эпохи.

"if (!revision)" - проверка условия, если "revision" равно "false".

Если "revision" равно "false", то:

• Происходит инициализация координат агентов "a[i].c[c]" с использованием случайных значений в заданных диапазонах.
• Устанавливается флаг "revision" в "true".
• Метод завершает работу.

Если "revision" не равно "false", то:

• Для каждого агента происходит вычисление новых координат с использованием определенных формул и вероятностей.
• Используются различные математические вычисления, случайные числа и вероятности для определения новых координат агентов.
• Новые координаты "x" вычисляются в соответствии с условиями и вероятностями.
• Новые координаты "a[i].c[c]" устанавливаются с использованием метода "SeInDiSp" для коррекции значений в соответствии с диапазонами поиска и шагами.

Данный метод отвечает за обновление координат агентов в алгоритме оптимизации WOAm в соответствии с текущей эпохой, случайными значениями и вероятностями. Давайте выделим цветом соответствующие участки кода, описывающие различные модели поведения китов:

Улучшение глобального решения: С каждой новой эпохой киты более тщательно исследуют окрестности найденного глобального решения по линейному закону и вычисленному коэффициенту "A", стремясь приблизиться к глобальному оптимуму.

Исследование окрестностей "лидера" популяции: С учётом коэффициента "A" киты исследуют окрестности "лидера" популяции, который выбирается случайным образом по равномерному закону распределения. Таким образом, продолжается исследование всех областей, где находятся киты в популяции.

Спиральное движение и "пузырьковая" сеть: Киты движутся по спирали, учитывая их лучшее индивидуальное положение и текущее местоположение, что обеспечивает сбор рыб в плотное облако и концентрацию пищи в одном месте.

Миграция китов: Миграция китов имитируется резким перемещением в сторону от глобального лучшего решения по степенному закону. Этот процесс определяет высокую вероятность оказаться в окрестностях глобального решения и малую, но ненулевую вероятность находиться очень далеко от него.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double aKo = 2.0 - epochNow * (2.0 / epochs);
      double r = u.RNDfromCI (-1, 1);
      double A = 2.0 * aKo * r - aKo;
      double C = 2.0 * r;
      double b = spiralCoeff;
      double l = u.RNDfromCI (-1, 1);
      double p = u.RNDprobab ();
      double x;

      if (p < refProb)
      {
        if (MathAbs (A) > 1.0)
        {
          x = cB [c] - A * MathAbs (cB [c] - agent [i].cPrev [c]);                                                      //Xbest - A * |Xbest - X|
        }
        else
        {
          int leaderInd = u.RNDminusOne (popSize);
          x = agent [leaderInd].cPrev [c] - A * MathAbs (agent [leaderInd].cPrev [c] - agent [i].cPrev [c]);            //Xlid - A * |Xlid - X|;
        }
      }
      else
      {
        if (u.RNDprobab () < spiralProb)
        {
          x = agent [i].cPrev [c] + MathAbs (agent [i].cPrev [c] - a [i].c [c]) * MathExp (b * l) * cos (2 * M_PI * l); //XbestPrev + |XbestPrev - X| * MathExp (b * l) * cos (2 * M_PI * l)
        }
        else
        {
          x = u.PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Revision" класса "C_AO_WOAm" используется для обновления лучшего глобального решения и обновления лучших позиций самих китов. Метод выполняет следующие действия:

1. Обновление лучшего глобального решения. В цикле "for" метод проходит по всем индивидуумам. Если значение функции приспособленности текущего индивидуума превышает текущее лучшее значение функции приспособленности, то обновляется лучшее значение и массив координат текущего индивидуума копируется в массив координат лучшего решения.

2. Обновление предыдущих значений функции приспособленности и координат агентов. В цикле "for" метод проходит по всем индивидуумам. Если значение функции приспособленности текущего индивидуума превышает предыдущее значение функции приспособленности этого агента, то обновляется предыдущее значение функции приспособленности и массив координат текущего индивидуума копируется в массив предыдущих координат этого агента.

Этот метод "Revision" отвечает за обновление лучших агентов на основе значений их функций, а также обновление предыдущих значений функций и координат агентов в рамках алгоритма оптимизации WOAm.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Базовая версия алгоритма, предложенная авторами, к сожалению, оставляет желать лучшего, демонстрируя относительно слабые результаты, которые можно увидеть ниже.

WOA|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.45323929163422483
25 Hilly's; Func runs: 10000; result: 0.3158990997230676
500 Hilly's; Func runs: 10000; result: 0.25544320870775555
=============================
5 Forest's; Func runs: 10000; result: 0.43485195446891795
25 Forest's; Func runs: 10000; result: 0.2454326019188397
500 Forest's; Func runs: 10000; result: 0.1557433572339264
=============================
5 Megacity's; Func runs: 10000; result: 0.3400000000000001
25 Megacity's; Func runs: 10000; result: 0.18800000000000003
500 Megacity's; Func runs: 10000; result: 0.10146153846153938
=============================
All score: 2.49007 (27.67%)

Однако благодаря усилиям и творческому подходу, внесены значительные улучшения, включая элементы, такие как миграция и степенное распределение. Кроме того, вместо использования текущего положения китов в качестве отправной точки для расчета следующего положения, теперь используются лучшие предыдущие положения китов. Эти модификации преобразовали алгоритм, придав ему новое качество и существенно улучшив результаты модифицированной версии. Таким образом, алгоритм стал более эффективным и способным к достижению более значительных успехов в решении поставленных задач.

Это распечатка результатов модифицированной версии WOAm, где присутствует улучшение результатов более чем на 22% (где 0% - самый худший возможный результат, а 100% - самый лучший достижимый теоретический результат).

WOAm|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8452089588169466
25 Hilly's; Func runs: 10000; result: 0.562977678943021
500 Hilly's; Func runs: 10000; result: 0.262626056156147
=============================
5 Forest's; Func runs: 10000; result: 0.9310009723200832
25 Forest's; Func runs: 10000; result: 0.5227806126625986
500 Forest's; Func runs: 10000; result: 0.1636489301696601
=============================
5 Megacity's; Func runs: 10000; result: 0.6630769230769229
25 Megacity's; Func runs: 10000; result: 0.41138461538461535
500 Megacity's; Func runs: 10000; result: 0.11356923076923182
=============================
All score: 4.47627 (49.74%)

На визуализации работы модифицированной версии можно заметить значительный разброс результатов на функции Hilly и небольшой разброс на дискретной Megacity. Интересно отметить, что обычно для большинства алгоритмов более сложной и с большим разбросом результатов является именно функция Megacity, и тем более удивительно, что на этой функции WOAm показывает очень стабильные и хорошие результаты.

Алгоритм успешно исследует локальные участки поверхности в различных областях пространства поиска, выделяя перспективные направления. Этому способствует разделение общего стайного поведения популяции на этапы поведения отдельных особей, направленных на улучшение положения каждого кита индивидуально.

Такой подход позволяет алгоритму эффективно исследовать пространство поиска оптимального решения, акцентируя внимание на улучшении позиций отдельных агентов в стае. Это способствует более точному и глубокому исследованию потенциально перспективных областей, что в свою очередь способствует повышению общей производительности алгоритма.

Базовая версия не представлена на данной визуализации. Дополнительно приведена визуализация работы алгоритма на тестовой функции Ackley, эта функция не участвует в расчете рейтинговой таблицы.

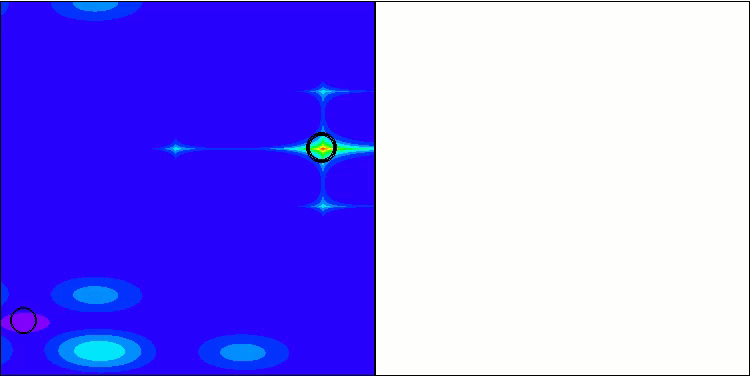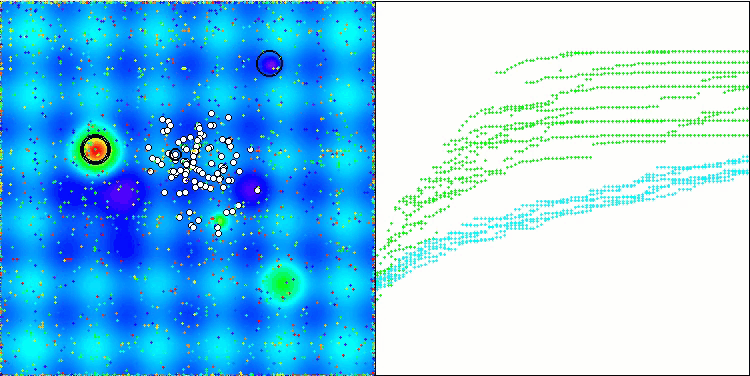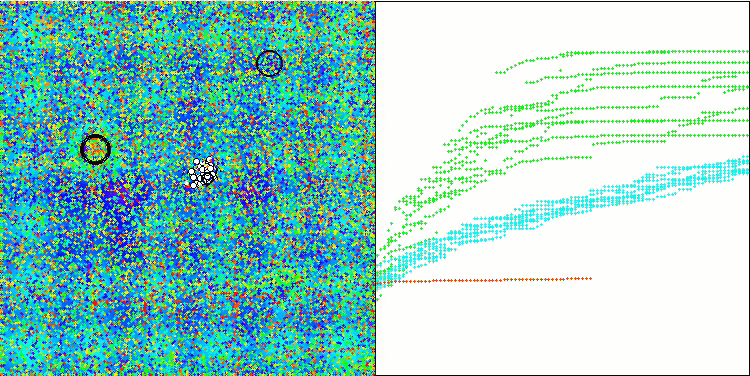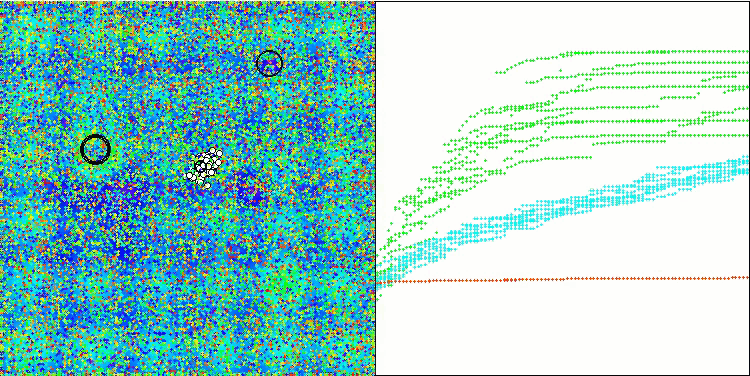
  WOAm на тестовой функции Hilly.

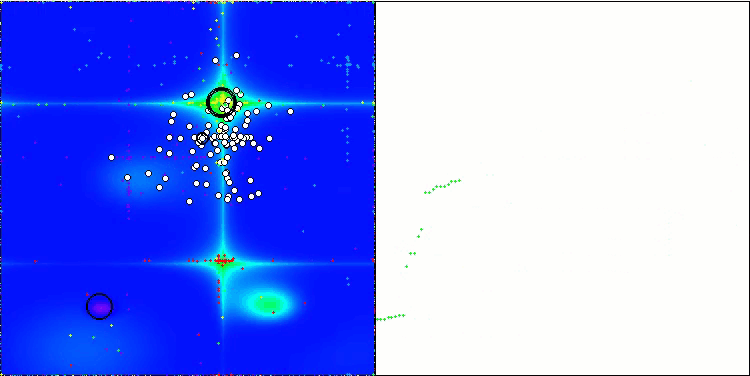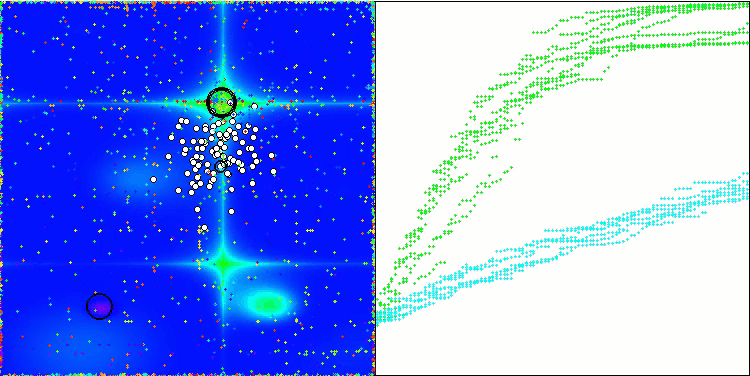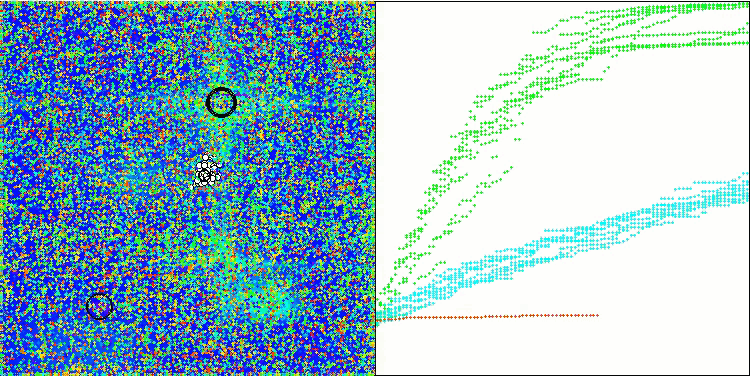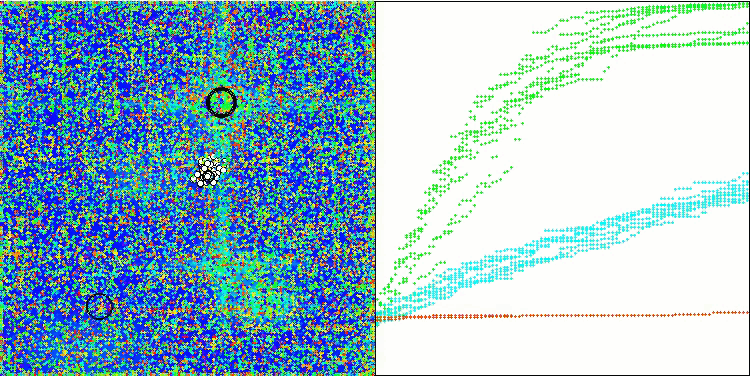
  WOAm на тестовой функции Forest.

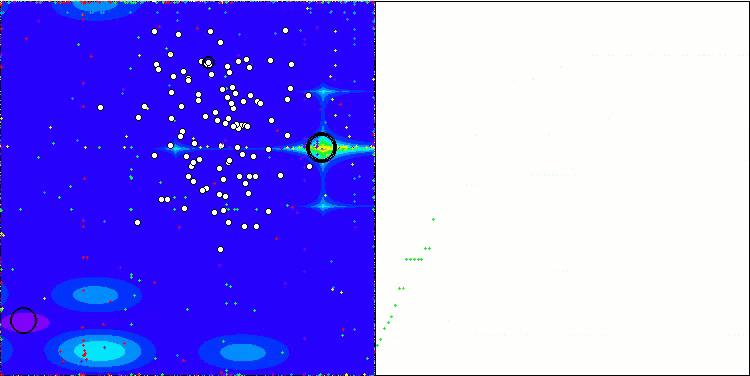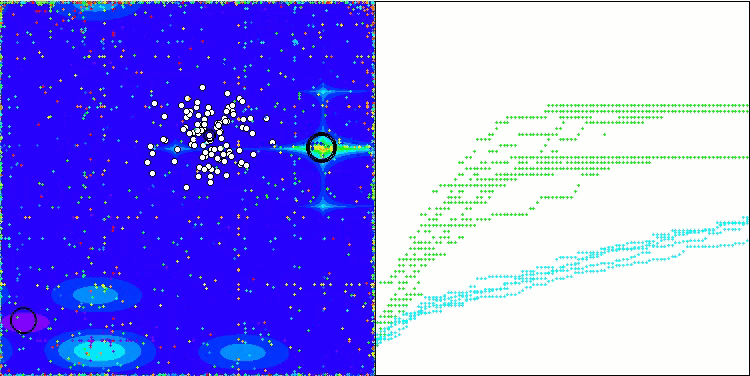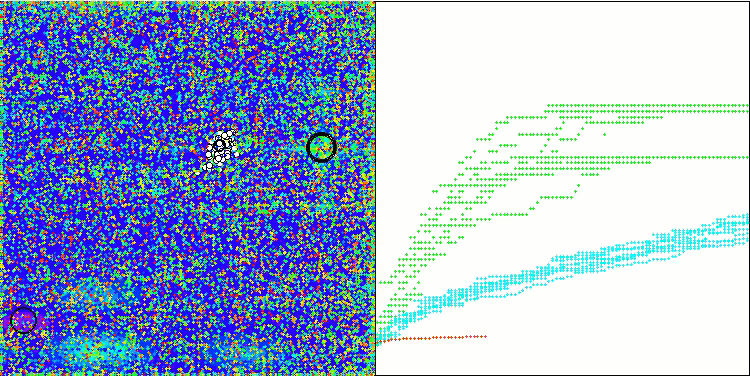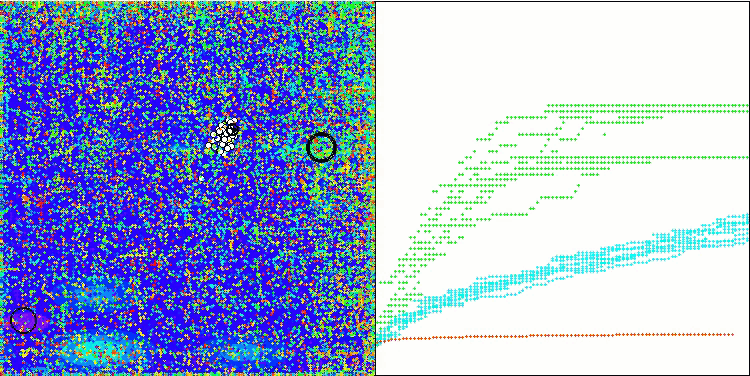
  WOAm на тестовой функции Megacity.

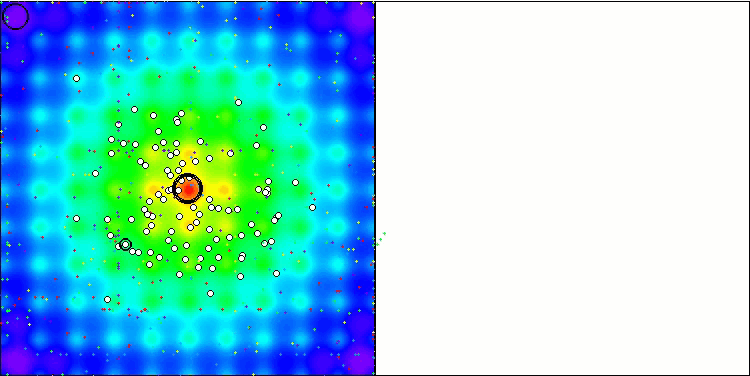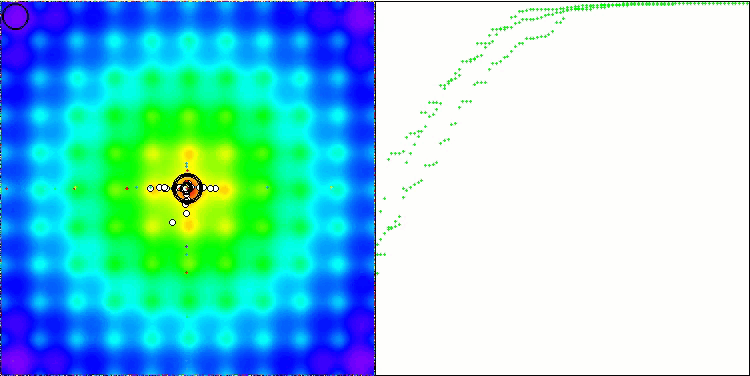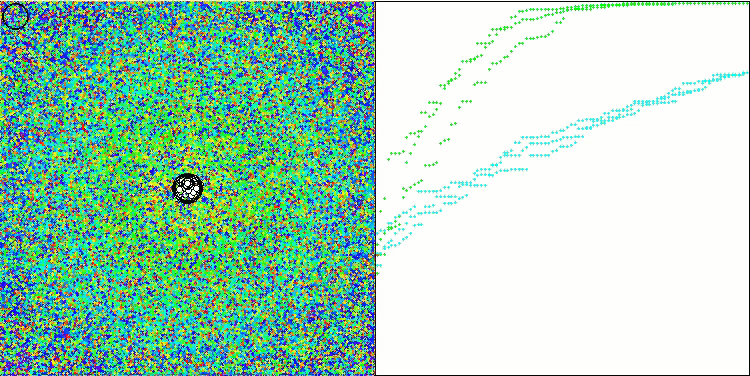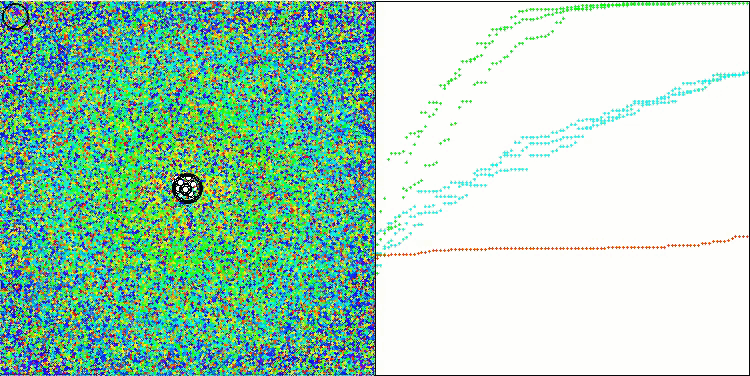
  WOAm на тестовой функции Ackley.

Модифицированный алгоритм WOAm разместился на почетном десятом месте в верхней части таблицы, демонстрируя итоговые хорошие и стабильные результаты. 

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99992	0,99484	0,50483	2,49959	1,00000	0,99975	0,32054	2,32029	0,90667	0,96400	0,23035	2,10102	6,921	76,90
2	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
3	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
4	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
5	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
6	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
7	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
8	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
9	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
10	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
11	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
12	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
13	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
14	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
15	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
16	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
17	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
18	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
19	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
20	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
21	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
22	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
23	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
24	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
25	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
26	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
27	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
28	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
29	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
30	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
31	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
32	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
33	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Выводы

В целом, я доволен внесенными улучшениями в данный алгоритм, описанными в этой статье. Однако, существуют более глубокие исследования по модификации данной версии, которые стоит рассмотреть тем, кто увлечен этой темой и стремится к дальнейшим экспериментам. Погружение в эти методы может открыть новые горизонты и вдохновить на создание еще более эффективных решений в области данного алгоритма.

Вот несколько стратегий, которые могут помочь улучшить алгоритм оптимизации китового поиска (WOA) и снизить вероятность застревания в локальных экстремумах:

1. Диверсификация популяции. Разнообразие в популяции может помочь избежать застревания в локальных оптимумах. Рассмотрите методы для поддержания разнообразия в популяции, такие как механизмы мутации, кроссовера или исследования окрестностей решений.

2. Стратегия элиты. Эта стратегия включает сохранение некоторого количества нескольких разных лучших решений (элиты) от поколения к поколению, что позволит избегать уменьшения разнообразия в популяции.

3. Мультистратегический механизм. Этот подход включает использование нескольких стратегий поиска одновременно, что может помочь алгоритму лучше исследовать пространство решений и избегать локальных ловушек.

4. Гибридизация с другими алгоритмами. Гибридизация WOA с другими алгоритмами оптимизации может также улучшить его производительность. Например, можно использовать дифференциальную эволюцию или частицы роя для улучшения фазы исследования алгоритма.

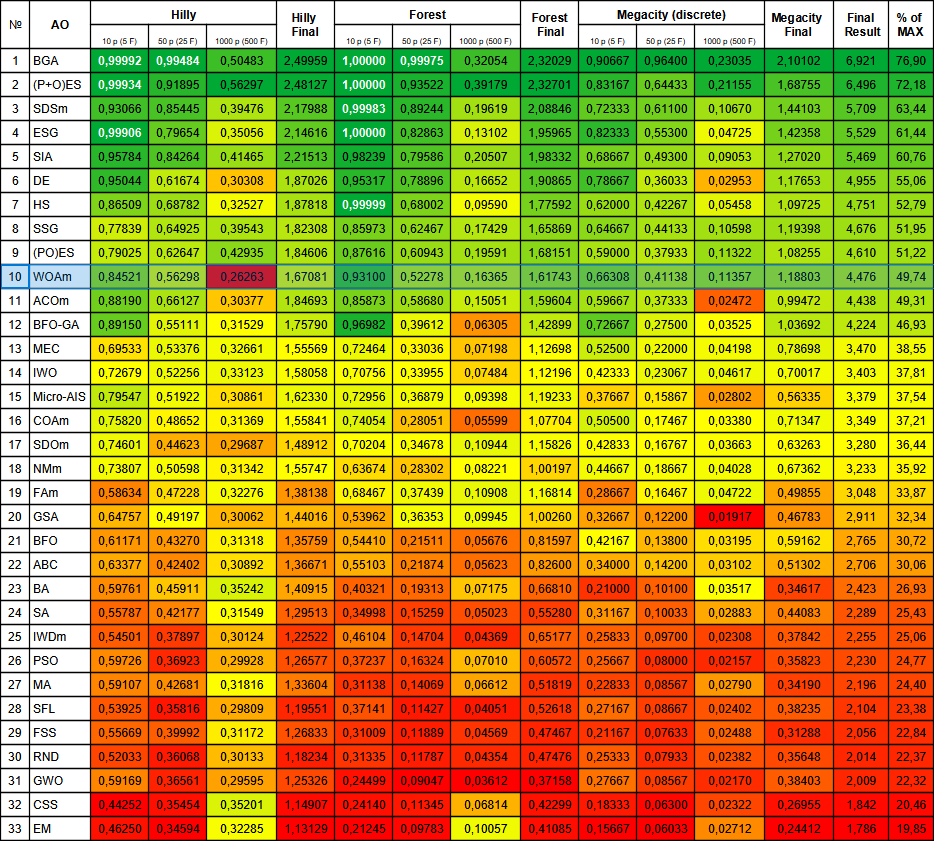
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99.

Обращает на себя внимание цвет ячейки значения на гладкой функции Hilly с 1000 переменными, указывая на то, что результат наихудший среди всех представленных в таблице алгоритмов. Причем, значительно хуже. Хотелось бы также отметить высокий показатель результата на функции Forest с 5 переменными, и в целом хорошие показатели на функциях Forest и Megacity.

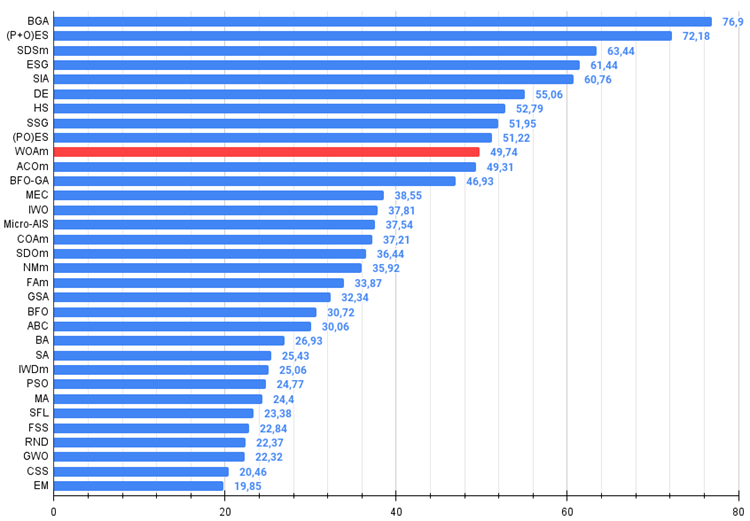
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы).

Плюсы и минусы алгоритма оптимизации китов (WOAm):

Плюсы:

1. Простая архитектура и реализация.
   
2. Стабильные и хорошие результаты на острой функции Forest и дискретной Megacity.
3. Не требователен к вычислительным ресурсам.

Минусы:

1. Невысокая сходимость (нет близких к 100% результатов).
2. Низкая масштабируемость на гладких функциях, таких как Hilly (проблемы с задачами высокой размерности).

К статье прикреплен архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.