Популяционные алгоритмы оптимизации: Бинарный генетический алгоритм (Binary Genetic Algorithm, BGA). Часть II

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

В предыдущей статье мы познакомились со всеми важными основными понятиями и методами, используемых не только в генетических алгоритмах, но, так или иначе, в любых популяционных алгоритмах оптимизации. Теперь, основываясь на этих знаниях, мы можем подробно рассмотреть основной предмет текущего "двухтомника" - бинарный генетический алгоритм (BGA). Начиная с общей информации перейдем к коду этой, во всех смыслах, замечательной стратегии поиска, и в завершении - к результатам тестов.

Генетический алгоритм (GA) относится к эволюционным алгоритмам, включающим в себя различные подходы, такие как генетические алгоритмы, генетическое программирование, эволюционные стратегии и другие. Они основаны на идеях эволюции и наследственности, где решения представляются в виде популяции, а генетические операторы, такие как скрещивание и мутация, применяются для создания новых поколений решений.

Генетические алгоритмы используют принципы естественного отбора и генетики для решения оптимизационных задач. Рассматриваемый в статье бинарный генетический алгоритм (BGA) появился первым среди всех видов генетических алгоритмов. Таким образом, BGA относится к классу эволюционных алгоритмов и является конкретным вариантом генетического алгоритма, который использует бинарное представление данных.

Работы над созданием генетических алгоритмов начались ещё в середине 20-го века. Одним из основоположников является Джон Холланд, который в 1975 году опубликовал книгу "Адаптивные системы искусственного интеллекта" (Adaptation in Natural and Artificial Systems), где впервые представил генетический алгоритм как целое направление подхода к решениям задач оптимизации.

Разработка генетического бинарного алгоритма была вдохновлена несколькими факторами и идеями. Основные из них:

• Естественный отбор и принципы эволюции: BGA основан на принципах естественного отбора и эволюции, которые были предложены Чарльзом Дарвином. Идея заключается в том, что в популяции существует разнообразие решений, и те, которые лучше приспособлены к среде, имеют больше шансов выжить и передать свои характеристики следующему поколению.
• Генетика и наследственность: BGA также использует концепции генетики, такие как ген, хромосома и наследственность. Решения в BGA представлены в виде бинарных строк, где отдельные группы битов представляют конкретные гены, а ген в свою очередь, представляет оптимизируемый параметр. Генетические операторы, такие как скрещивание и мутация, применяются к бинарным строкам для создания новых поколений решений.

В целом, разработка BGA была результатом сочетания идей из области эволюционных алгоритмов, генетики и оптимизации. Он был создан для решения оптимизационных задач, используя принципы естественного отбора и генетики, а его развитие продолжается и в настоящее время, создано огромное количество вариантов GA, а так же широкое использование идей и подходов в генетических алгоритмах в составе гибридных, в том числе и очень сложных, комплексных алгоритмов.

Генетический бинарный алгоритм, BGA, использует бинарное представление данных. Это значит, что каждый индивид (решение) представляется в виде строки из битов (0 и 1). Генетические операторы, такие как скрещивание и мутация, применяются к битовым строкам для создания новых поколений решений.

Интересный факт: генетические алгоритмы, включая BGA, могут использоваться для создания и улучшения искусственного интеллекта. Например, они могут применяться для эволюции нейронных сетей, позволяя создать более эффективные модели машинного обучения.

Генетические алгоритмы в целом и BGA в частности, представляют собой мощный инструмент для решения сложных оптимизационных задач, где традиционные методы могут быть недостаточно эффективными из-за отсутствия аналитического решения. В MetaTrader 5 используется бинарный ГА и поэтому вдвойне интересно изучить принципы работы этого замечательного алгоритма.

2. Описание алгоритма

Бинарный генетический алгоритм включает в себя следующие шаги:

1. Инициализация популяции: создать начальную популяцию, состоящую из хромосом со случайными бинарными значениями.
2. Оценка приспособленности: оценить приспособленность каждой особи (хромосомы) в дочерней популяции.
3. Селекция: выбрать родителей для создания потомства методом рулетки.
4. Кроссовер: разбить родительские хромосомы на участки и создать новые дочерние хромосомы с участками обоих родителей.
5. Инверсия: разбить хромосому дочерней особи в случайно выбранной точке и поменять местами полученные участки.
   
6. Мутация: случайным образом изменить биты в генах потомства с заданной вероятностью мутации.
7. Оценка приспособленности потомства: оценить приспособленность каждого нового потомка.
8. Формирование новой популяции: поместить популяцию потомков в конец общей популяции и выполнить сортировку по значению приспособленности.
9. Критерий остановки: повторять процесс с п.3 до достижения критерия остановки.

Для обеспечения работы BGA только с положительными числами, для упрощения операций с бинарными строками и повышения скорости вычислений, будем использовать расстояние между "max" и "min" оптимизируемых параметров. Полученные таким образом положительные значения расстояний представим в виде бинарного кода Грея разместим последовательно в один общий массив символов хромосомы так, как представлено на рисунке 1. Нужно отметить, что точки разрыва хромосом при выполнении метода кроссовера располагаются в случайных местах хромосомы и необязательно в точках стыковки генов, точки разрыва могут быть и внутри пространства гена.

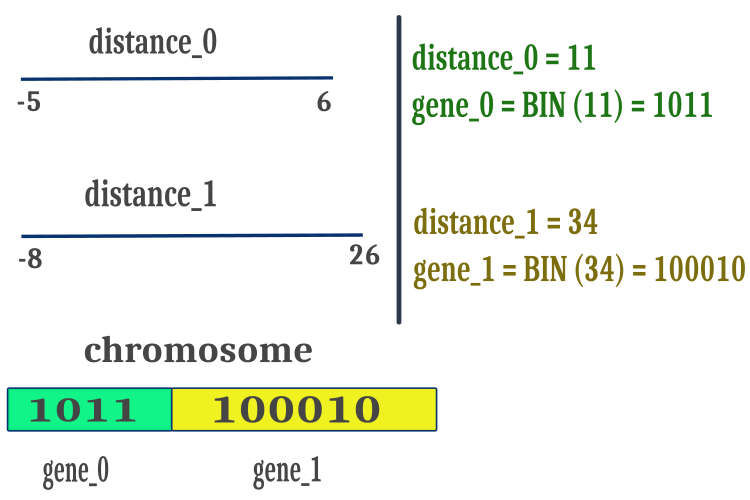
Рисунок 1. Размещение признаков особи (оптимизируемых параметров) в хромосоме.

Внешних параметров у генетического алгоритма существует значительное количество, поэтому целесообразно рассмотреть их более подробно. По умолчанию параметры практически полностью соответствуют рекомендациям многих авторов научных публикаций. Они были проверены мной и подобраны таким образом, чтобы обеспечить максимальную эффективность в большинстве типов задач. Однако, отклонение от этих параметров в любом направлении может привести к достижению 100% сходимости на тестах с 10 или даже 50 оптимизируемыми параметрами на отдельных функциях, но в то же время значительно снизить эффективность на других задачах. Поэтому параметры по умолчанию являются оптимальными для использования в большинстве практически значимых случаев.

• Population_P (размер популяции = 50): параметр определяет количество дочерних особей в каждом поколении популяции. Такой размер популяции используется в большинстве алгоритмов, рассматриваемых в тестах, и обеспечивает баланс между разнообразием решений и скоростью сходимости.
  

• ParentPopulation_P (размер родительской популяции = 50): параметр определяет количество родительских особей, выбранных для размножения и создания следующего поколения. Уменьшение значения этого параметра улучшает сходимость на гладких функциях (увеличивается точность), увеличение значения - на дискретных (повышается разнообразие генетического материала).
  

• CrossoverProbab_P (вероятность скрещивания = 1.0): параметр определяет вероятность выполнения операции скрещивания между двумя выбранными родительскими особями. Высокая вероятность скрещивания увеличивает комбинаторные возможности алгоритма, уменьшение значения - увеличивает скорость сходимости, но повышает вероятность застревания.
  

• CrossoverPoints_P (количество точек скрещивания = 3): параметр определяет количество точек, в которых происходит скрещивание между двумя родительскими хромосомами. Увеличение точек приводит к более интенсивному перемешиванию параметров между собой и в пределе сводится к случайному поведению алгоритма.
  

• MutationProbab_P (вероятность мутации = 0.001): параметр определяет вероятность мутации каждого бита в генотипе хромосомы. Мутация позволяет вносить случайные изменения в генетический материал и добавляет новые решения в популяцию. Низкая вероятность увеличивает скорость сходимости алгоритма, но уменьшает разнообразие, а слишком высокая вероятность приводит к потере полезной информации.

• InversionProbab_P (вероятность инверсии = 0.7): параметр определяет вероятность выполнения операции инверсии в хромосоме. Высокая вероятность инверсии увеличивает разнообразие генетического материала, но слишком высокая вероятность приводит к случайному поведению алгоритма.

• DoubleDigitsInChromo_P (количество десятичных знаков в гене): параметр определяет количество разрядов после запятой вещественного числа (оптимизируемого параметра), представленного в. бинарном виде в хромосоме. Увеличение значения приводит к увеличению сложности вычислений и увеличении времени оптимизации (без применения бинарного вида напрямую в решении задачи не имеет смысла устанавливать больше 16 - на выходе при конвертации в double разряды будут потеряны).

Переходим к рассмотрению кода.

При инициализации агентов необходимо определить количество битов в бинарном представлении оптимизируемого параметра. Допустим, нам требуется рассмотреть пять знаков после запятой, что соответствует определенной длине кода Грея. Однако в этом коде может быть закодировано число, превышающее требуемое. Поэтому нам необходимо определить максимальное вещественное число, которое может быть закодировано в бинарном виде. В дальнейшем мы сможем масштабировать закодированное число до требуемого диапазона оптимизируемого параметра на выходе. Для дробной части вещественного числа мы используем заданное количество разрядов (указанное в параметрах), а для целой части - столько сколько требуется в бинарном виде.

Например, если входной параметр функции "digitsInGrayCode" равно 3, то функция вернет максимальное значение типа "ulong" с использованием кода Грея для 3 битов, то есть 7 (111 в двоичной системе).

Для достижения этой цели - определения максимально возможного числа, которое может быть закодировано заданным количеством битов для дробной и целой части вещественного числа, мы будем использовать функцию "GetMaxDecimalFromGray".

//——————————————————————————————————————————————————————————————————————————————
//Calculation of the maximum possible ulong number using the Gray code for a given number of bits
ulong GetMaxDecimalFromGray (int digitsInGrayCode)
{
  ulong maxValue = 1;

  for (int i = 1; i < digitsInGrayCode; i++)
  {
    maxValue <<= 1;
    maxValue |= 1;
  }

  return maxValue;
}
//——————————————————————————————————————————————————————————————————————————————

Для представления каждого гена в хромосоме (положение гена в хромосоме) нам послужит структура  "S_BinaryGene", которая содержит поля и методы для работы с генами в двоичном формате:

• "gene": массив символов, представляющий ген.
• "integPart": массив символов целой части гена.
• "fractPart": массив символов дробной части гена.
• "integGrayDigits": количество цифр в коде Грея для целой части гена.
• "fractGrayDigits": количество цифр в коде Грея для дробной части гена.
• "length": общая длина гена.
• "minDoubleRange": минимальное значение диапазона вещественных чисел.
• "maxDoubleRange": максимальное значение диапазона вещественных чисел.
• "maxDoubleNumber": максимальное вещественное число, которое может быть представлено с использованием гена.
• "doubleFract": значение для преобразования дробной части гена в вещественное число.

Методы структуры:

• "Init": инициализирует поля структуры. Принимает минимальное и максимальное значения диапазона вещественных чисел, а также количество цифр в дробной части гена. Внутри метода вычисляются значения для максимального вещественного числа, кодирующих частей гена с использованием кода Грея.
  

• "ToDouble": преобразует ген в вещественное число. Принимает массив символов кода Грея "chromo" (хромосома) и индекс начала гена "indChr". Метод производит чтение участка хромосомы и преобразует считанный ген в десятичное значение, а затем масштабирует его в заданный диапазон вещественных чисел.

• "Scale": выполняет масштабирование входного значения "In" из диапазона "InMIN" и "InMAX" в выходной диапазон "OutMIN" и "OutMAX". Это вспомогательный метод, который используется в "ToDouble".

//——————————————————————————————————————————————————————————————————————————————
struct S_BinaryGene
{
  char   gene      [];
  char   integPart [];
  char   fractPart [];

  uint   integGrayDigits;
  uint   fractGrayDigits;
  uint   length;

  double minDoubleRange;
  double maxDoubleRange;
  double maxDoubleNumber;
  double doubleFract;

  //----------------------------------------------------------------------------
  void Init (double min, double max, int doubleDigitsInChromo)
  {
    doubleFract = pow (0.1, doubleDigitsInChromo);
    
    minDoubleRange = min;
    maxDoubleRange = max - min;

    ulong decInfr = 0;

    for (int i = 0; i < doubleDigitsInChromo; i++)
    {
      decInfr += 9 * (ulong)pow (10, i);
    }
    
    //----------------------------------------
    DecimalToGray (decInfr, fractPart);
    
    ulong maxDecInFr = GetMaxDecimalFromGray (ArraySize (fractPart));
    double maxDoubFr = maxDecInFr * doubleFract;
    
    
    //----------------------------------------
    DecimalToGray ((ulong)maxDoubleRange, integPart);
    
    ulong  maxDecInInteg = GetMaxDecimalFromGray (ArraySize (integPart));
    double maxDoubInteg  = (double)maxDecInInteg + maxDoubFr;

    maxDoubleNumber = maxDoubInteg;

    ArrayResize (gene, 0, 1000);
    integGrayDigits = ArraySize (integPart);
    fractGrayDigits = ArraySize (fractPart);
    length          = integGrayDigits + fractGrayDigits;

    ArrayCopy (gene, integPart, 0,                0, WHOLE_ARRAY);
    ArrayCopy (gene, fractPart, ArraySize (gene), 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double ToDouble (const char &chromo [], const int indChr)
  {
    double d;
    if(integGrayDigits > 0)d = (double)GrayToDecimal(chromo, indChr, indChr + integGrayDigits - 1);
    else                   d = 0.0;

    d +=(double)GrayToDecimal(chromo, indChr + integGrayDigits, indChr + integGrayDigits + fractGrayDigits - 1) * doubleFract;

    return minDoubleRange + Scale(d, 0.0, maxDoubleNumber, 0.0, maxDoubleRange);
  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

Для описания агента нам потребуется структура "S_Agent", которая представляет агента  и содержит в себе помимо хромосомы следующие данные:

• "c": массив значений координат агента в виде вещественного числа. 
• "f": значение приспособленности агента.
• "genes": массив структур "S_BinaryGene", описывающих положение каждого гена в хромосоме и правила конвертирования бинарного кода в вещественное число.
• "chromosome": массив символов хромосомы агента.
• "calculated": логическое значение, указывающее, были ли вычислены значения агента (поле присутствует, но в коде не задействовано).

Методы структуры:

• "Init": инициализирует поля структуры. Принимает количество координат "coords", массивы "min" и "max" с минимальными и максимальными значениями для каждого оптимизируемого параметра, а также "doubleDigitsInChromo" - количество разрядов вещественного числа в дробной части гена. Метод создает и инициализирует гены для каждой координаты, а также устанавливает начальное значение приспособленности и флаг "calculated".

• "ExtractGenes": извлекает значения генов из хромосомы и сохраняет их в массив "c", использует метод "ToDouble" из структуры "S_BinaryGene" для преобразования генов из хромосомы в вещественные числа.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }

    calculated = false;
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  double c []; //coordinates
  double f;    //fitness

  S_BinaryGene genes [];
  char chromosome    [];
  bool calculated;
};
//——————————————————————————————————————————————————————————————————————————————

Далее код представляет определение структуры "S_Roulette", которая представляет сегмент рулетки.

Поля структуры:

• "start": значение начальной точки сегмента рулетки.
• "end": значение конечной точки сегмента рулетки.

//——————————————————————————————————————————————————————————————————————————————
struct S_Roulette
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Обьявим класс "C_AO_BGA", реализующий генетический алгоритм:

• "cB": массив значений лучших координат.
• "fB": значение приспособленности лучших координат.
• "a": массив структур "S_Agent", представляющих агентов.
• "rangeMax": массив максимальных значений поискового диапазона.
• "rangeMin": массив минимальных значений поискового диапазона.
• "rangeStep": массив значений, представляющий шаг поиска.

Методы класса:

• "Init": инициализирует поля класса. Принимает параметры: количество координат "coordsP", размер популяции "popSizeP", размер родительской популяции "parentPopSizeP", вероятность скрещивания "crossoverProbabP", количество точек скрещивания "crossoverPointsP", вероятность мутации "mutationProbabP", вероятность инверсии "inversionProbabP", количество десятичных знаков в гене "doubleDigitsInChromoP". Метод инициализирует внутренние переменные и массивы, необходимые для работы генетического алгоритма.

• "Moving": основной метод генетического алгоритма, выполняет операции с популяцией, такие как скрещивание, мутация, инверсия и оценку приспособленности.

• "Revision": метод выполняет ревизию популяции, сортируя агентов и выбирая лучших.

Приватные поля и методы класса используются для внутренней реализации генетического алгоритма, включая операции с рулеткой, масштабирование значений, сортировку и другие операции.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BGA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP);//number of decimal places in the gene

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;               //coordinates number
  private: int    popSize;              //population size
  private: int    parentPopSize;        //parent population size
  private: double crossoverProbab;      //crossover probability
  private: int    crossoverPoints;      //crossover points
  private: double mutationProbab;       //mutation probability
  private: double inversionProbab;      //inversion probability
  private: int    doubleDigitsInChromo; //number of decimal places in the gene
  private: bool   revision;

  private: S_Agent    parents    [];  //parents
  private: int        ind        [];  //temporary array for sorting the population
  private: double     val        [];  //temporary array for sorting the population
  private: S_Agent    pTemp      [];  //temporary array for sorting the population
  private: char       tempChrome [];  //temporary chromosome for inversion surgery
  private: uint       lengthChrome;   //length of the chromosome (the length of the string of characters according to the Gray code)
  private: int        pCount;         //indices of chromosome break points
  private: uint       poRND      [];  //temporal indices of chromosome break points
  private: uint       points     [];  //final indices of chromosome break points
  private: S_Roulette roulette   [];  //roulette

  private: void   PreCalcRoulette ();
  private: int    SpinRoulette    ();
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: void   Sorting   (S_Agent &p [], int size);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
};
//——————————————————————————————————————————————————————————————————————————————

Далее код представляет реализацию метода "Init" класса "C_AO_BGA". Этот метод инициализирует поля класса и массивы, необходимые для работы генетического алгоритма.

Входные параметры метода:

• "coordsP": количество координат.
• "popSizeP": размер популяции.
• "parentPopSizeP": размер родительской популяции.
• "crossoverProbabP": вероятность скрещивания.
• "crossoverPointsP": количество точек скрещивания.
• "mutationProbabP": вероятность мутации.
• "inversionProbabP": вероятность инверсии.
• "doubleDigitsInChromoP": количество десятичных знаков в гене.

Метод "Init" используется для инициализации полей класса и массивов перед выполнением генетического алгоритма. Он устанавливает значения полей класса, проверяет и корректирует значения некоторых параметров, а также изменяет размеры массивов, выделяя память для них.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP) //number of decimal places in the gene
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords               = coordsP;
  popSize              = popSizeP;
  parentPopSize        = parentPopSizeP;
  crossoverProbab      = crossoverProbabP;
  crossoverPoints      = crossoverPointsP;
  pCount               = crossoverPointsP;
  mutationProbab       = mutationProbabP;
  inversionProbab      = inversionProbabP;
  doubleDigitsInChromo = doubleDigitsInChromoP;

  if (crossoverPoints < 1) crossoverPoints = 1;
  if (pCount < 1) pCount = 1;

  ArrayResize (poRND,  pCount);
  ArrayResize (points, pCount + 2);

  ArrayResize (ind,   parentPopSize + popSize);
  ArrayResize (val,   parentPopSize + popSize);
  ArrayResize (pTemp, parentPopSize + popSize);
  ArrayResize (a,     popSize);

  ArrayResize (parents,  parentPopSize + popSize);
  ArrayResize (roulette, parentPopSize);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Все основные операции по работе с генетическим материалом агентов выполняются методом "Moving" класса "C_AO_BGA". Метод "Moving" выполняет шаг генетического алгоритма, включая выборку родительских особей, скрещивание, инверсию и мутацию хромосом, а также применение операций к генам и координатам особей.

Метод логически разделен на несколько частей:

1. "if (!revision)" - если "revision" равно "false", выполняется инициализация особей популяции:

• Вызывается метод "Init" для инициализации особи с заданными параметрами.
• Генерируется случайная хромосома путем заполнения каждого гена случайным значением 0 или 1.
• Вызывается метод "ExtractGenes" для извлечения генов из хромосомы.
• Координаты особи "c" приводятся к диапазону с помощью функции "SeInDiSp".
• Значение приспособленности кадой особи "f" устанавливается в "-DBL_MAX".
• "lengthChrome = ArraySize (a [0].chromosome)" - определяется длина хромосомы особи (у всех особей одинаковая длина).
• "ArrayResize (tempChrome, lengthChrome)" - изменяется размер временного массива "tempChrome" на "lengthChrome".

2. Для каждой особи в популяции:

• Выполняется предварительный расчет рулетки выбора родительских особей с помощью метода "PreCalcRoulette".
• Выполняется выбор родительской особи с помощью метода "SpinRoulette".
• Копируется хромосома выбранной родительской особи в хромосому текущей особи.
• Выполняется операция скрещивания с вероятностью "crossoverProbab".
• Выбирается вторая родительская особь.
• Определяются точки разрыва хромосомы.
• Выполняется скрещивание хромосом родительских особей.
• Выполняется операция инверсии с вероятностью "inversionProbab".
• Определяется случайная точка разрыва хромосомы.
• Части хромосомы меняются местами.
• Выполняется операция мутации для каждого гена хромосомы с вероятностью "mutationProbab".
• Вызывается метод "ExtractGenes" для извлечения генов из хромосомы.
• Координаты особи "c" приводятся к диапазону с помощью функции "SeInDiSp".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      a [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);

      int r = 0;

      for (int len = 0; len < ArraySize (a [i].chromosome); len++)
      {
        r  = MathRand (); //[0,32767]

        if (r > 16384) a [i].chromosome [len] = 1;
        else           a [i].chromosome [len] = 0;
      }

      a [i].ExtractGenes ();

      for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].f = -DBL_MAX;
      a [i].calculated = true;
    }

    lengthChrome = ArraySize (a [0].chromosome);
    ArrayResize (tempChrome, lengthChrome);

    for (int i = 0; i < parentPopSize + popSize; i++)
    {
      parents [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);
      parents [i].f = -DBL_MAX;
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    pos       = 0;
  double r         = 0;
  uint   p1        = 0;
  uint   p2        = 0;
  uint   p3        = 0;
  uint   temp      = 0;

  for (int i = 0; i < popSize; i++)
  {
    PreCalcRoulette ();

    //selection, select and copy the parent to the child------------------------
    pos = SpinRoulette ();

    ArrayCopy (a [i].chromosome, parents [pos].chromosome, 0, 0, WHOLE_ARRAY);

    //crossover-----------------------------------------------------------------
    r = RNDfromCI (0.0, 1.0);

    if (r < crossoverProbab)
    {
      //choose a second parent to breed with------------------------------------
      pos = SpinRoulette ();

      //determination of chromosome break points--------------------------------
      for (int p = 0; p < pCount; p++)
      {
        poRND [p] = (int)RNDfromCI (0.0, lengthChrome);
        if (poRND [p] >= lengthChrome) poRND [p] = lengthChrome - 1;
      }
      ArraySort (poRND);
      ArrayCopy (points, poRND, 1, 0, WHOLE_ARRAY);
      points [0] = 0;
      points [pCount + 1] = lengthChrome - 1;

      r = RNDfromCI (0.0, 1.0);

      int startPoint = r > 0.5 ? 0 : 1;

      for (int p = startPoint; p < pCount + 2; p += 2)
      {
        if (p < pCount + 1)
        {
          for (uint len = points [p]; len < points [p + 1]; len++) a [i].chromosome [len] = parents [pos].chromosome [len];
        }
      }
    }

    //perform an inversion------------------------------------------------------
    //(break the chromosome, swap the received parts, connect them together)
    r = RNDfromCI (0.0, 1.0);

    if (r < inversionProbab)
    {
      p1 = (int)RNDfromCI (0.0, lengthChrome);
      if (p1 >= lengthChrome) p1 = lengthChrome - 1;

      //copying the second part to the beginning of the temporary array
      for (uint len = p1; len < lengthChrome; len++) tempChrome [len - p1] = a [i].chromosome [len];

      //copying the first part to the end of the temporary array
      for (uint len = 0; len < p1; len++)       tempChrome [lengthChrome - p1 + len] = a [i].chromosome [len];

      //copying a temporary array back
      for (uint len = 0; len < lengthChrome; len++)   a [i].chromosome [len] = tempChrome [len];
    }

    //выполнить мутацию---------------------------------------------------------
    for (uint len = 0; len < lengthChrome; len++)
    {
      r = RNDfromCI (0.0, 1.0);
      if (r < mutationProbab) a [i].chromosome [len] = a [i].chromosome [len] == 1 ? 0 : 1;
    }

    a [i].ExtractGenes ();

    for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

    a [i].calculated = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Revision" выполняет ревизию популяции, сортирует особи по значению их функции приспособленности и обновляет приспособленность лучшего решения "fB" и координаты лучшего решения "cB". Перед сортировкой популяции происходит копирование дочерней популяции в конец общей популяции.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = a [i - parentPopSize];
  }

  Sorting (parents, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Код предварительной разметки рулетки представляет метод "PreCalcRoulette". Этот метод предварительно вычисляет значения диапазонов для рулетки выбора особей на основе их функции приспособленности.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::PreCalcRoulette ()
{
  roulette [0].start = parents [0].f;
  roulette [0].end   = roulette [0].start + (parents [0].f - parents [parentPopSize - 1].f);

  for (int s = 1; s < parentPopSize; s++)
  {
    if (s != parentPopSize - 1)
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s].f - parents [parentPopSize - 1].f);
    }
    else
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s - 1].f - parents [s].f) * 0.1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Обеспечение исполнения вероятности выбора позиции родительской особи выполняет метод "SpinRoulette".

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BGA::SpinRoulette ()
{
  double r = RNDfromCI (roulette [0].start, roulette [parentPopSize - 1].end);

  for (int s = 0; s < parentPopSize; s++)
  {
    if (roulette [s].start <= r && r < roulette [s].end) return s;
  }

  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы бинарного генетического алгоритма BGA на тестовом стенде:

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs: 10000; result: 0.9999191151339382
25 Hilly's; Func runs: 10000; result: 0.994841435673127
500 Hilly's; Func runs: 10000; result: 0.5048331764136147
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.9997457419655973
500 Forest's; Func runs: 10000; result: 0.32054251149158375
=============================
5 Megacity's; Func runs: 10000; result: 0.9066666666666668
25 Megacity's; Func runs: 10000; result: 0.9640000000000001
500 Megacity's; Func runs: 10000; result: 0.23034999999999997
=============================
All score: 6.92090 (76.90%)

Визуализация процесса оптимизации BGA наглядно демонстрирует высокую сходимость алгоритма. Интересно отметить, что в процессе оптимизации некоторая часть популяции остается вдали от глобального экстремума, что указывает на исследование новых неизвестных областей пространства поиска, сохраняя разнообразие решений в популяции. Однако алгоритм сталкивается с определенными трудностями при работе с дискретной функцией "Megacity", которая является проблемной для большинства алгоритмов. Несмотря на некоторый разброс результатов при работе с этой сложной функцией, BGA проявляет себя значительно лучше, чем другие алгоритмы.

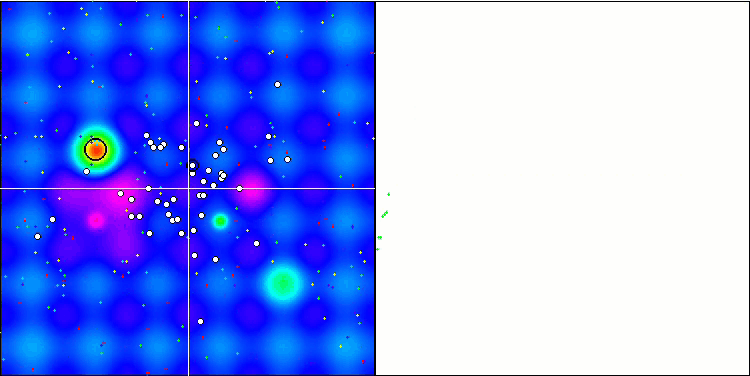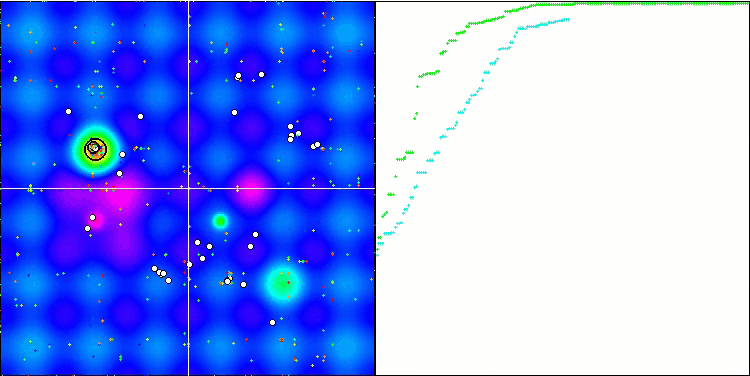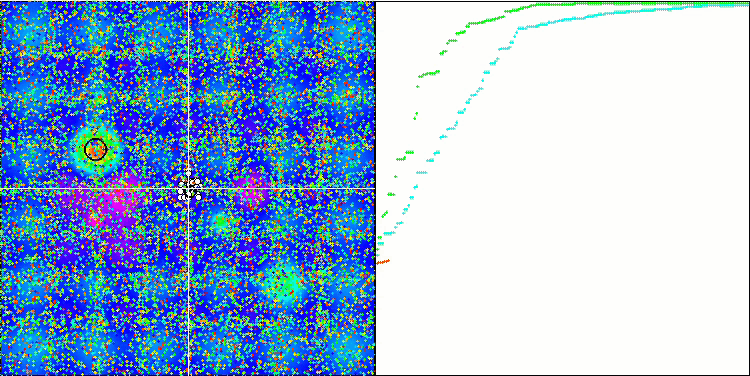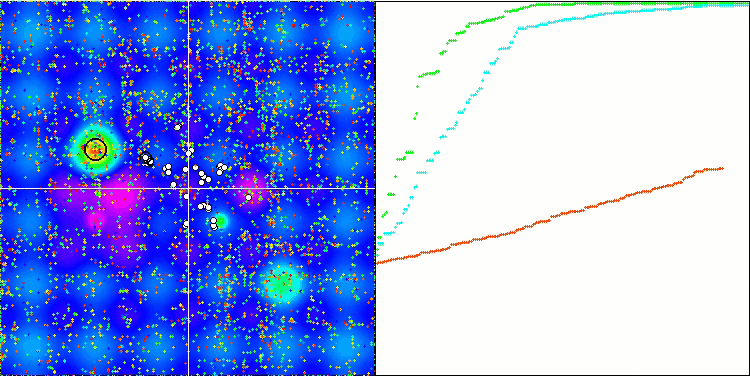
BGA на тестовой функции Hilly.

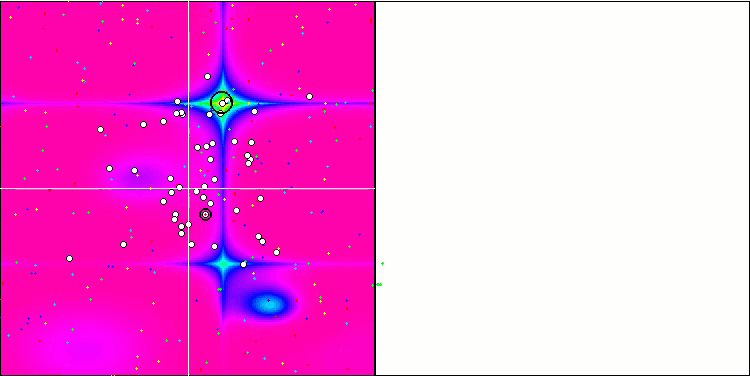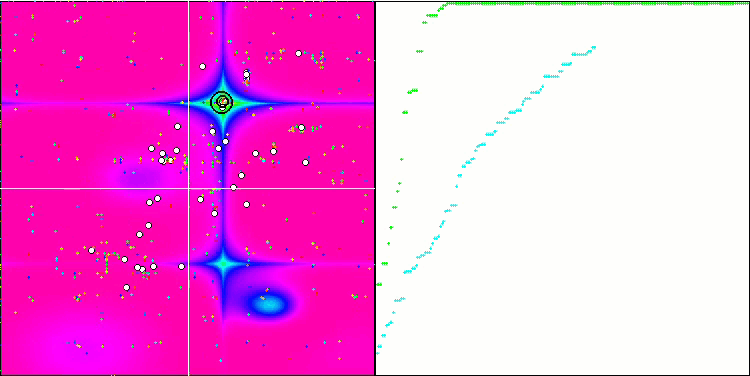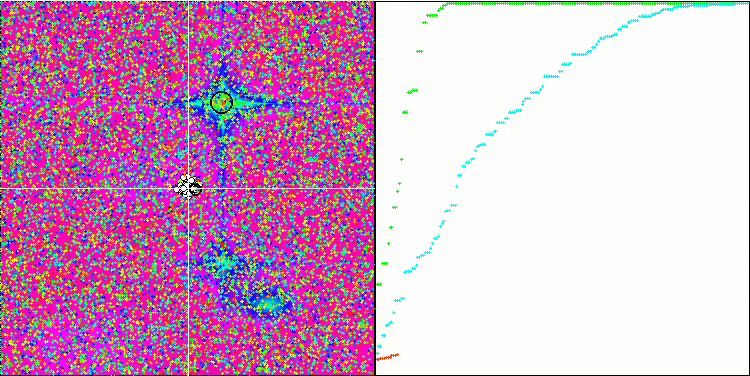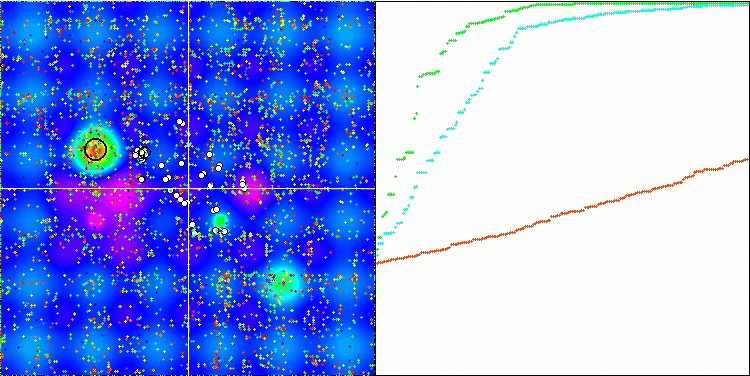
BGA на тестовой функции Forest.

BGA на тестовой функции Megacity.

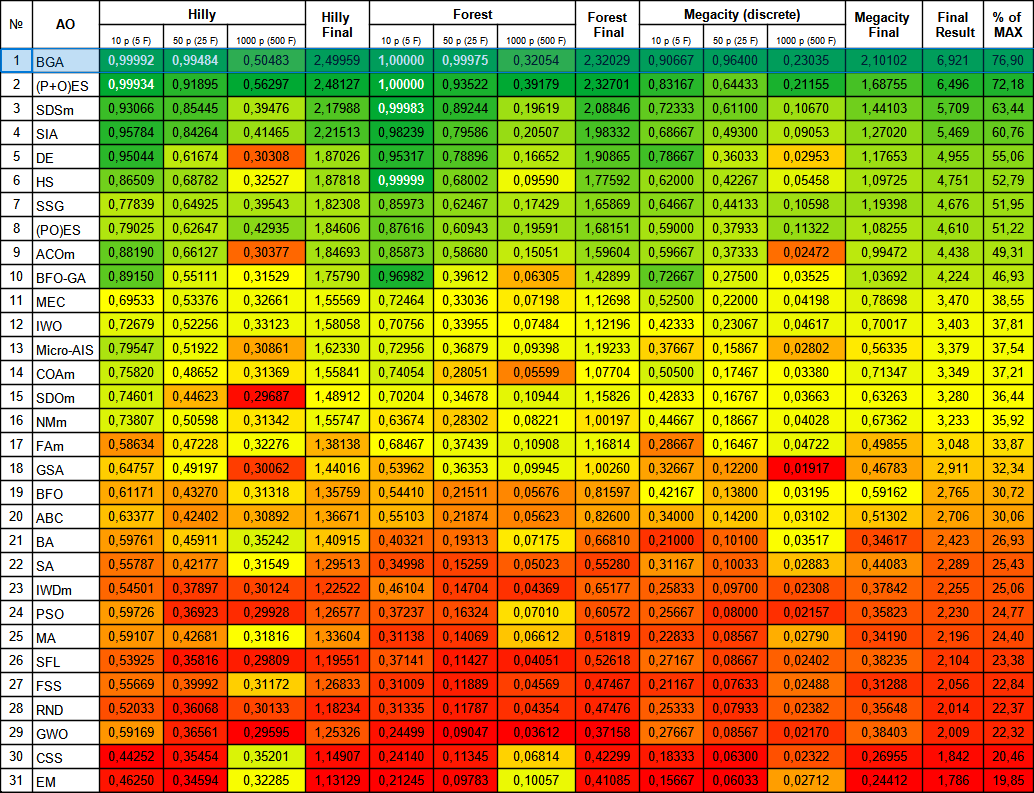
BGA занял первое место в рейтинговой таблице, продемонстрировав лучшие результаты в большинстве тестов для всех трех тестовых функций. Особенно впечатляющие результаты BGA продемонстрировал на дискретной функции Megacity, превзойдя другие алгоритмы.

№ AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 1 BGA binary genetic algorithm 0,99992 0,99484 0,50483 2,49959 1,00000 0,99975 0,32054 2,32029 0,90667 0,96400 0,23035 2,10102 6,921 76,90 2 (P+O)ES (P+O) evolution strategies 0,99934 0,91895 0,56297 2,48127 1,00000 0,93522 0,39179 2,32701 0,83167 0,64433 0,21155 1,68755 6,496 72,18 3 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44 4 SIA simulated isotropic annealing 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76 5 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06 6 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79 7 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95 8 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22 9 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31 10 BFO-GA bacterial foraging optimization - ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93 11 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55 12 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81 13 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54 14 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21 15 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44 16 NMm Nelder-Mead method M 0,73807 0,50598 0,31342 1,55747 0,63674 0,28302 0,08221 1,00197 0,44667 0,18667 0,04028 0,67362 3,233 35,92 17 FAm firefly algorithm M 0,58634 0,47228 0,32276 1,38138 0,68467 0,37439 0,10908 1,16814 0,28667 0,16467 0,04722 0,49855 3,048 33,87 18 GSA gravitational search algorithm 0,64757 0,49197 0,30062 1,44016 0,53962 0,36353 0,09945 1,00260 0,32667 0,12200 0,01917 0,46783 2,911 32,34 19 BFO bacterial foraging optimization 0,61171 0,43270 0,31318 1,35759 0,54410 0,21511 0,05676 0,81597 0,42167 0,13800 0,03195 0,59162 2,765 30,72 20 ABC artificial bee colony 0,63377 0,42402 0,30892 1,36671 0,55103 0,21874 0,05623 0,82600 0,34000 0,14200 0,03102 0,51302 2,706 30,06 21 BA bat algorithm 0,59761 0,45911 0,35242 1,40915 0,40321 0,19313 0,07175 0,66810 0,21000 0,10100 0,03517 0,34617 2,423 26,93 22 SA simulated annealing 0,55787 0,42177 0,31549 1,29513 0,34998 0,15259 0,05023 0,55280 0,31167 0,10033 0,02883 0,44083 2,289 25,43 23 IWDm intelligent water drops M 0,54501 0,37897 0,30124 1,22522 0,46104 0,14704 0,04369 0,65177 0,25833 0,09700 0,02308 0,37842 2,255 25,06 24 PSO particle swarm optimisation 0,59726 0,36923 0,29928 1,26577 0,37237 0,16324 0,07010 0,60572 0,25667 0,08000 0,02157 0,35823 2,230 24,77 25 MA monkey algorithm 0,59107 0,42681 0,31816 1,33604 0,31138 0,14069 0,06612 0,51819 0,22833 0,08567 0,02790 0,34190 2,196 24,40 26 SFL shuffled frog-leaping 0,53925 0,35816 0,29809 1,19551 0,37141 0,11427 0,04051 0,52618 0,27167 0,08667 0,02402 0,38235 2,104 23,38 27 FSS fish school search 0,55669 0,39992 0,31172 1,26833 0,31009 0,11889 0,04569 0,47467 0,21167 0,07633 0,02488 0,31288 2,056 22,84 28 RND random 0,52033 0,36068 0,30133 1,18234 0,31335 0,11787 0,04354 0,47476 0,25333 0,07933 0,02382 0,35648 2,014 22,37 29 GWO grey wolf optimizer 0,59169 0,36561 0,29595 1,25326 0,24499 0,09047 0,03612 0,37158 0,27667 0,08567 0,02170 0,38403 2,009 22,32 30 CSS charged system search 0,44252 0,35454 0,35201 1,14907 0,24140 0,11345 0,06814 0,42299 0,18333 0,06300 0,02322 0,26955 1,842 20,46 31 EM electroMagnetism-like algorithm 0,46250 0,34594 0,32285 1,13129 0,21245 0,09783 0,10057 0,41085 0,15667 0,06033 0,02712 0,24412 1,786 19,85

Выводы

В этой статье мы рассмотрели классический вариант BGA, частный случай общего класса генетических алгоритмов GA и все выводы относятся именно к нему. Несмотря на давнюю идею двоичного представления решений, подход с использованием двоичного кода остается актуальным до сих пор. Он объединяет независимые пространственные измерения задачи оптимизации в единое целое с помощью кодирования информации в одной хромосоме, что реализовать с помощью обычного вещественного кодирования признаков затруднительно, благодаря чему этот алгоритм выделяется среди других алгоритмов оптимизации.

Хотя математический аппарат и логика стратегии BGA мне полностью понятны, я до сих пор восхищаюсь происходящим с хромосомой. Это подобно тому, как если бы мы сравнили ее с магическим калейдоскопом. Когда мы вращаем калейдоскоп, разнообразные формы и цвета объединяются в уникальные узоры, создавая впечатляющую картину. Точно так же, оператор кроссовера в BGA случайным образом разрезает хромосому на несколько частей, включая внутренние области параметров. Затем эти части соединяются, подобно перемешиванию фрагментов калейдоскопа. Этот процесс позволяет объединить наилучшие характеристики разных решений и создать новую, более оптимальную комбинацию. Как и в случае с калейдоскопом, результаты кроссовера BGA могут быть удивительными и неожиданными, превращая простые хромосомы в истинные "алмазы" оптимальных решений.

Я уверен, что информация двух частей статьи о методах и инструментах, используемых в генетических алгоритмах, поможет вам расширить свои знания и достичь новых высот в работе и исследованиях. В природе, технике и человеческом разуме непрерывно проявляется сила эволюции, и BGA — это один из многих удивительных алгоритмов, которые помогут нам достигать новых высот и достижений.

BGA эффективно решает разнообразные задачи, будь то гладкие поверхности, дискретные проблемы или даже задачи большой размерности, в том числе используя стохастический подход, открывает новые возможности там, где аналитические решения ограничены.

<

Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99.

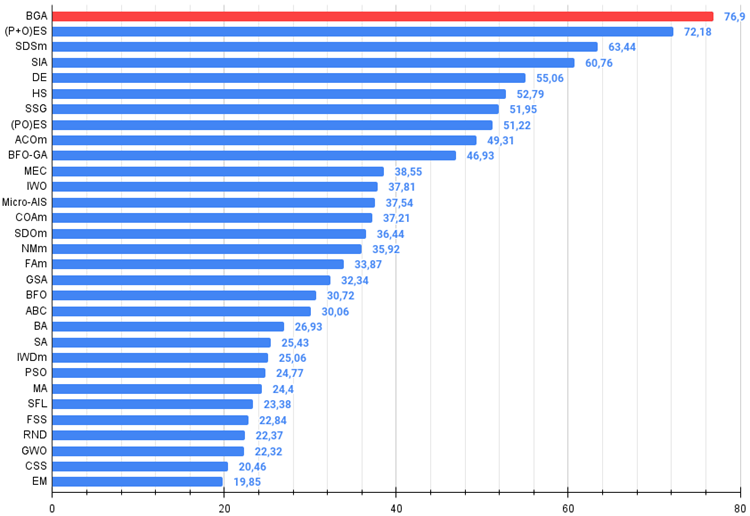
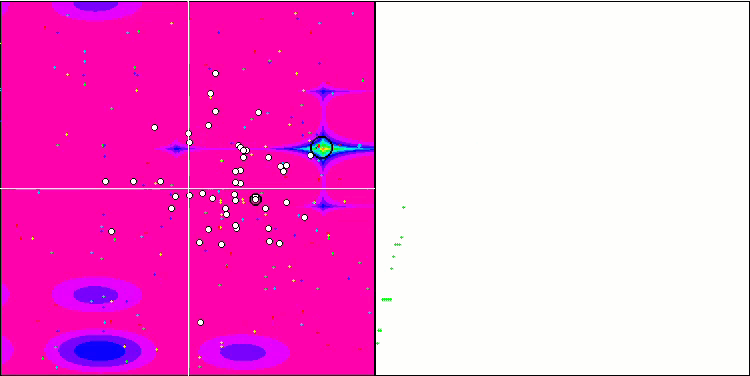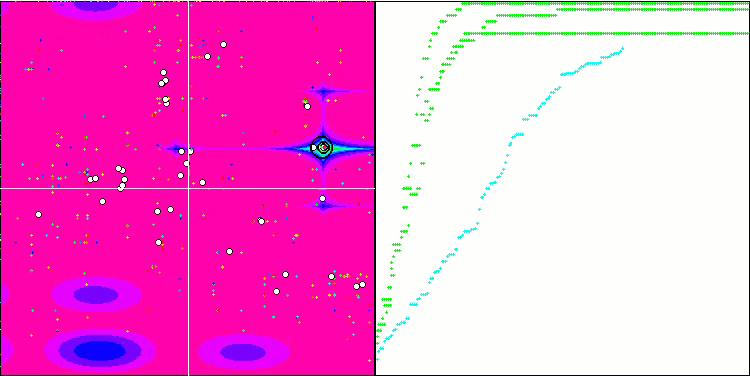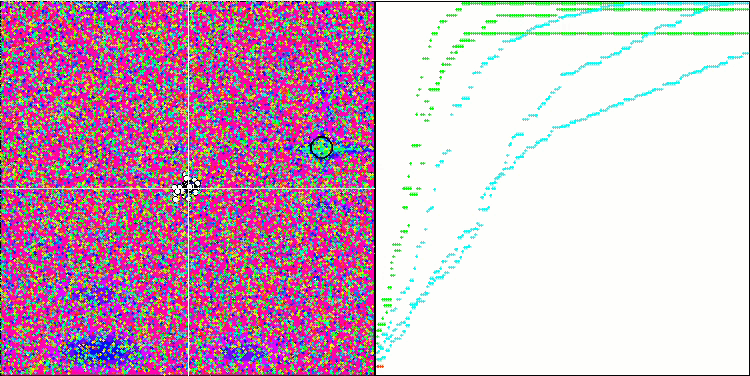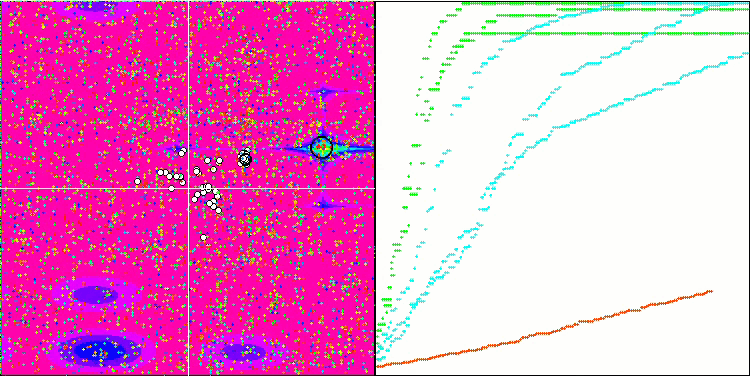
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы).

Плюсы и минусы бинарного генетического алгоритма (BGA), относятся исключительно к представленной реализации:

Плюсы:

1. Высокая эффективность при решении разнообразных задач.
2. Устойчивость к застреванию.
3. Высокие результаты как на гладких, так и на сложных дискретных функциях.
4. Высокая сходимость.

Минусы:

1. Большое количество внешних параметров.
   
2. Достаточно сложная реализации алгоритма.
   
3. Высокая вычислительная сложность.
   

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.