Популяционные алгоритмы оптимизации: Рой частиц (PSO)

MetaTrader 5 — Примеры | 14 октября 2022, 13:34

3 040

Andrey Dik

Они составляют отдельные рои, благодаря этому могут находиться в солнечных лучах,

либо двигаться за грозовыми тучами, не исключено, что они черпают энергию из атмосферных разрядов.

Но в момент опасности или, шире, внезапного изменения, которое грозит их существованию, объединяются…

Станислав Лем "Непобедимый"

Содержание:

1. Введение

Вероятно, найдется немало людей, кто читал замечательный фантастический бестселлер Станислава Лема, "Непобедимый". Удивительно, что одно из первых описаний "роевого" интеллекта родилось именно с выходом этого фантастического романа. В повествовании идет речь о роботах, которые выжили без централизации управления, причем выжили наиболее приспособленные, простейшие экземпляры— не самые сложные, интеллектуальные и мощные, а наиболее многочисленные и гибкие.

Эти автоматы за тысячи лет некроэволюции научились эффективно бороться с конкурентами, которые превосходили их и по интеллекту, и по энерговооружённости. Им пришлось сражаться не только с другими роботами, но и с живым миром планеты и победить. Элементы фантастики данного произведения можно со всей уверенностью сравнить непосредственно с действием самой природы и эволюции.

Еще с незапамятных времен людей интересовало поведение животных в группе, так называемое роевое поведение, каким способом функционируют птицы, когда стая направляется в теплые страны, как обеспечивает себя пропитанием рой пчел, каким способом выживает колония муравьев, создавая сложные структуры, как ведут себя рыбы в косяке, ведь так синхронизировано их поведение. Организация особей в социуме, как бы в присутствии единого управляющего разума, несмотря на децентрализацию управления, некоторые закономерности слаженного целостного организма, подсмотренные взаимосвязи у природы побуждают на создание и развитие новых идей в области алгоритмической оптимизации.

Роевый интеллект (Swarm intelligence) описывает имитацию коллективного поведения самоорганизующейся системы. Существует достаточно большое число таких алгоритмов. В каноническом варианте, написанном в 1995г. Кеннеди (J.Kennedy) и Эберхартом (R.Eberhart), модель, положенная в основу этого метода, была получена упрощением модели Рейнолдса. В результате этого упрощения отдельные особи популяции стали представляться отдельными объектами, не имеющими размера, но обладающими некоторой скоростью.

В силу крайней схожести с материальными частицами получившиеся простые объекты стали называться частицами, а их популяция — роем. В каждый момент времени (на каждой итерации) частицы имеют в пространстве некоторое положение и вектор скорости. Для каждого положения частицы вычисляется соответствующее значение целевой функции, и на этой основе по определённым правилам частица меняет своё положение и скорость в пространстве поиска, при определении следующего положения частицы учитывается информация о наилучшем положении из числа всех остальных соседних частиц, соответствующее задачам фитнесс-функции.

Примеры роевых алгоритмов:

Метод роя частиц
Муравьиный алгоритм
Пчелиный алгоритм
Искусственная иммунная система
Алгоритм серых волков
Алгоритм летучих мышей
Алгоритм гравитационного поиска
Алгоритм альтруизма
И многие другие

Переход от моделирования коллективного поведения к коллективной оптимизации основан на следующей биологической идее: организмы объединяются в колонии для улучшения своих условий существования — каждый организм в колонии в среднем имеет больше шансов на выживание в борьбе с хищниками, колония может более эффективно производить поиск, обработку и хранение пищи по сравнению с отдельными особями и т.д. Другими словами любая колония организмов в течение всего времени своего существования с той или иной степенью эффективности решает различные оптимизационные задачи, например, максимизация количества пищи с одновременной минимизацией потерь от хищников. Указанные соображения и легли в основу построения разнообразных математических методов оптимизации.

Рой частиц - один из самых известных и популярных алгоритмов оптимизации с самого момента его появления, многие авторы различных его реализаций утверждают, что алгоритм очень эффективен в оптимизации сложных со многими аргументами функций и даже подходит для обучения нейронных сетей.

В данной статье мы попытаемся выяснить, настолько ли хорош алгоритм для решения сложных задач. В классическом варианте алгоритма и во множестве его модификаций есть существенные ограничения, связанные с тем, что оптимизируемая функция должна быть гладкой и непрерывной, то есть совершенно не подходит для дискретных функций. Однако, как и задумывался цикл статей, все рассматриваемые алгоритмы будут изменены таким образом (если есть какие-либо ограничения), чтобы устранить недостатки, по крайней мере сделать так, что бы алгоритмы работали хотя бы чисто технически, то есть, все алгоритмы должны быть индифферентны к гладкости функций (такие, как в задачах трейдеров) и не иметь ограничений на шаг аргументов.

2. Принципы алгоритма

Поскольку предыдущая статья являлась основной вводной статьей в мир оптимизации, в ней не был освещен принцип взаимодействия основной программы (эксперт, скрипт, индикатор) с ядром алгоритма оптимизации, однако этому стоит уделить внимание, потому что в любом случае у внимательного читателя возникнет вопрос: почему алгоритмы и примеры программ написаны именно так. В открытом доступе существующие варианты алгоритмов оптимизации построены таким образом, что алгоритм обращается к фитнес-функции как к внешнему по отношении к нему объекту, а сам является основной исполняемой программой.

На рисунке 1 ниже представлена схема, где алгоритм передает оптимизируемые параметры в фитнес-функцию, а обратно получает значение приспособленности (оценочный критерий). Эта схема неудобна для построения программы для решения задач пользователями, в частности трейдерами. Почему неудобна? Потому что мы не можем вызвать, например, прогон тестера по истории.

Classic Scheme

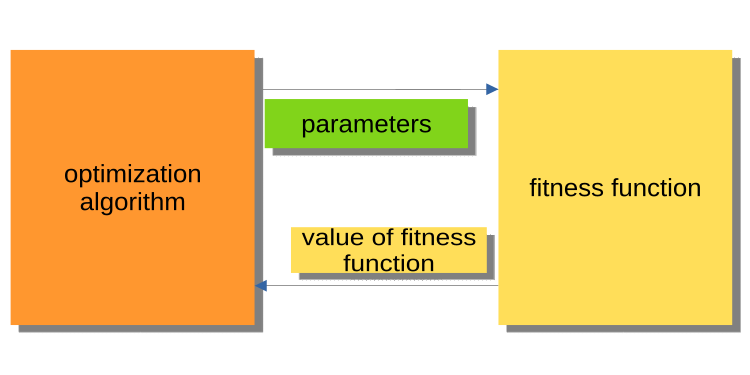
Рисунок 1. Схема взаимодействия алгоритма PSO и фитнес-функции.

Гораздо удобнее схема, отображенная на рисунке 2, при которой алгоритм оптимизации является не самостоятельной программой, а неким отдельным модулем или "черным ящиком". У данного модуля присутствуют параметры min, max, step для каждого оптимизируемого аргумента. Программа MQL получает по запросу оптимизируемые аргументы, а обратно возвращает значения приспособленности или, другими словами, значения фитнес-функции. Такая схема позволяет строить спектр очень гибких решений, от использования автоматической оптимизации в экспертах, до написания кастомного менеджера оптимизации.

MQL5 scheme

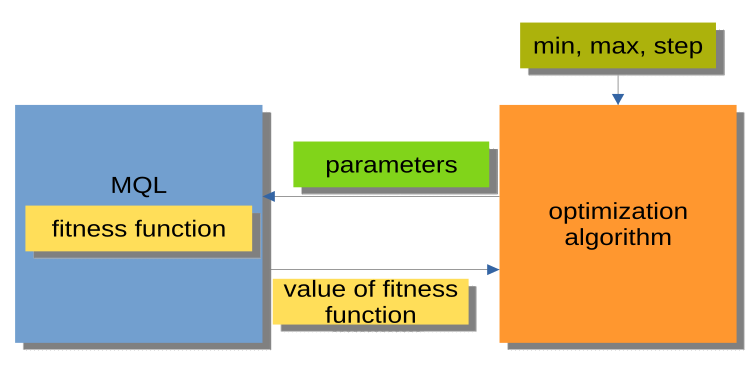
Рисунок 2. Схема взаимодействия программы MQL и PSO.

Отдельно стоит упомянуть организацию вызовов методов алгоритмов оптимизации (блок MQL на Рис.2), которую можно представить общей схемой, одинаковой для всех алгоритмов оптимизации (АО), так:

Инициализация_АО_0

Цикл итераций (эпох)
{
1) Метод_АО_1
2) Получение значений приспособленности для каждого варианта оптимизируемых параметров
3) Метод_АО_2
}

Таким образом видим, что используются всего лишь три публичных метода: Инициализация_АО_0, Метод_АО_1 и Метод_АО_2. Этого достаточно для организации процесса оптимизации в пользовательских проектах любой сложности.

Сама же схема работы PSO отображена на рисунке 3 и включает в себя следующие логические шаги:

Генерация случайных частиц (первый итерация)
Получение значения приспособленности для каждой частицы
Получение значения приспособленности для всех частиц в целом
Корректировка скорости частиц
Точка останова, либо переход к п.2
Завершение программы.

PSOscheme

Рисунок 3. Схема работы PSO.

Рассмотрим алгоритм "Рой частиц" более подробно.

Система роевого интеллекта состоит из множества частиц, взаимодействующих как между собой, так и с окружающей средой. Каждая частица следует простым правилам, несмотря на то, что нет централизованной системы управления поведения, которая бы указывала каждому из них на то, что ему следует делать, локальные и случайные взаимодействия между ними приводят к возникновению интеллектуального группового поведения, которое не контролируется отдельными особями.
Если проводить аналогию со стаей, то можно сказать, что все частицы, должны выполнять простые задачи:

избегать пересечения с другими частицами;
корректировать свою скорость в соответствии со скоростями окружающих частиц;
стараться сохранять достаточно малое расстояние между собой и окружением.

Алгоритм PSO начинается с инициализации популяции. Второй шаг — вычисление значений приспособленности каждой частицы, после чего обновляются индивидуальные и глобальные лучшие результаты, а затем обновляются скорость и положение частиц. При использовании PSO возможное решение задачи числовой оптимизации представляется позицией частицы. Вдобавок у каждой частицы есть текущая скорость, которая отражает ее абсолютную величину и направление к новому, предположительно лучшему, решению/позиции.

У частицы также хранится значение ее приспособленности, текущей позиции, лучшая известная позиция (т. е. предыдущая позиция с лучшей известной приспособленностью) и приспособленностью лучшей известной позиции. Шаги со второго по четвертый повторяются до тех пор, пока не будет выполнено условие завершения. В первой итерации все частицы рассредоточиваются, чтобы найти наилучшее решение (исследование). Каждая частица оценивается. Находятся наилучшие решения в отношении топологии соседства, и обновляются личные и глобальные лучшие частицы для каждого члена роя. Сходимость будет достигнута за счет притяжения всех частиц к частице с лучшим решением.

Хотя в своей основе алгоритм PSO довольно прост, нужно разобраться в нём, чтобы иметь возможность модифицировать код в этой статье под свои потребности. PSO является итеративным процессом. На каждой итерации в основном цикле обработки сначала обновляется текущая скорость каждой частицы; при этом учитываются текущая скорость частицы, локальная информация частицы и глобальная информация роя. Затем позиция каждой частицы обновляется с использованием значения новой скорости этой частицы.

С точки зрения математики эти два уравнения обновления координат частицы выглядят так:

v(t+1) = w * v(t) + c1 * rp * (p(t) – x(t)) + (c2 * rg * (g(t) – x(t))

x(t+1) = x(t) + v(t+1)

Процесс обновления позиции на самом деле намного проще, чем предлагаемые уравнения. Первое уравнение предназначено для обновления скорости частицы.

Член уравнения v(t+1) обозначает скорость в момент t+1. Новая скорость зависит от трех членов.

Первый: w * v(t). Множитель w называется весовой долей инерции и просто является константой; v(t) — это текущая скорость в момент t.
Второй член: c1 * rp * (p(t) – x(t)). Множитель c1 - константа, называемая когнитивной (или персональной, или локальной) весовой долей. Множитель rp является случайной переменной в диапазоне [0, 1]. Векторная величина p(t) - это лучшая позиция частицы, найденная на данный момент, а векторная величина x(t) — текущая позиция частицы.
Третий член: обновление скорости c2 * rg * (g(t) – x(t). Множитель c2 является константой, называемой социальной (или глобальной) весовой долей. Множитель rg - случайная переменная в диапазоне [0, 1]. Величина вектора g(t) - лучшая известная позиция, найденная на данный момент любой из частиц в рое. Как только определяется новая скорость, v(t+1), она используется для вычисления новой позиции частицы x(t+1).

3. Классическая реализация

Логической единицей, описывающей набор координат в пространстве (оптимизируемые параметры), является частица, которую можем представить в виде структуры, где c [] - координаты частицы, cB [] - лучшие координаты частицы за все итерации, v [] - скорость по каждой из координат частицы, ff - текущее значение приспособленности частицы, ffB - лучшее значение приспособленности частицы за все итерации. В конструкторе структуры частицы значение ff и ffB инициализируем минимально возможным значением, которое может быть представлено типом double, так как алгоритм предназначен для поиска максимума функции (для поиска минимума достаточно добавить знак "-" перед полученным значением приспособленности).

//——————————————————————————————————————————————————————————————————————————————
struct S_Particles
{
  public:
    double c  []; //coordinates
    double cB []; //best coordinates
    double v  []; //velocity

    double ff;    //the value of the fitness function
    double ffB;   //best value fitness function

    S_Particles ()
    {
      ff  = -DBL_MAX;
      ffB = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Собственно, сам алгоритм PSO запишем в виде класса, в котором всего лишь три публичных метода, InitPS (), Preparation (), и Dwelling () (Инициализация_АО_0, Метод_АО_1 и Метод_АО_2). Из приватных методов уникальными для PSO являются GenerateRNDparticles () и ParticleMovement (), а остальные мы уже рассматривали в предыдущей статье. Массив структур p [] - рой частиц. Кроме того, что каждая частица имеет значения приспособленности, своих координат и лучших координат, рой в целом имеет лучшие координаты cB и лучшее значение приспособленности ffB.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_PSO
{
  public:
  //----------------------------------------------------------------------------
  S_Particles p    []; //particles
  double rangeMax  []; //maximum search range
  double rangeMin  []; //manimum search range
  double rangeStep []; //step search
  double cB        []; //best coordinates
  double ffB;          //FF of the best coordinates

  void InitPS (const int    params,       //number of opt. parameters
               const int    size,         //swarm size
               const double inertiaP,     //inertia
               const double selfBoostP,   //boost
               const double groupBoostP); //group boost

  void Preparation ();
  void Dwelling ();

  private:
  //----------------------------------------------------------------------------
  int swarmSize; //swarm size
  int parameters;//number of optimized parameters

  double inertia;
  double selfBoost;
  double groupBoost;
  bool   dwelling;

  void   GenerateRNDparticles ();
  void   ParticleMovement     ();
  double SeInDiSp             (double in, double inMin, double inMax, double step);
  double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Метод InitPS () предназначен для инициализации алгоритма перед началом оптимизации (на схеме Инициализация_АО_0), в нем присваиваем приватным членам значения аргументов метода и назначаем размер рою и внутренним параметрам каждой частицы в рое.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::InitPS (const int    paramsP,
                       const int    sizeP,
                       const double inertiaP,
                       const double selfBoostP,
                       const double groupBoostP)
{
  ffB = -DBL_MAX;

  parameters = paramsP;
  swarmSize  = sizeP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);

  dwelling = false;

  inertia    = inertiaP;
  selfBoost  = selfBoostP;
  groupBoost = groupBoostP;

  ArrayResize (p, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (p [i].c,  parameters);
    ArrayResize (p [i].cB, parameters);
    ArrayResize (p [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

Метод Preparation () вызывается на каждой итерации (эпохе) первым (Метод_АО_1). Метод простой, но имеет очень важное значение. В зависимости от того, будет ли метод вызван на первой эпохе или на последующих (определяется флагом dwelling), будет сброшено значение приспособленности роя и создастся случайная популяция роя, либо произойдет перемещение частиц на новые координаты.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::Preparation ()
{
  if (!dwelling)
  {
    ffB = -DBL_MAX;
    GenerateRNDparticles ();
    dwelling = true;
  }
  else ParticleMovement ();
}
//——————————————————————————————————————————————————————————————————————————————

В методе GenerateRNDparticles (), генерируется случайная популяция роя, частицы имеют случайные координаты в заданном для каждой из них диапазоне, и случайную скорость по каждой из координат.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::GenerateRNDparticles ()
{
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      p [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      p [s].c  [k] = SeInDiSp (p [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      p [s].cB [k] = p [s].c [k];
      p [s].v  [k] = RNDfromCI (0.0, (rangeMax [k] - rangeMin [k]) * 0.5);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

В методе ParticleMovement () осуществляется алгоритм перемещения частиц на новые позиции, для этого необходимо рассчитать скорость по каждой координате согласно приведенной выше формуле. Я не знаю почему используется термин ''скорость", по сути, это значение перемещения, или другими словами, разность между тем положением, где находится частица в данный момент и положением, куда она должна переместиться. Вычислив эту разность по каждой из координат, мы просто прибавим к текущим значениям. После этого проверим недопустимость выхода за границы min/max оптимизированных параметров (для частицы - это координаты) с заданным шагом.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::ParticleMovement ()
{
  double rp;       //random component of particle movement
  double rg;
  double velocity;
  double posit;
  double positBest;
  double groupBest;

  for (int i = 0; i < swarmSize; i++)
  {
    for (int k = 0; k < parameters; k++)
    {
      rp = RNDfromCI (0.0, 1.0);
      rg = RNDfromCI (0.0, 1.0);
      
      velocity  = p [i].v  [k];
      posit     = p [i].c  [k];
      positBest = p [i].cB [k];
      groupBest = cB [k];

      p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit);
      p [i].c [k] = posit + p [i].v [k];

      p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод Dwelling () - третий публичный метод алгоритма, используемый пользователем в своей программе для оптимизации (по схеме Метод_АО_2). Назначение метода - обновить лучшие координаты и значения приспособленности каждой частицы относительно своих предыдущих показателей. И обновить, при необходимости, приспособленность роя и лучшие координаты роя. Метод вызывается после получения значений приспособленности в цикле итераций.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::Dwelling ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    //remember the best position for the particle
    if (p [i].ff > p [i].ffB)
    {
      p [i].ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k];
    }

    if (p [i].ff > ffB)
    {
      ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Функция для дискретизации числа double с заданным шагом в указанном диапазоне.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_PSO::SeInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

Функция получения случайного числа double в заданном диапазоне.

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval
double C_AO_PSO::RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

Теория закончилась. Приступим к практике.

Поскольку мы используем одну и ту же схему построения алгоритмов, что и в первой статье цикла (и в дальнейшем продолжим это делать), описанную на рис.2, то нам не составить труда подключить алгоритм к тестовому стенду.

Запустив стенд, мы увидим анимации, подобные тем, что показаны ниже. В данном случае мы хорошо видим, как ведет себя рой частиц. Рой ведет себя действительно как рой в природе. По тепловой карте функции он перемещается в виде плотного облака.

Напомню, что черным кружком обозначен глобальный оптимум (max) функции, а черной точкой - лучшие усредненные координаты алгоритма поиска, полученные на момент текущей итерации. Поясним откуда берутся усредненные значения. Тепловая карта двумерная по координатам, а оптимизируемая функция может включать сотни переменных (измерений) - поэтому результат, усредненный по координатам.

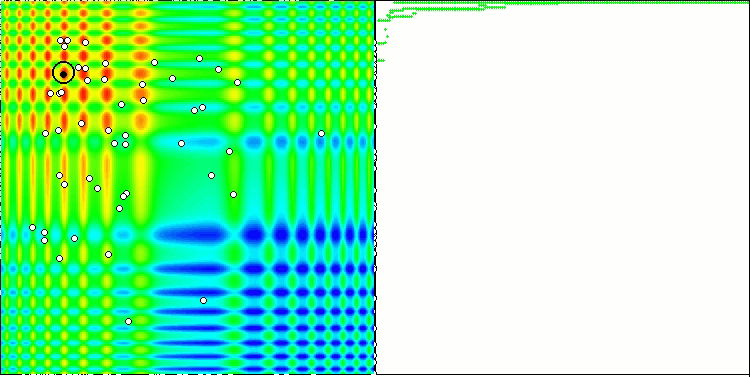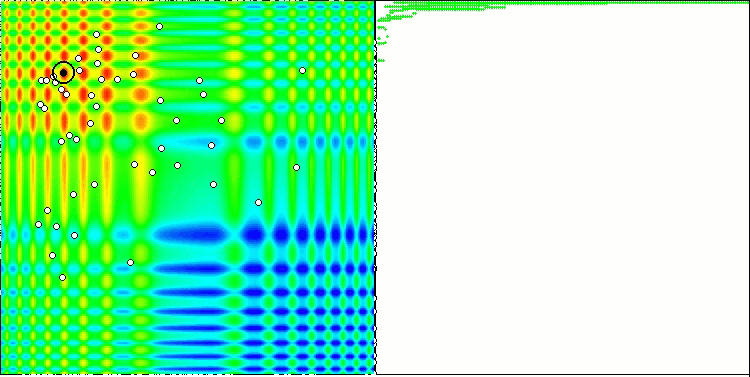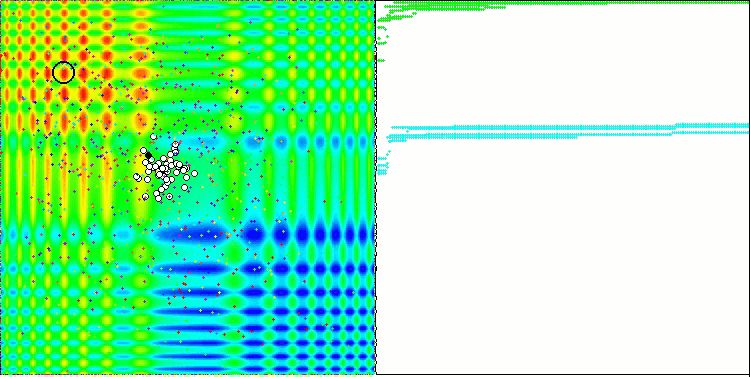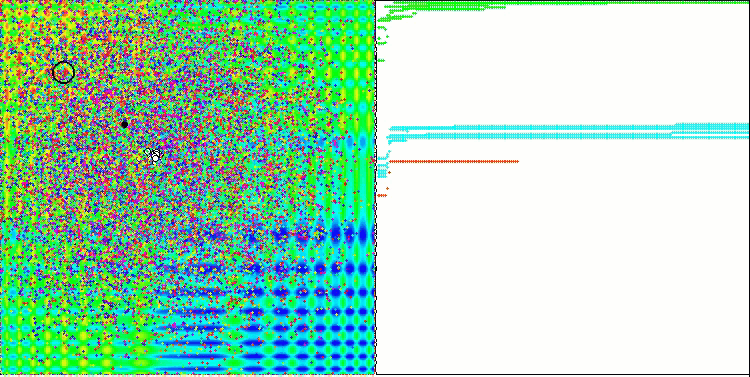
PSO на тестовой функции Skin.

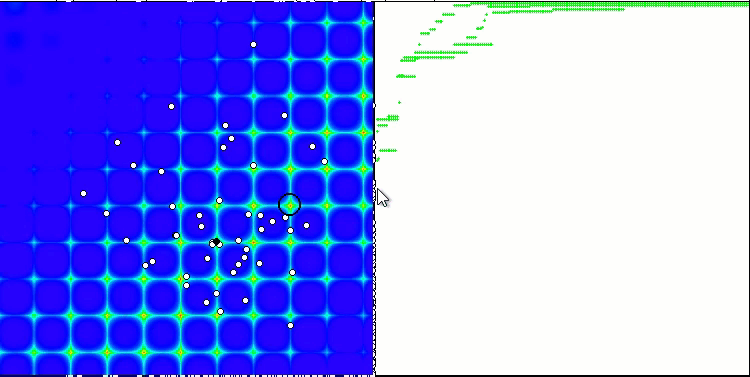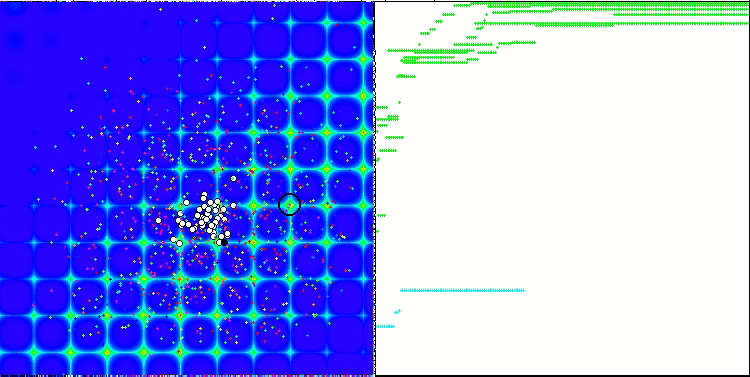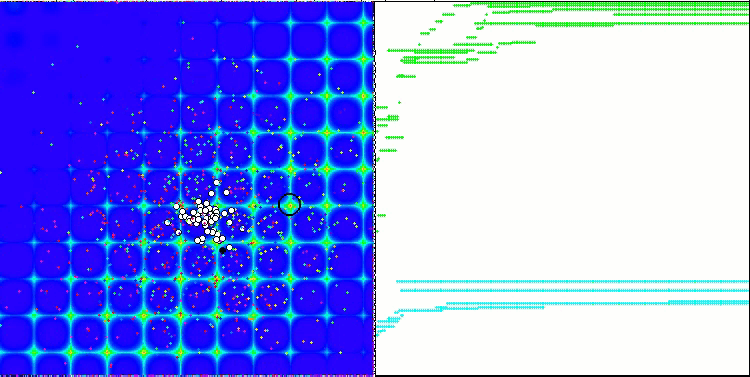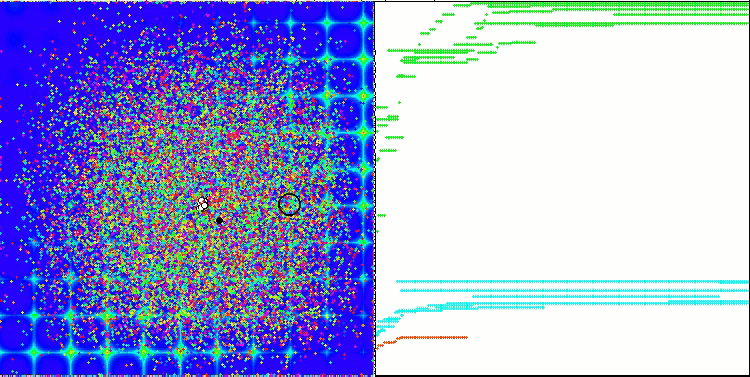
PSO на тестовой функции Forest.

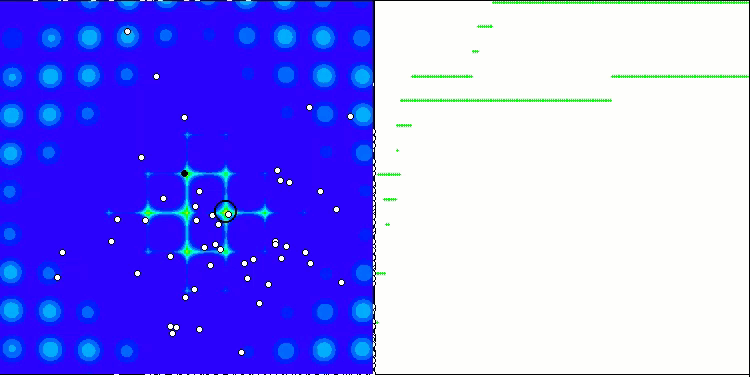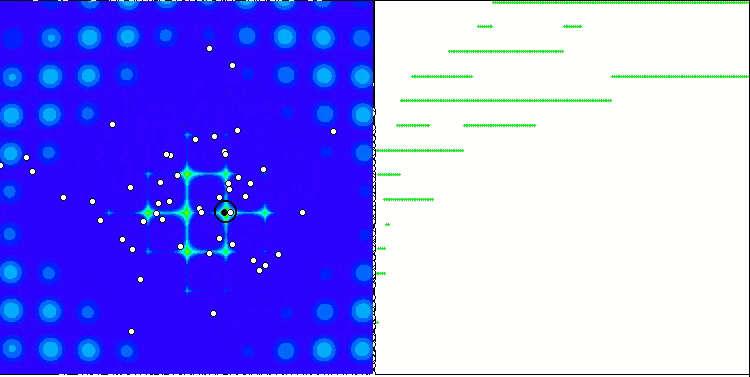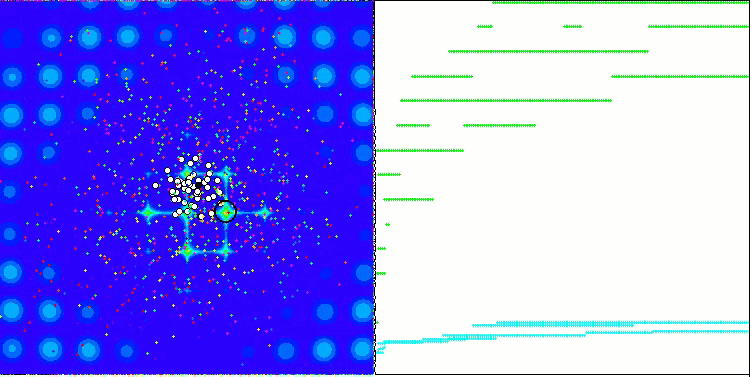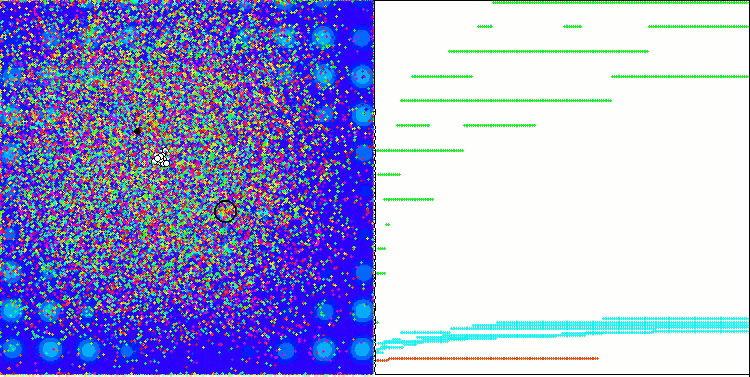
PSO на тестовой функции Megacity.

Как видим на анимации, тесты показали, что PSO достаточно хорошо справляется c гладкой первой функцией, но только при оптимизации двух переменных, с увеличением размерности пространства поиска, эффективность алгоритма резко падает, особенно это заметно на второй и дискретной третьей функциях. Результаты заметно хуже, чем у случайного алгоритма, описанного в предыдущей статье. К результатам мы еще вернёмся и подробно обсудим их при формировании сравнительной таблицы результатов.

Глядя на то, как знаменитый алгоритм PSO позорно проигрывает случайному, возникает желание дать алгоритму второй шанс - реванш. В следующем разделе статьи попытаемся модифицировать алгоритм PSO.

4. Модифицированная версия

На мой взгляд, слабыми сторонами PSO являются:

1) Каждая из координат обязательно, с вероятностью практически равной 1, будет изменена. Это означает, что каждая частица роя, на каждой итерации, колеблется в лучшем случае где-то в локальном экстремуме области глобального, а в худшем - никогда не попадет точно в точку глобального экстремума. Отсюда следует характерная черта алгоритма - застревание в локальных экстремумах, т.е. плохая сходимость.

2) Плохо работает с дискретными функциями, отчасти из-за первого недостатка. Координаты частиц перепрыгивают на ближайшие "площадки" поверхности оптимизируемой функции, не имея возможности детально исследовать окрестности какого-либо локального экстремума.

3) Слабые способности алгоритма исследовать новые области. Рой сосредотачивается где-то в одном месте и не пытается вырваться из локальной "ямы". В литературе упоминаются попытки создания реализации многороевой модификации, однако остаются открытыми вопросы оптимизации сложных многопеременных функций, так как неясен принцип взаимного отдаления, ведь должен выполняться не только принцип совместного движения, но и возможность взаимного отталкивания, иначе пропадает смысл в такой реализации, потому что отдельные рои просто сойдутся в одной области или точке. А для оптимизации простых одно-двух переменных функций и вовсе незачем городить огород, поскольку такие задачи выполняются простейшими методами при достижении превосходной сходимости.

Поскольку мы выяснили конкретные недостатки PSO, что можем предпринять что бы его улучшить?

Очевидно (хотя необязательно верно), что необходимо сделать - обеспечить передачу лучших отдельных координат частицам от других частиц с вероятностью тем большей, чем лучше в целом координаты частицы "донора". Схематично смещение вероятности выбора частицы представлено на рисунке 4. Генерируем случайное число от 0 до 1, преобразуем полученное число параболической функцией, а затем масштабируем в диапазон порядковых номеров частиц в рое от 0 до SwarmSize-1. Для этого нам понадобиться ввести дополнительный параметр для PSOm (такое имя дадим модифицированному алгоритму) - вероятность копирования координаты, а так же нужно сортировать рой так, что бы чем лучше частица, тем ближе она была к индексу 0.

ParabProbab

Рисунок 4. Смещённая вероятность выбора частицы.

Слегка изменим метод ParticleMovement (). Сгенерируем случайное число [0;1], если число окажется больше параметра copy, то выполним обычные операции с частицей, которые подробно были описаны выше, в противном случае скопируем координату у другой частицы с индексом, выбранным по правилу, графически показанному на рис.4.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSOm::ParticleMovement ()
{
  double rp;       //random component of particle movement
  double rg;
  double velocity;
  double posit;
  double positBest;
  double groupBest;

  for (int i = 0; i < swarmSize; i++)
  {
    for (int k = 0; k < parameters; k++)
    {
      rp = RNDfromCI (0.0, 1.0);
      rg = RNDfromCI (0.0, 1.0);

      double rC = RNDfromCI (0.0, 1.0);

      if (rC > copy)
      {
        velocity  = p [i].v  [k];
        posit     = p [i].c  [k];
        positBest = p [i].cB [k];
        groupBest = cB [k];

        p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit);
        p [i].c [k] = posit + p [i].v [k];

        p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      }
      else p [i].c [k] = p [GetPartcileAdress ()].cB [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Изменить понадобиться и метод Dwelling (). Добавим вызов функции сортировки SortParticles ().

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSOm::Dwelling ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    //remember the best position for the particle
    if (p [i].ff > p [i].ffB)
    {
      p [i].ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k];
    }

    if (p [i].ff > ffB)
    {
      ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k];
    }
  }

  SortParticles ();
}
//——————————————————————————————————————————————————————————————————————————————

Функция GetParticleAdress () обеспечивает выбор адреса частицы со смещённой в сторону лучшей частицы вероятностью.

//——————————————————————————————————————————————————————————————————————————————
//shift of probability in the smaller party (to an index 0)
int C_AO_PSOm::GetParticleAdress ()
{
  double x = RNDfromCI (-1.0, 0.0);
  x = x * x;
  x = Scale (x, 0.0, 1.0, 0, swarmSize - 1);
  x = SeInDiSp (x, 0, swarmSize - 1, 1);
  return ((int)x);
}
//——————————————————————————————————————————————————————————————————————————————

Функция SortParticles () - обычная пузырьковая сортировка.

//——————————————————————————————————————————————————————————————————————————————
//Sorting of particles
void C_AO_PSOm::SortParticles ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (int i = 0; i < swarmSize; i++)
  {
    ind [i] = i;
    val [i] = p [i].ffB; //ffPop [i];
  }

  while (cnt > 0)
  {
    cnt = 0;
    for (int i = 0; i < swarmSize - 1; i++)
    {
      if (val [i] < val [i + 1])
      {
        t0 = ind [i + 1];
        t1 = val [i + 1];
        ind [i + 1] = ind [i];
        val [i + 1] = val [i];
        ind [i] = t0;
        val [i] = t1;

        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (int u = 0; u < swarmSize; u++) pT [u] = p [ind [u]];

  // Copy the sorted array back
  for (int u = 0; u < swarmSize; u++) p [u] = pT [u];
}
//——————————————————————————————————————————————————————————————————————————————

Функция масштабирования числа из одного числового диапазона в другой.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_PSOm::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

5. Результаты тестов

Наконец, подведём итоги сегодняшнего исследования. Алгоритм PSO, как бы не хотелось нам надеяться на хорошие результаты, к сожалению, себя не оправдал. Проведенные исследования показали его слабую сходимость для дискретных функций, с изломами и с большим количеством аргументов, даже предпринятая попытка модифицировать алгоритм не увенчалась успехом, результаты оказались даже хуже, чем у классической реализации.

Увеличение параметра копирования до значений близких к 0.8 всё же способно показать моментальную сходимость, но это всего лишь для первой в тестах гладкой функции и при этом только с двумя аргументами, а для остальных тестов этот параметр только ухудшает результаты. Классическая реализация PSO как-то смогла отличиться лишь на функции Skin c 1000 аргументов, а на остальных тестах результаты оказались посредственными.

Финальный результат тестирования 0.47695 для классического и 0.45144 для модифицированного соответственно. Результаты приведены в таблице ниже. Тестовый стенд позволяет выбирать в настройках количество повторений тестов (по умолчанию установлено значение 5), поэтому читатели могут получить статистически более точные результаты установив этот параметр более высоким если позволяют мощности компьютера.

AO	Runs	Skin			Forest			Megacity (discrete)			Final result
AO	Runs	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	Final result
RND	1000	0,98744	0,61852	0,49408	0,89582	0,19645	0,14042	0,77333	0,19000	0,14283	0,51254
RND	10000	0,99977	0,69448	0,50188	0,98181	0,24433	0,14042	0,88000	0,20133	0,14283	0,51254
PSO	1000	0,98436	0,72243	0,65483	0,71122	0,15603	0,08727	0,53333	0,08000	0,04085	0,47695
PSO	10000	0,99836	0,72329	0,65483	0,97615	0,19640	0,09219	0,82667	0,10600	0,04085	0,47695
PSOm	1000	0,96678	0,64727	0,57654	0,80616	0,13388	0,06800	0,53333	0,08067	0,04211	0,45144
PSOm	10000	0,99505	0,64986	0,57654	0,90401	0,18194	0,07104	0,74667	0,10400	0,04211	0,45144

Если резюмировать всё выше сказанное, то можно подвести черту: PSO имеет тенденцию приводить к быстрой и преждевременной сходимости в средних оптимальных точках в дополнение к медленной сходимости в уточненной области поиска (имеющей слабую способность к локальному поиску). А если ещё проще: алгоритм очень слабый и не подходит для оптимизации сложных и тем более дискретных функций, в особенности функций многих аргументов.

Cуществует несколько подходов, которые можно использовать для улучшения PSO в целом. Размер роя является одним из важных факторов. Более высокий размер роя может увеличить вероятность более быстрой и точной конвергенции, однако зачастую в практических задачах существует порог на допустимое количество запусков фитнес-функции, и увеличение размера роя лишь пропорционально снизит количество эпох, а значит и снизит возможности эволюции роя.

Второй подход заключается в достижении баланса между разведкой и эксплуатацией. В начале итераций высокая степень разведки давала бы высокие шансы найти решение, близкое к глобальному оптимуму. Между тем, к концу итерации высокая степень эксплуатации дала бы частице шанс найти наиболее точное решение в перспективной области. Предварительная грубая оптимизация до роя другими методами — это еще один способ, который можно использовать для повышения базовой производительности PSO, который довольно часто используется в настоящее время. Распределение различных задач или целей для каждой подгруппы также может повысить эффективность PSO в многоцелевых задачах.

Другой подход к улучшению характеристик PSO состоит в том, чтобы установить составляющие компоненты уравнения скорости (динамическая регулировка скорости). Такой подход может направлять частицы в разных направлениях и приводить к более быстрой сходимости к глобальному оптимуму, но, это лишь предположение.

Плюсы:

Алгоритм очень прост и нетребователен к вычислительным ресурсам, код работает очень быстро, поскольку в классической реализации нет даже сортировки массивов.
Неплохо справляется с гладкими функциями. Пока PSO - явный лидер в таблице по оптимизации гладких функций со многими аргументами.

Минусы:

Низкое качество исследования оптимизируемой функции, алгоритм не может быть применим для решения задач, где требуется набор из нескольких уникальных решений.
Низкая скорость и точность сходимости.
Непригодность для оптимизации дискретных функций.
Практически немасштабируем.

Прикрепленные файлы |

Загрузить ZIP

r2_The_world_of_AO_4PSOf.ZIP (22.66 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

DoEasy. Элементы управления (Часть 22): SplitContainer. Изменение свойств созданного объекта

В статье реализуем возможность изменять свойства и внешний вид элемента управления SplitContainer после его создания.

Простое создание сложных индикаторов с помощью объектов

В статье представлен метод создания сложных индикаторов, позволяющий избежать проблем при работе с несколькими графиками и буферами, а также при объединении данных из нескольких источников.

Разработка торгового советника с нуля (Часть 25): Обеспечиваем надежность системы (II)

В этой статье мы сделаем финальный рывок к производительности советника... так что будьте готовы к долгому чтению. Чтобы сделать наш советник надежным, мы сначала удалим из кода всё, что не является частью торговой системы.

Разработка торгового советника с нуля (Часть 24): Обеспечиваем надежность системы (I)

В этой статье мы сделаем систему более надежной, чтобы обеспечить более стабильное и безопасное использование. Один из способов достижения нужной надежности — постараться как можно больше повторно использовать код, чтобы он постоянно проверялся в разных ситуациях. Однако, это только один из путей, а другой — использование ООП.