MetaTrader 5 / Тестер
English 中文 Español Deutsch 日本語 Português
preview
Популяционные алгоритмы оптимизации: Алгоритм обезьян (Monkey algorithm, MA)

Популяционные алгоритмы оптимизации: Алгоритм обезьян (Monkey algorithm, MA)

MetaTrader 5 — Тестер | 2 марта 2023, 15:31
2 369 0
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов


1. Введение

Алгоритм обезьян (МА) — это метаэвристический алгоритм поиска. В данной статье будут описаны основные составляющие алгоритма, представлены решения процесса восхождения (движения вверх), процесса локального прыжка и процесса глобального прыжка. Данный алгоритм предложили R. Zhao и W. Tang в 2007 г. Алгоритм моделирует поведение обезьян в процессе их перемещения и прыжков по горам в целях поиска пищи. Предполагается, что обезьяны исходят из того, что чем выше гора, тем больше пищи на ее вершине.

Местность, которую обследуют обезьяны, представляет собой ландшафт фитнес функции, поэтому решению задачи соответствует самая высокая гора (рассматриваем задачу глобальной максимизации). Из своего текущего положения каждая из обезьян движется вверх до тех пор, пока не достигнет вершины горы. Процесс набора высоты предназначен для постепенного улучшения значения целевой функции. Затем, обезьяна делает серию локальных прыжков в случайном направлении в надежде найти более высокую гору, и движение вверх повторяется. После выполнения некоторого числа подъемов и локальных прыжков, обезьяна полагает, что в достаточной степени исследовала ландшафт в окрестности своего начального положения.

Для того, чтобы обследовать новую область пространства поиска, обезьяна выполняет длинный глобальный прыжок. Указанные выше действия повторяются заданное число раз в параметрах алгоритма. Решением задачи объявляется самая высокая из вершин, найденных данной популяцией обезьян. Однако МА тратит значительное вычислительное время на поиск локальных оптимальных решений в процессе набора высоты. Процесс глобального прыжка может ускорить скорость сходимости алгоритма, цель этого процесса — заставить обезьян находить новые поисковые возможности, чтобы не попасть в локальный поиск. Алгоритм имеет такие преимущества, как простая структура, относительно высокая надежность и хороший поиск локальных оптимальных решений.

MA — это новый тип эволюционного алгоритма, который может решать множество сложных задач оптимизации, характеризующихся нелинейностью, недифференцируемостью и высокой размерностью. Отличие от других алгоритмов состоит в том, что время, затрачиваемое МА, в основном приходится на использование процесса набора высоты для поиска локальных оптимальных решений. В следующем разделе мы опишем основные компоненты алгоритма, представленные решения, инициализацию, процесс набора высоты, процесс наблюдения и прыжка.


2. Описание алгоритма

Для простоты понимания алгоритма обезьян, проще всего начать с псевдокода.

Псевдокод алгоритма MA:

1. Распределить случайным образом обезьян по пространству поиска.
2. Произвести замер высоты положения обезьяны.
3. Совершать локальные прыжки фиксированное количество раз.
4. Если новая вершина выше, полученная в п.3, тогда совершать локальные прыжки с этого места.
5. Если исчерпан лимит количества локальных прыжков и новая вершина не найдена, совершить глобальный прыжок.
6. После п.5 повторять п.3
7. Повторять с п.2 до выполнения критерия останова.

Итак, разберем каждый пункт псевдокода подробнее.

1. В самом начале оптимизации пространство поиска неизвестно для обезьян. Животные располагаются на неизведанной местности случайным образом, так как положение пищи равновероятно в любом месте.

2. Процесс замера высоты положения обезьян представляет собой выполнение задачи фитнес функции.

3. При совершении локальных прыжков есть ограничение на их количество, указанное в параметрах алгоритма. Это означает, что обезьяна пытается улучшить текущее положение, совершая небольшие локальные прыжки в области нахождения пищи. Если новый найденный источник пищи лучше, то переходим к п.4.

4. Новый источник пищи найден, счетчик количества локальных прыжков сбрасывается. Теперь поиск нового источника пищи будет производиться с этого места.

5. Локальные прыжки могут не дать обнаружить новый источник пищи лучше, обезьяна делает вывод, что текущая область пространства полностью исследована и пора искать новое место, но уже подальше. В этом месте возникает вопрос в какую же сторону тогда прыгать дальше? Идея алгоритма заключается в использовании центра координат всех обезьян, таким образом обеспечивается некоторая связь — общение между обезьянами в стае: обезьяны могут громко кричать и обладая хорошим объемным слухом способны определять точное положение своих сородичей. В то же время зная положение своих сородичей (сородичи не будут находиться в местах, где нет пищи) можно приблизительно вычислить оптимальное новое положение пищи, следовательно необходимо совершить прыжок именно в этом направлении.

В оригинальном алгоритме авторов обезьяна совершает глобальный прыжок по линии, проходящей через центр координат всех обезьян и текущее положение животного. Направление прыжка может быть как к центру координат, так и в противоположную сторону от центра. Прыжок в противоположном направлении от центра перечит самой логике нахождения пищи с аппроксимированными координатами по всем обезьянам, что и подтвердили мои эксперименты с алгоритмом — фактически это вероятность 50%, что будет удаление от глобального оптимума.

Практика показала, что выгоднее перепрыгивать за центр координат, чем не допрыгнуть или прыгнуть в противоположную сторону. Концентрации всех обезьян в одной точке не происходит, хотя подобная логика на первый взгляд должна приводить к этому. По факту обезьяны, исчерпав лимит локальных прыжков, перепрыгивают дальше центра, совершая тем самым ротацию положения всех обезьян в популяции. Если мысленно представить человекообразных, подчиняющихся данному алгоритму, то увидим стаю животных, перепрыгивающих время от времени через геометрический центр стаи, сама стая при этом кучно перемещается в сторону более богатого источника пищи, этот эффект "стайного перемещения" отчетливо прослеживается визуально на анимации алгоритма (у оригинального алгоритма данный эффект отсутствует и результаты хуже).

6. Совершив глобальный прыжок, обезьяна начинает уточнять положение источника пищи на новом месте. Процесс продолжается, пока не будет выполнен критерий останова.

Вся идея алгоритма легко умещается на схеме одного рисунка. Перемещение обезьяны обозначено окружностями с цифрами на рисунке 1. Каждая цифра — новое положение обезьяны. Маленькими желтыми окружностями показаны неудачные попытки локальных прыжков. Цифрой 6 обозначено положение, в котором лимит локальных прыжков исчерпан и при этом новое лучшее положение не найдено. Окружности без цифр символизируют местоположения остальных членов стаи. Геометрический центр координат стаи обозначен небольшой окружностью с координатами (x,y).


MA

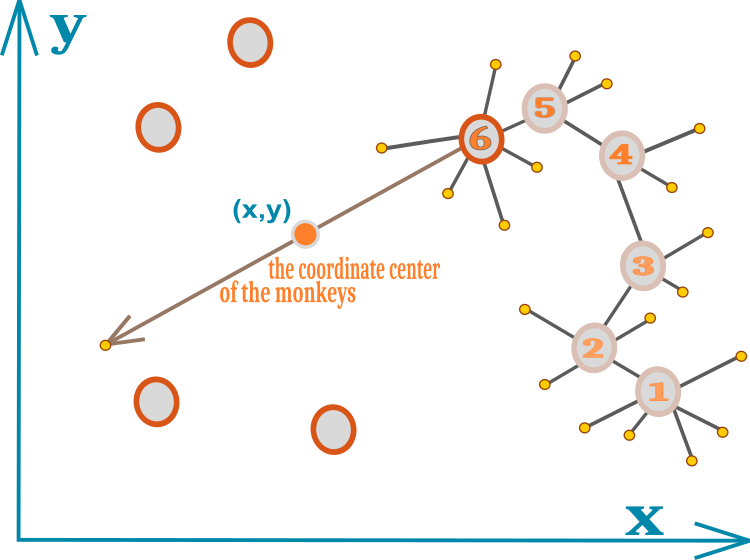
Рисунок 1. Схематичное представление перемещения обезьяны в стае.


Переходим к рассмотрению кода MA.

Обезьяну в стае удобно описать структурой S_Monkey. Структура содержит массив c []  с текущими координатами, массив cB [] с лучшими координатами пищи (именно от положения с этими координатами происходят локальные прыжки), h и hB — значение высоты текущей точки и значение наивысшей точки соответственно. lCNT — счетчик локальных прыжков, лимитирующий количество попыток улучшить местоположение.

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

Класс алгоритма обезьян C_AO_MA ничем особенным не отличается от алгоритмов, рассмотренных ранее. Стая обезьян представлена в классе как массив структур m []. Объявления в классе методов и членов небольшие по объему кода, поскольку алгоритм отличается лаконичностью, здесь нет сортировки, как во многих других алгоритмах оптимизации. Нам понадобится массивы для задания максимума, минимума и шага оптимизируемых параметров, константные переменные для передачи в них внешних параметров алгоритма. Переходим к описанию методов, в которых заключена основная логика MA. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Открытый метод Init () предназначен для инициализации алгоритма. Здесь зададим размер массивам. Показатель качества лучшей найденной обезьяной территории инициализируем минимально возможным числом double, так же поступим с соответствующими переменными массива структур MA. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Первый обязательный к исполнению на каждой итерации открытый метод Moving (), который осуществляет логику прыжков обезьян. На первой итерации, когда флаг revision равен false, необходимо инициализировать агентов случайными значениями в диапазоне координат исследуемого пространства, что равносильно случайному местонахождению обезьян на территории обитания стаи. Для того, чтобы сократить многократно повторяемые операции, такие как вычисления коэффициентов глобальных и локальных прыжков, сохраним значения величин для соответствующих координат (каждая из координат может иметь свою размерность) в массивах v []  и b []. Счетчик локальных прыжков каждой обезьяны сбросим на ноль.  

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

Для расчета центра координат всех обезьян используем массив cc [], размерность которого соответствует количеству координат. Расчет заключается в сложении координат обезьян и деление полученной суммы на размер популяции. Таким образом центр координат представляет собой арифметическое среднее координат.

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

Согласно псевдокоду, если лимит локальных прыжков не исчерпан, обезьяна будет прыгать из своего местоположения во все стороны равновероятно. Радиус окружности локальных прыжков регламентируется коэффициентом локальных прыжков, который пересчитан в соответствии с размерностью координат массив b [].

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Переходим к очень важной части логики MA — производительность алгоритма в большей степени зависит от реализации глобальных прыжков, разные авторы подходят к этому вопросу с различных сторон, предлагая всевозможные решения. Локальные прыжки, согласно проведенным исследованиям, мало влияют на сходимость алгоритма, именно глобальные прыжки определяют способность алгоритма "выпрыгивать" из локальных экстремумов. Мои эксперименты с глобальными прыжками выявили только один действенный подход именно для этого алгоритма, улучшающий результаты.

Выше мы обсуждали целесообразность прыжка в сторону центра координат, причем лучше, если конечная точка будет за центром, а не между центром и текущими координатами. Этот подход заключается в применении формулы полетов Леви, которую мы подробно описывали в статье, посвященной алгоритму поиска с кукушкой (COA).

Levi

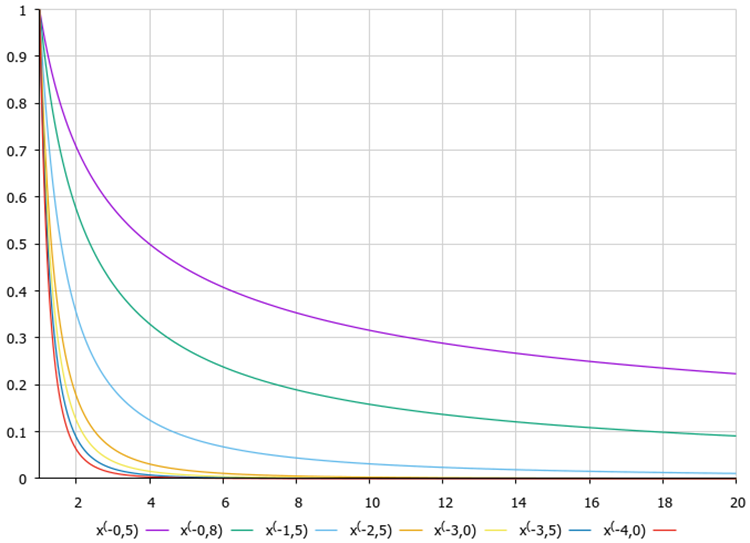
Рисунок 2. Графики функции полёта Леви в зависимости от степени в формуле.

Расчет координаты обезьяны произведен по следующей формуле:

m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);

где:

cc [c] — координата центра координат,

v [c] — коэффициент радиуса прыжка, пересчитанный в размерность пространства поиска,

r2 — число в диапазоне от 1 до 20.

Применяя полет Леви в данной операции, мы достигаем бо'льшую вероятность попадания обезьяны при прыжке в окрестности центра координат и меньшую вероятность оказаться далеко за центром. Таким образом обеспечиваем баланс между исследованием и эксплуатацией поиска, обнаруживая новые источники пищи. Если полученная координата, оказывается за нижней границей допустимого диапазона, то координата переносится на соответствующее расстояние к верхней границе диапазона, аналогично поступим при выходе за верхнюю границу. В завершении расчетов координаты проверим полученное значение на соответствие границ и шага исследования.

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

После совершения локальных/глобальных прыжков увеличим счетчик прыжков на единицу.

m [monk].lCNT++;

Второй открытый метод вызываемый на каждой итерации после вычисления фитнес функции Revision(). В этом методе обновляется глобальное решение, если найдено лучшее. Логика обработки результатов после локального и глобального прыжков отличается друг от друга, при локальном прыжке необходимо проверить улучшилось ли текущее положение и обновить его (на следующих итерациях совершаются прыжки уже с этого нового места), тогда как при глобальных прыжках проверки на улучшения нет — в любом случае новые прыжки будут совершены с этого места.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

В завершении описания кода можно заметить схожесть подходов этого алгоритма с группой алгоритмов роевого интеллекта, таких как рой частиц (PSO) и других, с похожей логикой стратегии поиска.


3. Результаты тестов

Распечатка работы алгоритма обезьян на тестовом стенде:

2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:36:26.877    Test_AO_MA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 64.89788419898215
2023.02.22 19:36:26.878    Test_AO_MA (EURUSD,M1)    Score: 0.80412
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 55.57339368461394
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    Score: 0.68859
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 41.41612351844293
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    Score: 0.51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.4307085210424681
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    Score: 0.24363
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.19875891413613866
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    Score: 0.11243
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06286212143582881
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    Score: 0.03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 2.8
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    Score: 0.23333
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 0.96
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    Score: 0.08000
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.34120000000000006
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    Score: 0.02843

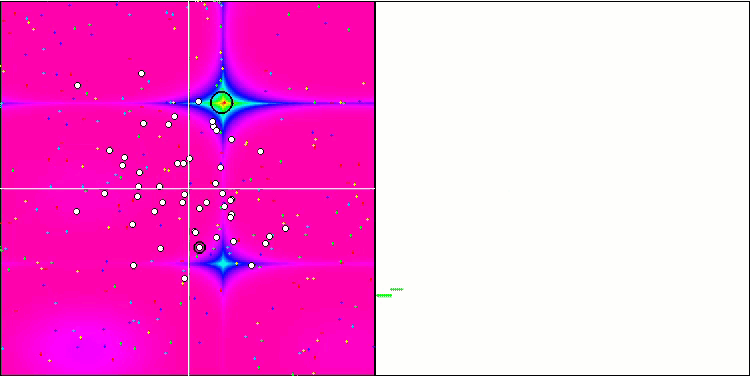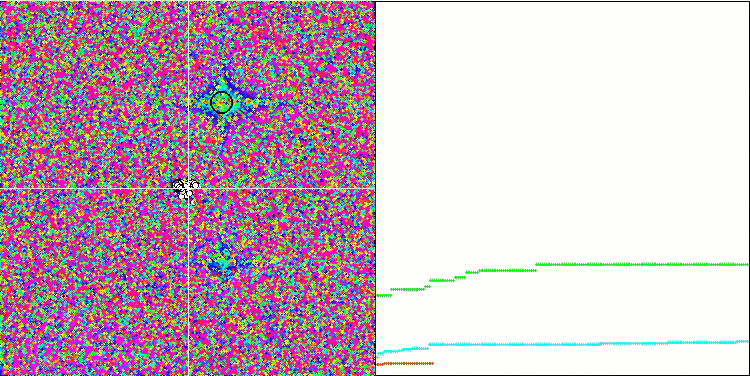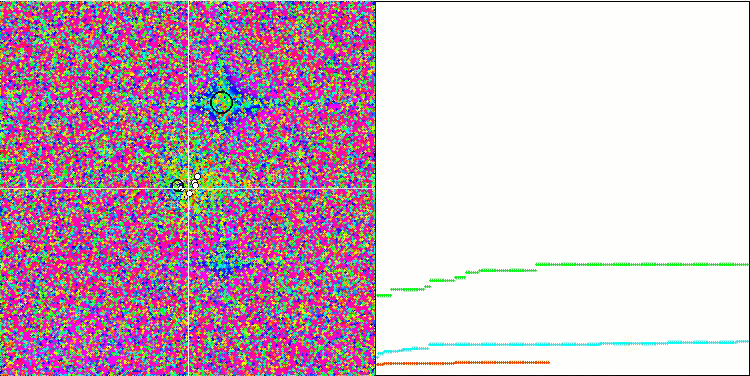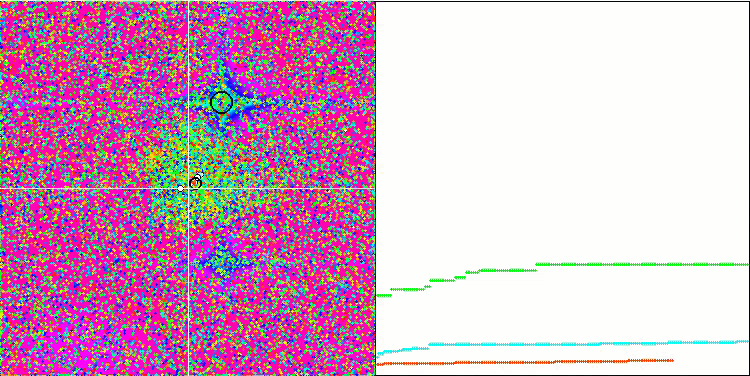
Обращая внимание на визуализацию работы алгоритма на тестовых функциях необходимо отметить отсутствие каких либо паттернов в поведении, очень схоже с алгоритмом RND. Присутствует некоторая небольшая концентрация агентов в локальных экстремумах, свидетельствующая о попытках алгоритма уточнять решение, но каких-то явных застреваний не проявляется.

rastrigin

  MA на тестовой функции Rastrigin.

forest

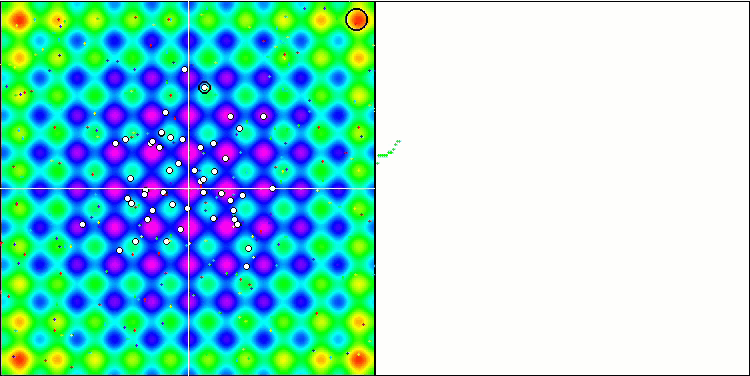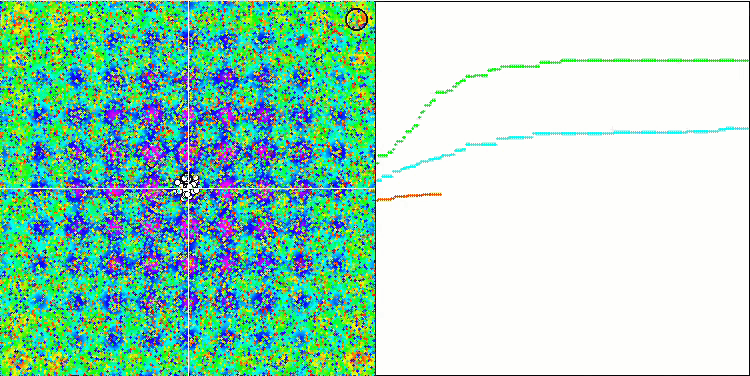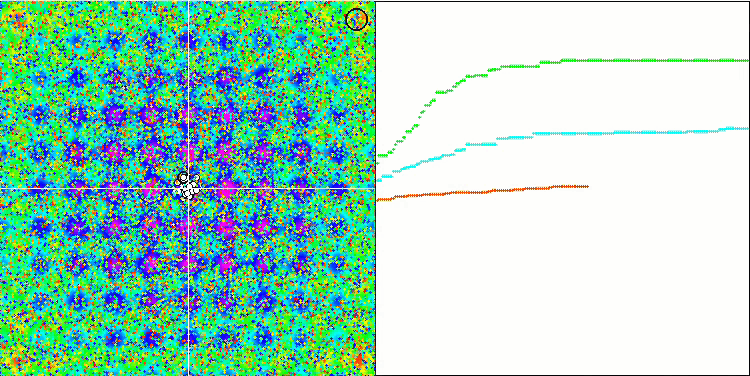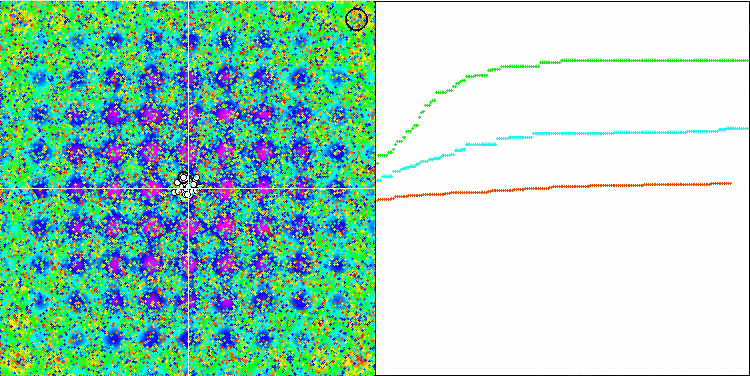
  MA на тестовой функции Forest.


  MA на тестовой функции Megacity.


Переходим к анализу результатов тестирования. По итогам подсчета баллов алгоритм MA занимает место в нижней части таблице между GSA и FSS. Хотелось бы отметить одно обстоятельство: поскольку тестирование алгоритмов построено по принципу сравнительного анализа, в котором оценки результатов представляют собой относительные величины между самым лучшим и самым худшим, то появление алгоритма с выдающимися результатами в каком то одном тесте и провальными результатами в других вызывает иногда изменение показателей у других участников тестирования.

Но результаты МА оказались такими, что не вызвали пересчет ни одного из результатов других участников тестов в таблице. У МА нет ни одного результата в тестах, который оказался бы самым худшим, хотя в таблице присутствуют алгоритмы с нулевыми относительными результатами, но имеют рейтинг выше (пример: GSA). Следовательно мы можем сделать некоторые выводы: хотя алгоритм ведет себя достаточно скромно, поисковая способность выражена недостаточно хорошо, как бы хотелось, однако алгоритм демонстрирует стабильные результаты, что для алгоритмов оптимизации является положительным качеством.

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

HS

harmony search

1,00000

1,00000

0,57048

2,57048

1,00000

0,98931

0,57917

2,56848

1,00000

1,00000

1,00000

3,00000

100,000

ACOm

ant colony optimization M

0,34724

0,18876

0,20182

0,73782

0,85966

1,00000

1,00000

2,85966

1,00000

0,88484

0,13497

2,01981

68,094

IWO

invasive weed optimization

0,96140

0,70405

0,35295

2,01840

0,68718

0,46349

0,41071

1,56138

0,75912

0,39732

0,80145

1,95789

67,087

COAm

cuckoo optimization algorithm M

0,92701

0,49111

0,30792

1,72604

0,55451

0,34034

0,21362

1,10847

0,67153

0,30326

0,41127

1,38606

50,422

FAm

firefly algorithm M

0,60020

0,35662

0,20290

1,15972

0,47632

0,42299

0,64360

1,54291

0,21167

0,25143

0,84884

1,31194

47,816

BA

bat algorithm

0,40658

0,66918

1,00000

2,07576

0,15275

0,17477

0,33595

0,66347

0,15329

0,06334

0,41821

0,63484

39,711

ABC

artificial bee colony

0,78424

0,34335

0,24656

1,37415

0,50591

0,21455

0,17249

0,89295

0,47444

0,23609

0,33526

1,04579

38,937

BFO

bacterial foraging optimization

0,67422

0,32496

0,13988

1,13906

0,35462

0,26623

0,26695

0,88780

0,42336

0,30519

0,45578

1,18433

37,651

GSA

gravitational search algorithm

0,70396

0,47456

0,00000

1,17852

0,26854

0,36416

0,42921

1,06191

0,51095

0,32436

0,00000

0,83531

35,937

MA

monkey algorithm

0,33300

0,35107

0,17340

0,85747

0,03684

0,07891

0,11546

0,23121

0,05838

0,00383

0,25809

0,32030

14,848

FSS

fish school search

0,46965

0,26591

0,13383

0,86939

0,06711

0,05013

0,08423

0,20147

0,00000

0,00959

0,19942

0,20901

13,215

PSO

particle swarm optimisation

0,20515

0,08606

0,08448

0,37569

0,13192

0,10486

0,28099

0,51777

0,08028

0,21100

0,04711

0,33839

10,208

RND

random

0,16881

0,10226

0,09495

0,36602

0,07413

0,04810

0,06094

0,18317

0,00000

0,00000

0,11850

0,11850

5,469

GWO

grey wolf optimizer

0,00000

0,00000

0,02672

0,02672

0,00000

0,00000

0,00000

0,00000

0,18977

0,03645

0,06156

0,28778

1,000


Выводы

Классический алгоритм МА в основном заключается в использовании процесса набора высоты для поиска локальных оптимальных решений. Шаг набора высоты играет решающую роль в точности аппроксимации локального решения. Чем меньше шаг набора высоты при локальных прыжках, тем выше точность решения, но требуется больше итераций, чтобы найти глобальный оптимум. Чтобы сократить время вычислений за счет снижения количества итераций, многие исследователи рекомендуют на начальных этапах оптимизации использовать другие методы оптимизации, такие как ABC, COA, IWO, а уже потом использовать MA для уточнения глобального решения. С таким подходом я не согласен, целесообразнее сразу использовать озвученные алгоритмы вместо МА, хотя потенциал развития у MA присутствует и является поводом дальнейших экспериментов и изучения. 

Алгоритм обезьян — это популяционный алгоритм, берущий свои корни из природы. Так же как и многие другие метаэвристические алгоритмы, данный алгоритм относится к числу эволюционных и способен решать ряд оптимизационных проблем, в числе которых нелинейность, недифференцируемость, высокая размерность пространства поиска с большой скоростью схождения. Ещё одно преимущество обезьяньего алгоритма заключается в том, что данный алгоритм регулируется малым числом параметров, делая его достаточно лёгким для реализации. Несмотря на стабильность результатов, невысокая скорость сходимости не позволяет рекомендовать алгоритм обезьян для решения задач с высокой вычислительной сложностью, поскольку требует значительное количество итераций, есть много других алгоритмов, совершающих ту же работу за менее продолжительное время (количество итераций).

Хотелось бы добавить в заключение, что классический вариант алгоритма, несмотря на мои многочисленные эксперименты, не мог выбраться выше третий снизу строчки рейтинговой таблицы, застревал в локальных экстремумах, чрезвычайно плохо работал на дискретных функциях, т.е. писать о нем статью не было особого желания, поэтому я предпринял попытки его улучшения, одна из которых показала некоторые улучшения показателей сходимости, повысила стабильность результатов за счет использования смещения вероятностей при глобальных прыжках, а так же пересмотра принципа самих глобальных прыжков. Многие исследователи MA указывают на необходимость модернизации алгоритма, поэтому существует большое количество модификаций алгоритма обезьян. Мной не ставилось целью рассматривать все виды модификаций МА, потому что алгоритм сам по себе не является выдающимся, скорее это вариация на тему роя частиц (PSO). Результатом проведенных экспериментов стал окончательный вариант алгоритма, приведенный в этой статье, без дополнительной маркировки m (модифицированный).

Гистограмма результатов тестирования алгоритмов на рисунке 3.

chart

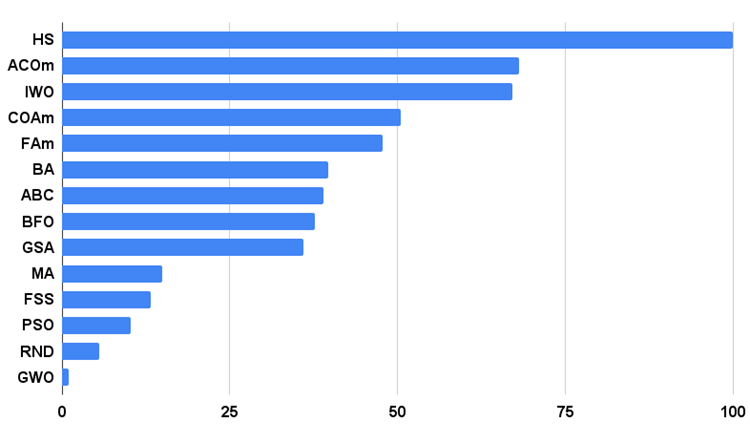
Рисунок 3. Гистограмма итоговых результатов тестирования алгоритмов.




Плюсы и минусы алгоритма обезьян (MA):

Плюсы:
1. Простота реализации.
2. Хорошая масштабируемость несмотря на низкую скорость сходимости.
3. Хорошие показатели на дискретных функциях.
4. Небольшое количество внешних параметров.

Минусы:
1. Низкая скорость сходимости.
2. Требует большого количества итераций для поиска.
3. Низкая общая эффективность.

К каждой статье я прикрепляю архив, который содержит обновленные актуальные версии кодов алгоритмов ко всем предыдущим статьям. Статья является накопленным опытом автора и личным мнением, выводы и суждения основаны на проведенных экспериментах.

Прикрепленные файлы |
Загрузить ZIP
14_The_world_of_AO_MA.ZIP (114.39 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Разработка экспериментальной DLL с поддержкой многопоточности в C++ для MetaTrader 5 на Linux Разработка экспериментальной DLL с поддержкой многопоточности в C++ для MetaTrader 5 на Linux
В статье рассмотрен процесс разработки для платформы MetaTrader 5 исключительно в системе Linux. При этом конечный продукт без проблем работает как в Windows, так и в Linux. Мы познакомимся с Wine и Mingw - важными инструментами кроссплатформенной разработки. В Mingw реализована потоковая передача (POSIX и Win32), что необходимо учитывать при выборе подходящего инструмента. Затем мы создадим DLL для проверки концепции и используем ее в коде MQL5, а также сравним производительность обеих реализаций потоков. Статья призвана стать отправной точкой для ваших собственных экспериментов. После прочтения статьи вы сможете создавать инструменты для MetaTrader в Linux.
Эксперименты с нейросетями (Часть 4): Шаблоны Эксперименты с нейросетями (Часть 4): Шаблоны
Нейросети наше все. Проверяем на практике, так ли это. MetaTrader 5 как самодостаточное средство для использования нейросетей в трейдинге. Простое объяснение.
Популяционные алгоритмы оптимизации: Алгоритм растущих деревьев (Saplings Sowing and Growing up — SSG) Популяционные алгоритмы оптимизации: Алгоритм растущих деревьев (Saplings Sowing and Growing up — SSG)
Алгоритм растущих деревьев (Saplings Sowing and Growing up, SSG) вдохновлен одним из самых жизнестойких организмов на планете, который является замечательным образцом выживания в самых различных условиях.
Нейросети — это просто (Часть 36): Реляционные модели обучения с подкреплением (Relational Reinforcement Learning) Нейросети — это просто (Часть 36): Реляционные модели обучения с подкреплением (Relational Reinforcement Learning)
В рассмотренных ранее моделях обучения с подкреплением мы использовали различные варианты сверточных сетей, которые способны идентифицировать различные объекты в исходных данных. Основное преимущество сверточных сетей в способности идентифицировать объекты вне зависимости от их расположением. В тоже время, сверточные сети не всегда справляются с различными деформациями объектов и шумом. Но эти проблемы способна решить реляционная модель.