
Методы оптимизации библиотеки Alglib (Часть II)
Содержание
- Введение
- Методы оптимизации библиотеки ALGLIB:
- BC (Box Constrained Optimization)
- NLC (Nonlinearly Constrained Optimization with Lagrangian Algorithm)
- LM (Levenberg-Marquardt Method)
- Таблица используемых функций в методах ALGLIB
- Тестирование методов
Введение
В первой части нашего исследования, посвященного алгоритмам оптимизации библиотеки ALGLIB в стандартной поставке терминала MetaTrader 5, мы детально познакомились с алгоритмами: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) и NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). Мы не только рассмотрели их теоретические основы, но и разобрали простой способ применения для задач оптимизации.
В настоящей статье мы продолжим исследование оставшихся методов из арсенала ALGLIB. Особое внимание будет уделено их тестированию на комплексных многомерных функциях, что позволит нам сформировать целостное представление об эффективности каждого метода. В завершение проведем всесторонний анализ полученных результатов и представим практические рекомендации по выбору оптимального алгоритма для конкретных типов задач.
BC (Box Constrained Optimization)
Оптимизация с учетом боксовых ограничений, подпрограмма минимизирует функцию F(x) с N аргументами при наличии боксовых ограничений (при этом некоторые из боксовых ограничений фактически являются равенствами). Этот оптимизатор использует алгоритм, аналогичный алгоритму BLEIC (оптимизатор с линейными ограничениями), но наличие только боксовых ограничений позволяет использовать более быстрые стратегии активации ограничений. На задачах большого масштаба, при наличии нескольких активных ограничений в решении, этот оптимизатор может быть быстрее чем BLEIC.
Давайте объясню более просто, что такое оптимизация с учетом боксовых ограничений. Это алгоритм оптимизации, который ищет наилучшее решение, работает с ограничениями типа "коробка" (когда каждая переменная должна быть в определенных пределах) и по сути, ищет минимум функции, где все переменные должны быть в заданных диапазонах. Главной особенностью алгоритма является то, что он похож на BLEIC, но работает быстрее, специально оптимизирован для работы с ограничениями-диапазонами.
Требования: начальная точка должна быть допустимой или близкой к допустимой области, и функция должна быть определена во всей допустимой области.
Для использования метода BC и других в библиотеке ALGLIB, нам понадобится подключить файл (библиотека поставляется вместе с терминалом MetaTrader 5, ничего дополнительно устанавливать пользователю не требуется).
#include <Math\Alglib\alglib.mqh> Напишем скрипт — пример для эффективной работы с методами ALGLIB. Необходимо выделить основные шаги, характерные для работы с методами ALGLIB, которые выделим соответствующим цветом идентичные блоки кода.
1. Определим граничные условия задачи, такие как количество запусков фитнес-функции (целевой функции), диапазоны оптимизируемых параметров и их шаг. Для методов ALGLIB необходимо назначить стартовые значения оптимизируемых параметров "x" (методы детерминированные и результаты полностью зависят от начальных значений, поэтому мы применим генерацию случайных чисел в диапазоне параметров задачи), а также масштаб "s" (методы чувствительны к масштабу параметров относительно друг друга, в данном случае устанавливаем масштаб "1").
2. Объявим объекты, необходимые для работы алгоритма.
3. Зададим внешние параметры алгоритма (настройки).
4. Выполним инициализацию алгоритма, передав в метод диапазоны и шаги оптимизируемых параметров, а также внешние параметры алгоритма.
5. Выполним оптимизацию.
6. Получим результаты оптимизации для дальнейшего использования.
Необходимо учесть важный аспект — пользователь не имеет возможности влиять на процесс оптимизации или остановить его в любой момент. Метод выполняет все операции самостоятельно, вызывая фитнес-функцию внутри своего процесса. Алгоритм может обращаться к фитнес-функции произвольное количество раз (хотя и ориентируется на параметр, указанный пользователем). Пользователь может контролировать максимальное допустимое число вызовов самостоятельно, передав методу команду останова.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Инициализация параметров оптимизации--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Создание и инициализация массивов для границ диапазона--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Генерация случайных начальных значений параметров в заданных диапазонах---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Создание объектов для оптимизации------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinBCReport rep; // Установка параметров алгоритма оптимизации BC------------------------------ double diffStep = 0.00001; double epsg = 1e-16; double epsf = 1e-16; CAlglib::MinBCCreateF (x, diffStep, fFunc.state); CAlglib::MinBCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinBCSetScale (fFunc.state, s); CAlglib::MinBCSetCond (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns); CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinBCResults (fFunc.state, x, rep); // Вывод результатов оптимизации----------------------------------------------- Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Так как метод обращается к фитнес-функции самостоятельно (а не из программы пользователя), потребуется обернуть вызов фитнес-функции в класс, который наследуется от родительского класса в ALGLIB (эти родительские классы отличаются для разных методов). Объявим класс-обертку как "C_OptimizedFunction" и пропишем в классе следующие методы:
1. Func () — это виртуальный метод, который переопределяется в производных классах.2. Init () — инициализирует параметры класса. Внутри метода:
- Инициализируются переменные, связанные с количеством запусков и лучшим найденным значением функции.
- Резервируются массивы "c" и "cB" для хранения координат.
Переменные:
- state — объект типа CMinBCState, характерный именно для метода BC, используется при вызове статических методов алгоритма и вызова метода останова.
- numberLaunches — текущее количество запусков (необходимо для предотвращения бесконтрольного или слишком долгого выполнения фитнес-функции).
- maxNumbLaunchesAllowed — максимально допустимое количество запусков.
- fB — лучшее найденное значение фитнес-функции.
- c [] — массив текущих координат.
- cB [] — массив для хранения лучших координат поиска.
//—————————————————————————————————————————————————————————————————————————————— // Класс для оптимизации функции, наследуется от CNDimensional_Func class C_OptimizedFunction : public CNDimensional_Func { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // Виртуальная функция, которая будет содержать оптимизируемую функцию-------- virtual void Func (CRowDouble &x, double &func, CObject &obj); // Инициализация параметров оптимизации--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinBCState state; // Состояние int numberLaunches; // Счетчик запусков double fB; // Лучшее найденное значение целевой функции (максимум) double cB []; // Координаты точки с лучшим значением функции private: //------------------------------------------------------------------- double c []; // Массив для хранения текущих координат int maxNumbLaunchesAllowed; // Максимально допустимое число вызовов функции }; //——————————————————————————————————————————————————————————————————————————————
Метод "Func" класса "C_OptimizedFunction" предназначен для обращения к фитнес-функции пользователя. Он принимает в качестве аргументов вектор "x" (один из вариантов оптимизируемых параметров задачи, предлагаемых методом оптимизации), аргумент "func", в который необходимо вернуть вычисленное значение фитнес-функции, и объект "obj" (предназначение которого для меня неясно, возможно зарезервировано для возможности передачи дополнительной информации в/из метода). Основные этапы выполнения метода:
- Увеличивается счетчик "numberLaunches", который отслеживает количество вызовов метода "Func".
- Если количество запусков превышает допустимое значение "maxNumbLaunchesAllowed", функция устанавливает значение "func" в "DBL_MAX" (максимальное значение типа "double", методы ALGLIB предназначены для минимизации функций, это значение означает наихудшее возможное решение). Затем вызывается функция "MinBCRequestTermination", которая предназначена сигнализировать методу BC о необходимости остановить процесс оптимизации.
- Далее в цикле происходит копирование значений из вектора "x" в массив "c". Это необходимо, чтобы использовать эти значения для передачи в фитнес-функцию пользователя.
- Вызывается функция "ObjectiveFunction", которая вычисляет значение целевой функции для текущих значений в массиве "c". Результат сохраняется в "ffVal", и значение "func" устанавливается в отрицательное значение "ffVal" (мы оптимизируем перевернутый параболоид, который необходимо максимизировать, а BC минимизирует функцию, поэтому значение переворачиваем).
- Если текущее значение "ffVal" больше, чем предыдущее лучшее значение "fB", то "fB" обновляется, и массив "cB" копирует текущее состояние "c". Это позволяет отслеживать лучшее найденное значение целевой функции с соответствующими параметрами и позволяет обращаться к ним позднее при необходимости.
Функция "Func" реализует вызов пользовательской фитнес-функции и отслеживает количество ее запусков, обновляет наилучшие результаты. Она также управляет условиями остановки, если количество запусков превышает установленный предел.
//—————————————————————————————————————————————————————————————————————————————— // Реализация оптимизируемой функции void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj) { // Увеличение счетчика запусков функции и контроль ограничений---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { func = DBL_MAX; CAlglib::MinBCRequestTermination (state); return; } // Копирование входных координат во внутренний массив------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Вычисление значения целевой функции---------------------------------------- double ffVal = ObjectiveFunction (c); func = -ffVal; // Обновление лучшего найденного решения-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
После запуска тестового скрипта с алгоритмом BC для оптимизации функции параболоида, получим в принт такой результат:
К сожалению, несмотря на запросы остановить оптимизацию с помощью метода "MinBCRequestTermination", алгоритм продолжал процесс и пытался обратиться к фитнес-функции сверх лимита в 10 000 запусков.
Теперь попробуем не ограничивать BC и дадим ему возможность действовать по своему усмотрению. Результат следующий:
Как можно заметить, BC способен полностью сойтись на функции параболоида, однако в этом случае заранее оценить требуемое количество запусков целевой функции невозможно.
В алгоритме важен шаг дифференцирования. Так, если использовать очень маленький шаг, например 1e-16 вместо 0.00001, то алгоритм преждевременно останавливается, по сути — застревает, с таким результатом:
NLC (Nonlinearly Constrained Optimization with Preconditioned Augmented Lagrangian Algorithm)
Этот алгоритм нелинейной оптимизации с ограничениями позволяет минимизировать сложную целевую функцию F(x) с N переменными, учитывая при этом различные ограничения: ограничения по границам переменных (min <= x <= max), линейные неравенства и равенства, нелинейные равенства G(x) = 0, нелинейные неравенства H(x) <= 0.
Представьте, что у вас есть какая-то сложная цель, которую вы хотите достичь, но при этом есть некоторые ограничения, которые нельзя нарушать. Например, вы хотите максимизировать прибыль от продаж, но при этом не можете превышать определенные накладные расходы. Алгоритм из ALGLIB помогает решить такого рода задачи оптимизации с ограничениями. Вот как он работает:
1. Вы даете алгоритму начальную точку — некоторое начальное предположение о том, как достичь цели. Эта точка должна быть возможной, то есть удовлетворять всем ограничениям.
2. Затем алгоритм начинает медленно двигаться от этой начальной точки, шаг за шагом приближаясь к оптимальному решению. На каждом шаге он решает некоторую вспомогательную задачу, чтобы понять, в каком направлении двигаться дальше.
3. Чтобы ускорить этот процесс, алгоритм использует специальный прием — "предобусловливание". Это значит, что он как бы подстраивает свои "шаги" под структуру задачи, чтобы двигаться быстрее.
4. В итоге, после нескольких итераций, алгоритм находит решение, которое минимизирует вашу целевую функцию (например, минимизирует накладные расходы) и при этом удовлетворяет всем ограничениям.
Пользователь может выбрать один из трех различных решателей, которые подходят для задач разного масштаба и сложности реализованных в ALGLIB:
SQP (последовательное квадратичное программирование) рекомендован для задач среднего размера с трудными целевыми функциями.
AUL (предобусловленный метод увеличенного лагранжа) рекомендован для крупномасштабных задач или с дешевыми (быстрыми) целевыми функциями.
SLP (последовательное линейное программирование) медленнее, но более устойчив в сложных случаях.
Эксперименты с тестовыми функциями показали эффективность решателя AUL, остальные решатели закомментированы в коде.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Инициализация параметров оптимизации--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Создание и инициализация массивов для границ диапазона--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Генерация случайных начальных значений параметров в заданных диапазонах---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Создание объектов для оптимизации------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinNLCReport rep; // Установка параметров алгоритма оптимизации NLC----------------------------- double diffStep = 0.00001; double rho = 1000.0; int outerits = 5; CAlglib::MinNLCCreateF (x, diffStep, fFunc.state); CAlglib::MinNLCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinNLCSetScale (fFunc.state, s); CAlglib::MinNLCSetCond (fFunc.state, rangeStep, numbTestFuncRuns); //CAlglib::MinNLCSetAlgoSQP (fFunc.state); CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits); //CAlglib::MinNLCSetAlgoSLP (fFunc.state); CAlglib::MinNLCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinNLCResults (fFunc.state, x, rep); // Вывод результатов оптимизации----------------------------------------------- Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
В NLC тип переменной "state" задаём "CMinNLCState".
//—————————————————————————————————————————————————————————————————————————————— // Класс для оптимизации функции, наследуется от CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // Виртуальная функция, которая будет содержать оптимизируемую функцию-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Инициализация параметров оптимизации--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinNLCState state; // Состояние int numberLaunches; // Счетчик запусков double fB; // Лучшее найденное значение целевой функции (максимум) double cB []; // Координаты точки с лучшим значением функции private: //------------------------------------------------------------------- double c []; // Массив для хранения текущих координат int maxNumbLaunchesAllowed; // Максимально допустимое число вызовов функции }; //——————————————————————————————————————————————————————————————————————————————
Остановку процесса оптимизации запрашиваем командой "MinNLCRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Реализация оптимизируемой функции void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Увеличение счетчика запусков функции и контроль ограничений---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); CAlglib::MinNLCRequestTermination (state); return; } // Копирование входных координат во внутренний массив------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Вычисление значения целевой функции---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Обновление лучшего найденного решения-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
После запуска тестового скрипта с алгоритмом NLC для оптимизации функции параболоида, получим в принт такой результат:
NLC, best result: 0.8858935739350294, number of function launches: 28007
Без ограничения на количество запусков целевой функции NLC полностью сходится, но при этом выполняет более одного миллиона итераций:
NLC, best result: 1.0, number of function launches: 1092273
С использованием очень маленького шага 1e-16 алгоритм преждевременно не останавливается, как, например, метод BC, но показывает результат немного хуже, чем при шаге 0.00001.
NLC, best result: 0.8543715192632731, number of function launches: 20005
LM (Levenberg-Marquardt Method)
Метод Левенберга-Марквардта (LM) это алгоритм оптимизации, широко используемый для решения задач нелинейных наименьших квадратов. Этот метод эффективен в задачах подгонки кривых и поверхностей.
Основная идея LM объединяет две техники оптимизации: метод градиентного спуска и метод Гаусса-Ньютона. Это позволяет алгоритму адаптироваться к форме целевой функции. Принцип работы:
- На каждой итерации алгоритм вычисляет направление шага, используя комбинацию градиентного спуска и приближения второго порядка.
- Коэффициент затухания (λ) автоматически корректируется, чтобы контролировать размер шага и баланс между двумя методами.
Представьте, что вы пытаетесь найти самую низкую точку в горной местности, но у вас есть только карта с размытыми контурами. Метод Левенберга-Марквардта — это как умный навигатор, который комбинирует два способа поиска пути:
1. Первый способ (метод Гаусса-Ньютона) быстрый, но рискованный. Как будто вы бежите прямо вниз по склону. Он отлично работает, когда вы близко к цели, но можете "споткнуться", если рельеф сложный.
2. Второй способ (градиентный спуск) медленный, но надежный. Как будто вы осторожно спускаетесь маленькими шажкам, медленнее, но безопаснее. Хорошо работает даже на сложном рельефе.
Алгоритм умно переключается между этими двумя способами. Когда путь понятен, использует быстрый способ, но когда ситуация сложная — переходит на осторожный режим. Автоматически подстраивает размер шага.
Он может застрять в локальном минимуме. Требует хорошего начального приближения (нужно примерно знать, где искать) и не очень эффективен для задач с большим числом параметров (больше 100).
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Инициализация параметров оптимизации--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; double rangeMin [], rangeMax [], rangeStep; ArrayResize (rangeMin, params); ArrayResize (rangeMax, params); for (int i = 0; i < params; i++) { rangeMin [i] = -10; rangeMax [i] = 10; } rangeStep = DBL_EPSILON; double x []; double s []; ArrayResize (x, params); ArrayResize (s, params); ArrayInitialize (s, 1); // Генерация случайных начальных значений параметров в заданных диапазонах---- for (int i = 0; i < params; i++) { x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0); } // Создание объектов для оптимизации------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinLMReportShell rep; // Установка параметров алгоритма оптимизации LM------------------------------ double diffStep = 1e-16;//0.00001; CAlglib::MinLMCreateV (1, x, diffStep, fFunc.state); CAlglib::MinLMSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinLMSetScale (fFunc.state, s); CAlglib::MinLMSetCond (fFunc.state, rangeStep, numbTestFuncRuns); CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj); CAlglib::MinLMResults (fFunc.state, x, rep); // Вывод результатов оптимизации----------------------------------------------- Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Для LM тип переменной "state" задаём "CMinLMStateShell".
//—————————————————————————————————————————————————————————————————————————————— // Класс для оптимизации функции, наследуется от CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // Виртуальная функция, которая будет содержать оптимизируемую функцию-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Инициализация параметров оптимизации--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinLMStateShell state; // Состояние int numberLaunches; // Счетчик запусков double fB; // Лучшее найденное значение целевой функции (максимум) double cB []; // Координаты точки с лучшим значением функции private: //------------------------------------------------------------------- double c []; // Массив для хранения текущих координат int maxNumbLaunchesAllowed; // Максимально допустимое число вызовов функции }; //——————————————————————————————————————————————————————————————————————————————
Так же как и в предыдущих методах оптимизации, мы ограничиваем количество обращений целевой функции, но метод LM единственный, для которого команды останова не предусмотрено, логично было бы ожидать наличие функции "MinLMRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Реализация оптимизируемой функции void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Увеличение счетчика запусков функции и контроль ограничений---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); //CAlglib::MinLMRequestTermination (state); //такого метода не существует return; } // Копирование входных координат во внутренний массив------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Вычисление значения целевой функции---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Обновление лучшего найденного решения-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
После запуска тестового скрипта с алгоритмом LM для оптимизации функции параболоида, получим в принт такой результат:
LM, best result: 0.6776047308612422, number of function launches: 4003
Метод LM остановился на 4003-м запуске целевой функции, соответственно, снятие ограничений на количество итераций даст тот же самый результат, потому что алгоритм застрял еще до достижения "потолка" в 10 000 итераций:
С использованием очень маленького шага 1e-16 алгоритм преждевременно останавливается ещё раньше, на 2001-м запуске целевой функции:
LM, best result: 0.6670839162547625, number of function launches: 2001
Таблица используемых функций в методах ALGLIB
В методах оптимизации ALGLIB используются различные типы переменных в качестве начальных значений и боксовых ограничений, а также разные типы родительских классов целевой функции и наборы объектов, необходимых для оптимизации, а также разный список вызываемых функций. Это может затруднить интуитивное написание программ, использующих эти методы.
Чтобы упростить понимание и структурировать знания о методах оптимизации ALGLIB, я подготовил сводную таблицу. Она поможет программистам быстро сориентироваться и правильно начать оптимизацию в своих проектах.
| Optimization algorithm | Type FF function | Type of variable | List of objects | List of called methods |
| BLEIC | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell | 1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination |
| LBFGS | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell | 1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination |
| NS | FVec | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState | 1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination |
| BC | Func | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState | 1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination |
| NLC | Fvec | CRowDouble | 1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState | 1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination |
| LM | FVec | double | 1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell | 1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist) |
Тестирование методов
После изучения методов оптимизации библиотеки ALGLIB, закономерно возникает вопрос о том, какие из этих методов выбрать для конкретных задач. Разные типы задач оптимизации могут быть решены с различной эффективностью в зависимости от выбранного метода. Чтобы ответить на этот важный вопрос, мы будем использовать сложные тестовые функции, которые зарекомендовали себя наиболее приближенными к реальным задачам. Эти функции отражают типичные случаи: гладкие функции представляют тестовая функция Hilly, гладкие с острыми вершинами (дифференцируемые не на всем своем определении) — Forest, а чисто дискретная функция — Megacity.
Тестирование будет проводиться с 50 перезапусками каждого теста и ограничением на количество вызовов целевой функции в 10 000. Мы подготовим стендовый скрипт для тестирования на примере метода BC. Этот подход позволит нам получить более точные и репрезентативные результаты, которые помогут выбрать наиболее подходящий метод оптимизации для каждой конкретной задачи.
Напишем функцию "FuncTests", которая будет производить тестовые запуски оптимизации с использованием соответствующего метода ALGLIB. Функция позволит собрать данные о производительности методов и визуализировать их работу, а также построить графики сходимости.
Перечислим коротко, что делает функция "FuncTests":
- Принимает тестовую целевую функцию, количество тестов, цвет для визуализации и переменные для общего результата.
- Если включено видео, строит график функции.
- Устанавливает границы для тестирования и инициализирует переменные для результатов.
- Генерирует случайные входные данные и выполняет оптимизацию с использованием библиотеки "CAlglib".
- Сохраняет количество вызовов целевой функции и лучшие результаты.
- Рассчитывает и выводит средние результаты.
- Обновляет общий балл на основе текущих тестов.
//—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, // Ссылка на объект целевой функции const int funcCount, // Количество тестируемых функций const color clrConv, // Цвет для визуализации double &allScore, // Общий балл всех тестов double &allTests) // Общее количество тестов { if (funcCount <= 0) return; // Если количество функций <= 0, выходим из функции allTests++; // Увеличиваем общее количество тестов if (Video_P) // Если включена визуализация { ST.DrawFunctionGraph (f); // Рисуем график функции ST.SendGraphToCanvas (); // Отправляем график на холст ST.MaxMinDr (f); // Определяем максимум и минимум функции ST.Update (); // Обновляем визуализацию } //---------------------------------------------------------------------------- C_AO_Utilities Ut; // Утилиты для работы с числами int xConv = 0.0; // Переменная для конвертации по оси X int yConv = 0.0; // Переменная для конвертации по оси Y double aveResult = 0.0; // Средний результат тестирования int aveRunsFF = 0; // Среднее количество запусков функции int params = funcCount * 2; // Количество параметров (по 2 для каждой функции) int epochCount = NumbTestFuncRuns_P / PopSize_P; // Количество эпох //---------------------------------------------------------------------------- CRowDouble bndl; bndl.Resize (params); // Массив для нижних границ CRowDouble bndu; bndu.Resize (params); // Массив для верхних границ for (int i = 0; i < funcCount; i++) // Заполняем границы для каждой функции { bndu.Set (i * 2, f.GetMaxRangeX ()); // Устанавливаем верхнюю границу по X bndl.Set (i * 2, f.GetMinRangeX ()); // Устанавливаем нижнюю границу по X bndu.Set (i * 2 + 1, f.GetMaxRangeY ()); // Устанавливаем верхнюю границу по Y bndl.Set (i * 2 + 1, f.GetMinRangeY ()); // Устанавливаем нижнюю границу по Y } CRowDouble x; x.Resize (params); // Массив для значений параметров CRowDouble s; s.Resize (params); // Массив для масштабирования s.Fill (1); // Заполняем массив единицами for (int test = 0; test < NumberRepetTest_P; test++) // Запускаем тесты { for (int i = 0; i < funcCount; i++) // Для каждой функции { x.Set (i * 2, Ut.RNDfromCI (bndl [i * 2], bndu [i * 2])); // Генерируем случайные значения по X x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Генерируем случайные значения по Y } //-------------------------------------------------------------------------- CObject obj; // Объект для хранения результатов C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Инициализация функции оптимизации CNDimensional_Rep frep; // Репрезентация многомерного пространства CMinBCState state; // Состояние метода минимизации CMinBCReport rep; // Отчет о минимизации double epsg = 1e-16; // Параметр для условия остановки по градиенту double epsf = 1e-16; // Параметр для условия остановки по значению функции CAlglib::MinBCCreateF (x, DiffStep_P, state); // Создание состояния минимизации CAlglib::MinBCSetBC (state, bndl, bndu); // Установка границ CAlglib::MinBCSetScale (state, s); // Установка масштабирования CAlglib::MinBCSetCond (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P); // Установка условий CAlglib::MinBCOptimize (state, fFunc, frep, obj); // Оптимизация CAlglib::MinBCResults (state, x, rep); // Получение результатов //-------------------------------------------------------------------------- aveRunsFF += fFunc.numberLaunches; // Суммируем количество запусков функции aveResult += -fFunc.bestMIN; // Суммируем лучший найденный минимум } aveRunsFF /= NumberRepetTest_P; // Вычисляем среднее количество запусков aveResult /= NumberRepetTest_P; // Вычисляем средний результат double score = aveResult; // Оценка на основе среднего результата Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Вывод результатов теста allScore += score; // Обновляем общий балл } //——————————————————————————————————————————————————————————————————————————————
Запустим тестовый стенд последовательно для всех рассмотренных методов оптимизации библиотеки ALGLIB. Ниже приведены распечатки результатов тестирования для соответсвующих методов, которые следует читать так:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|: Аббревиатура метода, полное наименование, шаг дифференцирования (опционально, дополнительные параметры методов).
5 Hilly's: Количество соответствующих тестовых целевых функций в составе многомерной задачи.
Func runs: 2178(10000): Количество запусков целевой функции — количество попыток обращения методов к целевой функции и заданный желаемый "потолок" по количеству запусков.
result: 0.38483704535107116: Средний результат за 50 запусков тестирования.
Распечатка работы метода BLEIC на тестовых целевых функциях:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
All score: 2.05290 (22.81%)
Распечатка работы метода L-BFGS на тестовых целевых функциях:
L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); result: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); result: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); result: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); result: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); result: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); result: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); result: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); result: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); result: 0.09022461538461606
=============================
All score: 1.84784 (20.53%)
Распечатка работы метода NS на тестовых целевых функциях:
NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
All score: 2.09251 (23.25%)
Распечатка работы метода BC на тестовых целевых функциях:
BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
All score: 2.03457 (22.61%)
Распечатка работы метода NLC на тестовых целевых функциях:
NLC|nonlinearly constrained optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
All score: 2.04604 (22.73%)
Распечатка работы метода LM на тестовых целевых функциях:
LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); result: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
All score: 1.54204 (17.13%)
Теперь мы можем наглядно проанализировать поведение алгоритмов на тестовых функциях. Для большинства методов характерна преждевременная остановка работы до исчерпания лимита на количество запусков целевой функции (в параметрах нами указан лимит в 10 000 итераций). Например, метод Левенберга-Марквардта (LM) на дискретной задаче "Megacity" с размерностью 1 000 параметров останавливался в среднем на 2 081 итерации, а при размерности 10 — всего на 21 итерации. В то же время, на гладких функциях "Hilly" этот метод пытался найти минимум за значительно большее количество итераций. Другие методы, напротив, совершали более миллиона обращений к целевой функции.
Ниже приведены визуализации работы методов NS (набравшего наибольшее количество баллов) и метода LM (набравшего наименьшее количество баллов).
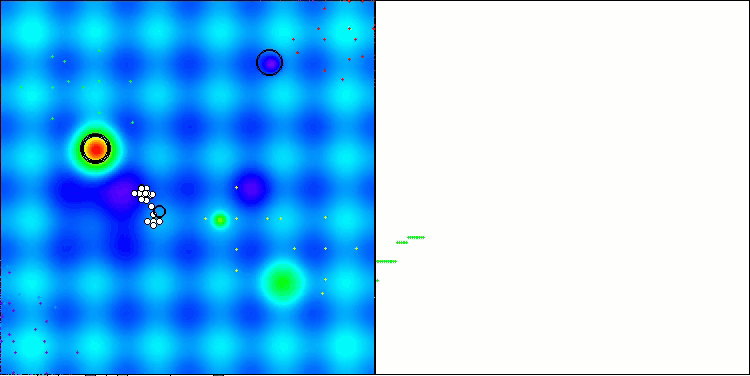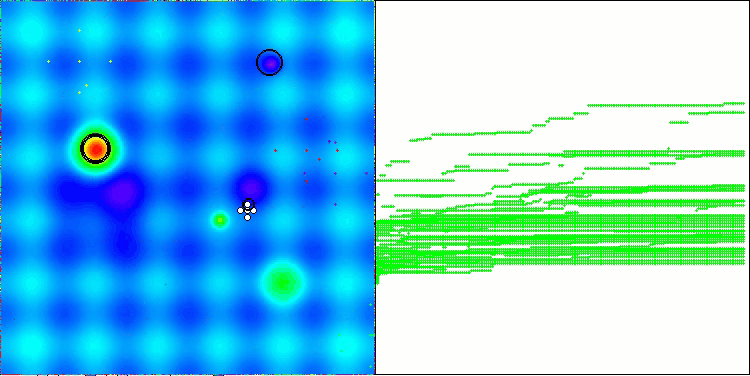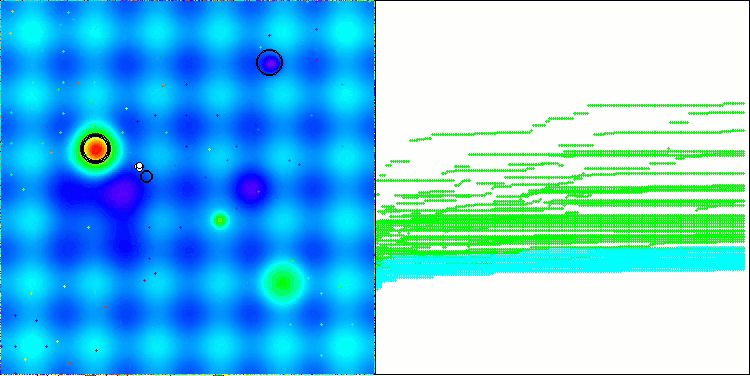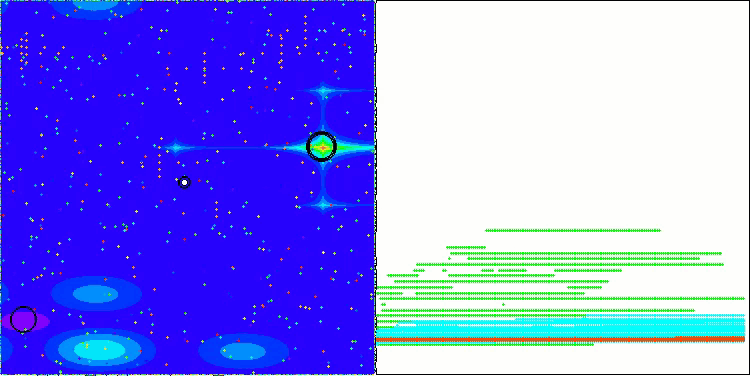
NS на тестовой функции Hilly
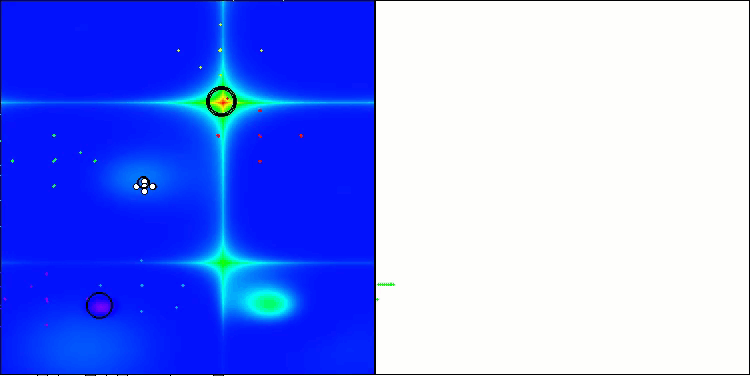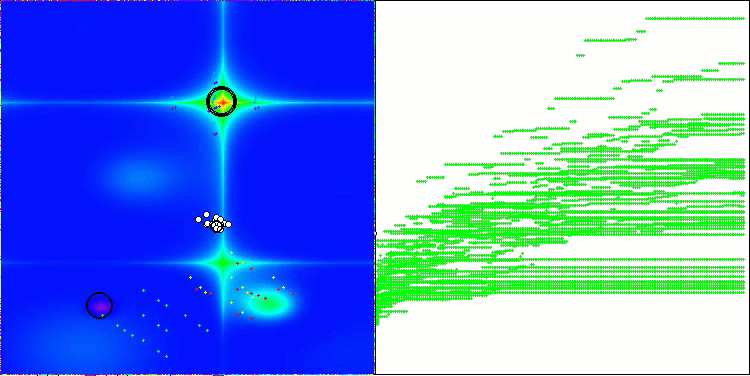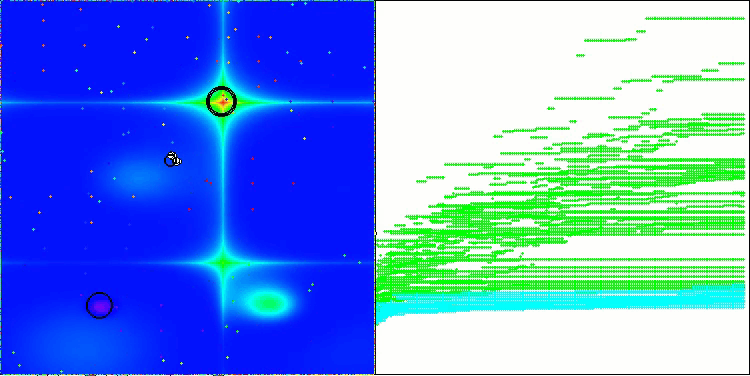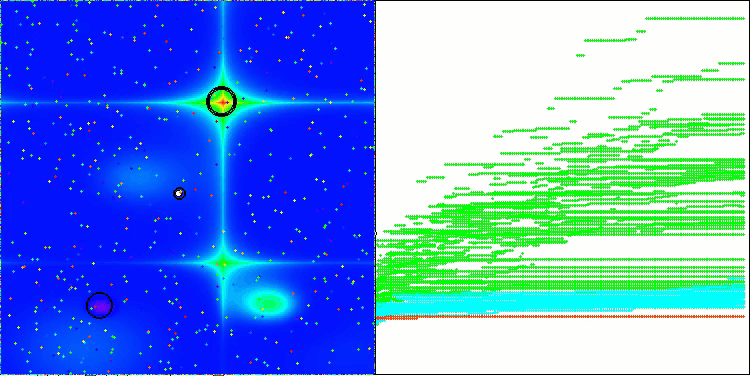
NS на тестовой функции Forest
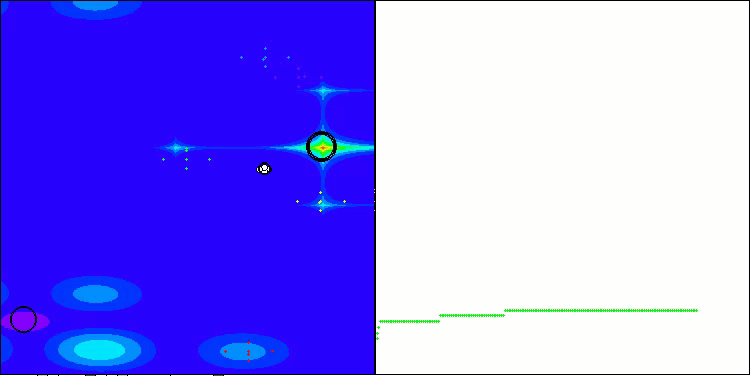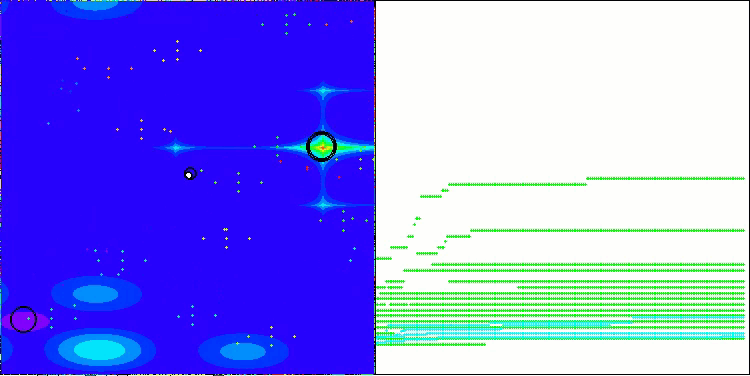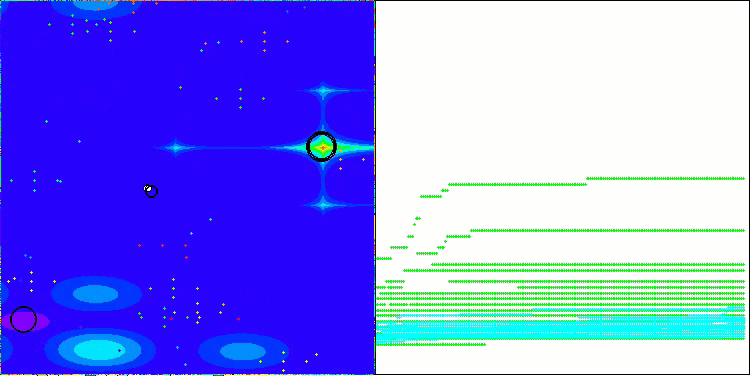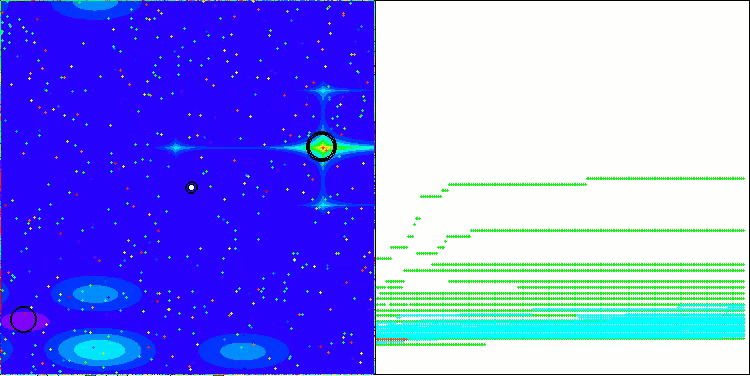
NS на тестовой функции Megacity
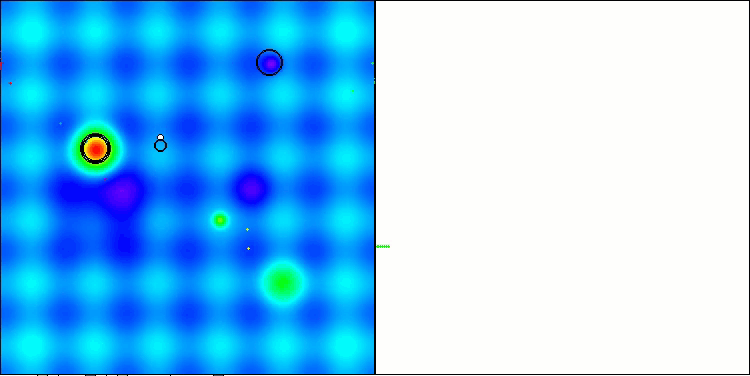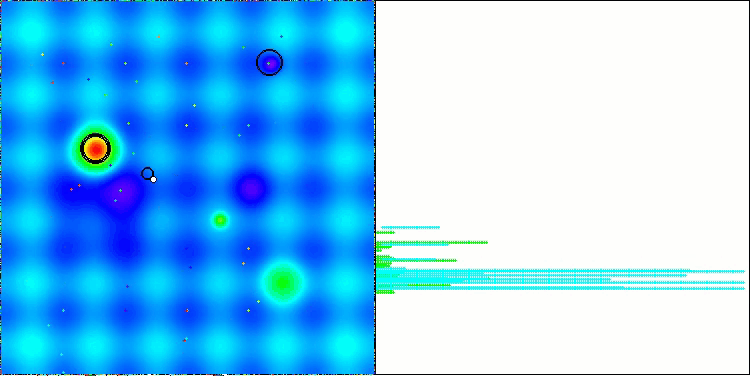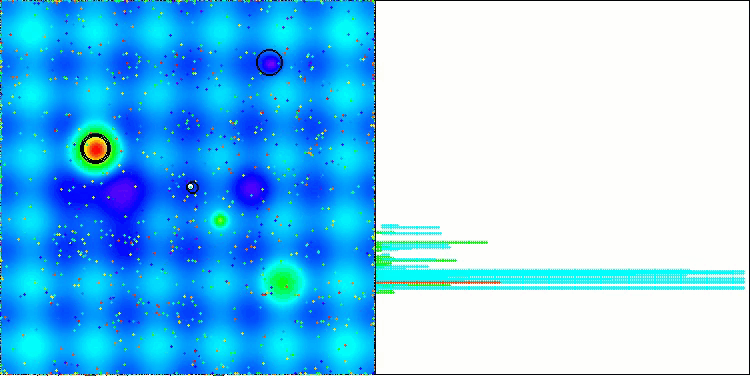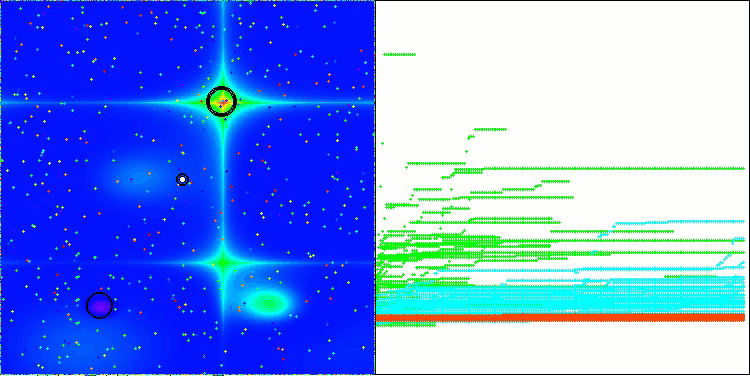
LM на тестовой функции Hilly
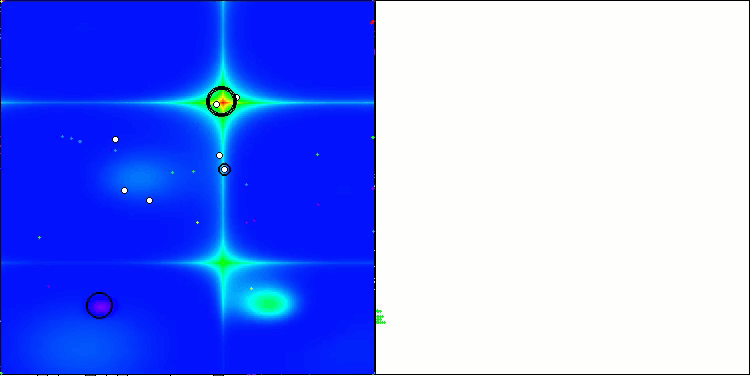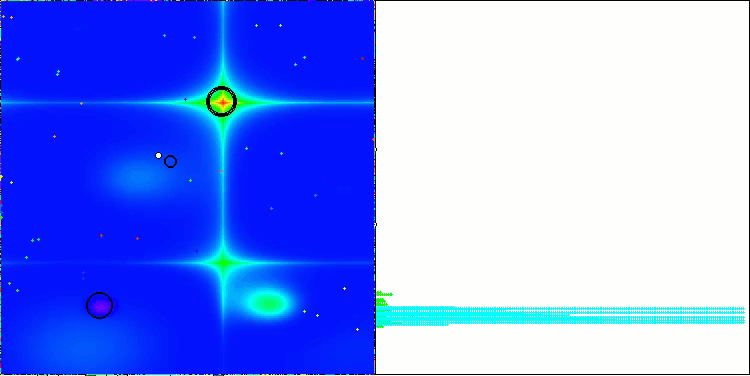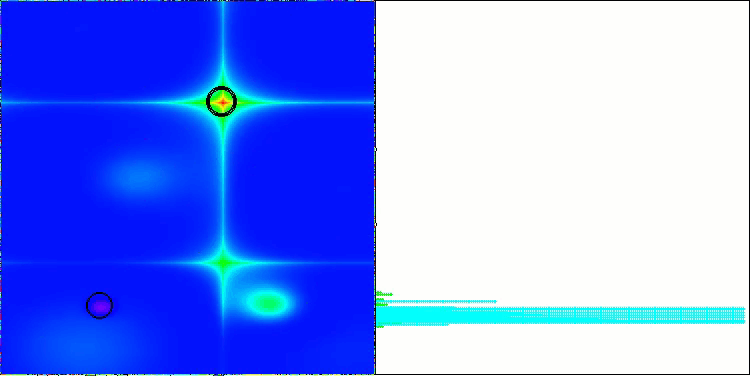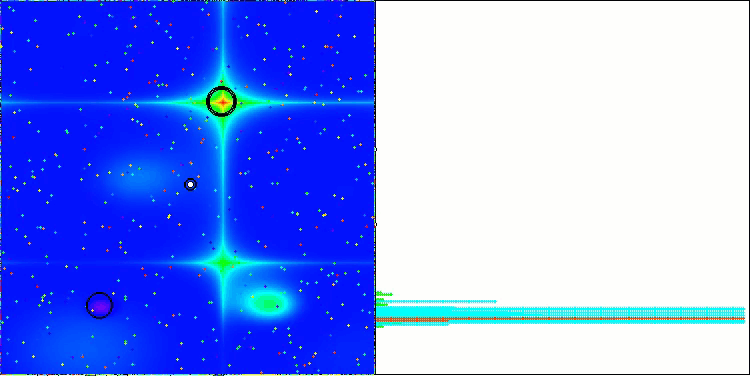
LM на тестовой функции Forest
LM на тестовой функции Megacity
Сведем полученные результаты в таблицу.

Цветовая градация алгоритмов по соответствующим тестам
Выводы
В двух статьях мы рассмотрели методы оптимизации из библиотеки ALGLIB, изучили способы их интеграции в пользовательские программы, а также особенности взаимодействия с функциями этих методов. Кроме того, мы провели тестирование, чтобы выявить сильные и слабые стороны алгоритмов. Кратко подведем итоги:
- На гладких функциях (Hilly) малой размерности наилучшие результаты показал метод NLC, в то время как на больших размерностях лидировал метод LM.
- На гладких функциях с острыми экстремумами (Forest) в малой размерности наилучшие результаты продемонстрировал метод NS, а в большой размерности — метод BC.
- На дискретной задаче "Megacity" в малой размерности лучшим оказался метод NS, в то время как в большой размерности лидировал метод BLEIC.
Различия в результатах работы методов несущественны, отклонения укладываются в разброс их собственных результатов, однако более универсальным можно назвать метод NS, при этом принудительно его остановить не представляется возможным.
Приложенные к статье коды включают все необходимое, чтобы начать использовать методы оптимизации в своих проектах, а также визуально увидеть и оценить их возможности.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Simple test ALGLIB BLEIC.mq5 | Скрипт | Тестовый скрипт для работы с BLEIC |
| 2 | Simple test ALGLIB LBFGS.mq5 | Скрипт | Тестовый скрипт для работы с L-BFGS |
| 3 | Simple test ALGLIB NS.mq5 | Скрипт | Тестовый скрипт для работы с NS |
| 4 | Simple test ALGLIB BC.mq5 | Скрипт | Тестовый скрипт для работы с BC |
| 5 | Simple test ALGLIB NLC.mq5 | Скрипт | Тестовый скрипт для работы с NLC |
| 6 | Simple test ALGLIB LM.mq5 | Скрипт | Тестовый скрипт для работы с LM |
| 7 | Test_minBLEIC.mq5 | Скрипт | Испытательный стенд для BLEIC |
| 8 | Test_minLBFGS.mq5 | Скрипт | Испытательный стенд для L-BFGS |
| 9 | Test_minNS.mq5 | Скрипт | Испытательный стенд для NS |
| 10 | Test_minBC.mq5 | Скрипт | Испытательный стенд для BC |
| 11 | Test_minNLC.mq5 | Скрипт | Испытательный стенд для NLC |
| 12 | Test_minLM.mq5 | Скрипт | Испытательный стенд для LM |
| 13 | CalculationTestResults.mq5 | Скрипт | Скрипт для расчета результатов в сравнительную таблицу |
| 14 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 15 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 16 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
 Возможности SQLite в MQL5: Пример интерактивной панели с торговой статистикой в разрезе символов и магиков
Возможности SQLite в MQL5: Пример интерактивной панели с торговой статистикой в разрезе символов и магиков
 Возможности Мастера MQL5, которые вам нужно знать (Часть 22): Условные генеративно-состязательные сети (cGAN)
Возможности Мастера MQL5, которые вам нужно знать (Часть 22): Условные генеративно-состязательные сети (cGAN)
 Нейросети в трейдинге: Модели направленной диффузии (DDM)
Нейросети в трейдинге: Модели направленной диффузии (DDM)
 Нейросети в трейдинге: Адаптивное представление графов (NAFS)
Нейросети в трейдинге: Адаптивное представление графов (NAFS)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
1. Ещё не факт, что правильно используются оптимизаторы из алглиба.
1. Можно ставить под сомнение всё что угодно, но всегда гораздо конструктивнее разговаривать с позиции полных исходных кодов и правильных воспроизводимых тестов.
2. Оптимальный результат можно получить на двумерном Мегасити если попросить 9 млрд человек случайно тыкнуть пальцем в чистый лист бумаги, за которым скрыта поверхность функции (кто-то из них обязательно окажется очень близко к глобалу и будет говорить, что именно он успешно решил задачу). Но нужно найти оптимальное решение не за 9 млрд попыток методом случайного тыка, а за 10 000 используя стратегию.
Чем выше получится средний результат за серию независимых испытаний (устойчивость, повторяемость результатов), тем выше тестируемый метод находится по сравнению со случайным тыком для конкретного типа задач (для одних задач некоторые методы мало отличимы от случайного тыка, а для других они очень эффективны).
В этом и смысл тестирования и сравнения разных алго, для которых взяты в качестве бенчмарков не просто одна кака-то тестовая функция, а три разных, с разными свойствами, чтобы можно было четко видеть применимость разных алго на различных задачах, их ограничения и возможности на различных задачах. Это позволяет осмысленно подходить к решению задач оптимизации.
В дальнейшем предпочитаю отвечать на конкретные вопросы по содержанию статьи и по кодам.
Берем методы для локальной оптимизации, применяем к задаче глобальной и сравниваем с методами для глобальной. Так что ли.
Я веду разговор о том, как можно адаптировать эти методы для глобальной оптимизации. Самым простым вариантом является увеличение кол-ва инициализаций.
Если я правильно понял, Адам и т.п. заточены на скорость, а не на качество.
Интересно глянуть рейтинг при ограничении по времени, а не количеству итераций.
Если я правильно понял, Адам и т.п. заточены на скорость, а не на качество.
Интересно глянуть рейтинг при ограничении по времени, а не количеству итераций.
Семейство алгоритмов ADAM (AdamW, RAdam, AdaBelief и другие) а так же SGD, SGRAD и прочие (их много) разработаны как современная замена классическим градиентным методам и задуманы для решения задач больших размерностей без знаний аналитической формулы, зачастую для обучения нейронных сетей (все они имеют свои достоинства и недостатки). Так же есть интересные методы Lion от Google (2023) и некоторые другие прям очень свежие. Эта тема очень интересная для изучения, в особенности в контексте обучения нейронных сетей, где будет полезно и познавательно построить на каком нибудь простом примере (а может быть и сложном) поверхность целевой и провести эксперименты (с разбором их внутренностей, с глубоким изучением свойств методов, тщательной оценкой их возможностей - всё как мы любим).
При ограничении по времени не к чему привязываться. У одного пользователя за 1 минуту будет произведено 1 млн обращений к целевой, а у другого 1 млрд. Как сравнивать в таких условиях алго между собой? Поэтому используем лимит по количеству обращений и сравниваем эффективность в рамках этого лимита.
При ограничении по времени не к чему привязываться. У одного пользователя за 1 минуту будет произведено 1 млн обращений к целевой, а у другого 1 млрд. Как сравнивать в таких условиях алго между собой? Поэтому используем лимит по количеству обращений и сравниваем эффективность в рамках этого лимита.
Привязка к ПК автора. Взять за базу время 10000 итераций ANS.
Мои результаты по коду fxsaber'а:
PS объем кода, как дополнительная метрика (на сколько сложна реализация алгоритма)