MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português
preview
Популяционные алгоритмы оптимизации: Алгоритм гравитационного поиска (Gravitational Search Algorithm - GSA)

Популяционные алгоритмы оптимизации: Алгоритм гравитационного поиска (Gravitational Search Algorithm - GSA)

MetaTrader 5 — Примеры | 15 февраля 2023, 16:09
1 583 0
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов


1. Введение

Алгоритм гравитационного поиска (GSA) был предложен Э. Рашеди первоначально для решения задачи оптимизации, особенно для нелинейных задач, следуя принципам закона тяготения Ньютона. В предлагаемом алгоритме частицы рассматриваются как объекты, и их производительность оценивается с учетом их масс. Гравитация – это стремление масс ускоряться друг к другу. Это одно из четырех фундаментальных взаимодействий в природе (остальные: электромагнитное взаимодействие, слабое ядерное взаимодействие и сильное ядерное взаимодействие).

Каждая частица во Вселенной притягивает любую другую частицу. Гравитация существует повсюду.  Хотя это самая слабая сила, она наиболее видима. Из-за работы гравитационной силы люди могут ходить по Земле, а планеты - вращаться по орбите вокруг Солнца. Сила гравитации любого объекта пропорциональна его массе. Таким образом, объекты с большей массой имеют большую гравитацию. Неизбежность гравитации отличает ее от всех других сил природы. То, как ведет себя гравитационная сила Ньютона, называется действием на расстоянии. Это общий физический закон, выведенный из эмпирических наблюдений с помощью того, что Исаак Ньютон назвал индуктивным умозаключением. Это часть классической механики, сформулированная в работе Ньютона "Philosophiae Naturalis Principia Mathematica" ("Начала"), впервые опубликованной 5 июля 1687 г.

Когда в апреле 1686 г. Ньютон представил Королевскому обществу первую книгу неопубликованного текста, Роберт Гук утверждал, что Ньютон получил от него закон обратных квадратов. Говоря сегодняшним языком, закон гласит, что каждая точечная масса притягивает любую другую точечную массу силой, действующей вдоль линии, пересекающей две точки.


2. Описание алгоритма

В данной статье представлен алгоритм оптимизации, основанный на ньютоновском законе гравитации: "Каждая частица во Вселенной притягивает любую другую частицу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними". В предлагаемом алгоритме поисковые агенты представляют собой совокупность масс, которые взаимодействуют друг с другом на основе ньютоновской гравитации и законов движения. При этом все агенты могут обмениваться между собой информацией, где бы они не находились в пространстве поиска, посредством силы притяжения зависящей от массы (рассчитывается из значений целевой функции) и расстояния между ними.

Агенты рассматриваются как объекты, а их приспособленность измеряется их массами. В общем виде (при настройках алгоритма приближенных к реальным физическим законам) все эти объекты притягиваются друг к другу силой гравитации, и эта сила вызывает глобальное движение всех объектов в сторону объектов с большей массой. Следовательно, массы взаимодействуют, используя прямую форму связи, через гравитационную силу.

В классическом GSA каждая частица имеет три вида масс:

a) активная масса
b) пассивная масса
c) инертная масса

В большинстве случаев удобно и целесообразно использовать равенство этих понятий с точки зрения упрощения кодов и расчетов и с точки зрения эффективности поисковых способностей алгоритма, следовательно масса в алгоритме будет одна, а не три. Используемые формулы физических законов в GSA представлены на рисунке 1.


formulas

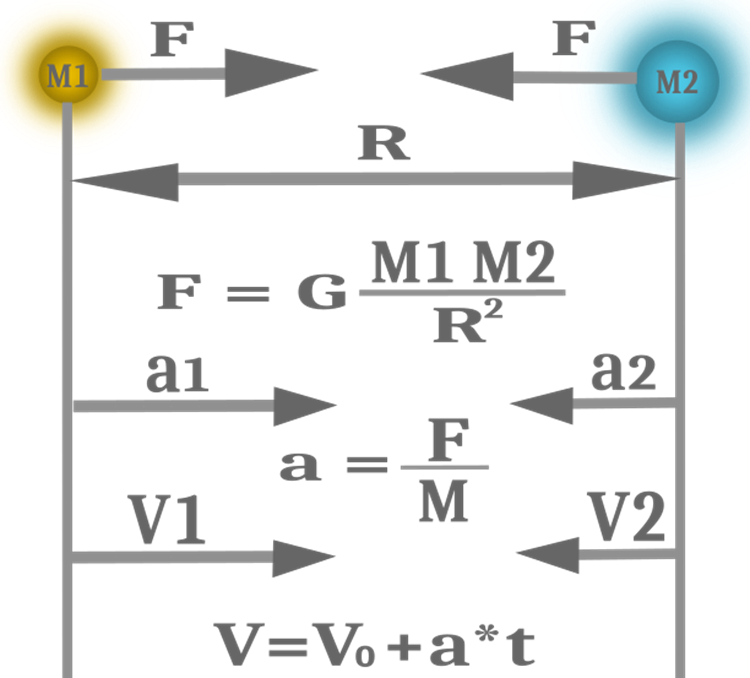
Рисунок 1. Сила гравитации, ускорения и скорости.



Положение частиц обеспечивает решение задачи, в то время как функция пригодности используется для вычисления масс. Алгоритм имеет два этапа: разведку и эксплуатацию. Этот алгоритм использует возможности разведки в начале, чтобы избежать проблемы застревания в локальным оптимуме, и после этого эксплуатирует области экстремумов.

Алгоритм гравитационного поиска должен превратить движущуюся в пространстве частицу в объект с определенной массой. Эти объекты притягиваются за счет гравитационного взаимодействия друг с другом, и каждая частица в пространстве будет притягиваться за счет взаимного притяжения частиц, создавая ускорения. Каждая частица притягивается другими частицами и движется в направлении действия силы. Можно сказать, что частицы с малой массой движутся к частицам с большей массой, но массивные объекты так же движутся, но с меньшей скоростью обратно пропорционально массе, оптимальное решение находят именно "крупные" объекты, которые уточняют решение двигаясь с небольшой скоростью по сравнению с более "мелкими" объектами, которые двигаются более быстро. GSA реализует передачу информации через взаимодействие между объектами.

Шаги для GSA:

1. Инициализация агентов
2. Эволюция фитнеса
3. Вычисление гравитационной постоянной
4. Расчет масс агентов


1. Инициализация агентов.
Все агенты инициализируются случайным образом. Каждый агент рассматривается как решение-кандидат. Для того чтобы анализ устойчивости был осмысленным и надежным, чрезвычайно важно указать равновесные начальные условия. В конце концов, если исходный "диск" объектов не находится в равновесии, его релаксация на первых временных шагах симуляции может вызвать нестабильности, которые мало важны для нашего понимания устойчивости "дисковых галактик". К сожалению, неизвестно аналитического решения для плотности, поля скоростей и температуры трехмерного газового диска, находящегося в гидростатическом равновесии во внешнем потенциале гало темной материи и/или звездного диска.

2. Эволюция фитнеса.
Надежность и эффективность GSA зависят от баланса между возможностями исследования и эксплуатации. В начальных итерациях процесса поиска решения предпочтение отдается исследованию пространства поиска. Этого можно добиться, позволив агентам использовать большой размер шага на ранних итерациях. В более поздних итерациях требуется уточнение пространства поиска, чтобы избежать ситуации пропуска глобальных оптимумов. Таким образом, решения-кандидаты должны иметь небольшие размеры шага для использования в последующих итерациях.

3. Вычисление гравитационной постоянной.
Гравитационная постоянная (также известная как "универсальная гравитационная постоянная", "ньютоновская постоянная тяготения" или "гравитационная постоянная Кавендиша"), обозначаемая буквой G, представляет собой эмпирическую физическую постоянную, участвующую в вычислении гравитационных эффектов в законе всемирного тяготения Исаака Ньютона и в общей теории относительности Альберта Эйнштейна. В законе Ньютона это константа пропорциональности, связывающая гравитационную силу между двумя телами с произведением их масс на обратный квадрат их расстояния. В уравнениях поля Эйнштейна количественно определяется связь между геометрией пространства-времени и тензором энергии-импульса.

4. Расчет масс агентов.
Масса – это количество вещества, присутствующего в пространстве.

Псевдокод алгоритма:

1. генерация системы объектов случайным образом.
2. определение приспособленности каждого объекта.
3. обновление значений гравитационной постоянной, расчет масс, лучшего и худшего объекта.
4. расчет сил, действующих по каждой координате.
5. расчет ускорений и скоростей объектов.
6. обновление позиций объектов.
7. определение приспособленности каждого объекта.
8. повторений с п.3 до выполнения критерия останова.

Рассмотрим код GSA. Для описания объекта в системе гравитационного взаимодействия нам понадобится структура S_Object, которая опишет все необходимые физические свойства объекта, достаточные для осуществления гравитационного поиска: с [] - координаты в пространстве поиска, v [] - вектор скоростей по каждой из координат (размерность массива - количество координат), M - масса объекта (в GSA масса - это относительная величина, которая представляет собой расчетное значение в зависимости от значения максимального и минимального фитнеса по всей системе объектов), f - значение фитнеса, R [] - евклидово расстояние до других объектов (размерность массива - количество объектов), F [] - вектор сил по каждой из координат (размерность массива - количество координат). 

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс алгоритма гравитационного поиска C_AO_GSA. Из физических свойств объектов, участвующих в алгоритме в качестве агентов, необходимо только одно: координаты, представляющие собой лучшее решение - значение fB. В классе объявлены допустимые диапазоны координат пространства поиска и шаг. Система гравитационно связанных объектов представим в виде массива структур S_Object. В классическом алгоритме только три внешних параметра: G_constant, a_constant, e_constant, определяющие свойства гравитационного взаимодействия объектов, а остальные константы заложены в формулы вычислений, но я счел целесообразным вынести эти константы во внешние параметры алгоритма, что позволяет более гибко регулировать свойства алгоритма в целом. Немного позднее рассмотрим все параметры подробнее, потому как они сильно влияют на поведение алгоритма. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Публичный метод алгоритма Init () предназначен для передачи внешних параметров алгоритма во внутренние константы, для инициализации сервисных переменных и назначение размеров массивам.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Первый публичный метод, вызываемый на каждой итерации Moving (). В этом методе заложена вся физика и логика алгоритма GSA, он достаточно большой поэтому рассмотрим его, разбив на части. Заметим, что метод принимает в качестве параметра текущую итерацию, параметр участвует в расчете гравитационной постоянной, регулируя баланс между исследованием и эксплуатацией.

На первой итерации происходит этап инициализации объектов. По всем координатам объектов назначаем случайные значения в допустимом диапазоне с равномерным распределением, проверяем на выход за диапазон. В начале процесса оптимизации все объекты имеют нулевую скорость, то есть объекты неподвижны в пространстве поиска относительно координат. Обратим внимание на то, что объекты не имеют массы, поэтому они должны были бы двигаться со скоростью света, но мы нарушим законы физики для первой итерации, ведь этот момент в какой-то степени эквивалентен Большому Взрыву. Приспособленность объектов в этот момент наименьшая из возможных значений числа double. При отладке алгоритма были трудности с поиском багов, связанных с нулевой массой, решение вы сможете увидеть ниже.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Остальной код метода Moving () относится ко второй и последующим итерациям, где объекты обретут массу, скорость и ускорение.

В первую очередь необходимо рассчитать массу, а поскольку, как говорилось выше, масса (по определению своему положительная скалярная величина) объектов рассчитывается из значений фитнесс - функции, то необходимо определить минимальное и максимальное значение приспособленности, и уже потом исходя из этих значений рассчитывать массу. К этому моменту на предыдущей итерации уже было получено значение фитнесс - функции.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

В этом месте кода расчитывается масса по формуле Mo=(Fo-Fmin)/(Fmax-Fmin), где:

  • Mo - масса объекта
  • Fo - фитнес объекта
  • Fmax - маскимальное значение фитнес среди всех объектов (лучшее значение)
  • Fmin - минимальное значение фитнес среди всех объектов (худшее значение)

Как видим из формулы масса может принимать только положительные значения в диапазоне от 0 до 1 включительно. Так как ранее мы обсуждали, что масса не должна быть равна нулю иначе скорость приравняется к скорости света, то ограничим нижнюю границу массы значением 0,1. Верхнее же значение вполне может быть равным 1. Стоит тут же отметить, что при равенстве минимального и максимального значения фитнесс - функции у всех объектов масса будет одинакова для всех и равна 1. Это соответствует случаю, когда пространство поиска однородно на участке, где расположены объекты и все объекты равноправны по качеству фитнесс - функции, а так же движение в любом направлении имеет равный приоритет. Казалось бы, в этом случае все объекты должны постепенно переместиться и сконцентрироваться к общему центру масс, но этого не происходит из-за нелинейного действия гравитационной силы.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Массу для объектов мы рассчитали, теперь необходимо рассчитать еще один компонент формулы R - евклидово расстояние от каждого объекта до каждого. Расчет заключается в двух циклах перебора объектов и цикла расчета по каждой из координат. Как мы помним, евклидово расстояние это корень из суммы квадратов разниц координат.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Теперь можем рассчитать векторы сил для объектов. Для этого понадобиться также перебрать все объекты в двух циклах и одном цикле для координат, поскольку по каждой координате скорость рассчитывается отдельно. Необходимо добавить условие, исключающее совпадение индексов объектов, чтобы объект исключил расчет самого себя в расчете сил. Здесь мы используем известную формулу Ньютона для расчета силы гравитации для двух объектов (рисунок 1) с поправкой расстояния на коэффициент e_constant. Предварительно произведем расчет гравитационной постоянной G, который должен изменяться на каждой итерации в сторону уменьшения предполагая усиливать интенсификацию алгоритма к окончанию оптимизации.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Для того, чтобы объекты начали двигаться осталось рассчитать скорость. Из формулы на рисунке 1 видно, что в расчете скорости участвует ускорение, а ускорение равно силе, действующей на тело деленное на массу. В формуле присутствует так же время V=V0+a*t,  В нашем алгоритме роль времени выполняет итерация, таким образом изменение скорости есть не что иное как приращение скорости за одну итерацию. Вектор скоростей уже рассчитан выше, осталось поделить на массу, дополнительно авторы вводят возмущение силы и возмущение скорости. Возмущение представляет собой равномерно распределенное случайное число от 0 до 1. Это добавляет случайную компоненту в движение объектов, без которой, движение было бы строго детерминировано и зависело бы только от первоначального положения тел. Я посчитал разумным вывести показатели возмущения во внешние параметры алгоритма, что позволит регулировать движение объектов от полностью детерминированного до полностью случайного.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Второй обязательный для исполнения на каждой итерации метод Revision (). Метод предназначен для определения лучшего значения фитнесс на текущей итерации. В цикле переберем все объекты и заменим глобальное лучшее решение. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. Результаты тестов

Переходим к результатам тестирования. Распечатка результатов тестового стенда с лучшими параметрами GSA, которые мне удалось найти:

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD,M1)    Score: 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD,M1)    Score: 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    Score: 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score: 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD,M1)    Score: 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    Score: 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD,M1)    Score: 0.44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD,M1)    Score: 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD,M1)    Score: 0.01950

Параметры алгоритма:

input double PowerOfdistance_P  = 2.0;   //Power of distance
input double GraviPert_Min_P    = 0.2;   //Gravitational perturbation Min
input double GraviPert_Max_P    = 0.6;   //Gravitational perturbation Max
input double VelocityPert_Min_P = 0.0;   //Velocity perturbation Min
input double VelocityPert_Max_P = 1.0;   //Velocity perturbation Max
input double G_constant_P       = 2.0;   //G constant
input double a_constant_P       = 20.0;  //a constant
input double e_constant_P       = 0.01;  //e constant

PowerOfdistance_P - показатель степени, в которую возводим расстояние между объектами, влияет на образование гравитационно связанных объектов. чем выше степень в формуле, тем меньшее влияние объекты оказывают на другие объекты.

  • GraviPert_Min_P - нижняя граница диапазона гравитационного возмущения.
  • GraviPert_Max_P - верхняя граница диапазона гравитационного возмущения.
  • При GraviPert_Min_P = 1.0 и GraviPert_Max_P = 1.0 отсутствует гравитационное возмущение.
  • VelocityPert_Min_P - нижняя граница диапазона возмущения скорости.
  • VelocityPert_Max_P - верхняя граница диапазона возмущения скорости.

При VelocityPert_Min_P = 1.0 и VelocityPert_Max_P = 1.0 отсутствует возмущение скорости.

  • G_constant_P - гравитационная постоянная, выполняет роль масштабного коэффициента, чем выше значение тем сильнее действуют силы гравитации и тем быстрее изменяется скорость объектов.
  • a_constant_P - поправочный коэффициент на гравитационную постоянную, предназначен для уменьшения поля поиска в течение всей оптимизации с целью уточнения найденных экстремумов.
  • e_constant_P - поправочный коэффициент на расстояние между объектами.

Обратим внимание на результаты тестирование на визуализации. Поведение алгоритма на тестовых функциях очень своеобразно и интересно. По сути, эксперимент отображает работу сил гравитации визуально. На перемещение объектов сильно влияют внешние параметры алгоритма, как и на получаемые результаты оптимизации. Первоначально, объекты, имеющие нулевую скорость распределены по пространству поиска случайным образом и уже на следующей итерации приходят в движение. Данные настройки, которые применялись в тестировании (лучшие из найденных мной), заставляют объекты перемещаться в сторону общего центра масс.

Не забываем, что каждый объект своей гравитацией действует на остальные объекты, законы движения которых описаны с достаточно высокой точностью в алгоритме. Приблизившись к общему центру масс объекты продолжают движение набрав уже высокую скорость, выглядит это как пульсирующие движение массы частиц к общему центру масс и от центра обратно. Через некоторое количество итераций движение объектов изменяет свою траекторию под воздействием рельефа пространства фитнес функции, которая выступает гравитационной неоднородностью, влияя на массу объектов. Как мы обсуждали ранее, масса объектов рассчитывается из значения фитнес функции. Хотя симметричная по осям функция Растригина достаточно однородно оказывает влияние на движение объектов и распад на группы особо не заметен.

Rastr

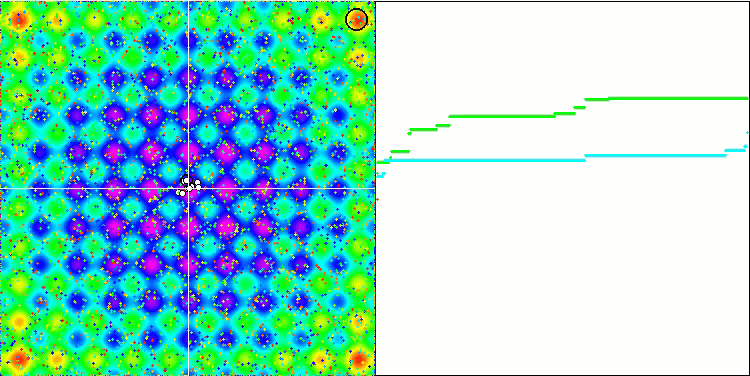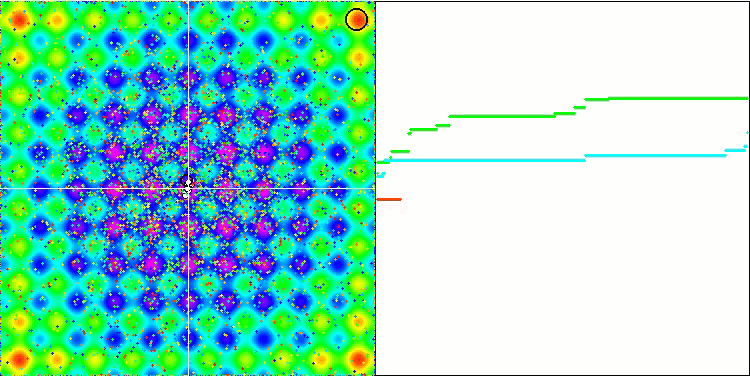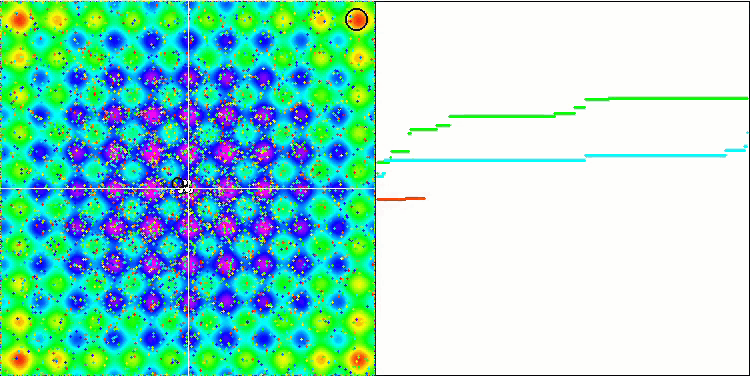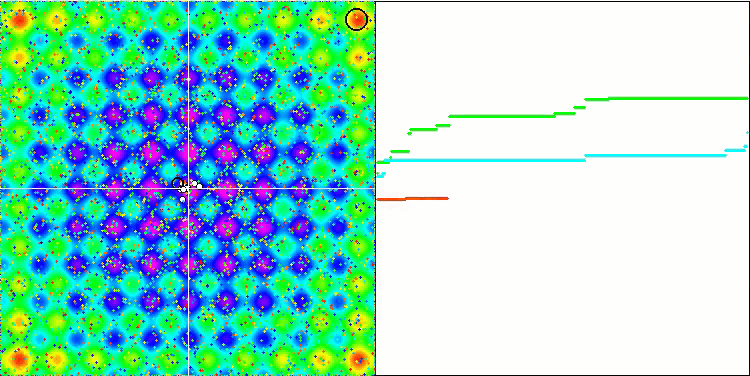
  GSA на тестовой функции Rastrigin.

Ещё более интересное поведение объекты показывают на функциях Forest и Megacity. Эти функции несимметричны и потому оказывают неоднородное воздействие на всю группу объектов.

Forest

  GSA на тестовой функции Forest.

Megacity

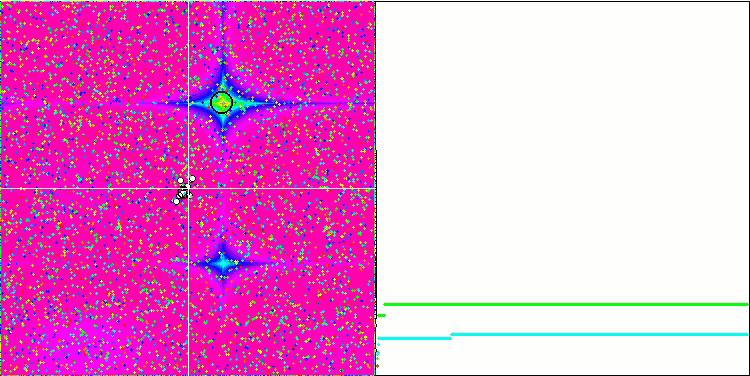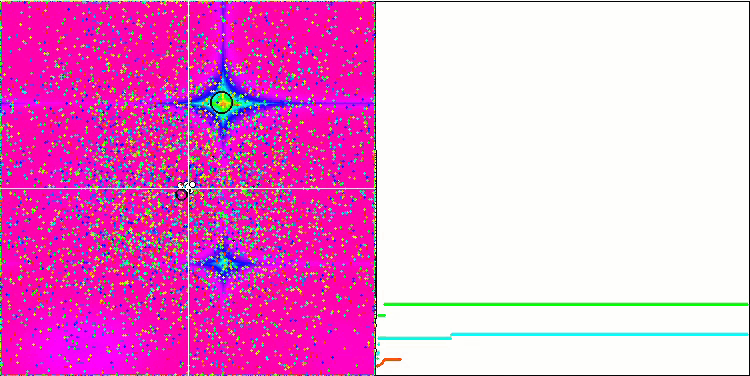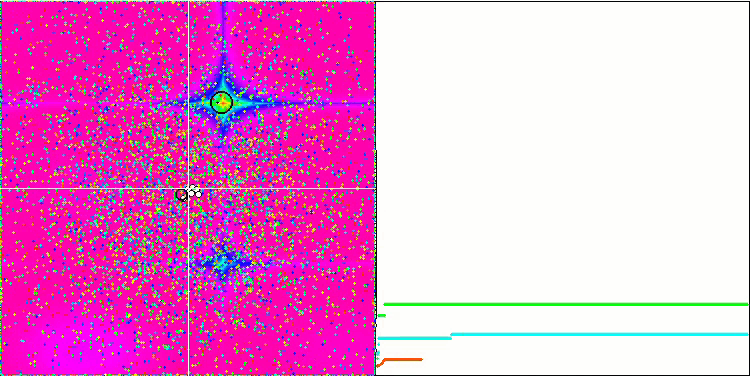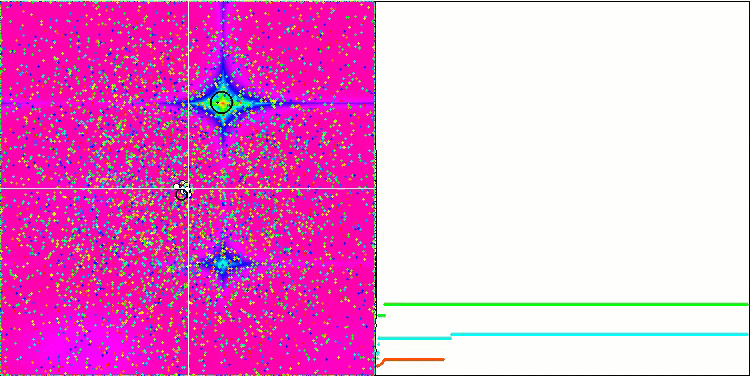
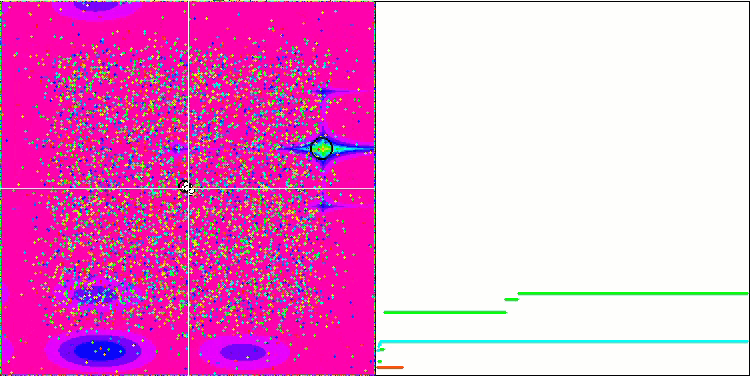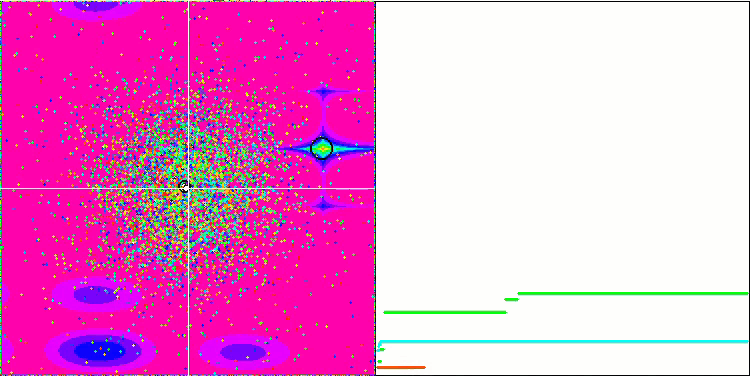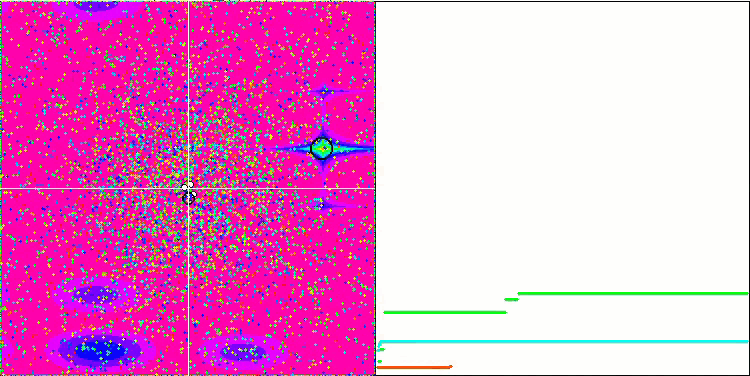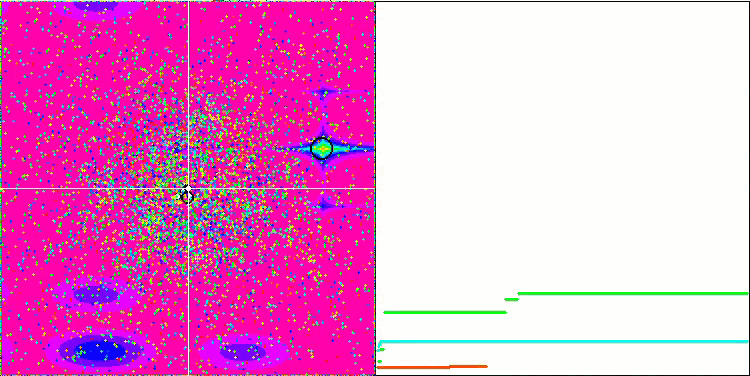
GSA на тестовой функции Megacity.

После продолжительных экспериментов с GSA мне пришла в голову идея сделать симулятор движения космических объектов. Практической ценности он не имеет, но дает представление о физических законах, действующих на планетарные  и звездные системы. Симулятор представляет собой версию GSA с отключенными факторами случайности. Дополнительно введены три объекта имитирующие три звезды, голубой гигант, желтая звезда и белый карлик, для них отдельно в настройках выведены параметры массы.

Специально для симулятора создана новая фитнес функция Universe, с однородным пространством. Симулятор наглядно показывает каким образом степень (параметр) расстояния между объектами влияет на их взаимное движение. Так на визуализации ниже применена степень 3, вместо стандартного значения ньютоновского закона 2. Становится понятно, каким образом степень влияет на формирование гравитационно связанных систем, таких как парные и тройные звездные системы.

Если бы в нашей вселенной степень расстояния была бы выше, то галактики образовались бы гораздо раньше, чем в реальности. На анимации мы видим, что уже на самых первых итерациях возникли парные объекты, обращающиеся вокруг общего центра масс. Как следовало ожидать, голубой гигант на визуализации собрал больше всего объектов вокруг себя.

Uni1

Визуализация работы симулятора движения космических объектов на базе алгоритма GSA.


Переходим к анализу результатов тестирования GSA. Оригинальные приемы, используемые в алгоритме, не позволили ему добиться серьезных результатов в нашем тестировании. Многочисленные вариации параметров, перепробованные мной, не позволили улучшить сходимость алгоритма. Некоторые положительные результаты по отношению к другим участникам тестирования алгоритм показал на гладкой функции Растригина с 10 переменными и Megacity. В остальных тестах GSA демонстрирует результаты ниже средних по таблице, GSA занимает 8 место из 12.

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

IWO

invasive weed optimization

1,00000

1,00000

0,35295

2,35295

0,79937

0,46349

0,41071

1,67357

0,75912

0,44903

0,94416

2,15231

100,000

ACOm

ant colony optimization M

0,36118

0,26810

0,20182

0,83110

1,00000

1,00000

1,00000

3,00000

1,00000

1,00000

0,15901

2,15901

96,805

COAm

cuckoo optimization algorithm M

0,96423

0,69756

0,30792

1,96971

0,64504

0,34034

0,21362

1,19900

0,67153

0,34273

0,48451

1,49877

74,417

FAm

firefly algorithm M

0,62430

0,50653

0,20290

1,33373

0,55408

0,42299

0,64360

1,62067

0,21167

0,28416

1,00000

1,49583

70,740

BA

bat algorithm

0,42290

0,95047

1,00000

2,37337

0,17768

0,17477

0,33595

0,68840

0,15329

0,07158

0,49268

0,71755

59,383

ABC

artificial bee colony

0,81573

0,48767

0,24656

1,54996

0,58850

0,21455

0,17249

0,97554

0,47444

0,26681

0,39496

1,13621

57,393

BFO

bacterial foraging optimization

0,70129

0,46155

0,13988

1,30272

0,41251

0,26623

0,26695

0,94569

0,42336

0,34491

0,53694

1,30521

55,563

GSA

gravitational search algorithm

0,73222

0,67404

0,00000

1,40626

0,31238

0,36416

0,42921

1,10575

0,51095

0,36658

0,00000

0,87753

52,786

FSS

fish school search

0,48850

0,37769

0,13383

1,00002

0,78060

0,05013

0,08423

0,91496

0,00000

0,01084

0,23493

0,24577

20,094

PSO

particle swarm optimisation

0,21339

0,12224

0,08478

0,42041

0,15345

0,10486

0,28099

0,53930

0,08028

0,02385

0,05550

0,15963

14,358

RND

random

0,17559

0,14524

0,09495

0,41578

0,08623

0,04810

0,06094

0,19527

0,00000

0,00000

0,13960

0,13960

8,117

GWO

grey wolf optimizer

0,00000

0,00000

0,02672

0,02672

0,00000

0,00000

0,00000

0,00000

0,18977

0,04119

0,07252

0,30348

1,000


В целом алгоритм GSA заметно чувствителен к наличию градиента в оптимизируемой функции, а низкая масштабируемость не позволяет использовать его для серьезных задач содержащих множество переменных, поэтому я бы не стал рекомендовать алгоритм для применения с нейронными сетями и для оптимизации торговых систем. Нужно отметить, что возможности алгоритма гравитационного поиска, как я считаю, полностью мной не изучены, и дополнительные исследования пользователями возможно откроют новые неизвестные положительные грани этого очень интересного и необычного со всех точек зрения алгоритма. К основным достоинствам алгоритма можно отнести независимость от текущего лучшего найденного глобального решения и способность всех агентов взаимодействовать между собой. 

Гистограмма результатов тестирования алгоритмов на рисунке 2.

chart

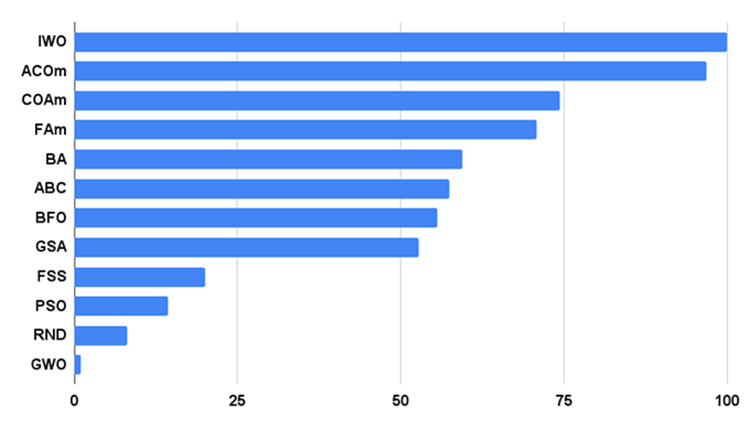
Рисунок 2. Гистограмма итоговых результатов тестирования алгоритмов.


Выводы по свойствам алгоритма оптимизации гравитационного поиска (GSA):

Плюсы:
1. Простота реализации.
2. Неплохая производительность на гладких функциях с небольшим количеством переменных.

Минусы:
1. Высокая вычислительная трудоёмкость.
2. Невысокие результаты на дискретных функциях.
3. Плохая масштабируемость.


Прикрепленные файлы |
Загрузить ZIP
12_The_world_of_AO_GSA.ZIP (100.62 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Алан Эндрюс и его приемы анализа временных рядов Алан Эндрюс и его приемы анализа временных рядов
Алан Эндрюс — один из известнейших "просветителей" современного мира в области трейдинга. Его "вилы" включены практически во все современные программы анализа котировок. Но большинство трейдеров не используют и пятой части тех возможностей, что заложены в этом инструменте. А оригинальный курс Эндрюса включает описание не только вил (хотя они всё же главные), но и некоторых других полезных прямых. Эта статья даёт представление о тех изумительных техниках анализа графиков, которым учил Эндрюс в своем оригинальном курсе. Осторожно, много картинок.
Пример создания комплекcной торговой стратегии Owl Пример создания комплекcной торговой стратегии Owl
Моя стратегия базируется на классических основах трейдинга и доработке индикаторов, широко применяемых на всех видах рынков. Фактически — это уже готовый инструмент, используя который, можно во всей полноте работать по предлагаемой новой прибыльной торговой стратегии.
Как построить советник, работающий автоматически (Часть 06): Виды счетов (I) Как построить советник, работающий автоматически (Часть 06): Виды счетов (I)
Сегодня мы рассмотрим, как создать советник, который просто и безопасно работает в автоматическом режиме. Пока наш советник может работать в любой ситуации, но он ещё не готов к автоматизации, поэтому нам нужно проработать несколько моментов.
Тестирование и оптимизация стратегий для бинарных опционов в MetaTrader 5 Тестирование и оптимизация стратегий для бинарных опционов в MetaTrader 5
Проверяем и оптимизируем стратегии для бинарных опционов в MetaTrader 5.