Базовый класс популяционных алгоритмов как основа эффективной оптимизации

Содержание:

1. Введение. Перспективы и возможности при наследовании от базового класса популяционных алгоритмов
2. Пишем базовый класс популяционных алгоритмов
3. Код алгоритмов - наследников
4. Код единого тестового стенда для всех алгоритмов
5. Добавим популярные известные тестовые функции
6. Построение тестовых функций 3D
7. Выводы

1. Введение. Перспективы и возможности при наследовании от базового класса популяционных алгоритмов

В мире современных вычислений и искусственного интеллекта базовый класс, спроектированный для интеграции алгоритмов оптимизации в конечные программные решения, представляет собой ключевой элемент, открывающий перед разработчиками бесконечные горизонты технических возможностей. Наследование от данного базового класса в контексте популяционных алгоритмов не только обеспечивает удобство и эффективность разработки новых методов оптимизации, но и расширяет перспективы создания гибридных алгоритмов, способных адаптироваться к самым разнообразным задачам.

Объединение алгоритмов оптимизации в рамках базового класса открывает двери для создания инновационных решений, объединяющих в себе лучшие характеристики различных методов. Гибридные алгоритмы, зародившиеся благодаря этому подходу, способны эффективно преодолевать ограничения отдельных методов и достигать новых высот в решении сложных задач оптимизации.

Кроме того, базовый класс для популяционных алгоритмов обеспечивает простоту использования и тестирования разработанных алгоритмов на стандартных наборах тестовых функций. Это позволяет исследователям и разработчикам быстро оценить эффективность новых методов оптимизации, сравнивая их производительность с уже существующими решениями.

Давайте представим себе, что мир оптимизации и поиска решений - это как удивительный кулинарный мир, где каждый метод оптимизации — это уникальный ингредиент, придающий свой неповторимый вкус блюду. Гибридизация в этом контексте — это как искусное сочетание разнообразных ингредиентов для создания новых, более вкусных и интересных блюд.

У вас есть широкий ассортимент различных методов оптимизации - генетические алгоритмы, эволюционные стратегии, муравьиные алгоритмы, оптимизация роя частиц и многие другие. Каждый из них обладает своими сильными сторонами и способностями, но также имеет свои ограничения.

Вот где на помощь приходит гибридизация! Вы можете взять лучшее из каждого метода, сочетая их в уникальные комбинации, как опытный шеф-повар. Таким образом, гибридные методы оптимизации могут объединить сильные стороны различных подходов, компенсируя их слабости и создавая более эффективные и мощные инструменты для поиска оптимальных решений.

Представьте, что сочетание генетического алгоритма с локальным поиском — это как идеальное сочетание пряного перца и сладкого меда в блюде, придающее ему глубокий и насыщенный вкус. Точно так же, гибридизация популяционных алгоритмов позволяет создавать инновационные методы, способные быстрее и точнее находить оптимальные решения в различных областях, будь то инженерные задачи, финансовая аналитика или искусственный интеллект.

Таким образом, гибридизация в оптимизации — это не просто смешивание методов, это искусство создания новых подходов, способных раскрыть потенциал каждого метода в максимальной степени и достичь выдающихся результатов. В итоге благодаря гибридизации мы можем создавать более эффективные, инновационные и мощные методы оптимизации, способные решать самые сложные задачи и приводить к новым открытиям и достижениям в различных областях.

Более того, унифицированный базовый класс позволяет интегрировать в пользовательские решения отдельные элементы каждого из алгоритмов для использования в проектировании новых, уникальных и мощных оптимизационных методов.

2. Пишем базовый класс популяционных алгоритмов

В контексте статьи о наследовании от базового класса для популяционных алгоритмов и создании гибридных методов оптимизации, можно рассмотреть в качестве примеров несколько интересных комбинаций:

• Генетический алгоритм с усиленным локальным поиском. В данной комбинации генетический алгоритм используется для глобального поиска оптимального решения, а локальный поиск применяется для уточнения найденного решения в окрестности. Это позволяет совместить преимущества глобального и локального поиска, повышая точность и скорость сходимости алгоритма.

• Эволюционная стратегия с муравьиным алгоритмом. Здесь эволюционная стратегия может использоваться для изменения параметров модели, а муравьиный алгоритм - для поиска оптимального пути в пространстве параметров. Такая комбинация может быть эффективной для оптимизации сложных задач, где требуется нахождение оптимальной комбинации параметров.

• Частицы роя с генетическим программированием. В данной комбинации частицы роя могут использоваться для исследования пространства решений, а генетическое программирование - для эволюции программных структур, решающих задачу оптимизации. Это позволяет эффективно исследовать как пространство параметров, так и структуры решений.

• Поиск симулированным отжигом с генетическим алгоритмом. Здесь симулированный отжиг может использоваться для исследования пространства решений с учетом температурного режима, а генетический алгоритм - для поиска оптимальных решений в заданном пространстве. Такая комбинация может обеспечить более глубокое исследование пространства решений и улучшить сходимость алгоритма.

Так же можно рассмотреть в качестве примера следующие направления в использовании возможностей объединённых в единый базовый класс популяционных алгоритмов:

• Метод комбинированного метаэвристического подхода. В этом методе можно объединить несколько различных метаэвристических алгоритмов, таких как генетические алгоритмы, муравьиные алгоритмы, алгоритмы оптимизации роя частиц, симулированный отжиг и т.д. Эти алгоритмы могут работать параллельно или последовательно, обмениваясь информацией и комбинируя свои сильные стороны для более эффективного поиска оптимального решения.

• Гибридный метод с адаптивным управлением стратегиями поиска. В этом подходе можно использовать механизмы адаптивного управления, чтобы динамически комбинировать различные стратегии оптимизации в зависимости от характеристик проблемы. Например, можно изменять веса или параметры каждого метода в зависимости от эффективности их работы на текущем этапе оптимизации.

• Гибридный метод с искусственными нейронными сетями. В данном подходе можно использовать искусственные нейронные сети для адаптивного управления параметрами и стратегиями оптимизации популяционных алгоритмов. Нейронные сети могут обучаться на лету, адаптируясь к изменениям в пространстве поиска, и предлагать оптимальные параметры для каждого метода оптимизации.

• Метод совместной оптимизации и обучения с подкреплением. В этом подходе можно объединить популяционные алгоритмы с методами обучения с подкреплением для создания гибридной системы, способной эффективно исследовать и оптимизировать сложные пространства решений. Агенты обучения с подкреплением могут учиться на основе результатов популяционных алгоритмов и наоборот, создавая взаимодействие между различными методами оптимизации.

Различное количество внешних параметров в каждом алгоритме оптимизации может создавать проблемы при наследовании и унифицированном применении. Для решения этой проблемы было принято решение прописывать внешние параметры алгоритмов по умолчанию в конструкторе, основываясь на результатах обширных тестирований. При этом сохраняется возможность изменения этих параметров перед инициализацией алгоритмов. Таким образом, объект каждого алгоритма будет представлять собой окончательное решение готовое к использованию. Ранее алгоритмы и их параметры представляли собой отдельные сущности.

Итак, начнём с параметров алгоритмов. Каждый параметр удобно описать структурой "S_AlgoParam", которая содержит имя и значение параметра. Соответственно, массив объектов этой структуры будет представлять набор внешних параметров алгоритмов.

struct S_AlgoParam
{
    double val;
    string name;
};

В каждом алгоритме оптимизации имеется поисковый агент — это элементарная единица и непременный участник поисковой стратегии, будь то нежное создание - светлячок в светлячковом алгоритме, или усердная пчела в пчелином, трудолюбивый муравей в муравьином и т.д. Они — неповторимые художники в лабиринте оптимизации, раскрывающие великолепие искусства поиска и открытия оптимальных путей к успеху. Их усилия и стремления, как магия, преображают хаос данных в гармонию решений, освещая путь к новым горизонтам идеальной оптимизации.

Ммм, о чем это я... ах да, про агентов оптимизации. :)

Таким образом, каждый агент представляет конкретное решение задачи оптимизации и имеет два обязательных минимально необходимых свойства: координаты в пространстве поиска (оптимизируемые параметры) и качество решения (приспособленность или фитнес-функция). Для возможности расширения функциональности и возможностей и реализации специфических свойств алгоритмов, оформим агента в виде класса "C_AO_Agent", который впоследствии сможем наследовать.

class C_AO_Agent
{
  public:
  ~C_AO_Agent () { }

  double c []; //coordinates
  double f;    //fitness
};

Большинство логических операций в алгоритмах оптимизации повторяются и могут быть оформлены обособленно в виде набора функций класса "C_AO_Utilities", объект которого в свою очередь может быть использован как в классах алгоритмов, так и в агентах.

Класс "C_AO_Utilities" содержит следующие методы:

• Scale: Перегруженный метод, который выполняет масштабирование входного значения "In" из диапазона [InMIN, InMAX] в диапазон [OutMIN, OutMAX]. Возможно также выполнение обратного масштабирования, если параметр "revers" установлен в "true".
• RNDfromCI: Генерирует случайное вещественное число в пределах заданного диапазона [min, max].
• RNDintInRange: Генерирует случайное целое число в пределах заданного диапазона [min, max].
• RNDbool: Генерирует случайное логическое значение (true/false).
• RNDprobab: Генерирует случайную вероятность (вещественное число от 0 до 1).
• SeInDiSp: Рассчитывает значение с учетом заданного шага "Step" внутри диапазона [InMin, InMax].
• Методы "DecimalToGray", "IntegerToBinary", "GrayToDecimal", "BinaryToInteger", "GetMaxDecimalFromGray": Выполняют преобразования между десятичными числами, двоичными числами и кодами Грея.
• Методы "GaussDistribution" и "PowerDistribution": Выполняют вычисления для нормального распределения и степенного распределения соответственно.
• Метод "Sorting" (шаблонный метод): Сортирует массив "p" типа "T" в порядке убывания.
• Структура "S_Roulette": Содержит поля "start" и "end" для представления диапазона.
• Методы "PreCalcRoulette" и "SpinRoulette": "PreCalcRoulette" вычисляет диапазоны для объектов типа "T" и сохраняет их в массиве "roulette". "SpinRoulette" выполняет операцию "кручения" рулетки на основе размера популяции "aPopSize".

//——————————————————————————————————————————————————————————————————————————————
class C_AO_Utilities
{
  public: //--------------------------------------------------------------------
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
  double Scale                 (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  double RNDfromCI             (double min, double max);
  int    RNDintInRange         (int min, int max);
  bool   RNDbool               ();
  double RNDprobab             ();
  double SeInDiSp              (double In, double InMin, double InMax, double Step);
  void   DecimalToGray         (ulong decimalNumber, char &array []);
  void   IntegerToBinary       (ulong number, char &array []);
  ulong  GrayToDecimal         (const char &grayCode [], int startInd, int endInd);
  ulong  BinaryToInteger       (const char &binaryStr [], const int startInd, const int endInd);
  ulong  GetMaxDecimalFromGray (int digitsInGrayCode);
  double GaussDistribution     (const double In, const double outMin, const double outMax, const double sigma);
  double PowerDistribution     (const double In, const double outMin, const double outMax, const double p);

  //----------------------------------------------------------------------------
  template<typename T>
  void Sorting (T &p [], T &pTemp [], int size)
  {
    int    cnt = 1;
    int    t0  = 0;
    double t1  = 0.0;
    int    ind [];
    double val [];

    ArrayResize (ind, size);
    ArrayResize (val, size);

    for (int i = 0; i < size; i++)
    {
      ind [i] = i;
      val [i] = p [i].f;
    }

    while (cnt > 0)
    {
      cnt = 0;
      for (int i = 0; i < size - 1; i++)
      {
        if (val [i] < val [i + 1])
        {
          t0 = ind [i + 1];
          t1 = val [i + 1];
          ind [i + 1] = ind [i];
          val [i + 1] = val [i];
          ind [i] = t0;
          val [i] = t1;
          cnt++;
        }
      }
    }

    for (int u = 0; u < size; u++) pTemp [u] = p [ind [u]];
    for (int u = 0; u < size; u++) p [u] = pTemp [u];
  }

  //----------------------------------------------------------------------------
  struct S_Roulette
  {
      double start;
      double end;
  };
  S_Roulette roulette [];

  template<typename T>
  void PreCalcRoulette (T &agents [])
  {
    int aPopSize = ArraySize (agents);
    roulette [0].start = agents [0].f;
    roulette [0].end   = roulette [0].start + (agents [0].f - agents [aPopSize - 1].f);

    for (int s = 1; s < aPopSize; s++)
    {
      if (s != aPopSize - 1)
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s].f - agents [aPopSize - 1].f);
      }
      else
      {
        roulette [s].start = roulette [s - 1].end;
        roulette [s].end   = roulette [s].start + (agents [s - 1].f - agents [s].f) * 0.1;
      }
    }
  }
  int  SpinRoulette (int aPopSize);
};
//——————————————————————————————————————————————————————————————————————————————

Поскольку стохастические алгоритмы оптимизации базируются на генерации случайных чисел, данная операция может выполняться сотнями или даже тысячами раз для получения каждого решения. Поэтому целесообразно оптимизировать процесс генерации случайных чисел путем разделения специфических задач. Учитывая, что стандартный генератор осуществляет генерацию целых чисел, существует потенциал для ускорения данного процесса.

Мы уже встречались ранее с методом "RNDfromCI", который генерирует случайное вещественное число в пределах заданного диапазона ["min", "max"]:

double C_AO_Utilities ::RNDfromCI (double min, double max)
{
  if (min == max) return min;
  if (min > max)
  {
    double temp = min;
    min = max;
    max = temp;
  }
  return min + ((max - min) * rand () / 32767.0);
}

Очень часто возникает необходимость в генерации случайного целого числа, например для случайного выбора агента в популяции. В этом нам поможет метод "RNDintInRange".

int C_AO_Utilities :: RNDintInRange (int min, int max)
{
  if (min == max) return min;
  if (min > max)
  {
    int temp = min;
    min = max;
    max = temp;
  }
  return min + rand () % (max - min + 1);
}

Получить случайную булеву величину с помощью метода "RNDbool" можно очень быстро, по сравнению с двумя методами выше, именно поэтому имел смысл разделения случайных величин на отдельные методы в зависимости от задачи.

bool C_AO_Utilities :: RNDbool ()
{
  return rand () % 2 == 0;
}

И ещё один метод "RNDprobab", позволяющий получить случайное вещественное число в диапазоне [0.0, 1.0]. Он прекрасно подходит для исполнения вероятности выполнения определённых операций, таких как вероятность кроссовера в генетическом алгоритме. Такие операции так же совершаются достаточно часто.

double C_AO_Utilities :: RNDprobab ()
{
  return (double)rand () / 32767;
}

Теперь рассмотрим базовый класс "C_AO" популяционных алгоритмов оптимизации. Этот класс описывает обязательные атрибуты всех популяционных алгоритмов, такие как:

• Методы и свойства класса "C_AO":

- SetParams: виртуальный метод для установки параметров алгоритма.
- Init: виртуальный метод для инициализации алгоритма с передачей минимального и максимального диапазона поиска, шага и количества эпох.
- Moving: виртуальный метод для выполнения шага алгоритма.
- Revision: виртуальный метод для проведения ревизии алгоритма.
- GetName: метод для получения имени алгоритма.
- GetDesc: метод для получения описания алгоритма.
- GetParams: метод для получения параметров алгоритма в виде строки.

• Защищенные свойства класса "C_AO":

- ao_name: имя алгоритма.
- "ao_desc: описание алгоритма.
- rangeMin, rangeMax, rangeStep: массивы для хранения минимального и максимального диапазона поиска, а также шага.
- coords: количество координат.
- popSize: размер популяции.
- revision: флаг для ревизии.
- u: объект класса "C_AO_Utilities" для выполнения вспомогательных функций.

#include "#C_AO_Utilities.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO
{
  public: //--------------------------------------------------------------------
  C_AO () { }
  ~C_AO () { for (int i = 0; i < ArraySize (a); i++) delete a [i];}

  double      cB     []; //best coordinates
  double      fB;        //FF of the best coordinates
  C_AO_Agent *a      []; //agents
  S_AlgoParam params []; //algorithm parameters

  virtual void SetParams () { }
  virtual bool Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
  { return false;}

  virtual void Moving   () { }
  virtual void Revision () { }

  string GetName   () { return ao_name;}
  string GetDesc   () { return ao_desc;}
  string GetParams ()
  {
    string str = "";
    for (int i = 0; i < ArraySize (params); i++)
    {
      str += (string)params [i].val + "|";
    }
    return str;
  }


  protected: //-----------------------------------------------------------------
  string ao_name;      //ao name;
  string ao_desc;      //ao description

  double rangeMin  []; //minimum search range
  double rangeMax  []; //maximum search range
  double rangeStep []; //step search

  int    coords;       //coordinates number
  int    popSize;      //population size
  bool   revision;

  C_AO_Utilities u;     //auxiliary functions

  bool StandardInit (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP []) //step search
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator
    fB       = -DBL_MAX;
    revision = false;

    coords  = ArraySize (rangeMinP);
    if (coords == 0 || coords != ArraySize (rangeMaxP) || coords != ArraySize (rangeStepP)) return false;

    ArrayResize (rangeMin,  coords);
    ArrayResize (rangeMax,  coords);
    ArrayResize (rangeStep, coords);
    ArrayResize (cB,        coords);

    ArrayCopy (rangeMin,  rangeMinP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeMax,  rangeMaxP,  0, 0, WHOLE_ARRAY);
    ArrayCopy (rangeStep, rangeStepP, 0, 0, WHOLE_ARRAY);

    return true;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Так же в этом же файле вместе с базовым классом находится перечисление "E_AO", содержащее идентификаторы оптимизационных алгоритмов и функция "SelectAO", позволяющая создать экземпляр соответствующего алгоритма и получить его указатель.

#include "AO_BGA_Binary_Genetic_Algorithm.mqh"
#include "AO_(P_O)ES_Evolution_Strategies.mqh"
#include "AO_DE_Differential_Evolution.mqh"
#include "AO_SDSm_Stochastic_Diffusion_Search.mqh"
#include "AO_ESG_Evolution_of_Social_Groups.mqh";

//——————————————————————————————————————————————————————————————————————————————
enum E_AO
{
  AO_BGA,
  AO_P_O_ES,
  AO_SDSm,
  AO_ESG,
  AO_DE,
  AO_NONE
};
C_AO *SelectAO (E_AO a)
{
  C_AO *ao;
  switch (a)
  {
    case  AO_BGA:
      ao = new C_AO_BGA (); return (GetPointer (ao));
    case  AO_P_O_ES:
      ao = new C_AO_P_O_ES (); return (GetPointer (ao));
    case  AO_SDSm:
      ao = new C_AO_SDSm (); return (GetPointer (ao));
    case  AO_ESG:
      ao = new C_AO_ESG (); return (GetPointer (ao));
    case  AO_DE:
      ao = new C_AO_DE (); return (GetPointer (ao));

    default:
      ao = NULL; return NULL;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Код алгоритмов - наследников

В качестве примера наследования от базового класса рассмотрим алгоритм стохастического диффузионного поиска, SDSm. Агента "C_SDS_Agent" этого алгоритма мы унаследуем от базового агента "C_AO_Agent". Заметим, что в методе инициализации агента присутствуют координаты "с" и приспособленность "f", однако в классе "C_SDS_Agent" они не объявлены. Это вполне логично, поскольку эти атрибуты являются обязательными для всех агентов алгоритмов оптимизации и наследуются от базового алгоритма, поэтому нет необходимости их повторно объявлять.

//——————————————————————————————————————————————————————————————————————————————
class C_SDS_Agent : public C_AO_Agent
{
  public: //--------------------------------------------------------------------
  ~C_SDS_Agent () { }

  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double cPrev     []; //previous coordinates (dishes)
  double fPrev;        //previous fitness

  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Класс "C_AO_SDSm" алгоритма SDSm наследуется от класса "C_AO". При объявлении объекта класса в конструкторе произведём инициализацию внешних параметров алгоритма, которые впоследствии могут быть изменены пользователем при особом желании, параметры будут доступны в виде массива и нам не придется беспокоиться о совместимости с тестовым стендом.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDSm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SDSm () { }
  C_AO_SDSm ()
  {
    ao_name = "SDSm";
    ao_desc = "Stochastic Diffusion Search";

    popSize    = 100; //population size

    restNumb   = 100;  //restaurants number
    probabRest = 0.05; //probability restaurant choosing

    ArrayResize (params, 3);

    params [0].name = "popSize";    params [0].val  = popSize;

    params [1].name = "restNumb";   params [1].val  = restNumb;
    params [2].name = "probabRest"; params [2].val  = probabRest;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;

    restNumb   = (int)params [1].val;
    probabRest = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    restNumb;          //restaurants number
  double probabRest;        //probability restaurant choosing

  C_SDS_Agent *agent []; //candidates

  private: //-------------------------------------------------------------------
  struct S_Riverbed //русло реки
  {
      double coordOnSector []; //coordinate on the sector (количество ячеек: количество секторов на координате, значение ячеек: конкретная координата на секторе)
  };

  double restSpace [];      //restaurants space
  S_Riverbed    rb [];      //riverbed

  void Research  (const double  ko,
                  const int     raddr,
                  const double  restSpace,
                  const double  rangeMin,
                  const double  rangeStep,
                  const double  pitOld,
                  double       &pitNew);
};
//——————————————————————————————————————————————————————————————————————————————

Далее, особо следует рассмотреть метод инициализации "Init" класса "C_AO_SDSm". По шагам метод выполняет следующее:

1. С самого начала необходимо вызвать метод базового класса "StandardInit" и передать в него "rangeMinP", "rangeMaxP", "rangeStepP". Если метод возвращает "false", функция "Init" также возвращает "false", сообщая о неудачной инициализации алгоритма.
2. Удаление агентов с помощью "delete". Это необходимо при многократном использовании объекта алгоритма.
3. Затем массивам "agent" алгоритма SDSm и "a" базового класса изменяем размер до "popSize" и производим приведение типов.
4. Далее выполняются действия, аналогичные алгоритму, описанному ранее в статье о SDSm.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SDSm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  for (int i = 0; i < ArraySize (agent); i++) delete agent [i];

  ArrayResize (agent, popSize);
  ArrayResize (a,     popSize);

  for (int i = 0; i < popSize; i++)
  {
    a     [i] = new C_SDS_Agent ();
    agent [i] = (C_SDS_Agent *)a [i];

    agent [i].Init (coords);
  }

  ArrayResize (restSpace, coords);
  ArrayResize (rb,        coords);
  for (int i = 0; i < coords; i++)
  {
    ArrayResize     (rb [i].coordOnSector, restNumb);
    ArrayInitialize (rb [i].coordOnSector, -DBL_MAX);
  }

  for (int i = 0; i < coords; i++)
  {
    restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

4. Код единого тестового стенда для всех алгоритмов

Хотя на данный момент нет необходимости "размножать" тестовые стенды, мы все же перенесем все функции стенда в класс "C_TestStand". Это позволит удобно инкапсулировать функционал стенда. Поскольку никаких существенных изменений в функциях стенда не произошло, не будем подробно описывать их. Достаточно просто посмотреть, как теперь выглядит это "тестовое хозяйство":

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>

//——————————————————————————————————————————————————————————————————————————————
class C_TestStand
{
  public: void Init (int width, int height)
  {
    W = width;  //750;
    H = height; //375;

    WscrFunc = H - 2;
    HscrFunc = H - 2;

    //creating a table ---------------------------------------------------------
    string canvasName = "AO_Test_Func_Canvas";

    if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
    {
      Print ("Error creating Canvas: ", GetLastError ());
      return;
    }

    ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
    ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

    ArrayResize (FunctScrin, HscrFunc);

    for (int i = 0; i < HscrFunc; i++) ArrayResize (FunctScrin [i].clr, HscrFunc);

  }

  struct S_CLR
  {
    color clr [];
  };

  //----------------------------------------------------------------------------
  public: void CanvasErase ()
  {
    Canvas.Erase (XRGB (0, 0, 0));
    Canvas.FillRectangle (1,     1, H - 2, H - 2, COLOR2RGB (clrWhite));
    Canvas.FillRectangle (H + 1, 1, W - 2, H - 2, COLOR2RGB (clrWhite));
  }

  //----------------------------------------------------------------------------
  public: void MaxMinDr (C_Function & f)
  {
    //draw Max global-------------------------------------------------------------
    int x = (int)Scale(f.GetMaxFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 1, W/2 - 1, false);
    int y = (int)Scale(f.GetMaxFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 1, H   - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 14, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 15, COLOR2RGB(clrBlack));

    //draw Min global-------------------------------------------------------------
    x = (int)Scale(f.GetMinFuncX(), f.GetMinRangeX(), f.GetMaxRangeX(), 0, W/2 - 1, false);
    y = (int)Scale(f.GetMinFuncY(), f.GetMinRangeY(), f.GetMaxRangeY(), 0, H - 1, true);

    Canvas.Circle(x, y, 12, COLOR2RGB(clrBlack));
    Canvas.Circle(x, y, 13, COLOR2RGB(clrBlack));
  }

  //----------------------------------------------------------------------------
  public: void PointDr (double &args [], C_Function & f, int shiftX, int shiftY, int count, bool main)
  {
    double x = 0.0;
    double y = 0.0;

    double xAve = 0.0;
    double yAve = 0.0;

    int width  = 0;
    int height = 0;

    color clrF = clrNONE;

    for(int i = 0; i < count; i++)
    {
      xAve += args [i * 2];
      yAve += args [i * 2 + 1];

      x = args [i * 2];
      y = args [i * 2 + 1];

      width  = (int)Scale(x, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
      height = (int)Scale(y, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

      clrF = DoubleToColor(i, 0, count - 1, 0, 270);
      Canvas.FillCircle(width + shiftX, height + shiftY, 1, COLOR2RGB(clrF));
    }

    xAve /=(double)count;
    yAve /=(double)count;

    width  = (int)Scale(xAve, f.GetMinRangeX(), f.GetMaxRangeX(), 0, WscrFunc - 1, false);
    height = (int)Scale(yAve, f.GetMinRangeY(), f.GetMaxRangeY(), 0, HscrFunc - 1, true);

    if(!main)
    {
      Canvas.FillCircle(width + shiftX, height + shiftY, 3, COLOR2RGB(clrBlack));
      Canvas.FillCircle(width + shiftX, height + shiftY, 2, COLOR2RGB(clrWhite));
    }
    else
    {
      Canvas.Circle (width + shiftX, height + shiftY, 5, COLOR2RGB (clrBlack));
      Canvas.Circle (width + shiftX, height + shiftY, 6, COLOR2RGB (clrBlack));
    }
  }

  //----------------------------------------------------------------------------
  public: void SendGraphToCanvas ()
  {
    for (int w = 0; w < HscrFunc; w++)
    {
      for (int h = 0; h < HscrFunc; h++)
      {
        Canvas.PixelSet (w + 1, h + 1, COLOR2RGB (FunctScrin [w].clr [h]));
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void DrawFunctionGraph (C_Function & f)
  {
    double ar [2];
    double fV;

    for (int w = 0; w < HscrFunc; w++)
    {
      ar [0] = Scale (w, 0, H, f.GetMinRangeX (), f.GetMaxRangeX (), false);
      for (int h = 0; h < HscrFunc; h++)
      {
        ar [1] = Scale (h, 0, H, f.GetMinRangeY (), f.GetMaxRangeY (), true);
        fV = f.CalcFunc (ar, 1);
        FunctScrin [w].clr [h] = DoubleToColor (fV, f.GetMinFunValue (), f.GetMaxFunValue (), 0, 270);
      }
    }
  }

  //----------------------------------------------------------------------------
  public: void Update ()
  {
    Canvas.Update ();
  }

  //----------------------------------------------------------------------------
  //Scaling a number from a range to a specified range
  public: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
    else
    {
      if (Revers)
      {
        if (In < InMIN) return (OutMAX);
        if (In > InMAX) return (OutMIN);
        return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
      else
      {
        if (In < InMIN) return (OutMIN);
        if (In > InMAX) return (OutMAX);
        return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
      }
    }
  }

  //----------------------------------------------------------------------------
  private: color DoubleToColor (const double In,    //input value
                                const double inMin, //minimum of input values
                                const double inMax, //maximum of input values
                                const int    loH,   //lower bound of HSL range values
                                const int    upH)   //upper bound of HSL range values
  {
    int h = (int) Scale (In, inMin, inMax, loH, upH, true);
    return HSLtoRGB (h, 1.0, 0.5);
  }

  //----------------------------------------------------------------------------
  private: color HSLtoRGB (const int    h, //0   ... 360
                           const double s, //0.0 ... 1.0
                           const double l) //0.0 ... 1.0
  {
    int r;
    int g;
    int b;
    if (s == 0.0)
    {
      r = g = b = (unsigned char)(l * 255);
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
    else
    {
      double v1, v2;
      double hue = (double) h / 360.0;
      v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
      v1 = 2.0 * l - v2;
      r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
      g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
      b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
      return StringToColor ((string) r + "," + (string) g + "," + (string) b);
    }
  }

  //----------------------------------------------------------------------------
  private: double HueToRGB (double v1, double v2, double vH)
  {
    if (vH < 0) vH += 1;
    if (vH > 1) vH -= 1;
    if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
    if ((2 * vH) < 1) return v2;
    if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
    return v1;
  }

  //----------------------------------------------------------------------------
  public: int W; //monitor screen width
  public: int H; //monitor screen height

  private: int WscrFunc; //test function screen width
  private: int HscrFunc; //test function screen height

  public:  CCanvas Canvas;      //drawing table
  private: S_CLR FunctScrin []; //two-dimensional matrix of colors
};
//——————————————————————————————————————————————————————————————————————————————

Теперь давайте взглянем на сам код тестового стенда. При изучении входных параметров стенда становится ясно, что теперь у нас есть возможность выбирать алгоритм оптимизации и тестовые функции в настройках. Это позволяет создавать уникальные наборы тестовых функций для проверки алгоритма. Теперь можно проводить тестирование только на гладких или только на дискретных функциях. Более того, теперь можно выбирать любую комбинацию тестовых функций, наиболее подходящую для потребностей пользователя.

#include "PAO\#C_TestStandFunctions.mqh"
#include "PAO\#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
input string AOparam            = "----------------"; //AO parameters-----------
input E_AO   AOexactly_P        = AO_NONE;

input string TestStand_1        = "----------------"; //Test stand--------------
input double ArgumentStep_P     = 0.0;   //Argument Step

input string TestStand_2        = "----------------"; //------------------------
input int    Test1FuncRuns_P    = 5;     //Test #1: Number of functions in the test
input int    Test2FuncRuns_P    = 25;    //Test #2: Number of functions in the test
input int    Test3FuncRuns_P    = 500;   //Test #3: Number of functions in the test

input string TestStand_3        = "----------------"; //------------------------
input EFunc  Function1          = Hilly;
input EFunc  Function2          = Forest;
input EFunc  Function3          = Megacity;

input string TestStand_4        = "----------------"; //------------------------
input int    NumbTestFuncRuns_P = 10000; //Number of test function runs
input int    NumberRepetTest_P  = 10;    //Test repets number

input string TestStand_5        = "----------------"; //------------------------
input bool   Video_P            = true;  //Show video
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_AO *AO = SelectAO (AOexactly_P);
  if (AO == NULL)
  {
    Print ("AO is not selected...");
    return;
  }

  Print (AO.GetName (), "|", AO.GetDesc (), "|", AO.GetParams ());

  //============================================================================
  C_TestStand ST; //stand
  ST.Init (750, 375);

  double allScore = 0.0;
  double allTests = 0.0;

  C_Function *F1 = SelectFunction (Function1);
  C_Function *F2 = SelectFunction (Function2);
  C_Function *F3 = SelectFunction (Function3);

  if (F1 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();

    FuncTests (AO, ST, F1, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F1, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F1, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F1;
  }

  if (F2 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F2, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F2, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F2, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F2;
  }

  if (F3 != NULL)
  {
    Print ("=============================");
    ST.CanvasErase ();
    FuncTests (AO, ST, F3, Test1FuncRuns_P, clrLime,      allScore, allTests);
    FuncTests (AO, ST, F3, Test2FuncRuns_P, clrAqua,      allScore, allTests);
    FuncTests (AO, ST, F3, Test3FuncRuns_P, clrOrangeRed, allScore, allTests);
    delete F3;
  }

  Print ("=============================");
  if (allTests > 0.0) Print ("All score: ", DoubleToString (allScore, 5), " (", DoubleToString (allScore * 100 / allTests, 2), "%)");
  delete AO;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_AO          &ao,
                C_TestStand   &st,
                C_Function    &f,
                const  int     funcCount,
                const  color   clrConv,
                double        &allScore,
                double        &allTests)
{
  if (funcCount <= 0) return;

  allTests++;

  if (Video_P)
  {
    st.DrawFunctionGraph (f);
    st.SendGraphToCanvas ();
    st.MaxMinDr          (f);
    st.Update            ();
  }

  int    xConv      = 0.0;
  int    yConv      = 0.0;
  double aveResult  = 0.0;
  int    params     = funcCount * 2;
  int    epochCount = NumbTestFuncRuns_P / (int)ao.params [0].val;

  //----------------------------------------------------------------------------
  double rangeMin  [], rangeMax  [], rangeStep [];
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeMax,  params);
  ArrayResize (rangeStep, params);

  for (int i = 0; i < funcCount; i++)
  {
    rangeMax  [i * 2] = f.GetMaxRangeX ();
    rangeMin  [i * 2] = f.GetMinRangeX ();
    rangeStep [i * 2] = ArgumentStep_P;

    rangeMax  [i * 2 + 1] = f.GetMaxRangeY ();
    rangeMin  [i * 2 + 1] = f.GetMinRangeY ();
    rangeStep [i * 2 + 1] = ArgumentStep_P;
  }

  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    //--------------------------------------------------------------------------
    if (!ao.Init (rangeMin, rangeMax, rangeStep)) break;

    // Optimization-------------------------------------------------------------
    for (int epochCNT = 1; epochCNT <= epochCount && !IsStopped (); epochCNT++)
    {
      ao.Moving ();

      for (int set = 0; set < ArraySize (ao.a); set++)
      {
        ao.a [set].f = f.CalcFunc (ao.a [set].c, funcCount);
      }

      ao.Revision  ();

      if (Video_P)
      {
        //drawing a population--------------------------------------------------
        st.SendGraphToCanvas  ();

        for (int i = 0; i < ArraySize (ao.a); i++)
        {
          st.PointDr (ao.a [i].c, f, 1, 1, funcCount, false);
        }
        st.PointDr (ao.cB, f, 1, 1, funcCount, true);

        st.MaxMinDr (f);

        //drawing a convergence graph---------------------------------------------
        xConv = (int)st.Scale (epochCNT, 1, epochCount, st.H + 2, st.W - 3, false);
        yConv = (int)st.Scale (ao.fB, f.GetMinFunValue (), f.GetMaxFunValue (), 2, st.H - 2, true);
        st.Canvas.FillCircle (xConv, yConv, 1, COLOR2RGB (clrConv));

        st.Update ();
      }
    }

    aveResult += ao.fB;
  }

  aveResult /= (double)NumberRepetTest_P;

  double score = aveResult;

  Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", NumbTestFuncRuns_P, "; result: ", aveResult);
  allScore += score;
}
//——————————————————————————————————————————————————————————————————————————————

5. Добавим популярные известные тестовые функции

Иногда меня спрашивают, почему я не включил в набор тестовых функций такие широко известные и часто используемые при исследованиях и разработках алгоритмов оптимизации. Причина кроется в том, что все они относятся к категории "простых" тестовых функций по моей классификации. Более половины их поверхностей сосредоточены вблизи глобального экстремума, что делает их слишком "предсказуемыми" для надлежащего тестирования. Но, несмотря на это, люди привыкли доверять им и стремятся проверять свои алгоритмы именно на таких функциях. Поэтому я решил включить в набор функции Экли, Гольдштейна-Прайса и Шафера №2. Это поможет сбалансировать выбор тестовых функций пользователям и обеспечить более всестороннее и надежное тестирование алгоритмов оптимизации, открывая новые горизонты для исследователей и способствуя более глубокому пониманию их эффективности.

Формула Экли:

f(x, y) = -(-20 * exp(-0.2 * sqrt(0.5 * (x^2 + y^2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20)

где:
- x, y - входные параметры функции,
- e - число Эйлера (приблизительно 2.71828),
- π - число пи (приблизительно 3.14159).

Код функции:

double Core (double x, double y)
{
  double res1 = -20.0 * MathExp (-0.2 * MathSqrt (0.5 * (x * x + y * y)));
  double res2 = -MathExp (0.5 * (MathCos (2.0 * M_PI * x) + MathCos (2.0 * M_PI * y)));
  double res3 = -(res1 + res2 + M_E + 20.0);

  return Scale (res3, -14.302667500265278, 0.0, 0.0, 1.0);
}

Формула Гольдштейна-Прайса :

f(x, y) = -([1 + (x + y + 1)^2 * (19 - 14x + 3x^2 - 14y + 6xy + 3y^2)] * [30 + (2x - 3y)^2 * (18 - 32x + 12x^2 + 48y - 36xy + 27y^2)])

Код функции:

double Core (double x, double y)
{
  double part1 = 1 + MathPow ((x + y + 1), 2) * (19 - 14 * x + 3 * x * x - 14 * y + 6 * x * y + 3 * y * y);
  double part2 = 30 + MathPow ((2 * x - 3 * y), 2) * (18 - 32 * x + 12 * x * x + 48 * y - 36 * x * y + 27 * y * y);

  return Scale (-part1 * part2, -1015690.2717980597, -3.0, 0.0, 1.0);
}

Формула Шафера №2:

f(x, y) = -(0.5 + ((sin(x^2 - y^2)^2 - 0.5) / (1 + 0.001 * (x^2 + y^2))^2))

Код функции:

double Core (double x, double y)
{
  double numerator   = MathPow (MathSin (x * x - y * y), 2) - 0.5;
  double denominator = MathPow (1 + 0.001 * (x * x + y * y), 2);
    
  return Scale (-(0.5 + numerator / denominator), -0.9984331449753265, 0, 0, 1.0);
}

Примечание: значения тестовых функций приведены к диапазону [0.0, 1.0].

6. Построение тестовых функций 3D

Иногда для более глубокого понимания тестовых функций и их рельефа необходимо не просто абстрагироваться от чисел и формул, а увидеть их визуально. Поэтому я решил воспользоваться возможностью построения 3D-сцен с помощью DirectX в платформе MetaTrader 5. Меня вдохновил файл "...\MQL5\Experts\Examples\Math 3D Morpher\Math 3D Morpher.mq5" от разработчиков, который входит в стандартную поставку и визуализирует функции, разработанные мной ранее (и которые я планирую добавить в список функций для тестового стенда). Таким образом, я принял решение создать визуализатор для тестовых функций.

Для этого мне пришлось расширить файл "Functions.mqh", где хранится класс тестовых функций, используемых в тестировании алгоритмов оптимизации. Дополнительные функции, которые я добавил, позволят не только изучить изменения функций визуально при их модификации если возникнет такая необходимость, но и более глубоко исследовать их свойства и особенности.

Этот процесс не только делает мое исследование более увлекательным и наглядным, но и помогает мне более полно понять поведение тестовых функций. В конечном итоге визуализация в 3D помогает мне не просто видеть числа на экране, а непосредственно взаимодействовать с формой и структурой функций, что важно при их модификации и анализе свойств.

Код дополнительных функций для построения модели для 3D-сцены:

//——————————————————————————————————————————————————————————————————————————————
//GenerateFunctionDataFixedSize
bool GenerateFunctionDataFixedSize (int x_size, int y_size, double &data [], double x_min, double x_max, double y_min, double y_max, C_Function &function)
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  double dx = (x_max - x_min) / (x_size - 1);
  double dy = (y_max - y_min) / (y_size - 1);

  ArrayResize (data, x_size * y_size);

  //---
  for (int j = 0; j < y_size; j++)
  {
    for (int i = 0; i < x_size; i++)
    {
      double x = x_min + i * dx;
      double y = y_min + j * dy;

      data [j * x_size + i] = function.Core (x, y);
    }
  }
  return (true);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//GenerateDataFixedSize
bool GenerateDataFixedSize (int x_size, int y_size, C_Function &function, double &data [])
{
  if (x_size < 2 || y_size < 2)
  {
    PrintFormat ("Error in data sizes: x_size=%d,y_size=%d", x_size, y_size);
    return (false);
  }

  return GenerateFunctionDataFixedSize (x_size, y_size, data,
                                        function.GetMinRangeX (),
                                        function.GetMaxRangeX (),
                                        function.GetMinRangeY (),
                                        function.GetMaxRangeY (),
                                        function);
}
//——————————————————————————————————————————————————————————————————————————————

Дополнительно я добавил дискретные варианты уже знакомых нам функций: SkinDiscrete и HillyDiscrete.

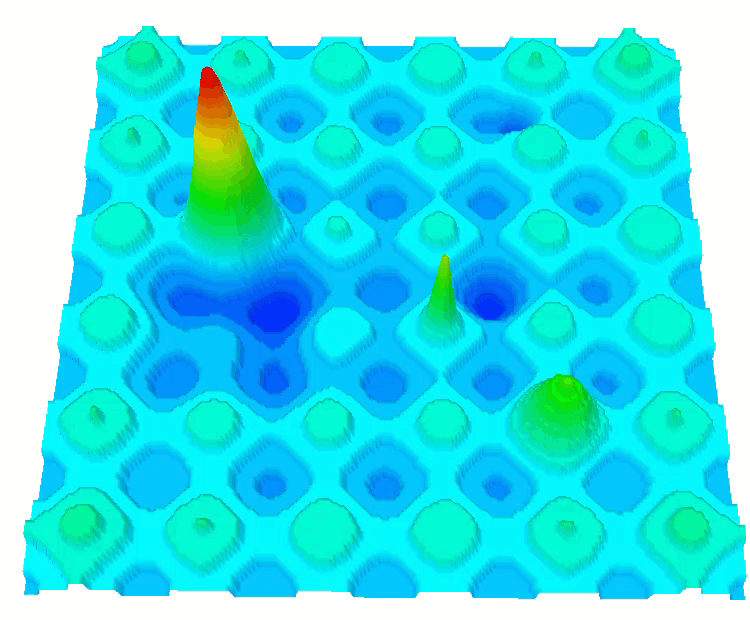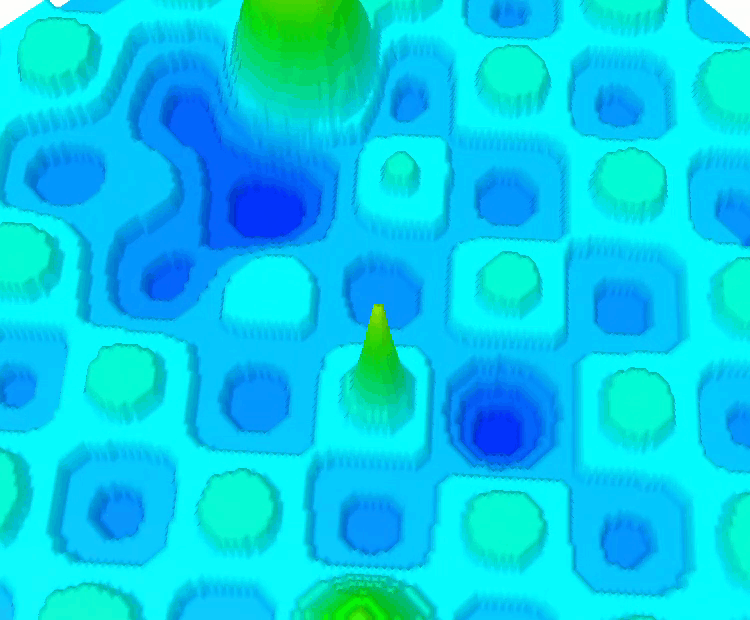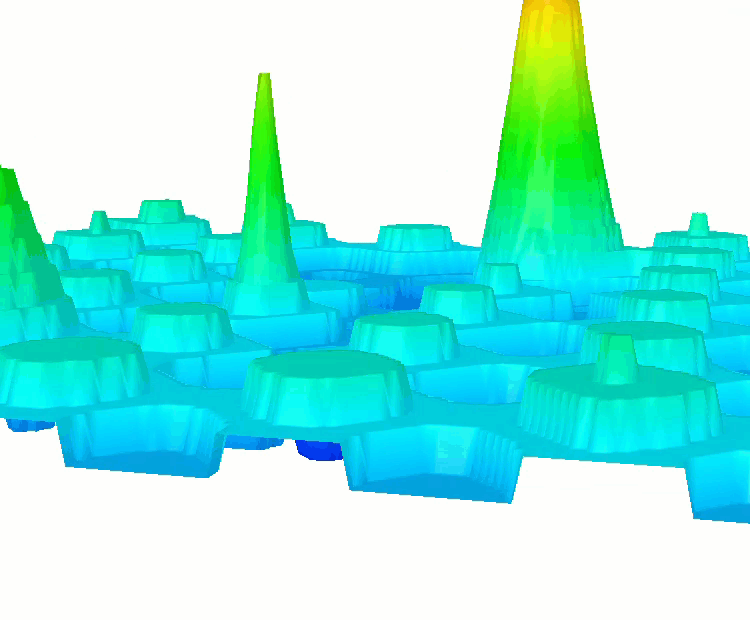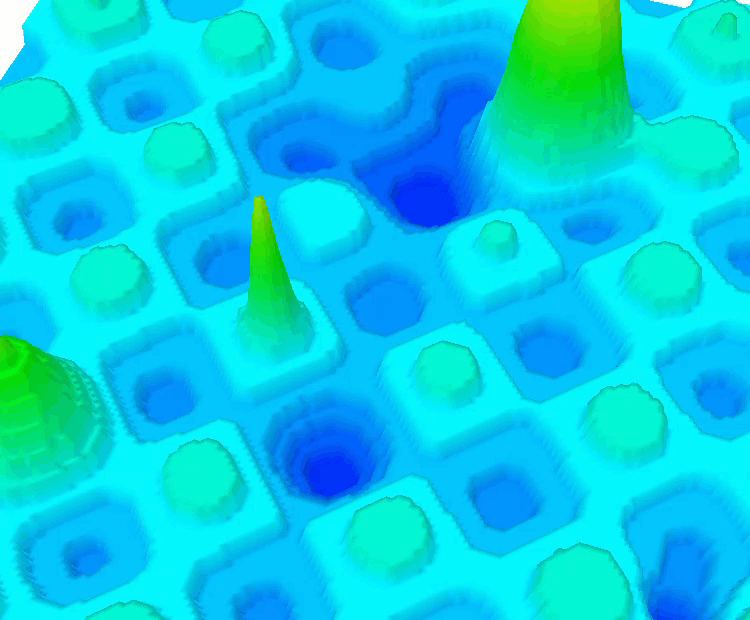
Функция HillyDiscrete.

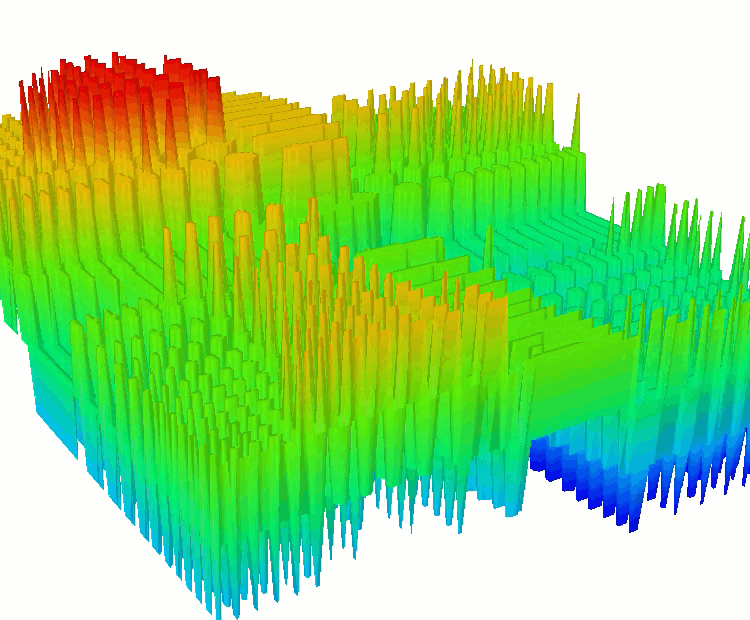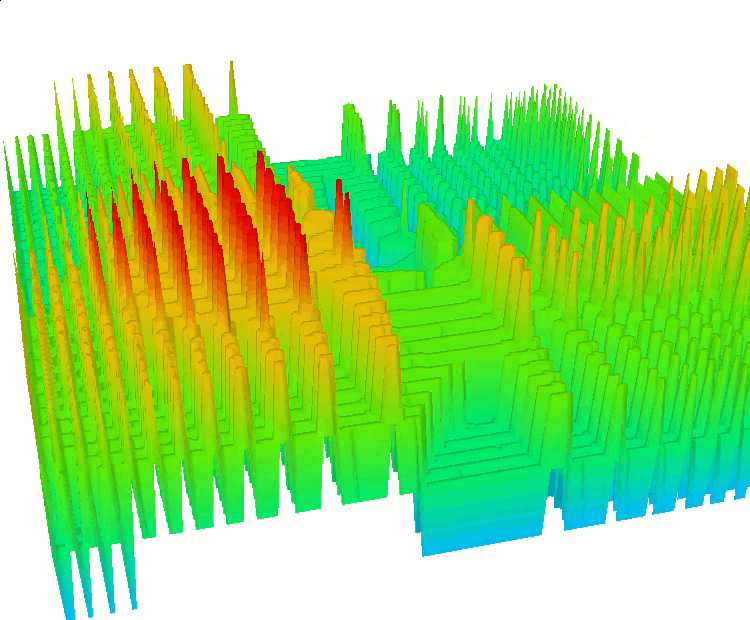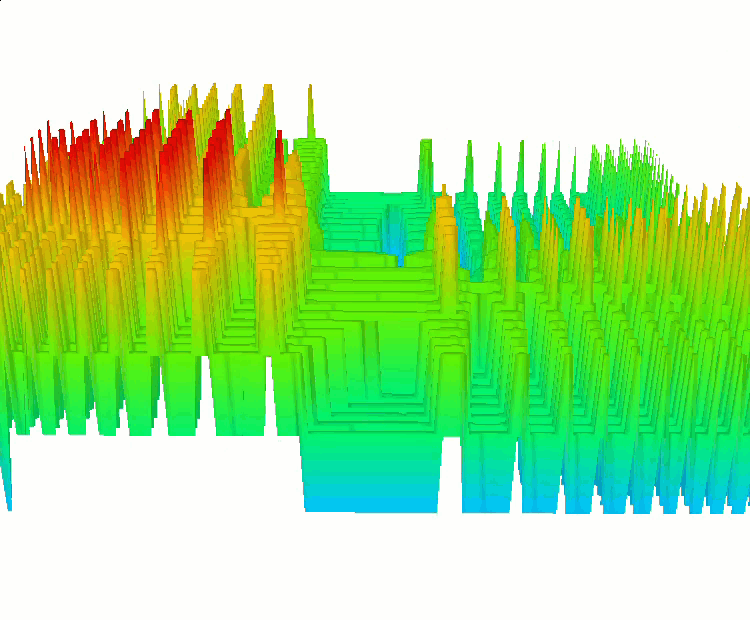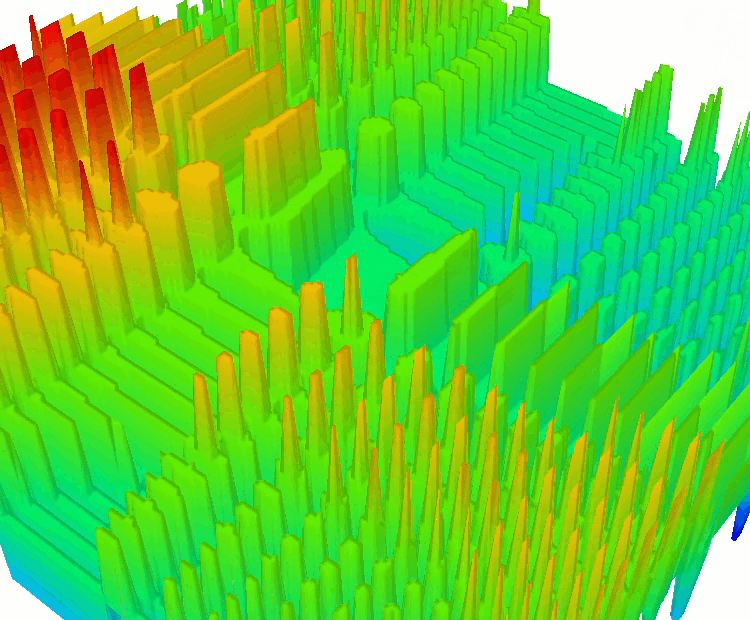
Функция SkinDiscrete.

Функция Shaffer #2.

7. Выводы

Мы продолжим пользоваться тестовыми функциями "Hilly", "Forest" и "Megacity", которые уже завоевали свою репутацию как настоящие испытания для алгоритмов оптимизации, помогая составить надежную рейтинговую таблицу. Однако, не стоит ограничиваться только этими функциями - ведь список тестовых функций успешно пополнился! Так что вам предоставляется свобода выбора: экспериментируйте, исследуйте, открывайте новые горизонты, ведь именно в этом заключается вся прелесть научных исследований.

В заключении нашего "кулинарного" исследования гибридных методов оптимизации через наследование от базового класса, мы видим, что создание такой отправной точки открывает двери перед бесконечными возможностями исследований. Объединение различных популяционных алгоритмов в один класс позволяет нам не только улучшить точность и скорость поиска оптимальных решений, но и создать универсальный инструмент для исследований.

Создание единого тестового стенда, который объединяет разнообразные тестовые функции — дискретные, гладкие, острые, недифференцируемые — открывает новые возможности для тестирования и сравнения различных методов оптимизации. Этот подход позволяет исследователям не только использовать стандартные наборы функций, но и создавать собственные тестовые стенды, адаптированные под конкретные задачи и требования.

Таким образом, объединение в один класс популяционных алгоритмов и создание универсального тестового стенда открывает перед нами увлекательный путь к созданию новых "гастрономических" комбинаций методов оптимизации, позволяя нам открывать новые вкусовые ноты в мире поиска оптимальных решений. Давайте продолжим этот "кулинарный" эксперимент и создадим новые шедевры на пути к совершенству и инновациям в области оптимизации!