Популяционные алгоритмы оптимизации: Стохастический диффузионный поиск (Stochastic Diffusion Search, SDS)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Алгоритм стохастического диффузионного поиска (Stochastic Diffusion Search, SDS) был предложен в 1989 году Бишопом (J. Bishop) и с тех пор активно развивается его автором и Насуто (S. Nasuto). Отличительной особенностью данного алгоритма является его глубокое математическое обоснование по сравнению с другими популяционными алгоритмами. Исходно SDS был разработан для дискретной оптимизации, но только в 2011 году была предложена его модификация для глобальной непрерывной оптимизации.

Интересные факты:

1. Стохастический диффузионный поиск (SDS) был первой метаэвристикой Swarm Intelligence, которая относится к семейству роевых интеллектов и естественных алгоритмов поиска и оптимизации. Другими примерами таких алгоритмов являются оптимизация колоний муравьев, оптимизация роя частиц и генетические алгоритмы.

2. В отличие от оптимизации муравьиных колоний, основанной на стигмергетическом общении, SDS использует прямую связь между агентами, аналогичную механизму тандемного вызова, используемому муравьями вида Leptothorax acervorum.

Алгоритм SDS основан на дешевой частичной оценке гипотезы (кандидатного решения проблемы поиска) агентами. Затем агенты обмениваются информацией о гипотезах через прямое личное общение. Посредством механизма диффузии высококачественные решения могут быть идентифицированы из кластеров агентов с одинаковой гипотезой.

Для лучшего понимания работы алгоритма SDS можно использовать простую аналогию – "Ресторанную игру".

В ресторанной игре участники играют роль агентов, а рестораны - гипотезы. Каждый агент выбирает ресторан, в котором хочет поесть, основываясь на своих предпочтениях и информации, которую он получает от других агентов. Затем агенты обмениваются информацией о своих выборах и предпочтениях. В результате этого процесса, кластеры агентов, выбравших один и тот же ресторан, образуются и могут быть идентифицированы как потенциально хорошие решения.

Алгоритм SDS имеет несколько преимуществ. Во-первых, он позволяет агентам делать дешевые частичные оценки гипотез, что снижает вычислительную сложность алгоритма. Во-вторых, он использует прямое личное общение между агентами, что позволяет эффективно распространять информацию. В-третьих, SDS имеет математическое обоснование, что делает его более надежным и предсказуемым.

Однако, алгоритм SDS также имеет свои ограничения. Во-первых, он может быть эффективен только в некоторых типах задач, где применимо понятие гипотезы. Во-вторых, он может страдать от проблемы преждевременной сходимости, когда агенты сходятся к одной гипотезе слишком быстро, не исследуя другие возможности. В-третьих, алгоритм требует настройки параметров, что может быть сложным и трудоемким процессом. Ограничения озвучены некоторыми авторами, проверим, так ли это.

В целом, SDS является интересным и эффективным алгоритмом для решения задач оптимизации. Он сочетает в себе преимущества популяционных алгоритмов и математическое обоснование, делая его привлекательным для исследования и применения в различных областях.

2. Описание алгоритма

Перейдем к более подробному рассмотрению алгоритма SDS.

Стохастический диффузионный поиск (SDS) — это популяционный алгоритм, основанный на двух идеях стратегии поиска:

1. Частичная оценка решений.
2. Распространение перспективных решений по всей популяции.

Есть две канонические игры, которые простым языком описывают принцип работы SDS.
1. Ресторанная игра
2. Золотодобывающая игра.

Игра "Ресторан"

Группа делегатов находится на продолжительной конференции в незнакомом городе. Каждый вечер они сталкиваются с проблемой выбора ресторана для обеда. В городе имеется огромное количество заведений, предлагающих разнообразные блюда. Цель группы - найти лучший ресторан, в котором каждый делегат сможет насладиться приятным обедом. Однако, проведение исчерпывающе полного поиска по всем возможным комбинациям ресторанов и блюд займет слишком много времени. Чтобы решить эту проблему, делегаты прибегают к использованию стохастического диффузионного поиска.

Каждый делегат выступает в роли агента, который делает предположение относительно выбора лучшего ресторана в городе. Каждый вечер делегаты проверяют свои гипотезы, посещая рестораны и случайным образом выбирая одно из ассортимента блюд ресторана. На следующее утро, за завтраком, каждый делегат, который остался недоволен ужином в предыдущий вечер, просит одного из коллег поделиться своими впечатлениями от обеда. Если впечатления коллеги положительные, делегат также выбирает этот ресторан. В противном случае, он случайным образом выбирает другое заведение из списка доступных ресторанов в этом городе.

Таким образом, благодаря данной стратегии, быстро формируется значительное количество делегатов, собирающихся вокруг лучшего ресторана города.

Этот процесс игры в ресторан имеет несколько интересных особенностей. При полном отсутствии внешнего контроля и управления, группа делегатов общаются, чтобы решить проблему, которую невозможно решить быстро в одиночку. Если качество обслуживания или меню текущего ресторана значительно снижается или он закрывается, делегаты эффективно переходят в следующее лучшее заведение. Главное требование - сравнимость ресторанов, меню и отдельных блюд. Каждый агент самостоятельно решает, был ли его опыт хорошим.

Делегаты проводят много вечеров в ресторане высокого качества до того, как будут оценены все блюда во всех заведениях города.
Критики указывают на то, что у делегатов, вероятно, разные предпочтения в еде, поэтому один делегат может найти ресторан, где ему нравятся все блюда, но это может не удовлетворить остальных участников группы. Если только один или небольшая часть делегатов остаются постоянно в таком ресторане, остальные продолжают действовать как обычно, и в итоге большинство все равно собирается в лучшем ресторане. Однако, в крайнем случае, все агенты могут оказаться обедающими в одиночку, даже если существует единственный превосходный ресторан, который удовлетворит большую часть делегатов. Этот ресторан никогда не будет найден, так как все делегаты удовлетворены своими текущими выборами и не будут искать новые заведения.

В нашей реализации сделаны небольшие изменения в логике стратегии поиска, благодаря которым делегаты продолжают поиск ресторанов даже тогда, когда нет ни одного делегата с более лучшим опытом, таким образом поиск ресторанов не прекращается в отличие от канонического варианта, в котором важен сам факт изменения текущего мнения о ресторане от предыдущего, если мнение не изменится в лучшую сторону у большинства делегатов, то они продолжат ходить в один и тот же ресторан, что означает застревание в локальном экстремуме.

"Золотодобывающая" игра

Группа друзей, состоящая из опытных шахтеров, узнает о возможности добычи золота на холмах горного хребта. Однако они не имеют информации о том, где именно находится самое богатое золотом место. На их картах горный массив разделен на несколько отдельных холмов, каждый из которых содержит набор пластов, требующих добычи. Вероятность обнаружить золото в течение времени пропорциональна его богатству.

Для максимизации своего коллективного богатства шахтеры должны определить холм с наиболее богатыми пластами золота, чтобы максимальное количество шахтеров могло добывать там. Однако эта информация недоступна заранее. Чтобы решить эту проблему, майнеры решают использовать простой стохастический диффузионный поиск.

Процесс добычи начинается с того, что каждому шахтеру случайным образом назначается холм для добычи (его гипотеза холма). Каждый день каждому шахтеру случайным образом выбирается пласт на его холме, который он будет разрабатывать.

В конце каждого дня вероятность того, что шахтер счастлив, пропорциональна количеству найденного им золота (значение фитнес - функции).
Вечером, после окончания работы, шахтеры собираются вместе. Недовольный шахтер случайным образом выбирает другого шахтера для разговора. Если выбранный шахтер доволен, он с "радостью" сообщает своему коллеге название холма, который он разрабатывает. Таким образом, оба шахтера поддерживают гипотезу холма. Если же выбранный шахтер недоволен, он ничего не говорит, и первоначальный шахтер снова вынужден выбирать новую гипотезу - определение холма, который он будет разрабатывать на следующий день наугад.

В контексте SDS (самоорганизующиеся динамические системы) агенты выступают в роли шахтеров. Активные агенты - это "счастливые шахтеры", а неактивные агенты - "несчастные шахтеры". Гипотеза каждого агента представляет собой "гипотезу холма" шахтера. Этот процесс изоморфен SDS, что позволяет шахтерам естественным образом самоорганизовываться и быстро собираться на холме(ах) горного хребта с высокой концентрацией золота.

Счастье шахтеров может быть измерено вероятностно или представлено абсолютным логическим значением, учитывая, что каждый шахтер к концу каждого дня либо счастлив, либо несчастен. Если золото моделируется как ограниченный ресурс, уменьшающийся со временем, то поиск становится достаточно адаптивным, и шахтеры перемещаются к местам с наибольшим количеством золота.

Хотя термин "счастливый" является субъективным, как и предпочтения в еде, в данном случае он используется в объективном смысле. Все шахтеры используют одинаковый процесс: количество золота, найденное ими за день, определяет вероятность того, что они объявят себя "счастливыми" в конце дня, когда они собираются вместе, чтобы потенциально поделиться информацией о холмах, которые они добывают.

Мы не будем использовать разделение шахтёров на "счастливых" и "несчастных", это позволит, как и в случае концепции игры "Ресторан", повысить активность агентов в поиске новых, неразведанных мест.

Для формализации алгоритма будем использовать понятие "кандидат", который эквивалентен делегату в игре "Ресторан" и шахтеру в золотодобывающей игре. Кандидат представляет собой поискового агента. Для более простого понимания сущности ресторан или холм можно представить себе пространство с двумя координатами, хотя в реальности для решения многомерных задач можно применять неограниченное количество координат. На рисунке 1 обозначениями С1, С2, С3 показаны кандидаты, которые хранят в себе номера ресторанов (соответствующие пространства на поле поиска). В процессе диффузионного обмена информацией о ресторанах кандидаты заимствуют номера ресторанов у случайным образом выбранных участников конференции в случае если значение фитнес функции у собеседника выше. Диапазон каждого параметра оптимизации (координаты пространства поиска) разбивается на количество ресторанов, указанного во внешних параметрах алгоритма, к примеру, если в параметрах алгоритма указано число 100 ресторанов, то это означает диапазон каждой координаты будет разбит на 100 частей.

Каждый ресторан предлагает в меню список блюд, каждое блюдо меню является конкретной координатой пространства поиска в пределах одного ресторана. Алгоритм реализует схему, при которой кандидат отведает только одно случайно выбранное блюдо ресторана.

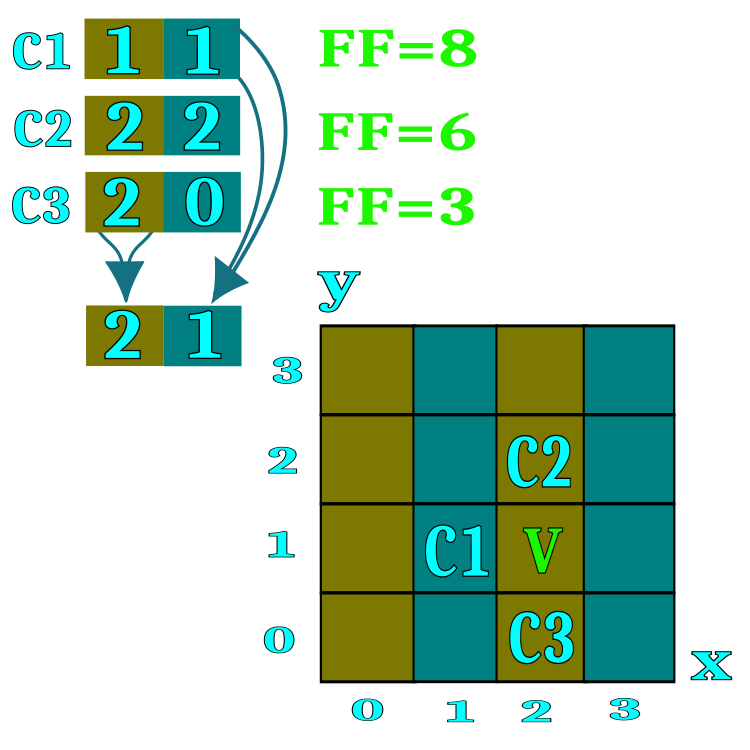
Рисунок 1. Визуальное представление принципа диффузионного обмена информацией о ресторанах.

Рассмотрим шаги алгоритма SDS в виде псевдокода.

1. Инициализация кандидатов (назначение случайных ресторанов и блюд).

2.0. Тестирование гипотезы и диффузионный обмен между кандидатами.

2.1. Сравнение текущего опыта кандидата с его предыдущим.

2.1.1. Если опыт лучше, назначаем адреса ресторанов как гипотезу для следующей итерации.

2.1.2. Если опыт хуже, тогда спрашиваем мнение случайно выбранного кандидата.

2.1.2.1. Если опыт собеседника - кандидата лучше, тогда берем адреса перспективных (для текущего кандидата) ресторанов.

2.1.2.2. Если опыт собеседника - кандидата хуже, тогда с долей вероятности либо выбираем адрес случайно выбранного ресторана, либо оставляем текущий.

3.0. Выбираем блюда, в сформированном списке ресторанов, как гипотезу для следующей итерации.

Логическая схема проверки гипотез представлена на рисунке 2. Большая часть схемы логики выполняет задачу выбора ресторана, а после завершения выбора ресторана, случайным образом, выбирается блюдо. Выбор ресторана является главной задачей алгоритма, однако выбор блюда совершенно случаен и независим от предыдущих итераций.

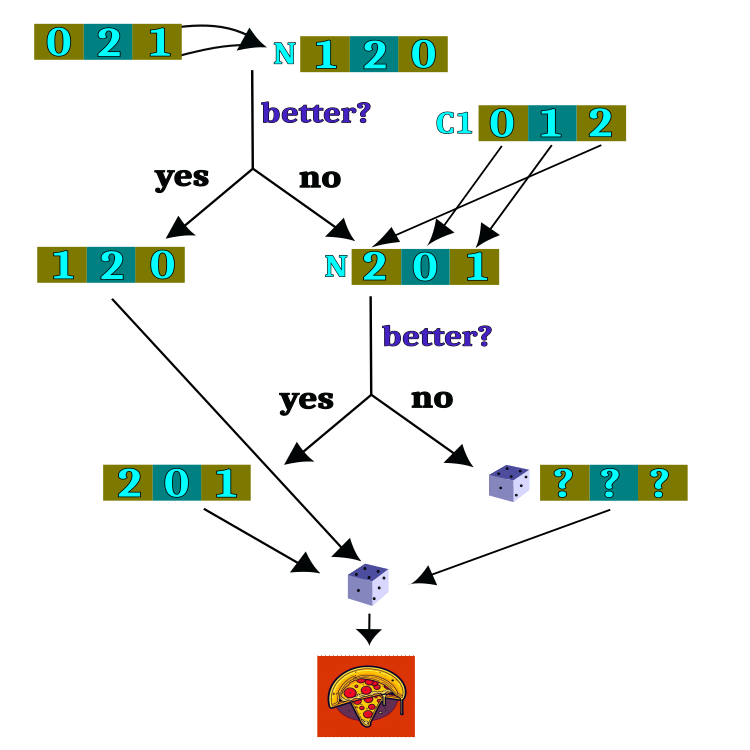
Рисунок 2. Логическая схема проверки гипотез.

Настало время рассмотреть код SDS (Stochastic Diffusion Search) и начать с сердца и души алгоритма - агента, он же кандидат, которого можно описать структурой S_Candidate. Она содержит следующие поля:

1. raddr: массив, содержащий адреса ресторанов. Каждый элемент массива представляет адрес одного ресторана.
2. raddrPrev: массив, содержащий предыдущие адреса ресторанов. Каждый элемент массива представляет предыдущий адрес одного ресторана.
3. c: массив, содержащий координаты (блюда). Каждый элемент массива представляет координату одного блюда.
4. cPrev: массив, содержащий предыдущие координаты (блюда). Каждый элемент массива представляет предыдущую координату одного блюда.
5. f: значение функции приспособленности (fitness) для текущего состояния агента.
6. fPrev: значение функции приспособленности (fitness) для предыдущего состояния агента.

Структура S_Candidate имеет метод Init, который инициализирует все массивы размерностью coords (количество координат - оптимизируемых параметров) и устанавливает начальные значения f и fPrev в -DBL_MAX, поскольку сравнивать опыт кандидата на первой итерации не с чем и не с кем.

//——————————————————————————————————————————————————————————————————————————————
struct S_Candidate
{
  void Init (int coords)
  {
    ArrayResize (c,         coords);
    ArrayResize (cPrev,     coords);
    ArrayResize (raddr,     coords);
    ArrayResize (raddrPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }
  int    raddr     []; //restaurant address
  int    raddrPrev []; //previous restaurant address
  double c         []; //coordinates (dishes)
  double cPrev     []; //previous coordinates (dishes)
  double f;            //fitness
  double fPrev;        //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс алгоритма SDS, содержащий следующее:

Поля класса:
- cB: массив, содержащий лучшие координаты
- fB: значение функции приспособленности для лучших координат
- cands: массив кандидатов для поиска оптимальных координат
- rangeMax: массив, содержащий максимальные значения для каждой координаты
- rangeMin: массив, содержащий минимальные значения для каждой координаты
- rangeStep: массив, содержащий шаги поиска для каждой координаты

Методы класса:
- Init: инициализация параметров алгоритма, таких как количество координат, размер популяции, количество ресторанов и вероятность выбора ресторана
- Moving: выполнение шага алгоритма, перемещение кандидатов в новые координаты
- Revision: выполнение шага ревизии, обновление лучших координат и функции приспособленности
- SeInDiSp: метод для вычисления новой координаты в заданном диапазоне с заданным шагом
- RNDfromCI: метод для генерации случайного числа в заданном интервале

Другие поля класса:
- coords: количество координат
- populationSize: размер популяции
- restNumb: количество ресторанов
- probabRest: вероятность выбора ресторана
- restSpace: пространство ресторанов
- revision: флаг, указывающий на необходимость выполнения ревизии

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDS
{
  //----------------------------------------------------------------------------
  public: double cB   [];       //best coordinates
  public: double fB;            //FF of the best coordinates
  public: S_Candidate cands []; //candidates

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search



  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP);         //probability restaurant choosing

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;            //coordinates number
  private: int    populationSize;    //population size

  private: int    restNumb;          //restaurants number
  private: double probabRest;        //probability restaurant choosing
  private: double restSpace [];      //restaurants space

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Метод инициализации алгоритма SDS начинается с установки начальных значений для некоторых переменных и массивов.

Входными параметрами метода являются:
- coordinatesNumberP: количество координат (размерность пространства поиска)
- populationSizeP: размер популяции (количество кандидатов)
- restaurantsNumberP: количество ресторанов
- probabRestP: вероятность выбора ресторана

Сначала происходит сброс генератора случайных чисел с помощью функции MathSrand и передачи ей текущего значения микросекунд. Затем переменные fB и revision инициализируются начальными значениями -DBL_MAX и false соответственно.
Далее присваиваются значения входным параметрам coordinatesNumberP и populationSizeP переменным coords и populationSize.
Переменные restNumb и probabRest инициализируются значениями restaurantsNumberP и probabRestP.
Создается массив restSpace размером coords с помощью функции ArrayResize.
Затем создается массив cands размером populationSize с помощью функции ArrayResize. В цикле происходит инициализация каждого элемента массива cands вызовом метода Init с параметром coords.
Также создаются массивы rangeMax, rangeMin, rangeStep и cB размером coords с помощью функции ArrayResize.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    restaurantsNumberP,   //restaurants number
                     const double probabRestP)          //probability restaurant choosing
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  populationSize = populationSizeP;

  restNumb   = restaurantsNumberP;
  probabRest = probabRestP;
  ArrayResize (restSpace, coords);

  ArrayResize (cands, populationSize);
  for (int i = 0; i < populationSize; i++) cands [i].Init (coords);

  ArrayResize (rangeMax,       coords);
  ArrayResize (rangeMin,       coords);
  ArrayResize (rangeStep,      coords);
  ArrayResize (cB,             coords);
}
//——————————————————————————————————————————————————————————————————————————————

Метод  Moving() хотя и будет вызываться на каждой итерации, но основная логика метода выполняется только один раз, контролируемая флагом revision.

В начале функции проверяется переменная revision, если она равна false, то выполняется инициализация переменных и массивов.
Затем происходит цикл по координатам точек пространства.

Внутри этого цикла вычисляется значение restSpace[i], которое представляет собой длину интервала для каждой координаты, определенную как разность между максимальным и минимальным значениями диапазона, деленная на restNumb.

Далее объявляются переменные min и max, которые будут использоваться для определения диапазона значений для пространства конкретного ресторана.

Затем инициализируются переменные n и dish, которые будут использоваться для определения случайных значений внутри диапазона выбранного ресторана.

Затем выполняется цикл по популяции размером populationSize, внутри которого выполняется цикл по координатам точек пространства. Внутри этого цикла генерируется случайное число n с помощью функции RNDfromCI(), которое используется для определения индекса в массиве restSpace. Если полученное значение n больше или равно restNumb, то оно присваивается restNumb - 1, для обеспечения равномерного распределения случайной величины. Затем вычисляются значения min и max, используя rangeMin, restSpace и n.

Генерируем случайное число dish (блюдо) с помощью функции RNDfromCI(), которое находится в диапазоне от min до max (пространство ресторана).

Затем значение dish используется для вычисления значения c[i] с помощью функции SeInDiSp(), использующей rangeMin, rangeMax, rangeStep для обеспечения корректного шага оптимизируемых параметров.

В результате выполнения этого алгоритма, каждая точка пространства получает случайные значения для каждой координаты в соответствии с пространством ресторана, имитируя случайный выбор блюда.

Переменная revision устанавливается в true, чтобы при следующем вызове функции Moving() не выполнялась инициализация переменных и массивов.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Moving ()
{
  if (!revision)
  {
    for (int i = 0; i < coords; i++)
    {
      restSpace [i] = (rangeMax [i] - rangeMin [i]) / restNumb;
    }

    double min = 0.0;
    double max = 0.0;

    int    n   = 0;
    double dish = 0.0;

    for (int i = 0; i < populationSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        n = (int)(RNDfromCI (0, restNumb));
        if (n >= restNumb) n = restNumb - 1;

        cands [i].raddr     [c] = n;
        cands [i].raddrPrev [c] = n;
        min = rangeMin [c] + restSpace [c] * n;
        max = min + restSpace [c];

        dish = RNDfromCI (min, max);

        cands [i].c [c] =  SeInDiSp (dish, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод Revision алгоритма SDS выполняет основную логику выбора ресторанов и блюд в ресторанах. Это не типично для алгоритмов, рассмотренных ранее, в которых основная логика перемещения агентов располагалась в методе Moving, хотя порядок обращения к методам алгоритма остаётся прежним и соответствует выбранной в первой статье серии статей концепции. Алгоритм состоит из следующих шагов:

1. Обновление лучшего найденного значения фитнес функции fB и соответствующего ему набора координат cB. Для каждого кандидата i в популяции, делается сравнение, если значение f (оценка функции) больше текущего глобального значения fB, то fB обновляется и в лучший глобальный набор координат cB копируется из кандидата i.

2. Обновление предыдущих значений оценок и наборов ресторанов для каждого кандидата. Для каждого кандидата i в популяции, если значение f больше предыдущего значения fPrev, то fPrev обновляется, а также копируются наборы ресторанов c и raddr из кандидата i в соответствующие предыдущие значения cPrev и raddrPrev.

3. Выбор нового набора ресторанов для каждого кандидата. Для каждого кандидата i в популяции и каждой координаты c, выбирается случайное число n в диапазоне от 0 до populationSize. Если значение fPrev для кандидата n больше значения fPrev для кандидата i, то набор ресторанов raddr для кандидата i обновляется значением raddrPrev для кандидата n. В противном случае, генерируется случайное число rnd в диапазоне от 0.0 до 1.0. Если rnd меньше вероятности probabRest, то выбирается случайное число n в диапазоне от 0 до restNumb и набор ресторанов raddr для кандидата i обновляется значением n. В противном случае, набор ресторанов raddr для кандидата i остается неизменным.

4. Генерация нового набора координат для каждого кандидата. Для каждого кандидата i в популяции и каждой координаты c, определяются минимальное и максимальное значения min и max на основе диапазона rangeMin и restSpace для соответствующей координаты. Затем генерируется случайное число в диапазоне от min до max с использованием функции SeInDiSp, и полученное значение присваивается соответствующей координате c в наборе c для кандидата i.

Таким образом, метод Revision алгоритма SDS выполняет каждую итерацию по популяции кандидатов, обновляет лучшее найденное значение и набор ресторанов, а также выбирает новые наборы ресторанов и генерирует новые наборы координат для каждого кандидата.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDS::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > fB)
    {
      fB = cands [i].f;
      ArrayCopy (cB, cands [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  double min = 0.0;
  double max = 0.0;
  double rnd = 0.0;
  int    n   = 0;

  for (int i = 0; i < populationSize; i++)
  {
    if (cands [i].f > cands [i].fPrev)
    {
      cands [i].fPrev = cands [i].f;
      ArrayCopy (cands [i].cPrev, cands [i].c, 0, 0, WHOLE_ARRAY);
      ArrayCopy (cands [i].raddrPrev, cands [i].raddr, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < populationSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, populationSize));
      if (n >= populationSize) n = populationSize - 1;

      if (cands [n].fPrev > cands [i].fPrev)
      {
        cands [i].raddr [c] = cands [n].raddrPrev [c];
      }
      else
      {
        rnd = RNDfromCI (0.0, 1.0);

        if (rnd < probabRest)
        {
          n = (int)(RNDfromCI (0, restNumb));
          if (n >= restNumb) n = restNumb - 1;
          cands [i].raddr [c] = n;
        }
        else
        {
          cands [i].raddr [c] = cands [i].raddrPrev [c];
        }
      }

      min = rangeMin [c] + restSpace [c] * cands [i].raddr [c];
      max = min + restSpace [c];

      cands [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы алгоритма стохастического диффузионного поиска на тестовом стенде:

C_AO_SDS:100;1000;0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.64253803557851
Score: 0.99921
25 Rastrigin's; Func runs 10000 result: 79.00996143538204
Score: 0.97898
500 Rastrigin's; Func runs 10000 result: 54.31544686388126
Score: 0.67300
=============================
5 Forest's; Func runs 10000 result: 1.677891584229713
Score: 0.94910
25 Forest's; Func runs 10000 result: 1.4089003503272384
Score: 0.79694
500 Forest's; Func runs 10000 result: 0.2437939668372883
Score: 0.13790
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.448
Score: 0.53733
500 Megacity's; Func runs 10000 result: 0.9551999999999999
Score: 0.07960
=============================
All score: 5.86873

Сразу при взгляде на принт результатов работы алгоритма можем обратить внимание на невероятно высокие результаты по сравнению с другими алгоритмами. Подробное сравнение представлено ниже в таблице.

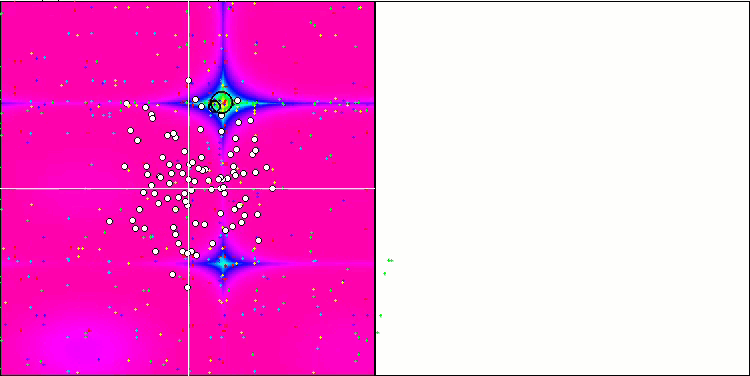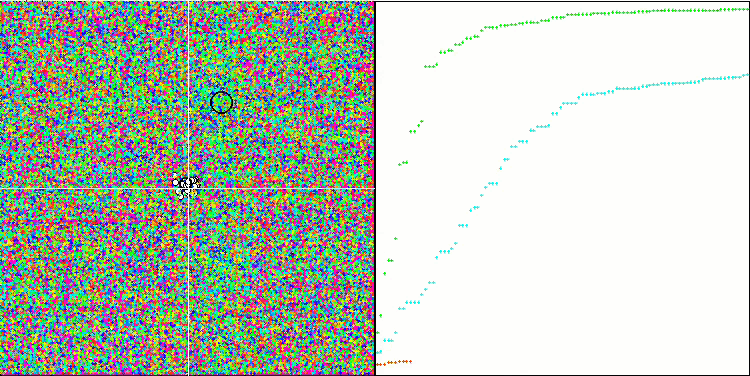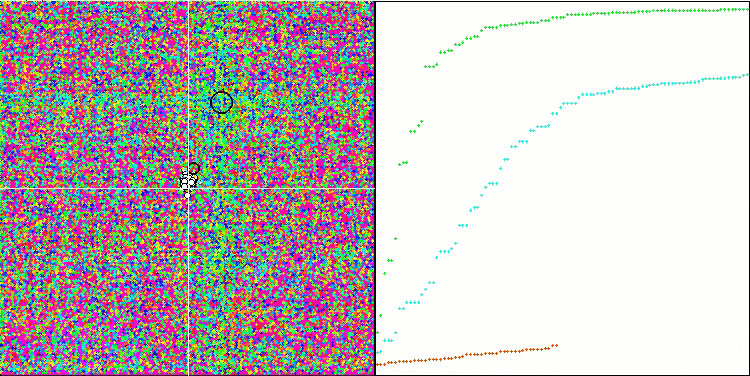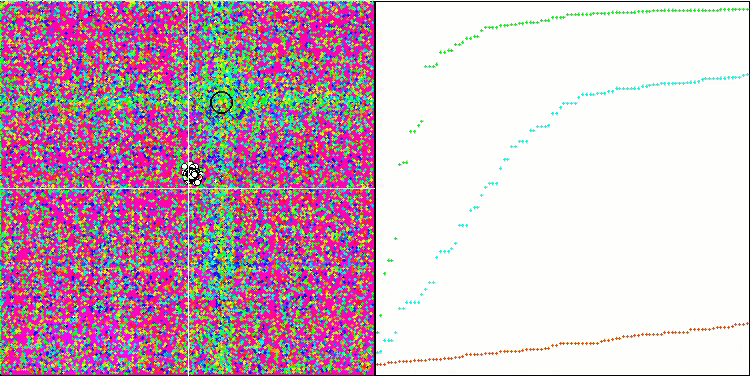
Особо следует отметить нетипичное поведение алгоритма при визуализации движения агентов. Агенты распределяются по количеству равномерно и пропорционально высоты холма фитнес функции, демонстрируя высокое качество кластеризации по локальным экстремумам. Создается впечатление, что ни один холм не будет упущен из вида алгоритма. Также обращает на себя внимание практически бесступенчатый рост сходимости алгоритма на каждой итерации, что говорит о малой склонности к застреванию в локальных экстремумах. Даже на сложнейшей функции Forest с острым глобальный экстремумом не наблюдается ступенчатости сходимости.

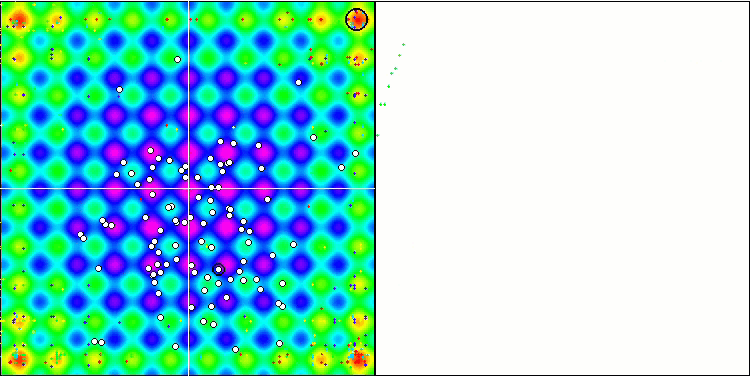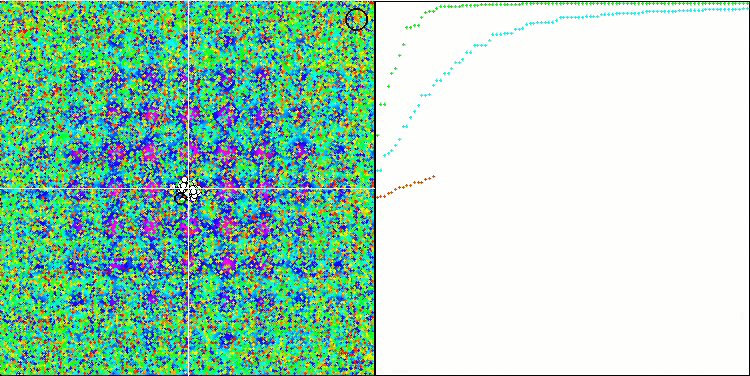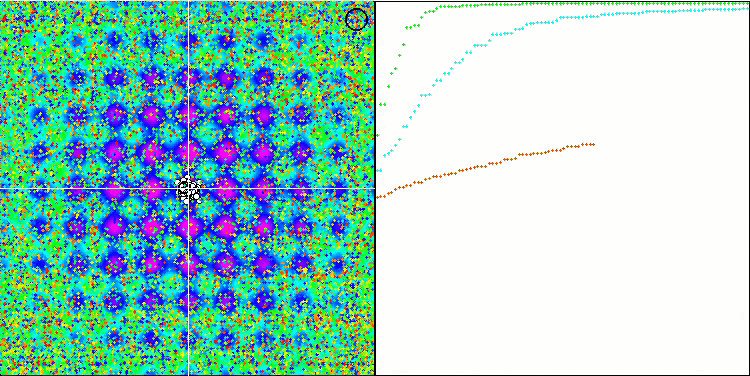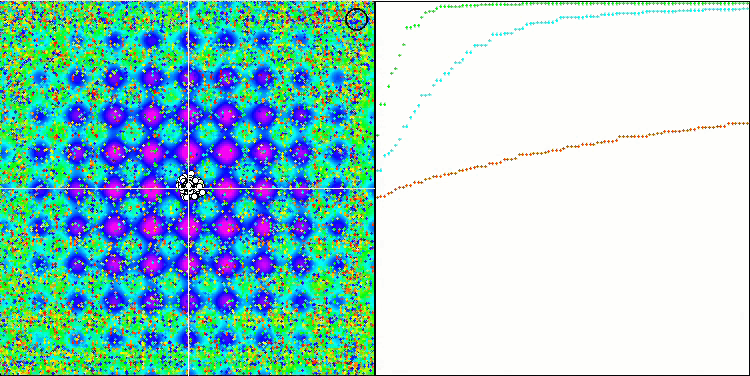
  SDS на тестовой функции Rastrigin.

  SDS на тестовой функции Forest.

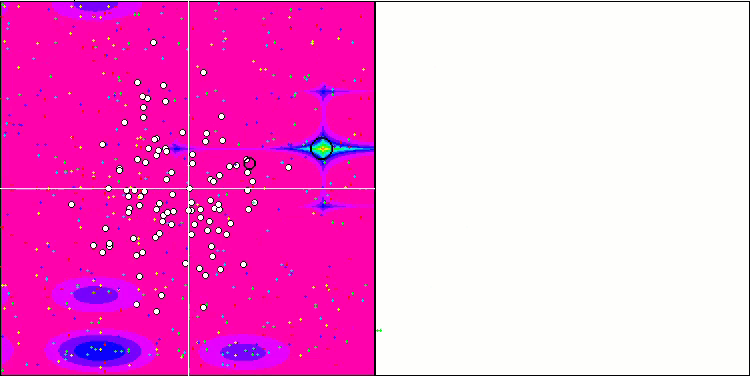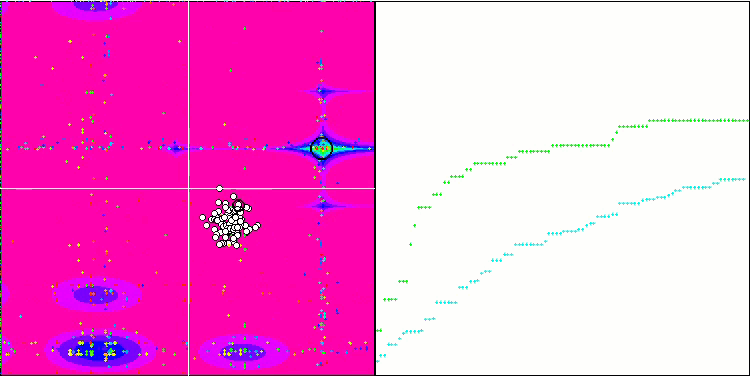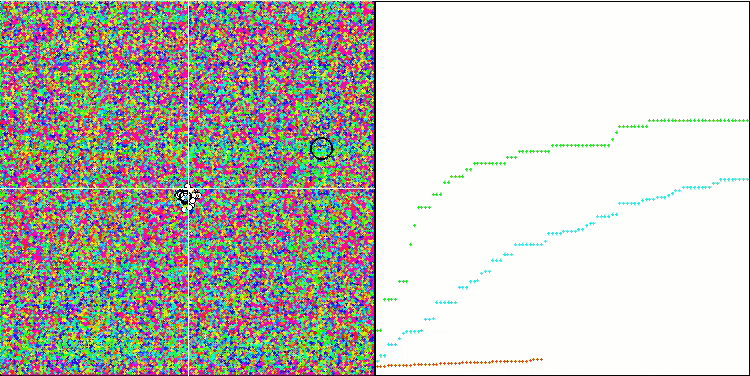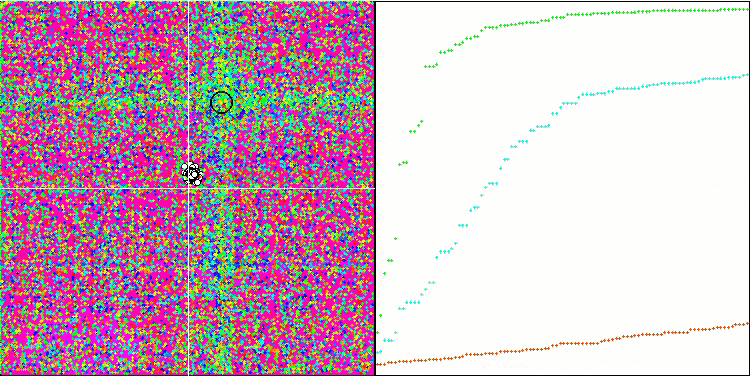
  SDS на тестовой функции Megacity.

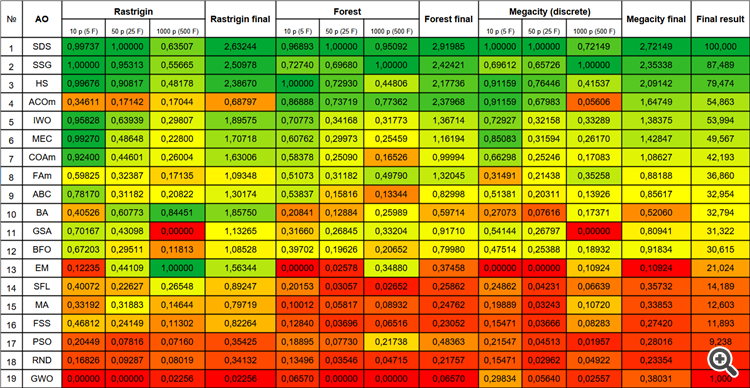
Хотелось бы отметить, что я никак не ожидал потрясающих результатов у такого очень простого, основанного на чистом случайном блуждании, алгоритма. Алгоритм SDS с большим превосходством, почти 13%, опередил все ранее рассмотренные алгоритмы, демонстрируя самые лучшие результаты во многих тестах (4 первых места из 9 возможных). Единственная дисциплина - многопеременная функция Растригина, лидер в которой далеко всех оставил позади, это алгоритм электромагнитного поиска (EM).

Даже на чрезвычайно сложной дискретной функции Megacity, алгоритм SDS показывает превосходные результаты, демонстрируя при этом практически полное отсутствие застревания, единственный, кто опередил SDS в тестах с 1000 переменных на Forest и Megacity - алгоритм растущих деревьев (SSG). 

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	stochastic diffusion search	0,99737	1,00000	0,63507	2,63244	0,96893	1,00000	0,95092	2,91985	1,00000	1,00000	0,72149	2,72149	100,000
2	SSG	saplings sowing and growing	1,00000	0,95313	0,55665	2,50978	0,72740	0,69680	1,00000	2,42421	0,69612	0,65726	1,00000	2,35338	87,489
3	HS	harmony search	0,99676	0,90817	0,48178	2,38670	1,00000	0,72930	0,44806	2,17736	0,91159	0,76446	0,41537	2,09142	79,474
4	ACOm	ant colony optimization M	0,34611	0,17142	0,17044	0,68797	0,86888	0,73719	0,77362	2,37968	0,91159	0,67983	0,05606	1,64749	54,863
5	IWO	invasive weed optimization	0,95828	0,63939	0,29807	1,89575	0,70773	0,34168	0,31773	1,36714	0,72927	0,32158	0,33289	1,38375	53,994
6	MEC	mind evolutionary computation	0,99270	0,48648	0,22800	1,70718	0,60762	0,29973	0,25459	1,16194	0,85083	0,31594	0,26170	1,42847	49,567
7	COAm	cuckoo optimization algorithm M	0,92400	0,44601	0,26004	1,63006	0,58378	0,25090	0,16526	0,99994	0,66298	0,25246	0,17083	1,08627	42,193
8	FAm	firefly algorithm M	0,59825	0,32387	0,17135	1,09348	0,51073	0,31182	0,49790	1,32045	0,31491	0,21438	0,35258	0,88188	36,860
9	ABC	artificial bee colony	0,78170	0,31182	0,20822	1,30174	0,53837	0,15816	0,13344	0,82998	0,51381	0,20311	0,13926	0,85617	32,954
10	BA	bat algorithm	0,40526	0,60773	0,84451	1,85750	0,20841	0,12884	0,25989	0,59714	0,27073	0,07616	0,17371	0,52060	32,794
11	GSA	gravitational search algorithm	0,70167	0,43098	0,00000	1,13265	0,31660	0,26845	0,33204	0,91710	0,54144	0,26797	0,00000	0,80941	31,322
12	BFO	bacterial foraging optimization	0,67203	0,29511	0,11813	1,08528	0,39702	0,19626	0,20652	0,79980	0,47514	0,25388	0,18932	0,91834	30,615
13	EM	electroMagnetism-like algorithm	0,12235	0,44109	1,00000	1,56344	0,00000	0,02578	0,34880	0,37458	0,00000	0,00000	0,10924	0,10924	21,024
14	SFL	shuffled frog-leaping	0,40072	0,22627	0,26548	0,89247	0,20153	0,03057	0,02652	0,25862	0,24862	0,04231	0,06639	0,35732	14,189
15	MA	monkey algorithm	0,33192	0,31883	0,14644	0,79719	0,10012	0,05817	0,08932	0,24762	0,19889	0,03243	0,10720	0,33853	12,603
16	FSS	fish school search	0,46812	0,24149	0,11302	0,82264	0,12840	0,03696	0,06516	0,23052	0,15471	0,03666	0,08283	0,27420	11,893
17	PSO	particle swarm optimisation	0,20449	0,07816	0,07160	0,35425	0,18895	0,07730	0,21738	0,48363	0,21547	0,04513	0,01957	0,28016	9,238
18	RND	random	0,16826	0,09287	0,08019	0,34132	0,13496	0,03546	0,04715	0,21757	0,15471	0,02962	0,04922	0,23354	5,108
19	GWO	grey wolf optimizer	0,00000	0,00000	0,02256	0,02256	0,06570	0,00000	0,00000	0,06570	0,29834	0,05640	0,02557	0,38031	1,000

Выводы

Алгоритм стохастического поиска (SDS) является эффективным методом оптимизации, который использует случайные выборки для нахождения глобального оптимума заданной функции.
В статье были представлены основные принципы работы алгоритма SDS. Он основывается на идее случайного выбора точек в разбитом на участки пространстве поиска. Результаты тестов показали, что SDS способен находить глобальные оптимумы в сложных функциях с большим числом локальных экстремумов, демонстрируя отличную сходимость. Одним из преимуществ алгоритма SDS является его простота и легкость реализации. Он не требует большого количества вычислений и может быть применен для различных типов задач оптимизации.

Для более наглядного представления преимуществ и недостатков отдельных алгоритмов в сравнении между собой таблицу выше можно представить с помощью цветовой шкалы на рисунке 3.

Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам.

Гистограмма результатов тестирования алгоритмов на рисунке 3 (по шкале от 0 до 100, чем больше тем лучше, в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье):

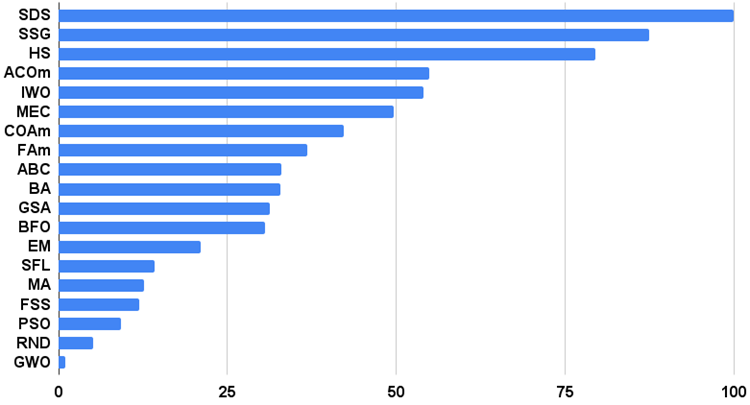
Рисунок 4. Гистограмма итоговых результатов тестирования алгоритмов.

Плюсы и минусы алгоритма стохастического диффузионного поиска (SDS):

Плюсы:
1. Минимальное количество внешних параметров.
2. Высокая эффективность при решении разнообразных задач.
3. Низкая нагрузка на вычислительные ресурсы.
4. Легкость в реализации алгоритма.
5. Устойчивость к застреванию.
6. Высокие результаты как на гладких, так и на сложных дискретных функциях.
7. Высокая сходимость.

Минусы:
1. Не замечены.

К каждой статье я прикрепляю архив, содержащий обновленные актуальные версии кодов алгоритмов, описанных в предыдущих статьях. Однако, следует отметить, что я не несу ответственность за абсолютную точность в описании канонических алгоритмов. Часто я также добавляю свои идеи и улучшения, основываясь на накопленном опыте и личном мнении. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.