Популяционные алгоритмы оптимизации: Дифференциальная эволюция (Differential Evolution, DE)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Метаэвристические методы оптимизации - это класс алгоритмов, которые используют эвристические подходы для решения сложных оптимизационных задач. Они отличаются от численных методов оптимизации, которые обычно основаны на математическом анализе и требуют знания градиента или производной целевой функции. Основное отличие метаэвристических методов заключается в их способности исследовать большие пространства поиска и находить глобальные оптимумы, даже в случаях, когда функция имеет множество локальных оптимумов или не является непрерывно-дифференцируемой. Преимущества метаэвристических методов состоит в том, что они могут работать с "черным ящиком", то есть функцией, для которой нет аналитического решения. Они основаны на стохастических вероятностных принципах и обеспечивают хорошее качество решения.

Эволюционные алгоритмы (ЭА) - это отдельный класс метаэвристических методов оптимизации, которые моделируют процесс естественной эволюции для решения сложных оптимизационных задач. Они основаны на принципах наследственности, мутации, скрещивания и естественного отбора. Процесс эволюции в эволюционных алгоритмах моделирует естественный отбор, где более приспособленные решения имеют большую вероятность выжить и передать свои характеристики следующему поколению. Таким образом, постепенно популяция сходит к оптимальному решению. Некоторые из наиболее известных эволюционных алгоритмов включают: генетические алгоритмы (GA), эволюционное программирование (EP), стратегии эволюции (ES) и генетическое программирование (GP). Каждый из этих алгоритмов имеет свои особенности и применяется в различных областях.

В целом, эволюционные алгоритмы являются мощным инструментом для решения сложных оптимизационных задач, особенно в случаях, когда нет доступа к аналитическому выражению функции или градиенту. Они позволяют исследовать пространство поиска и находить оптимальные решения, комбинируя информацию из разных индивидуальных решений.

Дифференциальная эволюция (DE) является одним из метаэвристических методов оптимизации. Она отличается от других методов своей простотой и эффективностью. DE использует популяцию векторов, которые мутируют и скрещиваются для создания новых решений. Она не требует знания градиента и способна находить глобальные оптимумы.

Алгоритм DE был разработан в 90-х годах Сторном и Прайсом (был опубликован в работе "Дифференциальная эволюция - простая и эффективная эвристика для глобальной оптимизации в непрерывных пространствах"), и с тех пор стал одним из наиболее популярных методов оптимизации, который использует популяцию векторов параметров для поиска оптимального решения.

2. Описание алгоритма

Идея дифференциальной эволюции - это совокупность простоты и эффективности. В алгоритме дифференциальной эволюции используется популяция векторов, представляющих потенциальные решения. Каждый вектор состоит из компонентов, которые представляют значения переменных оптимизационной задачи.

В DE роль поискового агента выполняет вектор. Алгоритм начинается с создания случайной популяции векторов. Затем происходит итеративный процесс, в котором каждый вектор мутирует и скрещивается с другими векторами в популяции. Мутация осуществляется путем добавления разницы между двумя случайно выбранными векторами из популяции к третьему вектору. Это создает новый вектор, который представляет потенциальное решение задачи.

После мутации происходит скрещивание мутировавшего вектора с исходным вектором. Скрещивание позволяет комбинировать информацию из двух векторов и создавать новые варианты решений. Полученный результат сравнивается с текущим лучшим решением в популяции. Если новый вектор лучше, он заменяет старый вектор и становится частью популяции. Мутация позволяет исследовать пространство поиска, а скрещивание позволяет комбинировать информацию из разных векторов и создавать новые варианты решений.

Этот процесс мутации, скрещивания и замены повторяется в течение нескольких итераций, пока не будет достигнуто условие остановки, например, заданное количество итераций или достижение требуемой точности решения, в нашем случае достижения 10000 запусков фитнес-функции.

DE - это один из эволюционных алгоритмов, который широко используется для решения задач оптимизации. В дифференциальном алгоритме используется оператор дифференциации, чтобы создать новые кандидаты на основе текущей популяции. Вот основные формулы, используемые в дифференциальном алгоритме:

1. Формула для создания нового кандидата (дифференциации):

r = r1 + F * (r2 - r3)

где:

• v - представляет компонент нового вектора
• r1, r2 и r3 - компоненты случайно выбранных векторов (индивидуальные решения из популяции)
• F - коэффициент дифференциации, который контролирует степень изменчивости решения (разброс получаемых значений), по умолчанию принимается в диапазоне (0.0;1.0]
  

2. Формула для скрещивания (crossover):

u = crossover (x, v)

Данная формула описывает процесс скрещивания между текущим решением x и новым кандидатом v. Оператор скрещивания определяет, какие компоненты решения будут взяты из нового кандидата. Это вероятность использования нового компонента вектора, в противном случае компонент остаётся без изменений, используются значения (0.0;1.0].

Составим псевдокод алгоритма DE, который прост и понятен из-за простоты самого алгоритма (на самом деле код получится не намного сложнее, чем его псевдокод):

1. Создать случайную популяцию векторов
   
2. Вычислить фитнес-функцию
3. Обновить лучшее решение
4. Обновить популяцию (заменить вектора лучшими мутантами)
5. Создать мутантный компонент вектора или оставить прежний в зависимости от того, который из них лучше
   
6. Повторить с п.2.

Для описания вектора в алгоритме DE напишем структуру, так и назовём её, S_Vector, которая представляет собой вектор в n-мерном пространстве. Структура имеет следующие поля:

•  Init (int coords): функция инициализирует вектор заданной длины coords. Она создает два массива: "c" и "cPrev", представляющие координаты вектора и его предыдущие координаты соответственно. Также устанавливает начальные значения для f и fPrev равными -DBL_MAX. 
• c []: массив, содержащий координаты вектора
• cPrev []: массив содержащий координаты вектора на предыдущей итерации 
• f: значение функции приспособленности для текущего вектора 
• fPrev: значение функции приспособленности вектора на предыдущей итерации

//——————————————————————————————————————————————————————————————————————————————
struct S_Vector
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

У такого элементарно-простого алгоритма, как DE и описание класса очень простое, объявим класс C_AO_DE. Поля класса C_AO_DE содержат информацию о текущем состоянии алгоритма и его параметрах, а методы выполняют различные операции, связанные с оптимизацией функции.

Класс имеет следующие поля и методы:

• cB []: массив содержит лучшие координаты, найденные алгоритмом
• fB: значение функции приспособленности для лучших координат
• v []: массив структур S_Vector, представляющий популяцию векторов
• rangeMax[]: массив содержит максимальные значения для каждой координаты вектора
• rangeMin[]: массив содержит минимальные значения для каждой координататы вектора
• rangeStep[]: массив содержит значения шага для каждой координаты вектора
• Init (int coordsP, int popSizeP, double diffWeightP, double crossProbabP): функция инициализирует параметры алгоритма. Она принимает количество координат "coordsP", размер популяции "popSizeP", дифференциальный вес "diffWeightP" и вероятность кроссовера "crossProbabP".
• Moving (): функция выполняет один шаг алгоритма дифференциальной эволюции
• Revision (): функция выполняет ревизию популяции векторов
• SeInDiSp (double In, double InMin, double InMax, double Step): метод вычисляет новое значение координаты в заданном диапазоне с заданным шагом
• RNDfromCI (double min, double max): функция генерирует случайное число в диапазоне [min, max]

//——————————————————————————————————————————————————————————————————————————————
class C_AO_DE
{
  //----------------------------------------------------------------------------
  public: double cB  []; //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Vector v []; //vector

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,       //coordinates number
                     const int    popSizeP,      //population size
                     const double diffWeightP,   //differential weight
                     const double crossProbabP); //crossover robability

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double diffWeight;   //differential weight
  private: double crossProbab;  //crossover robability

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Метод Init класса C_AO_DE инициализирует параметры алгоритма дифференциальной эволюции. Метод принимает четыре параметра:

• "coordsP" - количество координат,
• "popSizeP" - размер популяции,
• "diffWeightP" - дифференциальный вес
• "crossProbabP" - вероятность кроссовера.

В начале метод использует функцию MathSrand для сброса генератора случайных чисел. Это гарантирует, что каждый раз, когда алгоритм запускается, он использует новую последовательность случайных чисел.

Затем метод инициализирует переменные "fB" и "revision". Переменная "fB" содержит лучшее значение функции приспособленности, найденное алгоритмом. Изначально оно устанавливается на "-DBL_MAX", то есть на очень маленькое число. Переменная "revision" устанавливается на "false", что означает, что популяция векторов не была еще пересмотрена.

Затем метод инициализирует переменные "coords", "popSize", "diffWeight" и "crossProbab" значениями, переданными в качестве параметров.

Далее метод создает массив "v" размера "popSize", который содержит популяцию векторов.

Затем метод создает три массива: "rangeMax", "rangeMin" и "rangeStep", каждый размера coords (количество координат).

Наконец, метод создает массив "cB" размера coords, который содержит лучшие координаты, найденные алгоритмом.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Init  (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double diffWeightP,  //differential weight
                     const double crossProbabP) //crossover robability
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordsP;
  popSize = popSizeP;

  diffWeight  = diffWeightP;
  crossProbab = crossProbabP;

  ArrayResize (v, popSize);
  for (int i = 0; i < popSize; i++) v [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Для изменения векторов-решений в пространстве поиска напишем метод "Moving" класса C_AO_DE. Метод применяет мутационный и кроссоверный операторы для генерации новых векторов-кандидатов и выбирает наилучшее решение на основе функции приспособленности.

Первый блок кода, который начинается с условия "if (!revision)", выполняется только при первом запуске метода "Moving" или после вызова метода "Init". Он инициализирует начальную популяцию векторов случайными значениями в заданных пределах и с шагом, указанным в массиве "rangeStep".

Затем метод использует цикл "for" для обновления каждого вектора в популяции. Для каждого вектора метод выбирает три разных случайных вектора из популяции (r1, r2, r3), не совпадающих с текущим вектором (i), и применяет мутационный и кроссоверный операторы, чтобы получить новый вектор-кандидат. Мутационный оператор вычисляет разность между векторами "r2" и "r3", умноженную на дифференциальный вес "diffWeight", и добавляет результат к вектору "r1". Кроссоверный оператор выбирает координату вектора и заменяет ее на соответствующую координату нового вектора-кандидата с вероятностью crossProbab. Если вероятность кроссовера не выполняется, то текущая координата вектора остается неизменной.

Внимательный читатель, разбирая код ниже, обнаружит, что метод изменения векторов "Moving" не предусматривает создание координат в пространстве, кроме тех, которые могут быть получены из существующих. Таким образом стохастичность алгоритма заключается только выбором векторов для скрещивания, но не создания новых, оригинальных. Это особенность определяет далеко идущие последствия, о которых мы поговорим ниже.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        v [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;
  int    r   = 0;
  int    r1  = 0;
  int    r2  = 0;
  int    r3  = 0;

  for (int i = 0; i < popSize; i++)
  {
    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r1 = r;
    }
    while (r1 == i);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r2 = r;
    }
    while (r2 == i || r2 == r1);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r3 = r;
    }
    while (r3 == i || r3 == r1 || r3 == r2);

    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (0, 1.0);

      if (rnd < crossProbab)
      {
        v [i].c [c] = v [r1].cPrev [c] + diffWeight * (v [r2].cPrev [c] - v [r3].cPrev [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        v [i].c [c] = v [i].cPrev [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

И наконец, нам понадобится, метод "Revision" класса C_AO_DE, который обновляет лучшее решение в популяции и сохраняет предыдущие значения функции приспособленности и координат векторов.

Сначала метод инициализирует переменную "ind" значением "-1". Затем он использует цикл "for" для перебора всех векторов в популяции и проверяет, если функция приспособленности текущего вектора больше, чем "fB" (лучшая функция приспособленности, найденная до сих пор), то он сохраняет индекс этого вектора в переменной "ind".

Если "ind" не равен "-1", то метод обновляет значение "fB" на значение функции приспособленности вектора с индексом "ind" и сохраняет его координаты в массиве "cB".

Затем метод использует еще один цикл "for" для перебора всех векторов в популяции и проверяет, если функция приспособленности текущего вектора больше, чем его предыдущее значение, то метод сохраняет текущее значение функции приспособленности и координаты вектора в соответствующих полях v[i].fPrev и v[i].cPrev.

Этот метод позволяет классу C_AO_DE сохранять лучшее решение в популяции и предыдущие значения функции приспособленности и координат векторов для использования в дальнейшем при оптимизации функции приспособленности.

Можно заметить, что популяция никак не сдвинется далее в пространстве поиска, пока не будет найден вектор лучше, чем его исходная (родительская) версия. Этот момент дополняет вышесказанное.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = v [ind].f;
    ArrayCopy (cB, v [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > v [i].fPrev)
    {
      v [i].fPrev = v [i].f;
      ArrayCopy (v [i].cPrev, v [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы алгоритма дифференциальной эволюции на тестовом стенде:

C_AO_DE:50;0.2;0.8
=============================
5 Rastrigin's; Func runs 10000 result: 80.30183306326985
Score: 0.99498
25 Rastrigin's; Func runs 10000 result: 76.15178282331799
Score: 0.94356
500 Rastrigin's; Func runs 10000 result: 52.17316317703311
Score: 0.64645
=============================
5 Forest's; Func runs 10000 result: 1.7348423083855402
Score: 0.98131
25 Forest's; Func runs 10000 result: 1.28572746338484
Score: 0.72727
500 Forest's; Func runs 10000 result: 0.20833645141168078
Score: 0.11785
=============================
5 Megacity's; Func runs 10000 result: 9.640000000000002
Score: 0.80333
25 Megacity's; Func runs 10000 result: 3.9199999999999995
Score: 0.32667
500 Megacity's; Func runs 10000 result: 0.3548
Score: 0.02957
=============================
All score: 5.57100

По выходным значениям алгоритма мы видим превосходные результаты тестов.

На визуализации можем видеть феноменальную сходимость алгоритма, но также можно заметить и особенность, о которой говорили выше в описании методов "Moving" и "Revision". При создании визуализации, после нескольких попыток, я специально выбрал самые удачные, на самом деле результаты получаются далеко не всегда такими замечательными. Это объясняется вырождением популяции, когда полностью вся популяция, все до единого вектора, сходятся к какому-то одному экстремуму. Но, это может оказаться вовсе не глобальный оптимум. Как говорилось выше, у алгоритма отсутствуют механизмы, позволяющие продолжать исследовать пространство поиска, создавая новые уникальные вектора. Алгоритм DE не создаёт новых векторов, а только генерирует комбинации из существующих. Этим и объясняется полное вырождение популяции, никакой "новой крови" не создаётся, что бы разнообразить "генофонд" популяции.

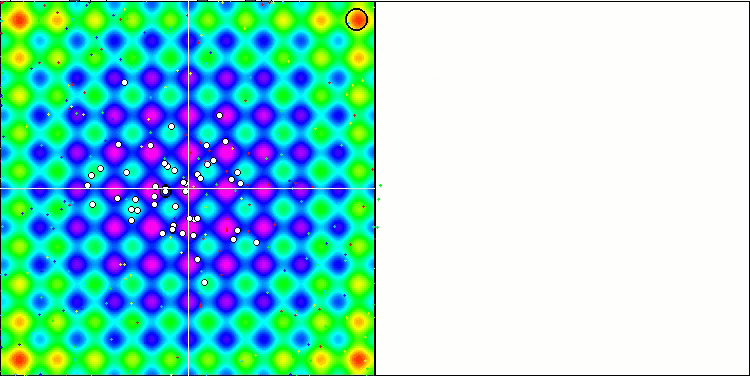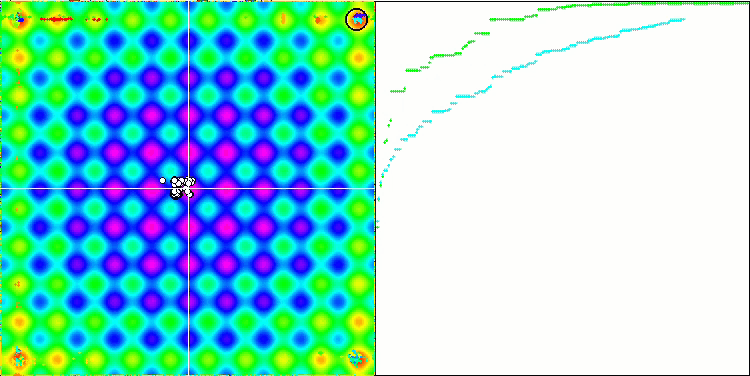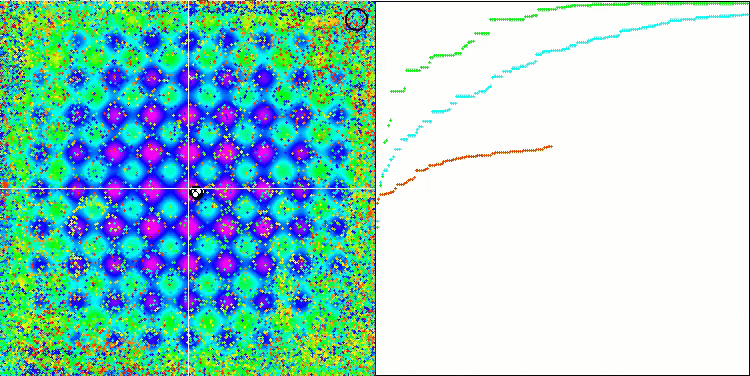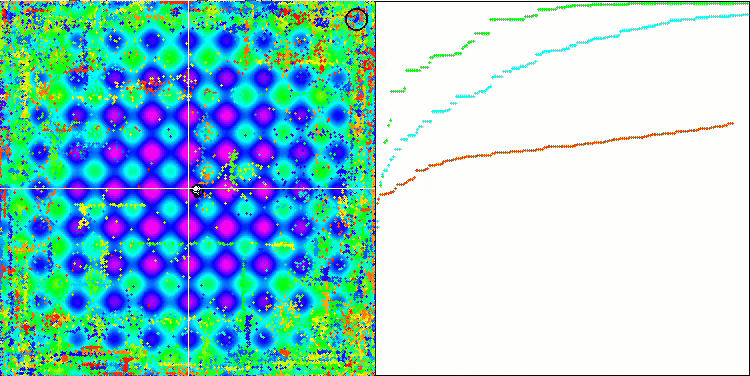
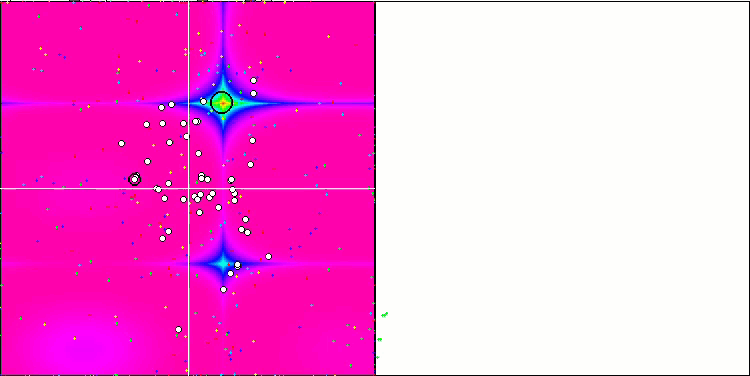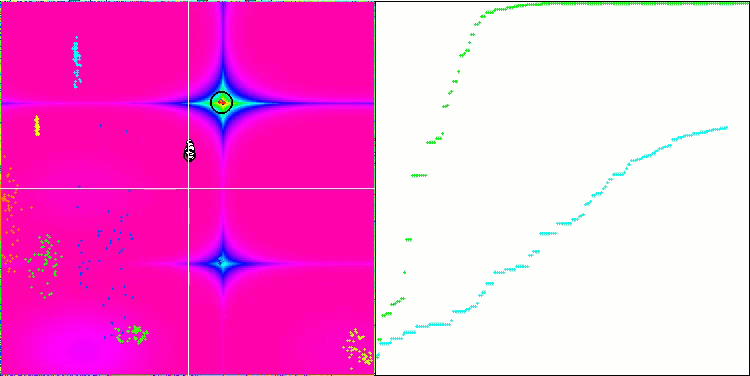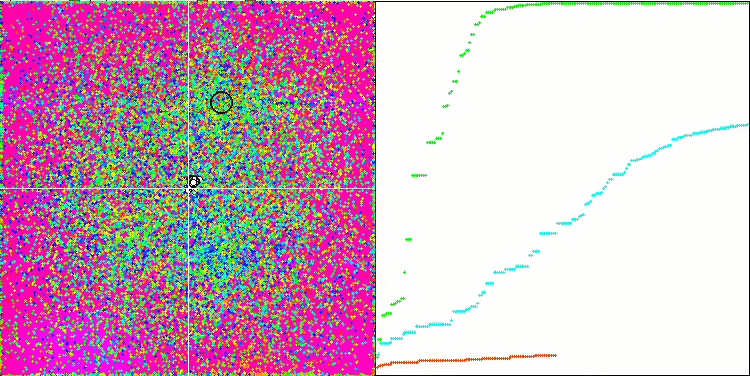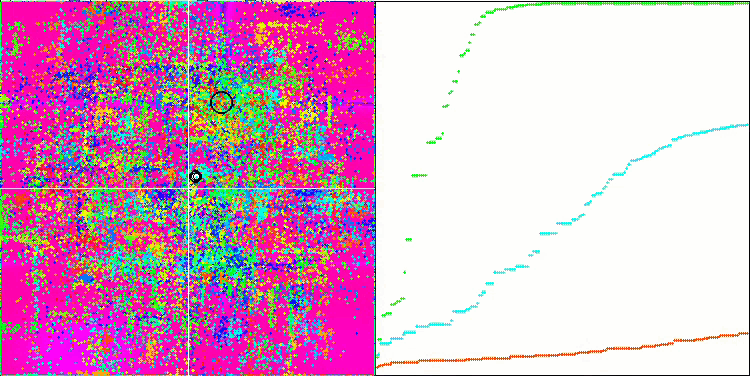
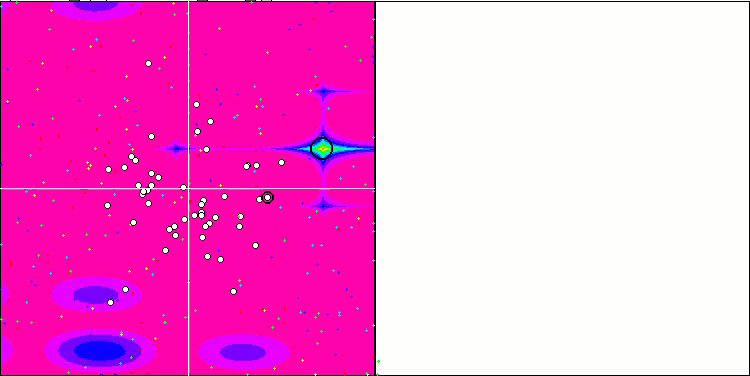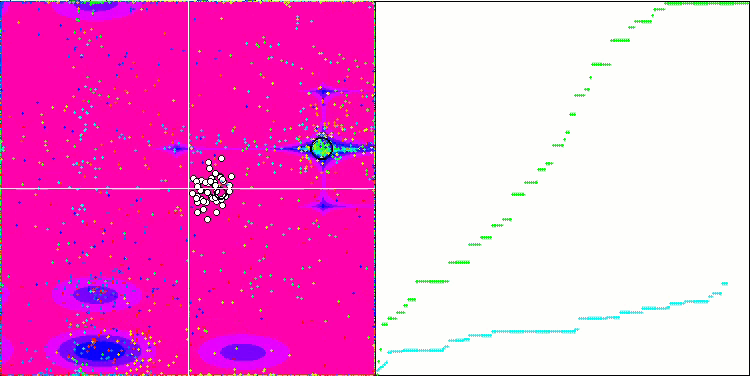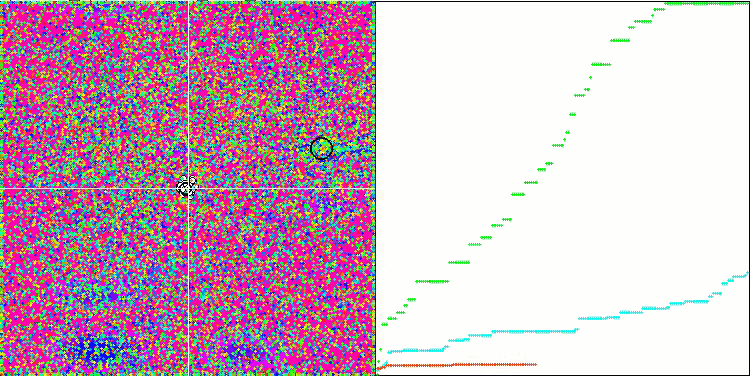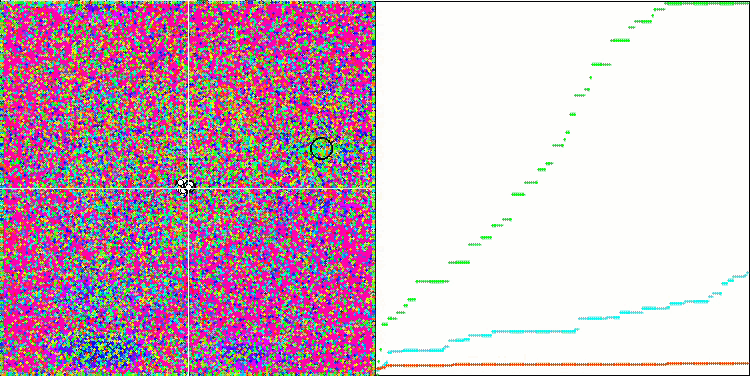
  DE на тестовой функции Rastrigin.

  DE на тестовой функции Forest.

  DE на тестовой функции Megacity.

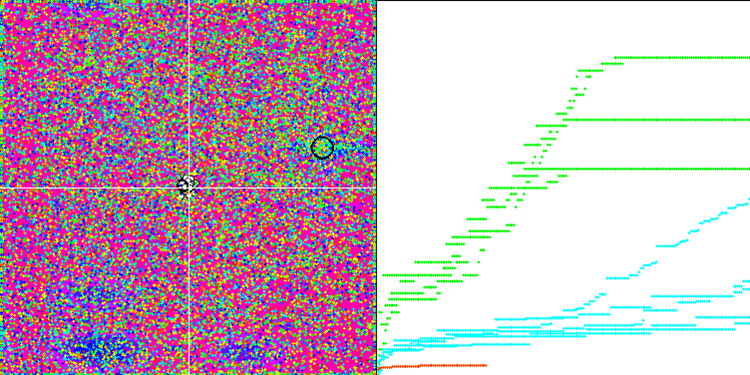
Пример огромного разброса сходимости. Особенно выражено на функциях Forest и Megacity.

Перейдем к рассмотрению итоговой рейтинговой таблицы с новым участником - DE. Алгоритм смог вырвать у текущего лидера SDSm призовое место в тесте Forest с 10-ю переменными. Результаты остальных тестов тоже очень хорошие и DE занял четвёртое место после SSG. Необходимо отметить, что вместо обычного 5-ти кратного запуска тестов для каждой из тестовых функций, мне пришлось произвести 10-ти кратное тестирование из-за огромного разброса результатов на функциях Forest и Megacity. На гладкой функции Rastrigin разброс результатов менее выражен. 

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	0,99265	1,00000	1,00000	2,99265	1,00000	1,00000	1,00000	3,00000	100,000
2	SDS	stochastic Diffusion Search	0,99737	0,97322	0,58904	2,55963	0,96067	0,93572	0,79649	2,69288	0,78696	0,93815	0,71804	2,44315	88,201
3	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72120	0,65201	0,83760	2,21081	0,54782	0,61841	0,99522	2,16146	77,683
4	DE	differential evolution	0,98295	0,89236	0,51375	2,38906	1,00000	0,84602	0,65510	2,50112	0,90000	0,52237	0,12031	1,54268	73,099
5	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99148	0,68242	0,37529	2,04919	0,71739	0,71842	0,41338	1,84919	70,623
6	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70170	0,31972	0,26613	1,28755	0,57391	0,30527	0,33130	1,21048	48,250
7	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86147	0,68980	0,64798	2,19925	0,71739	0,63947	0,05579	1,41265	47,387
8	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60244	0,28046	0,21324	1,09615	0,66957	0,30000	0,26045	1,23002	44,049
9	SDOm	spiral dynamics optimization M	0,69840	0,52988	0,33168	1,55996	0,59818	0,38766	0,37600	1,36183	0,35653	0,15262	0,25842	0,76758	40,289
10	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,57881	0,23477	0,13842	0,95200	0,52174	0,24079	0,17001	0,93254	37,830
11	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,50637	0,29178	0,41704	1,21519	0,24783	0,20526	0,35090	0,80398	33,139
12	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53379	0,14799	0,11177	0,79355	0,40435	0,19474	0,13859	0,73768	29,766
13	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20664	0,12056	0,21769	0,54488	0,21305	0,07632	0,17288	0,46225	29,499
14	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,13961	0,01853	0,13638	0,29452	0,07392	0,00000	0,03465	0,10856	27,930
15	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31390	0,25120	0,27812	0,84322	0,42609	0,25525	0,00000	0,68134	27,807
16	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39364	0,18364	0,17298	0,75026	0,37392	0,24211	0,18841	0,80444	27,542
17	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,29215	0,31628	0,00000	0,00527	0,10872	0,11399	19,002
18	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,19981	0,02861	0,02221	0,25063	0,19565	0,04474	0,06607	0,30646	13,200
19	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,09927	0,05443	0,07482	0,22852	0,15652	0,03553	0,10669	0,29874	11,777
20	FSS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12730	0,03458	0,05458	0,21647	0,12175	0,03947	0,08244	0,24366	11,332
21	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28358	0,05445	0,05112	0,38916	0,22609	0,05659	0,05054	0,33322	10,423
22	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18734	0,07233	0,18207	0,44175	0,16956	0,04737	0,01947	0,23641	8,426
23	RND	random	0,16826	0,09038	0,07438	0,33302	0,13381	0,03318	0,03949	0,20648	0,12175	0,03290	0,04898	0,20363	5,054
24	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06514	0,00000	0,00000	0,06514	0,23478	0,05789	0,02545	0,31812	1,000

Выводы

Алгоритм дифференциальной эволюции способен находить очень быстро глобальные оптимумы и обладает отличной сходимостью, если принимать во внимание весьма посредственные результаты в отдельных тестах. DE широко применяется в различных областях, таких как оптимизация параметров моделей, настройка нейронных сетей, оптимизация функций в физике и экономике, и многих других. Я бы рекомендовал производить несколько запусков оптимизации с помощью этого алгоритма, так как результаты очень сильно зависят от начальной популяции на первой итерации. Полезным может быть увеличение размера популяции с одновременным увеличением количества итераций.

При своей простоте и скорости работы, алгоритм дифференциальной эволюции имеет очевидные недостатки, такие как вырождение популяции и как следствие застревание в локальных экстремумах, необходимо учитывать эти моменты при выборе DE для своих задач оптимизации.

Алгоритм DE, рассмотренный в данной статье, является своего рода шаблоном, на основе которого созданы несколько модификаций. Мои предложения по улучшению алгоритма дифференциальной эволюции (DE) заключается в следующем:

1. Использование адаптивных методов контроля параметров: DE имеет несколько параметров, которые необходимо настроить вследствие их значительного влияния на результататы.

Рекомендуемый авторами параметр дифференциального веса "0.2", это значение принято мной по умолчанию в скрипте для тестирования DE. Этот параметр оказывает значительное влияние на разнообразие популяции, если выбрать значение менее "0.2", то можно получить сходимость алгоритма ещё лучше, но при этом получить ещё больший разброс в результатах. И наоборот, если увеличивать значение этого параметра, то алгоритм становится устойчивым против вырождения популяции и застреванию в локальных экстремумах, но при этом качество сходимости стремительно снижается за ограниченное тестами количество итераций, соответственно, неизбежно увеличивается время поиска.

Так же влияет на качество оптимизации параметр вероятности скрещивания. Авторами рекомендовано значение "0.9", но мои эксперименты показали более удачное, на мой взгляд, значение - "0.8". 

Учитывая вышесказанное видится целесообразным использовать адаптивные методы для контроля и динамичного изменения параметров, чтобы алгоритм мог автоматически настраиваться в зависимости от поставленной задачи.

2. Использование различных стратегий мутации и кроссовера.

3. Использование гибридных методов: можно комбинировать DE с другими методами оптимизации, такими как генетические алгоритмы, методы оптимизации на основе градиентов, методы оптимизации на основе роя частиц и т.д. Это может улучшить производительность алгоритма и помочь повысить эффективность алгоритма в целом.

4. Улучшение сходимости: применение дополнительного создания случайных векторов с целью повышения разнообразия в популяции.

5. Использование различных стратегий выбора особей для мутации: в данном алгоритме рассмотрен полностью случайный метод выбора особей для скрещивания, однако так же можно дополнять или полностью заменить этот способ на использование других различных стратегии выбора особей для кроссовера/мутации, такие как стратегия выбора особей на основе их пригодности. Это может помочь улучшить разнообразие популяции и значительно повысить устойчивость алгоритма к застреванию.

В целом, алгоритм DE оставляет очень хорошее впечатление о своей работе, но необходимо либо постоянно помнить об особенностях этого интересного алгоритма, либо предпринять некоторые попытки для улучшения дифференциальной эволюции за счет применения комбинирования различных стратегий и методов. DE уверенно продемонстрировал, что алгоритмы могут быть очень эффективными и при этом оставаться невероятно простыми и быстрыми. Алгоритм дифференциальной эволюции может быть рекомендован для решения сложных задач оптимизации с большой размерностью, так как влияние падения разнообразия во время эволюции менее выражено при большом количестве оптимизируемых параметров.

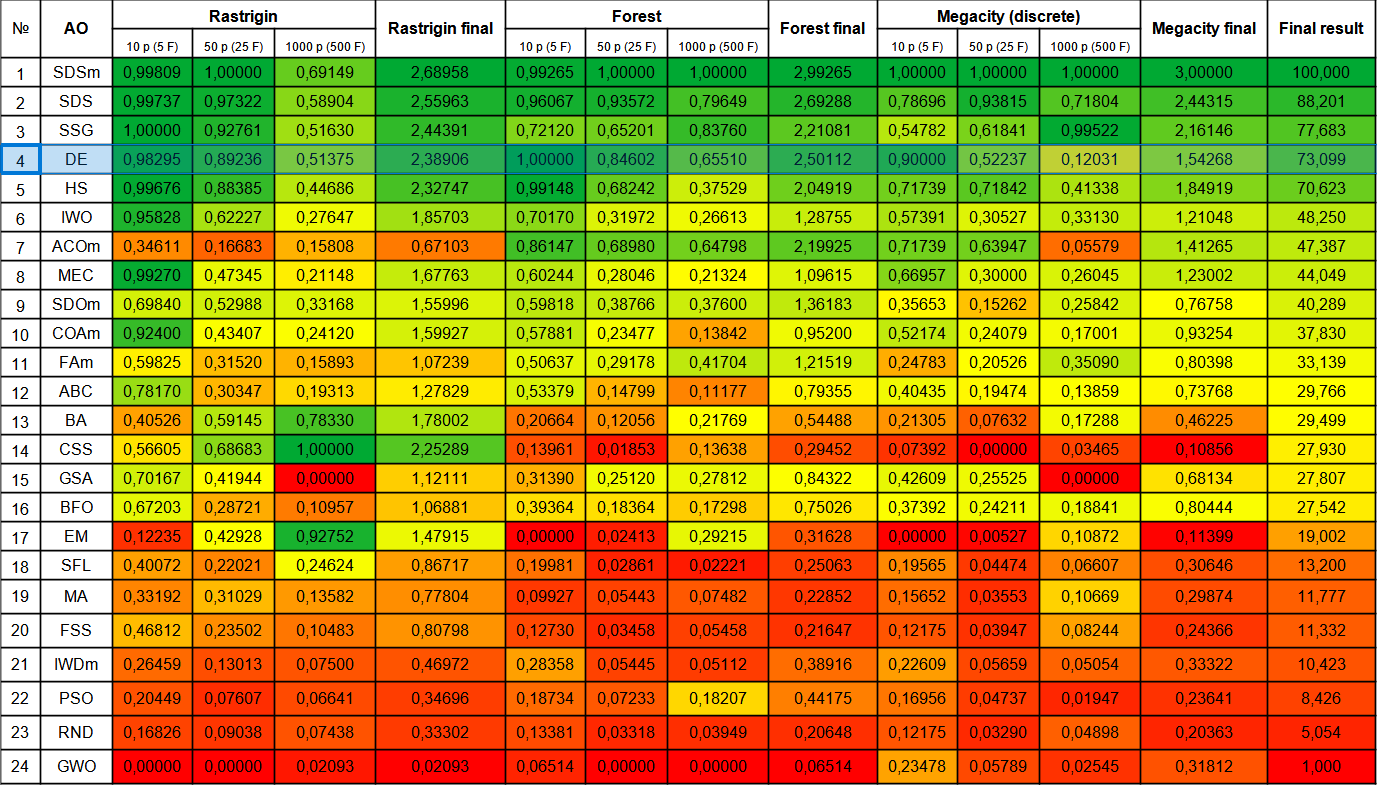
Рисунок 1. Цветовая градация алгоритмов по соответствующим тестам.

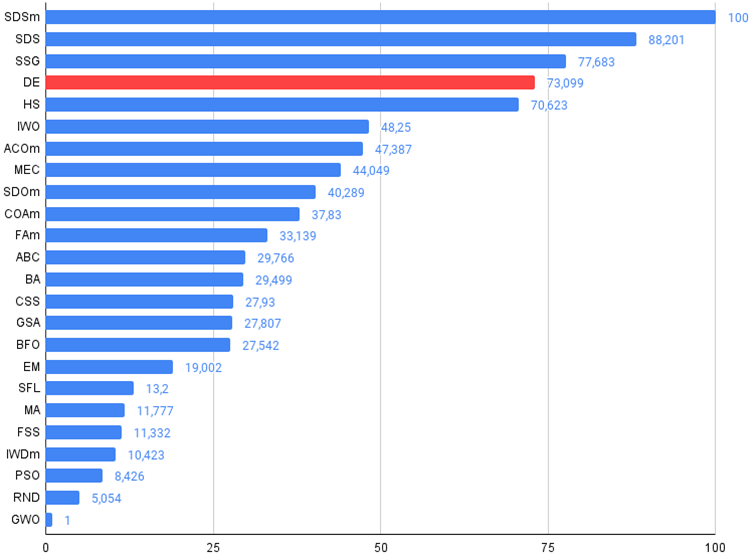
Рисунок 2. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье).

Плюсы и минусы алгоритма дифференциальной эволюции (DE)

Плюсы:

1. Небольшое количество внешних параметров.
2. Простая реализация.
3. Скорость работы.
4. Хорошая масштабируемость.
5. Очень хорошие показатели на разного типа функциях (принимая во внимание пункты минусов).

Минусы:

1. Очень высокий разброс результатов.
2. Склонность к застреванию в локальных экстремумах.

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.