
Redes neurais em trading: Otimizando Transformer para previsão de séries temporais (LSEAttention)
Introdução
A previsão multivariada de séries temporais é vital em diversas áreas, como finanças e saúde, por exemplo, onde o objetivo é prever valores futuros com base em dados históricos. Essa tarefa se torna especialmente desafiadora na previsão de longo prazo, pois exige modelos capazes de capturar eficientemente correlações entre características e dependências de longo alcance em séries temporais multivariadas. Pesquisas recentes têm se concentrado no uso da arquitetura Transformer para essa finalidade, devido à sua capacidade de capturar interações temporais complexas por meio do mecanismo de Self-Attention. No entanto, apesar de seu potencial, os métodos atuais de previsão multivariada de séries temporais ainda dependem majoritariamente de modelos lineares, o que levanta questionamentos sobre a real eficácia da arquitetura Transformer nesse contexto.
O mecanismo de Self-Attention, que é o núcleo da arquitetura Transformer, é formulado da seguinte forma:
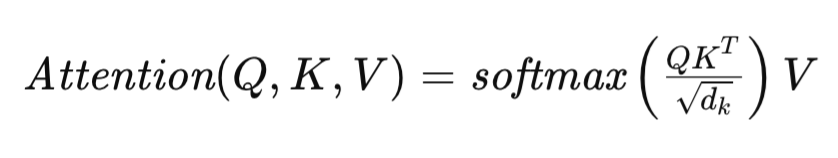
onde Q, K e V representam as matrizes Query, Key e Value, respectivamente, e dk denota a dimensionalidade dos vetores que descrevem cada elemento da sequência nessas matrizes. Essa formulação permite que o Transformer avalie dinamicamente a relevância dos diferentes elementos da sequência original, facilitando a identificação de dependências complexas nos dados.
Diversas estratégias de adaptação da arquitetura Transformer são aplicadas à previsão de séries temporais de longo prazo. Por exemplo, o FEDformer utiliza um módulo avançado de Fourier, que alcança complexidade linear em tempo e espaço, aumentando significativamente a escalabilidade e eficiência no processamento de sequências longas.
O PatchTST abandona a atenção pontual e foca no nível de blocos (patches) em vez de passos temporais individuais, permitindo que o modelo capture informações semânticas mais amplas em séries temporais multivariadas, o que é essencial para uma previsão de longo prazo eficaz.
Em visão computacional e processamento de linguagem natural, as matrizes de atenção podem sofrer com entropia ou colapso de posto. Essa problema se agrava na previsão de séries temporais devido às frequentes oscilações inerentes aos dados temporais, o que leva a uma queda significativa no desempenho do modelo. As causas fundamentais do colapso entrópico ainda são pouco compreendidas, o que exige estudos mais aprofundados sobre seus mecanismos principais e seus efeitos sobre o desempenho do modelo. Esses problemas são abordados pelos autores do trabalho "LSEAttention is All You Need for Time Series Forecasting".
1. Algoritmo LSEAttention
O objetivo da previsão de séries temporais multivariadas é determinar os P valores futuros mais prováveis para cada um dos C canais, representados na forma de um tensor Y ∈ RC×P. Essa previsão se baseia em dados históricos de séries temporais de comprimento L com C canais, encapsulados na matriz de dados brutos X ∈ RC×L. Para resolver essa tarefa, é necessário treinar o modelo preditivo fωRC×L →RC×P com parâmetros ω, de forma a minimizar o erro quadrático médio (MSE) entre os valores previstos e os reais.
O Transformer depende fortemente do seu mecanismo de Self-Attention pontual para capturar associações temporais. No entanto, essa dependência pode levar ao fenômeno conhecido como colapso de atenção, quando as matrizes de atenção convergem para os mesmos valores em todos os conjuntos de dados brutos e tendem a se tornar matrizes idênticas. Isso compromete a capacidade de generalização do modelo.
Os autores do LSEAttention fazem uma analogia entre a definição dos coeficientes de dependência pela função SoftMax com LSE (Log-Sum-Exp) e propõem aí a origem de uma instabilidade numérica, que pode ser a principal causa do colapso da atenção.
O número de condicionamento de uma função determina sua sensibilidade a pequenas mudanças nos dados brutos. Um número de condicionamento elevado indica que pequenas perturbações nos dados podem resultar em grandes alterações na saída.
Essa instabilidade pode se manifestar na forma de problemas como atenção excessiva ou colapso entrópico, caracterizados por matrizes de atenção com valores muito altos na diagonal (indicando estouro) e valores extremamente baixos fora da diagonal (indicando subestimação).
Para resolver esses problemas, foi proposto o módulo LSEAttention, que integra o truque Log-Sum-Exp (LSE) com a função de ativação de unidade linear com erro gaussiano (GELU). O truque LSE atenua a instabilidade numérica decorrente de estouros e subestimações por meio da normalização. A função SoftMax pode ser reformulada com LSE da seguinte forma:
![]()
onde o exponencial de LSE(x) representa o valor exponencial da função log-sum-exp, aumentando a estabilidade numérica.
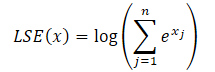
Utilizando a propriedade das potências, sempre podemos representar o valor exponencial de qualquer número como o produto de dois valores exponenciais.
![]()
onde a é uma constante usada para normalização. Na prática, utiliza-se geralmente o valor máximo como constante. Substituímos o produto de exponenciais na fórmula LSE e colocamos o valor comum para fora do sinal de soma:
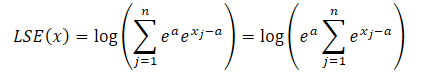
O logaritmo do produto é igual à soma dos logaritmos, e o logaritmo natural de um valor exponencial é igual ao expoente. Isso nos permite simplificar a expressão apresentada:
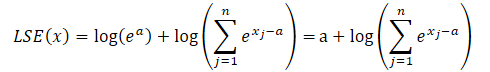
Substituímos a expressão obtida na função SoftMax e utilizamos a propriedade das potências:
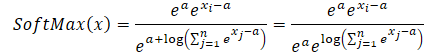
É fácil perceber que o valor exponencial constante comum ao numerador e denominador é cancelado. E o exponencial do logaritmo natural é igual à própria expressão logarítmica. Assim, obtemos uma forma numericamente estável da expressão SoftMax.
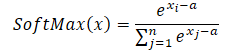
Ao utilizar o valor máximo como constante (a = max(x)), temos sempre x-a menor ou igual a 0. Nesse caso, o valor exponencial de x-a fica no intervalo entre 0 e 1, sem incluir o 0. Consequentemente, o denominador da função fica no intervalo (1, n].
Além disso, os autores do framework LSEAttention propõem o uso da função de ativação GELU, que proporciona uma ativação probabilística mais suave. Isso ajuda a estabilizar valores extremos de probabilidade logarítmica antes da aplicação da função exponencial, suavizando, assim, transições abruptas nas estimativas de atenção. Por meio da aproximação da função ReLU, com uma curva suave que incorpora a função de distribuição acumulada (CDF) da distribuição normal padrão, o GELU reduz mudanças bruscas nas ativações, que podem ocorrer com o uso do ReLU. Essa característica é especialmente útil para estabilizar os mecanismos de atenção baseados em Transformer, nos quais alterações abruptas nas ativações podem causar instabilidade numérica e explosão de gradientes.
A função GELU é formalmente definida da seguinte forma:
![]()
onde Φ(x) representa a CDF da distribuição normal padrão. Essa formulação garante que o GELU aplique diferentes níveis de escalonamento às entradas com base em sua magnitude, reduzindo a amplificação de valores extremos. O caráter suave e probabilístico do GELU permite uma transição gradual dos valores de entrada, o que, por sua vez, suaviza o impacto de grandes variações de gradiente durante o treinamento.
Essa característica se torna importante quando combinada com o truque Log-Sum-Exp (LSE), que normaliza a função SoftMax de forma numericamente estável. Juntos, LSE e GELU evitam estouros e subestimações nas operações exponenciais do SoftMax, o que resulta em um intervalo de estimativas de atenção mais estável. Essa sinergia aumenta a confiabilidade dos modelos Transformer, garantindo uma boa distribuição dos coeficientes de atenção entre os tokens. No fim das contas, isso leva a gradientes mais estáveis e melhor convergência durante o treinamento.
Nas arquiteturas Transformer tradicionais, a função de ativação ReLU (Rectified Linear Unit), usada no bloco Feed Forward (FFN), está sujeita ao problema do “ReLU morto”, no qual os neurônios podem se tornar inativos, gerando saída zero para todas as entradas negativas. Isso resulta em um cenário de gradiente nulo para esses neurônios, o que efetivamente interrompe seu processo de aprendizado e contribui para instabilidade durante o treinamento.
Para resolver esses problemas, é utilizada como alternativa a função de ativação ReLU paramétrica (PReLU). O PReLU introduz uma inclinação treinável para as entradas negativas, o que permite obter uma saída diferente de zero mesmo com entrada negativa. Essa adaptação não apenas alivia o problema do ReLU morto, mas também favorece uma transição mais suave entre ativações negativas e positivas, aumentando assim a capacidade do modelo de aprender em todas as regiões do espaço dos dados brutos. A presença de gradiente diferente de zero para valores negativos melhora o fluxo de gradientes, o que é essencial para o treinamento de arquiteturas mais profundas. Portanto, o uso de PReLU favorece a estabilidade geral do treinamento e ajuda a manter representações ativas, o que, no final, contribui para um melhor desempenho do modelo.
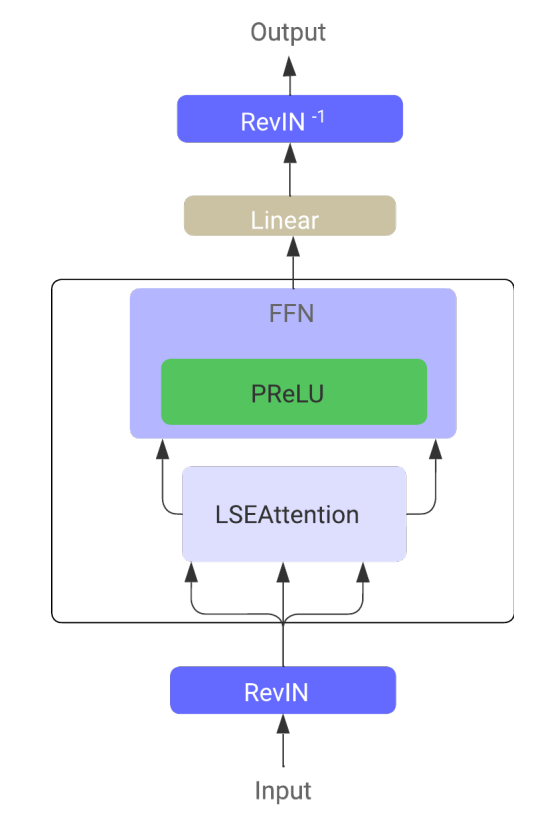
No Transformer para séries temporais LSEAttention (LATST), os autores do framework também adicionam a normalização reversível de dados, que é particularmente eficaz para eliminar discrepâncias entre a distribuição dos dados de treinamento e dos dados de teste em tarefas de previsão de séries temporais.
A arquitetura preserva o mecanismo temporal tradicional de Self-Attention, incorporado ao módulo LSEAttention.
De modo geral, a arquitetura LATST consiste em uma estrutura Transformer de nível único, complementada por módulos de substituição, o que permite um aprendizado adaptativo mantendo a confiabilidade dos mecanismos de atenção. Essa estrutura facilita o modelamento eficiente de dependências temporais e melhora o desempenho em tarefas de previsão de séries temporais. A visualização do framework proposta pelos autores está apresentada a seguir.
2. Implementação com MQL5
Após discutirmos os aspectos teóricos do framework LSEAttention, passamos agora à parte prática do nosso trabalho, na qual será explorada uma das formas de implementar as abordagens propostas utilizando os recursos do MQL5. E já adiantamos que este trabalho será diferente de todos os anteriores. O motivo é que, nesta implementação, não criaremos um novo objeto para aplicar as abordagens propostas. Em vez disso, vamos incorporar as abordagens nos classes previamente implementadas.
2.1 Ajuste da camada SoftMax
Tomemos como exemplo a classe CNeuronSoftMaxOCL, na qual está estruturada a camada da função SoftMax. Utilizamos amplamente essa classe, tanto como camada isolada do nosso modelo quanto integrada a diferentes frameworks. Em particular, utilizamos o objeto CNeuronSoftMaxOCL na construção do módulo de pooling baseado em dependências CNeuronMHAttentionPooling, empregado em diversos trabalhos recentes. Assim, é perfeitamente lógico adicionar ao seu algoritmo a abordagem de cálculo numericamente estável dos valores da função SoftMax.
Com esse objetivo, vamos modificar o funcionamento do kernel SoftMax_FeedForward. Nos parâmetros do kernel, recebemos ponteiros para dois buffers de dados: os valores brutos e os resultados.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs) { const uint total = (uint)get_local_size(0); const uint l = (uint)get_local_id(0); const uint h = (uint)get_global_id(1);
A execução do kernel está planejada para ocorrer em um espaço de tarefas bidimensional. A dimensão do primeiro eixo corresponde à quantidade de valores a serem normalizados dentro de uma única sequência unitária. Na segunda dimensão, indicamos a quantidade de sequências unitárias (ou cabeças de normalização). Unificamos os fluxos em grupos de trabalho dentro de cada sequência unitária.
No corpo do kernel, identificamos imediatamente o fluxo atual em todos os eixos do espaço de tarefas.
Em seguida, declaramos um array de dados na memória local, que será utilizado para a troca de informações entre os fluxos dentro dos grupos de trabalho.
__local float temp[LOCAL_ARRAY_SIZE];
E definimos constantes de deslocamento nos buffers globais até os elementos correspondentes.
const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE); uint shift_head = h * total;
Para reduzir o número de acessos à memória global, copiamos os dados brutos para variáveis locais e realizamos o controle dos valores obtidos.
float inp = inputs[shift_head + l]; if(isnan(inp) || isinf(inp) || inp<-120.0f) inp = -120.0f;
Vale notar que limitamos o valor bruto no nível de -120, o que equivale, na prática, ao menor valor possível de expoente para o tipo float, sendo uma forma adicional de prevenir a subestimação dos valores. Ao mesmo tempo, não limitamos o valor superior, pois o problema de estouro será tratado subtraindo-se o valor máximo.
Em seguida, precisamos determinar o valor máximo da sequência unitária que está sendo analisada. Para isso, organizamos um laço que coleta os valores máximos em sub-sequências individuais dentro do grupo de trabalho, armazenando-os nos elementos de um array local.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp); barrier(CLK_LOCAL_MEM_FENCE); }
Depois disso, identificamos o maior valor dentro do nosso array local, criando um laço adicional para percorrer os valores.
uint count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float max_value = temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
O valor máximo obtido dos elementos do grupo de trabalho atual é então armazenado em uma variável local, e é fundamental sincronizar os fluxos neste ponto. É extremamente importante garantir que todos os fluxos do grupo de trabalho tenham corretamente registrado o valor máximo antes que qualquer modificação ocorra nos elementos da memória local.
Agora podemos subtrair do valor original a magnitude do maior elemento. E, novamente, verificamos o limite inferior dos valores. Afinal, ao subtrair um valor máximo positivo, corremos o risco de sair da faixa permitida. Em seguida, calculamos o exponencial do valor corrigido.
inp = fmax(inp - max_value, -120); float inp_exp = exp(inp); if(isinf(inp_exp) || isnan(inp_exp)) inp_exp = 0;
Utilizando dois laços sequenciais, somamos os valores exponenciais obtidos dentro do grupo de trabalho. O algoritmo para construção dos laços é semelhante ao utilizado anteriormente para encontrar o valor máximo. Apenas modificamos a operação dentro do corpo dos laços.
for(int i = 0; i < total; i += ls) { if(l >= i && l < (i + ls)) temp[l] = (i > 0 ? temp[l] : 0) + inp_exp; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)total); do { count = (count + 1) / 2; if(l < ls) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); if(l + count < ls) temp[l + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Agora que já temos todos os valores necessários, podemos calcular os valores finais da função SoftMax, dividindo cada valor exponencial individual pela soma total dos valores no grupo de trabalho.
//--- float sum = temp[0]; outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f); }
O resultado dessas operações é armazenado no elemento correspondente do buffer global de resultados.
Vale destacar que as alterações feitas no algoritmo de cálculo da função SoftMax durante a propagação para frente não exigem alterações nos algoritmos da propagação reversa. Como pode ser observado nas deduções matemáticas apresentadas na parte teórica deste artigo, o uso do truque LSE não altera os valores finais da função. Sendo assim, a influência dos dados brutos sobre o resultado final permanece inalterada. E, portanto, temos total liberdade para continuar utilizando o algoritmo de distribuição de gradiente de erro já existente.
2.2 Implementação de alterações no módulo de atenção relativa
No entanto, é importante observar que o algoritmo SoftMax nem sempre é utilizado como uma camada isolada. Em praticamente todas as nossas versões de implementação dos diferentes blocos de Self-Attention, nós incorporamos sua execução diretamente dentro de um único kernel de construção da funcionalidade de atenção. Vejamos o módulo de atenção relativa CNeuronRelativeSelfAttention. Nele, todo o algoritmo do Self-Attention modificado é implementado dentro do kernel MHRelativeAttentionOut. E, claro, é essencial garantir um processo de aprendizado estável para todos os nossos modelos, independentemente da arquitetura. Por isso, precisaremos implementar o SoftMax numericamente estável em todos os algoritmos similares. Ao fazer isso, buscamos manter os parâmetros do kernel e do espaço de tarefas o mais intactos possível. Essa foi exatamente a abordagem adotada durante a modernização do kernel MHRelativeAttentionOut.
Entretanto, vale destacar que alterações nos parâmetros do kernel e no espaço de tarefas durante seu enfileiramento para execução devem ser acompanhadas pelas devidas atualizações em todos os métodos de encapsulamento do kernel na função principal. Caso contrário, há o risco de ocorrer uma falha crítica durante a submissão do kernel para execução. Isso se aplica não apenas à alteração do espaço global de tarefas, mas também à modificação do tamanho dos grupos de trabalho.
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_local_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_local_size(1); const int heads = get_global_size(2);
No corpo do kernel, como de costume, identificamos o fluxo atual dentro do espaço de tarefas. Também determinamos todas as dimensões desse espaço.
Nesse momento, definimos uma série de constantes necessárias, incluindo ponteiros de deslocamento nos buffers globais de dados e algumas variáveis auxiliares.
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension);
Em seguida, declaramos um array na memória local, que utilizaremos para troca de dados entre os fluxos do grupo de trabalho.
__local float temp[LOCAL_ARRAY_SIZE];
Para calcular o coeficiente de atenção, conforme o algoritmo do Self-Attention tradicional, primeiramente realizamos a multiplicação de dois vetores correspondentes dos tensores Query e Key. No entanto, os autores do framework R-MAT adicionaram elementos de viés global e dependente do contexto. O fato de todos os vetores envolvidos terem o mesmo tamanho nos permite realizar essas operações dentro de um único laço, com número de iterações igual ao tamanho dos vetores. No corpo do laço, realizamos a multiplicação elemento a elemento entre os vetores, seguida pela soma dos resultados obtidos.
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef;
O valor resultante é então ajustado pela raiz quadrada da dimensionalidade dos vetores. Os autores do Transformer original afirmam que essa operação melhora a estabilidade do modelo. E não há razão para discordar disso.
Em seguida, os valores obtidos são convertidos em probabilidades usando a função SoftMax. Aqui, adicionamos as operações para aumentar a estabilidade numérica do algoritmo. Primeiramente, devemos identificar o valor máximo entre os coeficientes obtidos dentro de um grupo de trabalho. Para isso, dividimos todos os fluxos do grupo em subgrupos, sendo que cada subgrupo escreverá seu valor máximo em um dos elementos do nosso array na memória local.
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); }
Em seguida, organizamos um laço para determinar o valor máximo entre os elementos do array.
uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
E calculamos o valor exponencial do coeficiente de atenção atual subtraído do valor máximo. E não nos esquecemos de sincronizar os fluxos. Isso é essencial porque, na próxima etapa, iremos modificar os valores dos elementos do array local, correndo o risco de sobrescrever o valor máximo antes que ele seja utilizado por todos os fluxos do grupo de trabalho.
sc = exp(fmax(sc - temp[0], -120)); if(isnan(sc) || isinf(sc)) sc = 0; barrier(CLK_LOCAL_MEM_FENCE);
O próximo passo é calcular a soma dos valores exponenciais obtidos dentro do grupo de trabalho. Para isso, como anteriormente, utilizamos um algoritmo composto por dois laços sequenciais.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Agora podemos converter os coeficientes de atenção em valores de probabilidade, dividindo os valores atuais pela soma total.
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Os valores obtidos são armazenados nos elementos correspondentes do buffer global de dados, e sincronizamos os fluxos das operações dentro do grupo de trabalho.
Por fim, é hora de calcular a soma ponderada dos elementos do tensor Value para cada elemento da sequência original. Como você já sabe, essa ponderação será feita com base nos coeficientes de atenção calculados anteriormente. Para um único elemento da sequência, essa operação corresponde à multiplicação do vetor de coeficientes de atenção pelo tensor Value, ao qual os autores do framework R-MAT adicionaram um tensor de viés global.
Para executar essas operações, criamos um sistema de laços, sendo o laço externo responsável por iterar sobre os elementos da última dimensão do tensor Value.
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0;
No corpo do laço, cada fluxo calcula seu valor para o elemento correspondente, que em seguida será somado dentro do grupo de trabalho por meio de dois laços sequenciais aninhados.
//--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
A soma dos valores obtidos é então armazenada por um dos fluxos do grupo de trabalho no elemento correspondente do buffer global de resultados.
//--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); barrier(CLK_LOCAL_MEM_FENCE); } }
Após isso, os fluxos do grupo de trabalho são sincronizados novamente, e seguimos para a próxima iteração do laço.
Como discutido anteriormente, as alterações feitas no algoritmo da função SoftMax não afetam a dependência dos resultados em relação aos dados brutos. Portanto, continuamos utilizando os algoritmos previamente implementados para a funcionalidade da propagação reversa, sem modificações.
2.3 Função de ativação GELU
Além da estabilização numérica da função SoftMax, os autores do framework LSEAttention sugerem o uso da função de ativação GELU. Os criadores dessa função de ativação propuseram duas formas de implementação. Uma delas está apresentada a seguir.
![]()
A implementação dessa função é simples. Apenas adicionamos à função de cálculo de ativações uma nova opção.
float Activation(const float value, const int function) { if(isnan(value) || isinf(value)) return 0; //--- float result = value; switch(function) { case 0: result = tanh(clamp(value, -20.0f, 20.0f)); break; case 1: //Sigmoid result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f))); break; case 2: //LReLU if(value < 0) result *= 0.01f; break; case 3: //SoftPlus result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value)))); break; case 4: //GELU result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f))); break; default: break; } //--- return result; }
No entanto, por trás da simplicidade da propagação para frente, enfrentamos um desafio considerável ao implementar a propagação reversa dessa função. O ponto é que a derivada do GELU depende tanto do valor original quanto da sigmoide. E na nossa implementação padrão, esses valores não estão disponíveis.
![]()
Não é possível expressar com precisão a derivada da função GELU com base apenas no resultado da propagação para frente. Por isso, tivemos que recorrer a algumas heurísticas e aproximações.
Para começar, vamos relembrar o gráfico da sigmoide.
Quando o argumento é maior que "5", ela tende a "1", e quando é menor que "-5", tende a "0". Portanto, para valores suficientemente negativos de X, a derivada do GELU tende a "0", pois o primeiro fator da equação vai a "0". Para valores suficientemente positivos de X, a derivada tende a "1", já que ambos os fatores se aproximam de "1". Isso é confirmado pelo gráfico abaixo.
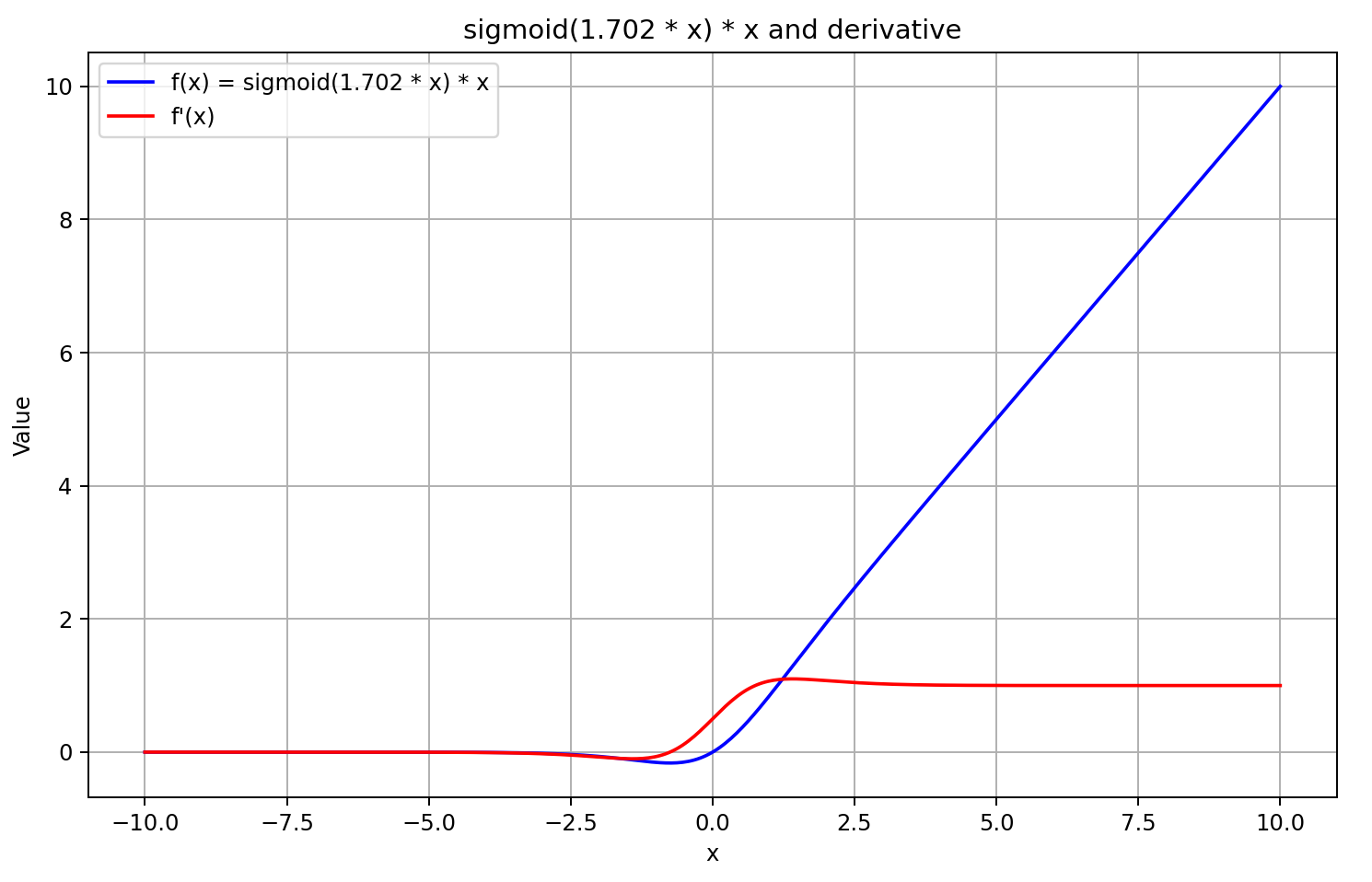
Com base nesses pressupostos, aproximamos a derivada como a sigmoide do resultado da propagação para frente multiplicado por 5. Essa abordagem nos permite calcular rapidamente o valor da derivada com boa precisão para resultados do GELU maiores ou iguais a "0". Para valores negativos da função após a propagação para frente, a derivada é fixada em 0.5, o que impede o prosseguimento do treinamento do modelo. Enquanto isso, a derivada real da função tende a "0", bloqueando a transmissão do gradiente de erro.
![]()

Decisão tomada. Vamos à implementação. Para isso, adicionamos mais um item na função de cálculo da derivada.
float Deactivation(const float grad, const float inp_value, const int function) { float result = grad; //--- if(isnan(inp_value) || isinf(inp_value) || isnan(grad) || isinf(grad)) result = 0; else switch(function) { case 0: //TANH result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value; result *= 1.0f - pow(inp_value, 2.0f); break; case 1: //Sigmoid result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value; result *= inp_value * (1.0f - inp_value); break; case 2: //LReLU if(inp_value < 0) result *= 0.01f; break; case 3: //SoftPlus result *= Activation(inp_value, 1); break; case 4: //GELU if(inp_value < 0.9f) result *= Activation(5 * inp_value, 1); break; default: break; } //--- return clamp(result, -MAX_GRAD, MAX_GRAD); }
Vale observar que a função de ativação só é calculada quando o resultado da propagação para frente for menor que "0.9". Em todos os outros casos, assumimos que a derivada é igual a "1", o que corresponde à realidade. Isso reduz o número de operações realizadas durante a distribuição do gradiente de erro.
Os autores do framework sugerem o uso da função GELU para introduzir não linearidade entre as camadas do bloco FeedForward. Na classe CNeuronRMAT utilizamos o módulo convolucional com retroalimentação CResidualConv como esse bloco. Vamos modificar nele a função de ativação entre as camadas. Essa alteração é feita no método de inicialização da classe. A modificação pontual está destacada no código com sublinhado.
bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_out, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch)) return false; //--- if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch)) return false; if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[0].SetActivationFunction(GELU); if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch)) return false; if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization)) return false; cNorm[1].SetActivationFunction(None); //--- ........ ........ ........ //--- return true; }
Com isso, concluímos a implementação das abordagens propostas pelos autores do framework LSEAttention. O código completo de todas as alterações está disponível no anexo. Lá você também encontrará o código integral de todos os programas utilizados na elaboração deste artigo.
Devo dizer que todos os programas de interação com o ambiente e de treinamento dos modelos foram completamente reaproveitados do artigo anterior. Da mesma forma, a arquitetura dos modelos foi mantida sem alterações. Isso torna ainda mais interessante avaliar os resultados do treinamento. Afinal, os únicos fatores que podem influenciar os resultados são os métodos incorporados.
3. Testes
Neste artigo, implementamos as abordagens de otimização do algoritmo Transformer tradicional, propostas pelos autores do framework LSEAttention para previsão de séries temporais. Como já mencionado, este trabalho difere dos anteriores. Não criamos novas camadas neurais, como foi feito anteriormente. Pelo contrário, incorporamos as abordagens propostas nos objetos já implementados. De fato, utilizamos o framework HypDiff, desenvolvido no artigo anterior, e adicionamos a ele algumas otimizações de algoritmo que não alteraram a arquitetura do modelo. Exceto, claro, pela mudança na função de ativação do bloco FeedForward. No entanto, as abordagens aplicadas ajustaram ligeiramente as operações computacionais, conferindo-lhes estabilidade numérica. E, naturalmente, estamos curiosos para ver como isso impacta os resultados do treinamento do modelo.
Para manter a integridade do experimento, repetimos integralmente o algoritmo de treinamento do modelo HypDiff. Utilizamos o mesmo conjunto de dados para treinamento. No entanto, desta vez não aplicamos atualizações iterativas ao conjunto de treinamento. Sim, isso pode afetar negativamente os resultados do aprendizado, mas nos permite comparar corretamente o desempenho do modelo antes e depois da otimização do algoritmo.
Para a verificação dos resultados do treinamento, utilizamos dados históricos reais do primeiro trimestre de 2024. Os resultados dos testes são apresentados a seguir.
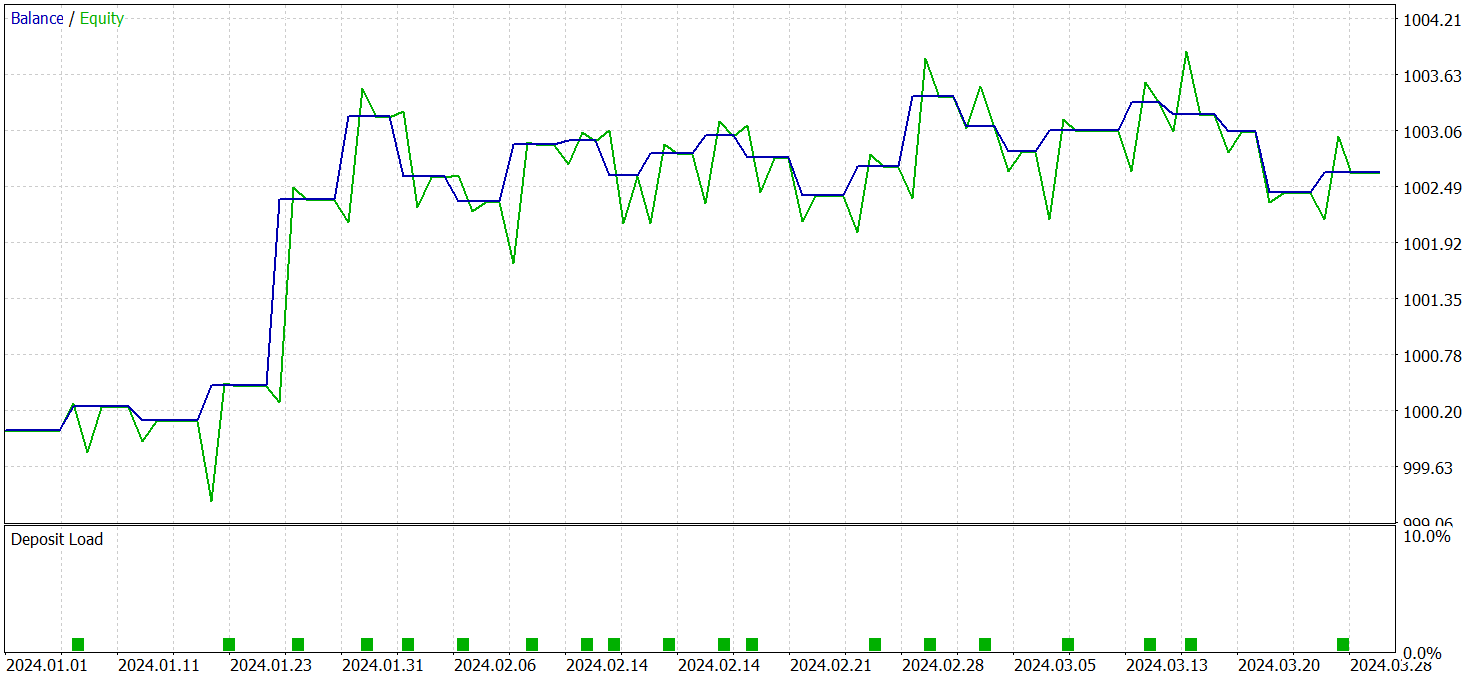
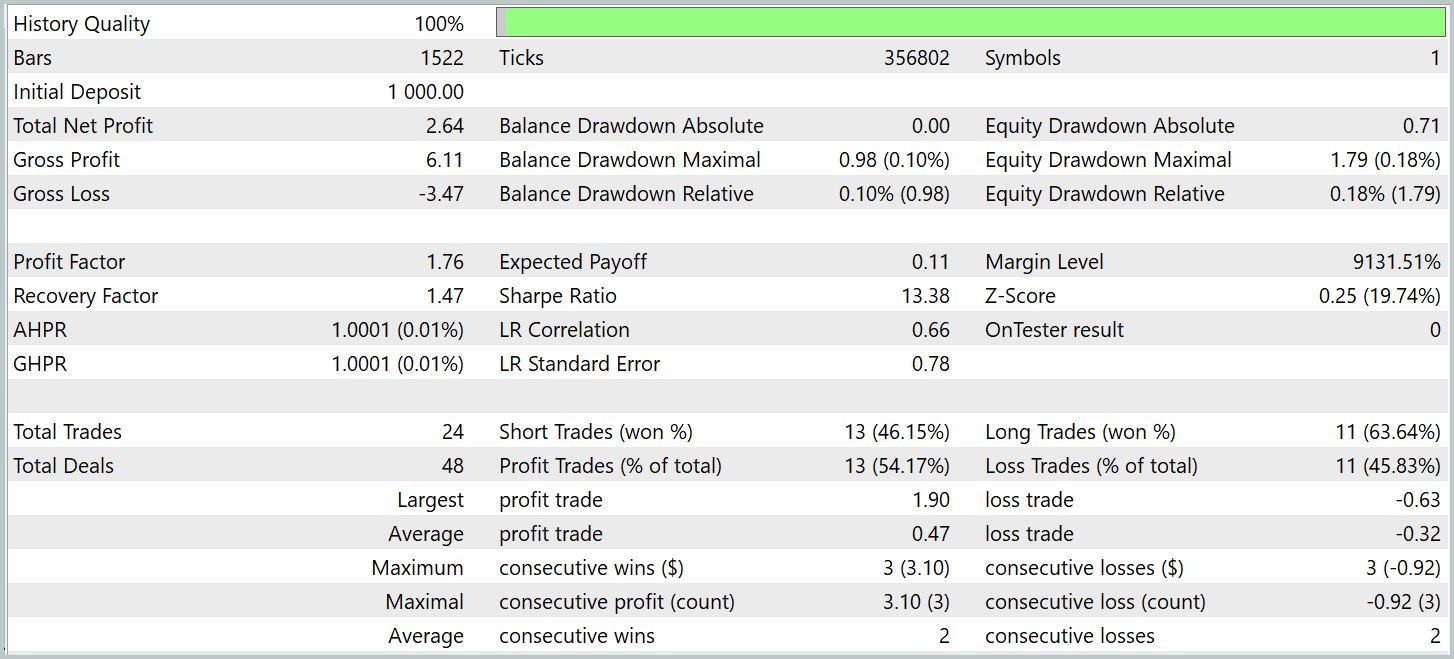
É importante destacar que os resultados do modelo na base de testes, antes e depois da modificação, são bastante próximos. Durante o período de testes, o modelo atualizado realizou 24 operações. A diferença de 1 operação em relação ao modelo base está dentro da margem de erro. Ambos os modelos registraram 13 operações lucrativas. A única melhoria visível foi a ausência de rebaixamento no mês de fevereiro.
Conclusão
O método LSEAttention representa uma evolução dos mecanismos de atenção, especialmente eficaz em tarefas que exigem alta resistência a ruído e variabilidade dos dados. Sua principal vantagem está no uso do suavizamento logarítmico, implementado por meio da função Log-Sum-Exp. Isso permite evitar efeitos de estouro e subestimação numérica, que são críticos em redes neurais profundas.
Na parte prática, implementamos as abordagens propostas utilizando os recursos do MQL5 nos objetos previamente desenvolvidos. Treinamos e testamos os modelos com essas abordagens aplicadas, utilizando dados históricos reais. Com base nos resultados obtidos, podemos concluir que os métodos propostos aumentam a estabilidade do processo de treinamento do modelo.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de amostras |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA de coleta por método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA de treinamento de modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código para OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16360
 Reimaginando Estratégias Clássicas (Parte VII): Mercados de Forex e Análise da Dívida Soberana no USDJPY
Reimaginando Estratégias Clássicas (Parte VII): Mercados de Forex e Análise da Dívida Soberana no USDJPY
 Média Móvel em MQL5 do zero: Simples e acessível
Média Móvel em MQL5 do zero: Simples e acessível
 Está chegando o novo MetaTrader 5 e MQL5
Está chegando o novo MetaTrader 5 e MQL5
 Análise volumétrica com redes neurais como chave para tendências futuras
Análise volumétrica com redes neurais como chave para tendências futuras
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso