Redes neurais em trading: Modelo hiperbólico de difusão latente (Conclusão)

Introdução

O espaço geométrico hiperbólico é capaz de representar estruturas discretas em forma de árvore ou hierárquicas, aplicáveis a diversas tarefas de aprendizado em grafos. Ele também possui um grande potencial para resolver o problema da anisotropia estrutural dos espaços não euclidianos nos processos de difusão latente de grafos. A geometria hiperbólica une as dimensões angulares e radiais das coordenadas polares, fornecendo medições geométricas com interpretabilidade e semântica física.

E, nesse contexto, o framework HypDiff representa um método avançado de criação de ruído gaussiano hiperbólico, que resolve o problema da falha aditiva das distribuições gaussianas no espaço hiperbólico. Os autores do framework introduziram restrições geométricas de semelhança angular, aplicadas no processo de difusão anisotrópica para preservar a estrutura local dos grafos.

A visualização do framework pelos autores é apresentada abaixo.

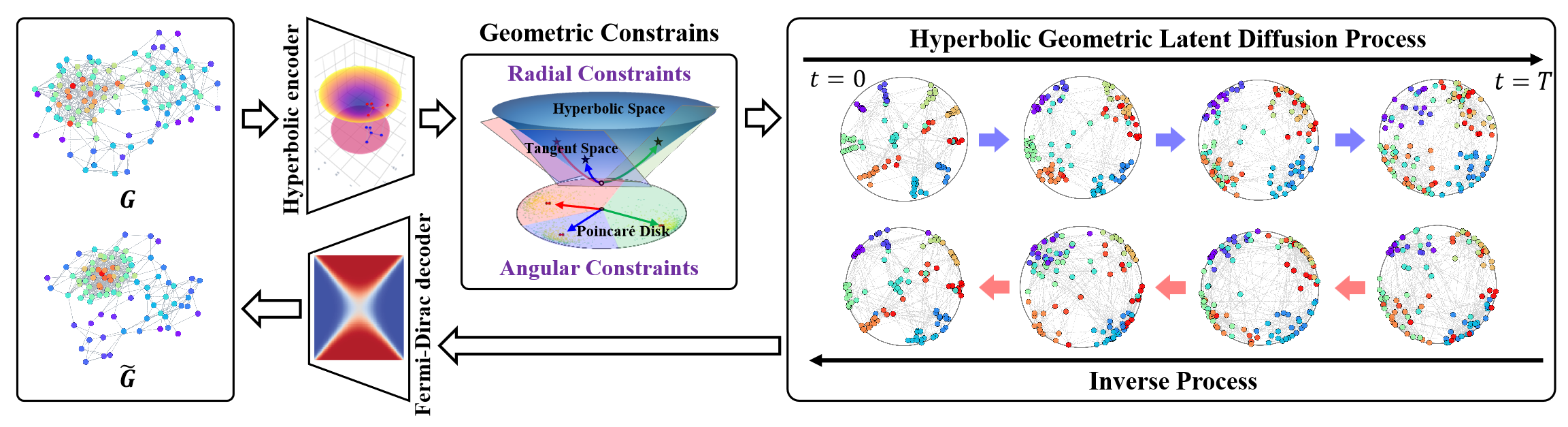
No artigo anterior, começamos a preparar a implementação das abordagens propostas usando MQL5. No entanto, o volume de trabalho é considerável. Conseguimos analisar apenas os blocos de implementação no lado do programa OpenCL. Neste artigo, continuaremos o trabalho iniciado. Concluiríamos a implementação do framework HypDiff. No entanto, em nossa implementação, faremos algumas alterações em relação ao algoritmo original, que discutiremos ao longo da construção dos algoritmos.

1. Projeção dos dados no espaço hiperbólico

Nosso trabalho no lado do programa OpenCL começou com a construção dos kernels de propagação para frente e reversa da projeção dos dados brutos no espaço hiperbólico (HyperProjection e HyperProjectionGrad, respectivamente). A implementação das abordagens do framework HypDiff no programa principal também começará com a construção dos algoritmos dessa funcionalidade. Para isso, criaremos uma nova classe CNeuronHyperProjection, cuja estrutura é apresentada abaixo.

class CNeuronHyperProjection   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronHyperProjection(void) : iWindow(-1), iUnits(-1) {};
                    ~CNeuronHyperProjection(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperProjection;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
  };

Na estrutura apresentada, vemos a declaração de duas variáveis internas para registrar constantes que definem a arquitetura do objeto, além de um conjunto de métodos sobrescrevíveis já familiar. Mas, observe que o método de atualização dos parâmetros do modelo updateInputWeights é apresentado como uma "função simulada" com retorno positivo fixo. E isso não é por acaso. Os kernels de propagação para frente e de propagação reversa da projeção dos dados que implementamos executam um algoritmo explicitamente definido, sem parâmetros treináveis. No entanto, a presença do método de atualização de parâmetros é necessária para o funcionamento correto do modelo. Por isso, somos obrigados a sobrescrever esse método com um retorno fixo positivo.

A ausência de declarações de novos objetos internos nos permite deixar o construtor e o destrutor da classe em branco. Já a inicialização dos objetos herdados e das variáveis internas declaradas é feita no método Init.

O algoritmo do método de inicialização é bastante simples. Nos parâmetros do método, como de costume, recebemos as principais constantes que permitem identificar de forma inequívoca a arquitetura do objeto que está sendo criado.

bool CNeuronHyperProjection::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                  uint window, uint units_count, 
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + 1)*units_count, optimization_type, batch))
      return false;
   iWindow = window;
   iUnits = units_count;
//---
   return true;
  }

E no corpo do método, chamamos imediatamente o método homônimo da classe-pai, passando a ele os parâmetros recebidos necessários. Como você já sabe, os algoritmos de verificação dos parâmetros recebidos e de inicialização dos objetos herdados estão implementados no corpo da classe-pai. Basta verificarmos o resultado lógico da execução do método da classe-pai. Em seguida, salvamos as constantes da arquitetura do objeto, fornecidas pelo programa externo, nas variáveis internas.

E é isso. Não declaramos novos objetos internos, e os herdados foram inicializados pelo método da classe pai. Resta apenas retornar o resultado lógico da execução das operações para o programa chamador e encerrar a execução do método.

Sugiro que você explore por conta própria os métodos de propagação para frente e reversa dessa classe. Ambos são apenas "encapsulamentos" para invocar os kernels correspondentes do programa OpenCL. Métodos semelhantes já foram descritos diversas vezes ao longo da nossa série de artigos. E acredito que a implementação dos seus algoritmos não causará problemas. Você pode consultar o código completo dessa classe e de todos os seus métodos no anexo.

2. Projeção nos planos tangentes

Após a projeção dos dados brutos no espaço hiperbólico, o framework HypDiff prevê a construção de um Codificador para gerar incorporações hiperbólicas dos nós. Pretendemos utilizar os recursos já existentes em nossa biblioteca para cobrir essa funcionalidade. As incorporações obtidas são projetadas nos planos tangentes correspondentes aos k centroides. Os algoritmos de projeção nos planos tangentes e de redistribuição reversa dos gradientes já foram implementados nos kernels LogMap e LogMapGrad, respectivamente, do lado do programa OpenCL. No entanto, a questão dos centroides permanece em aberto.

Aqui é importante destacar que os autores do framework HypDiff definiram os centroides a partir do conjunto de dados de treinamento na fase de preparação dos dados. Infelizmente, essa abordagem não é viável para nós. E não se trata apenas da complexidade do processo. Essa abordagem não é adequada para a análise de um mercado dinâmico de instrumentos financeiros. No contexto da análise técnica dos movimentos de preço, às vezes, os padrões formados recebem mais atenção do que os valores específicos do ativo. Além disso, para situações de mercado semelhantes, observadas em diferentes intervalos de tempo, podem ser relevantes centroides distintos. Dessa forma, concluímos que é necessário criar um modelo dinâmico de adaptação ou geração de centroides e seus parâmetros. Em nossa implementação, decidimos gerar centroides com base nas incorporações dos dados brutos. E decidimos, também, unir os processos de geração de centroides e projeção dos dados nos respectivos planos tangentes dentro da classe CNeuronHyperboloids. Sua estrutura é apresentada abaixo.

class CNeuronHyperboloids  :  public CNeuronBaseOCL
  {
protected:
   uint              iWindows;
   uint              iUnits;
   uint              iCentroids;
   //---
   CLayer            cHyperCentroids;
   CLayer            cHyperCurvatures;
   //---
   int               iProducts;
   int               iDistances;
   int               iNormes;
   //---
   virtual bool      LogMap(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                            CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   virtual bool      LogMapGrad(CNeuronBaseOCL *featers, CNeuronBaseOCL *centroids, 
                                CNeuronBaseOCL *curvatures, CNeuronBaseOCL *outputs);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronHyperboloids(void) : iWindows(0), iUnits(0), iCentroids(0), 
                                                 iProducts(-1), iDistances(-1), iNormes(-1) {};
                    ~CNeuronHyperboloids(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint units_count, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronHyperboloids;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual void      TrainMode(bool flag);
  };

Na estrutura apresentada da nova classe, é possível notar a declaração de 2 arrays dinâmicos e 6 variáveis divididas em 2 grupos.

Os arrays dinâmicos são destinados ao registro de ponteiros para os objetos das camadas neurais de dois modelos aninhados. Sim, em nossa implementação, decidimos dividir o funcional de geração dos parâmetros dos centroides em dois modelos. O primeiro modelo é responsável pela geração das coordenadas dos centroides no espaço hiperbólico. O segundo modelo retornará os parâmetros de curvatura do espaço nos respectivos pontos.

A divisão das variáveis internas em dois grupos também tem uma justificativa lógica. Em um grupo, reunimos os parâmetros da arquitetura do objeto que está sendo criado, os quais receberemos do programa externo. No segundo grupo, colocamos as variáveis para armazenar ponteiros dos buffers de gravação de valores intermediários, que criaremos somente no contexto do OpenCL, sem cópia de dados para a memória RAM do dispositivo.

Todos os objetos internos foram declarados de forma estática, o que nos permite deixar o construtor e o destrutor da classe em branco. Já a inicialização de todos os objetos herdados e declarados é feita no método Init.

bool CNeuronHyperboloids::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                               uint window, uint units_count, uint centroids,
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window*units_count*centroids, optimization_type, batch))
      return false;

Nos parâmetros do método, como de costume, recebemos uma série de constantes que permitem interpretar de forma inequívoca a arquitetura do objeto que está sendo criado. Neste caso, são:

• units_count — número de elementos na sequência analisada;
• window — tamanho do vetor de incorporação de cada elemento da sequência analisada;
• centroids — número de centroides que o modelo gera para uma análise abrangente dos dados brutos.

No corpo do método, conforme o esquema já consolidado, chamamos o método homônimo da classe-pai para inicializar os objetos e variáveis herdados. Aqui é importante destacar que, diferentemente do algoritmo original do HypDiff, nossa implementação não separamos os elementos da sequência bruta com base na associação a este ou aquele centroide. Em vez disso, com o objetivo de fornecer à nossa modelo o máximo possível de informações, geramos projeções de toda a sequência sobre todos os planos tangentes. Isso, naturalmente, aumenta o volume do tensor de resultados proporcionalmente ao número de centroides gerados. Por esse motivo, ao chamar o método de inicialização da classe-pai, especificamos o produto das três constantes recebidas do programa externo como o tamanho da camada a ser criada.

E após a execução bem-sucedida das operações do método da classe-pai, como indicado pelo seu resultado lógico, salvamos as constantes recebidas nas variáveis internas.

   iWindows = window;
   iUnits = units_count;
   iCentroids = centroids;

Na etapa seguinte, preparamos nossos arrays dinâmicos para registrar os ponteiros dos objetos dos modelos de geração dos parâmetros dos centroides.

   cHyperCentroids.Clear();
   cHyperCurvatures.Clear();
   cHyperCentroids.SetOpenCL(OpenCL);
   cHyperCurvatures.SetOpenCL(OpenCL);

E então passamos ao trabalho direto de inicialização dos objetos do modelo. Primeiro, inicializamos o modelo de geração das coordenadas dos centroides.

Aqui, planejamos construir um modelo linear que, ao analisar o conjunto de dados brutos, nos retorne um pacote de coordenadas para os centroides relevantes. No entanto, o uso de camadas totalmente conectadas para essa finalidade leva à criação de um grande número de parâmetros treináveis e ao aumento da carga computacional. O uso de camadas convolucionais permite reduzir tanto o número de parâmetros treináveis quanto o volume de cálculos. Além disso, o uso de camadas convolucionais em sequências unitárias isoladas é bastante lógico. Para aplicar essa abordagem, primeiro precisaremos transpor os dados brutos obtidos.

   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 0, OpenCL, iUnits, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction(None);

Em seguida, adicionamos uma camada convolucional de redução dimensional das sequências unitárias.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 1, OpenCL, iUnits, iUnits, iCentroids, iWindows, 1, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);

Aqui utilizamos um único conjunto de parâmetros para todas as sequências unitárias. E na saída da camada, usamos a tangente hiperbólica como função de ativação para introduzir não linearidade.

Depois, adicionamos mais uma camada convolucional sem função de ativação, mas desta vez contendo parâmetros treináveis distintos para cada sequência unitária.

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 2, OpenCL, iCentroids, iCentroids, iCentroids, 1, iWindows, optimization, iBatch) ||
      !cHyperCentroids.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Dessa forma, duas camadas convolucionais consecutivas nos permitem criar uma MLP única para cada série unitária da sequência bruta. Cada uma dessas MLP nos fornecerá uma coordenada para a quantidade necessária de centroides. Em outras palavras, criamos uma MLP para cada dimensão do espaço de coordenadas, que, em conjunto, geram as coordenadas da quantidade especificada de centroides.

E agora, só nos resta retornar as coordenadas dos centroides à sua representação original. Para isso, adicionamos uma camada extra de transposição de dados.

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 3, OpenCL, iWindows, iCentroids, optimization, iBatch) ||
      !cHyperCentroids.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Em seguida, criaremos os objetos do segundo modelo, que indicará os parâmetros de curvatura do espaço hiperbólico nos pontos dos centroides. Determinaremos esses parâmetros com base nas coordenadas dos centroides gerados. É bastante lógico que o parâmetro de curvatura dependa apenas dessas coordenadas específicas. Afinal, supomos que a noção do espaço hiperbólico utilizada será aprendida pela modelo durante o processo de treinamento e refletida em seus parâmetros treináveis. Por isso, no modelo de definição dos parâmetros de curvatura, não utilizamos camadas de transposição. Simplesmente criamos uma MLP única para cada centroide a partir de duas camadas convolucionais consecutivas.

   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 4, OpenCL, iWindows, iWindows, iWindows, iCentroids, 1, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 5, OpenCL, iWindows, iWindows, 1, 1, iCentroids, optimization, iBatch) ||
      !cHyperCurvatures.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Aqui também utilizamos a tangente hiperbólica para introduzir não linearidade entre as camadas do modelo.

Com isso, concluímos o trabalho de inicialização dos objetos dos modelos de geração dos parâmetros dos centroides. Agora, nos resta preparar os objetos necessários para o suporte aos kernels de projeção dos dados nos planos tangentes e de distribuição do gradiente do erro. Aqui, quero lembrar que, ao construir esses algoritmos, falamos sobre a criação de buffers de armazenamento temporário dos resultados das operações intermediárias. São três buffers de dados, cada um contendo um elemento por par "centroide — Elemento da sequência".

Esses buffers de dados são usados apenas para transmitir informações do kernel de propagação para frente para o kernel de distribuição do gradiente do erro. Portanto, sua criação só se justifica dentro do contexto OpenCL. Em outras palavras, criar esses buffers na memória RAM do dispositivo e realizar cópias de dados entre a memória do contexto OpenCL e a memória principal seria desnecessário. Também não há necessidade de gravar esses dados ao salvar os parâmetros do modelo, pois eles são atualizados a cada propagação para frente. Assim, no lado do programa principal, criamos apenas variáveis para armazenar os ponteiros desses buffers de dados.

Mas ainda precisamos criá-los no contexto OpenCL. Para isso, primeiro definimos o tamanho necessário dos buffers de dados. Como já foi mencionado acima, todos os 3 buffers têm o mesmo tamanho.

   uint size = iCentroids * iUnits * sizeof(float);
   iProducts = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iProducts < 0)
      return false;
   iDistances = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iDistances < 0)
      return false;
   iNormes = OpenCL.AddBuffer(size, CL_MEM_READ_WRITE);
   if(iNormes < 0)
      return false;
//---
   return true;
  }

Depois disso, criamos os buffers de dados na memória do contexto OpenCL, salvando os ponteiros obtidos nas variáveis correspondentes. E não nos esquecemos de verificar a validade do ponteiro obtido.

E após a inicialização de todos os objetos, retornamos o resultado lógico da execução das operações para o programa chamador e encerramos o método.

A próxima etapa do nosso trabalho é a construção dos algoritmos de propagação para frente da nossa classe CNeuronHyperboloids. Aqui vale dizer que os métodos LogMap e LogMapGrad são encapsulamentos para a chamada dos kernels de mesmo nome. E os deixaremos para estudo independente.

Vamos analisar o método de propagação para frente feedForward. Nos parâmetros deste método, recebemos um ponteiro para o objeto da camada neural que contém o tensor dos dados brutos.

bool CNeuronHyperboloids::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *prev = NeuronOCL;
   CNeuronBaseOCL *centroids = NULL;
   CNeuronBaseOCL *curvatures = NULL;

E no corpo do método, primeiro realizaremos uma pequena preparação: declaramos variáveis locais para armazenar temporariamente os ponteiros para os objetos das camadas neurais internas. Um deles receberá o ponteiro para o objeto de dados brutos recebido. Os outros dois permanecerão vazios por ora.

Observe que, neste momento, não verificamos a validade do ponteiro recebido para o objeto de dados brutos. Não pretendemos acessar diretamente os buffers desse objeto dentro das operações do método atual. Por isso, esse controle seria desnecessário.

A seguir, devemos gerar as coordenadas dos centroides para o conjunto atual de dados brutos. Para isso, organizamos um laço iterando sobre os objetos do modelo interno correspondente.

//--- Centroids
   for(int i = 0; i < cHyperCentroids.Total(); i++)
     {
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.FeedForward(prev))
         return false;
      prev = centroids;
     }

No corpo do laço, pegamos sequencialmente os ponteiros para os objetos das camadas neurais e verificamos sua validade. Em seguida, chamamos o método de propagação para frente do objeto extraído e passamos a ele, como dados de entrada, o ponteiro da variável local correspondente. Após a execução bem-sucedida do método de propagação para frente da camada interna, ela se torna a fonte de dados brutos para a próxima camada do modelo. Portanto, salvamos seu ponteiro na variável local de dados de entrada.

Observe que, inicialmente, a variável local continha o ponteiro para o objeto de dados brutos recebido do programa externo. Portanto, na primeira iteração do laço, utilizamos esse ponteiro como dados de entrada. Dessa Gapforma, a verificação da validade do ponteiro para o objeto recebido do programa externo foi realizada dentro da execução do método de propagação para frente da camada interna do modelo. Dessa forma, todos os pontos de controle foram atendidos e o fluxo de informações a partir do objeto de dados brutos foi respeitado.

Realizamos um laço semelhante para determinar os parâmetros de curvatura do hiperespaço nos pontos dos centroides. E aqui vale destacar que, após o término das iterações do laço anterior, as variáveis locais prev e centroids contêm o ponteiro para o mesmo objeto da última camada do modelo de geração das coordenadas dos centroides. E como planejamos determinar os parâmetros de curvatura com base nas coordenadas dos centroides, podemos continuar trabalhando tranquilamente com a variável prev.

//--- Curvatures
   for(int i = 0; i < cHyperCurvatures.Total(); i++)
     {
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.FeedForward(prev))
         return false;
      prev = curvatures;
     }

E após obtermos com sucesso todos os parâmetros necessários dos centroides, podemos projetar os dados brutos nos respectivos planos tangentes. Para isso, chamamos o método encapsulador do kernel LogMap, criado no artigo anterior.

   if(!LogMap(NeuronOCL, centroids, curvatures, AsObject()))
      return false;
//---
   return true;
  }

Observe que, como objeto receptor dos resultados, passamos o ponteiro para o objeto atual. Isso nos permitirá armazenar os resultados das operações nos buffers das interfaces da nossa classe, que serão acessados pelas próximas camadas neurais do nosso modelo.

Resta apenas retornar o resultado lógico da execução das operações para o programa chamador e encerrar o método de propagação para frente.

Após construirmos os métodos de propagação para frente, passamos a trabalhar nos algoritmos de propagação reversa. E aqui, proponho que analisemos o algoritmo do método de distribuição do gradiente do erro calcInputGradients. Já o método de atualização dos parâmetros do modelo updateInputWeights deve ser estudado individualmente.

Como de costume, nos parâmetros do método de distribuição do gradiente do erro calcInputGradients, recebemos um ponteiro para o objeto da camada anterior, no buffer do qual devemos transmitir o gradiente do erro, de acordo com a influência dos dados brutos no resultado final do modelo.

bool CNeuronHyperboloids::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Desta vez, verificamos imediatamente a validade do ponteiro recebido. Afinal, se o ponteiro não for válido, todas as operações seguintes perderão o sentido.

Assim como na propagação para frente, declaramos variáveis locais para armazenar temporariamente os ponteiros dos objetos dos modelos internos. Desta vez, porém, extraímos imediatamente os ponteiros para as últimas camadas desses modelos.  

   CObject *next = NULL;
   CNeuronBaseOCL *centroids = cHyperCentroids[-1];
   CNeuronBaseOCL *curvatures = cHyperCurvatures[-1];

Em seguida, chamamos o método encapsulador do kernel de distribuição do gradiente por meio das operações de projeção dos dados brutos nos planos tangentes.

   if(!LogMapGrad(prevLayer, centroids, curvatures, AsObject()))
      return false;

E distribuímos o gradiente do erro no modelo interno de definição da curvatura do hiperespaço nos pontos dos centroides, criando um laço de iteração reversa pelas camadas neurais do modelo.

//--- Curvatures
   for(int i = cHyperCurvatures.Total() - 2; i >= 0; i--)
     {
      next = curvatures;
      curvatures = cHyperCurvatures[i];
      if(!curvatures ||
         !curvatures.calcHiddenGradients(next))
         return false;
     }

E em seguida, precisamos transmitir o gradiente do erro do modelo de definição da curvatura para o modelo de geração das coordenadas dos centroides. Mas aqui observamos que o buffer da última camada do modelo de geração das coordenadas dos centroides já contém o gradiente do erro das operações de projeção dos dados nos planos tangentes. E é desejável preservar os valores existentes. Como de costume, nesses casos recorremos à substituição temporária dos ponteiros dos buffers de dados. Primeiro, salvamos o ponteiro atual do buffer de gradientes de erro da última camada do modelo de geração das coordenadas dos centroides em uma variável local e, se necessário, ajustamos os valores pela derivada da função de ativação da camada neural.

   CBufferFloat *temp = centroids.getGradient();
   if(centroids.Activation()!=None)
      if(!DeActivation(centroids.getOutput(),temp,temp,centroids.Activation()))
        return false;
   if(!centroids.SetGradient(centroids.getPrevOutput(), false) ||
      !centroids.calcHiddenGradients(curvatures.AsObject()) ||
      !SumAndNormilize(temp, centroids.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !centroids.SetGradient(temp, false)
     )
      return false;

Depois, substituímos temporariamente esse ponteiro por um buffer não utilizado, com o tamanho correspondente. Chamamos o método de distribuição do gradiente do erro para a última camada do modelo de geração das coordenadas dos centroides, passando como próximo objeto a primeira camada do modelo de definição da curvatura do hiperespaço nos pontos dos centroides. Somamos os valores dos dois buffers de dados e restauramos os ponteiros à condição original. Não nos esquecemos de controlar cuidadosamente a execução de cada operação descrita.

Agora, com o gradiente de erro total no buffer da última camada do modelo de definição das coordenadas dos centroides, podemos organizar um laço de iteração reversa sobre as camadas neurais do modelo. Nesse laço, distribuímos o gradiente do erro entre as camadas do modelo, conforme a contribuição de cada uma para o resultado final.

//--- Centroids
   for(int i = cHyperCentroids.Total() - 2; i >= 0; i--)
     {
      next = centroids;
      centroids = cHyperCentroids[i];
      if(!centroids ||
         !centroids.calcHiddenGradients(next))
         return false;
     }

Depois disso, só nos resta transmitir o gradiente do erro ao nível dos dados brutos. Mas aqui novamente nos deparamos com a questão da preservação do gradiente do erro previamente acumulado. E repetimos o truque anteriormente descrito da substituição dos buffers de dados, só que desta vez para o objeto dos dados brutos.

   temp = prevLayer.getGradient();
   if(prevLayer.Activation()!=None)
      if(!DeActivation(prevLayer.getOutput(),temp,temp,prevLayer.Activation()))
        return false;
   if(!prevLayer.SetGradient(prevLayer.getPrevOutput(), false) ||
      !prevLayer.calcHiddenGradients(centroids.AsObject()) ||
      !SumAndNormilize(temp, prevLayer.getGradient(), temp, iWindows, false, 0, 0, 0, 1) ||
      !prevLayer.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

Agora, basta retornarmos o resultado lógico da execução das operações para o programa chamador e encerrar o método.

Com isso, finalizamos a análise dos algoritmos de construção dos métodos da nossa classe CNeuronHyperboloids. Você pode consultar por conta própria o código completo dessa classe e de todos os seus métodos no anexo.

3. Montamos o framework HypDiff

Concluímos o trabalho de construção dos novos blocos individuais do framework HypDiff e chegamos ao momento de montar o objeto unificado da implementação de alto nível do framework. Para isso, criaremos uma nova classe CNeuronHypDiff, cuja estrutura é apresentada abaixo.

class CNeuronHypDiff :  public CNeuronRMAT
  {
public:
                     CNeuronHypDiff(void) {};
                    ~CNeuronHypDiff(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint centroids,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronHypDiff; }
   //---
   virtual uint      GetWindow(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetWindow() - 1);
     }
   virtual uint      GetUnits(void) const override
     {
      CNeuronRMAT* neuron = cLayers[1];
      return (!neuron ? 0 : neuron.GetUnits());
     }
  };

Como se pode notar na estrutura apresentada acima da nova classe, sua funcionalidade principal é herdada do objeto CNeuronRMAT. Esse objeto possui os recursos necessários para organizar o funcionamento de um pequeno modelo linear, o que é mais do que suficiente para a implementação do HypDiff. Por isso, nesta etapa, basta sobrescrever o método de inicialização do objeto, especificando a arquitetura correta do modelo aninhado. Todos os demais processos já estão cobertos pelos métodos da classe pai.

Nos parâmetros do método de inicialização do objeto, recebemos as principais constantes que permitem interpretar de forma inequívoca a arquitetura do objeto que está sendo criado.

bool CNeuronHypDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint units_count, 
                          uint heads, uint layers, uint centroids, 
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

E no corpo do método, chamamos diretamente o método homônimo do objeto base das camadas neurais, no qual está implementada a inicialização das interfaces principais. Intencionalmente, não utilizamos neste ponto o método de inicialização da classe-pai direta, pois a arquitetura do modelo interno que estamos criando é significativamente diferente.

Depois disso, preparamos o array dinâmico herdado para armazenar os ponteiros para os objetos internos.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   int layer = 0;

E então passamos ao processo direto de construção da arquitetura interna do framework HypDiff.

Os dados brutos recebidos na entrada do modelo são inicialmente projetados no espaço hiperbólico. Para isso, adicionamos um objeto da classe CNeuronHyperProjection criada anteriormente.

//--- Projection
   CNeuronHyperProjection *lorenz = new CNeuronHyperProjection();
   if(!lorenz ||
      !lorenz.Init(0, layer, OpenCL, window, units_count, optimization, iBatch) ||
      !cLayers.Add(lorenz))
     {
      delete lorenz;
      return false;
     }
   layer++;

Em seguida, o framework HypDiff prevê o uso de um codificador hiperbólico destinado à geração das incorporações dos nós do grafo analisado. Os autores do framework utilizaram modelos neurais de grafos em conjunto com camadas convolucionais. Em nossa implementação, substituímos as redes neurais de grafos por um Transformer com codificação relativa.

//--- Encoder
   CNeuronRMAT *rmat = new CNeuronRMAT();
   if(!rmat ||
      !rmat.Init(0, layer, OpenCL, window + 1, window_key, units_count, heads, layers, optimization, iBatch) ||
      !cLayers.Add(rmat))
     {
      delete rmat;
      return false;
     }
   layer++;
//---
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, window + 1, window + 1, 2 * window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;
   conv.SetActivationFunction(TANH);
//---
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 2 * window, 2 * window, 3, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   layer++;

É importante observar que, ao projetar as incorporações obtidas nos planos tangentes, aumentamos significativamente o volume de informações processadas, pois realizamos projeções sobre todos os planos tangentes do volume completo de dados. Para compensar parcialmente os efeitos negativos dessa abordagem, reduzimos o tamanho da incorporação de cada nó.

As incorporações dos dados brutos obtidas deverão ser projetadas nos planos tangentes dos centroides. O funcional de geração dos centroides e projeção dos dados brutos nos planos correspondentes já foi estruturado na classe CNeuronHyperboloids. E agora, basta adicionarmos uma instância desse objeto ao nosso modelo linear.

//--- LogMap projecction
   CNeuronHyperboloids *logmap = new CNeuronHyperboloids();
   if(!logmap ||
      !logmap.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(logmap))
     {
      delete logmap;
      return false;
     }
   layer++;

Na saída, obtemos projeções dos dados brutos em múltiplos planos. E agora podemos aplicar a elas o algoritmo de difusão direcionada, originalmente desenvolvido para modelos euclidianos. Em nossa implementação, utilizamos o objeto CNeuronDiffusion.

//--- Diffusion model
  CNeuronDiffusion *diff = new CNeuronDiffusion();
  if(!diff ||
     !diff.Init(0, layer, OpenCL, 3, window_key, heads, units_count*centroids, 2, layers, optimization, iBatch) ||
     !cLayers.Add(diff))
    {
     delete diff;
     return false;
    }
  layer++;

Aqui vale destacar que optamos por não agrupar as diferentes projeções de um mesmo elemento da sequência em uma única entidade. Pelo contrário, em nossa implementação, o modelo de difusão direcionada trata cada projeção como um objeto separado. Dessa forma, propomos que o modelo aprenda a correlacionar as projeções individuais de uma mesma sequência e, a partir delas, forme uma representação volumétrica dos dados analisados.

Outro ponto implícito que merece menção é o ruído adicionado. Não tentamos unificar o ruído das diferentes projeções de um mesmo elemento da sequência, pois isso complicaria o modelo. Afinal, o próprio processo de adição de ruído pressupõe um "borramento" dos dados brutos em torno de sua vizinhança. A adição diferenciada de ruído em cada projeção torna esse "borramento" tridimensional.

Na saída do modelo de difusão, esperamos obter representações dos dados brutos, em suas diferentes projeções, já depuradas do ruído. E é aqui que iniciamos nossos desvios mais significativos do framework original. Os autores do HypDiff realizavam uma projeção reversa dos dados para o espaço hiperbólico e, com o auxílio de um decodificador de Fermi-Dirac, reconstruíam a representação original do grafo. Já o nosso objetivo é obter uma representação latente informativa dos dados brutos, para posterior envio ao modelo do Ator e treinamento de uma política lucrativa de atuação do nosso agente. Por isso, utilizamos uma camada de pooling baseada em dependências, para obter uma visão geral de cada elemento da sequência.

//--- Pooling
   CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling();
   if(!pooling ||
      !pooling.Init(0, layer, OpenCL, 3, units_count, centroids, optimization, iBatch) ||
      !cLayers.Add(pooling))
     {
      delete pooling;
      return false;
     }
   layer++;

E ajustamos o tamanho do tensor de resultados para o nível dos dados brutos.

//--- Resize to source size
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer, OpenCL, 3, 3, window, units_count, 1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }

Agora, só nos resta substituir os ponteiros dos buffers de dados das interfaces pelos buffers correspondentes da última camada do nosso modelo. E encerrar o método de inicialização da nossa classe.

//---
   if(!SetOutput(conv.getOutput(), true) ||
      !SetGradient(conv.getGradient(), true))
      return false;
//---
   return true;
  }

Com isso, concluímos a implementação da nossa visão sobre as abordagens do framework HypDiff com os recursos do MQL5. O código completo de todas as classes e métodos apresentados no artigo está disponível no anexo. Lá também estão os códigos dos programas de interação com o ambiente e de treinamento dos modelos, que foram mantidos inalterados em relação aos trabalhos anteriores.

E algumas palavras sobre a arquitetura dos modelos treináveis. As arquiteturas dos modelos do Ator e do Crítico permaneceram inalteradas. No entanto, fizemos pequenos ajustes no modelo do Codificador do estado do ambiente. Os dados brutos alimentados no modelo, como antes, passam por um pré-processamento inicial em uma camada de normalização em lote.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, eles são imediatamente enviados para o nosso modelo de difusão latente hiperbólica.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronHypDiff;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=10;                                        // centroids
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

O algoritmo descrito acima representa um processo bastante complexo e abrangente, pois é baseado no modelo de difusão latente hiperbólica. Por esse motivo, optamos por não realizar processamento adicional dos dados. Utilizamos apenas uma camada totalmente conectada para ajustar os dados ao tamanho necessário do tensor, com o qual o modelo do Ator será alimentado.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Com isso, encerramos a implementação das abordagens do framework HypDiff e passamos à etapa mais empolgante: a avaliação prática dos resultados obtidos com dados históricos reais.

4. Testes

Implementamos o framework HypDiff com os recursos do MQL5 e agora chegamos à fase final: o treinamento dos modelos e a avaliação da política de comportamento aprendida pelo Ator. Seguimos o algoritmo de treinamento descrito em trabalhos anteriores, treinando simultaneamente três modelos: Codificador do estado da conta, Ator e Crítico. Codificador analisa a situação do mercado. Ator toma decisões de negociação com base na política aprendida. O Crítico avalia as ações do Ator e indica direções para ajustes de sua política.

O treinamento foi realizado com dados históricos reais de todo o ano de 2023 do instrumento financeiro EURUSD, no timeframe H1. Os parâmetros de todos os indicadores analisados foram usados em suas configurações padrão.

O processo de treinamento é iterativo e inclui a atualização regular do conjunto de dados de treino.

Para avaliar a eficácia da política treinada, foram utilizados dados históricos reais do primeiro trimestre de 2024. Os resultados dos testes são apresentados abaixo.

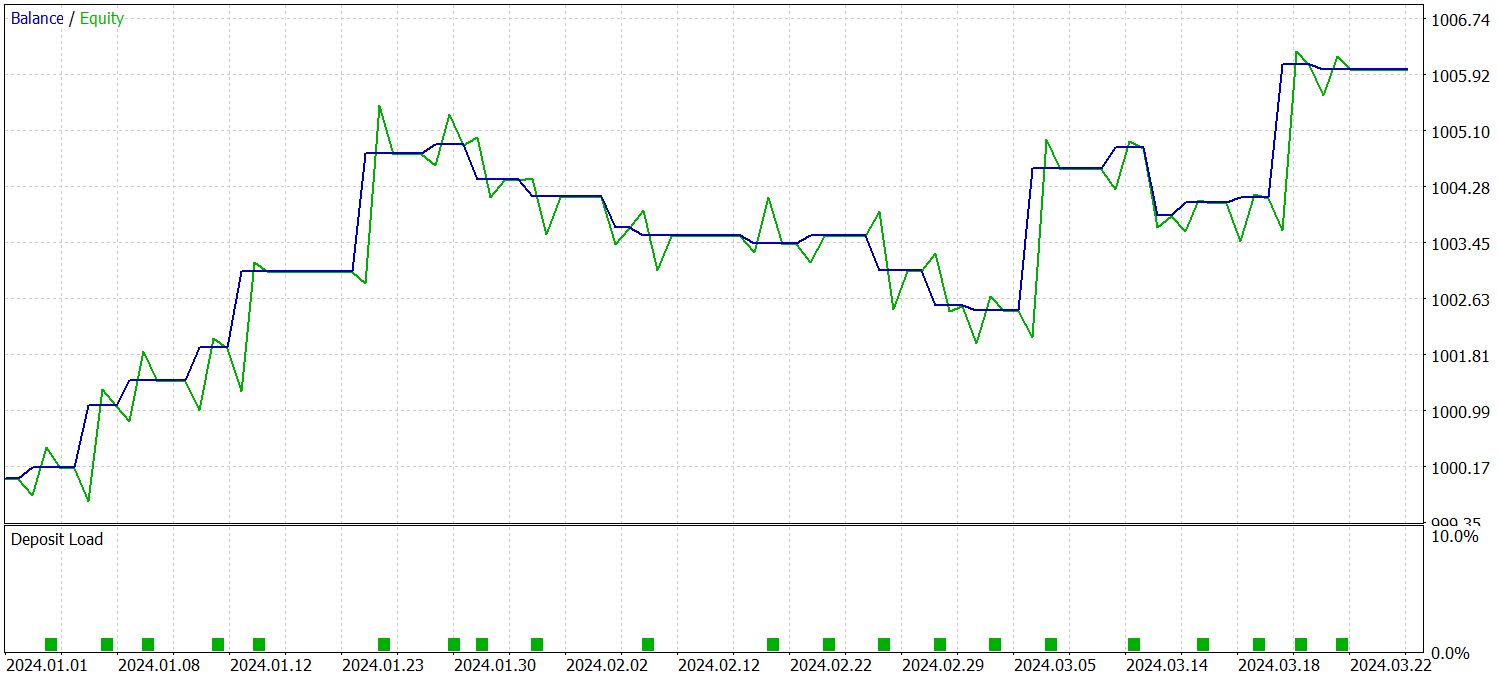
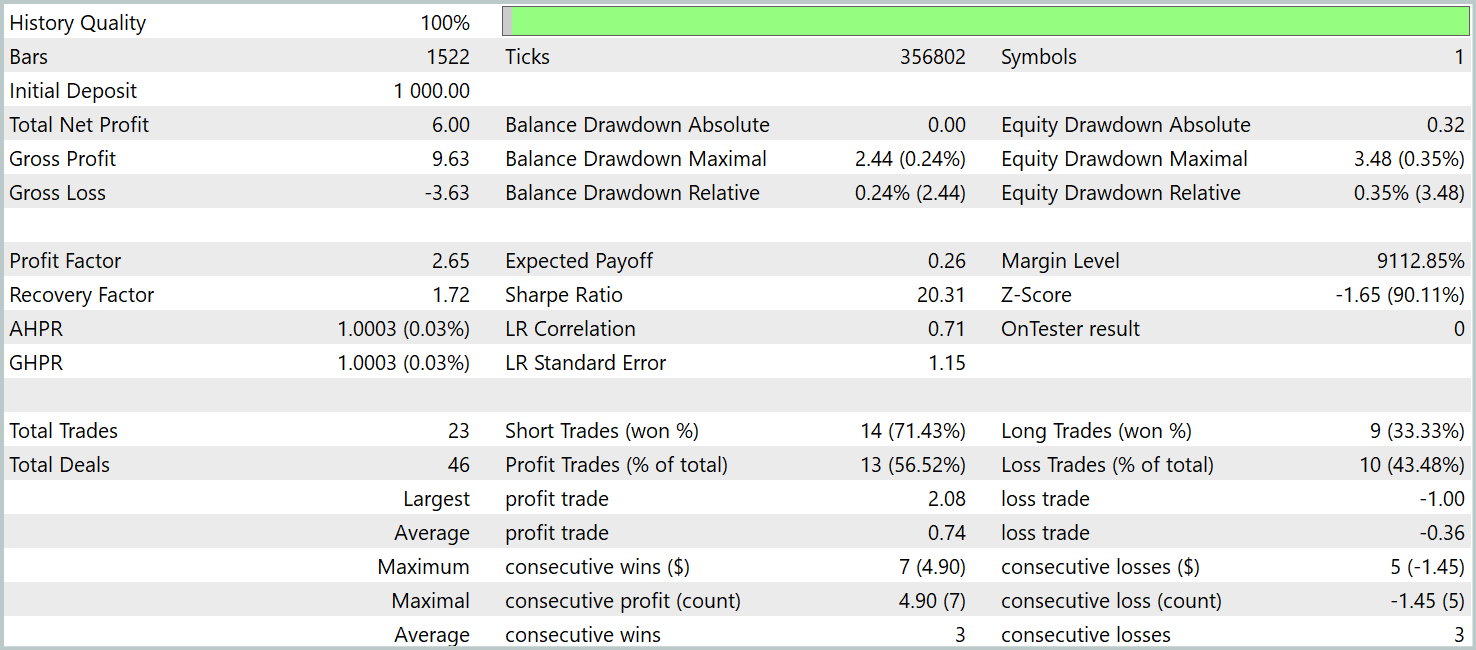
Como se pode notar pelos dados apresentados, o modelo obteve lucro no período de teste. Foram realizadas 23 operações comerciais ao longo de 3 meses, o que é pouco evidentemente. Mais de 56% dessas operações foram encerradas com lucro. Além disso, tanto o lucro máximo quanto o lucro médio por operação superaram em duas vezes os valores correspondentes das operações com prejuízo.

No entanto, ainda mais interessante é a análise detalhada das operações. Dos 3 meses de teste, o modelo obteve lucro em apenas 2. Fevereiro foi completamente negativo. Ainda assim, das 8 operações realizadas em janeiro de 2024, apenas a última foi fechada com prejuízo. Isso confirma a teoria anteriormente levantada sobre a perda de representatividade do conjunto de treino de um ano após o primeiro mês de operação do modelo.

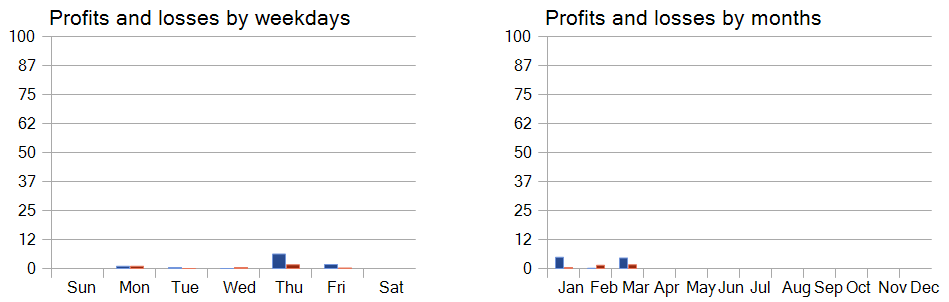
A análise da rentabilidade das operações por dia da semana permite concluir que há uma clara preferência do modelo por operar nas quintas e sextas-feiras.

Considerações finais

A aplicação da geometria hiperbólica ajuda a superar os problemas decorrentes do conflito entre a natureza discreta dos dados em grafos e o modelo contínuo de difusão. O framework HypDiff propõe um método avançado de geração de ruído gaussiano hiperbólico, capaz de resolver o problema das falhas aditivas das distribuições gaussianas no espaço hiperbólico. Para preservar a estrutura local durante a difusão anisotrópica, são introduzidas restrições geométricas à semelhança angular.

Na parte prática, implementamos nossa própria visão das abordagens propostas utilizando os recursos do MQL5. Treinamos os modelos com base nessas abordagens, utilizando dados históricos reais. Além disso, realizamos testes da política de comportamento do Ator, treinada fora do conjunto de dados de treinamento. Os resultados obtidos demonstram o potencial existente das abordagens propostas e indicam possíveis caminhos para melhorar a eficiência do funcionamento do modelo.

Referências

• Hyperbolic Geometric Latent Diffusion Model for Graph Generation
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento dos Modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação da rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL