Redes neurais em trading: Modelo hiperbólico de difusão latente (HypDiff)

Introdução

Os grafos apresentam uma variedade e importância nas topologias dos dados brutos. Essas características topológicas frequentemente refletem princípios físicos e modelos de desenvolvimento. Modelos tradicionais de grafos aleatórios, baseados na teoria dos grafos, exigem heurísticas artificiais para criar algoritmos com topologia específica e não conseguem modelar de forma flexível a variedade de grafos complexos. Por isso, diversos modelos de aprendizado profundo foram criados para gerar grafos. Os modelos probabilísticos de difusão, desenvolvidos com função de redução de ruído, demonstraram alta eficácia e potencial na resolução de tarefas de visualização.

No entanto, devido à estrutura irregular e não euclidiana dos grafos, a aplicação do modelo de difusão neste contexto apresenta duas limitações principais:

1. Alta complexidade computacional. A geração de grafos consiste no processamento da natureza discreta, esparsa e de outras propriedades topológicas da estrutura não euclidiana. Como a perturbação por ruído gaussiano usada no modelo de difusão padrão não é adequada para dados discretos, o modelo de difusão de grafo discreto geralmente apresenta alta complexidade temporal e espacial devido ao problema de esparsidade estrutural. Além disso, o modelo de difusão de grafos discretos depende de um processo contínuo de ruído gaussiano para criar grafos completamente conectados e ruidosos, o que resulta na perda de informações estruturais e das propriedades topológicas subjacentes.
2. Anisotropia da estrutura não euclidiana. Ao contrário dos dados com estrutura regular, as estruturas “irregulares” não euclidianas das incorporações de grafos são anisotrópicas no espaço latente contínuo. As incorporações de nós de grafos no espaço euclidiano demonstram anisotropia significativa em várias direções específicas. A difusão isotrópica da incorporação do nó do grafo no espaço latente interpretará a informação estrutural anisotrópica como ruído, e essa informação útil será perdida no processo de redução de ruído.

O espaço geométrico hiperbólico é amplamente reconhecido como a variedade contínua ideal para representar estruturas discretas em forma de árvore ou hierárquicas, sendo utilizado em diversas tarefas de aprendizado com grafos. E, conforme afirmam os autores do trabalho "Hyperbolic Geometric Latent Diffusion Model for Graph Generation", a geometria hiperbólica apresenta grande potencial para lidar com a anisotropia estrutural não euclidiana nos processos de difusão latente de grafos. No espaço hiperbólico, observa-se que a distribuição das incorporações dos nós tende a ser globalmente isotrópica. Ao mesmo tempo em que mantém a anisotropia localmente. Além disso, a geometria hiperbólica unifica as medições angulares e radiais das coordenadas polares e pode oferecer medições geométricas com semântica física e interpretabilidade. É interessante notar que a geometria hiperbólica pode fornecer um espaço latente com características geométricas apriorísticas do grafo.

Com base nessas conclusões, os autores do trabalho mencionado buscam definir um espaço latente adequado, baseado na geometria hiperbólica, para desenvolver um processo de difusão eficaz dentro de estruturas não euclidianas na geração de grafos com preservação topológica. Paralelamente, dois problemas principais são abordados:

1. A aditividade de distribuições gaussianas contínuas não é definida no espaço latente hiperbólico;
2. O desenvolvimento de um processo eficaz de difusão anisotrópica para estruturas não euclidianas.

Com o objetivo de resolver esses problemas, foi proposto o modelo de difusão latente em espaço hiperbólico (HypDiff). Para a questão aditiva da distribuição gaussiana contínua nesse espaço, foi proposto um processo de difusão baseado em medidas radiais. Já a restrição angular foi usada para limitar o ruído anisotrópico, visando preservar a aprioridade estrutural e direcionar o modelo de difusão para detalhes mais refinados da estrutura do grafo.

1. Algoritmo HypDiff

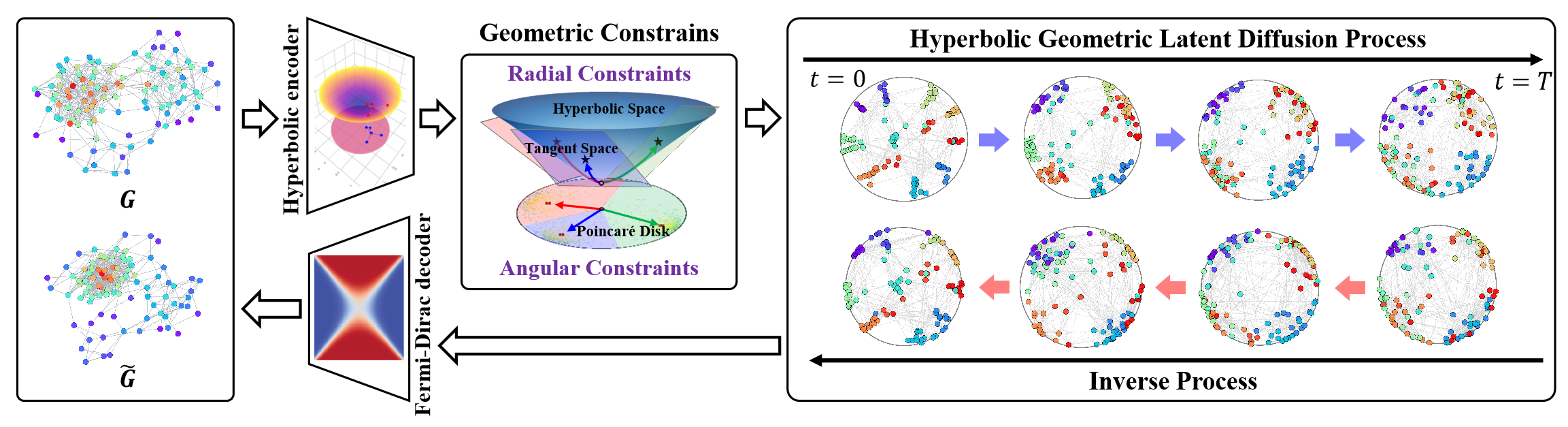
O modelo de difusão latente hiperbólica (HypDiff) resolve dois problemas principais. Ele utiliza a geometria hiperbólica para abstrair a hierarquia implícita dos nós do grafo e introduz duas restrições geométricas para preservar propriedades topológicas importantes. Os autores do método aplicam uma estratégia de aprendizado em duas etapas. Primeiro, é treinado um autocodificador hiperbólico para obter incorporações de nós pré-treinadas, e em seguida é treinado o processo de difusão latente geométrica hiperbólica.

Primeiro, é necessário integrar os dados do grafo 𝒢 = (𝐗, A) no espaço hiperbólico de baixa dimensionalidade, o que permitirá melhorar o processo de difusão latente do grafo.

O autocodificador hiperbólico proposto pelos autores do método é composto por um codificador geométrico hiperbólico e um decodificador de Fermi-Dirac. O codificador geométrico hiperbólico codifica o grafo 𝒢 = (𝐗, A) em um espaço geométrico hiperbólico para obter uma representação hiperbólica adequada, enquanto o decodificador de Fermi-Dirac decodifica a representação hiperbólica de volta para o domínio dos dados do grafo. A variedade hiperbólica Hd e o espaço tangente 𝒯x podem ser mapeados um no outro por meio das transformações exponencial e logarítmica. Em seguida, perceptrons multicamadas (MLP) ou redes neurais de grafos (GNN) podem ser utilizados para as representações exponenciais e logarítmicas, atuando como codificadores geométricos hiperbólicos. No trabalho, os autores utilizaram redes neurais convolucionais com grafos hiperbólicos (HGCN) como codificador geométrico hiperbólico.

Devido à falha aditiva da distribuição gaussiana no espaço hiperbólico, não é possível utilizar diretamente a distribuição normal Riemanniana ou a distribuição normal enrolada. Em vez da difusão hiperbólica das incorporações, é utilizado o espaço de produto de múltiplas variedades. Os autores do método HypDiff propuseram um novo processo de difusão no espaço hiperbólico. Para fins de eficiência computacional, a distribuição gaussiana no espaço hiperbólico é aproximada por uma distribuição gaussiana no plano tangente 𝒯μ.

Ao contrário da soma linear no espaço euclidiano, o espaço hiperbólico utiliza a adição de Möbius. Isso gera problemas para a difusão sobre a variedade hiperbólica. Além disso, o ruído isotrópico leva a uma rápida queda na relação sinal/ruído, dificultando a preservação das informações topológicas.

A anisotropia do grafo no espaço latente contém um viés indutivo da estrutura do grafo, sendo o principal desafio identificar as direções dominantes das características anisotrópicas. Para resolver esses problemas, os autores do HypDiff propuseram uma estrutura de difusão anisotrópica hiperbólica. A ideia central é selecionar a direção principal da difusão (ou seja, o ângulo) com base na clusterização dos nós por similaridade. Isso equivale a dividir o espaço latente hiperbólico em vários setores. Em seguida, os nós de cada cluster são projetados no plano tangente de seu centro para a realização da difusão.

Os clusters podem ser obtidos por meio de qualquer algoritmo de clusterização baseado em similaridade durante a etapa de pré-processamento.

O parâmetro de clusterização hiperbólica k ∈ [1, n] representa a quantidade de setores que dividem o espaço hiperbólico. A difusão anisotrópica hiperbólica é equivalente à difusão direcionada no modelo de Klein 𝕂c,n com curvatura múltipla Ci ∈|k|, a qual representa uma projeção aproximada em um conjunto de planos tangentes 𝒯𝐨i∈{|k|} dos centroides Oi∈{|k|}.

Essa propriedade estabelece de forma elegante a conexão entre o algoritmo de aproximação proposto pelos autores do HypDiff e o modelo de Klein com curvatura múltipla.

O algoritmo proposto demonstra um comportamento específico, com base no valor de k. Isso permite representar de maneira mais flexível e detalhada a anisotropia fundamentada na geometria hiperbólica, o que melhora a precisão e a eficiência na adição de ruído e no treinamento do modelo.

A geometria hiperbólica pode descrever de forma natural e geométrica o esquema de conexão dos nós durante o crescimento do grafo. A popularidade de um nó pode ser abstraída por suas coordenadas radiais, e a similaridade pode ser expressa pelas distâncias angulares das coordenadas no espaço hiperbólico.

O objetivo principal é modelar a difusão com crescimento radial geométrico. No qual esse crescimento radial esteja em conformidade com as propriedades hiperbólicas.

A principal razão pela qual o modelo geral de difusão não funciona muito bem com grafos está na rápida queda da relação sinal/ruído. No HypDiff, a direção da geodésica entre o ponto central de cada cluster e o polo norte O é usada como direção-alvo de difusão ao aplicar restrições aos processos de propagação para frente.

Seguindo o processo padrão de redução de ruído e treinamento de modelo para absorção de ruído com o objetivo de modelar o processo de propagação reversa, os autores do HypDiff utilizam a arquitetura DDM baseada em UNET para treinar a previsão de X0.

Além disso, os autores do HypDiff demonstram que, para aumentar a eficiência, é possível realizar a amostragem simultaneamente em um mesmo espaço tangente em vez de amostrar em diferentes espaços tangentes dos centros dos clusters.

A visualização do framework HypDiff criada pelos autores é apresentada abaixo.

2. Implementação com MQL5

Após analisar os aspectos teóricos do framework HypDiff, partimos para a parte prática deste artigo, na qual implementamos nossa própria visão das abordagens propostas por meio do MQL5. E já podemos adiantar que embarcaremos em uma jornada longa e empolgante. Portanto, é importante se preparar mentalmente para a realização de um grande volume de trabalho.

2.1 Complemento do programa OpenCL

Iniciamos nosso trabalho adicionando modificações ao nosso programa OpenCL. Primeiro, organizamos a projeção dos dados brutos no espaço hiperbólico. Durante o processo de transformação dos dados, é fundamental considerar a posição de cada elemento na sequência, já que o espaço hiperbólico combina os parâmetros do espaço euclidiano e do tempo. Seguindo a implementação dos autores, utilizamos o modelo de Lorentz. Essa tarefa será realizada no kernel HyperProjection.

__kernel void HyperProjection(__global const float *inputs,
                              __global float *outputs
                             )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_local_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_local_size(1);

Nos parâmetros desse kernel, passaremos ponteiros para os buffers de dados, ou seja, a sequência analisada e os resultados da transformação. Os parâmetros exatos dos buffers transmitidos serão definidos por meio do espaço de tarefas. A primeira dimensão indicará a dimensionalidade da sequência analisada, enquanto a segunda corresponderá ao tamanho do vetor de descrição de um único elemento dessa sequência. Os fluxos serão agrupados em grupos de trabalho pela última dimensão. 

Aqui é importante destacar que o vetor de descrição de um único elemento da sequência conterá 1 elemento a mais.

Em seguida, declaramos um array local que nos permitirá estabelecer a troca de dados entre os fluxos do grupo de trabalho.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

E definimos as constantes de deslocamento nos buffers de dados.

   const int shift_in = pos * dimension + d;
   const int shift_out = pos * (dimension + 1) + d + 1;

Carregamos os dados brutos do buffer global nos elementos locais correspondentes do fluxo de operações e calculamos os valores quadráticos. Durante esse processo, verificamos a validade dos resultados dessas operações.

   float v = inputs[shift_in];
   if(isinf(v) || isnan(v))
      v = 0;
//---
   float v2 = v * v;
   if(isinf(v2) || isnan(v2))
      v2 = 0;

Depois, devemos calcular a norma do vetor de dados brutos. Para isso, somamos o quadrado de seus valores usando nosso array local. Afinal, cada fluxo do grupo de trabalho contém 1 elemento.

//---
   if(d < ls)
      temp[d] = v2;
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += v2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Aqui vale destacar que a norma do vetor é necessária apenas para o cálculo do valor do primeiro elemento em nosso vetor de descrição das coordenadas hiperbólicas do elemento da sequência analisada. Todos os demais elementos são transferidos sem alterações, mas com deslocamento de posição.

   outputs[shift_out] = v;

E, para evitar operações redundantes, o cálculo do valor do primeiro elemento do vetor hiperbólico será realizado apenas no primeiro fluxo de cada grupo de trabalho.

Primeiramente, calculamos a fração de deslocamento do elemento analisado na sequência original. Em seguida, subtraímos o quadrado desse valor da norma do vetor do elemento analisado calculada anteriormente. E então extraímos a raiz quadrada do valor obtido.

   if(d == 0)
     {
      v = ((float)pos) / ((float)total);
      if(isinf(v) || isnan(v))
         v = 0;
      outputs[shift_out - 1] = sqrt(fmax(temp[0] - v * v, 1.2e-07f));
     }
  }

Observe que, para extrair a raiz quadrada, garantimos que os valores utilizados sejam sempre maiores que 0. Isso nos permite evitar erros de execução e resultados inválidos.

Com o objetivo de implementar os algoritmos de propagação reversa, criamos imediatamente o kernel HyperProjectionGrad, no qual os gradientes do erro serão distribuídos por meio das operações de propagação para frente descritas anteriormente. Aqui, devemos observar dois pontos importantes. Primeiro, a posição do elemento na sequência é estática e não é parametrizada. Portanto, não aplicamos a ela o gradiente do erro.

Em segundo lugar, o gradiente do erro dos demais elementos chega por dois fluxos de informação. A transferência direta de dados resulta na transmissão direta do gradiente do erro. Ao mesmo tempo, todos os elementos do vetor original de descrição do elemento da sequência são utilizados para calcular a norma do vetor, que participa da definição do primeiro elemento da representação hiperbólica. Sendo assim, cada elemento deve receber sua parte do gradiente de erro proveniente do primeiro elemento do vetor da representação hiperbólica.

Vamos observar a implementação desses conceitos no código. Nos parâmetros do kernel HyperProjectionGrad, são passados agora três ponteiros para buffers de dados. Adiciona-se o buffer de gradientes do erro no nível dos dados de entrada (inputs_gr). E o buffer da representação hiperbólica da sequência original é substituído pelo buffer correspondente aos gradientes do erro (outputs_gr).

__kernel void HyperProjectionGrad(__global const float *inputs,
                                  __global float *inputs_gr,
                                  __global const float *outputs_gr
                                 )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_global_size(1);

O espaço de tarefas do kernel permanece o mesmo da propagação para frente, mas agora os fluxos não são agrupados em grupos de trabalho. No corpo do kernel, primeiro identificamos o fluxo atual no espaço de tarefas. E com os valores obtidos, definimos o deslocamento nos buffers de dados.

   const int shift_in = pos * dimension + d;
   const int shift_start_out = pos * (dimension + 1);
   const int shift_out = shift_start_out + d + 1;

No bloco de carregamento de dados dos buffers globais, lemos o valor do elemento analisado na representação original e seu gradiente do erro no nível da representação hiperbólica.

   float v = inputs[shift_in];
   if(isinf(v) || isnan(v))
      v = 0;
   float grad = outputs_gr[shift_out];
   if(isinf(grad) || isnan(grad))
      grad = 0;

Em seguida, determinamos a fração do gradiente do erro proveniente do primeiro elemento da representação hiperbólica, definida como o produto do seu gradiente do erro pelo valor original do elemento analisado.

   v = v * outputs_gr[shift_start_out];
   if(isinf(v) || isnan(v))
      v = 0;

E não devemos esquecer de verificar, em cada etapa, a validade dos resultados obtidos.

O gradiente total do erro será armazenado no buffer global de dados correspondente.

//---
   inputs_gr[shift_in] = v + grad;
  }

Neste ponto, realizamos a projeção dos dados brutos no espaço hiperbólico. No entanto, os autores do método propõem realizar o processo de difusão em projeções do espaço hiperbólico nos planos tangentes.

À primeira vista, pode parecer um tanto estranho projetar os dados de uma representação plana para a hiperbólica e depois de volta apenas para adicionar ruído. Mas a questão é que a representação plana original, com grande probabilidade, será diferente da projeção final. Afinal, o plano dos valores originais e o plano da projeção da representação hiperbólica são planos distintos.

Talvez isso possa ser comparado à criação de um desenho técnico a partir da fotografia de um objeto. Primeiro, em nossa mente, formamos uma representação tridimensional do objeto mostrado na fotografia, com base em nossa experiência e conhecimento prévio. Em seguida, transferimos para o papel o desenho técnico do objeto representado, nas vistas lateral, frontal e superior. De maneira semelhante, o HypDiff projeta os dados em diversos planos tangentes com diferentes centros.

Para implementar essa funcionalidade, criaremos o kernel LogMap. Nos parâmetros desse kernel, recebemos ponteiros para 7 buffers de dados, o que, convenhamos, é uma quantidade considerável. Desses buffers, 3 são de dados brutos:

1. O buffer features contém o tensor das incorporações da representação hiperbólica dos dados brutos. 
2. O buffer centroids contém as coordenadas dos centroides. São esses os pontos onde os planos tangentes serão definidos, e nos quais devemos projetar os dados brutos.
3. 3. O buffer curvatures armazena os parâmetros de curvatura dos respectivos centroides.

Não é difícil deduzir que o buffer outputs é destinado ao registro dos resultados das operações. E adicionamos ainda mais 3 buffers de dados para armazenar os resultados intermediários, que serão utilizados durante a execução da propagação reversa.

E aqui vale destacar que nossa implementação se afasta um pouco do framework original dos autores. Na fase de preparação dos dados, os autores do HypDiff agruparam os elementos da sequência analisada e projetaram apenas os elementos de determinados grupos nos planos tangentes. Nós, por outro lado, não realizaremos a divisão prévia dos elementos da sequência em grupos. Portanto, projetaremos todos os elementos em todos os planos tangentes. Isso, naturalmente, aumentará o número de operações executadas. Porém, enriquecerá a compreensão da sequência analisada por parte do modelo.

__kernel void LogMap(__global const float *features,
                     __global const float *centroids,
                     __global const float *curvatures,
                     __global float *outputs,
                     __global float *product,
                     __global float *distance,
                     __global float *norma
                    )
  {
//--- identify
   const size_t f = get_global_id(0);
   const size_t cent = get_global_id(1);
   const size_t d = get_local_id(2);
   const size_t total_f = get_global_size(0);
   const size_t total_cent = get_global_size(1);
   const size_t dimension = get_local_size(2);

No corpo do método, identificamos o fluxo de operação atual em um espaço de tarefas tridimensional. A primeira dimensão indica o elemento da sequência original. A segunda corresponde ao centroide. E a terceira aponta a posição no vetor de descrição do elemento analisado da sequência. Nesse caso, os fluxos são agrupados em grupos de trabalho pela última dimensão.

Em seguida, declaramos um array local para troca de dados dentro do grupo de trabalho.

//--- create local array
   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

E definimos as constantes de deslocamento nos buffers de dados.

//--- calc shifts
   const int shift_f = f * dimension + d;
   const int shift_out = (f * total_cent + cent) * dimension + d;
   const int shift_cent = cent * dimension + d;
   const int shift_temporal = f * total_cent + cent;

Depois disso, carregamos os dados brutos dos buffers globais, com a devida verificação da validade dos valores obtidos.

//--- load inputs
   float feature = features[shift_f];
   if(isinf(feature) || isnan(feature))
      feature = 0;
   float centroid = centroids[shift_cent];
   if(isinf(centroid) || isnan(centroid))
      centroid = 0;
   float curv = curvatures[cent];
   if(isinf(curv) || isnan(curv))
      curv = 1.2e-7;

Em seguida, devemos calcular os produtos entre os tensores dos dados brutos e os centroides. Mas, como estamos trabalhando com uma representação hiperbólica, utilizaremos o produto de Minkowski. Para isso, primeiro multiplicamos os valores escalares correspondentes.

//--- dot(features, centroids)
   float fc = feature * centroid;
   if(isnan(fc) || isinf(fc))
      fc = 0;

E somamos os valores obtidos dentro do grupo de trabalho.

//---
   if(d < ls)
      temp[d] = (d > 0 ? fc : -fc);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += fc;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
   float prod = temp[0];
   if(isinf(prod) || isnan(prod))
      prod = 0;

Observe que, diferentemente da multiplicação usual de vetores no espaço euclidiano, aqui tomamos o produto dos primeiros elementos dos vetores com sinal invertido.

Verificamos a validade do resultado das operações realizadas e armazenamos o valor obtido no respectivo elemento do buffer global de armazenamento temporário de dados. Esse valor será necessário durante a propagação reversa.

   product[shift_temporal] = prod;

Isso nos permite determinar a direção e a magnitude do deslocamento do elemento analisado em relação ao centroide.

//--- project
   float u = feature + prod * centroid * curv;
   if(isinf(u) || isnan(u))
      u = 0;

Calculamos a norma de Minkowski do vetor de deslocamento obtido. Como antes, elevamos ao quadrado cada elemento.

//--- norm(u)
   float u2 = u * u;
   if(isinf(u2) || isnan(u2))
      u2 = 0;

E somamos os valores dentro do grupo de trabalho, utilizando o quadrado do primeiro elemento com sinal invertido.

   if(d < ls)
      temp[d] = (d > 0 ? u2 : -u2);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += u2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
   float normu = temp[0];
   if(isinf(normu) || isnan(normu) || normu <= 0)
      normu = 1.0e-7f;
   normu = sqrt(normu);

O valor obtido também será necessário no contexto da propagação reversa. Por isso, armazenamos esse dado no buffer de armazenamento temporário.

   norma[shift_temporal] = normu;

Na etapa seguinte, determinamos a distância entre o ponto analisado e o centroide no espaço hiperbólico, levando em consideração os parâmetros de curvatura do centroide. Nesse processo, não recalculamos o produto vetorial, mas usamos o valor já obtido anteriormente. 

//--- distance features to centroid
   float theta = -prod * curv;
   if(isinf(theta) || isnan(theta))
      theta = 0;
   theta = fmax(theta, 1.0f + 1.2e-07f);
   float dist = sqrt(clamp(pow(acosh(theta), 2.0f) / curv, 0.0f, 50.0f));
   if(isinf(dist) || isnan(dist))
      dist = 0;

Verificamos a validade do valor resultante e armazenamos o resultado no buffer global de armazenamento temporário de dados.

   distance[shift_temporal] = dist;

Ajustamos os valores do vetor de deslocamento.

   float proj_u = dist * u / normu;

E então realizamos a projeção dos valores obtidos no plano tangente. Aqui, de forma semelhante à projeção de Lorentz feita anteriormente, devemos ajustar o primeiro elemento do vetor de projeção. Para isso, calculamos o produto vetorial entre a projeção e o centroide, desconsiderando os primeiros elementos.

   if(d < ls)
      temp[d] = (d > 0 ? proj_u * centroid : 0);
   barrier(CLK_LOCAL_MEM_FENCE);
   for(int i = ls; i < (int)dimension; i += ls)
     {
      if(d >= i && d < (i + ls))
         temp[d % ls] += proj_u * centroid;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (int)dimension);
//---
   do
     {
      count = (count + 1) / 2;
      if(d < count)
         temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
      if(d + count < dimension)
         temp[d + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Corrigimos o valor do primeiro elemento da projeção.

//---
   if(d == 0)
     {
      proj_u = temp[0] / centroid;
      if(isinf(proj_u) || isnan(proj_u))
         proj_u = 0;
      proj_u = fmax(u, 1.2e-7f);
     }

E salvamos os resultados obtidos.

//---
   outputs[shift_out] = proj_u;
  }

Como se pode notar, o algoritmo do kernel ficou bastante robusto, com diversas interconexões complexas. Isso torna difícil compreender o caminho percorrido pelo gradiente do erro durante a propagação reversa. Entretanto, precisamos desembaraçar esse "nó". Vamos nos concentrar nos detalhes e começar o trabalho. O algoritmo de propagação reversa é implementado no kernel LogMapGrad.

__kernel void LogMapGrad(__global const float *features, __global float *features_gr,
                         __global const float *centroids, __global float *centroids_gr,
                         __global const float *curvatures, __global float *curvatures_gr,
                         __global const float *outputs, __global const float *outputs_gr,
                         __global const float *product,
                         __global const float *distance,
                         __global const float *norma
                        )
  {
//--- identify
   const size_t f = get_local_id(0);
   const size_t cent = get_global_id(1);
   const size_t d = get_local_id(2);
   const size_t total_f = get_local_size(0);
   const size_t total_cent = get_global_size(1);
   const size_t dimension = get_local_size(2);

Nos parâmetros do kernel, adicionamos buffers de gradientes do erro no nível dos dados brutos e dos resultados, o que nos forneceu 4 buffers de dados adicionais.

O espaço de tarefas do kernel foi mantido igual ao da propagação para frente, apenas alteramos o critério de agrupamento nos grupos de trabalho. Pois agora devemos acumular valores não apenas no contexto dos vetores dos elementos individuais da sequência, mas também os gradientes dos centroides. Afinal, cada centroide interage com todos os elementos da sequência analisada. Consequentemente, o gradiente do erro deve receber contribuição de cada um deles.

No corpo do kernel, identificamos o fluxo de operações em todas as dimensões do espaço de tarefas. Em seguida, criamos um array local para troca de dados entre os elementos do grupo de trabalho.

//--- create local array
   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);

E definimos as constantes de deslocamento nos buffers globais de dados.

//--- calc shifts
   const int shift_f = f * dimension + d;
   const int shift_out = (f * total_cent + cent) * dimension + d;
   const int shift_cent = cent * dimension + d;
   const int shift_temporal = f * total_cent + cent;

Depois disso, carregamos os dados dos buffers globais. Primeiro, extraímos os dados brutos e os valores intermediários. 

//--- load inputs
   float feature = features[shift_f];
   if(isinf(feature) || isnan(feature))
      feature = 0;
   float centroid = centroids[shift_cent];
   if(isinf(centroid) || isnan(centroid))
      centroid = 0;
   float centroid0 = (d > 0 ? centroids[shift_cent - d] : centroid);
   if(isinf(centroid0) || isnan(centroid0) || centroid0 == 0)
      centroid0 = 1.2e-7f;
   float curv = curvatures[cent];
   if(isinf(curv) || isnan(curv))
      curv = 1.2e-7;
   float prod = product[shift_temporal];
   float dist = distance[shift_temporal];
   float normu = norma[shift_temporal];

Aqui mesmo, calculamos os valores do vetor de deslocamento do elemento analisado em relação ao centroide. Ao contrário das operações de propagação para frente, já temos todos os dados necessários aqui.

   float u = feature + prod * centroid * curv;
   if(isinf(u) || isnan(u))
      u = 0;

Em seguida, carregamos o gradiente de erro disponível no nível dos resultados.

   float grad = outputs_gr[shift_out];
   if(isinf(grad) || isnan(grad))
      grad = 0;
   float grad0 = (d>0 ? outputs_gr[shift_out - d] : grad);
   if(isinf(grad0) || isnan(grad0))
      grad0 = 0;

Vale ressaltar que carregamos o gradiente de erro não apenas do elemento analisado, mas também do primeiro valor no vetor de descrição desse elemento na sequência. A razão para isso é a mesma já descrita anteriormente no kernel HyperProjectionGrad.

Depois, inicializamos variáveis locais para acumulação dos gradientes do erro.

   float feature_gr = 0;
   float centroid_gr = 0;
   float curv_gr = 0;
   float prod_gr = 0;
   float normu_gr = 0;
   float dist_gr = 0;

Primeiramente, propagamos o gradiente do erro da projeção dos dados no plano tangente até o vetor de deslocamento.

   float proj_u_gr = (d > 0 ? grad + grad0 / centroid0 * centroid : 0);

Aqui é importante notar que o primeiro elemento do vetor de deslocamento não influenciou o resultado. Portanto, seu gradiente é igual a "0". Enquanto isso, os demais elementos receberam tanto o gradiente direto do erro quanto uma fração proveniente do primeiro elemento dos resultados.

Neste ponto, também definimos os valores iniciais dos gradientes do erro para os centroides. Eles serão calculados em um laço, acumulando os valores vindos de todos os elementos da sequência.

   for(int id = 0; id < dimension; id += ls)
     {
      if(d >= id && d < (id + ls))
        {
         int t = d % ls;
         for(int ifeat = 0; ifeat < total_f; ifeat++)
           {
            if(f == ifeat)
              {
               if(d == 0)
                  temp[t] = (f > 0 ? temp[t] : 0) + outputs[shift_out] / centroid * grad;
               else
                  temp[t] = (f > 0 ? temp[t] : 0) + grad0 / centroid0 * outputs[shift_out];
              }
            barrier(CLK_LOCAL_MEM_FENCE);
           }

Após a coleta dos gradientes do erro de todos os elementos da sequência no array local, utilizamos um único fluxo para transferir os valores acumulados para uma variável local.

         if(f == 0)
           {
            if(isnan(temp[t]) || isinf(temp[t]))
               temp[t] = 0;
            centroid_gr += temp[0];
           }
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Nesse processo, é fundamental garantir que todos os fluxos de operação alcancem os pontos de barreira sem exceções.

Em seguida, calculamos os gradientes do erro para os vetores de distância, norma e deslocamento.

   dist_gr = u / normu * proj_u_gr;
   float u_gr = dist / normu * proj_u_gr;
   normu_gr = dist * u / (normu * normu) * proj_u_gr;

Aqui devemos destacar que os elementos do vetor de deslocamento são específicos para cada fluxo. Já a norma do vetor e a distância são valores discretos. Por isso, devemos somar os respectivos gradientes do erro no escopo de um único elemento da sequência analisada. Primeiro, acumulamos os gradientes do erro da distância. A soma será feita usando um array local.

   for(int ifeat = 0; ifeat < total_f; ifeat++)
     {
      if(d < ls && f == ifeat)
         temp[d] = dist_gr;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += dist_gr;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      int count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(f == ifeat)
        {
         if(isinf(temp[0]) || isnan(temp[0]))
            temp[0] = 0;
         dist_gr = temp[0];

E em seguida, determinamos o gradiente do erro para o parâmetro de curvatura do centroide correspondente e para o produto vetorial.

         if(d == 0)
           {
            float theta = -prod * curv;
            float theta_gr = 1.0f / sqrt(curv * (theta * theta - 1)) * dist_gr;
            if(isinf(theta_gr) || isnan(theta_gr))
               theta_gr = 0;
            curv_gr += -pow(acosh(theta), 2.0f) / (2 * sqrt(pow(curv, 3.0f))) * dist_gr;
            if(isinf(curv_gr) || isnan(curv_gr))
               curv_gr = 0;
            temp[0] = -curv * theta_gr;
            if(isinf(temp[0]) || isnan(temp[0]))
               temp[0] = 0;
            curv_gr += -prod * theta_gr;
            if(isinf(curv_gr) || isnan(curv_gr))
               curv_gr = 0;
           }
        }
      barrier(CLK_LOCAL_MEM_FENCE);

No entanto, é importante observar que o gradiente do erro para o parâmetro de curvatura é apenas acumulado para posterior armazenamento no buffer global de dados. Diferentemente dele, o gradiente do erro do produto vetorial é um valor intermediário, que será posteriormente distribuído entre os elementos afetados. Por isso, é essencial sincronizá-lo dentro do grupo de trabalho. Neste estágio, armazenamos esse valor em um elemento do array local. E em seguida o transferimos para uma variável local.

      if(f == ifeat)
         prod_gr += temp[0];
      barrier(CLK_LOCAL_MEM_FENCE);

Acredito que você tenha notado a grande quantidade de verificações repetidas. Isso torna o código um pouco mais complexo, mas é uma medida necessária para garantir a correta sincronização dos fluxos dentro do grupo de trabalho.

Em seguida, da mesma forma, somamos o gradiente do erro da norma do vetor de deslocamento.

      if(d < ls && f == ifeat)
         temp[d] = normu_gr;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += normu_gr;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(f == ifeat)
        {
         normu_gr = temp[0];
         if(isinf(normu_gr) || isnan(normu_gr))
            normu_gr = 1.2e-7;

E ajustamos o gradiente do erro do vetor de deslocamento.

         u_gr += u / normu * normu_gr;
         if(isnan(u_gr) || isinf(u_gr))
            u_gr = 0;

E o distribuímos entre os dados brutos e o centroide.

         feature_gr += u_gr;
         centroid_gr += prod * curv * u_gr;
        }
      barrier(CLK_LOCAL_MEM_FENCE);

Vale destacar aqui que o gradiente do erro do vetor de deslocamento deve ser distribuído tanto ao nível do produto vetorial quanto ao parâmetro de curvatura. No entanto, essas entidades são escalares. Portanto, devemos somar os valores dentro do escopo de um único elemento da sequência analisada. Neste ponto, realizamos a soma dos produtos entre os respectivos gradientes do erro do vetor de deslocamento e os elementos dos centroides. Ou seja, basicamente, o produto vetorial entre eles.

      //--- dot (u_gr * centroid)
      if(d < ls && f == ifeat)
         temp[d] = u_gr * centroid;
      barrier(CLK_LOCAL_MEM_FENCE);
      for(int id = ls; id < (int)dimension; id += ls)
        {
         if(d >= id && d < (id + ls) && f == ifeat)
            temp[d % ls] += u_gr * centroid;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (int)dimension);
      //---
      do
        {
         count = (count + 1) / 2;
         if(f == ifeat)
           {
            if(d < count)
               temp[d] += ((d + count) < dimension ? temp[d + count] : 0);
            if(d + count < dimension)
               temp[d + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

Os valores obtidos serão utilizados para distribuir o gradiente do erro entre essas entidades correspondentes.

      if(f == ifeat && d == 0)
        {
         if(isinf(temp[0]) || isnan(temp[0]))
            temp[0] = 0;
         prod_gr += temp[0] * curv;
         if(isinf(prod_gr) || isnan(prod_gr))
            prod_gr = 0;
         curv_gr += temp[0] * prod;
         if(isinf(curv_gr) || isnan(curv_gr))
            curv_gr = 0;
         temp[0] = prod_gr;
        }
      barrier(CLK_LOCAL_MEM_FENCE);

Em seguida, sincronizamos o valor do gradiente do erro no nível do produto vetorial dentro do grupo de trabalho.

      if(f == ifeat)
        {
         prod_gr = temp[0];

E distribuímos o valor obtido entre os dados brutos.

         feature_gr += prod_gr * centroid * (d > 0 ? 1 : -1);
         centroid_gr += prod_gr * feature * (d > 0 ? 1 : -1);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Após a execução bem-sucedida de todas as operações e a coleta completa dos gradientes do erro nas variáveis locais, transferimos os valores obtidos para os buffers globais de dados.

//--- result
   features_gr[shift_f] = feature_gr;
   centroids_gr[shift_cent] = centroid_gr;
   if(f == 0 && d == 0)
      curvatures_gr[cent] = curv;
  }

E finalizamos a execução do kernel.

Como se pode ver, o algoritmo é bastante complexo, mas ao mesmo tempo fascinante. Sua compreensão exige atenção aos detalhes.

Como mencionado, a implementação do framework HypDiff exige um esforço considerável. Aqui, discutimos apenas a implementação dos algoritmos no lado do programa em OpenCL, cujo código completo está disponível no anexo. Com isso, praticamente esgotamos o conteúdo deste artigo. Por isso, proponho que o estudo da implementação dos algoritmos do framework no lado do programa principal seja continuado em um próximo artigo. Dessa forma, dividiremos o trabalho realizado em dois blocos lógicos.

Considerações finais

O uso da geometria hiperbólica permite resolver os conflitos entre os dados de grafos discretos e o modelo de difusão contínua. O framework HypDiff propõe um método aprimorado para a geração de ruído gaussiano hiperbólico, com o objetivo de superar a falha aditiva das distribuições gaussianas no espaço hiperbólico. Restrições geométricas baseadas em similaridade angular são aplicadas ao processo de difusão anisotrópica para preservar a estrutura local.

Na parte prática do artigo, iniciamos a implementação das abordagens propostas utilizando MQL5. Porém, o volume de trabalho excede o escopo de um único artigo. E continuaremos a construção do framework proposto em um artigo subsequente.

Referências

• Hyperbolic Geometric Latent Diffusion Model for Graph Generation
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL