Reimaginando Estratégias Clássicas (Parte VII): Mercados de Forex e Análise da Dívida Soberana no USDJPY

A Inteligência Artificial tem o potencial de criar novas estratégias de negociação para o investidor moderno. É improvável que um único investidor tenha tempo suficiente para avaliar cuidadosamente cada estratégia possível antes de decidir em qual confiar seu capital. Nesta série de artigos, nosso objetivo é fornecer as informações necessárias para que você tome uma decisão informada sobre qual estratégia melhor se adapta ao seu perfil de investidor.

Resumo da Estratégia de Negociação

Os títulos de renda fixa são investimentos que permitem aos investidores diversificar seus portfólios de forma segura. Eles são uma classe de investimentos que paga uma taxa fixa ou flutuante de retorno até o vencimento. Ao atingir o vencimento, o principal do investidor é devolvido, e nenhum pagamento adicional será feito ao investidor. Existem muitos tipos diferentes de títulos de renda fixa, como títulos e Certificados de Depósito.

Os títulos estão entre as formas mais populares de títulos de renda fixa e serão o foco da nossa discussão. Os títulos podem ser emitidos por uma corporação ou por um governo. Os títulos do governo, em particular, estão entre os investimentos mais seguros do mundo. Se um investidor deseja comprar um título de um governo específico, ele deve fazê-lo na moeda do estado emissor. Se um título de um governo específico tiver alta demanda internacional, todo investidor que desejar adquirir o título primeiro converterá sua moeda doméstica na moeda desejada. Isso pode, por sua vez, mudar as crenças do mercado sobre uma avaliação justa da taxa de câmbio das duas moedas. 

O desempenho de um título é medido pelo rendimento do título. Há uma relação inversa entre o rendimento de um título e o nível de demanda por esse título. Em outras palavras, à medida que a demanda por um título específico diminui, o rendimento do título sobe para atrair demanda por ele. Alguns traders bem-sucedidos nos mercados de câmbio incorporam essa análise fundamental em sua estratégia de negociação. Ao comparar os rendimentos de títulos do governo de médio e longo prazo de dois países em qualquer taxa de câmbio, os traders de câmbio podem obter uma intuição sobre as condições econômicas dos dois países em questão

Normalmente, o título que oferece aos investidores taxas de juros mais altas será mais popular e, de acordo com a estratégia, a moeda do país emissor também se apreciará ao longo do tempo, enquanto a moeda do país que emite títulos com taxas de juros mais baixas se depreciará ao longo do tempo. 

Resumo da Metodologia

Para avaliar a estratégia, treinamos diversos modelos para prever o preço de fechamento da taxa de câmbio USDJPY. Tivemos 3 conjuntos de preditores para os modelos:

1. Dados do tipo Open, High, Low, Close, Tick Volume (OHLCV) retirados do mercado USDJPY.
2. Dados OHLCV do Título do Governo Japonês de 10 Anos e do Título do Tesouro dos Estados Unidos de 10 Anos.
3. Um super conjunto dos dois primeiros.

Nosso objetivo era identificar qual conjunto de preditores produziria o modelo com o menor RMSE em dados não vistos. Embora os níveis de correlação entre os preços históricos dos títulos e o USDJPY fossem significativamente fortes, -0,85 para ambos os títulos do governo, a menor taxa de erro nos testes foi produzida pelos modelos treinados a partir do primeiro conjunto de preditores.

O melhor modelo que identificamos foi o modelo de Regressão Linear (LR). No entanto, ele não tem parâmetros que possamos ajustar. Portanto, selecionamos o Regressor de Vetores de Suporte Linear (LSVR) como nossa solução candidata. Realizamos com sucesso a sintonia de hiperparâmetros no modelo LSVR sem sobreajuste ao conjunto de treinamento. Além disso, nosso modelo LSVR personalizado foi capaz de superar o desempenho de referência definido pelo modelo mais simples de LR nos dados de validação. Os modelos foram treinados e comparados usando validação cruzada de séries temporais sem embaralhamento aleatório.

Após a sintonia bem-sucedida do nosso modelo, exportamos ele para o formato ONNX e o integramos ao nosso Expert Advisor personalizado. 

Buscando Dados.

Vamos começar, primeiro importaremos as bibliotecas que precisamos.

#Import the libraries we need
import pandas as pd
import numpy as np
import MetaTrader5 as mt5
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import sklearn
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split

Aqui estão as versões das bibliotecas que estamos utilizando.

#Show library versions
print(f"Pandas version: {pd.__version__}")
print(f"Numpy version: {np.__version__}")
print(f"MetaTrader 5 version: {mt5.__version__}")
print(f"Matplotlib version: {matplotlib.__version__}")
print(f"Seaborn version: {sns.__version__}")
print(f"Scikit-learn version: {sklearn.__version__}")

Versão do Pandas: 1.5.3

Versão do Numpy: 1.24.4

Versão do MetaTrader 5: 5.0.45

Versão do Matplotlib: 3.7.1

Versão do Seaborn: 0.13.0

Versão do Scikit-learn: 1.2.2

Vamos inicializar nosso terminal.

#Initialize the terminal
mt5.initialize()

Verdadeiro

Definindo até onde no futuro desejamos prever.

#Define how far ahead into the future we should forecast
look_ahead = 20

Buscando os dados de séries temporais que precisamos do terminal MetaTrader 5.

#Fetch historical market data 
usa_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("UST10Y_U4",mt5.TIMEFRAME_M1,0,100000))
jpn_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("JGB10Y_U4",mt5.TIMEFRAME_M1,0,100000))
usd_jpy      = pd.DataFrame(mt5.copy_rates_from_pos("USDJPY",mt5.TIMEFRAME_M1,0,100000))

A coluna de tempo do DataFrame precisa ser formatada.

#Convert the time from seconds
usa_10y_bond["time"] = pd.to_datetime(usa_10y_bond["time"],unit="s")
jpn_10y_bond["time"] = pd.to_datetime(jpn_10y_bond["time"],unit="s")
usd_jpy["time"] = pd.to_datetime(usd_jpy["time"],unit="s")

Devemos definir a coluna de tempo como nosso índice, isso facilitará a fusão dos nossos 3 DataFrames em 1.

#Prepare to merge the data
usa_10y_bond.set_index("time",inplace=True)
jpn_10y_bond.set_index("time",inplace=True)
usd_jpy.set_index("time",inplace=True)

Fazendo a fusão dos DataFrames.

#Merge the data
merged_data = usa_10y_bond.merge(jpn_10y_bond,how="inner",left_index=True,right_index=True,suffixes=(" usa"," japan"))
merged_data = merged_data.merge(usd_jpy,left_index=True,right_index=True)

Análise Exploratória de Dados

Vamos criar uma cópia do DataFrame que usaremos para fins de plotagem.

data_visualization = merged_data

Precisamos redefinir o índice dos dados de visualização.

#Reset the index
data_visualization.reset_index(inplace=True)

Escalar todos os valores das colunas para que todos comecem com o valor 1.

#Let's scale the data so all the first values in the column are one
for i in np.arange(1,data_visualization.shape[1]):
    data_visualization.iloc[:,i] = data_visualization.iloc[:,i] / data_visualization.iloc[0,i]

Vamos plotar as 3 séries temporais para ver se há relações observáveis.

#Let's create a plot
plt.figure(figsize=(10, 5))
plt.plot(data_visualization.loc[:,"open usa"])
plt.plot(data_visualization.loc[:,"open japan"])
plt.plot(data_visualization.loc[:,"open"])
plt.legend(["USA 10Y T-Note","JGB 10Y Bond","USDJPY Fx Rate"])

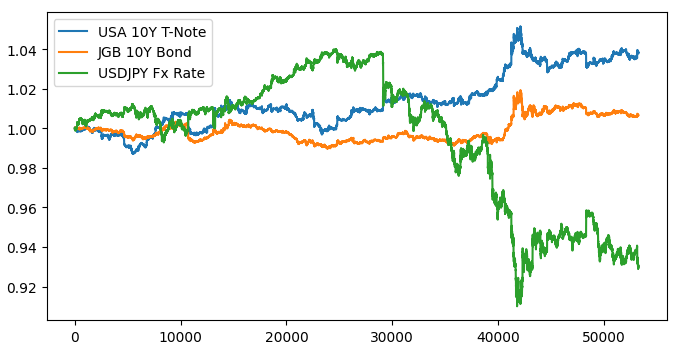
Figura 1: Visualizando nossos dados de mercado.

Parece não haver uma relação discernível quando sobrepomos os 3 mercados. Vamos tentar tornar o gráfico mais legível, plotando o spread entre os títulos americanos e japoneses. Assim, precisamos considerar apenas a taxa de câmbio USDJPY e o spread do título japonês de 10 anos. Ou seja, as 3 curvas que plotamos acima podem ser representadas completamente por apenas 2 curvas.

Primeiro, precisamos calcular o spread entre os títulos.

#Let's create a new feature to show the spread between the securities
data_visualization["spread"] = data_visualization["open usa"] - data_visualization["open japan"]

No lado esquerdo do gráfico, vemos uma amostra da taxa de câmbio USDJPY. Sempre que a taxa de câmbio ultrapassa 1, o dólar está se saindo melhor que o iene, o oposto ocorre quando a taxa de câmbio cai abaixo de 1. Além disso, sempre que o spread sobe acima de 0, os títulos americanos estão se saindo melhor que os títulos japoneses, e o contrário é verdadeiro quando o spread cai abaixo de 0. Portanto, quando o spread está abaixo de 0, significando que os títulos japoneses estão se saindo melhor no mercado, também esperaríamos ver o câmbio de equilíbrio mudar a favor do iene. No entanto, ao inspecionar visualmente os gráficos, podemos rapidamente observar que essa expectativa nem sempre se confirma.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,2,sharex=True,sharey=False,figsize=(8,4))
columns = ["open","spread"]

for i,ax in enumerate(axs.flat):
    ax.plot(data_visualization.loc[:,columns[i]])
    ax.set_title(columns[i])

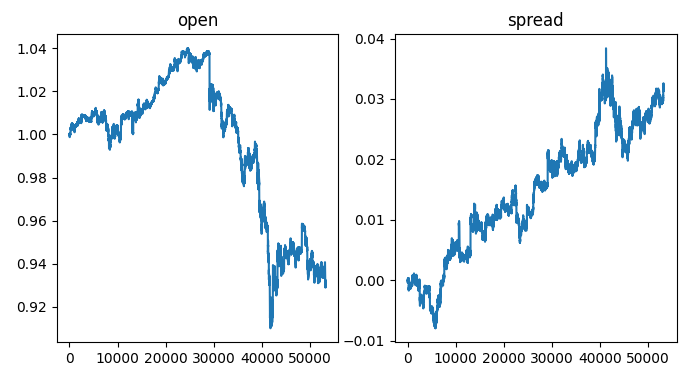
Figura 2: Visualizando o spread dos títulos na taxa de câmbio.

Agora vamos rotular nossos dados. 

#Label the data
merged_data["target"] = merged_data["close"].shift(-look_ahead)
merged_data["binary target"] = np.nan
merged_data.loc[merged_data["close"] > merged_data["target"],"binary target"] = 0
merged_data.loc[merged_data["close"] < merged_data["target"],"binary target"] = 1
merged_data.dropna(inplace=True)
merged_data.reset_index(inplace=True)
merged_data

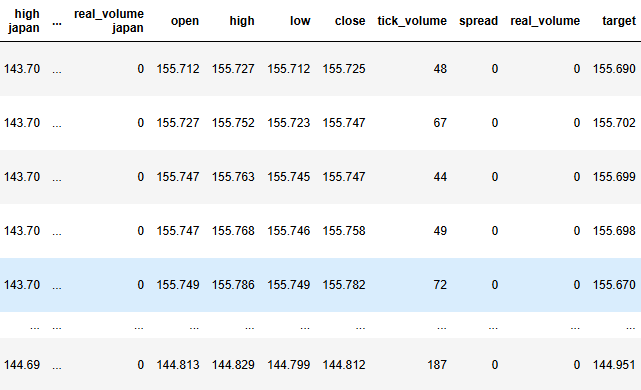
Figura 3: O estado atual do nosso DataFrame.

Agora precisamos definir nosso alvo e entradas.

#Define the predictors and target
target = "target"
ohlc_predictors = ['open', 'high', 'low', 'close','tick_volume']
bonds_predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan']
predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan','open', 'high', 'low', 'close','tick_volume']

Vamos analisar os níveis de correlação em nosso conjunto de dados.

#Analyze correlation levels
plt.subplots(figsize=(8,6))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True)

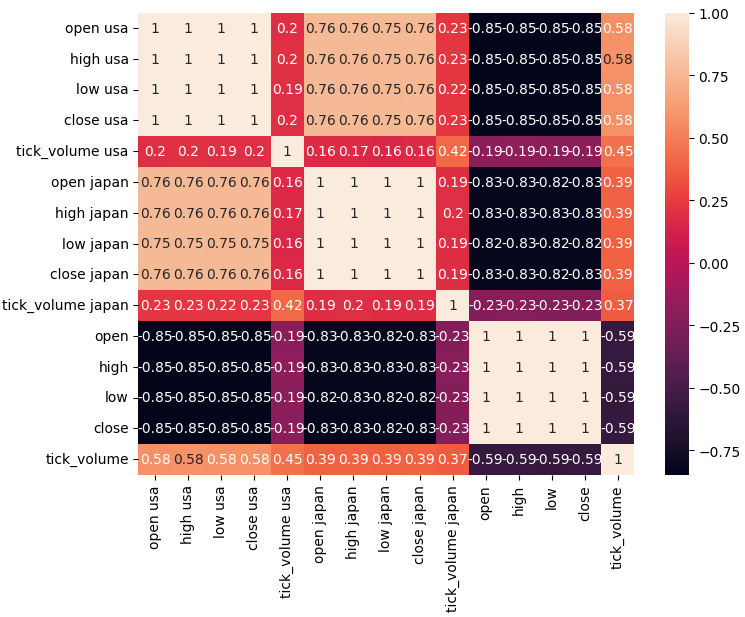
Figura 4: Nossa matriz de correlação.

Como podemos observar, existem níveis fortes de correlação entre os títulos americanos e japoneses, 0,76. Além disso, tanto os títulos americanos quanto os japoneses têm níveis fortes de correlação negativa com a taxa de câmbio USDJPY. 

Os gráficos de dispersão nos permitem visualizar relações entre variáveis em 2 dimensões. Vamos criar gráficos de dispersão usando os dados que coletamos do mercado de títulos. Começaremos criando um gráfico de dispersão do preço de abertura do título do Tesouro americano contra o preço de abertura da taxa de câmbio USDJPY.

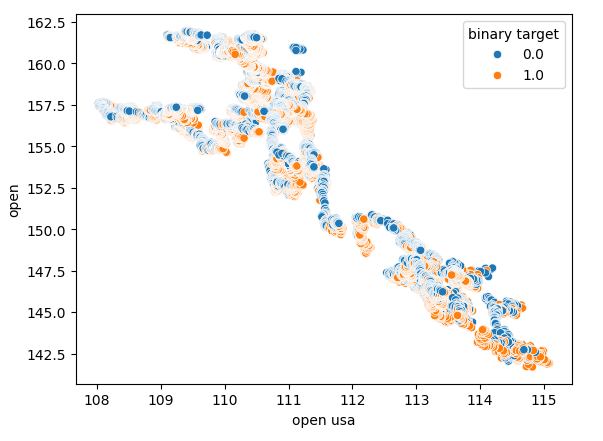
Figura 5: Um gráfico de dispersão do preço de abertura do título dos EUA contra o preço de abertura do USDJPY.

Como pode ser observado, não há um padrão claro ou dependência sendo exposta pelo gráfico de dispersão. Parece que a taxa de câmbio pode se valorizar ou depreciar, independentemente das mudanças que ocorrem no mercado de títulos.

Também realizamos outro gráfico de dispersão usando o preço de abertura do título do governo japonês no eixo x e o preço de abertura da taxa de câmbio USDJPY no eixo y. Infelizmente, ainda não houve relação visível nos dados.

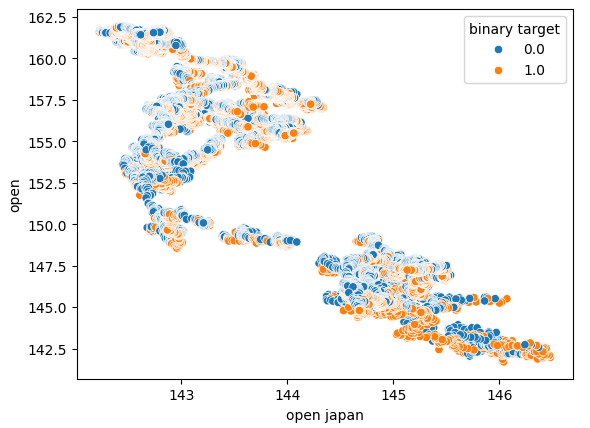
Figura 6: Um gráfico de dispersão do preço de abertura do título do governo japonês contra o preço de abertura do USDJPY.

Também tentamos criar outro gráfico de dispersão, desta vez usando ambos os títulos do governo em cada eixo. Usamos o preço de abertura do título do governo japonês no eixo x e os títulos do Tesouro americano no eixo y. Nosso gráfico de dispersão não revelou padrões interessantes nos dados, isso pode nos indicar que pode haver outras variáveis que não estamos considerando e que também estão afetando os dados.

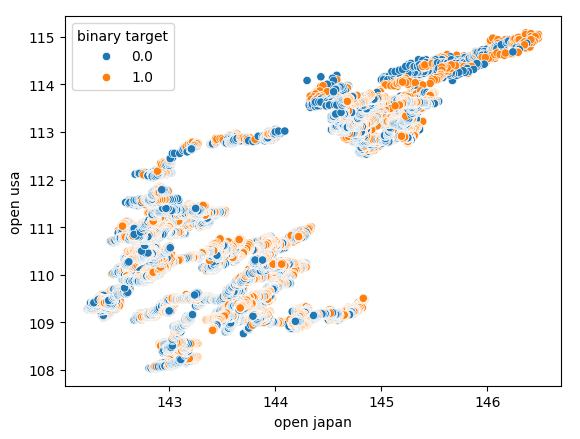
Figura 7: Um gráfico de dispersão do preço de abertura do título do governo japonês contra o preço de abertura do título do governo americano.

Agora, vamos verificar se há alguma relação entre o volume de ticks do mercado de títulos americanos e o preço de fechamento da taxa de câmbio USDJPY. Infelizmente, não há separação clara no gráfico de dispersão, observamos muitos casos em que o preço subiu e caiu na mesma leitura de volume de ticks.

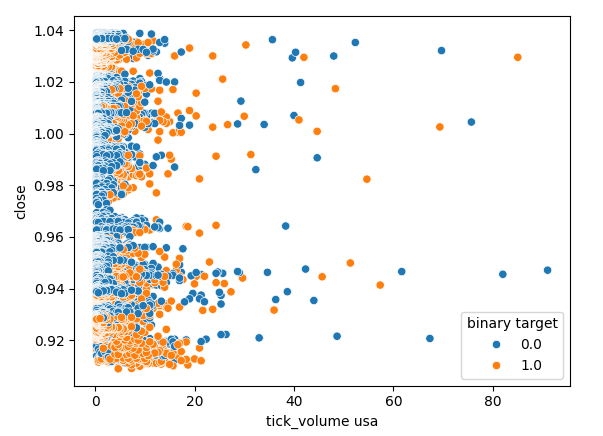
Figura 8: Um gráfico de dispersão do volume de ticks do título do governo americano contra o preço de fechamento do USDJPY.

Modelando os Dados

Agora estamos prontos para começar a modelar nossos dados, começaremos escalando e padronizando nosso conjunto de dados. Isso ajuda nossos modelos de aprendizado de máquina a aprenderem de forma eficaz.

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

Em seguida, vamos dividir nosso conjunto de dados em duas partes: uma metade será usada para treinar e otimizar nossos modelos, enquanto a outra metade será usada para validar nossos modelos e testar se há sobreajuste.

#Partition the data
train_X , test_X, train_y, test_y = train_test_split(scaled_data,merged_data.loc[:,target],shuffle=False,test_size=0.5)

Para testar efetivamente vários modelos, manteremos nossos modelos em uma lista para que possamos iterar sobre eles e validar o desempenho de cada um deles. Também precisaremos criar 3 DataFrames:

1. O primeiro DataFrame armazenará nossos níveis de erro quando usarmos apenas dados OHLCV ordinários do mercado USDJPY.
2. O segundo DataFrame armazenará nossos níveis de erro quando dependeremos apenas dos dados OHCLV dos dois mercados de títulos.
3. E o último DataFrame armazenará nossos níveis de erro quando incorporarmos todos os dados disponíveis.

#Model selection
from sklearn.linear_model import LinearRegression , Lasso , SGDRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import GradientBoostingRegressor , RandomForestRegressor , BaggingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error 
from sklearn.model_selection import TimeSeriesSplit

#Define the columns
columns = [
    "Linear Model",
    "Lasso",
    "SGD",
    "Linear SV",
    "Gradient Boost",
    "Random Forest",
    "Bagging",
    "K Neighbors",
    "Neural Network"
]

#Define the models
models = [
    LinearRegression(),
    Lasso(),
    SGDRegressor(),
    LinearSVR(),
    GradientBoostingRegressor(),
    RandomForestRegressor(),
    BaggingRegressor(),
    KNeighborsRegressor(),
    MLPRegressor(hidden_layer_sizes=(100,40,20,10),shuffle=False)
]

#Create 2 dataframes to store our error on the training and test sets respectively
ohlc_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
ohlc_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Agora vamos validar cruzadamente cada um de nossos modelos. O loop externo iterará sobre cada modelo disponível, enquanto o loop interno validará cada modelo e armazenará os níveis de erro de treinamento e teste respectivos. Observe que estamos validando os modelos apenas no conjunto de treinamento.

#Now perform cross validation
for j in np.arange(0,len(models)):
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],predictors],train_y.loc[train[0]:train[-1]])
        all_training_loss.iloc[i,j] = mean_squared_error(train_y.loc[train[0]:train[-1]],model.predict(train_X.loc[train[0]:train[-1],predictors]))
        all_validation_loss.iloc[i,j] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],predictors]))

Agora vamos observar nossos níveis de erro ao usar os dados OHLCV do mercado USDJPY. Como podemos ver, o modelo linear teve um bom desempenho e o Regressor de Vetor de Suporte Linear (LSVR) teve um desempenho notavelmente bom nessa configuração.

#Our results using the OHLC data
ohlc_validation_loss

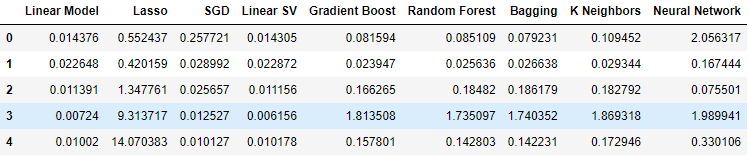
Figura 9: Níveis de erro dos nossos dados OHLCV.

Agora vamos visualizar os resultados. Começaremos com um gráfico de linha do desempenho de cada modelo em nossa validação cruzada de 5 dobras.

#Visualizing the results of using the OHLC predictors
plt.plot(ohlc_validation_loss)
plt.legend(columns)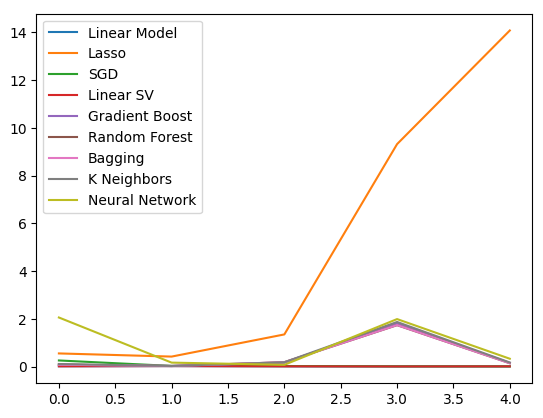

Figura 10: Gráficos de linha dos nossos valores de erro OHLCV. 

Podemos ver claramente que o Lasso foi o modelo com pior desempenho, sua taxa de erro de validação foi a maior por uma margem significativa. No entanto, como não está claro qual modelo está obtendo a menor taxa de erro, podemos usar boxplots para responder a essa pergunta.

Boxplots nos ajudam a identificar rapidamente quais modelos estão tendo bom desempenho nesta tarefa específica. Como podemos ver no gráfico abaixo, a regressão linear apresenta os menores níveis médios de erro, além disso, parece estável e possui o menor valor de outlier.

#Visualizing the results of using the OHLC predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(ohlc_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

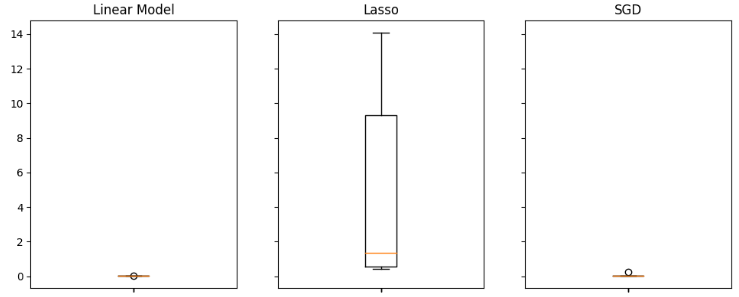
Fig 11: Alguns dos nossos níveis de erro ao utilizar dados OHLCV comuns do USDJPY

Quando utilizamos dados relacionados a títulos do governo, nossos níveis de desempenho caíram de maneira geral. No entanto, o Regressor Linear de Vetores de Suporte (Linear SVR) parece conseguir lidar bem com esses dados.

#Our results using the bonds data
bonds_validation_loss

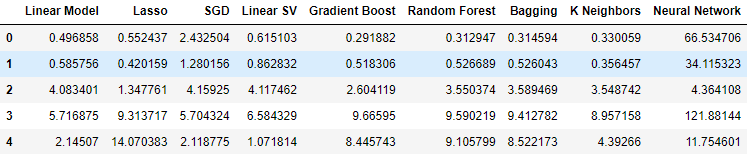
Fig 12: Nossos níveis de erro ao utilizar os dados dos Títulos.

Agora vamos visualizar os resultados.

#Visualizing the results of using the bonds predictors
plt.plot(bonds_validation_loss)
plt.legend(columns)

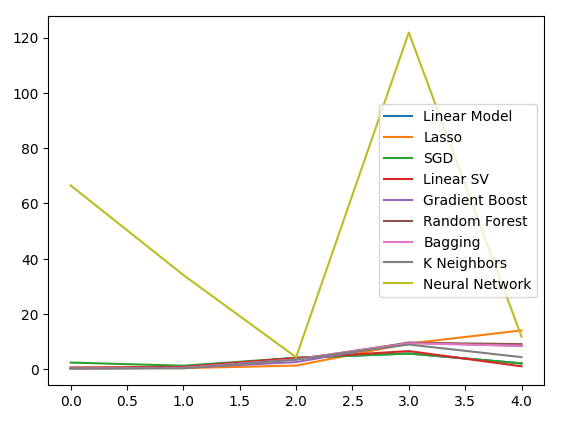
Fig 13: Um gráfico de linhas do nosso erro de validação ao usar dados dos Títulos para prever a taxa de câmbio do USDJPY.

Também podemos empregar boxplots para avaliar nossos níveis de erro.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(bonds_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

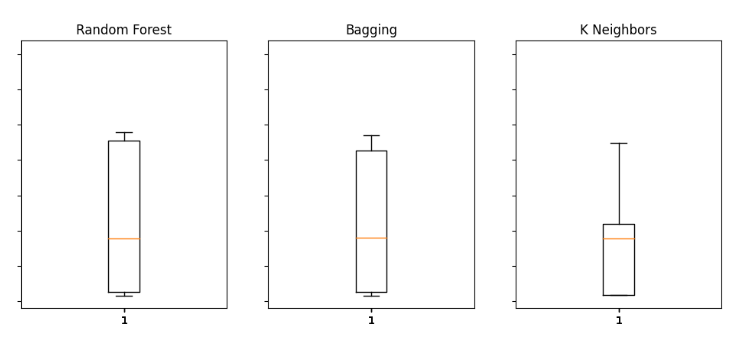
Fig 14: Alguns dos nossos níveis de erro ao usar dados OHLCV do mercado de Títulos para prever o preço de fechamento futuro do USDJPY

Por fim, ao incorporarmos todos os dados disponíveis, nossos níveis de erro melhoraram em comparação ao passo anterior, porém ainda não foram tão satisfatórios quando comparados aos níveis de erro ao usar apenas as cotações do mercado USDJPY.

#Our results using all the data we have
all_validation_loss

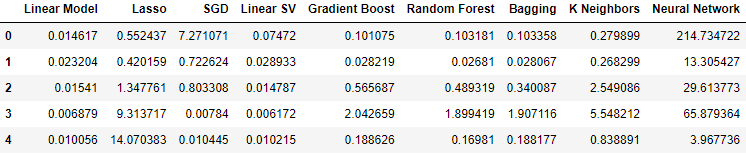
Fig 15: Nossos níveis de erro ao usar todos os dados disponíveis.

Vamos visualizar nosso desempenho.

#Visualizing the results of using the bonds predictors
plt.plot(all_validation_loss)
plt.legend(columns)

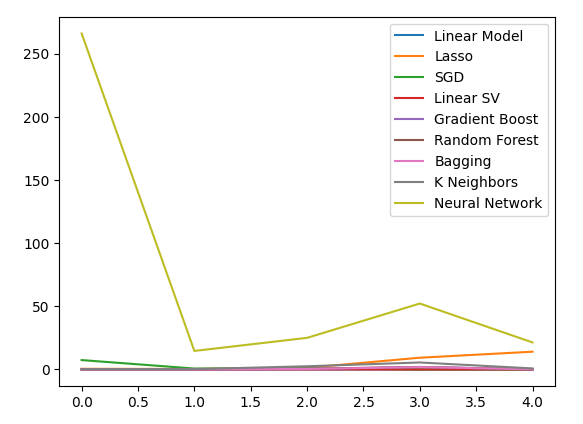
Fig 16: Nossos níveis de erro ao prever o fechamento do USDJPY usando todos os dados disponíveis.

O modelo de Regressão Linear é claramente nossa melhor opção aqui. No entanto, ele não possui hiperparâmetros de interesse para nós. Portanto, selecionaremos o segundo melhor modelo, o Linear SVR, e tentaremos ajustá-lo para superar o modelo Linear sem sobreajuste ao conjunto de treinamento. Antes de otimizar o modelo, vamos avaliar quais atributos são importantes para o modelo. Se nossa estratégia for viável, esperamos que nossos algoritmos de eliminação de atributos mantenham a coluna. Caso contrário, se os dados dos títulos forem descartados, poderemos ter motivo para revisar a estratégia.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(all_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

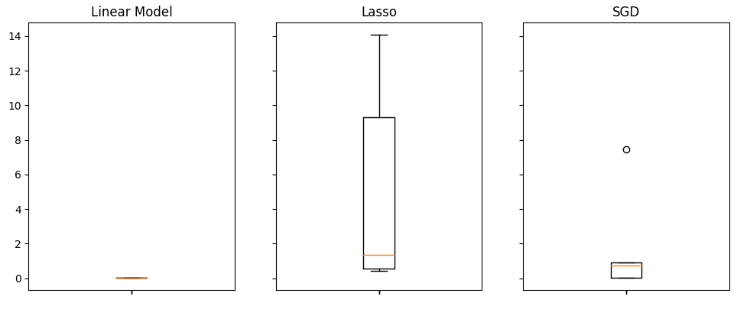
Fig 17: Nosso Modelo Linear teve o melhor desempenho ao usar todos os dados disponíveis.

Seleção de Atributos

Vamos começar calculando os valores de Shapley (SHAP). Os valores SHAP são uma métrica projetada para nos informar o impacto que cada entrada tem nas previsões do nosso modelo, quando comparado a um valor de referência para cada coluna. Por exemplo, considere um modelo que prevê a probabilidade de um motorista receber uma multa por excesso de velocidade. Se quisermos avaliar se nosso modelo é capaz de fazer previsões razoáveis, podemos perguntar: “Como nosso modelo interpreta o fato de que o nível de álcool no sangue do motorista está alto?”.

Obviamente, esperaríamos que nosso modelo previsse maiores probabilidades de receber uma multa se o motorista estiver dirigindo sob a influência de álcool. Os valores SHAP nos ajudam a responder perguntas dessa natureza ao reformular a pergunta incluindo um valor de referência: “Como nosso modelo interpreta o fato de que o nível de álcool no sangue do motorista está acima do limite legal?”.

Ao incluir o limite legal, definimos um valor de referência. Portanto, calculamos nossos valores SHAP realizando cálculos com base na diferença entre as previsões do modelo quando os níveis de álcool estão abaixo e acima dos limites legais. 

Vamos importar a biblioteca SHAP.

#Feature selection
import shap

Agora, precisamos treinar nosso modelo.

#The SVR performed quite well, let's inspect it further
model = LinearSVR()
model.fit(train_X,train_y)

Vamos ajustar o explicador SHAP.

#Calculate SHAP Values
explainer = shap.Explainer(model.predict,test_X)
shap_values = explainer(test_X)

Vamos visualizar o gráfico SHAP.

shap.plots.beeswarm(shap_values)

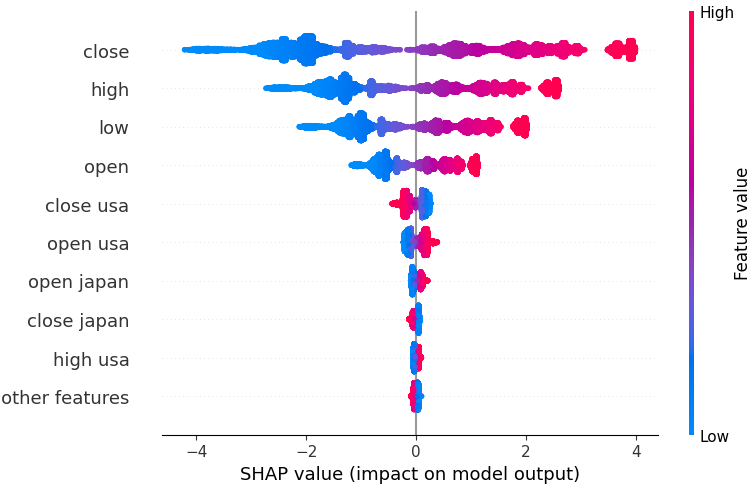
Fig 18: Nossos valores SHAP a partir do modelo Linear SVR.

Os atributos estão organizados em ordem, começando com o mais importante no topo. Portanto, parece que o valor de fechamento do USDJPY é o atributo mais importante, de acordo com nossas explicações SHAP. Além disso, também podemos ver que nossos dados relacionados aos títulos do governo aparecem logo após todos os dados de preço do par de moedas. Isso é uma boa evidência em apoio à nossa estratégia: nossos valores SHAP consideram que os dados dos títulos são mais importantes do que o volume por tick do próprio mercado USDJPY.

No entanto, todas as explicações de modelo devem ser interpretadas com cautela. Elas não estão isentas de erro.

Vamos também considerar a seleção regressiva (backward selection). O algoritmo de seleção regressiva começa ajustando um modelo completo e elimina atributos sequencialmente até que o erro de teste não possa mais ser melhorado. 

Vamos importar a biblioteca mlxtend.

#Let's also perform backward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

Inicialize os modelos.

#Reinitialize the model
model = LinearSVR()

Crie o objeto de seleção de atributos.

#Prepare the feature selector
sfs = SFS(model,
         k_features=(1,train_X.shape[1]),
         forward=False,
          n_jobs = -1,
          scoring="neg_mean_squared_error",
          cv=5)

Ajuste o seletor de atributos.

#Fit the feature selector
sfs_results = sfs.fit(train_X,train_y)

Vamos ver os atributos selecionados.

#The best features we identified
sfs_results.k_feature_names_

('open usa',

 'high usa',

 'tick_volume usa',

 'open japan',

 'low japan',

 'close',

 'tick_volume')

Nosso algoritmo de eliminação regressiva atribuiu mais importância aos dados do mercado de títulos do que nossos valores SHAP. Portanto, podemos concluir razoavelmente que pode haver uma relação confiável entre nossos dados dos títulos e a taxa de câmbio futura do par USDJPY.

Agora vamos plotar os resultados.

#Prepare the plot
fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev")
plt.title("Backward Selection on our Linear SVR")
plt.grid()

Fig 19: Nossos resultados da seleção regressiva.

Parece que as taxas de erro do nosso modelo não flutuam violentamente, o que significa que nosso modelo pode ser estável mesmo em circunstâncias com dados limitados. Lembre-se, o algoritmo elimina atributos um por um até que a taxa de erro não possa mais ser melhorada removendo qualquer um dos atributos selecionados.

Ajuste de Hiperparâmetros

Agora vamos otimizar nosso modelo para superar a Regressão Linear.

Primeiro, importe as bibliotecas necessárias.

#Parameter tuning 
from sklearn.model_selection import RandomizedSearchCV

Inicialize os modelos.

#Reinitialize the model
model = LinearSVR()

Defina o objeto de ajuste (tuner).

tuner = RandomizedSearchCV(model,
                          {
                              "epsilon":[0,0.001,0.01,0.1,25,50,100],
                              "tol": [0.1,0.01,0.001,0.0001,0.00001],
                              "C" : [1,5,10,50,100,1000,10000,100000],
                              "loss":["epsilon_insensitive", "squared_epsilon_insensitive"],
                              "fit_intercept": [False,True]
                          },
                           n_jobs=-1,
                           n_iter=100,
                           scoring="neg_mean_squared_error"
                          )

Ajuste o modelo.

tuner_results = tuner.fit(train_X,train_y)

É bastante interessante notar que nossos melhores parâmetros são quase idênticos às configurações padrão. No entanto, vamos observar a diferença no desempenho.

tuner_results.best_params_

{'tol': 0.0001,

 'loss': 'epsilon_insensitive',

 'fit_intercept': True,

 'epsilon': 0,

 'C': 1}

Testando para Overfitting

Agora vamos testar se houve overfitting no conjunto de treinamento. Vamos instanciar nossos modelos.

#Testing for overfitting
baseline_model = LinearRegression()
default_model =  LinearSVR()
customized_model = LinearSVR(tol=0.0001,loss='epsilon_insensitive',fit_intercept=True,epsilon=0,C=1)

Agora, vamos ajustar todos os 3 modelos.

#Fit the models
baseline_model.fit(train_X,train_y)
default_model.fit(train_X,train_y)
customized_model.fit(train_X,train_y)

Preparando para validar por cross-validation o desempenho de cada modelo.

#Create a list of models
models = [
    baseline_model,
    default_model,
    customized_model
]

columns = [
    "Linear Regression",
    "Default Linear SVR",
    "Customized Linear SVR"
]

We need to reset the index of our datasets.
#Let's assess our new accuracy levels
test_y = test_y.reset_index()
test_X.reset_index(inplace=True)

Redefina o objeto de divisão da série temporal e crie um DataFrame para armazenar nosso erro de validação.

#Create our time-series test object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
overfitting_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Cross-validate each model.
for j in np.arange(0,len(columns)):
    model = models[j]
    for i , (train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],predictors],test_y.loc[train[0]:train[-1],"target"])
        overfitting_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"target"],model.predict(test_X.loc[test[0]:test[-1],predictors]))

Vamos ver os resultados.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,3,sharex=True,sharey=True,figsize=(8,4))

for i,ax in enumerate(axs.flat):
    ax.boxplot(overfitting_error.iloc[:,i])
    ax.set_title(columns[i])

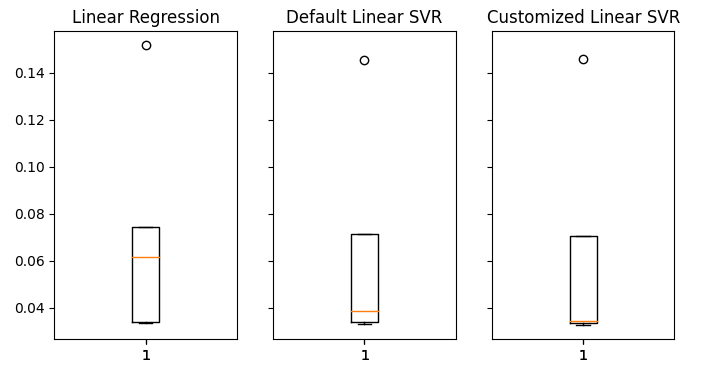
Fig 20: Nossos níveis de erro sobre dados não vistos.

Podemos ver claramente que nosso modelo LinearSVR produziu o menor erro médio na validação. Portanto, conseguimos superar o benchmark estabelecido pelo Modelo Linear. Além disso, também superamos a taxa de erro padrão sem overfitting no conjunto de treinamento.

Exportando para ONNX

Agora vamos nos preparar para exportar nosso modelo no formato ONNX para que possamos integrá-lo facilmente ao nosso programa em MQL5.

Antes de prosseguirmos, devemos primeiro padronizar nossos dados de uma forma que possamos reproduzir no MQL5. Podemos fazer isso subtraindo a média da coluna de cada valor correspondente da coluna e, subsequentemente, dividindo cada coluna pelo seu desvio padrão.

Vamos escrever os respectivos valores em um arquivo CSV, no caminho de arquivos do nosso Terminal.

#Create scaling factors
scaling_factors = pd.DataFrame(index=("mean","standard deviation"),columns=predictors)

#Write our the values
for i in np.arange(0,scaling_factors.shape[1]):
    scaling_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
    scaling_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std()
    merged_data.loc[:,predictors[i]] = ((merged_data.loc[:,predictors[i]] - scaling_factors.iloc[0,i]) / scaling_factors.iloc[1,i])

scaling_factors

Fig 21: Nossos fatores de escala.

Agora vamos salvar o arquivo CSV.

#Save the scaling factors
scaling_factors.to_csv("C:\\Enter \\Your\\Path\\Here\\MetaQuotes\\Terminal\\D0E82094358C8CF3394F550E51FF075\\MQL5\\Files\\usdjpy scaling factors.csv")

Vamos treinar o modelo com todos os dados disponíveis.

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,"target"])

Importe as bibliotecas que precisamos.

#Let's import the libraries we need
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import netron
import onnx

Defina o tipo de entrada e a forma do nosso modelo ONNX.

#Define the initial input types
initial_types = [('float_input',FloatTensorType([1,len(predictors)]))]

Criar modelos ONNX

#Create an ONNX representation of the model
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

Salve o modelo ONNX em um arquivo com a extensão .onnx.

#Save the ONNX model
onnx_name = "USDJPY M1 FLOAT.onnx"
onnx.save(onnx_model,onnx_name)

Vamos visualizar o modelo no netron.

#Visualize the model
netron.start(onnx_name)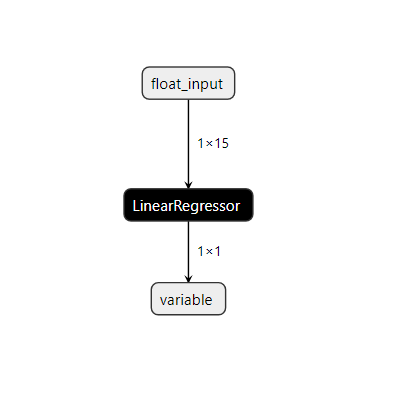

Fig 22: Visualizando nosso modelo Linear SVR.

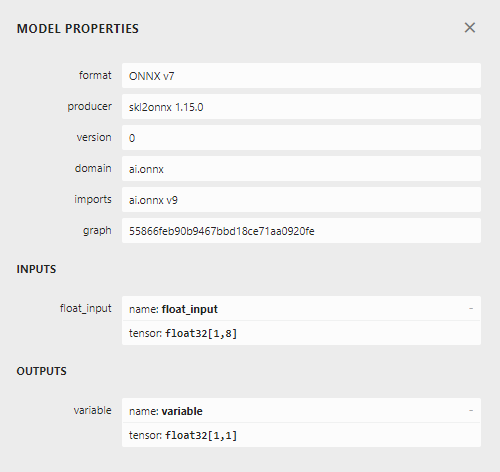
Fig 23: Forma de entrada e saída do nosso modelo ONNX.

A entrada e saída do nosso modelo estão de acordo com nossas especificações. Vamos prosseguir para construir o Expert Advisor.

Implementação no MQL5

Primeiro vamos requerer nosso modelo ONNX como um recurso que será compilado dentro do nosso programa.

//+------------------------------------------------------------------+
//|                                                 USDJPY Bonds.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource "\\Files\\USDJPY M1 FLOAT.onnx" as const uchar onnx_model_buffer[];

Agora vamos definir algumas variáveis globais que precisaremos ao longo do programa.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
float mean_values[15],std_values[15];
vector model_output = vector::Zeros(1);
int state = 0;
int prediction = 0;

Importe a biblioteca de trade para que possamos abrir e gerenciar posições com facilidade.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Agora vamos definir funções auxiliares para o nosso Expert Advisor. Precisamos de uma função que carregue nosso modelo ONNX e defina suas formas de entrada e saída. Se falharmos em qualquer ponto do procedimento, nossa função retornará uma flag que interromperá o processo de inicialização.

//+------------------------------------------------------------------+
//| Load our onnx file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT);

//--- Set the input shape
   ulong input_shape [] = {1,15};

//--- Check if the input shape is valid
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model));
      return(false);
     }

//--- Set the output shape
   ulong output_shape [] = {1,1};

//--- Check if the output shape is valid
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model));
      return(false);
     }
//--- Everything went fine
   return(true);
  }

Também precisamos de uma função para ler o arquivo CSV que contém os valores de escala e armazená-los em um array para uso posterior, na nossa função de previsão. Observe que a primeira linha contém apenas os títulos das colunas. A primeira entrada da segunda linha é o rótulo do índice, e a segunda entrada da segunda linha é a média da primeira coluna. Portanto, nossa função verificará a iteração atual do loop para acompanhar onde está e quais valores são importantes.

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
void load_scaling_factors(void)
    {
//--- Read in the file
   string file_name = "usdjpy scaling factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). 

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file
      
      int counter = 0;
      string value = "";
      
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end 
       {
       
         if (counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read
           break; //stop the reading progress
         
         value = FileReadString(result);
         Print("Trying to read string: ",value," count value: ",counter);
         
         //--- Check where we are
         if((counter >= 17) && (counter < 32))
            {
               mean_values[counter - 17] = (float) value;
            }   
         //--- Check where we are
         if((counter >= 33) && (counter < 48))
            {
               std_values[counter - 33] = (float) value;
            }   
         //--- Reading a new row
         if(FileIsLineEnding(result))
           { 
             Print("row++");
           }
         
         counter++;
       }
      //---Close the file
      ArrayPrint(mean_values);
      ArrayPrint(std_values);
      FileClose(result);
     }
//--- We failed to find the file
else 
   {
      Print("Failed to find the file");
   }

  }

Esta função buscará os valores de entrada do modelo e os padronizará antes de obter uma previsão do nosso modelo. Subsequentemente, a previsão do modelo será armazenada como um estado binário: 1 é uma previsão de alta e 2 é uma posição de baixa. Isso nos ajudará a identificar quando nosso modelo está prevendo uma reversão.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void model_predict(void)
   {
     //--- Fetch input values
      string symbols[3] = {"UST10Y_U4","JGB10Y_U4","USDJPY"};
      vectorf model_inputs = {iOpen(symbols[0],PERIOD_CURRENT,0),iHigh(symbols[0],PERIOD_CURRENT,0),iLow(symbols[0],PERIOD_CURRENT,0),iClose(symbols[0],PERIOD_CURRENT,0),iTickVolume(symbols[0],PERIOD_CURRENT,0),
                      iOpen(symbols[1],PERIOD_CURRENT,0),iHigh(symbols[1],PERIOD_CURRENT,0),iLow(symbols[1],PERIOD_CURRENT,0),iClose(symbols[1],PERIOD_CURRENT,0),iTickVolume(symbols[1],PERIOD_CURRENT,0),
                      iOpen(symbols[2],PERIOD_CURRENT,0),iHigh(symbols[2],PERIOD_CURRENT,0),iLow(symbols[2],PERIOD_CURRENT,0),iClose(symbols[2],PERIOD_CURRENT,0),iTickVolume(symbols[2],PERIOD_CURRENT,0)
                     };
     //--- Normalize and scale our inputs
     for(int i=0;i < 15;i++)
         {
            model_inputs[i] = ((model_inputs[i] - mean_values[i])/std_values[i]);
         }
     //--- Show the inputs
     Print("Model inputs: ",model_inputs);
     //--- Fetch a forecast from our model
     OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
     //--- Give the user feedback
     Comment("Model forecast: ",model_output[0]);
     
     //--- Store the prediction
     if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 1;
         }
     else if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 2;
         }       
   }

Nosso procedimento de inicialização exigirá primeiro que carreguemos com sucesso o arquivo ONNX, antes de lermos os valores de escala e, por fim, testarmos se nosso modelo funciona.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Load the ONNX file
   if(!load_onnx_file())
     {
      //--- We failed to load our onnx model
      return(INIT_FAILED);
     }
     
//--- Load scaling factors
load_scaling_factors();

//--- Test if our ONNX model works
model_predict();

//--- Everything worked out
   return(INIT_SUCCEEDED);
   
  }

Sempre que nosso programa não estiver mais em uso, devemos liberar os recursos que não são mais necessários.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we used for our onnx model
   OnnxRelease(onnx_model);
//--- Release the expert advisor
   ExpertRemove();
  }

Por fim, sempre que houver mudanças nos níveis de preço, primeiro obteremos uma previsão do nosso modelo. Se não tivermos posições abertas, seguiremos a previsão do modelo e armazenaremos uma flag para representar nossa posição atual aberta. Caso contrário, se já tivermos posições abertas, verificaremos se a previsão do modelo está alinhada com nossas posições abertas; caso não esteja, fecharemos nossas posições abertas.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
      //--- Obtain a forecast from our model
      model_predict();
      
      //--- Check if we have any positions
      if(PositionsTotal() == 0)
         {
            //--- Reset the state of our system
            state = 0;
            
            //--- Check for an entry
            if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Buy(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_ASK),SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,"USDJPY Bonds AI");
                  state = 1;
               }
            
             if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Sell(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_BID),SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,"USDJPY Bonds AI");
                  state = 2;
               }
         }
         
      //--- Check for reversals
      if(state != prediction)
         {
            Alert("Reversal detected by the AI system!");
            Trade.PositionClose("USDJPY");
         }
  }
//+------------------------------------------------------------------+

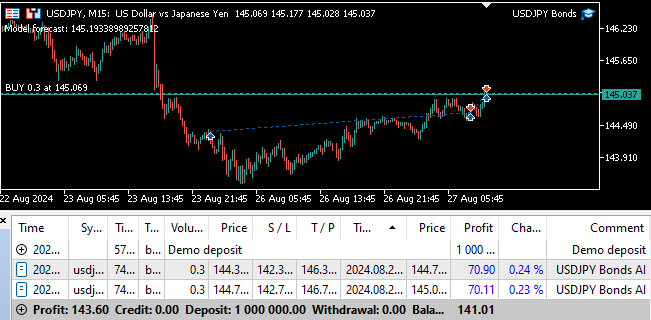
Fig 24: Testando nosso programa em forward.

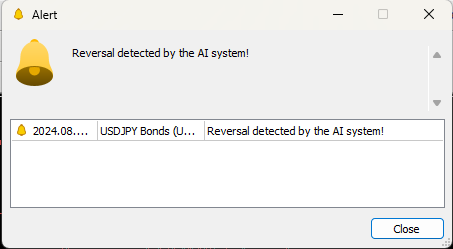
Fig 25: Nosso Expert Advisor pode fechar posições automaticamente sempre que detectar uma reversão.

Conclusão

Neste artigo, demonstramos como você pode empregar IA para dar nova vida a uma estratégia clássica de negociação. Se nossa estratégia vale sua complexidade é algo debatível — poderíamos ter obtido níveis de acurácia menores com um modelo mais simples. Portanto, podemos concluir razoavelmente que, a menos que mais tempo seja investido na transformação das variáveis para melhor expor a relação, talvez seja mais vantajoso usar uma estratégia mais simples baseada apenas nas cotações normais do mercado.