Redes neurais em trading: Transformer com codificação relativa

Introdução

Prever preços e tendências de mercado é fundamental para o sucesso na negociação e na gestão de riscos. Previsões precisas dos movimentos de preços ajudam os traders a tomar decisões no momento oportuno e a evitar perdas financeiras. No entanto, em mercados altamente voláteis, os modelos tradicionais de aprendizado de máquina podem ter sua capacidade limitada.

A transição do treinamento de modelos do zero para o pré-treinamento em grandes conjuntos de dados brutos não rotulados, seguida de um ajuste fino para tarefas específicas, permite alcançar alta precisão de previsão sem a necessidade de coletar enormes volumes de novos dados. Por exemplo, modelos baseados na arquitetura Transformer, adaptados para dados financeiros, podem usar informações sobre correlações entre ativos, dependências temporais e outros fatores para construir previsões mais precisas. A introdução de mecanismos alternativos de atenção ajuda a considerar dependências importantes do mercado, aumentando significativamente o desempenho dos modelos. Isso possibilita a criação de estratégias de negociação, minimizando a necessidade de configurações manuais e modelos complexos baseados em regras.

Um desses algoritmos alternativos de atenção foi apresentado no trabalho "Relative Molecule Self-Attention Transformer". Os autores desenvolveram uma nova fórmula Self-Attention para grafos moleculares, que processa cuidadosamente várias funções de entrada para obter maior precisão e confiabilidade em muitas áreas da química. Relative Molecule Attention Transformer (R-MAT) é um modelo pré-treinado baseado em Transformer. Trata-se de uma nova variação de Self-Attention relativa, que permite combinar de maneira eficaz informações sobre distância e vizinhança. R-MAT oferece um desempenho moderno e competitivo em uma ampla gama de tarefas.

1. Algoritmo R-MAT

Durante o processamento de linguagem natural, a camada Self-Attention padrão (vanilla) não considera a informação posicional dos tokens de entrada, ou seja, ao alterar a ordem dos dados brutos, o resultado permanece o mesmo. Para incorporar a informação posicional aos dados brutos, o Transformer padrão adiciona uma codificação de posição absoluta. Por outro lado, a codificação posicional relativa adiciona a distância relativa entre cada par de tokens, o que resulta em um ganho significativo em algumas tarefas. No algoritmo R-MAT, é usada a codificação relativa da posição dos tokens.

A ideia principal é aumentar a flexibilidade no processamento de informações sobre grafos e distâncias. Os autores do método R-MAT adaptaram a codificação posicional relativa com o objetivo de enriquecer o bloco Self-Attention com uma representação eficiente das posições relativas dos elementos na sequência original.

A posição relativa entre dois átomos em uma molécula é caracterizada por três fatores interligados:

• a distância relativa entre eles,
• a distância no grafo molecular,
• e sua relação físico-química.

Dois átomos são representados por vetores 𝒙i, 𝒙j com dimensão D. Os autores propõem codificar sua relação utilizando uma incorporação de relação atômica 𝒃ij com dimensão D′. Essa incorporação será então usada no módulo Self-Attention após a camada de projeção.

Primeiramente, a ordem da vizinhança entre dois átomos é codificada, com a informação sobre quantos outros vértices existem entre os nós i e j no grafo molecular original. Em seguida, aplica-se a codificação de distância com base radial. Por fim, cada ligação é destacada para refletir a relação física entre os pares de átomos.

Os autores do método observam que, embora essas funções possam ser facilmente aprendidas durante o pré-treinamento, essa construção pode ser muito útil para treinar o R-MAT em conjuntos de dados pequenos.

O token 𝒃ij obtido para cada par de átomos em uma molécula é usado para definir uma nova camada Self-Attention, que os autores do método chamaram de Relative Molecule Self-Attention.

Na nova arquitetura, os autores do método espelham o design Query-Key-Value do Self-Attention padrão, o token 𝒃ij é transformado em vetores específicos para chave e valor 𝒃ijV, 𝒃ijK utilizando duas redes neurais φV e φK. Cada rede neural é composta por duas camadas. Uma camada oculta, comum a todas as cabeças de atenção e uma camada de saída que gera uma incorporação relativa distinta para diferentes cabeças de atenção. O Self-Attention relativo pode ser expresso da seguinte maneira:

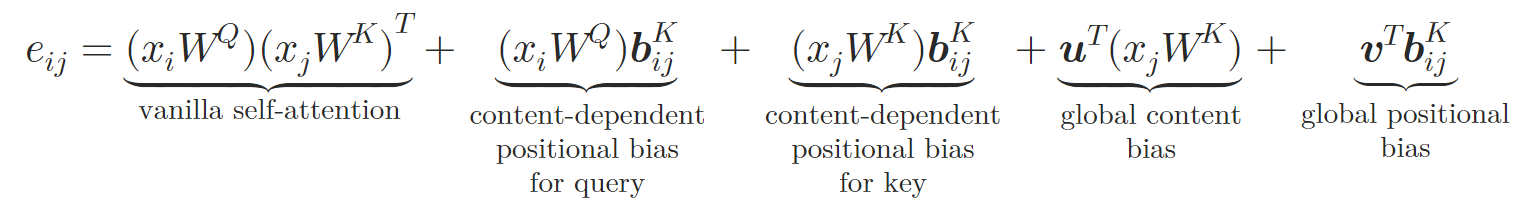
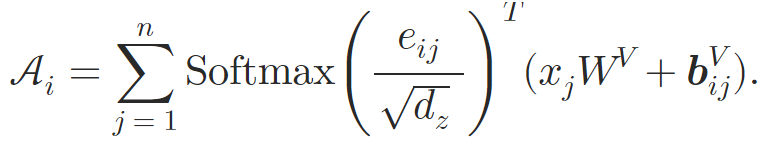
onde 𝒖, 𝒗 são vetores treináveis.

Assim, os autores enriquecem o bloco Self-Attention por meio da incorporação das relações atômicas. Na etapa de cálculo dos pesos de atenção, são adicionados um deslocamento posicional dependente do conteúdo, um deslocamento global de contexto e um deslocamento posicional global, todos calculados com base em 𝒃ijK. Em seguida, durante o cálculo da média ponderada da atenção, os autores também incluem a informação proveniente de outra incorporação 𝒃ijV.

O bloco de Self-Attention relativo é utilizado para construir a arquitetura Transformer de atenção molecular relativa (Relative Molecule Attention Transformer — R-MAT).

Os dados brutos são fornecidos como uma matriz de tamanho Nátomos×36, que são processados por meio de uma pilha de N camadas de atenção Relative Molecule Self-Attention. Cada camada de atenção é seguida por um MLP com conexão residual, similar ao modelo Transformer padrão.

Após o processamento dos dados brutos com as camadas de atenção, os autores do método combinam a representação em um vetor de tamanho fixo. Para isso, utilizam o Self-Attention pooling.

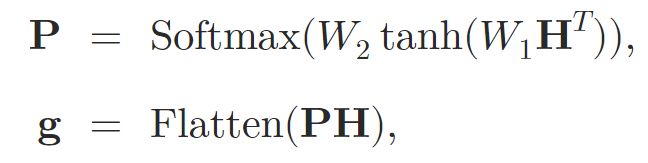
onde 𝐇 é o estado oculto obtido das camadas Self-Attention, W1 e W2 são os pesos de atenção agregadores.

A incorporação dos grafos 𝐠 é então passada para um MLP de dois níveis com função de ativação leaky-ReLU, cujo resultado é a saída de previsões.

A visualização do método pelos autores é apresentada abaixo.

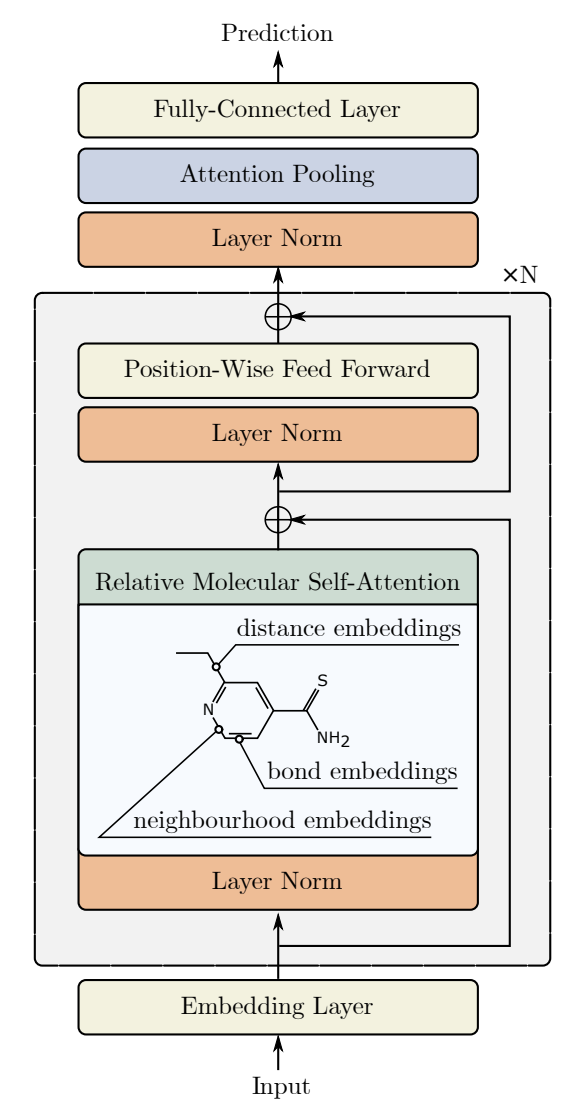
2. Implementação com MQL5

Após analisar os aspectos teóricos do método proposto, Relative Molecule Attention Transformer (R-MAT), passamos à construção de nossa própria versão dos conceitos apresentados, utilizando MQL5. Quero deixar claro desde já que decidi dividir a construção do algoritmo proposto em blocos. Primeiro, criaremos um objeto separado para implementar o algoritmo de Self-Attention relativo, e depois montaremos o modelo R-MAT em uma classe de nível superior.

#2.1 Módulo de Self-Attention relativo

Como você sabe, a maior parte dos cálculos foi transferida para o contexto OpenCL. Portanto, ao iniciarmos a implementação do novo algoritmo, devemos adicionar os kernels faltantes ao nosso programa em OpenCL. O primeiro kernel que criaremos é o de propagação para frente MHRelativeAttentionOut. Embora esse kernel tenha sido desenvolvido com base nas implementações anteriores do algoritmo Self-Attention, é fácil notar um aumento significativo no número de buffers globais, cuja finalidade exploraremos ao longo da construção do algoritmo.

__kernel void MHRelativeAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                     __global const float *k,         ///<[in] Matrix of Keys
                                     __global const float *v,         ///<[in] Matrix of Values
                                     __global const float *bk,        ///<[in] Matrix of Positional Bias Keys
                                     __global const float *bv,        ///<[in] Matrix of Positional Bias Values
                                     __global const float *gc,        ///<[in] Global content bias vector
                                     __global const float *gp,        ///<[in] Global positional bias vector
                                     __global float *score,           ///<[out] Matrix of Scores
                                     __global float *out,             ///<[out] Matrix of attention
                                     const int dimension              ///< Dimension of Key
                                    )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Este kernel será executado em um espaço tridimensional de tarefas, cada uma correspondendo às dimensões de Query, Key e Heads. Dentro da segunda dimensão, criamos grupos de trabalho.

No corpo do kernel, identificamos imediatamente a thread atual em todas as dimensões do espaço de tarefas, assim como definimos seus limites. Em seguida, definimos constantes de deslocamento nos buffers de dados para acessar os elementos necessários.

   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Logo depois, criamos um array na memória local para troca de informações dentro do grupo de trabalho.

   __local float temp[LOCAL_ARRAY_SIZE];

A seguir, conforme o algoritmo de Self-Attention relativo, precisamos calcular os coeficientes de atenção. Para isso, devemos calcular o produto escalar de vários vetores e somar os resultados obtidos. Aqui, aproveitamos o fato de que as dimensões de todos os vetores multiplicados são iguais. Sendo assim, um único laço é suficiente para multiplicar todos os vetores necessários.

//--- score
   float sc = 0;
   for(int d = 0; d < dimension; d++)
     {
      float val_q = q[shift_q + d];
      float val_k = k[shift_kv + d];
      float val_bk = bk[shift_kv + d];
      sc += val_q * val_k + 
	    val_q * val_bk + 
            val_k * val_bk + 
            gc[shift_q + d] * val_k + 
            gp[shift_q + d] * val_bk;
     }

O próximo passo é normalizar os coeficientes de dependência obtidos para cada Query. Para normalizar, usamos a função SoftMax, de forma análoga ao algoritmo padrão. Por isso, o algoritmo de normalização foi reaproveitado das implementações anteriores sem alterações. Primeiro, calculamos o valor exponencial do coeficiente.

   sc = exp(sc / koef);
   if(isnan(sc) || isinf(sc))
      sc = 0;

Depois, somamos os coeficientes obtidos dentro do grupo de trabalho usando o array criado anteriormente na memória local.

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Agora podemos dividir o coeficiente obtido anteriormente pela soma total e armazenar o valor normalizado no buffer global correspondente.

//--- score
   float sum = temp[0];
   if(isnan(sum) || isinf(sum) || sum <= 1e-6f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Após o cálculo dos coeficientes de dependência normalizados, podemos calcular o resultado da operação de atenção. Aqui, o algoritmo é muito próximo do padrão. Apenas adicionamos a soma dos vetores Value e bijV antes da multiplicação pelo coeficiente de atenção.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = sc * (val_v + val_bv);
      if(isnan(val) || isinf(val))
         val = 0;
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]);
     }
  }

Provavelmente vale a pena reforçar a necessidade de cautela ao utilizar barreiras para sincronizar operações entre as threads do grupo de trabalho. A inserção dessas barreiras no código do kernel deve ser feita de forma que cada thread do grupo de trabalho atinja a barreira o mesmo número de vezes. O código não deve conter desvios das barreiras nem saídas antecipadas antes que todas as threads cheguem aos pontos de sincronização. Caso contrário, corremos o risco de travar a execução do kernel, quando algumas threads ficarem esperando outras que já finalizaram suas operações.

O algoritmo de propagação reversa está implementado no kernel MHRelativeAttentionInsideGradients. Sua implementação inverte completamente as operações do kernel de propagação para frente discutido acima e, em grande parte, reaproveita elementos das implementações anteriores. Por isso, recomendo que você explore esse kernel por conta própria. O código completo de todos os programas em OpenCL está incluído em anexo.

E agora passamos ao trabalho com o programa principal. Aqui vamos criar a classe CNeuronRelativeSelfAttention, onde implementaremos o algoritmo de Self-Attention relativo. Mas antes de começar sua implementação, é necessário discutir alguns aspectos da codificação posicional relativa.

Os autores do framework R-MAT propuseram seu algoritmo para resolver tarefas na indústria química. Eles construíram o algoritmo de descrição posicional dos átomos das moléculas com base na especificidade dos problemas abordados. Para nós, a distância entre as velas e seus atributos também é importante, mas há um detalhe. Além da distância, a direção também é fundamental. Somente o movimento de preço unidirecional forma tendências que evoluem para trends.

Outro ponto é o tamanho da sequência analisada. O número de átomos em uma molécula muitas vezes é limitado a uma quantidade relativamente pequena. E, nesse caso, é possível calcular o vetor de desvio para cada par de átomos. No nosso caso, porém, o volume de histórico analisado pode ser bastante grande. E assim, o cálculo e armazenamento de vetores de desvio individuais para cada par de velas analisadas pode se tornar uma tarefa bastante exigente em termos de recursos.

Por isso, decidimos abandonar a metodologia proposta pelos autores para o cálculo dos desvios entre elementos individuais da sequência. Em busca de um mecanismo alternativo, adotamos uma solução bastante simples: multiplicar a matriz de dados brutos por sua cópia transposta. Matematicamente, a multiplicação de dois vetores equivale ao produto dos comprimentos escalares desses vetores pelo cosseno do ângulo entre eles. Assim, o produto de vetores perpendiculares é igual a zero. Enquanto isso, vetores na mesma direção produzem um valor positivo, e vetores em direções opostas resultam em um valor negativo. Consequentemente, ao comparar um vetor com uma série de outros, o valor do produto dos vetores cresce à medida que o ângulo entre eles diminui e o comprimento do segundo vetor aumenta.    

E agora que definimos a metodologia, podemos partir para a construção do nosso novo objeto, cuja estrutura está apresentada a seguir.

class CNeuronRelativeSelfAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                    iWindow;
   uint                    iWindowKey;
   uint                    iHeads;
   uint                    iUnits;
   int                     iScore;
   //---
   CNeuronConvOCL          cQuery;
   CNeuronConvOCL          cKey;
   CNeuronConvOCL          cValue;
   CNeuronTransposeOCL     cTranspose;
   CNeuronBaseOCL          cDistance;
   CLayer                  cBKey;
   CLayer                  cBValue;
   CLayer                  cGlobalContentBias;
   CLayer                  cGlobalPositionalBias;
   CLayer                  cMHAttentionPooling;
   CLayer                  cScale;
   CBufferFloat            cTemp;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionGraadient(void);

   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRelativeSelfAttention(void) : iScore(-1) {};
                    ~CNeuronRelativeSelfAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRelativeSelfAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Como se pode notar, a estrutura da nova classe possui uma quantidade considerável de objetos internos. Vamos nos familiarizar com suas funcionalidades à medida que implementamos os métodos da classe. Por ora, o mais importante é que todos os objetos são declarados como estáticos. Isso significa que podemos deixar o construtor e o destruidor da classe em branco. A inicialização de todos os objetos declarados e herdados, como sempre, ocorre no método Init. Os parâmetros deste método fornecem as constantes que nos permitem definir com precisão a arquitetura do objeto que estamos criando. É fácil notar que todos os parâmetros do método foram mantidos sem alterações em relação ao Multi-Head Self-Attention padrão. Apenas o parâmetro que define o número de camadas internas “se perdeu pelo caminho”. Essa foi uma escolha deliberada, já que nesta implementação o número de camadas será definido pelo objeto de nível superior por meio da criação da quantidade adequada de objetos internos.

bool CNeuronRelativeSelfAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                        uint window, uint window_key, uint units_count, uint heads, 
                                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

No corpo do método, chamamos imediatamente o método homônimo da classe pai, passando a ele parte dos parâmetros recebidos. Como você sabe, o método da classe pai já contém algoritmos para o controle mínimo dos parâmetros recebidos e para a inicialização dos objetos herdados. Apenas verificamos o resultado lógico da execução dessas operações.

Em seguida, armazenamos as constantes recebidas em variáveis internas da classe para uso posterior.

   iWindow = window;
   iWindowKey = window_key;
   iUnits = units_count;
   iHeads = heads;

E damos início à inicialização dos objetos internos declarados. Primeiro, inicializamos as camadas convolucionais para geração das entidades Query, Key e Value nos respectivos objetos internos. Os parâmetros das três camadas são usados de forma idêntica.

   int idx = 0;
   if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;

Depois, devemos preparar os objetos para o cálculo da nossa matriz de distâncias. Para isso, começamos criando um objeto de transposição dos dados brutos.

   idx++;
   if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

Em seguida, criamos um objeto para armazenar os resultados. A operação de multiplicação de matrizes em si já está implementada na classe pai.

   idx++;
   if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnits, optimization, iBatch))
      return false;

O próximo passo é organizar o processo de geração dos tensores BK e BV. Conforme descrito na parte teórica do método, sua geração é feita usando um MLP com 2 camadas. A primeira camada é comum a todas as cabeças de atenção, e a segunda gera tokens distintos para cada cabeça. Em nossa implementação, utilizamos duas camadas convolucionais sequenciais para cada entidade. E aplicamos a tangente hiperbólica para introduzir não linearidade entre as camadas.

   idx++;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;

Também precisamos de vetores treináveis de deslocamento global de contexto e de posição. Para criá-los, usamos a abordagem já adotada em trabalhos anteriores. Refiro-me à criação de um MLP com duas camadas. Uma delas é estática e contém o valor "1", e a outra é treinável e gera o tensor necessário. Os ponteiros para os objetos criados são armazenados nos arrays cGlobalContentBias e cGlobalPositionalBias.

   idx++;
   CNeuronBaseOCL *neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;
   idx++;
   CBufferFloat *buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;
   idx++;
   buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;

Nesta etapa, preparamos todos os objetos necessários para a preparação correta dos dados brutos do nosso módulo de atenção relativa. Na etapa seguinte, passamos aos objetos de processamento dos resultados da atenção. Primeiro, criamos o objeto de gravação dos resultados do mecanismo de atenção multig cabeça e adicionamos seu ponteiro ao array cMHAttentionPooling.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(neuron)
     )
      return false;

Depois, adicionamos o MLP das operações de pooling.

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, 
                                                                       optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;

E adicionamos a camada SoftMax na saída.

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   softmax.SetHeads(iUnits);

Observe que, na saída do MLP de pooling, obtemos os coeficientes normalizados de influência das cabeças de atenção para cada elemento da sequência. Agora basta multiplicar os vetores obtidos pelos respectivos resultados do bloco de atenção multig cabeça para gerar os resultados finais. Porém, o tamanho do vetor de descrição de um único elemento da sequência será igual à nossa dimensionalidade interna. Por isso, adicionamos também objetos para escalonar os resultados até o nível dos dados brutos.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iUnits, optimization, iBatch) ||
      !cScale.Add(neuron)
     )
      return false;
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(LReLU);
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(None);

Agora só resta fazer a substituição dos buffers de dados, a fim de evitar operações de cópia desnecessárias, e retornar o resultado lógico da execução do método ao programa chamador.

//---
   if(!SetGradient(conv.getGradient(), true))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Vale destacar que, neste caso, estamos substituindo apenas o ponteiro do buffer de gradientes. Isso se deve à criação das conexões residuais dentro do bloco de atenção. Mas esse assunto será abordado ao implementarmos o método de propagação para frente feedForward.

Nos parâmetros do método de propagação para frente, recebemos o ponteiro para o objeto de dados brutos, que é imediatamente repassado ao método homônimo dos objetos internos para geração das entidades Query, Key e Value.

bool CNeuronRelativeSelfAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL) ||
      !cKey.FeedForward(NeuronOCL) ||
      !cValue.FeedForward(NeuronOCL)
     )
      return false;

Perceba que não verificamos a validade do ponteiro recebido do programa externo para o objeto de dados brutos. Essa verificação já é realizada nos métodos dos objetos internos. Portanto, esse ponto de controle é desnecessário neste caso.

Em seguida, passamos à geração das entidades para definição das distâncias entre os objetos analisados. Transpomos o tensor dos dados brutos.

   if(!cTranspose.FeedForward(NeuronOCL) ||
      !MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnits, iWindow, iUnits, 1)
     )
      return false;

E então realizamos a multiplicação matricial do tensor de dados brutos com sua cópia transposta. O resultado dessa operação será usado para gerar as entidades BK e BV. Para isso, organizamos laços de iteração sobre as camadas dos respectivos modelos internos.

   if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) ||
      !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject())
     )
      return false;
   for(int i = 1; i < cBKey.Total(); i++)
      if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1]))
         return false;
   for(int i = 1; i < cBValue.Total(); i++)
      if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1]))
         return false;

Depois, organizamos os laços para geração das entidades de deslocamento global.

   for(int i = 1; i < cGlobalContentBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1]))
         return false;
   for(int i = 1; i < cGlobalPositionalBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1]))
         return false;

E com isso, a etapa preparatória está concluída. Chamamos o método wrapper do kernel de propagação para frente do mecanismo de atenção relativa criado anteriormente.

   if(!AttentionOut())
      return false;

Em seguida, passamos ao processamento dos resultados. Primeiro, utilizamos o MLP de pooling para gerar o tensor de influência das cabeças de atenção.

   for(int i = 1; i < cMHAttentionPooling.Total(); i++)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1]))
         return false;

Depois, multiplicamos os vetores obtidos pelos resultados da atenção multig cabeça.

   if(!MatMul(((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).getOutput(),
              ((CNeuronBaseOCL*)cMHAttentionPooling[0]).getOutput(),
              ((CNeuronBaseOCL*)cScale[0]).getOutput(),
              1, iHeads, iWindowKey, iUnits)
     )
      return false;

Agora só precisamos escalonar os valores obtidos com o MLP de escalonamento.

   for(int i = 1; i < cScale.Total(); i++)
      if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1]))
         return false;

E somamos os resultados obtidos com os dados brutos, registrando o resultado no buffer de resultados de nível superior, herdado da classe pai. Foi exatamente para executar essa operação que deixamos o ponteiro do buffer de resultados sem substituição.

   if(!SumAndNormilize(NeuronOCL.getOutput(), 
                       ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), 
                       Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Após a implementação do método de propagação para frente, normalmente passamos à construção dos algoritmos de propagação reversa, que organizamos nos métodos calcInputGradients e updateInputWeights. No primeiro, os gradientes do erro são distribuídos para todos os elementos do modelo conforme sua influência no resultado final. No segundo, os parâmetros do modelo são ajustados para reduzir o erro. Recomendo que você explore esses métodos por conta própria no material em anexo. Lá, você também encontrará o código completo desta classe e de todos os seus métodos. Agora, partimos para a próxima etapa do nosso trabalho — a construção do objeto de nível superior com a implementação do framework R-MAT.

#2.2 implementação do framework R-MAT

Para organizar o algoritmo de nível superior do framework R-MAT, vamos criar uma nova classe chamada CNeuronRMAT. Sua estrutura está apresentada abaixo.

class CNeuronRMAT :  public CNeuronBaseOCL
  {
protected:
   CLayer               cLayers;
   //---
   virtual bool         feedForward(CNeuronBaseOCL *NeuronOCL)
   override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRMAT(void) {};
                    ~CNeuronRMAT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRMAT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Diferentemente da classe anterior, esta contém apenas um objeto interno de array dinâmico. À primeira vista, isso pode parecer insuficiente para implementar uma arquitetura tão complexa. No entanto, declaramos um array dinâmico no qual serão armazenados os ponteiros dos objetos necessários à construção do algoritmo.

O array dinâmico foi declarado como estático, o que nos permite deixar vazios o construtor e o destrutor da classe. A inicialização dos objetos internos e herdados é feita no método Init.

bool CNeuronRMAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint window_key, uint units_count, uint heads, 
                       uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Nos parâmetros do método de inicialização, recebemos as constantes que nos permitem interpretar claramente os requisitos do usuário em relação ao objeto a ser criado. Aqui vemos o conjunto habitual de parâmetros do bloco de atenção, incluindo o número de camadas internas.

A primeira operação que executamos é a já conhecida chamada do método homônimo da classe pai. Em seguida, preparamos as variáveis locais.

   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CResidualConv *conv = NULL;

E geramos um laço com número de iterações igual ao número de camadas internas a serem criadas.

   for(uint i = 0; i < layers; i++)
     {
      attention = new CNeuronRelativeSelfAttention();
      if(!attention ||
         !attention.Init(0, i * 2, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
         !cLayers.Add(attention)
        )
        {
         delete attention;
         return false;
        }

No corpo do laço, primeiro criamos uma nova instância do objeto de atenção relativa implementado anteriormente e o inicializamos, passando as constantes recebidas do programa externo.

Como você se lembra, no método de propagação para frente da classe de atenção relativa, estabelecemos o fluxo das conexões residuais. Portanto, podemos omitir essa operação neste nível e seguir adiante.

O próximo passo é criar o bloco FeedForward de forma semelhante ao Transformer padrão. No entanto, para tornar o objeto de nível superior mais simples e direto, decidimos alterar um pouco a arquitetura do bloco. Em vez disso, inicializamos um bloco convolucional com conexão residual chamado CResidualConv. Como o nome sugere, esse bloco também contém conexões residuais, eliminando a necessidade de implementá-las na classe de nível superior.

      conv = new CResidualConv();
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window, window, units_count, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
     }

Dessa forma, é suficiente criarmos apenas 2 objetos para criamos uma camada de atenção relativa. Adicionamos os ponteiros dos objetos criados ao nosso array dinâmico na ordem em que serão posteriormente chamados e seguimos para a próxima iteração do laço de geração das camadas internas de atenção.

Após a execução bem-sucedida de todas as iterações do laço, realizamos a substituição dos ponteiros dos buffers de dados do nosso último bloco interno pelos buffers correspondentes do nível superior.

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

Em seguida, retornamos ao programa chamador o resultado lógico da execução das operações e encerramos o método.

Como se pode observar, graças à divisão do algoritmo do framework R-MAT em blocos distintos, conseguimos construir um objeto de nível superior bastante conciso.

Vale destacar que essa mesma concisão se reflete em outros métodos da classe. Tomemos como exemplo o método de propagação para frente feedForward. Nos parâmetros, o método recebe um ponteiro para o objeto de dados brutos.

bool CNeuronRMAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *neuron = cLayers[0];
   if(!neuron.FeedForward(NeuronOCL))
      return false;

No corpo do método, primeiro chamamos o método homônimo do primeiro objeto interno. Em seguida, criamos um laço para iterar sequencialmente por todos os objetos internos, chamando seus respectivos métodos. Para isso, passamos como entrada o ponteiro do objeto anterior.

   for(int i = 1; i < cLayers.Total(); i++)
     {
      neuron = cLayers[i];
      if(!neuron.FeedForward(cLayers[i - 1]))
         return false;
     }
//---
   return true;
  }

E após a conclusão de todas as iterações, nem precisamos copiar os dados, pois já realizamos anteriormente a substituição dos buffers de dados. Assim, apenas encerramos a execução do método retornando o resultado lógico das operações ao programa chamador.

A mesma lógica se aplica aos métodos de propagação reversa, que recomendo que você analise por conta própria. Com isso, encerramos a apresentação dos algoritmos de implementação do framework R-MAT com MQL5. O código completo das classes apresentadas neste artigo e de todos os seus métodos pode ser encontrado no anexo.

Lá você também encontrará o código completo dos programas de interação com o ambiente e de treinamento dos modelos. Eles foram completamente transferidos dos trabalhos anteriores, sem alterações. Quanto à arquitetura das redes, foram feitas apenas modificações pontuais, substituindo uma camada no Codificador do estado do ambiente.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRMAT;
   descr.window=BarDescr;
   descr.count=HistoryBars;
   descr.window_out = EmbeddingSize/2;                // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A descrição completa da arquitetura dos modelos treináveis também está disponível no anexo.

3. Testes

Realizamos um intenso trabalho de implementação do framework R-MAT com MQL5. Agora, passamos à parte final do nosso projeto — o treinamento dos modelos e o teste da política obtida. Neste estudo, seguiremos o algoritmo de treinamento de modelos descrito anteriormente. Neste caso, treinamos simultaneamente os três modelos: Codificador do estado da conta, Ator e Crítico. O primeiro modelo executa o trabalho preparatório de interpretação da situação de mercado. Ator toma decisões sobre a execução de operações de trading com base na política aprendida. E Crítico avalia as ações do Ator e aponta a direção para ajuste da política.

Como antes, o treinamento dos modelos é realizado com dados históricos reais do instrumento financeiro EURUSD, no timeframe H1, cobrindo todo o ano de 2023. Os parâmetros de todos os indicadores analisados foram mantidos com seus valores padrão.

O treinamento dos modelos é realizado de forma iterativa, com atualização periódica do conjunto de treinamento.

A eficácia da política treinada é avaliada com dados históricos de janeiro de 2024. Os resultados dos testes são apresentados abaixo.

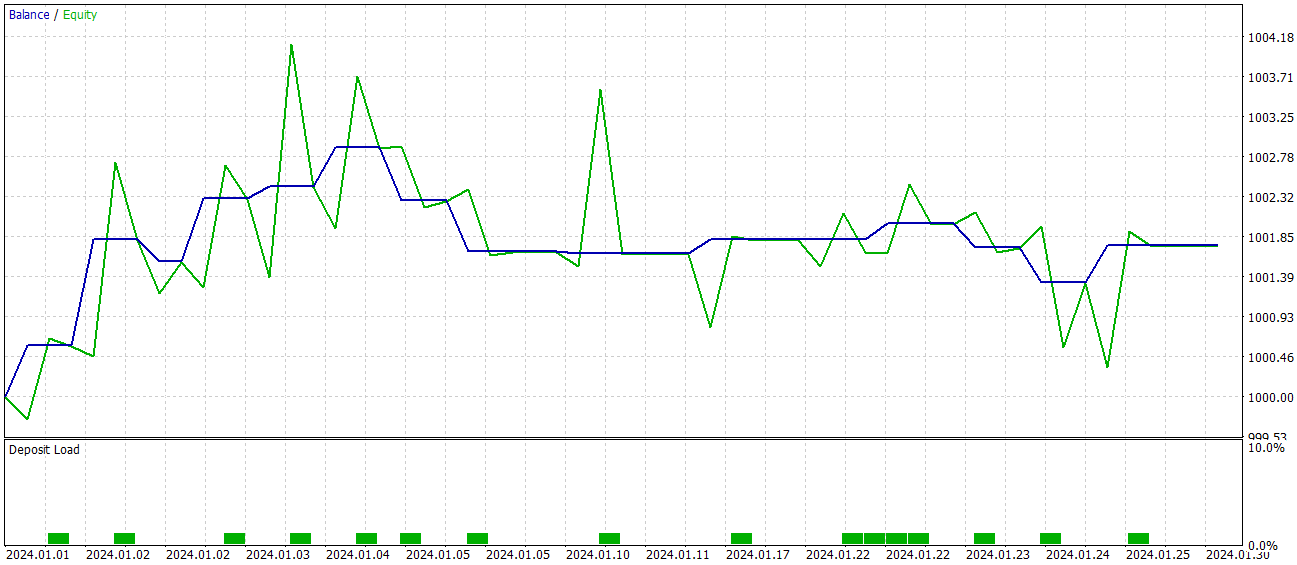
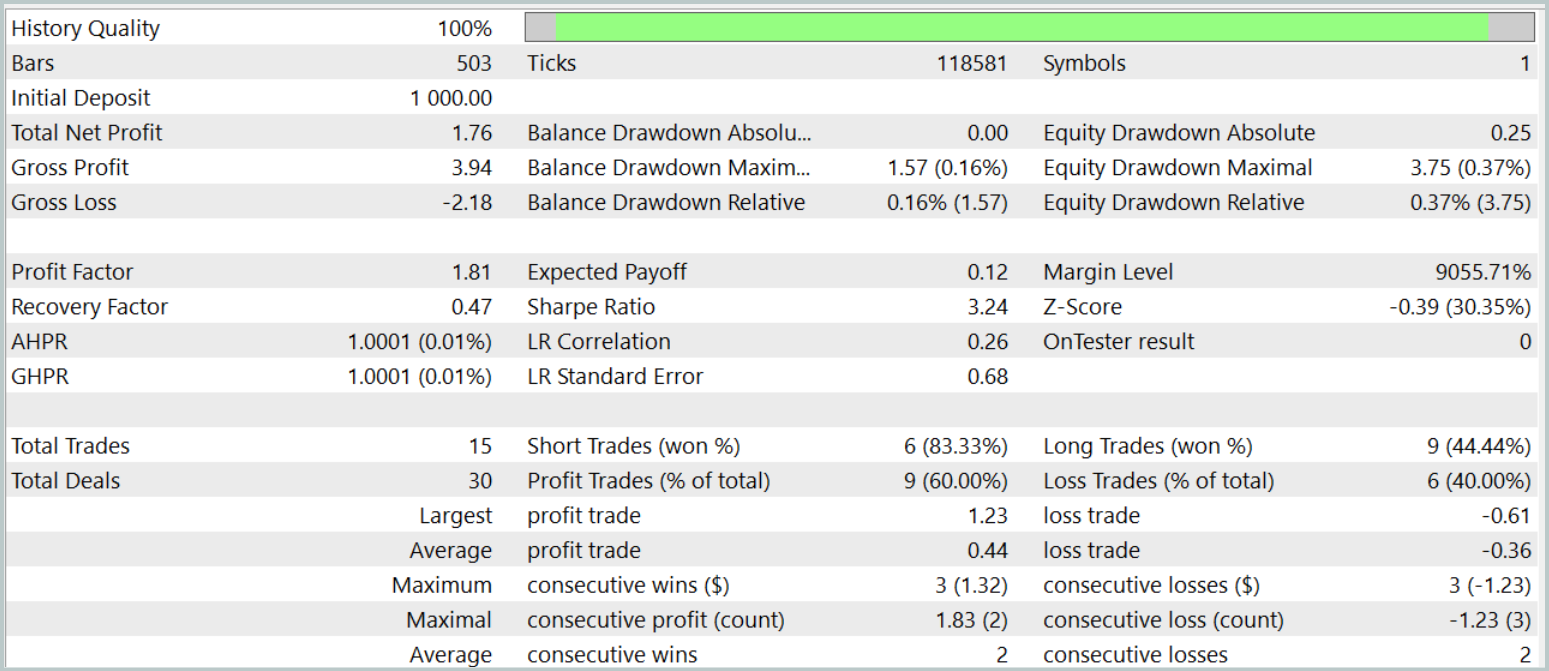
Como se pode observar, de acordo com os testes, o modelo atingiu um nível de 60% de operações lucrativas. Além disso, tanto a média quanto a posição mais lucrativa superaram os valores correspondentes das operações com prejuízo.

No entanto, nessa "colher de mel há um pingo de fel". Durante o período de teste, o modelo realizou apenas 15 operações de trading. E no gráfico de saldo, vemos que a maior parte dos lucros foi obtida no início do mês. Depois disso, observou-se um movimento lateral. Portanto, neste caso, podemos apenas afirmar o potencial do modelo, mas ele ainda precisa ser melhorado para operar em intervalos de tempo mais longos.

Considerações finais

O modelo Relative Molecule Attention Transformer (R-MAT) representa um avanço significativo na previsão de propriedades complexas. No contexto do trading, o R-MAT pode ser visto como uma poderosa ferramenta para analisar inter-relações complexas entre diferentes fatores de mercado, considerando tanto suas distâncias relativas quanto as dependências temporais.

Na parte prática, implementamos nossa versão dos conceitos apresentados com MQL5 e treinamos os modelos resultantes com dados reais. Os resultados dos testes permitem discutir o potencial da solução proposta. No entanto, o modelo ainda requer ajustes antes de ser utilizado em operações de negociação reais.

#Links

• Relative Molecule Self-Attention Transformer
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL