
Redes neurais em trading: Modelos de difusão direcionada (DDM)
Introdução
O aprendizado não supervisionado de representações com modelos de difusão tornou-se uma área de pesquisa importante na visão computacional. Os resultados de experimentos realizados por diferentes pesquisadores confirmam a eficácia dos modelos de difusão no aprendizado de representações visuais relevantes. A recuperação de dados distorcidos por certos níveis de ruído fornece uma base adequada para o modelo aprender conceitos visuais complexos, e priorizar certos níveis de ruído durante o treinamento melhora o desempenho dos modelos de difusão.
Os autores do trabalho "Directional diffusion models for graph representation learning" propuseram o uso de modelos de difusão para aprendizado não supervisionado de representação de grafos. No entanto, na prática, enfrentaram uma limitação dos modelos de difusão padrão. Os experimentos realizados por eles mostraram que os dados em grafos podem possuir estruturas anisotrópicas e direcionais bem definidas, que são menos evidentes em imagens. Modelos de difusão padrão com processo de propagação para frente isotrópico levam a uma rápida diminuição da relação sinal/ruído (Signal-to-Noise Ratio — SNR), tornando-os menos eficazes na aprendizagem de estruturas anisotrópicas. Por isso, foram propostas novas abordagens que permitem capturar tais estruturas de maneira eficiente. Esses modelos são os de difusão direcionada, que conseguem atenuar de forma eficaz o problema da rápida queda da relação sinal/ruído. A estrutura proposta inclui a geração de ruído dependente dos dados e direcionado no processo de propagação para frente. As ativações intermediárias obtidas pelo modelo de absorção de ruído capturam, de maneira eficiente, informações semânticas e topológicas úteis, necessárias para tarefas posteriores.
Como resultado, os modelos de difusão direcionada oferecem uma abordagem generativa promissora para o aprendizado de representação de grafos. Os resultados dos experimentos conduzidos pelos autores do método demonstram desempenho superior em comparação ao aprendizado contrastivo e às abordagens generativas. É notável que, em tarefas de classificação de grafos, os modelos de difusão direcionada superam até mesmo modelos básicos com aprendizado supervisionado, destacando o enorme potencial dos modelos de difusão na área de aprendizado de representação de grafos.
A aplicação de modelos de difusão no contexto do trading abre perspectivas para melhorar os métodos de representação e análise de dados de mercado. Modelos de difusão direcionada, que consideram estruturas anisotrópicas dos dados, podem ser potencialmente úteis. Como os mercados financeiros muitas vezes se caracterizam por movimentos assimétricos e direcionais, modelos com ruído direcionado podem reconhecer com mais eficiência padrões estruturais em movimentos de tendência e de correção. Isso permitirá identificar dependências ocultas e padrões sazonais.
1. Algoritmo DDM
Existem diferenças notáveis nas propriedades estruturais dos dados entre grafos e imagens. No processo padrão de propagação para frente, o ruído gaussiano isotrópico é adicionado de forma sequencial aos dados brutos até que a sequência analisada se transforme em ruído branco. Esse processo faz sentido quando os dados seguem distribuições isotrópicas, pois transforma gradualmente o ponto de dado em ruído e gera dados ruidosos com uma ampla faixa de SNR. No entanto, no caso de distribuições de dados anisotrópicas, a adição de ruído isotrópico pode rapidamente corromper a estrutura dos dados, o que leva a uma queda acelerada do SNR até zero.
Consequentemente, o modelo de supressão de ruído não consegue aprender representações significativas e discriminatórias de características que possam ser usadas de forma eficaz na resolução de tarefas subsequentes. Por outro lado, ao utilizar modelos de difusão direcionada, que incorporam um processo de propagação para frente dependente dos dados, a relação sinal/ruído diminui mais lentamente. Essa diminuição mais gradual permite extrair representações detalhadas de características com diferentes SNR, preservando informações importantes sobre estruturas anisotrópicas. As informações obtidas podem ser usadas para resolver tarefas futuras de classificação de grafos e de nós.
O processo de geração de ruído direcionado envolve transformar o ruído gaussiano isotrópico original em ruído anisotrópico por meio da adição de duas restrições adicionais. Essas duas restrições desempenham um papel crítico na melhoria dos modelos de difusão.
Seja Gt = (A, Xt) a solução de trabalho no passo t do processo de propagação para frente, onde 𝐗t = {xt,1, xt,2, …, xt,N} representa as características em estudo.
![]()
![]()
![]()
onde x0,i é o vetor de características brutas do nó i, μ ∈ ℛ e σ ∈ ℛ representam os tensores de médias e desvios padrão de dimensão d das características entre todos os N nós, respectivamente, e ⊙ representa a multiplicação elemento a elemento. Durante o treinamento, em cada mini-lote, μ e σ são calculados para os grafos dentro do lote. O parâmetro ɑt representa um cronograma de desvios fixos e é parametrizado por uma sequência decrescente {β ∈ (0, 1)}.
Ao contrário do processo de difusão padrão, os modelos de difusão direcionada incluem duas restrições adicionais. Uma delas define a transformação do ruído gaussiano, independente dos dados, em ruído anisotrópico, dependente do minilote. Nessa restrição, cada coordenada do vetor de ruído possui a mesma média e o mesmo desvio padrão empírico que a coordenada correspondente nos dados. Isso limita o processo de difusão à vizinhança local do lote, evitando desvios excessivos e mantendo a coerência local. A outra restrição é introduzida como uma direção angular, que rotaciona o ruído ε para o mesmo hiperplano do objeto x0,i, preservando a direção do objeto original. Essa restrição ajuda a manter a estrutura interna dos dados durante a propagação para frente.
Essas duas restrições atuam em conjunto, garantindo que o processo de propagação para frente considere a estrutura subjacente dos dados e evite o rápido desvanecimento dos sinais. Como resultado, a relação sinal/ruído se atenua lentamente, o que permite aos modelos de difusão direcionada extrair representações significativas de características em diferentes escalas de SNR. Isso melhora o desempenho em tarefas posteriores, pois fornece representações mais robustas e informativas.
Os autores do método seguem a mesma estratégia de treinamento usada em modelos de difusão padrão, treinando o modelo de supressão de ruído fθ para aproximar o processo de propagação reversa. Como o caminho reverso do processo direto com ruído direcionado não pode ser expresso em forma fechada, foi proposto que o modelo de supressão de ruído fθ previsse diretamente a sequência original.
A visualização desenvolvida pelos autores do framework Directional diffusion models é apresentada abaixo.
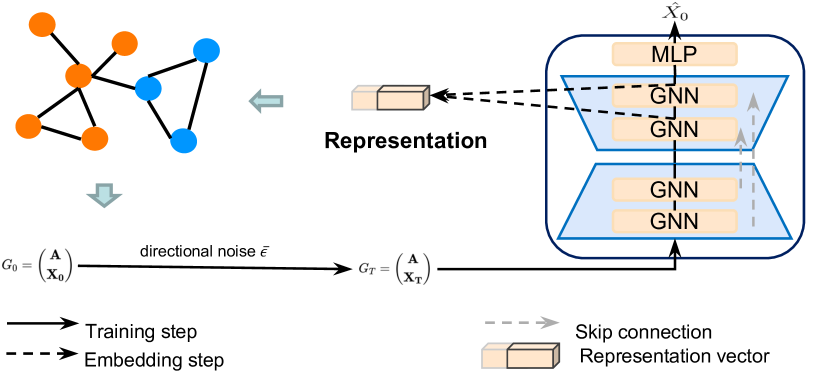
2. Implementação com MQL5
Após discutir os aspectos teóricos do framework Directional diffusion models, passamos para a parte prática do nosso artigo, na qual analisamos uma das possíveis formas de implementar as abordagens propostas usando MQL5.
Dividiremos nosso trabalho em 2 blocos. Na primeira etapa, adicionaremos ruído direcionado aos dados analisados, e em seguida implementaremos o framework dentro de uma única classe.
2.1 Adição de ruído direcionado
E antes de começarmos a codificação, vamos discutir o algoritmo de geração do ruído direcionado. Primeiro, precisaremos de ruído proveniente de uma distribuição normal. Podemos obtê-lo facilmente usando as bibliotecas padrão do MQL5.
Em seguida, conforme o algoritmo proposto pelos autores do framework, precisamos transformá-lo em ruído anisotrópico dependente dos dados brutos. Para isso, vamos precisar do valor médio e da variância de cada característica. Se pensarmos bem, já resolvemos uma tarefa semelhante ao construir a camada de normalização em minilotes CNeuronBatchNormOCL. Aqui, é importante lembrar que o algoritmo de normalização por lote transforma os dados brutos em uma média igual a zero e uma variância igual a um. No entanto, durante a etapa de deslocamento e escalonamento, a distribuição dos dados é alterada. E provavelmente poderíamos obter essa informação da camada de normalização dos dados brutos. Até porque já implementamos o procedimento de obtenção dos parâmetros da distribuição original ao desenvolver a classe de reversão da normalização CNeuronRevINDenormOCL. Mas esse tipo de abordagem nos limita no uso deste framework.
Por isso, fomos um pouco além. E decidimos unir a adição de ruído direcionado com a normalização dos dados. E aí surge a pergunta: em que ponto devemos adicionar o ruído?
De fato, podemos adicionar o ruído ANTES da normalização dos dados brutos. Mas nesse caso, vamos distorcer o próprio processo de normalização. Afinal, adicionar ruído modifica a distribuição dos dados. Portanto, ao normalizar usando média e variância previamente definidas, obteremos uma distribuição distorcida na saída. E isso não é desejável.
A segunda opção seria adicionar o ruído na saída da camada de normalização. Nesse caso, seria necessário ajustar o ruído gaussiano com os coeficientes de escala e deslocamento. Mas, se observarmos as fórmulas do algoritmo proposto pelos autores, notamos que, ao ajustar a direção do ruído, ele se desloca na direção do nosso coeficiente de deslocamento. Logo, com o aumento do coeficiente de deslocamento, temos um ruído também deslocado e “tendencioso”. O que também não é desejável.
Após ponderar os prós e os contras, optamos por um caminho diferente e adicionamos o ruído entre a normalização dos dados e a etapa de deslocamento e escalonamento. Nesse caso, excluímos a etapa de transformação do ruído, pois após a normalização esperamos obter dados com média zero e variância um. É justamente com essa distribuição que geramos o ruído. E na etapa de escalonamento e deslocamento, já alimentamos o modelo com dados ruidosos, o que permitirá que ele aprenda os coeficientes corretos.
Definidos os princípios da implementação, podemos agora passar à parte prática. Esse algoritmo será implementado no contexto do OpenCL. Para isso, vamos criar um novo kernel chamado BatchFeedForwardAddNoise. Já adiantamos que o algoritmo deste kernel foi, em grande parte, inspirado no kernel de propagação para frente da camada de normalização por lote. No entanto, adicionamos um buffer de dados de ruído gaussiano e um coeficiente de desvios ɑ.
__kernel void BatchFeedForwardAddNoise(__global const float *inputs, __global float *options, __global const float *noise, __global float *output, const int batch, const int optimization, const int activation, const float alpha) { if(batch <= 1) return; int n = get_global_id(0); int shift = n * (optimization == 0 ? 7 : 9);
No corpo do método, começamos verificando o tamanho do minilote de normalização, que deve ser maior que "1". Em seguida, determinamos o deslocamento nos buffers de dados com base no identificador da thread atual.
Depois, verificamos se há números válidos no buffer dos parâmetros de normalização. Os elementos incorretos são substituídos por valores nulos.
for(int i = 0; i < (optimization == 0 ? 7 : 9); i++) { float opt = options[shift + i]; if(isnan(opt) || isinf(opt)) options[shift + i] = 0; }
Em seguida, realizamos a normalização dos dados brutos em total conformidade com o algoritmo do kernel base.
float inp = inputs[n]; float mean = (batch > 1 ? (options[shift] * ((float)batch - 1.0f) + inp) / ((float)batch) : inp); float delt = inp - mean; float variance = options[shift + 1] * ((float)batch - 1.0f) + pow(delt, 2); if(batch > 0) variance /= (float)batch; float nx = (variance > 0 ? delt / sqrt(variance) : 0);
Nesse estágio, obtemos os dados brutos normalizados com média zero e variância unitária. E é nesse momento que adicionamos o ruído, após corrigirmos previamente sua direção.
float noisex = sqrt(alpha) * nx + sqrt(1-alpha) * fabs(noise[n]) * sign(nx);
A seguir, executamos o algoritmo de escalonamento e deslocamento, salvando os resultados nos buffers de dados correspondentes, da mesma forma que na implementação do kernel doador. Só que, desta vez, aplicamos escalonamento e deslocamento aos valores com ruído.
float gamma = options[shift + 3]; if(gamma == 0 || isinf(gamma) || isnan(gamma)) { options[shift + 3] = 1; gamma = 1; } float betta = options[shift + 4]; if(isinf(betta) || isnan(betta)) { options[shift + 4] = 0; betta = 0; } //--- options[shift] = mean; options[shift + 1] = variance; options[shift + 2] = nx; output[n] = Activation(gamma * noisex + betta, activation); }
A propagação para frente já foi implementada. Mas e quanto à propagação reversa? Aqui vale dizer que, para realizar as operações de propagação reversa, decidimos utilizar integralmente a implementação dos algoritmos da camada de normalização por lote. O ponto é que o ruído não é treinado. Consequentemente, o gradiente do erro é transmitido integralmente para os dados brutos. O uso do coeficiente ɑ apenas cria uma leve difusão em uma área com centro próximo aos dados originais. Portanto, podemos ignorar esse coeficiente e transferir completamente o gradiente de erro para o nível dos dados brutos, conforme o algoritmo da camada de normalização por lote.
Com isso, encerramos o trabalho no que se refere à programação OpenCL. O código completo está disponível no anexo. Agora, passaremos ao desenvolvimento da parte principal do programa, onde criaremos a nova classe CNeuronBatchNormWithNoise. Como se pode imaginar, a funcionalidade principal será herdada da classe de normalização por lote. Aqui, apenas sobrescreveremos o método de propagação para frente. A seguir, apresentamos a estrutura da nova classe.
class CNeuronBatchNormWithNoise : public CNeuronBatchNormOCL { protected: CBufferFloat cNoise; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); public: CNeuronBatchNormWithNoise(void) {}; ~CNeuronBatchNormWithNoise(void) {}; //--- virtual int Type(void) const { return defNeuronBatchNormWithNoise; } };
Como vocês devem ter notado, buscamos simplificar ao máximo o desenvolvimento da nova classe CNeuronBatchNormWithNoise. No entanto, para implementar a funcionalidade necessária, precisaremos de um buffer para transferir o ruído, que será gerado na parte principal do programa, para o contexto OpenCL. No entanto, não reimplementamos o método de inicialização do objeto nem os métodos de manipulação de arquivos. Afinal, não faz sentido salvar o ruído aleatório. Por isso, toda a lógica foi centralizada no método de propagação para frente feedForward, cujos parâmetros incluem o ponteiro para o objeto de dados brutos.
bool CNeuronBatchNormWithNoise::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!bTrain) return CNeuronBatchNormOCL::feedForward(NeuronOCL);
Aqui vale destacar que o ruído será adicionado apenas durante o processo de treinamento do modelo. Isso permitirá que ele aprenda as estruturas significativas dos dados brutos. Já na fase de utilização prática, queremos usar o modelo treinado como um filtro, que restaurará as estruturas relevantes da informação a partir de dados reais que contenham certo nível de ruído. Por isso, durante a utilização, executamos apenas a normalização dos dados com os recursos da classe pai.
O código a seguir é executado apenas durante o treinamento do modelo. Primeiro, verificamos a validade do ponteiro recebido para o objeto de dados brutos.
if(!OpenCL || !NeuronOCL) return false;
Depois, armazenamos esse ponteiro em uma variável interna.
PrevLayer = NeuronOCL;
Em seguida, verificamos o tamanho do minilote de normalização. E, se ele for menor ou igual a 1, simplesmente sincronizamos as funções de ativação e encerramos o método com resultado positivo. Afinal, nesse caso, o resultado da normalização será igual aos dados brutos. Para evitar trabalho desnecessário, apenas transmitimos esses dados brutos diretamente para a próxima camada.
if(iBatchSize <= 1) { activation = (ENUM_ACTIVATION)NeuronOCL.Activation(); return true; }
Caso todas as verificações anteriores sejam bem-sucedidas, primeiro geramos ruído a partir de uma distribuição normal.
double random[]; if(!Math::MathRandomNormal(0, 1, Neurons(), random)) return false;
Depois, precisamos transferi-lo para o contexto OpenCL. Como não reimplementamos o método de inicialização do objeto, primeiro verificamos se o nosso buffer de dados tem elementos suficientes e se já há um buffer criado no contexto.
if(cNoise.Total() != Neurons() || cNoise.GetOpenCL() != OpenCL) { cNoise.BufferFree(); if(!cNoise.AssignArray(random)) return false; if(!cNoise.BufferCreate(OpenCL)) return false; }
Se alguma dessas verificações retornar um valor negativo, ajustamos o tamanho do buffer e criamos um novo ponteiro no contexto OpenCL.
Caso contrário, apenas copiamos os dados para o buffer e os transferimos para a memória do contexto OpenCL.
else { if(!cNoise.AssignArray(random)) return false; if(!cNoise.BufferWrite()) return false; }
Depois disso, ajustamos o tamanho real do minilote e definimos aleatoriamente o nível de ruído nos dados brutos.
iBatchCount = MathMin(iBatchCount, iBatchSize); float noise_alpha = float(1.0 - MathRand() / 32767.0 * 0.01);
E agora, com todos os dados preparados, resta apenas passá-los como parâmetros para o kernel que criamos anteriormente.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = Neurons(); int kernel = def_k_BatchFeedForwardAddNoise; ResetLastError(); if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_inputs, NeuronOCL.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_noise, cNoise.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_options, BatchOptions.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_output, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_activation, int(activation))) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_alpha, noise_alpha)) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_batch, iBatchCount)) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_optimization, int(optimization))) { printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } //--- if(!OpenCL.Execute(kernel, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), GetLastError(), __LINE__); return false; } iBatchCount++; //--- return true; }
E então colocamos o kernel na fila de execução. Durante esse processo, monitoramos a execução das operações passo a passo. Após a conclusão, retornamos o resultado lógico da execução das operações para o programa principal.
Com isso, concluímos o desenvolvimento da nossa nova classe CNeuronBatchNormWithNoise. Seu código completo está disponível no anexo.
2.2 Classe do framework DDM
Acima, implementamos o objeto de adição de ruído direcionado aos dados brutos. E agora passamos à construção do framework Directional diffusion models na nossa interpretação.
Desde já, destacamos que estamos utilizando a estrutura de abordagens proposta pelos autores do framework. Embora façamos alguns desvios no contexto da resolução das nossas tarefas. Em nossa implementação, também utilizamos a arquitetura em formato de U sugerida pelos autores do método, mas substituímos as redes neurais de grafos (GNN) por blocos codificadores do Transformer. Além disso, enquanto os autores aplicam os dados já com ruído na entrada do modelo, nós adicionamos os ruídos dentro do próprio modelo. Mas vamos por partes.
Para implementar nossa solução, criamos a nova classe CNeuronDiffusion. Como objeto pai, utilizamos o U-образный Трансформер. A seguir, apresentamos a estrutura da nova classe.
class CNeuronDiffusion : public CNeuronUShapeAttention { protected: CNeuronBatchNormWithNoise cAddNoise; CNeuronBaseOCL cResidual; CNeuronRevINDenormOCL cRevIn; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronDiffusion(void) {}; ~CNeuronDiffusion(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, uint inside_bloks, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronDiffusion; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Na estrutura apresentada da classe, vemos a declaração de três objetos, cuja finalidade conheceremos ao longo da implementação dos métodos da classe. Para construir a arquitetura principal do modelo de filtragem de ruído, utilizamos objetos herdados.
Todos os novos objetos são declarados como estáticos, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos é feita no método Init.
Nos parâmetros do método, recebemos as constantes principais que definem a arquitetura do objeto criado. É importante dizer que, neste caso, mantivemos integralmente a estrutura de parâmetros do método da classe pai, sem alterações.
bool CNeuronDiffusion::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, uint inside_bloks, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Contudo, ao desenvolver os novos algoritmos, modificaremos levemente a sequência de uso dos objetos herdados. Por isso, dentro do corpo do método, chamamos o método homônimo da classe base, no qual apenas as interfaces principais são inicializadas.
Em seguida, inicializamos o objeto de normalização dos dados brutos com adição de ruído. Esse será o objeto usado para o pré-processamento inicial dos dados brutos.
if(!cAddNoise.Init(0, 0, OpenCL, window * units_count, iBatch, optimization)) return false;
Depois, estruturamos o Transformer em formato de U. Começamos com o bloco de atenção com múltiplas cabeças.
if(!cAttention[0].Init(0, 1, OpenCL, window, window_key, heads, units_count, layers, optimization, iBatch)) return false;
Logo em seguida, adicionamos uma camada convolucional para redução de dimensionalidade.
if(!cMergeSplit[0].Init(0, 2, OpenCL, 2 * window, 2 * window, window, (units_count + 1) / 2, optimization, iBatch)) return false;
E formamos de maneira recorrente os objetos do pescoço da arquitetura.
if(inside_bloks > 0) { CNeuronDiffusion *temp = new CNeuronDiffusion(); if(!temp) return false; if(!temp.Init(0, 3, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, inside_bloks - 1, optimization, iBatch)) { delete temp; return false; } cNeck = temp; } else { CNeuronConvOCL *temp = new CNeuronConvOCL(); if(!temp) return false; if(!temp.Init(0, 3, OpenCL, window, window, window, (units_count + 1) / 2, optimization, iBatch)) { delete temp; return false; } cNeck = temp; }
Vale ressaltar que complicamos um pouco a arquitetura do modelo. E, com isso, a própria tarefa que o modelo resolve. Isso porque, como objeto do pescoço, adicionamos de forma recorrente objetos semelhantes de difusão direcionada. Isso significa que cada nova camada adiciona ruído aos dados brutos. Portanto, o modelo aprende a trabalhar e recuperar dados a partir de dados com alto nível de ruído.
Essa abordagem não entra em conflito com a ideia das modelos de difusão, que são, essencialmente, modelos generativos. Eles foram criados justamente para gerar dados iterativamente a partir de ruído. No entanto, também é possível usar os objetos da classe pai no pescoço do modelo.
Depois, adicionamos o segundo bloco de atenção ao nosso modelo de supressão de ruído.
if(!cAttention[1].Init(0, 4, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, optimization, iBatch)) return false;
E a camada convolucional de restauração da dimensionalidade ao nível dos dados brutos.
if(!cMergeSplit[1].Init(0, 5, OpenCL, window, window, 2 * window, (units_count + 1) / 2, optimization, iBatch)) return false;
De acordo com a arquitetura do U-образный Трансформер, o resultado obtido é complementado com dados das conexões residuais. Para registrá-los, vamos criar uma camada neural básica.
if(!cResidual.Init(0, 6, OpenCL, Neurons(), optimization, iBatch)) return false; if(!cResidual.SetGradient(cMergeSplit[1].getGradient(), true)) return false;
Em seguida, sincronizamos os buffers de gradientes da camada de conexões residuais e da restauração de dimensionalidade.
Depois, adicionamos a camada de reversão da normalização, que não é mencionada pelos autores do framework, mas decorre da lógica de funcionamento dele.
if(!cRevIn.Init(0, 7, OpenCL, Neurons(), 0, cAddNoise.AsObject())) return false;
O fato é que, na versão original do framework, não se utiliza normalização dos dados. Considera-se que os dados dos grafos já estão preparados e são processados por redes de grafos. Na saída do modelo, espera-se a recuperação dos dados originais livres de ruído. E durante o treinamento, o erro de reconstrução dos dados é minimizado. Já em nossa solução, utilizamos normalização dos dados. Portanto, para comparar os resultados com os valores reais, precisamos devolver aos dados sua distribuição original. Essa tarefa é executada pela camada de reversão da normalização.
Agora, resta apenas realizar a substituição dos ponteiros dos buffers de dados para evitar operações de cópia desnecessárias e retornar o resultado lógico da execução das operações para o programa chamador.
if(!SetOutput(cRevIn.getOutput(), true)) return false; //--- return true; }
Mas vale destacar que, nesse caso, substituímos apenas o ponteiro do buffer de resultados. O buffer de gradientes de erro permanece inalterado. Os motivos dessa decisão serão discutidos ao abordar os algoritmos dos métodos de propagação reversa.
Por ora, seguimos para o método de propagação para frente feedForward.
bool CNeuronDiffusion::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cAddNoise.FeedForward(NeuronOCL)) return false;
Nos parâmetros do método, recebemos o ponteiro para o objeto de dados brutos, que imediatamente encaminhamos para o método homônimo da camada interna de adição de ruído.
Os dados com ruído são então passados para o primeiro bloco de atenção.
if(!cAttention[0].FeedForward(cAddNoise.AsObject())) return false;
Depois, alteramos a dimensionalidade dos dados e os enviamos ao objeto do pescoço da arquitetura.
if(!cMergeSplit[0].FeedForward(cAttention[0].AsObject())) return false; if(!cNeck.FeedForward(cMergeSplit[0].AsObject())) return false;
Os resultados vindos do pescoço são direcionados para o segundo bloco de atenção.
if(!cAttention[1].FeedForward(cNeck)) return false;
Em seguida, restauramos a dimensionalidade dos dados ao nível original e somamos com os dados ruidosos.
if(!cMergeSplit[1].FeedForward(cAttention[1].AsObject())) return false; if(!SumAndNormilize(cAddNoise.getOutput(), cMergeSplit[1].getOutput(), cResidual.getOutput(), 1, true, 0, 0, 0, 1)) return false;
E para concluir o método, devolvemos os dados ao subespaço da distribuição original.
if(!cRevIn.FeedForward(cResidual.AsObject())) return false; //--- return true; }
Feito isso, retornamos o resultado lógico da execução das operações ao programa chamador.
Acredito que o algoritmo do método de propagação para frente não tenha apresentado maiores dificuldades. Mas nem tudo é tão simples nos métodos de propagação do gradiente de erro calcInputGradients. É justamente aqui que nos lembramos de que estamos lidando com um modelo de difusão.
bool CNeuronDiffusion::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Nos parâmetros do método, assim como na propagação para frente, recebemos o ponteiro para o objeto de dados brutos. Só que agora precisamos transmitir para ele o gradiente de erro, conforme a influência dos dados brutos no resultado final do modelo. E já começamos verificando a validade do ponteiro recebido, pois do contrário todas as operações seguintes perdem o sentido.
Em seguida, quero lembrar que, durante a inicialização, propositalmente não substituímos os ponteiros para o buffer de gradientes de erro. E, neste momento, o gradiente de erro vindo da camada seguinte está presente apenas no buffer correspondente à interface. Isso nos permite resolver nossa segunda tarefa, que é treinar o modelo de difusão. Conforme mencionado na parte teórica do artigo, o modelo de difusão é treinado para recuperar os dados brutos a partir do ruído. Por isso, vamos calcular a diferença entre os dados obtidos na saída da camada durante a propagação para frente e os dados brutos recebidos na entrada sem ruído.
float error = 1; if(!cRevIn.calcOutputGradients(prevLayer.getOutput(), error) || !SumAndNormilize(cRevIn.getGradient(), Gradient, cRevIn.getGradient(), 1, false, 0, 0, 0, 1)) return false;
No entanto, queremos ajustar o filtro de forma que ele seja capaz de destacar estruturas significativas no contexto da tarefa principal. Por isso, ao gradiente de erro de recuperação dos dados, somamos o gradiente de erro vindo da rota principal, que indica a imprecisão do desempenho do modelo principal.
Depois, transmitimos o gradiente de erro total até o nível da camada de conexões residuais.
if(!cResidual.calcHiddenGradients(cRevIn.AsObject())) return false;
Neste ponto, já utilizamos a substituição dos buffers de dados e seguimos com a propagação do gradiente de erro para o segundo bloco de atenção.
if(!cAttention[1].calcHiddenGradients(cMergeSplit[1].AsObject())) return false;
E então continuamos transmitindo o gradiente de erro pela cadeia: pescoço, camada de redução de dimensionalidade, primeiro bloco de atenção, objeto de adição de ruído.
if(!cNeck.calcHiddenGradients(cAttention[1].AsObject())) return false; if(!cMergeSplit[0].calcHiddenGradients(cNeck.AsObject())) return false; if(!cAttention[0].calcHiddenGradients(cMergeSplit[0].AsObject())) return false; if(!cAddNoise.calcHiddenGradients(cAttention[0].AsObject())) return false;
Aqui é necessário pausar e adicionar o gradiente de erro das conexões residuais.
if(!SumAndNormilize(cAddNoise.getGradient(), cResidual.getGradient(), cAddNoise.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Em seguida, transmitimos o gradiente de erro até o nível dos dados brutos e encerramos o método, retornando previamente o resultado lógico da execução das operações para o programa chamador.
if(!prevLayer.calcHiddenGradients(cAddNoise.AsObject())) return false; //--- return true; }
Com isso, concluímos a análise dos algoritmos de construção dos métodos da nossa classe do framework de difusão direcionada. Você pode consultar o código completo de todos os métodos dessa classe no anexo. Lá também estão os programas de interação com o ambiente e de treinamento dos modelos, que foram transferidos do trabalho anterior sem alterações.
As arquiteturas dos modelos também foram herdadas do artigo anterior. A única modificação foi a substituição da camada de representação adaptativa de grafos no Codificador do ambiente por uma camada de difusão direcionada treinável.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDiffusion; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = BarDescr; descr.layers=2; descr.step=3; { int temp[] = {4}; // Heads if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
A arquitetura completa dos modelos treináveis pode ser encontrada no anexo.
E agora passamos à etapa final do nosso trabalho — a verificação da eficácia das abordagens implementadas em dados reais.
3. Testes
Realizamos um trabalho significativo na implementação das abordagens de difusão direcionada utilizando os recursos do MQL5. E chegou o momento de verificar sua eficácia na resolução de tarefas de trading. Treinamos os modelos com base nas abordagens propostas, utilizando dados reais do instrumento EURUSD referentes ao ano de 2023. Durante o treinamento, foram utilizados dados históricos do timeframe H1.
Como de costume, aplicamos o treinamento offline dos modelos, com atualização regular do conjunto de dados de treinamento, com o objetivo de manter sua aderência à política atual do Ator.
Já havíamos mencionado que a nova estrutura do Codificador de estado do ambiente foi praticamente herdada da versão anterior apresentada no artigo anterior. E para efeito de comparação de resultados, testamos o novo modelo mantendo integralmente os parâmetros de teste da versão base. Os resultados dos testes referentes aos primeiros três meses de 2024 são apresentados a seguir.
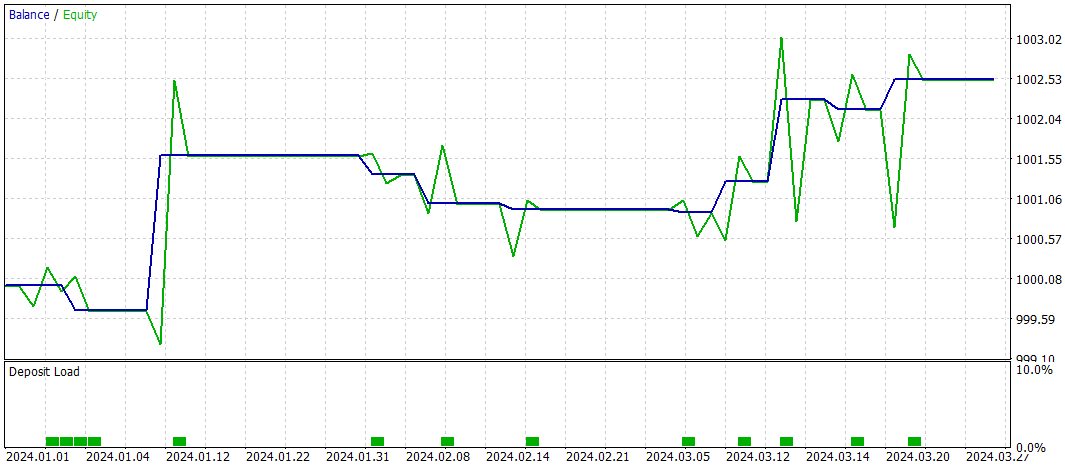
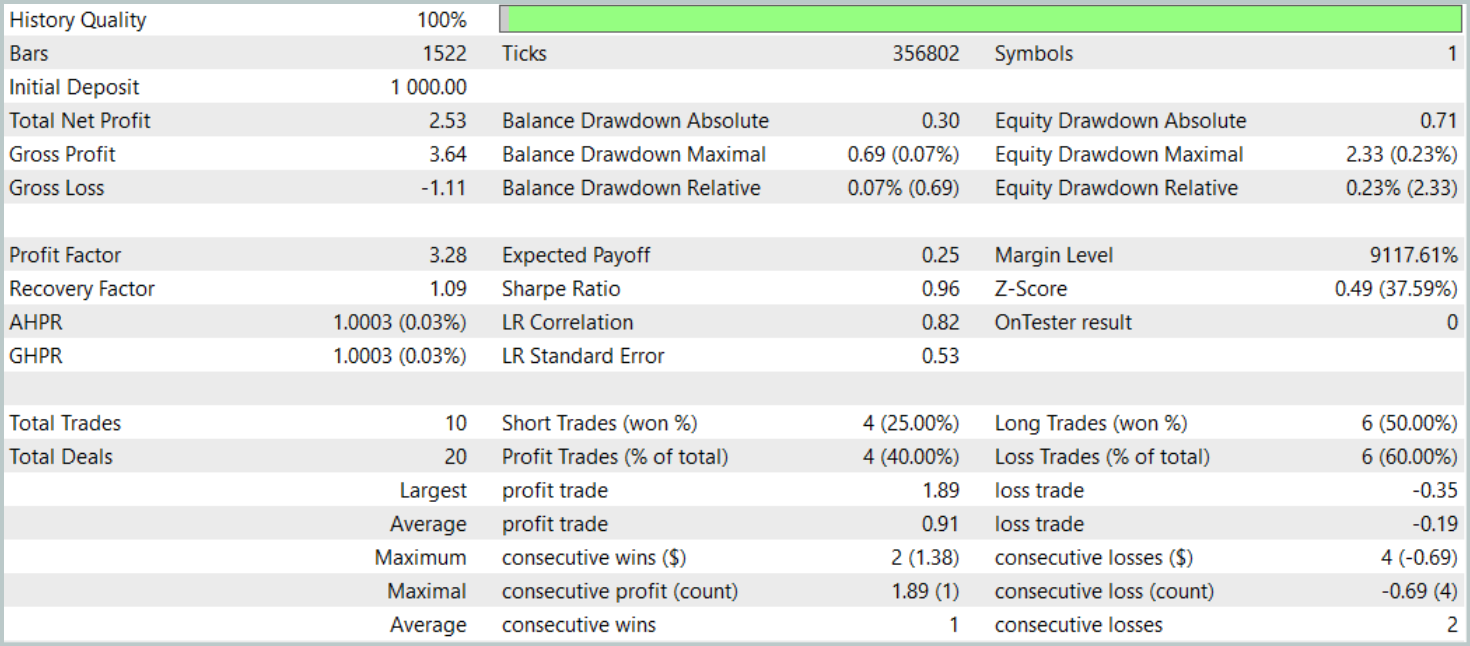
Durante o período de teste, o modelo realizou apenas 10 operações de trading. E isso é muito pouco. Além disso, apenas 4 dessas operações foram encerradas com lucro. Não é um resultado impressionante. No entanto, a média e o valor máximo das operações lucrativas superaram em cinco vezes os valores das operações com prejuízo. Isso permitiu ao modelo registrar um profit factor de 3.28.
De modo geral, o modelo apresentou uma boa relação entre lucro e prejuízo, mas o número extremamente baixo de operações de trading exige que se busquem formas de aumentar a frequência das operações. O ideal é fazer isso sem comprometer a qualidade das entradas.
Considerações finais
Os modelos de difusão direcionada (Directional diffusion model — DDM) são uma ferramenta promissora para a análise e representação de dados de mercado no trading. Considerando que os mercados financeiros frequentemente apresentam padrões anisotrópicos e direcionais, devido a estruturas complexas e a fatores externos, os modelos de difusão tradicionais, com processos isotrópicos, nem sempre são capazes de capturar essas características de forma eficaz. DDM, com sua capacidade de adaptação à direção dos dados por meio do uso de ruído direcionado, permitem identificar padrões e tendências importantes com maior eficiência, mesmo em cenários de alto ruído e volatilidade do mercado.
Na parte prática, implementamos nossa própria interpretação das abordagens propostas utilizando MQL5. Treinamos os modelos com dados históricos reais e realizamos testes fora do conjunto de dados de treinamento. Com base nos resultados obtidos, podemos concluir que os DDM possuem um potencial real. No entanto, o modelo que desenvolvemos ainda precisa de otimizações adicionais.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos com o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código para o programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16269
 Redes neurais em trading: Modelo hiperbólico de difusão latente (HypDiff)
Redes neurais em trading: Modelo hiperbólico de difusão latente (HypDiff)
 Análise da influência do clima nas moedas de países agrícolas usando Python
Análise da influência do clima nas moedas de países agrícolas usando Python
 Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt
Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 34): Embedding de Preços com um RBM Não Convencional
Técnicas do MQL5 Wizard que você deve conhecer (Parte 34): Embedding de Preços com um RBM Não Convencional
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso