パターン検索、主なパターンの説明
ピンとこない
原理的には、RMSは時系列(RT)を含む一連の数字に埋め込まれたあらゆるパターンを、その数字の出現の性質に関係なく検出することを示すと思う。このような微妙な違いを、乱数系列解析などの具体的な例を使って説明します。
RMSは有効な、あるいは架空のパターンを見つけますが、分布の正規性がないため、モデルの予測値は0になります。これは微妙な問題ではなく、基本的なことです。
具体的には、何が分からなかったのですか?
RMSは実数または虚数のパターンを見つけるが、分布の正規性がないため、モデルの予測値は0になる。これは微妙なことではなく、基礎の部分である。
RMSは、派生した依存関係ではなく、最も適切な依存関係を見つけます。また、初期データの分布の正規性の有無については、別途議論を行い、このベースの専門家に並行して発言してもらうことにしましょう。
了解です......。そして、右-忘れてください、正常な状態!ただ、邪魔になるんです。
追伸:モデルの予測値は0に近くなります
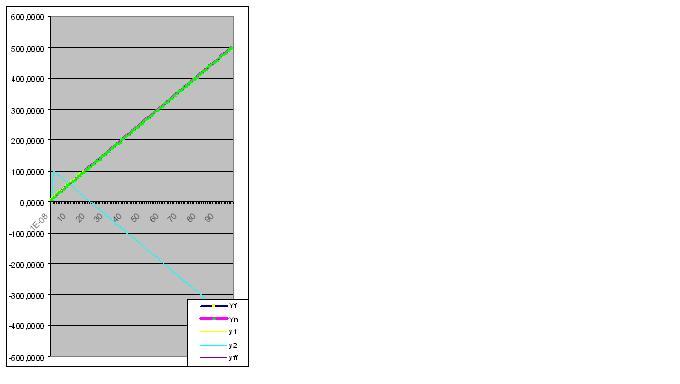
まずは一次関数から。
Yi = a+bxi という数で与えられる系列を想像してみよう。
xi イー
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
実際の値と計算値のグラフを示しますが、モデルの誤差は2.78163E-14%です。
了解です......。そして、当然のことながら、「普通なんて、くそくらえ!」です。邪魔になるだけです。
追伸:モデルの予測値は0に近くなります。
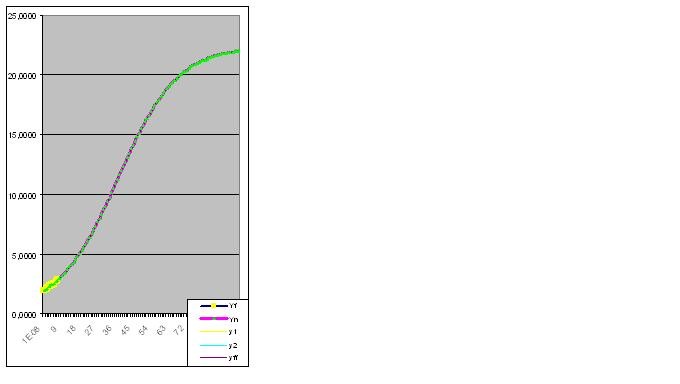
せっかくなので、まずは関数Y=tg(0,1x)+2を解析して、最初の8桁の組を紹介しながら、モデルの予測能力を示すことから始めなければなりません。
xi イー
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
誤差0.427140953%。
しかし、9桁目の数字を入力すると、その物体の将来の「奇妙な」振る舞いを即座に予測する。
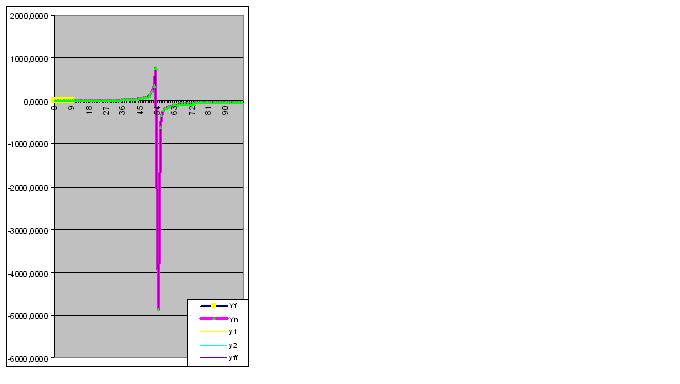
さらにデータを入力すると、予測される「異常値」が元のデータに近づいていく。
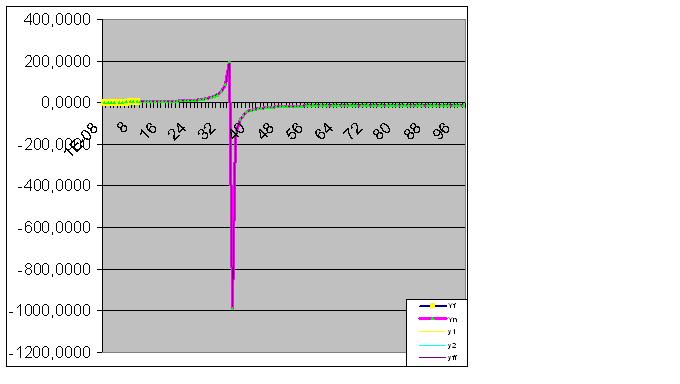
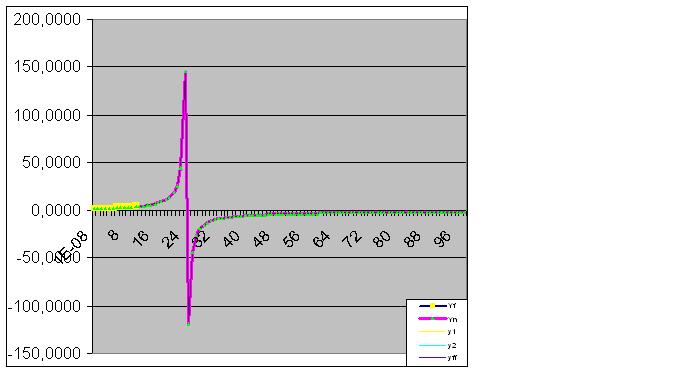
ここでは、生データも予測された「フェイント」を行い始めている。
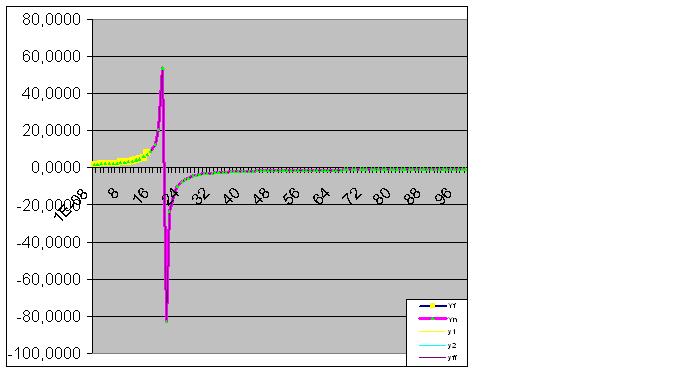
そしてついに、その予言は完璧に的中する。
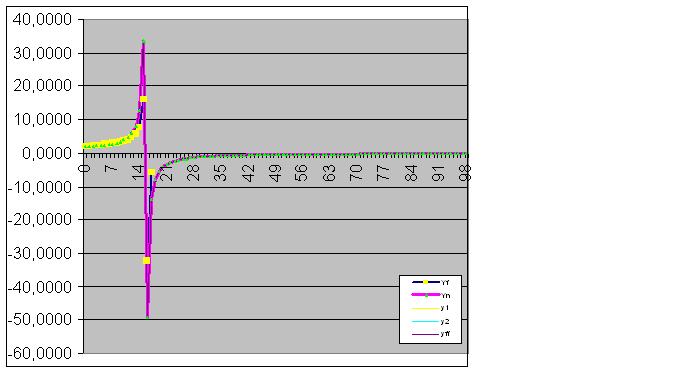
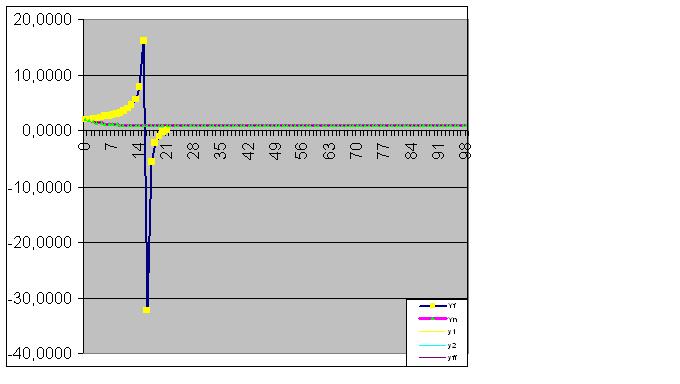
次に、関数の実際の値の合計が計算されたRMSと等しくなるように、モデルはオブジェクトの最終的な状態を完全に捕らえ、コンピュータの精度で
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
フォーラムメンバーの皆様、市場の基本パターンを記述する依存関係を見つける問題は、重要な問題であることは周知の事実です。ここでは、この問題についての参加者のさまざまな提案や、この瞬間までに蓄積されたあらゆる可能な限りの理論的・実践的資料など、あらゆる分析手段によって、この問題にアプローチしようとするものである。この仕事の結果、この機能の一端でも眺めれば、時間と労力は決して無駄ではなかったと思えるのではないでしょうか。
まず、市場に確実に存在する線形、放物線、双曲線、指数、サイン、コサイン、タンジェント、コタンジェントなどの有名なパターンの記述とその組み合わせを簡単な例にして、RMSの機能を紹介することから始める。このような私の衝動を、必要であれば建設的な提案や健全な批評でサポートしてください。