母集団最適化アルゴリズム：SSG（Saplings Sowing and Growing up、苗木の播種と育成）

内容：

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

自然界に存在するすべての生物は、ある法則にしたがって生きています。これにより、変化する環境条件の中で生き残ることができるのです。植物が環境に適応するためには、さまざまな選択肢があります。季節の変化に対応できるものもあれば、水分不足、高温・低温、送粉者の不在に適応できるものもあります。植物の中で最も安定した生物の1つである木の中には、コロニーを形成して5万年以上生き続けるものもあります。

自然は、計算手法の開発・発明において、多くの有効なアイデアを生み出す無尽蔵のインスピレーションの場です。実は、進化的計算とは、進化をコンピュータシミュレーションに投影したものです。進化的計算、人工免疫学、集団法等、自然界で起こるプロセスに着想を得た最適化手法は数多く存在します。SSGは基本的に、苗木と呼ばれる潜在的な解の庭で働く、反復的な生成と組み合わせのプロセスと定義されます。SSG（Saplings Sowing and Growing up、苗木の播種と育成）アルゴリズムは、2002年にA. Karciと共著者により提案されました。このアルゴリズムは、成長する木の進化にヒントを得て、木の成長と枝分かれをモデル化したものです。

2.アルゴリズム

このアルゴリズムは、著者による明確な説明がない（一般的な規定とアイデアしか提供されていない）数少ないものです。また、著者が提示したアルゴリズム演算子は、プログラムのアルゴリズム実装のための既成の指示書ではありません。子木と親木、その相互作用について明確な指示はありません。演算子の実行順序に決まりはなく、ユーザーはより良い苗を得るために順序を変更することができます。

広い意味では、SSGは最適化アルゴリズムではなく、他のアルゴリズムを補完して最適化の質を向上させるために設計された一般的なルールセットです。つまり、SSGはあらゆる進化的集団アルゴリズムのアドオンであるため、想像の余地があり、最適化アルゴリズムの具体的な実装を試す機会もあるのです。これまでのアルゴリズムを書きながら自分なりに考えたことや経験したことを、SSGとの連携に応用しました。以下、読者の判断のために、実験結果を紹介します。

アルゴリズムを理解し始めるには、木を最適化エージェントとして考える必要があります。木は最適化問題の解であり、各枝は問題の最適化されたパラメータです。子木と親木の抽象的かつ芸術的な図解を図1に示します。木の幹は、最適化すべきパラメータの集合体です。各枝は別々の最適化されたパラメータであり、枝の長さは対応するパラメータの値の許容範囲によって制限されます。枝の向きは関係なく、その違いを強調するために図に示しただけです。

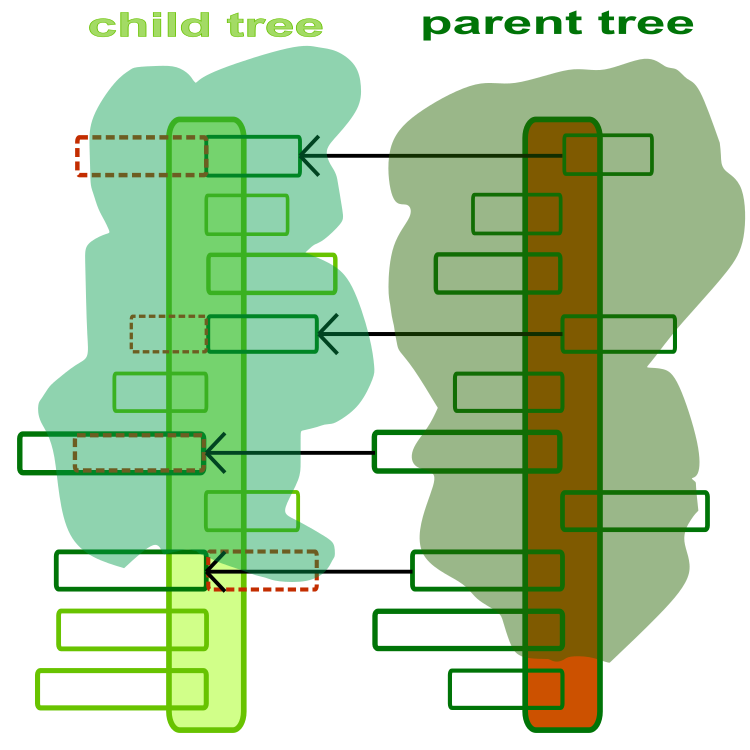
図1：子木と親木。点線は、親枝に置き換わった子枝を示す

したがって、木の枝は、探索空間における木の座標となります。

SSGアルゴリズムは、新しい解、つまり解の共通プールの候補を生成する変動演算子で構成されています。主なバリエーション演算子は、交配、枝分かれ、予防接種です。苗の植え付けは、互いに等距離の各方向（東西南北）でおこなうことが望ましく、これが方法の初期段階です。座標（最適化されたパラメータ）が3つよりはるかに多い場合、「均一」な植え付けは、探索空間上で苗を単純にランダムに分布させることになります。そして、苗が育ち、交配し、枝分かれして、予防接種がおこなわれます。

SSGアルゴリズムの手順と演算子を考えてみましょう。

1）苗を植える。

探索空間は苗の庭と考えることができるので、すべての苗が庭に均等に配置されている必要があります。苗を蒔くとき、農家は等間隔に蒔くことで、苗同士が干渉することなく早く成長することができます。苗の栽培をシミュレーションして問題を解くためには、最初に生成する任意解が有効な探索空間に均等に分布している必要があります。

座標が2～3個の場合は、苗を均等に配置することに問題はありませんが、座標が3個を大きく超える場合は、ランダムな配置にする方が簡単です。実際には、座標数が少ない場合、苗の均一分布に気を配る必要はありません。その作業は大きな問題ではなく、高い精度で解が得られることが分かっているためです。したがって、アルゴリズムの座標数にかかわらず、庭の苗の分布はランダムなものを使うことになります。

2）苗（木）を育てるには、3つの演算子を順番に実行する。

2.1) 交配

「交配」演算子の目的は、現在存在する苗から、苗間の情報を交換して新しい苗を作ることです。交配とは、本来、親木から子木に枝のコピーを移植することです（図1）。苗のペアごとに、交配の確率を表す交配係数が異なるものを使用します。交配の確率は、1組の苗の距離によって異なり、距離が長いほど交配の確率は低くなります。交配演算子は、組み合わせ的なメカニズムを提供するアルゴリズムの非常に重要な手法です。エージェント間の情報を組み合わせることで、最適化アルゴリズム全体の品質を大幅に向上させることができます。

2.2）枝分かれ

この演算子は、枝の成長をモデル化します。成長には、プラス（伸長）とマイナス（乾燥）があります。「苗の体のどの場所でも枝を伸ばすためには、近くに以前そこに芽生えた枝がない」ということになります。これはアルゴリズムの作者による演算子の近似的な記述です。実はこの処理は一見すると単純明快で、子木の既存の枝を修正するものです（具体的な修正方法は明記されていません）。

個々の枝の修正の可能性は、現在の反復と最後に枝の修正がおこなわれた反復の間により多くの反復が経過しているほど高くなります。私の実験では、この演算子の非効率性が明らかになりました。それに、修正法を使ったという直接的な指標はなく、この件に関しては私が主導して、レヴィ飛行分布則に従った枝の長さの変化を適用しました。アルゴリズムの外部パラメータとして指定された確率と強度で修正がおこなわれます。

2.3）予防接種

苗が似ている場合、2つの異なる苗の間で予防接種がおこなわれます。苗の類似度は予防接種の成否に影響し、加重距離の算術平均に比例します。この演算子は交配演算子と似ており、枝の交換で構成され、アルゴリズムにエージェント間の情報を結合する追加の方法を提供します。この演算子は記事の中で強調されますが、この演算子はソースコードでコメントアウトされており、テスト結果はこの演算子が参加しない形で提示されています。予防接種によって結果が悪化するためです。

3）木の適応度を計算する。

4）庭に新しい苗を植える。

交配、枝分かれ、予防接種の演算子の協力で得られた苗は、一時的な解決策（娘園）です。この段階で、最良の苗木をn本選び（アルゴリズムの外部パラメータ）、庭の最悪の木n本と入れ替えて庭に配置することが必要です。なお、苗木への交換はどのような場合でもおこなわれます。たとえ庭の最悪の苗木よりも悪いものであってもです。

このタイミングで成長木アルゴリズムのコードを見ると、この研究のクライマックスであるテスト結果のレビューに着実に近づいていることがわかります。

そこで、それぞれの木をGarden構造体として表現するのが便利です。これは、花壇を作る際のベースとなります。このアルゴリズムにおいて、「木」の実体ほど単純なものはありません。「木」の実体は、[]を持つ座標と適応度値fという2つの要素しか必要としません。

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

SGアルゴリズムのC_AO_SSGクラスは、特別なものではありません。ここでのすべては、先に検討したアルゴリズムから非常に馴染みのあるものです。クラスでは、親子園を操作するためのメンバーやメソッドを宣言します。一時的な庭は、並び替えメソッドが機能するためのものです。子園と親園の両方を並び替える必要があるためです。全体としての解の最適な座標の配列と最高の適応度値、アルゴリズムの外部パラメータを格納するための定数変数を宣言しておきましょう。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

Init()初期化メソッドで、配列のメモリを確保し、定数パラメータに値を代入します。seedlingsReplacementPパラメータは、親園に植える子苗の数を担当します。園の大きさの割合（0.0～1.0）で設定されているので、園の大きさを表す整数に変換する必要があります。庭の苗の初期フラグをリセットして、グローバル決定変数を最小の2倍値で初期化しましょう。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

反復毎に最初に呼ばれるSowing() publicメソッドが播種です。アルゴリズムを実行したばかりの最初の反復では、庭（探索空間）の周りに苗を一様な分布でランダムに散布することになります。ここでは、最適化されたパラメータのminとmaxの間の許容範囲でランダムに座標を生成し、許容範囲からの抜けを確認してから、最適化ステップに沿った座標値にもっていくことを確認しています。

この段階では、苗の適応性は最低限です。vec[]ベクトルを設定します。これは、枝分かれ演算子で枝分かれの増分をスケーリングしたり、探索空間での最大可能ユークリッド距離rを計算するために必要です。ペアの木の間の距離に依存する確率を決定することは、交配演算子において有用でしょう。

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

次に、Sowing()メソッドでは、2回目以降の繰り返しで、交配、枝分かれ、予防接種の各演算子が実行されます。演算子はメインループの中で順次実行されます。

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

演算子を実行する場合、「子」「親」という概念は非常に恣意的です。実は、それらは新しい苗を作るための基本的な情報源に過ぎないのです。新しい苗木は、子木からすべての枝をコピーし（覚えているかもしれませんが、枝は最適化されるべきパラメータです）、親木から新しい枝を受け取ります。

新しい苗木1本に対して、庭から2本の木が個別に選ばれ、子と親がランダムに1本ずつ、庭のすべての木に対して等しい確率で選ばれます。つまり、すべての木は、その適応度に関係なく、等しい確率で新しい苗の創造に参加することができるのです。したがって、子と親は、単に親園配列の元の2本の木のインデックスです。

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

最初の演算子は、交配、つまり接合（交尾）です。インデックスtの苗木に対して交配演算子を実行するには、「子」「親」をインデックスとする子木と親木の間のユークリッド空間を計算する必要があります。

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

ユークリッド距離は、探索空間における最大可能ユークリッド距離rに正規化することで交配確率の計算式に関与しています。

eM = 1.0 - (ed / r);

[0.0;1.0]の範囲で乱数を発生させます。その結果、算出された確率eMの範囲内の数値であれば、各枝のprobabMatingOperatorの確率で親木から枝をコピーする交配を実行します。eM確率が満たされない場合、苗木は、子木のすべての原枝で次の文の実行に進みます。

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

次に、枝分かれ演算子が実行されます。枝分かれでは、長くしたり短くしたりという枝のバリエーションが用意されています。新しい長さの枝を作る主な演算子です。残りの演算子は組み合わせの役割を果たすだけで、新しいユニークな枝を作ることはありません。各枝分かれについて、[0.0;1.0]の範囲で乱数を生成し、probabBranchOperatorの確率が満たされた場合、ここで考えたレヴィ飛行分布則に従って、枝分かれの長さを変化させて枝分かれをおこなうものです。

ご覧のように、苗木のすべての枝が変化するわけではありません。前のステートメントで親木からコピーされた枝か、元の子枝かにかかわらず、変更されます。枝分かれを修正した後、範囲外の値がないか確認し、最適化のステップに合わせます。

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

3つ目の演算子は予防接種です。予防接種演算子は、著者らが連結演算子として考案したもので、子木と親木の枝が組の全枝の平均差以上の差がある場合に、親木から枝をコピーするように実行するものらしいです。非常に複雑に聞こえますが、この演算子の使用はほとんどないため、ソースファイルではこの演算子はコメントアウトされています。この場合、私は専門家としての役を務めることはできないので、この演算子について正しい理解ができていない可能性があることを認めます。

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

最後に、このアルゴリズムの最後の、しかし最も重要な操作である「発芽」があります。各反復で実行が必須となる2番目のpublic Germination ()メソッドを実行します。

最初の反復が終わりに近づいている（sowingフラグで確実にわかる）場合、これは親園が空であることを意味します。子園の苗は、若木を1本ずつすべて写すだけで親園に植えます。その後、Sorting()メソッドで親園を適応度値で並び替えます。もし木が並び替えられていれば、インデックス0の木が最高の適応度を持つことになり、すでに大域的最適解でない場合は、それを更新することができます。

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

さらにコードを進めると、sowingフラグがtrueに設定されているため、アルゴリズムの2回目以降の繰り返しにしかたどり着けません。2回目以降の繰り返しでは、苗を親園に移す前に子園を並び替え、最悪の木を入れ替える必要があります。大域解が改善されたかどうかを確認し、ベストnの苗を親園の端にコピーしましょう。

結論としては、あとは親園を仕分けるだけです。古い世代の木に代わって、庭の社会に新しいメンバーが登場し、最適化問題の解決と花で私たちを喜ばせるのです。

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);

3.テスト結果

次は、SSGテストスタンドの結果です。

2023.03.09 12:50:37.207 Test_AO_SSG (GBPUSD,M1) C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:50:45.954 Test_AO_SSG (GBPUSD,M1) 5 Rastrigin's; Func runs 10000 result：80.7052793572295
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    Score:0.99998
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) 25 Rastrigin's; Func runs 10000 result：77.3972262608643
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) Score：0.95900
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) 500 Rastrigin's; Func runs 10000 result：52.24518909141432
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    Score:0.64735
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:52:31.419 Test_AO_SSG (GBPUSD,M1) 5 Forest's; Func runs 10000 result：1.331178589711503
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    Score:0.75298
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) 25 Forest's; Func runs 10000 result：1.019329018074209
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) Score：0.57658
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) 500 Forest's; Func runs 10000 result：0.25410121872226443
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    Score:0.14373
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    5 Megacity's; Func runs 10000 result:6.4
2023.03.09 12:53:57.201 Test_AO_SSG (GBPUSD,M1) Score：0.53333
2023.03.09 12:54:08.004 Test_AO_SSG (GBPUSD,M1) 25 Megacity's; Func runs 10000 result：4.504
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    Score:0.37533
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) 500 Megacity's; Func runs 10000 result：1.2336
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Score:0.10280
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    All score:5.09109

これはアルゴリズムに手を加えた結果ですが、SSGのパラメータはあまりありません（元のSSGはさらに少ないパラメータを持ちます）。ただし、すべてのパラメータには特別な注意を払う必要があります。テストでは、以下のパラメータを使用しました。覚えていらっしゃるかもしれませんが、各記事では、テストにおいて可能な限り高い結果をもたらす最適なアルゴリズムパラメータを紹介しています。

C_AO_SSG:50;0.3;0.5;0.4;0.1

input int NumberTrees_P = 50; - 庭にある木の本数。このパラメータはデフォルト値（私の実験のデフォルト値）のままで、実験はしていません。100の場合、アルゴリズムはさらに優れた集計結果をもたらしますが、庭の大きさに応じて庭ごとに許容される反復回数が減少するため、拡張能力は低下します。枝の数が多い庭は、進化する暇がありません。

input double SeedlingsReplacement_P = 0.3; - 娘園の苗を親園に移植する割合。
input double ProbabMatingOperator_P = 0.5; - 一対の木の間の距離を考慮した確率を満たした場合に、交差（親木から枝をコピーする）する確率。
input double ProbabBranchOperator_P = 0.4; - 枝分かれの確率（枝の成長・縮小）。アルゴリズムの性能に大きく影響する重要なパラメータです（一般的にはすべてのパラメータが重要です）。
input double PowerBranchOperator_P = 0.1; - 枝分かれの強さ。これは最適化されるパラメータの次元のスケーリングファクターです。1.0以上だと庭の境界まで枝が伸びます。0.0だと枝が伸びません。つまり新しい枝のサイズが生じず、アルゴリズムは単純な組み合わせ学のツールに退化します。これはSSGを使う上で素晴らしいアイデアかもしれませんが、ここではもっと研究が必要です。

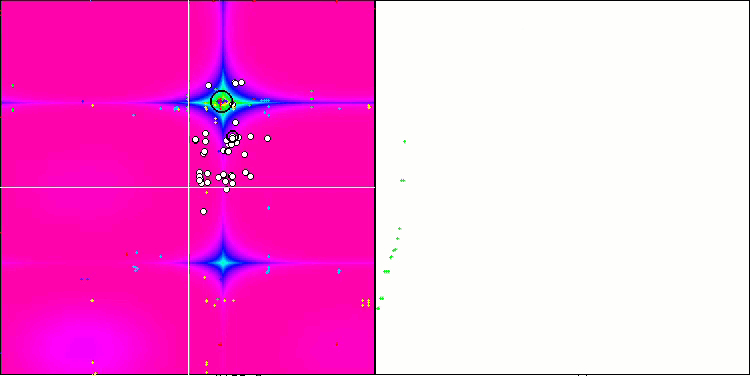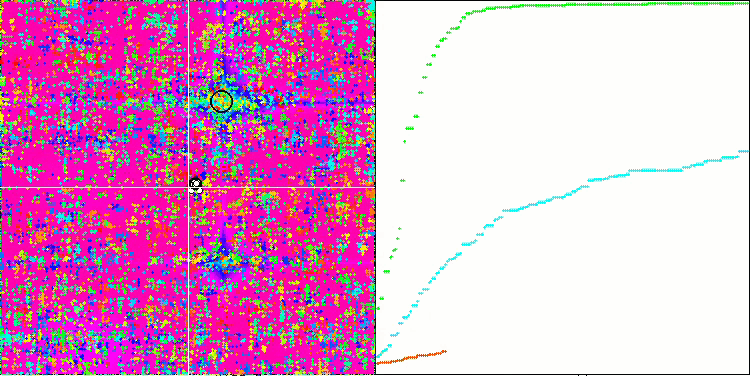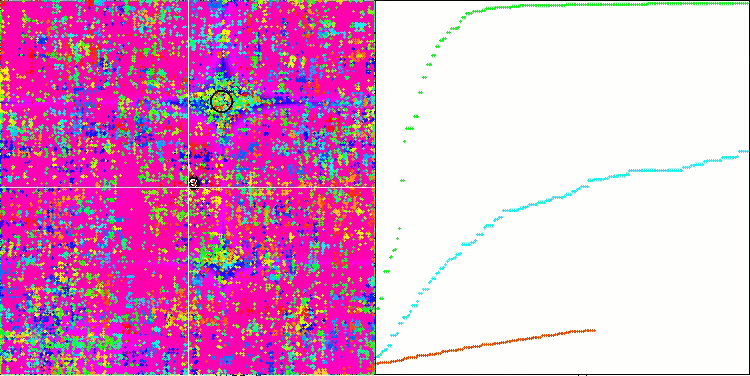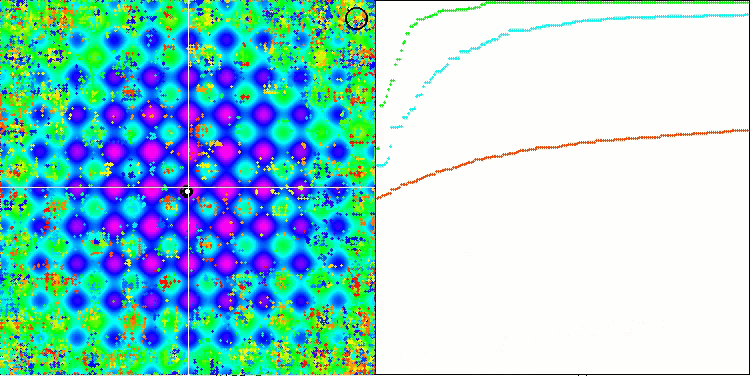
テスト関数に対するSSEアルゴリズムのアニメーションに注目すると、庭の木の動きのパターンがなく、局所極値におけるいくつかの「かたまり」が目立つだけであることに気づきます。しかし、以前に検討されたアルゴリズムと比較すると、収束の質の高さがすぐにわかります。また、安定した再現性も特筆すべき点です。

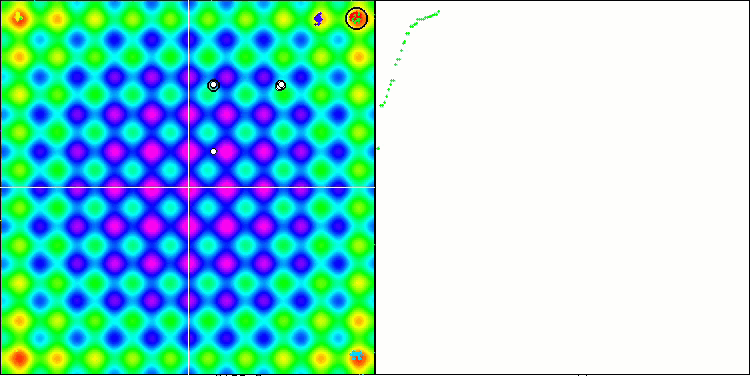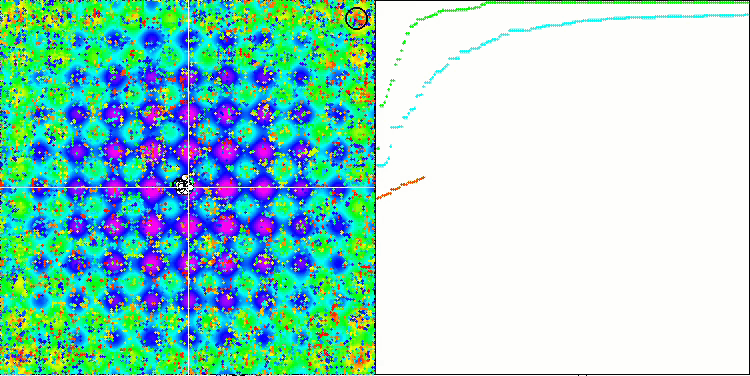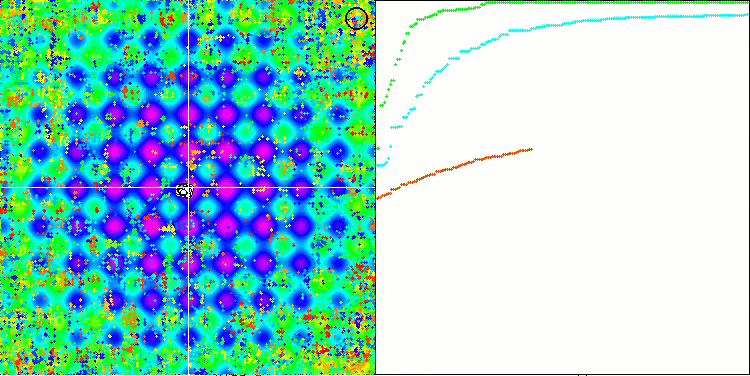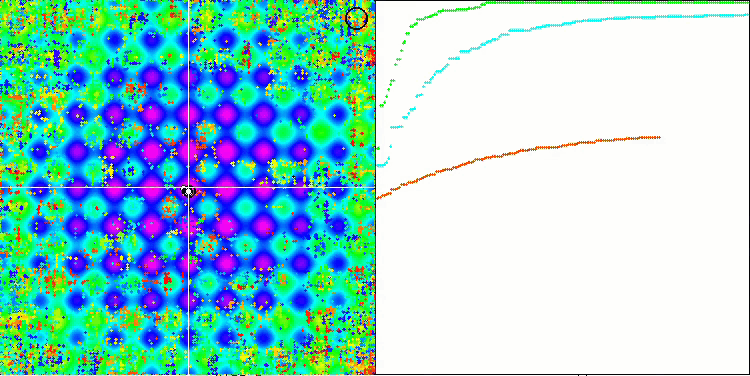
  Rastriginテスト関数のSSG

  Forestテスト関数のSSG

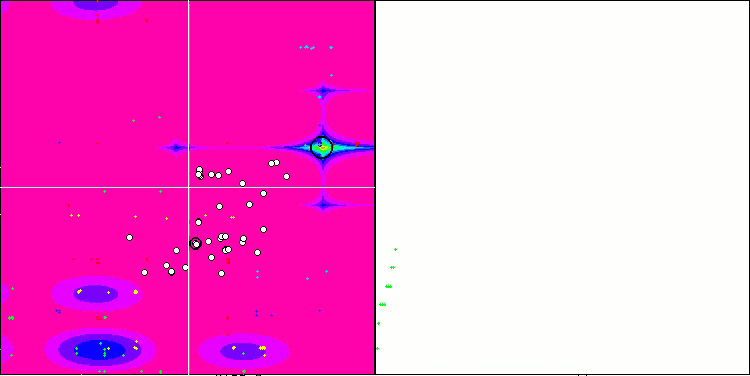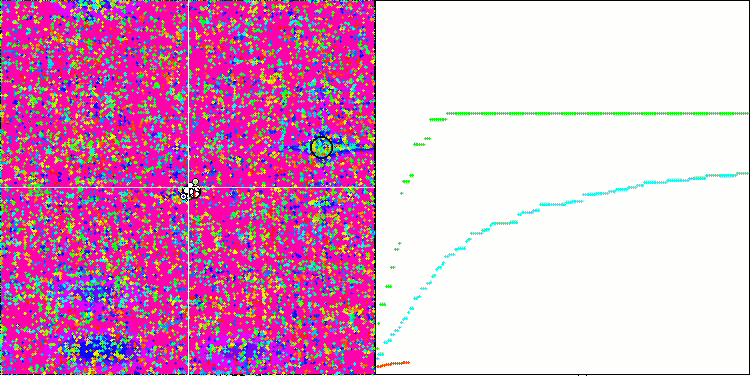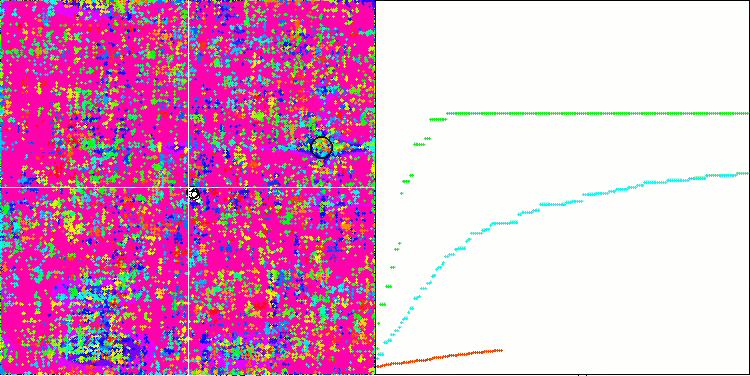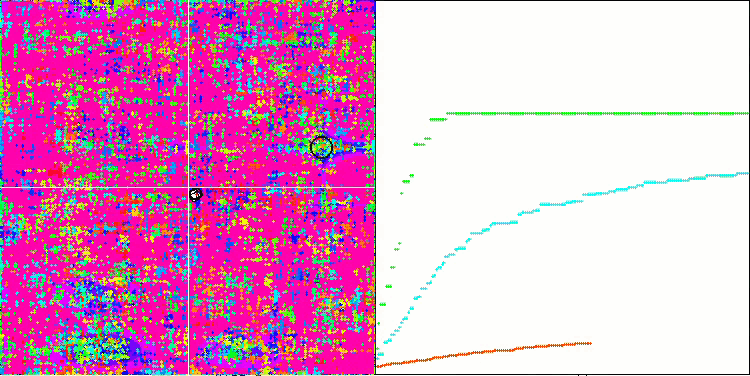
  Megacityテスト関数のSSG

それでは、SSGアルゴリズムの結果についての説明に移ります。話すべきことは確実にあります。このアルゴリズムは、ライバルを抜いて、見事に評価の1位に躍り出ました。このアルゴリズムでは、決定木を修正するために適応度の知識を直接使用することはありません。適応度は子園と親園の振り分けにしか必要ないので、このアルゴリズムがテストでこれほど顕著な結果を示せたことは、より驚きです。

これは、オリエンテーリングで目の見えない人のチームが目の見える人のチームに勝つのと同じことです。このアルゴリズムは、6つのテストのうち4つで表の参加者をリードし、リーダーでないテストでは遠く及ばないままでした。SSGは、Megacity離散関数において、最も近い競合のHSを約60%上回り、ライバルを圧倒しています！これは、本アルゴリズムの優れたスケーラビリティを示すものです。また、「シャープ」なForestテスト関数でも最高のスケーラビリティ結果が得られています。SSGは、このテストで最も優れた競合他社(ACOm)を約30%上回りました。

AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity(discrete)			Megacity最終	最終結果
		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）
SSG	苗木の播種と育成	1.00000	1.00000	0.65914	2.65914	0.70823	0.94522	1.00000	2.65345	0.71532	0.85412	1.00000	2.56944	100.000
HS	ハーモニーサーチ	0.99676	0.95282	0.57048	2.52006	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	93.370
ACOm	蟻コロニー最適化M	0.34611	0.17985	0.20182	0.72778	0.85966	1.00000	0.77362	2.63327	1.00000	0.88484	0.05606	1.94090	66.407
IWO	侵入雑草最適化	0.95828	0.67083	0.35295	1.98207	0.68718	0.46349	0.31773	1.46840	0.75912	0.39732	0.33289	1.48933	61.691
COAm	カッコウ最適化アルゴリズムM	0.92400	0.46794	0.30792	1.69987	0.55451	0.34034	0.16526	1.06012	0.67153	0.30326	0.17083	1.14561	48.226
FAm	ホタルアルゴリズムM	0.59825	0.33980	0.20290	1.14095	0.47632	0.42299	0.49790	1.39721	0.21167	0.25143	0.35258	0.81568	41.042
ABC	人工蜂コロニー	0.78170	0.32715	0.24656	1.35541	0.50591	0.21455	0.13344	0.85390	0.47444	0.23609	0.13926	0.84979	37.204
BA	コウモリアルゴリズム	0.40526	0.63761	1.00000	2.04287	0.15275	0.17477	0.25989	0.58741	0.15329	0.06334	0.17371	0.39034	36.703
GSA	重力探索法	0.70167	0.45217	0.00000	1.15384	0.26854	0.36416	0.33204	0.96475	0.51095	0.32436	0.00000	0.83531	35.834
BFO	細菌採餌の最適化	0.67203	0.30963	0.13988	1.12154	0.35462	0.26623	0.20652	0.82736	0.42336	0.30519	0.18932	0.91786	34.700
MA	モンキーアルゴリズム	0.33192	0.33451	0.17340	0.83983	0.03684	0.07891	0.08932	0.20508	0.05838	0.00383	0.10720	0.16941	13.185
FSS	魚群検索	0.46812	0.25337	0.13383	0.85532	0.06711	0.05013	0.06516	0.18240	0.00000	0.00959	0.08283	0.09242	12.089
PSO	粒子群最適化	0.20449	0.08200	0.08478	0.37127	0.13192	0.10486	0.21738	0.45415	0.08028	0.02110	0.01957	0.12095	9.696
RND	ランダム	0.16826	0.09743	0.09495	0.36065	0.07413	0.04810	0.04715	0.16938	0.00000	0.00000	0.04922	0.04922	4.916
GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.02557	0.25179	1.000

まとめ

SSGの特徴は、最適化された関数の微分可能性と連続性の要件がなく、適用される表現と符号化の種類に制約がないということです。このアルゴリズムでは、個々のエージェントの適応度情報を使わず、全体として最適解を求めます。これらの特徴により、SSGは非常に複雑な問題を含む様々な最適化問題に容易に適用することができます。トレーダーの問題や機械学習へのSSGの利用は間違いなく推奨できます。本稿執筆時点では、収束の質、結果の安定性、拡張性において、SSG（Saplings Sowing and Growing up、苗木の播種と育成）アルゴリズムが紛れもなくリーダーです。

図2は、本アルゴリズムのテスト結果です。

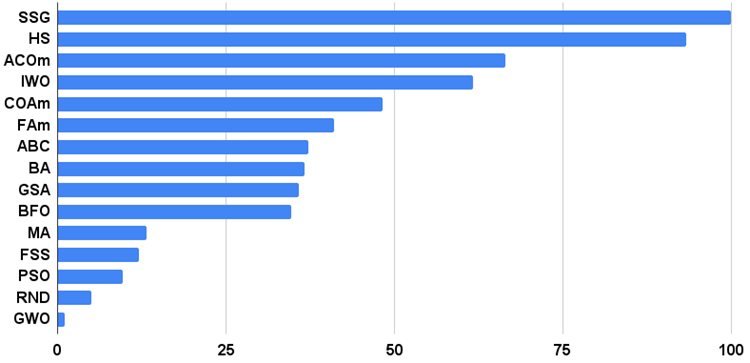
図2：アルゴリズムのテスト結果のヒストグラム

SSGアルゴリズムの長所と短所：

長所：
1.簡単に実装できる
2.あらゆる種類の関数において、例外なく優れた収束性を発揮する
3.圧倒的なスケーラビリティ

短所：
1.直感的にわかりやすいが、カスタマイズのオプションが多い。

各記事には、過去の記事のアルゴリズムコードを最新版に更新したアーカイブが用意されています。本記事は、著者の蓄積された経験に基づくものであり、個人的な意見を述べたものです。結論や判断は、実験に基づくものです。