MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
母集団最適化アルゴリズム：コウモリアルゴリズム(BA)

母集団最適化アルゴリズム：コウモリアルゴリズム(BA)

MetaTrader 5 — 例 | 3 3月 2023, 14:49
608 0
Andrey Dik
Andrey Dik

内容

1.はじめに
2.アルゴリズムの説明
3.テスト結果


1.はじめに

コウモリはすごい動物です。科学者たちは、最初のコウモリが6500万年前から1億年前に出現し、恐竜と共存していたと考えています。コウモリは哺乳類の中で唯一の有翼動物です。コウモリは1300種以上を誇ります。極地を除くほとんどの地域で見ることができます。日中はシェルターに隠れています。コウモリは、暗い洞窟内を移動したり、日没後に狩りをしたりするために、音波で物体を感知する「エコーロケーション」（反響定位）というシステムを利用しています。高周波の音を出して前進し、物体に当たって反射して戻ってくることでエコロケーションをおこないます。エコーロケーションはソナーの一種で、コウモリは大きく短いパルス状の音を発します。音が物体に届くと、しばらくしてその反響音がコウモリの耳に戻ってきます。このようにしてコウモリは空間の位置を確認し、獲物の位置を判断しているのです。 

コウモリアルゴリズム(BA)は、2010年にYangが発表した、コウモリのエコーロケーション行動を模倣して大域的最適化をおこなうヒューリスティックアルゴリズムです。メタヒューリスティックは、通常、自然や物理的なプロセスから着想を得ており、現在、多くの複雑な最適化問題を解くための最も強力な技術の1つとして利用されています。最適化とは、効率的な多数の選択肢の中から、ある基準に対して最適な要素を選択することであり、計算効率や全体最適の可能性など、さまざまなメリットやデメリットを示します。

特徴量最適化は、パラメータを入力とする「目的」関数を提供することで、多くの特定の問題をモデル化し、解決するための正式な枠組みを提供します。目標は、最適な値を返すパラメータ値の組み合わせを見つけることです。この枠組みは、様々な問題を「特徴最適化」の問題として解釈できるように抽象化されています。


しかし、従来の特徴量最適化は、一部の小さな問題を解決するためにのみ使用され、実際には適用できないことが多いです。そこで、科学者たちは、これらの問題を解決するための豊富なモデルを提供してくれる自然界に目を向けています。自然界の生物システムをモデル化することで、従来にない手法で応用問題を解決する知的群最適化アルゴリズムが数多く提案されており、その優れた性能から、様々な最適化問題に広く利用されています。BAは、本物のコウモリの自然な超音波パルスの音量と発光周波数を模擬した人工コウモリを探索エージェントとして、探索処理をおこなう新しい最新の群アルゴリズムです。


2.アルゴリズムの説明

基本的なコウモリアルゴリズムでは、各コウモリは解空間の有効解を表す「質量もサイズもない」粒子として扱われます。異なる適応度関数に対して、各コウモリは対応する特徴量を持ち、特徴量を比較することで現在の最適な個体を決定します。そして、音響波の周波数、速さ、インパルスの放出速度、集団内の各コウモリの体積を更新し、反復進化を続け、現在の最適解を近似的に生成し、最後に大域的最適解を求めます。アルゴリズムは、各コウモリの周波数、速さ、位置を更新します。

標準的なアルゴリズムでは、周波数、ラウドネス、リップル、ラウドネスとリップルの比率の5つの基本パラメータが必要です。この周波数は、過去のベストポジションが現在のポジションに与える影響のバランスをとるために使用されます。個々のコウモリは、探索周波数範囲が大きいと集団の歴史的位置から遠く離れた場所を探索し、その逆もまた然りです。

先に検討したものと比べて、アルゴリズムのパラメータはかなり多くなっています。

input double MIN_FREQ_P          = 0.0;
input double MAX_FREQ_P         = 1.0;
input double MIN_LOUDNESS_P  = 0.0;
input double MAX_LOUDNESS_P = 1.5;
input double MIN_PULSE_P        = 0.0;
input double MAX_PULSE_P        = 1.0;
input double ALPHA_P               = 0.3;
input double GAMMA_P              = 0.3;

BAアルゴリズムを実装する際、多くの文献で著者が全く異なる方法でアルゴリズムを記述していることに気づきました。その違いは、要点を説明する際の用語の使い方と、基本的なアルゴリズムの特徴の両方にあるので、私自身がどのように理解したかを説明します。エコロケーションの基礎となる基本的な物理原理は、大きな留保と慣習を伴って、アルゴリズムに適用することができます。コウモリはMinFreqからMaxFreqまでの周波数の超音波パルスを使用すると仮定しています。周波数はコウモリの速度に影響します。また、ラウドネスという条件付き概念を用い、コウモリの現在位置での局所探索の状態から、最適解の近傍での大域探索の状態への遷移に影響を与えるようにしました。最適化の過程で脈動周波数は増加し、音の大きさは減少します。

次は、BAアルゴリズムの擬似コードです（図1）。

1.コウモリの個体数を初期化する
2.周波数、速さ、新しいソリューションを創出する
3.局地的な解を模索する
4.大域的な解を更新する
5.音量を小さくし、脈動周波数を大きくする
6.停止基準に達するまで、手順2を繰り返す

スキーム

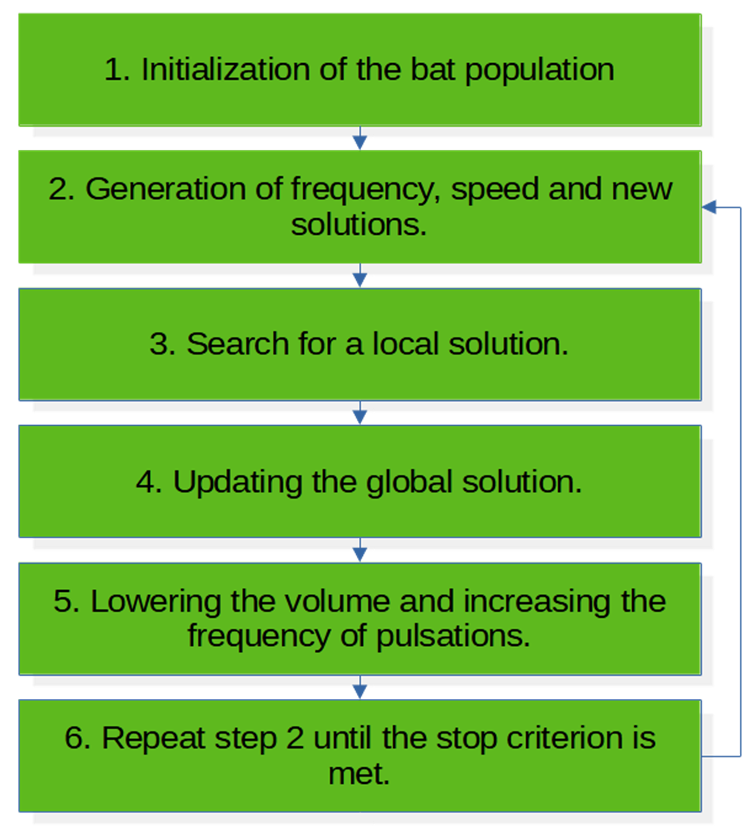
図1：BAアルゴリズムブロック図

それでは、コードの記述に入ります。コウモリ」探索エージェントを記述するためには、各反復の時点での状態を完全に記述するために必要なすべての特性を記述する構造が必要です。position[]配列は、空間における最適な位置座標を格納するために使用され、auxPosition[]配列は、現在の「操作」座標のために使用されます。speed[]配列は，座標による速度ベクトルの計算に必要です。frequency - 超音波パルスの周波数、initPulseRate - 初期パルスレート（最適化の最初から各コウモリごと），pulseRate - 現在の反復におけるパルスレート、loudness - 超音波パルスの音量、fitness - 最後の移動後の適応度関数値、fitnessBest - すべての反復におけるエージェントの適応度関数の最高値です。  

//——————————————————————————————————————————————————————————————————————————————
struct S_Bat
{
  double position    [];
  double auxPosition [];
  double speed       [];
  double frequency;
  double initPulseRate;
  double pulseRate;
  double loudness;
  double fitness;
  double fitnessBest;
};
//——————————————————————————————————————————————————————————————————————————————

コウモリアルゴリズムクラスは、探索エージェント、探索空間の境界とステップ、アルゴリズムが見つけた最適な座標、適応度関数の最適値、アルゴリズムパラメータを格納する定数などの構造体の配列と、public初期化メソッド、アルゴリズムでの操作に必要な2つのpublicメソッド、アルゴリズム固有のprivateメソッドから構成されています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BA
{
  //============================================================================
  public: S_Bat  bats      []; //bats
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,
                     const int    batsNumberP,
                     const double min_FREQ_P,
                     const double max_FREQ_P,
                     const double min_LOUDNESS_P,
                     const double max_LOUDNESS_P,
                     const double min_PULSE_P,
                     const double max_PULSE_P,
                     const double alpha_P,
                     const double gamma_P,
                     const int    maxIterP);

  public: void Flight (int epoch);
  public: void Preparation ();

  //============================================================================
  private: void Walk               (S_Bat &bat);
  private: void AproxBest          (S_Bat &bat, double averageLoudness);
  private: void AcceptNewSolutions (S_Bat &bat);
  private: int  currentIteration;
  private: int  maxIter;

  private: double MIN_FREQ;
  private: double MAX_FREQ;

  private: double MIN_LOUDNESS;
  private: double MAX_LOUDNESS;

  private: double MIN_PULSE;
  private: double MAX_PULSE;

  private: double ALPHA;
  private: double GAMMA;

  private: int    params;
  private: int    batsNumber;

  private: bool   firstFlight;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

パラメータを設定するアルゴリズムのInit() publicメソッドでは、配列のためのメモリを割り当て、最高の適応度を格納するために最小値に変数をリセットし、最初の反復のフラグをリセットします。一般的に、この方法は複雑でも特別でもありません。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Init (const int    paramsP,
                    const int    batsNumberP,
                    const double min_FREQ_P,
                    const double max_FREQ_P,
                    const double min_LOUDNESS_P,
                    const double max_LOUDNESS_P,
                    const double min_PULSE_P,
                    const double max_PULSE_P,
                    const double alpha_P,
                    const double gamma_P,
                    const int    maxIterP)
{
  MathSrand (GetTickCount ());

  fB = -DBL_MAX;

  params       = paramsP;
  batsNumber   = batsNumberP;
  MIN_FREQ     = min_FREQ_P;
  MAX_FREQ     = max_FREQ_P;
  MIN_LOUDNESS = min_LOUDNESS_P;
  MAX_LOUDNESS = max_LOUDNESS_P;
  MIN_PULSE    = min_PULSE_P;
  MAX_PULSE    = max_PULSE_P;
  ALPHA        = alpha_P;
  GAMMA        = gamma_P;
  maxIter      = maxIterP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);

  firstFlight = false;

  ArrayResize (bats, batsNumber);

  for (int i = 0; i < batsNumber; i++)
  {
    ArrayResize (bats [i].position,    params);
    ArrayResize (bats [i].auxPosition, params);
    ArrayResize (bats [i].speed,       params);

    bats [i].fitness  = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

各反復で最初に呼ばれるメソッドはFlight()です。ここには探索ロジックのメインフレームが集中し、残りの詳細はこの最適化アルゴリズムに特化した補助的なprivateメソッドに配置されます。最初の反復では、firstFlightフラグがリセットされます（リセットはInit()メソッドの初期化中に発生）。これは、各コウモリに初期状態（探索空間内のランダムな位置）を割り当てる必要があることを意味します。

  • 0の速さ
  • パラメータで指定された範囲の乱数で割り当てられた超音波パルスの個々の周波数
  • 初期個別脈動周波数をパラメータ範囲内の乱数で定義
  • パラメータ範囲内の超音波パルスの大きさを設定

このように、人工コウモリにはそれぞれ音信号の特徴があり、より自然界に存在する本物のコウモリに近づけることができます。数十万とも言われる個体群の中で、母親はその子が発する独特の音信号によって、たった一匹の子を見つけることができるのです。

firstFlightフラグが有効な場合、コウモリを動かすための基本的な操作をおこなう必要があります。このアルゴリズムの興味深い特徴の一つは、母集団全体の平均的な音の大きさの概念にあります。一般に，すべての反復処理において，音の大きさは「α」係数を介して減少します。ここでは、2種類のコウモリの動きがあります。Walk() - 各座標成分の速度ベクトルを計算し、最適解の近傍を局所的に移動する個別移動。

次の繰り返しごとに、脈動の強さは減少し、近傍探索の強さに影響を与えます。このように、探査と開拓は最適化を通じて動的に変化します。次に、現在の反復がコウモリの挙動にどのような影響を与えるかを見ていきます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Flight (int epoch)
{
  currentIteration = epoch;

  //============================================================================
  if (!firstFlight)
  {
    fB = -DBL_MAX;

    //--------------------------------------------------------------------------
    for (int b = 0; b < batsNumber; b++)
    {
      for (int p = 0; p < params; p++)
      {
        bats [b].position    [p] = RNDfromCI (rangeMin [p], rangeMax [p]);
        bats [b].position    [p] = SeInDiSp (bats [b].position [p], rangeMin [p], rangeMax [p], rangeStep [p]);
        bats [b].auxPosition [p] = bats [b].position    [p];
        bats [b].speed       [p] = 0.0;
        bats [b].frequency       = RNDfromCI (MIN_FREQ, MAX_FREQ);
        bats [b].initPulseRate   = RNDfromCI (MIN_PULSE, MAX_PULSE / 2);
        bats [b].pulseRate       = bats [b].initPulseRate;
        bats [b].loudness        = RNDfromCI (MAX_LOUDNESS / 2, MAX_LOUDNESS);
        bats [b].fitness         = -DBL_MAX;
        bats [b].fitnessBest     = -DBL_MAX;
      }
    }

    firstFlight = true;
  }
  //============================================================================
  else
  {
    double avgLoudness = 0;

    for (int b = 0; b < batsNumber; b++)
    {
      avgLoudness += bats [b].loudness;
    }

    avgLoudness /= batsNumber;

    for (int b = 0; b < batsNumber; b++)
    {
      Walk (bats [b]);

      if (RNDfromCI (MIN_PULSE, MAX_PULSE) > bats [b].pulseRate)
      {
        AproxBest (bats [b], avgLoudness);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

各反復で呼び出される2番目の必須publicメソッド-Preparation()は、大域的な最適解を更新するために必要です。ここでは、「ラウドネス」という概念がどのように使われているかを見ることができます。各反復ごとに各マウスの体積は係数（「α」アルゴリズムチューニングパラメータ）を介して減少するので、ローカル研究の確率は大域的な解の研究の強度と一緒に減少します。つまり、各コウモリの最適位置が更新される確率は、反復するごとに減少していきます。アルゴリズムの中で、少なくとも私にとっては、最も理解できない瞬間のひとつです。しかし、アルゴリズムの作者がこれを実装したのですから、必要なことなのでしょう。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Preparation ()
{
  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (bats [b].fitness > fB)
    {
      fB = bats [b].fitness;
      ArrayCopy (cB, bats [b].auxPosition, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (RNDfromCI (MIN_LOUDNESS, MAX_LOUDNESS) < bats [b].loudness && bats [b].fitness >= bats [b].fitnessBest)
    {
      AcceptNewSolutions (bats [b]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

private Walk()メソッドは、大域的な最適解が与えられたときに、各コウモリがこれまでの現在の最適位置に対して個別に移動することを保証します。MIN_FREQ;MAX_FREQ]の範囲内でランダムに変化する超音波パルスの周波数を利用する方法です。周波数は探索エージェントの移動の速さを計算するのに必要で、周波数とマウスの最適位置と大域的な最適解との差の積となります。その後、コウモリベクトルの現在の最適解に速さの値をベクトル単位で加算していきます。このように、私たちは不釣り合いな物理量を操作しているわけですが、何ができるのでしょうか。これはあくまで現実の物理的な対象への近似値です。この場合、妥当性は無視せざるを得ません。新しい位置を計算した後、SeInDiSp()メソッドで座標が範囲外でないかを確認する必要があります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Walk (S_Bat &bat)
{
  for (int j = 0; j < params; ++j)
  {
    bat.frequency       = MIN_FREQ + (MAX_FREQ - MIN_FREQ) * RNDfromCI (0.0, 1.0);
    bat.speed       [j] = bat.speed [j] + (bat.position [j] - cB [j]) * bat.frequency;
    bat.auxPosition [j] = bat.position [j] + bat.speed [j];

    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

2番目のprivateメソッドAproxBest()は、大域的な最適解に対してコウモリを相対的に移動させ、座標をさらに精緻化する役割を担っています。コウモリの全個体間の平均的な大きさに[-1.0;1.0]の範囲の乱数をかけた形の増分の座標にベクトルごとに加算していくこの動作の物理的意味を理解することは私には不可能です。定義域の有効値のベクトルを介して最適化する関数の次元まで値を小さくしてみましたが、テスト結果は筆者版のアルゴリズムより悪いことが判明したので、すべてそのままにしています。しかし、BAアルゴリズムの効率は改善できるはずですが、それには追加の研究が必要で、今回は目的外でした。座標計算後、SeInDiSp()メソッドで値が範囲外かどうかを確認します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AproxBest (S_Bat &bat, double averageLoudness)
{
  for (int j = 0; j < params; ++j)
  {
    bat.auxPosition [j] = cB [j] + averageLoudness * RNDfromCI (-1.0, 1.0);
    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

もう1つの具体的なprivateメソッドはAcceptNewSolutions()で、これは各コウモリの超音波パルスの周波数のテスト条件が満たされたときに呼び出されるものです。新しい最適な個別解が受け入れられると同時に、ここで個別ラウドネスと個別脈動周波数が再計算されます。ここでは、脈動周波数の算出に反復の序数がどのように関わっているかを見ることができます。

このとき、アルゴリズムのロジックを少し自由に変えて、結果を総反復回数の次元に依存しないようにしたことで、結果的にアルゴリズムの効率が少し上がりました。オリジナル版では、パルス周波数を計算するための非線形式に、繰り返し回数が直接関わっていました。BAにはすでに多くの決まりがあります。この場合、もう1つに目をつぶることができませんでした。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AcceptNewSolutions (S_Bat &bat)
{
  ArrayCopy(bat.position, bat.auxPosition, 0, 0, WHOLE_ARRAY);
  bat.fitnessBest = bat.fitness;
  bat.loudness    = ALPHA * bat.loudness;
  double iter     = Scale (currentIteration, 1, maxIter, 0.0, 10.0, false);
  bat.pulseRate   = bat.initPulseRate *(1.0 - exp(-GAMMA * iter));
}
//——————————————————————————————————————————————————————————————————————————————

脈動周波数の現在の反復回数（グラフ上のx）およびGAMMA設定パラメータへの依存性を図2に示します。

ガンマ

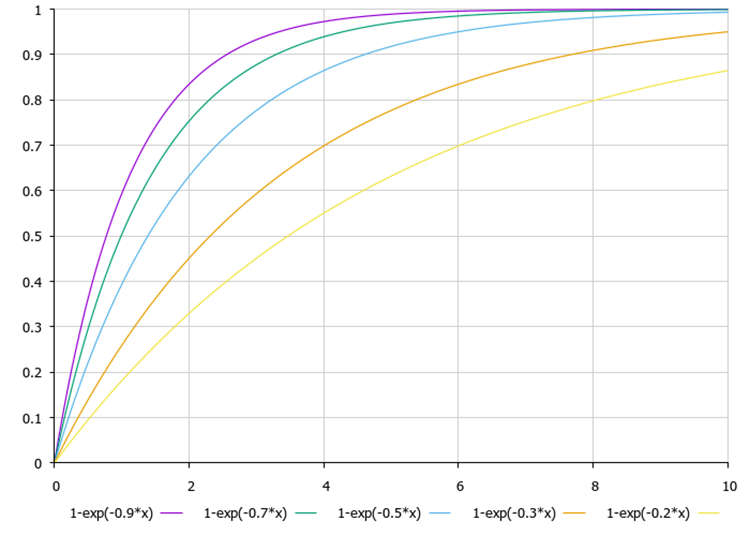
図2：脈動周波数の現在の反復回数とGAMMA設定パラメータへの依存性（値：0.9、0.7、0.5、0.3、0.2）

3.テスト結果

前回、テストしたアルゴリズムの評価算出方法を見直す予定であることを紹介しました。まず、ほとんどのアルゴリズムが2変数のテスト関数に容易に対応でき、結果の差もほとんどないことから、すべてのテスト関数について、最初の2回のテストで変数の数を増やすことにしました。ここで、変数の数は10、50、1000となります。

第二に、Skintest関数を、広く使われているRastrigin関数に置き換えました（図3）。この関数はSkinのように滑らかです。多くの極値を持ち、4点で最大値、座標軸の中心で1つの最小値を持つ複雑な曲面を持っています。

第三に、表中の全アルゴリズムの中で、最も良い結果を1.0、最も悪い結果を0.0として、テスト結果を数値の範囲に正規化することにしました。これにより、テスト中の各最適化アルゴリズムの結果に応じて関数の複雑さを考慮しつつ、テスト結果を均等に評価することができるようになりました。

その後、アルゴリズムのテスト結果を集計しています。最大値には100（基準最大値）が、最小値には1が割り当てられています。これにより、テスト関数の複雑さを考慮することなく、アルゴリズム同士を直接比較することができるようになりました。これで、Print()で出力された結果は、各アルゴリズムのテストスクリプトのソースファイルにそれぞれ保存されます。テストの点数を計算するスクリプトを以下に添付します。今後、検討中の新アルゴリズムの結果を追加して更新していく予定です。



rastrigin

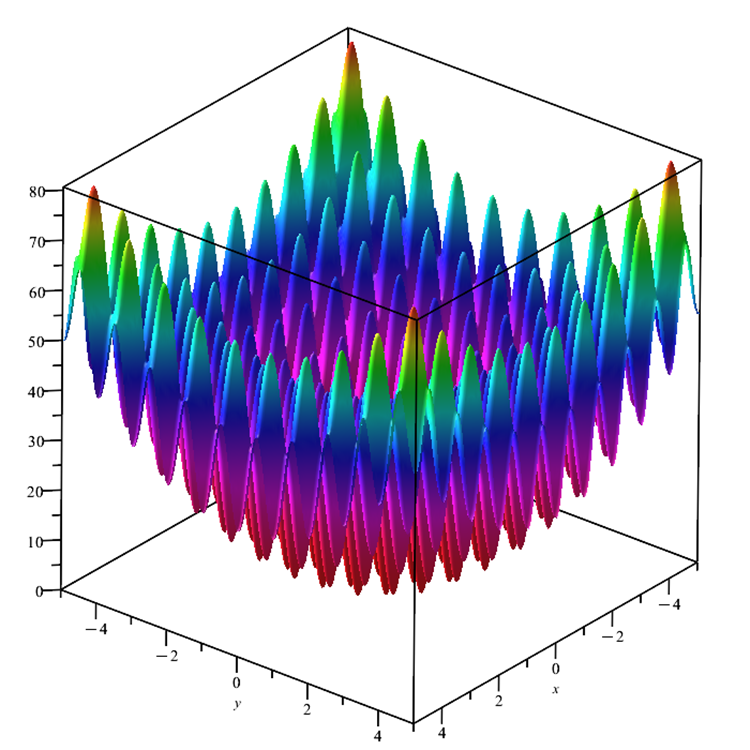
図3：Rastriginテスト関数

テストスタンドの結果は以下のようになります。

2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 66.63334336098077
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    Score: 0.82562
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 65.51391114042588
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    Score: 0.81175
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 59.84512760590815
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    Score: 0.74151
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.5861602092218606
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    Score: 0.33156
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.2895682720055589
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    Score: 0.16379
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.09867854051596259
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    Score: 0.05582
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 3.3199999999999994
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    Score: 0.27667
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 1.2079999999999997
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    Score: 0.10067
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.40759999999999996
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    Score: 0.03397

コウモリアルゴリズムは、滑らかなRastrigin関数に対して印象的な結果を示しました。興味深いことに、関数の変数数が増えるにつれて、結果の安定性（再現性）が増し、滑らかな関数に対するBAの優れたスケーラビリティが示されました。特に、50変数と1000変数のRastrigin関数では、全テスト参加者の中でBAが最も優れていることが判明し、複雑な平滑関数やニューラルネットワークを扱う際にコウモリアルゴリズムを推奨できるようになりました。Forest関数とMegacity関数では、コウモリアルゴリズムは平均的な結果を示し、極値にはまり込む傾向があることがわかりました。座標はグループに局所化されており、変化や大域的な最適値に向かう動きのダイナミクスを示すことはありません。これは、このアルゴリズムが、研究対象の関数の表面に勾配があることに敏感だからだと思います。勾配がない場合、アルゴリズムは適応度関数値が大きく増加しない局所領域の近傍ですぐに停止します。さらに、BAアルゴリズムには、COAで実装されているような新しい未知の領域への「ジャンプ」を可能にするメカニズムがありません（レヴィフライト）。

また、BAの設定項目が多いことも特筆すべき点です。パラメータ（自由度）が多いだけでなく、それぞれのパラメータが探索特性の性質と全体の収束率の両方に大きく影響します。パラメータによっては、滑らかな関数で優れた結果を得られるものと、離散的な関数や亀裂のある関数で優れた結果を得られるものがあります。異なる種類のテスト機能に等しく対応できるような普遍的なパラメータを見つけることは困難です。この記事には、私にとって最も最適と思われるパラメータを用いたコウモリアルゴリズムのソースコードが掲載されています。一般的に、最適化の結果が大きく変わる可能性があるため、最適化アルゴリズムを扱った経験の少ないユーザーには、BAの利用をお勧めしません。 

rastrigin

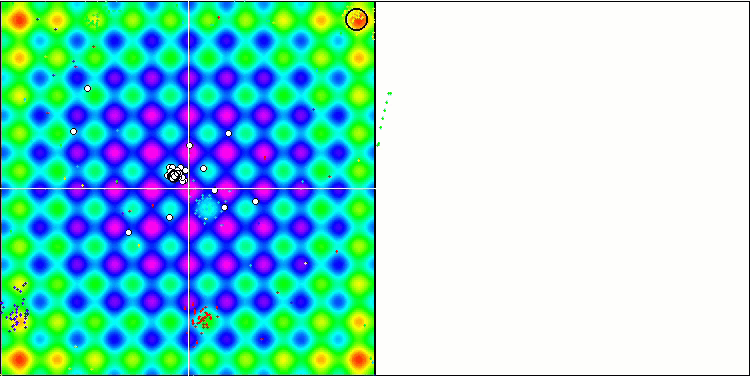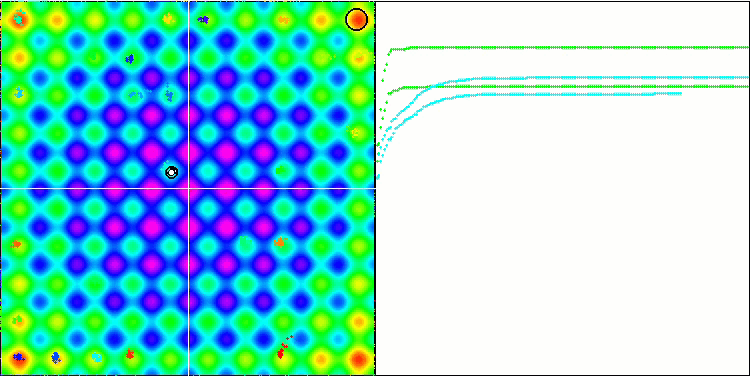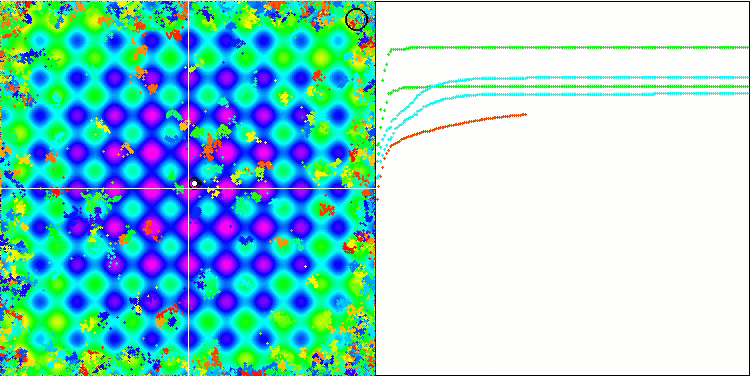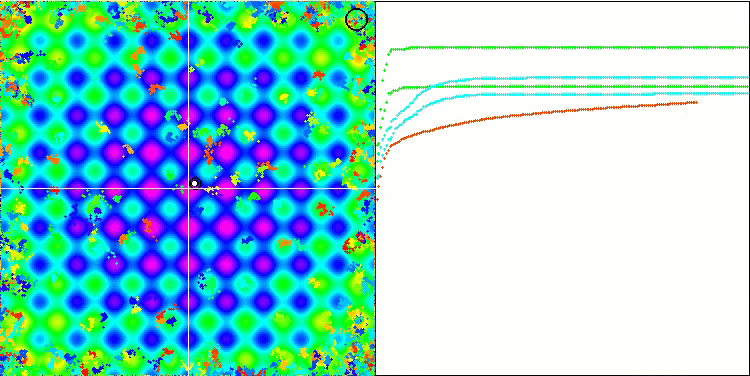
  Rastriginテスト関数のBA

Forest

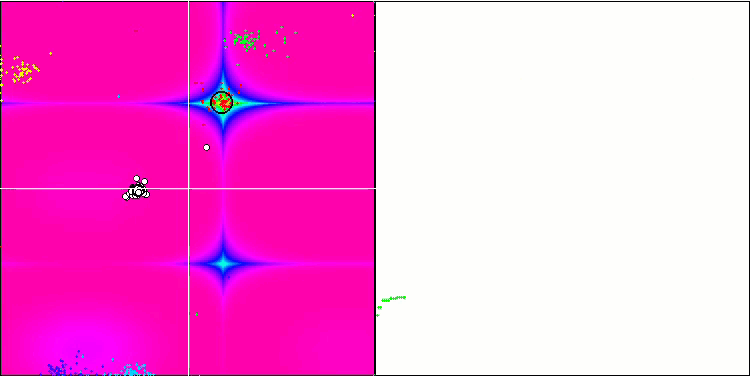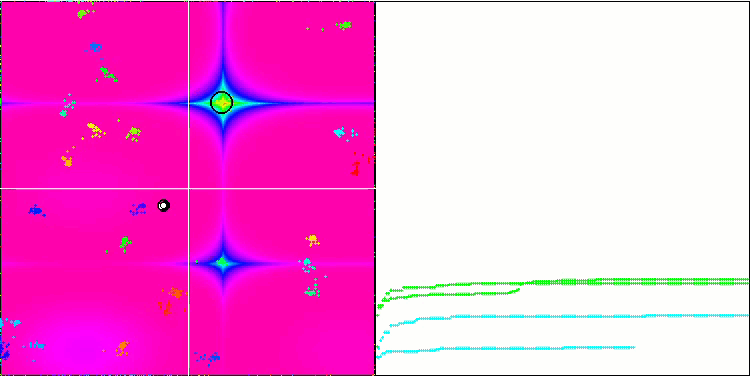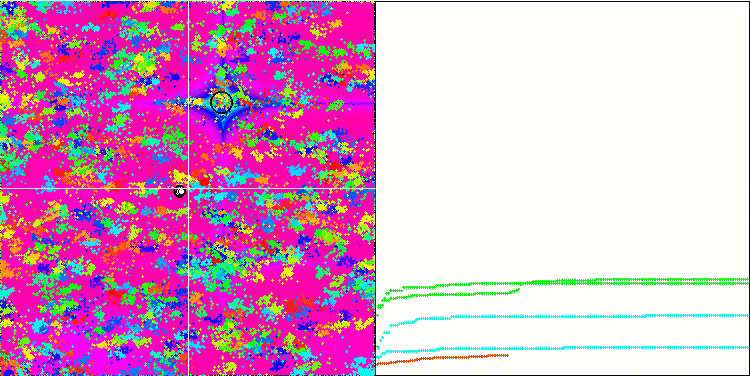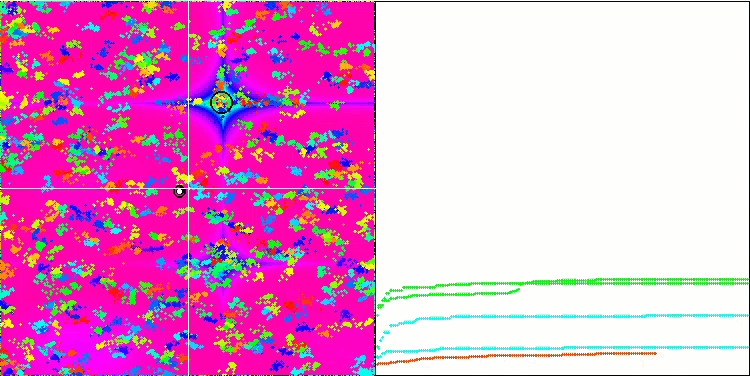
Forestテスト関数のBA

Megacity

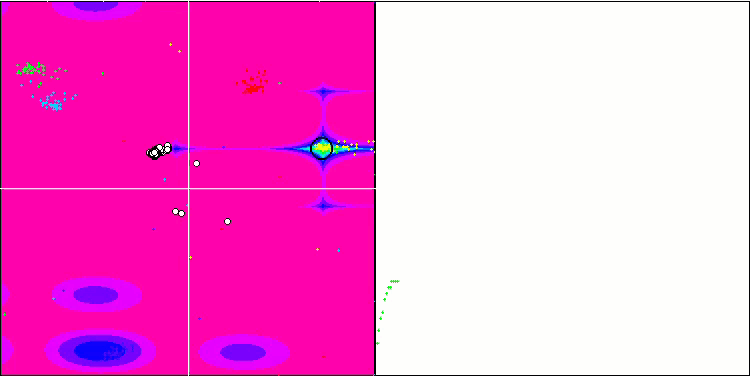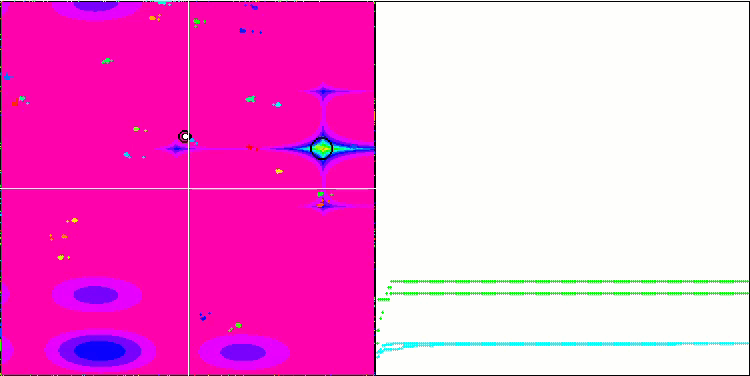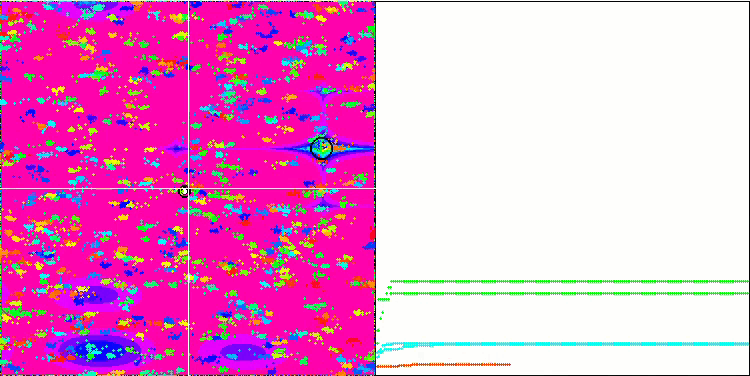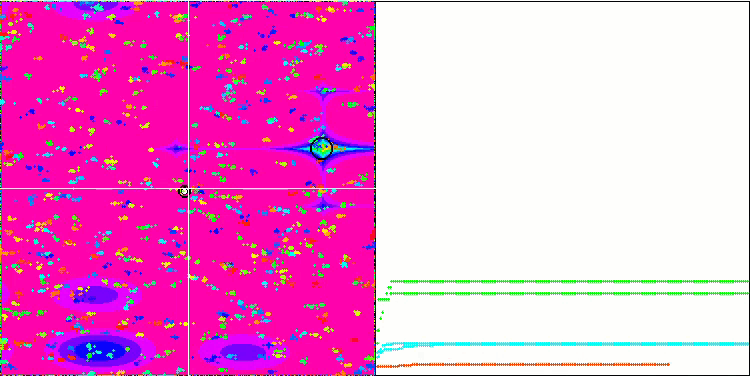
Megacityテスト関数のBA

テスト関数の可視化に着目すると、コウモリアルゴリズムの特徴的な機能を把握することができます。特に、すべてのテスト関数で作業する場合、アルゴリズムは非常に小さな局所領域で座標をグループ化することを特徴とします。滑らかな関数では、この機能により適応度関数の勾配がわずかに変化しても移動することができるが、離散関数ではこの機能は平坦なプラトーで止まってしまうという欠点があることがわかる。

最適化アルゴリズムのスコアを計算するスクリプトで得られた結果。

2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_RND=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18210 | 0.15281 | 0.07011 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08623 | 0.04810 | 0.06094 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.08904 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.6893397068905002
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_PSO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.22131 | 0.12861 | 0.05966 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15345 | 0.10486 | 0.28099 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08028 | 0.02385 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.053004072893302
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ACOm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.37458 | 0.28208 | 0.17991 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 0.10959 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ABC=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.84599 | 0.51308 | 0.22588 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.58850 | 0.21455 | 0.17249 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.47444 | 0.26681 | 0.35941 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.661160435265267
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_GWO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18977 | 0.04119 | 0.01802 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_COAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 0.73390 | 0.28892 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64504 | 0.34034 | 0.21362 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.67153 | 0.34273 | 0.45422 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.690306586791184
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FSS=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.50663 | 0.39737 | 0.11006 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.07806 | 0.05013 | 0.08423 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.01084 | 0.18998 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.4272897567648186
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64746 | 0.53292 | 0.18102 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.55408 | 0.42299 | 0.64360 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.21167 | 0.28416 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.477897116029613
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_BA=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.43859 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.17768 | 0.17477 | 0.33595 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15329 | 0.07158 | 0.46287 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.8147314003892507
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956 | 5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_RND: 8.652
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_PSO: 14.971
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ACOm: 100.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ABC: 60.294
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_GWO: 1.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_COAm: 78.177
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FSS: 21.475
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FAm: 74.486
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_BA: 62.962

それでは、最終的な評価表を見てみましょう。以上のように、アルゴリズムの推定特性の算出方法が変わったことで、アルゴリズムが新たな地位を獲得しました。いくつかの古典的なアルゴリズムは表から削除され、テストにおいてより高い性能を示したそれらの修正版のみが残されています。今までのような絶対的なテスト結果（テスト関数値の絶対正規化結果）ではなく、アルゴリズム同士を比較した結果に基づく相対的なテスト結果になりました。

この表から、ACOm（蟻コロニー最適化）が現時点でのリーダーであることがわかります。このアルゴリズムは、9回のテストのうち5回で最良の結果を示したので、最終結果は100点です。カッコー最適化アルゴリズムの改良版であるCOAmは2位です。このアルゴリズムは、滑らかなRastrigin関数で最良であることが判明し、また他のテストでも他のテスト参加者と比較して良い結果を示しました。修正ホタルアルゴリズムFAmが3位を獲得しています。Megacityの離散関数で最も良い結果を示しました。このテストでは、FSSだけが同じ結果を示しました。

AO

詳細

Rastrigin

Rastrigin最終

Forest

Forest最終

Megacity (discrete)

Megacity最終

最終結果

10パラメータ(5F)

50パラメータ(25F)

1000パラメータ（500F）

10パラメータ(5F)

50パラメータ(25F)

1000パラメータ（500F）

10パラメータ(5F)

50パラメータ(25F)

1000パラメータ（500F）

ACOm

蟻コロニー最適化M

0.37458

0.28208

0.17991

0.83657

1.00000

1.00000

1.00000

3.00000

1.00000

1.00000

0.10959

2.10959

100.000

COAm

カッコウ最適化アルゴリズムM

1.00000

0.73390

0.28892

2.02282

0.64504

0.34034

0.21362

1.19900

0.67153

0.34273

0.45422

1.46848

78.177

FAm

ホタルアルゴリズムM

0.64746

0.53292

0.18102

1.36140

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

74.486

BA

コウモリアルゴリズム

0.43859

1.00000

1.00000

2.43859

0.17768

0.17477

0.33595

0.68840

0.15329

0.07158

0.46287

0.68774

62.962

ABC

人工蜂コロニー

0.84599

0.51308

0.22588

1.58495

0.58850

0.21455

0.17249

0.97554

0.47444

0.26681

0.35941

1.10066

60.294

FSS

魚群検索

0.64746

0.53292

0.18102

1.36140

0.55408

0.42299

0.64360

1.62067

0.21167

0.28416

1.00000

1.49583

21.475

PSO

粒子群最適化

0.22131

0.12861

0.05966

0.40958

0.15345

0.10486

0.28099

0.53930

0.08028

0.02385

0.00000

0.10413

14.971

RND

ランダム

0.18210

0.15281

0.07011

0.40502

0.08623

0.04810

0.06094

0.19527

0.00000

0.00000

0.08904

0.08904

8.652

GWO

灰色オオカミオプティマイザ

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.00000

0.18977

0.04119

0.01802

0.24898

1.000


図4のアルゴリズムテスト結果のヒストグラム

レーティング

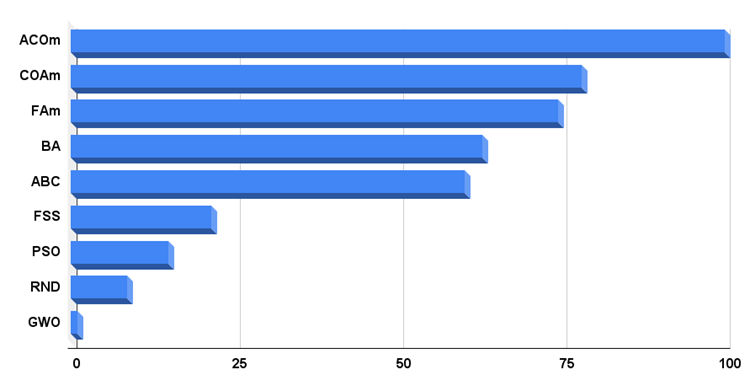
図4：テストアルゴリズムの最終結果のヒストグラム

次は、コウモリアルゴリズム(BA)の特性に関する結論です。

賛成：
1.高速
2.滑らかな関数でうまく機能する
3.スケーラビリティ

反対：
1.設定が多すぎる
2.離散関数に関する中途半端な結果


MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11915

添付されたファイル |
ZIPをダウンロード
9_The_world_of_AO_gBAs.zip (68.81 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
母集団最適化アルゴリズム：侵入雑草最適化(IWO) 母集団最適化アルゴリズム：侵入雑草最適化(IWO)
雑草がさまざまな条件で生き残る驚くべき能力は、強力な最適化アルゴリズムのアイデアになっています。IWO(Invasive Weed Optimization)は、以前にレビューされたものの中で最高のアルゴリズムの1つです。
自動で動くEAを作る（第03回）：新しい関数 自動で動くEAを作る（第03回）：新しい関数
今日は、自動モードでシンプルかつ安全に動作するエキスパートアドバイザー(EA)を作成する方法を紹介します。前回は、自動売買EAで使用するオーダーシステムの開発に着手しましたが、必要な関数のうち1つしか作っていません。
自動で動くEAを作る（第04回）：手動トリガー(I) 自動で動くEAを作る（第04回）：手動トリガー(I)
今日は、自動モードでシンプルかつ安全に動作するエキスパートアドバイザー(EA)を作成する方法を紹介します。
自動で動くEAを作る（第02回）：コードを始める 自動で動くEAを作る（第02回）：コードを始める
今日は、自動モードでシンプルかつ安全に動作するエキスパートアドバイザー(EA)を作成する方法を紹介します。前回は、自動売買をおこなうEAの作成に進む前に、誰もが理解しておくべき最初のステップについて説明しました。概念と構造が検討されました。