母集団最適化アルゴリズム：微小人工免疫系(Micro-AIS)

MetaTrader 5 — 例 | 13 5月 2024, 17:40

249

Andrey Dik

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

免疫系は、私たちの体を外部の脅威から守る重要な役割を果たす驚くべきメカニズムです。免疫系は、目に見えない盾のように、細菌、ウイルス、真菌と戦い、私たちの体を健康に保ちます。しかし、この強力なメカニズムを使って、複雑な最適化や学習の問題を解くことができるとしたらどうでしょうか。これはまさに、人工免疫系(AIS)最適化手法で使用されているアプローチです。

身体の免疫系は、細胞、組織、臓器からなる複雑なシステムであり、感染症、病気、その他の外的影響から身体を守っています。身体の免疫系は、細菌、ウイルス、真菌などの異物や微生物を認識し、破壊することで機能します。

AISアルゴリズムは、抗原（入力）、抗体（解）、キラー細胞（最適化プロセス）の概念を用いてこれらのプロセスをモデル化し、問題を最適に解決します。抗原は最適化されるべき入力を表します。抗体はこの問題に対する潜在的な解です。キラー細胞は、最適化問題に対する最適解を探索する最適化プロセスです。

人工免疫系(AIS)最適化法は1990年代に提案されました。この手法に関する初期の研究は1980年代半ばまでさかのぼり、Farmer、Packard、Perelson (1986)、Bersini and Varela (1990)が大きく貢献しています。

それ以来、AIS法は発展を続け、科学界で継続的な研究の対象となっています。この方法は、様々な最適化問題や学習問題への応用と同様に、多くのバリエーションや修正が提案されています。身体の免疫系は、感染症や腫瘍などの外的影響から身を守るためにも重要な役割を果たしています。敵対的なエージェントを識別し、将来の使用のために情報を保存する能力を維持しながら、異常を認識し、検出し、攻撃する能力を持ちます。

Micro-AIS (Micro-Immune Algorithm)は、最適化問題を解くために開発された免疫系(AIS)アルゴリズムを改良したものです。従来のAISとの違いは、より単純な免疫系のモデルと、より単純な免疫情報処理操作を用いる点です。

Micro-AISの基本的な考え方は、免疫細胞を模倣したエージェントの集団の創造と進化です。エージェントは解探索空間内を、相互に作用することなく、また解に関する情報を交換することなく移動します。同時に、エージェントは学習し、変化するタスク状況に適応することができます。

従来のAISでは、B細胞、T細胞、抗体、サイトカインなど、多くの種類の細胞や分子を含む複雑な免疫系モデルを用いています。Micro-AISは、抗体のみを含む、より単純なモデルを使用しています。さらにMicro-AISは、突然変異や選択といった、より単純な免疫情報処理操作を用います。

AISと比較した場合のMicro-AISの利点の1つは、そのシンプルさと実装の容易さです。しかし、場合によっては、複雑な問題を解決するためには、より複雑な免疫系のモデルの方が効果的かもしれません。

全体として、Micro-AISと従来のAISのどちらを選択するかは、特定の使い道の状況に依存します。最適化問題が比較的単純で、迅速に解が必要な場合は、Micro-AISが良い選択かもしれません。問題がより複雑で、より正確な解が必要な場合は、従来のAISの方が適しているかもしれません。

2.アルゴリズム

Micro-AISでは、抗体と抗原の類似性を示す「親和性」の概念を用いて適合性を判定します。親和性とは、抗体と抗原の類似性の度合いを示します。親和性が高ければ高いほど、抗体と抗原は類似していることになります。Micro-AISでは、親和性を利用して最適な抗体を選択し、突然変異と交叉によって新しい抗体を作り出します。親和性の高い抗体は、新しい抗体を作るために選択されやすくなります。

親和性は、オブジェクトの特徴ベクトルと分類器の重みベクトルの間の距離として定義することができます。距離が小さいほどベクトルは似ており、親和性は高いです。一般に、親和性は2つの浮動小数点数間の距離の関数として定義できます。距離関数は、特定の使い道とMicro-AISアルゴリズムの要件に応じて選択することができます。例えば最適化問題では、距離は通常、ユークリッド距離、マンハッタン距離、あるいは他のタイプの距離として定義されます。

ただし、Micro-AISを使用した実験によると、この探索戦略では親和性を使用するのは最も効率的なアプローチではなく、代わりに適合度関数の値を直接使用することができます。

元のMicro-AISでは、突然変異を遺伝子に確率的に適用しています。適合度が高ければ高いほど、突然変異の確率は低くなります。このアプローチも非効率のために断念せざるを得ませんでしたが、それを検証するのは簡単です。それには、コードを何行か追加するだけです。

以下は、Micro-AISの疑似コードです。

抗体クローンの母集団を作り、探索空間全体に無作為に分布させます。抗体とそのクローンは、最適化問題の潜在的な解です。クローンは、最適化問題のパラメータ値を決定する遺伝子型を無作為に生成することによって作成されます。
解の質を測る尺度である適合度を定義します。適合度値は、各抗体の目的関数を推定することで計算できます。
各抗体について、減少数列のルールに対応する量のクローンを作成します。（適合度の点から）最初の抗体は2番目の抗体より多くのクローンを作成し、2番目の抗体は3番目の抗体より多くのクローンを作成する、などです。このように、クローンの数は適合度の度合いではなく、厳密に定義された数列ルールに対応しています。適応度の高い抗体は、適応度の低い抗体よりも多くのクローンを作りますが、その比率は常に同じです。
クローン遺伝子に変異を適用します。クローンごとに遺伝子型の突然変異が起こり、新しい解を作り出し、最適化問題のパラメータ空間を探索することができます。
クローンの適合度を決定します。
突然変異と適合度計算の後、クローン母集団は親抗体母集団に加えられます。
母集団（抗体＋クローン）を適合度の降順に並べ替え、次の反復でクローンの新しい母集団を作成するための最適解を選択します。これにより、子孫クローンと親抗体との間の競合を実装します。
停止基準を満たすまで、ステップ2から繰り返します。停止基準は、ある適合度値に達するとか、最大反復回数に達するとか、あらかじめ定義しておくことができます。

クローンにおける遺伝子の突然変異とは、式に従って一様分布の乱数を発生させることです。

X' = X + dist * rnd * k * mutation

ここで

X' ：クローン遺伝子の新しい値（座標）
X：親抗体遺伝子の値
dist ：親遺伝子への増分
rnd ：[-1.0;1.0] の範囲で一様分布する乱数
k：現在のエポックに応じて一様に減少する比率
mutation：変異率、実際は拡大係数（外部パラメータ）

「k」比率は以下のように計算されます。

k = (epochs - epochsCNT) / epochs

ここで

epochs：エポック数の制限値
epochsCNT：エポック（繰り返し）カウンタ

dist増分サイズは、rndが0より大きければ、最適化されたパラメータの最大値からXまでの距離であり、そうでなければ、Xから最適化されたパラメータの最小値までの距離です。

このように、突然変異によって解パラメータの値を無作為に変化させることができるため、問題空間の探索を確実におこなうことができます。係数kを減少させることで、後の反復でパラメータが急激に変化する可能性を減らし、最適解へのアルゴリズムの収束を向上させ、発見された座標を洗練させることができます。

抗体として機能する構造体S_Agentを書いてみましょう。この構造体には2つのフィールドしかありません。

c：エージェント座標の配列
f：適合度インデックス

Initメソッドは、構造体のフィールドを初期化し、c配列のサイズを変更し、fフィールドに初期値「-DBL_MAX」を割り当てます。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

微小免疫系アルゴリズムクラスC_AO_Micro_AISを宣言し、様々なフィールドとメソッドを定義します。

クラスのフィールド

cB: 最適座標の配列
fB：最良の座標に対する適合度指数
a：S_Agent型のエージェントの配列
rangeMax：検索範囲の最大値の配列
rangeMin：検索範囲の最小値の配列
rangeStep：検索ステップの配列

cords、popSize、minClonesNumber、cloneStep、mutation、epochsは、アルゴリズムの外部パラメータを受け取ります。

クラスのメソッド

Init：与えられた値でクラスのフィールドを初期化する
Moving：エージェントを移動する
Revision：リビジョンを実行する

このクラスはまた、それぞれ正規化、乱数生成、並び替えのための SeInDiSp、RNDfromCI、Sorting privateメソッドを定義しています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_Micro_AIS
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,          //coordinates number
                     const int    popSizeP,         //population size
                     const int    minClonesNumberP, //minimum number of clones
                     const int    cloneStepP,       //clone step
                     const double mutationP,        //mutation
                     const int    epochP);          //total epochs

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;          //coordinates number
  private: int    popSize;         //population size
  private: int    minClonesNumber; //minimum number of clones
  private: int    cloneStep;       //clone step
  private: double mutation;        //mutation
  private: int    epochs;          //total epochs
  private: int    epochsCNT;       //epoch counter
  private: int    parentsNumb;     //number of parents
  private: bool   revision;

  private: S_Agent parents [];  //parents
  private: int     ind     [];
  private: double  val     [];
  private: S_Agent pTemp   [];

  private: int     cCnt    [];  //clone counters for each antibody

  private: double SeInDiSp           (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI          (double min, double max);
  private: void   Sorting            (S_Agent &p [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

クラスオブジェクトを初期化するには、Initメソッドを実装して、指定された値でクラスのフィールドを初期化します。

メソッドの冒頭で、乱数生成器はMathSrand関数を使って初期化され、その状態はGetMicrosecondCount関数を使ってリセットされます。

そして、fB変数とrevision変数にそれぞれ「-DBL_MAX」とfalseが代入されます。また、メソッドの入力でprivateフィールドを初期化します。

次に、cCnt配列の値が計算され、ループを使用して各抗体のクローン数を格納するために使用されます。数列方程式を適用し、数列の最初の項をa1、数列の差をd、数列のすべての項の和をSnとします。数列値はcCnt配列に格納されます。

このメソッドは、その後、parentsNumb変数の値をcCnt配列のサイズとして決定します。

次に、ind、val、pTemp、a、parents、rangeMax、rangeMin、rangeStep、cB各配列のサイズを変更します。配列のサイズはpopSizeとparentsNumbの値に従って設定されます。

次にループの中で、配列aの要素がS_AgentクラスのInitメソッドを使って初期化され、配列parentsの要素もInitメソッドを使って初期化されます。

メソッドの最後に、rangeMax、rangeMin、rangeStep、cB各配列のサイズは、coords値に応じて変更されます。

したがって、InitメソッドはC_AO_Micro_AISクラスのフィールドを初期化し、配列 cCntの数列値を計算します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Micro_AIS::Init (const int    coordsP,          //coordinates number
                           const int    popSizeP,         //population size
                           const int    minClonesNumberP, //minimum number of clones
                           const int    cloneStepP,       //clone step
                           const double mutationP,        //mutation
                           const int    epochP)           //total epochs
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords          = coordsP;
  popSize         = popSizeP;
  minClonesNumber = minClonesNumberP;
  cloneStep       = cloneStepP;
  mutation        = mutationP;
  epochs          = epochP;
  epochsCNT       = 1;

  //----------------------------------------------------------------------------
  int Sn = popSize;         //sum
  int a1 = minClonesNumber; //first member of progression
  int d  = cloneStep;       //progression difference

  int an   = 0;             //n th member of progression,
  int Ssum = 0;

  ArrayResize (cCnt, 1);

  for (int n = 1;; n++)
  {
    an = a1 + (n - 1) * d;
    Ssum = n * (a1 + an) / 2;

    if (Ssum == Sn)
    {
      ArrayResize (cCnt, n);
      cCnt [n - 1] = an;
      break;
    }
    else
    {
      if (Ssum < Sn)
      {
        ArrayResize (cCnt, n);
        cCnt [n - 1] = an;
      }
      else
      {
        if (n == 1)
        {
          ArrayResize (cCnt, n);
          cCnt [n - 1] = Sn;
          break;
        }
        else
        {
          n--;
          an = a1 + (n - 1) * d;
          int diff = Sn - ((n) * (a1 + an) / 2);

          int index = ArraySize (cCnt) - 1;

          while (true)
          {
            if (index < 0) index = ArraySize (cCnt) - 1;

            cCnt [index]++;

            index--;
            diff--;

            if (diff <= 0) break;
          }

          break;
        }
      }
    }
  }
  
  
  parentsNumb   = ArraySize (cCnt);
  ArrayReverse (cCnt, 0, WHOLE_ARRAY);

  ArrayResize (ind,   popSize + parentsNumb);
  ArrayResize (val,   popSize + parentsNumb);
  ArrayResize (pTemp, popSize + parentsNumb);
  ArrayResize (a,     popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (parents, popSize + parentsNumb);
  for (int i = 0; i < popSize + parentsNumb; i++) parents [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Movingクラスメソッドを使って、探索空間内での抗体の動きを実装します。

メソッドの最初で、変数revisionの値が確認されます。falseであれば、抗体クローンは一様分布の座標を生成して探索空間に配置されます。

母集団に抗体クローンを生成した後、revision変数をtrueに設定し、メソッドを終了します。

変数revisionの値がfalseでなければ、次のコードブロックが実行されます。

続いて、parentsNumb親エージェントの数反復するforループがネストされます。このループの中で、以下のことが起こります。

ネストされたforループが、与えられたcCnt[i]親抗体に対するクローン数反復します。
このループの中で、ネストされたforループがすべてのエージェントc座標を繰り返し処理します。
a[indx].c[c]座標の値がparents[i].c[c]座標の値と等しく設定されます。

そして、次のコードのブロックが実行されます。

k変数の値は、epochsとepochsCNTの差をepochsで割ったものとして計算されます。
rnd乱数は[-1.0;1.0]の範囲で生成されます。
rndが0.0より大きい場合、dist変数の値は rangeMax[c]とa[indx].c[c]の差として計算されます。そうでなければ、distは a[indx].c[c]と rangeMin[c]の差に等しくなります。
a[indx].c[c]は「a[indx].c[c] + dist * rnd * k * mutation」という式を使って再計算されます。ここでmutationは突然変異率です。
a[indx].c[c]はSeInDiSp関数を通過し、rangeMin[c]からrangeMax[c]までの範囲でrangeStep[c]ステップで正規化されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Micro_AIS::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    indx = 0;
  double min  =  DBL_MAX;
  double max  = -DBL_MAX;
  double dist = 0.0;
  int    cnt  = 0;
  double rnd  = 0.0;
  
  for (int i = 0; i < parentsNumb; i++)
  {
    for (int cl = 0; cl < cCnt [i]; cl++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [indx].c [c] = parents [i].c [c];
        
        //----------------------------------------------------------------------
        double k = ((double)epochs - (double)epochsCNT) / (double)epochs;
        rnd = RNDfromCI (-1.0, 1.0);

        if (rnd > 0.0) dist = (rangeMax [c] - a [indx].c [c]);
        else           dist = (a [indx].c [c] - rangeMin [c]);

        a [indx].c [c] = a [indx].c [c] + dist * rnd * k * mutation;
        a [indx].c [c] = SeInDiSp  (a [indx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }

      indx++;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

最後に、Revisionメソッドを実装してみましょう。この方法は、Micro-AISアルゴリズムにおけるエージェントの母集団の現在の状態の監査を実行します。

コメントで区切られた最初のコードのブロックは、クローンの母集団の適合度値を確認することで、最適な大域解を更新します。

次にループで、クローンを配列の最後尾の親抗原母集団にコピーします。

この後、parentsと「parentsNumb + popSize」を引数として、並び替え関数が呼び出されます。この関数は、parents配列を適合度スコアの降順で並び替えます。

メソッドの最後に、epochsCNT変数が増分され、アルゴリズムのエポック数をカウントします。

したがって、Revisionメソッドは、抗体（エージェント）母集団の現在の状態を修正し、最良の適合度指標値を持つエージェントを見つけ、親エージェントの配列を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Micro_AIS::Revision ()
{
  //----------------------------------------------------------------------------
  int indx = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) indx = i;
  }

  if (indx != -1)
  {
    fB = a [indx].f;
    ArrayCopy (cB, a [indx].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = parentsNumb; i < parentsNumb + popSize; i++)
  {
    parents [i] = a [i - parentsNumb];
  }

  Sorting (parents, parentsNumb + popSize);
  
  epochsCNT++;
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

テストベンチ上のMicro-AISアルゴリズムの出力

C_AO_Micro_AIS:50:1:2:0.3
=============================
5 Hilly's; Func runs:10000; result:0.7954680903046107
25 Hilly's; Func runs:10000; result:0.5192246492565626
500 Hilly's; Func runs:10000; result:0.30860655744850657
=============================
5 Forest's; Func runs:10000; result:0.7295587642801589
25 Forest's; Func runs:10000; result:0.36878621216829993
500 Forest's; Func runs:10000; result:0.09398090798741626
=============================
5 Megacity's; Func runs:10000; result:0.37666666666666665
25 Megacity's; Func runs:10000; result:0.15866666666666668
500 Megacity's; Func runs:10000; result:0.028016666666666672
=============================
All score:3.37898 (37.54%)

前回の記事から、テスト結果の絶対値に移行したので、異なるアルゴリズムの結果を表にしてナビゲートし、比較することが非常に簡単になりました。37.54％は傑出した結果とは言えませんが、それでも上位半分の位置に入ります。

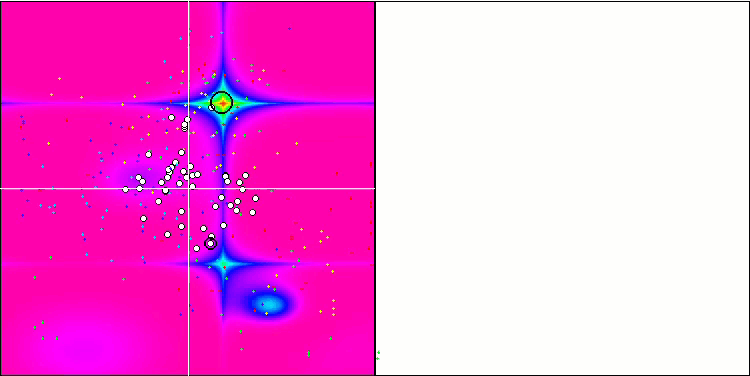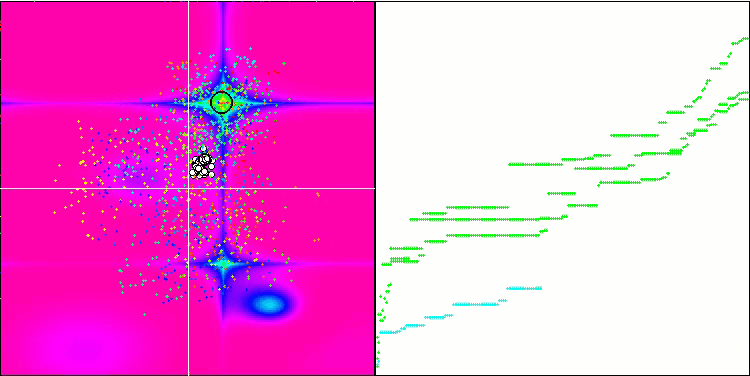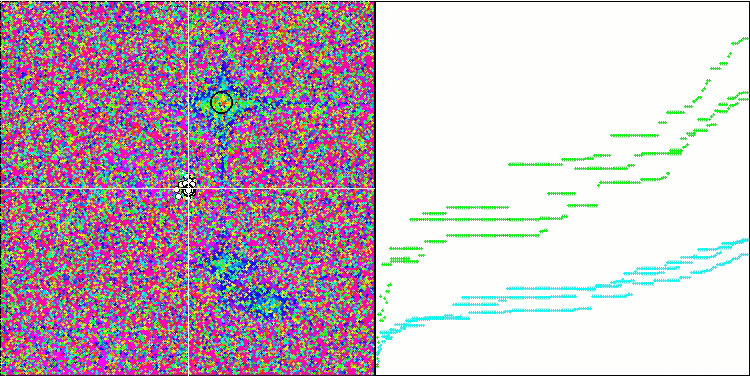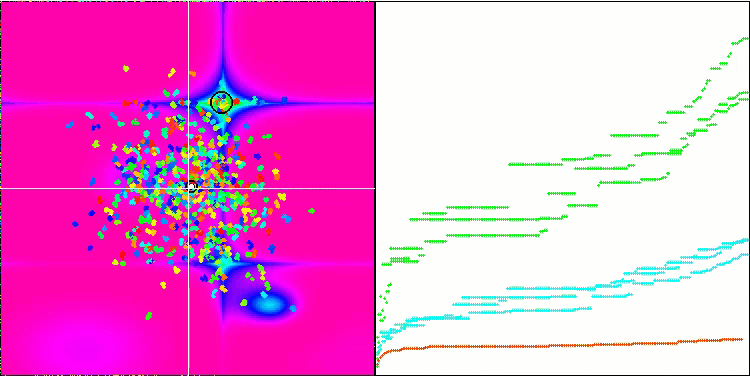
最適化プロセスの視覚化により、アルゴリズムはより良い解を得るために重要な局所的極値を粘り強く探索することが示されました。その結果、エージェントが空間の異なる領域に集中することになります。収束グラフは異常な挙動を示しました。一般的に、検討したアルゴリズムでは、反復の前半で収束率が急激に上昇し、その後収束率は徐々に低下します。しかし、このアルゴリズムでは収束グラフがS字型になります。収束の急激な増加は、反復の最初の10-20％でのみ観察され、その後、収束の速度は低下しますが、最適化の終わりに近づくにつれて、収束の大幅な加速が再び見られます。

この収束グラフの挙動は、線形法則に従って突然変異の間に増分の範囲を狭める戦略によって説明することができます。しかし、テスト関数の表面に関するアルゴリズムによる不均一な情報の「蓄積」のため、収束は線形法則には従いません。変異の範囲を狭めることは、最適化の終わりに近づいて初めて、より顕著な役割を果たすようになります。突然変異の範囲を狭める線形法則を非線形法則の他の変形に置き換えても収束の改善には至りませんでした。範囲を狭める法則の他の変形を選択することに研究者の建設的な想像力の余地があるのかもしれません。

収束グラフには大いに不満が残りますが、このグラフの出現は、検索戦略のさらなる改善の可能性を期待させます。

Hilly

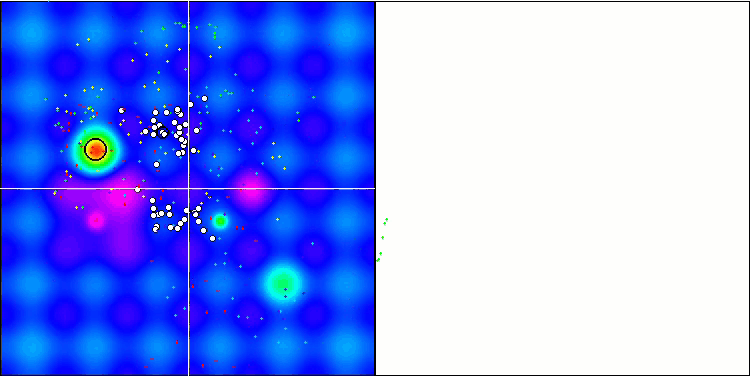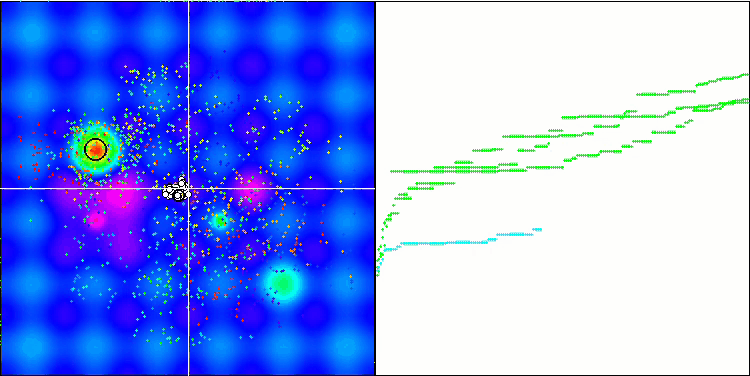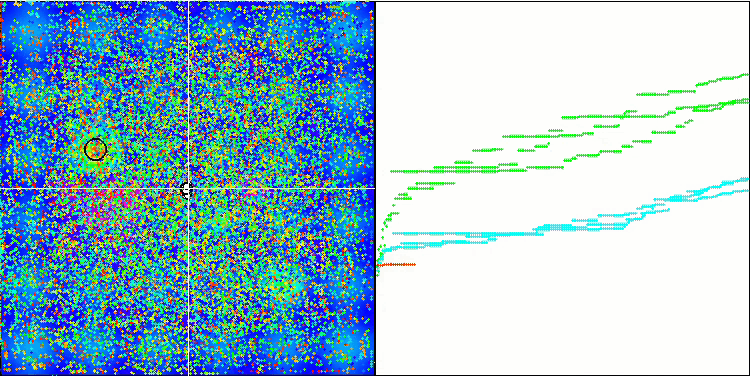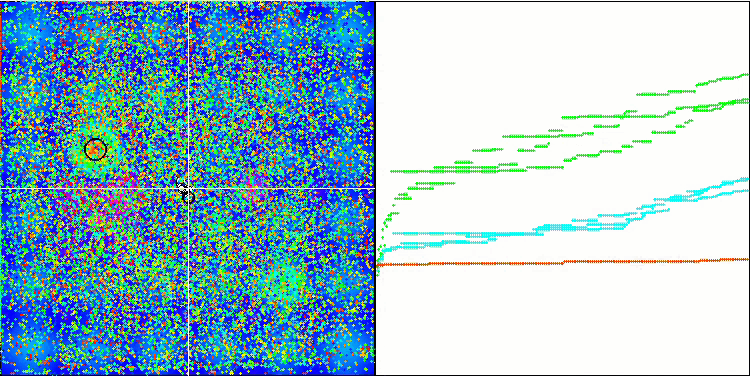
Hillyテスト関数でのMicro-AIS

Forest

Forestテスト関数でのMicro-AIS

Megacity

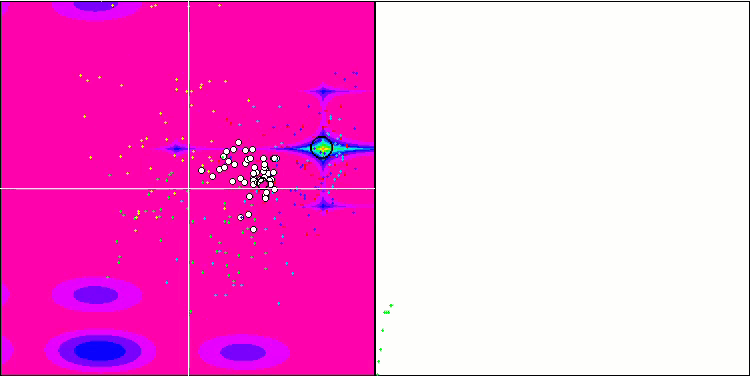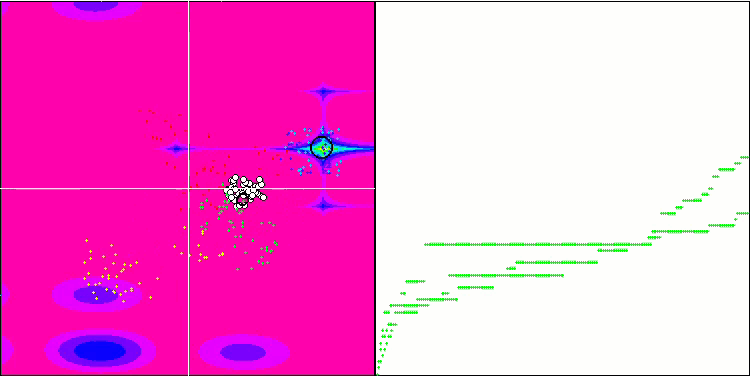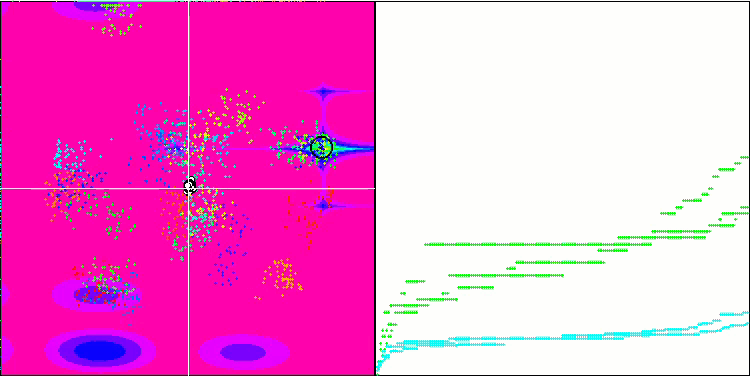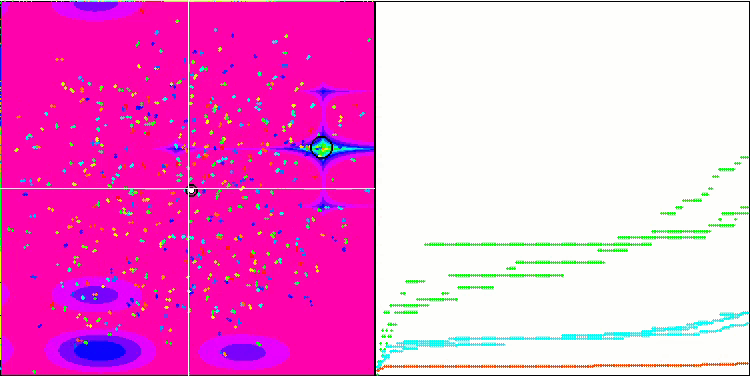
Megacityテスト関数でのMicro-AIS

Micro-AISアルゴリズムは、カッコー最適化アルゴリズム、人工蜂コロニー、焼きなましといった有名で人気のあるアルゴリズムを抑えて、評価表の11行目に正当な位置を占めました。これは、複雑な最適化問題を解く上で、このアルゴリズムが効率的であることを示しています。

しかし、カラーテーブルによると、変数の数が多い関数では性能が低下していることがわかります。これは、アルゴリズムがスケールする能力が弱いことを示しています。これは、Micro-AISが、より単純な免疫系のモデルと、より単純な免疫情報処理操作を使用しているため、高次元空間での最適解を見つける能力が制限されているために起こる可能性があります。

しかし、これはMicro-AISが変数の数が多い問題を解くのに使えないということではありません。おそらく、アルゴリズムを修正したり、他の最適化手法と組み合わせたりすることで、その性能を向上させることができるでしょう。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最終	最終結果	MAXの%
1	(P+O)ES	(P+O）進化戦略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
2	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
3	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
4	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
5	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
6	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
7	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
8	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
9	MEC	MindEvolutionaryComputation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
10	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
11	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
12	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
13	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
14	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
15	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
16	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
17	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
18	BFO	細菌採餌の最適化	0.54626	0.43533	0.31907	1.30066	0.41626	0.23156	0.06266	0.71048	0.35500	0.15233	0.03627	0.54360	2.555	28.39
19	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
20	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
21	IWDm	インテリジェント水滴M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
22	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
23	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
24	SFL	ShuffledFrog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
25	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
26	RND	無作為	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
27	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
28	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
29	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

まとめ

微小人工免疫系（Micro-AIS）最適化手法は、免疫系の機能原理に基づく最適化問題を解くための興味深く有望なアプローチです。免疫系の強力なメカニズムを利用して、複雑な最適化問題や学習問題を解くことができます。

Micro-AISの利点は、外部パラメータの数が少ないことと、アルゴリズムの実装が簡単なことです。そのため、実用的な作業に使用するにはかなり魅力的です。

しかし、Micro-AISアルゴリズムにも欠点があります。局所的な極端にはまりやすく、収束性が低いです。さらに、変数の数が多い関数ではアルゴリズムの性能が低下しており、これはスケーリング能力が弱いことを示しています。

しかし、Micro-AISは有望な最適化手法であり、アルゴリズムを修正したり、他の最適化手法と組み合わせたりすることで改善することができます。全体として、人工微小免疫系を用いた最適化手法は、最適化分野への重要な貢献であり、機械学習、人工知能、バイオインフォマティクスなどの様々な分野における複雑な問題の解決に有用なツールとなり得ます。

このアルゴリズムは、様々な方法で構築することができ、検索能力を拡張することができる、一種の「テンプレート」であるという印象を残します。これはシンプルなアーキテクチャーによって容易になっており、この非常に興味深いアルゴリズムを実験するための大きな余地を残しています。

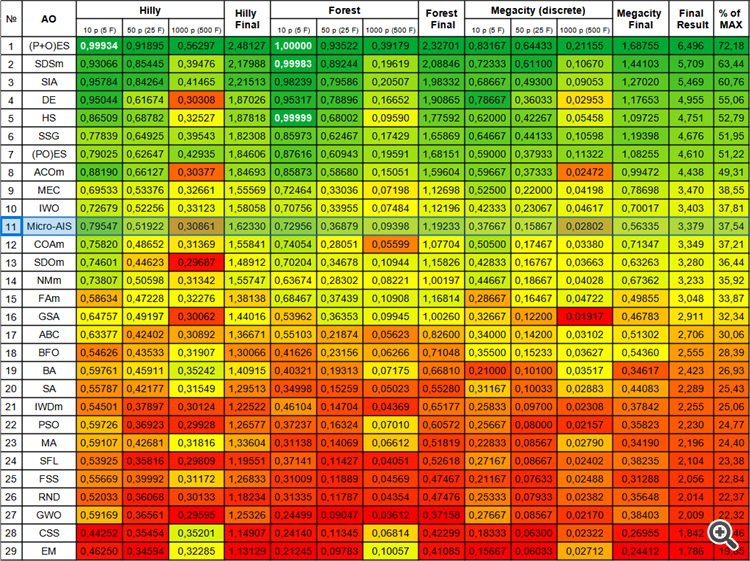
図1：関連テストによるアルゴリズムのカラーグラデーション

チャート

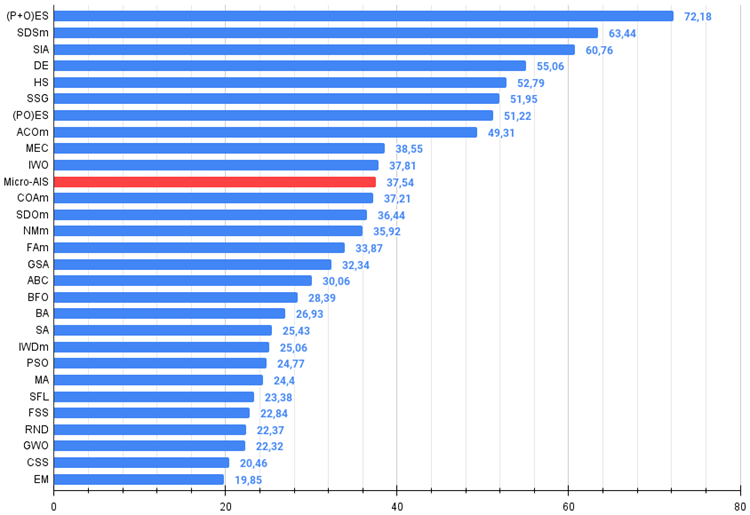
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果です（アーカイブにはレーティングテーブルを計算するスクリプトがある）。

Micro-AISアルゴリズムの長所と短所：

長所：

外部パラメータの数が少ない
シンプルなアルゴリズムの実装

短所

動けなくなる傾向がある
収束性が低い

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13951

添付されたファイル |

ZIPをダウンロード

29_The_world_of_AO_Micro_AIS.zip (536.94 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

リプレイシステムの開発（第33回）：発注システム（II）

今日も発注システムの開発を続けます。ご覧のように、他の記事ですでに紹介したものを大量に再利用することになります。とはいえ、この記事にはささやかなご褒美があります。まず、デモ口座からでもリアル口座からでも、取引サーバーで使えるシステムを開発します。MetaTrader 5プラットフォームを幅広く活用し、当初から必要なサポートをすべて提供します。

MQL5でマーケットメイク系アルゴリズムを作成する

マーケットメーカーはどのように機能するのでしょうか。この問題を考えて、原始的なマーケットメイク系アルゴリズムを作ってみましょう。

リプレイシステムの開発（第34回）：発注システム (III)

今回は、構築の第一段階を完成させます。この部分はかなり短時間で終わりますが、前回までに説明しなかった詳細をカバーします。多くの方が理解していない点をいくつか説明します。なぜShiftキーやCtrlキーを押さなければならないかご存じでしょうか。

母集団最適化アルゴリズム：細菌採餌最適化-遺伝的アルゴリズム(BFO-GA)

本稿では、細菌採餌最適化(BFO)アルゴリズムのアイデアと遺伝的アルゴリズム(GA)で使用される技術を組み合わせ、ハイブリッドBFO-GAアルゴリズムとして最適化問題を解くための新しいアプローチを紹介します。最適解を大域的に探索するために細菌の群れを使い、局所最適解を改良するために遺伝的演算子を使用します。元のBFOとは異なり、細菌は突然変異を起こし、遺伝子を受け継ぐことができるようになっています。