母集団最適化アルゴリズム：等方的焼きなまし（Simulated Isotropic Annealing、SIA）アルゴリズム（第2部）

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

第1部では、従来バージョンの焼きなまし(SA)アルゴリズムを検討しました。このアルゴリズムは、無作為性を適用する、より悪い決断を下す、より悪い決断を下す可能性を徐々に減らしていくという、3つの主要な概念に基づいています。無作為性を適用することで、検索空間のさまざまな領域を探索することができ、局所的最適解から抜け出せなくなるのを防ぐことができます。ある確率でより悪い決定を受け入れることで、アルゴリズムは局所的最適解から一時的に「抜け出して」、検索空間の他の場所でより良い解を探すことができます。これにより、まず検索空間をより広範囲に探索し、次に解の改善に集中できるようになります。

SAアルゴリズムのアイデアは、金属の焼きなましのアナロジーに基づいています。予熱された金属は徐々に冷やされ、構造が変化します。同様に、焼きなましアルゴリズムは、高い温度（より悪い決定を下す確率が高い）で開始し、徐々に温度を下げる（より悪い決定を下す確率を下げる）ことで、アルゴリズムが最適解に収束するのを助けると考えられています。

このアルゴリズムは、初期解から作業を開始します。初期解は無作為でもよいし、以前の反復から得られたものでもいいです。そして、解の状態を変化させる操作を適用します。この操作は無作為でも制御されていてもよく、現在の状態より悪くても新しい状態を得ることができます。より悪い決断を下す確率は「冷却」機能によって決定され、時間の経過とともにより悪い決断を下す確率は減少します。

焼きなましを記述するために、いくつかの簡単な方程式が用いられます。エネルギーの変化を計算する式によって、連続する2回の反復における適合度関数の値の差を求めることができます。より悪い判断を下す確率の計算式は、エネルギーと現在の温度の差を考慮して、新しい状態を受け入れる確率を決定します。

焼きなましアルゴリズムを使用する際に調整する必要がある重要なパラメータは、初期温度と冷却比です。これらのパラメータを設定することは、解のパフォーマンスと品質に大きな影響を与える可能性があり、パフォーマンスに与える影響が明らかでないためにパラメータを選択することが難しいという、アルゴリズムの弱点の1つです。加えて、これらのパラメータは相互に影響し合います。温度の上昇は、ほぼ等しく温度低下比の低下に置き換えられます。

記事の前半では、アルゴリズムの主な問題点を明らかにしました。

• パラメータ調整：初期温度や冷却係数といったSAアルゴリズムのパラメータは、そのパフォーマンスや効率に大きく影響します。これらのパラメータの設定は難しく、最適な値を得るためには試行錯誤が必要です。

• 極値から抜け出せなくなる問題：これを克服するためには、既存のアルゴリズム戦略ツールと組み合わせて新しい解を生成する際に、最も適切な確率変数の分布を選択したり、組み合わせ能力を向上させるための可能な解決策を検討したりするなど、さまざまな戦略を適用することができます。

• 収束速度の向上：収束を早めるために、冷却関数に修正を加え、システム温度をより早く下げることができるようにする（あるいは、別の形式の冷却関数を使用する）オプションがあります。また、アルゴリズムで次の状態を選択する方法を見直すこともできます。これは、以前に通過した状態に関する情報を考慮するものです。

• 変数の数が多い場合のSAアルゴリズムの効率改善：これは、大多数のアルゴリズムにとって最も難しい問題の1つです。変数の数が増えるにつれて、検索空間の複雑さは、探索戦略における特別な方法を用いて考慮できるよりもはるかに速く成長します。 

多次元空間における主な問題の1つは、可能な変数の組み合わせの組み合わせ論的爆発です。変数の数が増えると、探索が必要なシステム状態の可能性の数は指数関数的に増加します。そのため、最適化アルゴリズムは空間的複雑性の問題に直面することになります。

空間的複雑性とは、変数の数が増えるにつれて検索空間のサイズが指数関数的に大きくなることを意味します。例えば、10個の変数があり、それぞれが10個の値を取り得るとすると、可能な組み合わせの総数は10^10に等しく、1万回の試行回数（適合度関数の実行回数）しかないにもかかわらず、100億回に等しくなります。これだけ多くの組み合わせの中から最適解を見つけるのは、非常に難しい作業になります。これとは別に、テストでは、関数パラメータを0ステップで最適化していることは注目に値します。つまり、アルゴリズムにとっては信じられないほど難しい条件なのです。このような複雑なテスト問題で満足のいく結果を出したものは、（他の条件がすべて同じであれば）それほど複雑でない実際の問題でも、ほぼ確実にうまくいくでしょう。

2.アルゴリズム

焼きなましアルゴリズムは非常にシンプルで、これ以上どう改良できるかを想像するのは本当に難しいです。コップの水を魅惑的なワインに変える、魔法のようなものです。実際、新しい値の生成が均等に分散され、最悪の決定を下すという考え方が、最適化アルゴリズムを構築する通常の論理に完全に反している場合、何を改善できるのでしょうか。

前回の記事の結果の出力を見て、その後の実験結果と元の焼きなまし(SA)アルゴリズムの最初の参照結果を視覚的に比較してみましょう。

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result:65.78409729002105
Score:0.81510
25 Rastrigin's; Func runs 10000 result:52.25447043222567
Score:0.64746
500 Rastrigin's; Func runs 10000 result:40.40159931988021
Score:0.50060
=============================
5 Forest's; Func runs 10000 result:0.5814827554067439
Score:0.32892
25 Forest's; Func runs 10000 result:0.23156336186841173
Score:0.13098
500 Forest's; Func runs 10000 result:0.06760002887601002
Score:0.03824
=============================
5 Megacity's; Func runs 10000 result:2.92
Score:0.24333
25 Megacity's; Func runs 10000 result:1.256
Score:0.10467
500 Megacity's; Func runs 10000 result:0.33840000000000003
Score:0.02820
=============================
All score:2.83750

システムの新しい状態を生成する際に、確率変数の一様分布を正規分布に置き換えて結果を改善してみましょう。

新しいSIAアルゴリズムの基礎として焼きなましアルゴリズムクラスを使用します。このクラスのメソッドと機能については説明しません。この記事の最初の部分ですべてがすでにおこなわれているためです。

次に、逆関数法を用いて正規分布の乱数を生成することができます。ミュー（平均）とシグマ（標準偏差）の正規分布を持つx数を生成するとすると、次の式を使用することができます。

x = z0 * sigma + mu

ここで

• z0：以下の方程式を使って計算します

z0 = sqrt (-2 * log (u1)) * cos(2 * Pi * u2)

ここで

• u1*：範囲 (0.0;1.0] の乱数（ここではmin は範囲に含まれない）
  

• u2**：範囲 [0.0;1.0] の乱数

• *と**：一様分布の2つの独立した乱数
  

前回の記事では、SAアルゴリズムに乱数発生範囲を制限する拡散率パラメータを追加しました。乱数を発生させるのはこの領域です。

拡散をシミュレートするC_AO_SIAクラスのDiffusionメソッドを書いてみましょう。この方法は、最大2標準偏差の正規分布を持つ乱数を生成します。分布の形状を失うことなく、これらの境界を超えた値を「内側」に包み込みます（これについては、次の記事で詳しく見ていきます）。

標準偏差（シグマ）の値を知っていれば、この値の範囲を拡散のシミュレーションに必要な範囲に変換することができます。そのために、スケーリング関数Scaleを使用します。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SIA::Diffusion (const double value, const double rMin, const double rMax, const double step)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN))* cos (2 * M_PI * u2);

  double sigma = 2.0;//Sigma > 8.583864105157389 ? 8.583864105157389 : Sigma;

  if (z0 >=  sigma) z0 = RNDfromCI (0.0,    sigma);
  if (z0 <= -sigma) z0 = RNDfromCI (-sigma, 0.0);

  double dist = d * (rMax - rMin);

  if (z0 >= 0.0) return Scale (z0, 0.0,    sigma, value,        value + dist, false);
  else           return Scale (z0, -sigma, 0.0,   value - dist, value,        false);
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドでは、次のようにDiffusionメソッドを使用します。

for (int i = 0; i < popSize; i++)
{
   for (int c = 0; c < coords; c++)
   {
     a [i].c [c] = Diffusion (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
     a [i].c [c] = SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
   } 
}

変更（一様分布を正規分布に置き換える）を加えてテストを実行した結果、以下のような結果が得られました。

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result:60.999013617749895
Score:0.75581
25 Rastrigin's; Func runs 10000 result:47.993562806349246
Score:0.59467
500 Rastrigin's; Func runs 10000 result:40.00575378955945
Score:0.49569
=============================
5 Forest's; Func runs 10000 result:0.41673083215719087
Score:0.23572
25 Forest's; Func runs 10000 result:0.16700842421505407
Score:0.09447
500 Forest's; Func runs 10000 result:0.049538421252065555
Score:0.02802
=============================
5 Megacity's; Func runs 10000 result:2.7600000000000002
Score:0.23000
25 Megacity's; Func runs 10000 result:0.9039999999999999
Score:0.07533
500 Megacity's; Func runs 10000 result:0.28
Score:0.02333
=============================
All score:2.53305

他のアルゴリズムと同様に、焼きなましアルゴリズムで確率変数の分布を変更すると、その動作と結果に確実に影響を与えます。アルゴリズムの元の式は、解空間を探索するための無作為なステップを生成するために一様分布を使用しています。この分布は、すべての可能なステップについて等しい確率を保証します。

一様分布を正規分布に置き換えると、アルゴリズムの確率的性質が変化しました。正規分布は平均付近でピークに達し、平均から離れるにつれて減少します。これは、正規分布を用いて生成された無作為ステップは、平均値の周りに集中することを意味します。平均値から離れたステップは起こりにくいです。ここでの場合、「平均値」は改善したい元の座標値です。

この分布の変化は、解空間を探索する際のステップのバリエーションを減らすことにつながります。アルゴリズムはより局所的になり、解空間のより遠い領域や可能性の低い領域を探索することができなくなるようです。

上記のテストは、この場合、正規分布の使用は、（記事の最初の部分に反映されているように）一様分布の確率変数と比較して、最終結果にわずかではあるが統計的に有意な悪化をもたらしたことを示しています。これらの結果は2つの標準偏差を使って得られたもので、シグマ（標準偏差）の値を大きくすると、さらに統計的に有意に結果が悪化します。

このことから、分布の形状をより鋭角的なものに変えると、この特定のケースでは結果が悪化すると結論づけられます。

さて、元のアルゴリズムで分布の形状を「シャープにする」ことは有益ではないことがわかったので、別のアプローチを見てみましょう。本来のアルゴリズムでは、金属中の分子、あるいは拡散ゾーン内の結晶全体が、金属の体積全体に均等にエネルギーを分配するために、エネルギーを交換する十分な機会がないと仮定しましょう。この場合、結晶がエネルギーを交換しながら分子を交換できるようにするというアイデアを提案することができます。

エネルギーの異なる結晶間で分子を交換することで、エージェント間の座標の移動が可能になります。こうして分子は、金属の体積全体にわたってエネルギー分布を平滑化することができる、ある種のエネルギーキャリアとなります。結晶格子と分子間のこの相互作用の結果、エネルギーはより均等に分散され、より安定した最適なシステム構成を達成することができます。つまり、金属構造の等方性を高めようとするのです。

等方性とは、物体や系があらゆる方向に対して同じ特性や性質を保持する性質のことです。もっと簡単に言えば、物体やシステムがどの方向から見ても同じように見え、同じように振る舞う場合、その物体やシステムは等方的です。したがって、等方性とは、好ましい方向や向きがないことを意味し、物体やシステムはすべての方向において同じか均質であるとみなされます。

金属中の特性が全方向に等しくなる（等方性が増す）ことをシミュレートするには、Movingメソッドを変更する必要があります。

コードのロジックは以下の通りです。反復はpopSize母集団の各要素と各coords座標に対して実行されます。

• RNDfromCI関数を使用して、0からpopSizeの範囲で無作為な整数rを生成し、母集団内のエージェントを無作為に選択する
  
• 条件を確認し、選択されたエージェントの適合度関数の値が変更されるエージェントの適合度より大きければ、最適なエージェントの座標をコピーし、そうでなければエージェントの座標は変更しない
  
• RNDfromCI関数を使用して、範囲[-0.1;0.1]の乱数rndを生成する
• 座標値を、rnd、（rangeMax[c]-rangeMin[c]）とdの積、つまり拡散範囲に無作為な増分を加えることによって更新する
• SeInDiSp関数を使用して、結果の座標が許容範囲内であり、必要なステップであることを確認する
  

int    r   = 0;
double rnd = 0.0;

for (int i = 0; i < popSize; i++)
{
  for (int c = 0; c < coords; c++)
  {
      
    r = (int)RNDfromCI (0, popSize);
    if (r >= popSize) r = popSize - 1;

    if (a [r].fPrev > a [i].fPrev)
    {
      a [i].c [c] = a [r].cPrev [c];
    }
    else
    {
      a [i].c [c] = a [i].cPrev [c];
    }
      
    rnd = RNDfromCI (-0.1, 0.1);
    a [i].c [c] = a [i].c [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
    a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

同じパラメータを使用して一様分布と等方性で焼きなましした結果：

C_AO_SIA:50:1000.0:0.1:0.1
=============================
5 Rastrigin's; Func runs 10000 result:80.52391137534615
Score:0.99774
25 Rastrigin's; Func runs 10000 result:77.70887543197314
Score:0.96286
500 Rastrigin's; Func runs 10000 result:57.43358792423487
Score:0.71163
=============================
5 Forest's; Func runs 10000 result:1.5720970326889474
Score:0.88926
25 Forest's; Func runs 10000 result:1.0118351454323513
Score:0.57234
500 Forest's; Func runs 10000 result:0.3391169587652742
Score:0.19182
=============================
5 Megacity's; Func runs 10000 result:6.76
Score:0.56333
25 Megacity's; Func runs 10000 result:5.263999999999999
Score:0.43867
500 Megacity's; Func runs 10000 result:1.4908
Score:0.12423
=============================
All score:5.45188

異なるエネルギーを持つ結晶間で分子を交換する等方性の増加を利用することで、アルゴリズムの結果が大幅に改善されました。これはリーダーシップの主張です。

説明されたプロセスに基づいて導き出される結論は、次の通りです。

• エージェント間の座標移動：異なるエネルギーを持つ結晶間で分子を交換することで、アルゴリズム内のエージェント間で座標情報の移動が可能になります。これは、最適解に関する情報が他のエージェントに伝達されるため、最適解をより効率的かつ迅速に探索することに貢献します。
• エネルギー分布の平滑化：エネルギーの異なる結晶間で分子が交換される過程で、金属体積全体のエネルギー分布が平滑化されます。これは、エネルギーがより均等に分散されることを意味し、極小値を回避し、より安定した最適なシステム構成を達成するのに役立ちます。

さて、等方性を加えることで結果が大幅に改善されたので、もう一度正規分布を加えてみましょう（まず等方性を増加させる操作をおこない、その結果得られる値に正規分布による増分を加える）。

等方性による改善と正規分布を加えた焼きなましの結果：

C_AO_SIA:50:1000.0:0.1:0.05
=============================
5 Rastrigin's; Func runs 10000 result:78.39172420614801
Score:0.97132
25 Rastrigin's; Func runs 10000 result:66.41980717898778
Score:0.82298
500 Rastrigin's; Func runs 10000 result:47.62039509425823
Score:0.59004
=============================
5 Forest's; Func runs 10000 result:1.243327107341557
Score:0.70329
25 Forest's; Func runs 10000 result:0.7588262864735575
Score:0.42923
500 Forest's; Func runs 10000 result:0.13750740782669305
Score:0.07778
=============================
5 Megacity's; Func runs 10000 result:6.8
Score:0.56667
25 Megacity's; Func runs 10000 result:2.776
Score:0.23133
500 Megacity's; Func runs 10000 result:0.46959999999999996
Score:0.03913
=============================
All score:4.43177

結果は大幅に悪化しました。

焼きなましアルゴリズムで正規分布インクリメントを生成しても、改善は見られませんでした。等方性を適用した後、正規分布のインクリメントで期待通りの効果が得られるでしょうか。この期待は確認されていません。これは、等方性が適用された後、依然として一様な分布が解空間をより一様に探索することを可能にし、アルゴリズムが選好を強く偏らせることなく様々な領域を探索することを可能にするという事実によって説明することができます。正規分布を使用して既存の座標を改良しようと試みましたが、うまくいきませんでした。このため、アルゴリズム領域の広範な探索には限界があります。

最後に、等方性を高めた後の確率変数の増分の分布が一様であることを支持する結論を導き出すために、最後の実験をおこなってみましょう。2次分布を使用することで、既知の座標の近傍をさらに正確に探索します。一様に分布する確率変数を2乗すると、得られる分布は確率変数の2乗分布または2次分布と呼ばれます。

焼きなましアルゴリズムの結果（等方性による改善＋シャープな2次分布を含む同じパラメータ）：

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result:70.23675927985173
Score:0.87027
25 Rastrigin's; Func runs 10000 result:56.86176837508631
Score:0.70455
500 Rastrigin's; Func runs 10000 result:43.100825665204596
Score:0.53404
=============================
5 Forest's; Func runs 10000 result:0.9361317757226002
Score:0.52952
25 Forest's; Func runs 10000 result:0.25320813586138297
Score:0.14323
500 Forest's; Func runs 10000 result:0.0570263375476293
Score:0.03226
=============================
5 Megacity's; Func runs 10000 result:4.2
Score:0.35000
25 Megacity's; Func runs 10000 result:1.296
Score:0.10800
500 Megacity's; Func runs 10000 result:0.2976
Score:0.02480
=============================
All score:3.29667

一様分布の確率変数を2乗しても、プラスの効果は得られませんでした。パフォーマンスの低下は、正規分布を使った場合よりもさらに強かったです。

さて、焼きなましアルゴリズムのもう1つの欠点、すなわち、温度と減温比の設定と組み合わせの選択が難しいという欠点を解消しましょう。これらのパラメータは両方とも相互に影響を与えるためです。この2つのパラメータを連動させるために、温度低減機能と確率的悪化判断機能を組み合わせます。双曲弧余弦関数を適用してみましょう。

(1 - delta) * (acosh (-(x^3 - 3))) / 1,765

ここで

• delta：直近の2回の反復における適合度関数の値の差で、[0.0;1.0]の範囲で正規化される
• x：正規化アルゴリズムのエポックステップ

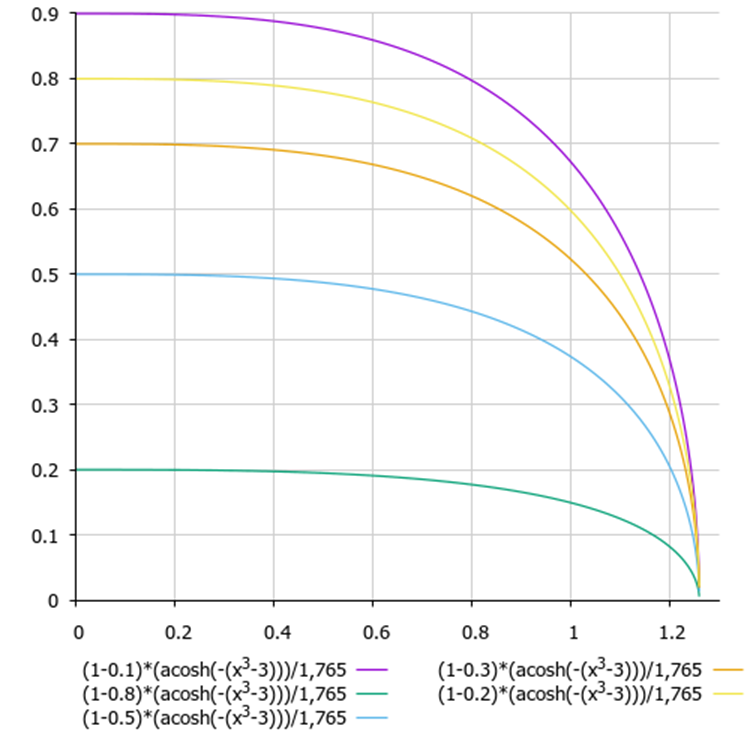
図1：最悪判定のエネルギー差と現在のエポック数依存性のグラフ（y：エネルギー差、x：エポック数）

3.テスト結果

SIAテストスタンドの結果：

C_AO_SIA:100:0.01:0.1
=============================
5 Rastrigin's; Func runs 10000 result:80.49732910930824
Score:0.99741
25 Rastrigin's; Func runs 10000 result:78.48411039606445
Score:0.97246
500 Rastrigin's; Func runs 10000 result:56.26829697982381
Score:0.69720
=============================
5 Forest's; Func runs 10000 result:1.6491133508905373
Score:0.93282
25 Forest's; Func runs 10000 result:1.3608802086313785
Score:0.76978
500 Forest's; Func runs 10000 result:0.31584037846210056
Score:0.17866
=============================
5 Megacity's; Func runs 10000 result:8.6
Score:0.71667
25 Megacity's; Func runs 10000 result:6.152
Score:0.51267
500 Megacity's; Func runs 10000 result:1.0544
Score:0.08787
=============================
All score:5.86552

結果は印象的です。その上、パラメータの数も1つ減っています。

アルゴリズム動作の視覚化は、すべての重要な局所極端をカバーするエージェントの別々のクラスタへの明確な分割を示しています。そのイメージは、金属が凝固して結晶化する様子に似ています。多くの変数を含むすべてのテストにおいて、優れた収束性があることがはっきりとわかります。

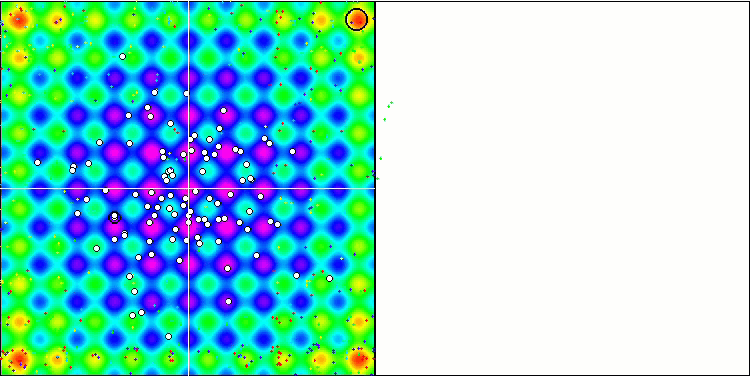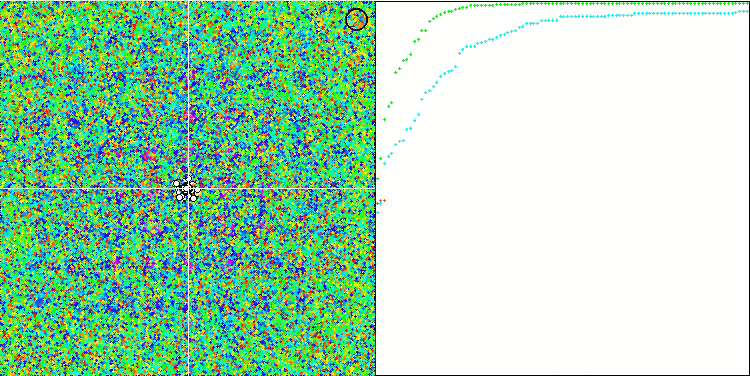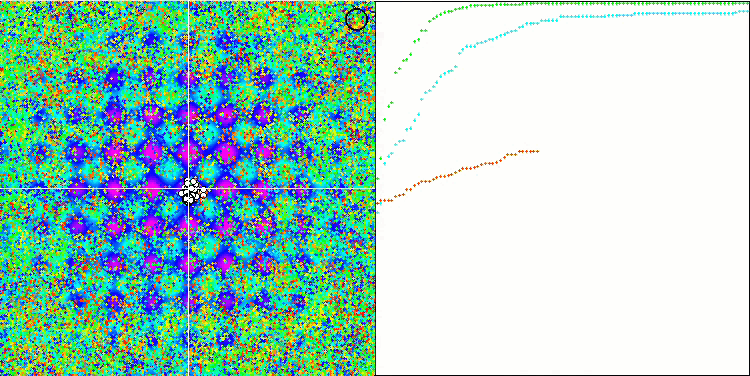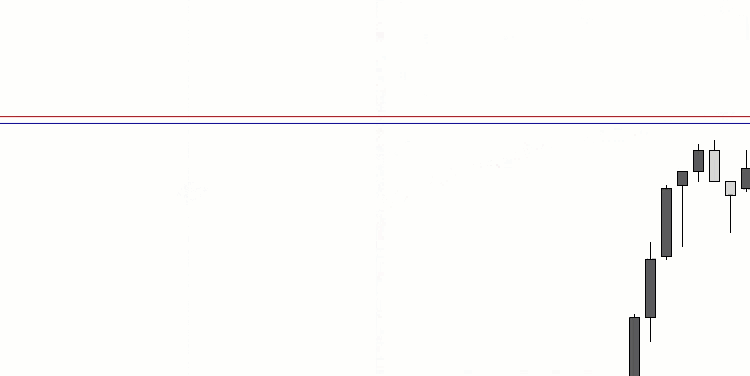
Rastriginテスト関数のSIA

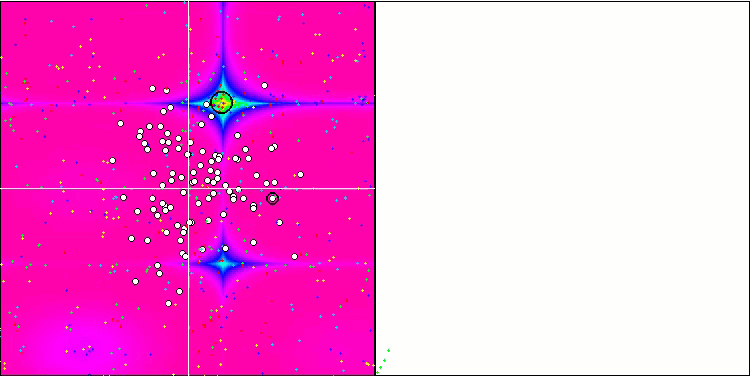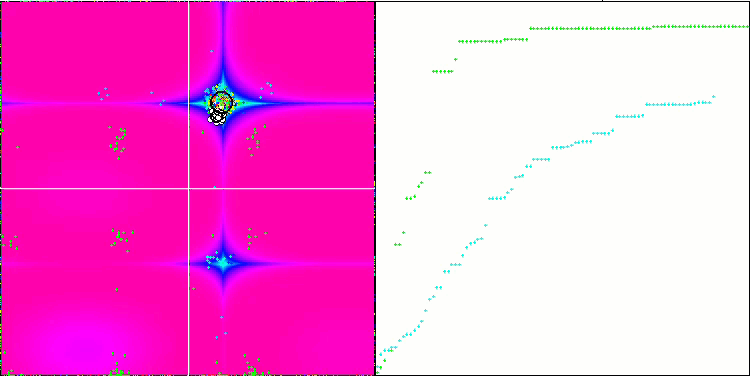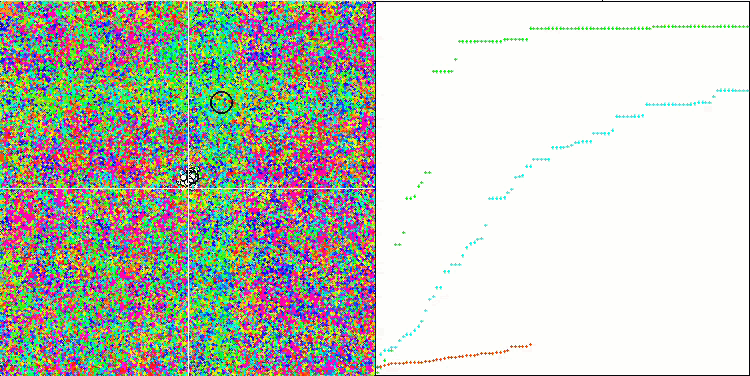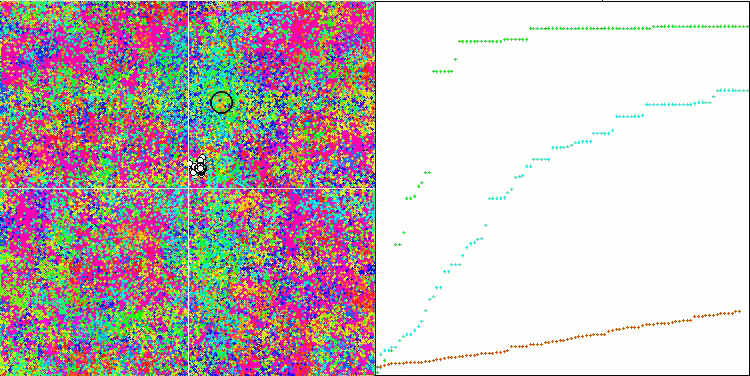
Forestテスト関数のSIA

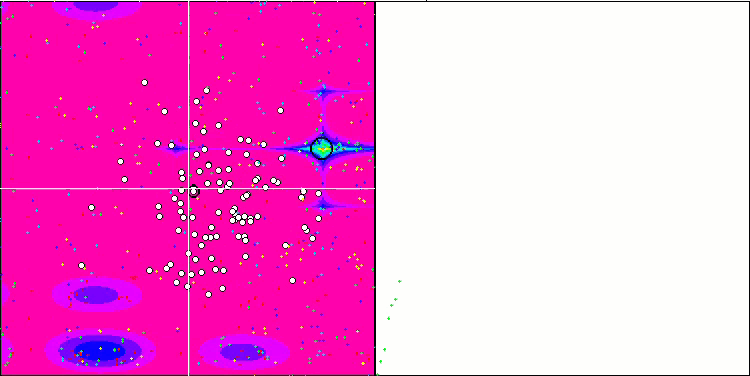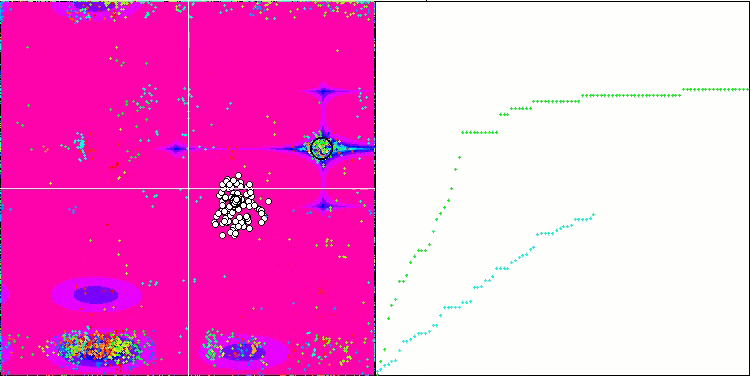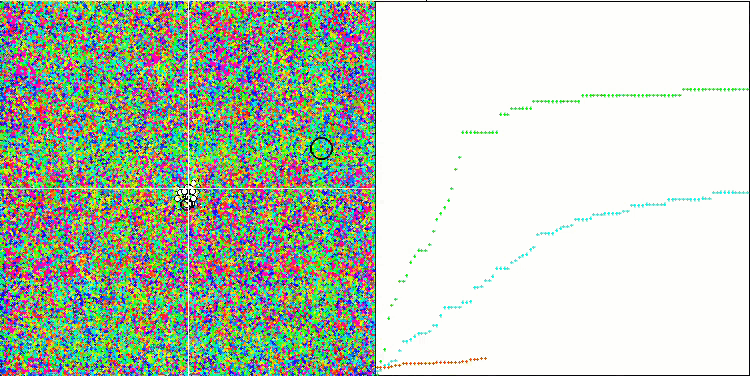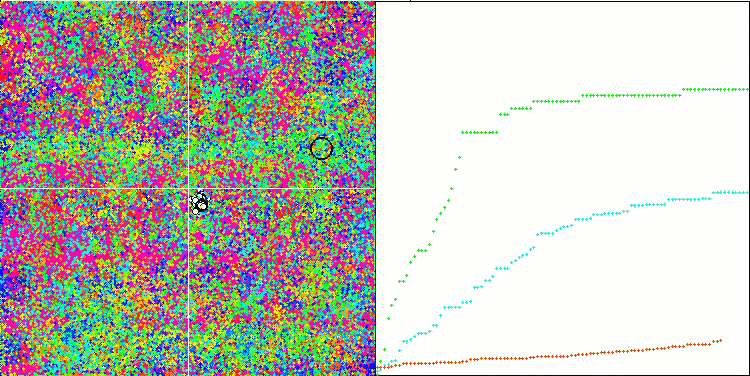
 Megacityテスト関数のSIA

等方的焼きなまし（SIA、2023）の新しいアルゴリズムは、最も難しい2つのテスト（急性Forestと1000変数による離散Megacity）で、SDSmに代わって評価表の2位を獲得しました。

#	AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果
			10p(5F)	50p(25F)	1000p(500F)		10p(5F)	50p(25F)	1000p(500F)		10p(5F)	50p(25F)	1000p(500F)
1	SDSm	確率的拡散探索M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	0,84982	2,84247	1.00000	1.00000	0,79920	2,79920	100.000
2	SIA	シミュレーション等方性アニーリング	0.99236	0.93642	0.69858	2.62736	0.88760	0.64655	1.00000	2.53416	0.58695	0.74342	1.00000	2.33038	89.524
3	SSG	苗木の播種と育成	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.71181	2.08502	0.54782	0.61841	0.79538	1.96161	77.027
4	DE	差分進化	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.55672	2.40274	0.90000	0.52237	0.09615	1.51852	74.777
5	HS	ハーモニー検索	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.31893	1.99283	0.71739	0.71842	0.33037	1.76618	71.983
6	IWO	侵入雑草最適化	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.22616	1.24758	0.57391	0.30527	0.26478	1.14395	49.045
7	ACOm	蟻コロニー最適化M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.55067	2.10194	0.71739	0.63947	0.04459	1.40145	48.119
8	MEC	MindEvolutionaryComputation	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.18122	1.06412	0.66957	0.30000	0.20815	1.17772	44.937
9	SDOm	螺旋ダイナミクス最適化M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.31953	1.30537	0.35653	0.15262	0.20653	0.71568	40.713
10	NMm	ネルダー=ミード法M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.18613	0.89148	0.46088	0.25658	0.13435	0.85180	40.577
11	COAm	カッコウ最適化アルゴリズムM	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.11764	0.93121	0.52174	0.24079	0.13587	0.89840	38.814
12	FAm	ホタルアルゴリズムM	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.35441	1.15256	0.24783	0.20526	0.28044	0.73352	32.943
13	ABC	人工蜂コロニー	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.09498	0.77676	0.40435	0.19474	0.11076	0.70985	30.528
14	BA	コウモリアルゴリズム	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.18499	0.51219	0.21305	0.07632	0.13816	0.42754	29.964
15	CSS	荷電系探索	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.11590	0.27404	0.07392	0.00000	0.02769	0.10161	28.825
16	GSA	重力探索法	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.23635	0.80145	0.42609	0.25525	0.00000	0.68134	28.518
17	BFO	細菌採餌の最適化	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.14700	0.72428	0.37392	0.24211	0.15058	0.76660	27.966
18	EM	電磁気学的アルゴリズム	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.24828	0.27240	0.00000	0.00527	0.08689	0.09216	19.030
19	SFL	ShuffledFrog-Leaping	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.01888	0.24729	0.19565	0.04474	0.05280	0.29320	13.588
20	SA	焼きなまし	0.36938	0.21640	0.10018	0.68595	0.20341	0.07832	0.07964	0.36137	0.16956	0.08422	0.08307	0.33685	13.295
21	MA	モンキーアルゴリズム	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.06358	0.21729	0.15652	0.03553	0.08527	0.27731	11.903
22	FSS	魚群検索	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.04638	0.20827	0.12175	0.03947	0.06588	0.22710	11.537
23	IWDm	インテリジェント水滴M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.04345	0.38148	0.22609	0.05659	0.04039	0.32307	10.675
24	PSO	粒子群最適化	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.15473	0.41440	0.16956	0.04737	0.01556	0.23250	8.423
25	RND	無作為	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03356	0.20055	0.12175	0.03290	0.03915	0.19380	5.097
26	GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02034	0.31301	1.000

まとめ

実施した実験と結果の分析に基づき、以下の結論を導き出すことができます。

1. 新しい等方的焼きなまし（Simulated Isotropic Annealing、SIA）アルゴリズムは、複数の変数を持つ関数の最適化において素晴らしい結果を示します。これは、高次元空間における最適解を求めるアルゴリズムの効率の高さを示しています。
2. このアルゴリズムは、鋭く離散的な特徴を持つ関数に対して特に優れた結果を示します。SIAによって解空間を一様に探索し、複雑で不規則な領域でも最適点を見つけることができることが理由だと思われます。
3. 全体として、新しいSIAアルゴリズムは強力な最適化ツールです。探索戦略をうまく組み合わせることで、このアルゴリズムは質的に新しい特性を持ち、最適解の探索において高い効率を発揮します。

新しいSIAアルゴリズムでは、母集団サイズに加えて、SAのような3つのパラメータではなく、2つのパラメータ（温度と拡散比）しかありません。さらに、温度パラメータは非常にわかりやすく、抽象的な温度の単位で表され、デフォルトでは0.01に等しくなっています。

研究および結果の分析に基づき、私たちは、ニューラルネットワークの訓練や、多くのパラメータを持つ取引問題や複雑な組合せ問題にSIAアルゴリズムを使用することを自信を持って推奨することができます。

図2：関連テストによるアルゴリズムのカラーグラデーション

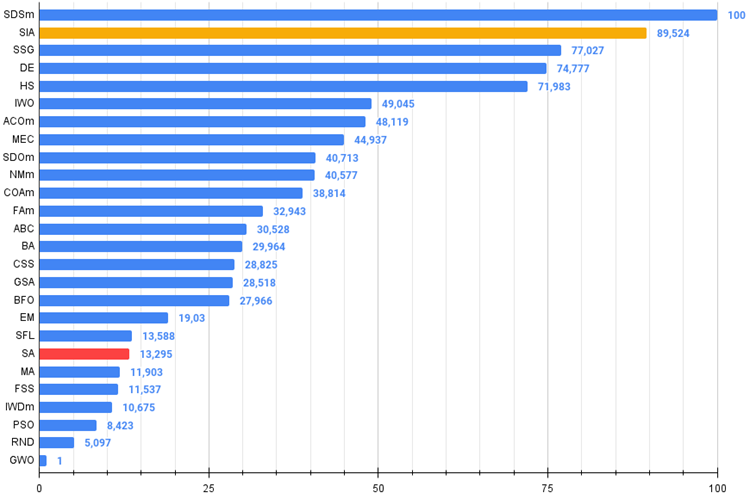
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

アーカイブには、記事で適用されている方法で格付けを計算するためのスクリプトが含まれています）。

SIAの長所と短所

長所

1. 外部パラメータ数が最小
2. 様々な問題を高い効率で解決
3. 計算リソースへの負荷が低い
4. 実装が容易
5. 行き詰まりにくい
6. 平滑離散関数と複雑な離散関数の両方で有望な結果
7. 収束性が高い

短所

1. なし

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。