母集団最適化アルゴリズム：Mind Evolutionary Computation (MEC)アルゴリズム

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

進化的計算は、計算知能、機械学習、人工知能の一分野であり、最適化問題、ロボット設計、決定木の作成、データ分析アルゴリズムのチューニング、ニューラルネットワークの訓練、ハイパーパラメータのチューニングなどに広く利用されています。進化的計算は、古典的な数値計算手法を使う代わりに、生物進化からヒントを得て優れた解を開発します。これらは、適応度関数の導関数がわからない場合や、適応度関数に局所極値が多く逐次的な手法の妨げになる場合に特に有効です。

複雑な高次元問題を解く際に、進化的計算で使われる集団アルゴリズムには、古典的なアルゴリズムに比べて多くの利点があります。最適解に十分に近い準最適解をより効率的に見つけることができるため、実用的な最適化問題ではしばしば許容されます。

進化的計算における興味深いアプローチのひとつに、1998年にChengaiとその共著者たちによって提案されたMind Evolutionary Computation (MEC)アルゴリズムがあります。人間の脳のモデリングが期待されるのとは異なり、MECアルゴリズムは社会における人間の行動のいくつかの側面をモデル化しています。このアルゴリズムでは、各個人は、人々の集団の中で機能する知的エージェントとみなされます。意思決定をするとき、個人は自分の集団のメンバーからも、他の集団のメンバーからも影響を受けます。社会で高い地位を得るためには、その集団の中で最も成功した人物から学ばなければなりません。同時に、自分の集団が他の集団よりも成功するためには、すべての個人が集団間競争において同じ原則に導かれなければなりません。MECアルゴリズムの重要な側面は、集団内および集団間の個人間の情報交換です。これは、知的な個人の社会が成功裏に発展するためには、継続的で自由な情報交換が必要であることを反映しています。

MECアルゴリズムは、局所的探索と大域的探索をそれぞれ担当する局所競合演算と異化演算を用いて、提示された概念を実装します。提示版は、アルゴリズムが集団の進化史に関する情報を保存するために使用します。最適化プロセスは、この情報に基づいて制御されます。

2.アルゴリズム

MECアルゴリズムは、先行集団と後行集団からなる多個体群アルゴリズムと解釈することができます。各集団のエージェントの数は同じとします。各集団には、それぞれの局所的掲示板があり、また、全複数集団共通の大域的掲示板もあります。

Simple MEC (SMEC)として知られるMECアルゴリズムの元のバージョンは、集団初期化、局所競合、異化演算を使用します。

初期化操作では、集団を作成し、検索エリアに配置します。各集団について、その集団の個人を識別するランダムなベクトルが生成されます。次に、集団の残りのエージェントの初期座標が決定され、正規分布の法則を用いて集団の個体の周りに無作為に配置されます。

局所競争操作は、各集団の最大適応度関数の局所探索を実行します。各集団について、現在の優勝エージェントに関する情報が掲示板から読み取られます。その後、集団内の残りのエージェントの新しい座標が決定され、正規分布の法則を用いて勝者の周囲に無作為に配置されます。集団エージェントの新規口座が計算され、現在の口座が最大となる新たな集団勝者が決定されます。新しい勝者に関する情報は、集団掲示板に掲載されます。

異化操作は大域的な探索を制御します。まず、掲示板の全集団のアカウントを読みます。そして、これらのアカウントは互いに比較されます。先行集団のスコアが後行集団のスコアを下回った場合、後行集団が先行集団の代わりになり、先行集団は後行集団となります。ある集団のスコアが、すべての遅れている集団のスコアよりも低い場合、その集団は母集団から除外されます。削除された集団の代わりに、新しい集団が初期化操作を使って初期化されます。

このように、MECアルゴリズムは、初期化、局所競争、異化操作を含む多個体群アルゴリズムです。

上記は、Simple MECアルゴリズムの作者による一般的な説明です。このような説明では、多次元空間における検索戦略の根底にある原理を理解するのは難しいと私は思います。その結果、「掲示板とは何なのか、集団の中の特定の個人の特徴とどう違うのか」など、多くの疑問が生じるので、その機微を詳しく見ていきましょう。

アルゴリズムは人間社会とそのメンバー間の相互作用をモデル化したものだと前述しました。「アイデア」という概念を想像する最も単純で明確な方法は、科学的なアイデア、芸術的なアイデア、文学的なアイデア、その他どんなものでも構わないということです。社会には常に支配的な考え方と代替的な考え方があります。著者らとは異なり、私は集団との関係でアイデアを「先行」と「後行」に分けるつもりはありません。後述するように、これは基本的なバージョンと比較してアルゴリズムに何らかの利点をもたらします。各アイデアには少なくとも1つのテーゼが含まれるため（テーゼは適応度関数の最適化されたパラメータ）、科学にさまざまな科学理論や運動があるように、1つのアイデアにもイデオロギーの分岐ができます。図1は、i1、i2などとラベル付けされたアイデアを模式的に示しています。それぞれのアイデアは、思考力（アルゴリズムの外部パラメータ）によって決定される範囲内で枝分かれすることができます。イデオロギーの分岐が思想から遠ざかれば遠ざかるほど、その可能性は低くなります（イデオロギーの分岐の確率と境界は、拡大する同心円で示されている）。もしそのアイデアが、イデオロギー的な親アイデアよりも一貫性がある（適合度関数の値が優れている）ことを示したなら、この分岐は親アイデアに取って代わります（イデオロギーの分岐の結果としての新しいアイデアは、図ではi5として示されている）。この図を見ると、イデオロギーの境界を越えることには何の制約もないことがわかります。これは、同じ主張を持つイデオロギーの分岐が出現する可能性があることを意味します。

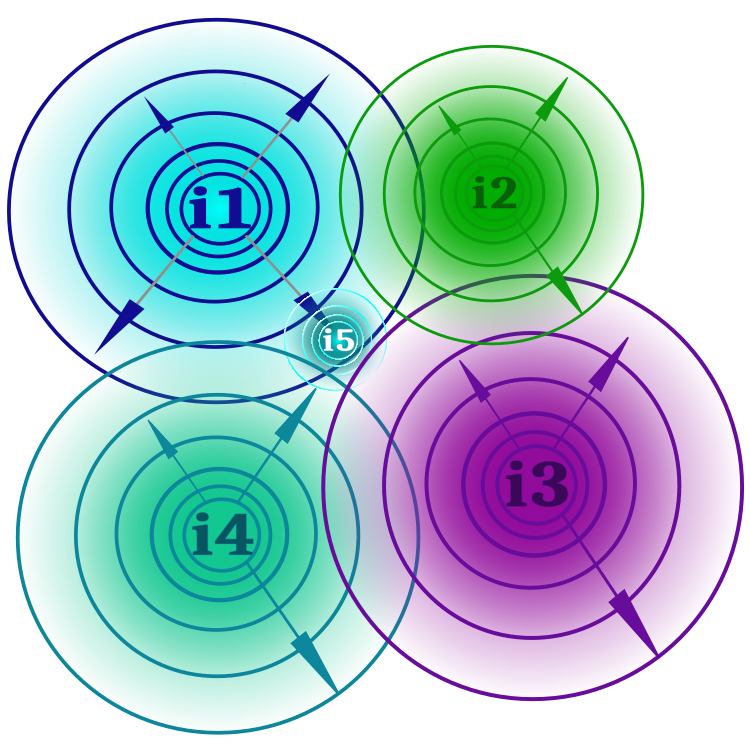
図1：アイデアi1、i2、i3、i4、それらの境界、境界の交差、アイデアi1の分岐による新しいアイデアi5の出現

アイデア分岐は、各アイデア内での局所的な競争を実装し、局所的な極値近傍での探索を提供します。すべてのアイデアの複数の枝は多人数を表し、単一のアイデアとその枝は単一集団を表します。各アイデアは、そのテーゼと実用的な価値を保存しているだけであり、ユーザープログラムはイデオロギーの分岐を参照するのであって、アイデアそのものを参照するわけではありません。

大域的探索を確実にするためには、母集団内の現在のアイデアを超える新しいアイデアの出現を保証する必要があります。そうでなければ、アイデアは局所的極値から抜け出せなくなり、より良い適合度関数の値が出現しなくなります。異化（破壊）のプロセスは、この目的のためにあります。アイデアの支配集団（緑色）と代替集団（青色）の間のアイデアの交換には、元のアルゴリズムとは少し異なる方式を使用します。各集団のアイデアを別々に分類した後、支配集団から最悪のものを取り除き、代替集団から最高のものに置き換えることで、イデオロギーの交換を保証します。代替集団の空いた場所には、支配集団から無作為に選ばれたアイデア（最後のものを除く）の抜粋から組み立てられた新しいアイデアを配置します。変動性を提供するために、このアクションにランダムコンポーネントを追加できます。これは、最適化アルゴリズムの研究者によるさらなる実験の可能性のために残しておきます。支配集団のアイデアから抜粋を選択することで、アルゴリズムの組み合わせ能力が高まります。下の図2は、代替集団からアイデアを置き換えて、新しいアイデアを生み出す図です。

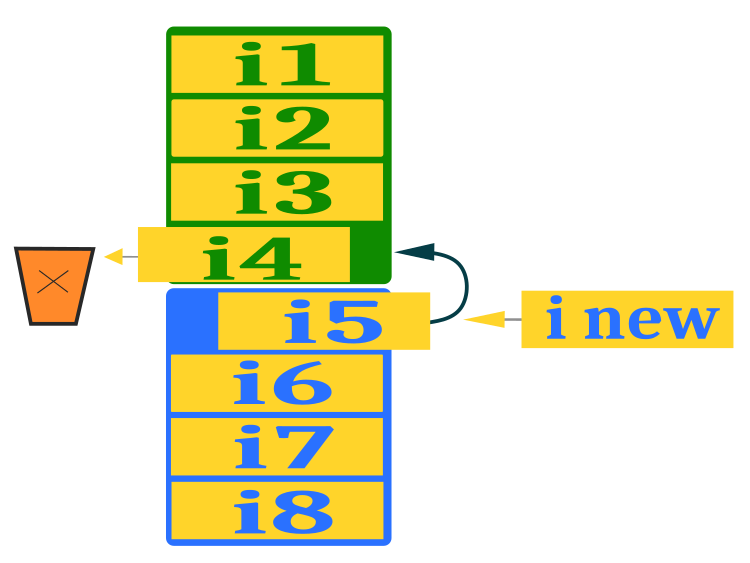
図2：代替集団のアイデアを置き換え、新たなアイデアを生み出す

アルゴリズムのコードを書くのを簡単にするために、MECの疑似コードを書いてみましょう。

1.1 アルゴリズムの最初の実行の場合
1.1.1 アイデアの集団（支配集団と代替集団）に従って、無作為に2つのアイデアの集団を作成

1.2 アルゴリズムの2回目以降の実行の場合
1.2.1 レヴィの法則*に従って支配的なアイデアが分岐する場合、分岐の1つは支配的なアイデアからのテーゼの組み合わせの結果となる
1.2.2 代替案として、すべての分岐はレヴィの法則*に従って作られる

2 イデオロギーの分岐の価値を計算する

3.1 より優れたイデオロギーの分岐があれば、対応するイデオロギーを置き換える
3.2 支配集団と代替集団を別々に分類する
3.3 支配集団の最悪のアイデアを、代替集団のより良いアイデアで置き換える
3.4 代替集団の空っぽのアイデアの代わりに、支配集団**の要素に基づく新しいアイデアを作る（最後に置き換えたもの以外すべて）


*著者が提案した正規分布の代わりに
**著者が提案したテーゼを無作為に作成するのではなく

擬似コードから、元のアルゴリズムに変更が加えられていることがわかります。

第一に、アルゴリズムの著者によって提案された正規分布法則の代わりに、ここではレヴィ飛行法則を使用し、アルゴリズムの研究と改良能力を増加させました。なお、レヴィの飛行法則を正規分布や一様分布の代わりに使おうとしても、各最適化アルゴリズムの効率を必ずしも向上させることはできません。これは主に、アルゴリズムの検索戦略の特殊性によるものです。例えば、前回の記事では、Shuffled Frog-Leapingアルゴリズムを見てみました。正規分布の代わりにカエル跳びにおけるレヴィの法則を使ってみましたが、検索性能に顕著な改善は見られませんでした。

第二に、元のアルゴリズムでは、探索戦略に組み合わせのメカニズムが用意されていません。なぜこれが極めて重要なのか、考えてみましょう。例えば、アルミニウムのボール（軽いボール）と金のボール（重いボール）が入ったカゴがいくつかあるとします。私たちの仕事は、空のカゴにボールを集め、それらがすべて金色になるようにすることです。一方、カゴの中の新しいボールの化学組成を滑らかに変化させることが許されており、これによって質量が増加するかどうかは不明です。そのうちのひとつが金でなければならないことはわかっています。重さを量れるのはカゴ全体だけで、玉ひとつひとつを量ることはできません。カゴがいっぱいになったら、重さを量らなければなりません。この問題は、単純な組み合わせによって、より少ないステップでカゴいっぱいの金の玉を集められることを示しています。

アルゴリズムコードの説明に移りましょう。

アルゴリズムの基本的な論理単位はアイデアであり、それはイデオロギーの分岐を表すものでもあります。S_Idea構造体は、アイデアを記述するのに最適です。これは、アイデアの座標と適合性に関する情報を含むオブジェクトです。この構造体は、DBL_MAXの負の値で適応度を簡単に初期化できるInitメソッドを備えています。

//——————————————————————————————————————————————————————————————————————————————
struct S_Idea
{
  void Init (int size)
  {
    ArrayResize (c, size);
    f = -DBL_MAX;
  }
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_MECクラスで、MECアルゴリズムを説明します。これには多くの変数と、これらの変数を扱うためのメソッドが含まれています。

クラス変数：
-cB：最適な座標を含む配列
-fB：最適座標の適応度関数値
-idBr：イデオロギーの分岐を含む配列

-rangeMax：最大検索値を含む配列
-rangeMin：検索値の最小値を含む配列
-rangeStep：検索ステップを含む配列

-leadIdeolGroup：先行イデオロギー集団を含む配列
-alteIdeolGroup：代替イデオロギー集団を含む配列
-tempIdeolGroup：一時的なイデオロギー集団を含む配列

-coordinatesNumber：座標の数
-populationSize：母集団のサイズ
-ideasNumber：アイデアの数
-thoughtPower：アイデアの力
-ideasBr：イデオロギーの分岐
-leadIdGroupSize：先行イデオロギー集団のサイズ
-alteIdGroupSize：代替イデオロギー集団のサイズ

-vect：座標インクリメントを使用するベクトル
-ind：インデックスの配列
-val：値の配列
-revision：改訂フラグ

クラスのメソッド：
-Init：パラメータを渡してクラスを初期化する
- Moving：動作をおこなう
- Revision

- Sorting：イデオロギー集団を選別する
-SeInDiSp：検索間隔計算
-RNDfromCI：与えられた区間から乱数を生成する

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MEC
{
  //----------------------------------------------------------------------------
  public: double cB   []; //best coordinates
  public: double fB;      //FF of the best coordinates
  public: S_Idea idBr []; //ideological branches


  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search


  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    ideasNumberP,         //ideas number
                     const double thoughtPowerP);       //thought power

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: S_Idea leadIdeolGroup []; //leading ideological group
  private: S_Idea alteIdeolGroup []; //alternative ideological group
  private: S_Idea tempIdeolGroup []; //temporal ideological group

  private: int    coordinatesNumber; //coordinates number
  private: int    populationSize;    //population size
  private: int    ideasNumber;       //ideas number
  private: double thoughtPower;      //thought power
  private: int    ideasBr;           //number of ideological branches
  private: int    leadIdGroupSize;   //leading ideological group size
  private: int    alteIdGroupSize;   //alternative ideological group size

  private: double vect    [];        //vector
  private: int    ind     [];
  private: double val     [];
  private: bool   revision;

  private: void   Sorting   (S_Idea &ideas []);
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Init初期化メソッドは、以下のアクションを実行します。

- コードの冒頭で、乱数発生器の初期値が設定され、変数fBにdouble型の最小値が設定されます。
- 次に、coordinatesNumber、opulationSize、ideasNumber、thoughtPower変数に、Init関数に渡された値が設定されます。
- ideasBr、leadIdGroupSize、alteIdGroupSizeの値は、opulationSizeとideasNumberの値に基づいて計算されます。
- rangeMax、rangeMin、rangeStep、vect、ind、val、tempIdeolGroup、cB配列は、ArrayResize関数を使用してサイズを変更します。
- その後、forループとInit関数を使って、leadIdeolGroup配列とalteIdeolGroup配列にIdeologyクラスのオブジェクトが作成されます。
-イデオロギークラスオブジェクトは、forループとInit関数を使って、idBr配列の中に次に生成されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MEC::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    ideasNumberP,         //ideas number
                     const double thoughtPowerP)        //thought power
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  populationSize    = populationSizeP;
  ideasNumber       = ideasNumberP;
  thoughtPower      = thoughtPowerP;

  ideasBr         = populationSize / ideasNumber;
  leadIdGroupSize = ideasNumber / 2;
  alteIdGroupSize = ideasNumber - leadIdGroupSize;

  ArrayResize (rangeMax,       coordinatesNumber);
  ArrayResize (rangeMin,       coordinatesNumber);
  ArrayResize (rangeStep,      coordinatesNumber);
  ArrayResize (vect,           coordinatesNumber);
  ArrayResize (ind,            alteIdGroupSize, alteIdGroupSize);
  ArrayResize (val,            alteIdGroupSize, alteIdGroupSize);
  ArrayResize (tempIdeolGroup, alteIdGroupSize, alteIdGroupSize);
  ArrayResize (cB,             coordinatesNumber);

  ArrayResize (leadIdeolGroup, leadIdGroupSize);
  for (int i = 0; i < leadIdGroupSize; i++) leadIdeolGroup [i].Init (coordinatesNumber);

  ArrayResize (alteIdeolGroup, alteIdGroupSize);
  for (int i = 0; i < alteIdGroupSize; i++) alteIdeolGroup [i].Init (coordinatesNumber);

  ArrayResize (idBr, populationSize);
  for (int i = 0; i < populationSize; i++) idBr [i].Init (coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

イデオロギー分岐を作成するMovingメソッドは、MECの検索戦略の核となるロジックを実行します。コードの一部はアルゴリズムの最初の反復でのみ実行され、残りのコードは各反復で実行されます。

最初の反復では、ベクトルを初期化する必要があります。このベクトルには、範囲と思考力に基づいて計算された値（これが分岐時の増分である）が格納され、支配集団と代替集団の2つにアイデアを作成します。そのために、両集団のアイデア（両者は等価である）を、検索フィールド全体に等確率で散りばめていきます。

//============================================================================
if (!revision)
{
  fB = -DBL_MAX;
  int cnt = 0;

  for (int c = 0; c < coordinatesNumber; c++) vect [c] = (rangeMax [c] - rangeMin [c]) * thoughtPower;

  //--------------------------------------------------------------------------
  for (int i = 0; i < leadIdGroupSize; i++)
  {
    for (int c = 0; c < coordinatesNumber; c++)    
    {
      coord = RNDfromCI (rangeMin [c], rangeMax [c]);
      leadIdeolGroup [i].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    leadIdeolGroup [i].f = -DBL_MAX;
  }

  //--------------------------------------------------------------------------
  for (int i = 0; i < alteIdGroupSize; i++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      coord = RNDfromCI (rangeMin [c], rangeMax [c]);
      alteIdeolGroup [i].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    alteIdeolGroup [i].f = -DBL_MAX;
  }

  revision = true;
}

さらに、最初の反復とそれ以降の反復ではすでにアイデアそのものを生み出しているので、イデオロギーの分岐を生み出すことになります。適応度関数を用いて評価できるイデオロギーの分岐にこそ興味があるのです。

分岐を作るための主な作業は、レヴィの飛行の法則に従って、思考力の係数によって正規化されたアイデアの抽象に移行する作業です。代替集団のすべてのアイデアと、支配集団の最後のアイデア以外のアイデアについて、式に従ってこれをおこないます。

coord = leadIdeolGroup [i].c [c] + r1 * vect [c] * pow (r2, -2.0);

支配集団の最後のアイデアについては、この集団から無作為にアイデアを選択し、対応するインデックスのテーマを取ります。

r1 = RNDfromCI (0.0, leadIdGroupSize - 1);
idBr [cnt].c [c] = leadIdeolGroup [(int)r1].c [c];

以下は、両集団のイデオロギーの分岐を作成するためのコード全体です。

//----------------------------------------------------------------------------
for (int i = 0; i < leadIdGroupSize; i++)
{
  for (int b = 0; b < ideasBr; b++)
  {
    if (b < ideasBr -1)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        r1 = RNDfromCI (0.0, 1.0);
        r1 = r1 > 0.5 ? 1.0 : -1.0;
        r2 = RNDfromCI (1.0, 20.0);

        coord = leadIdeolGroup [i].c [c] + r1 * vect [c] * pow (r2, -2.0);
        idBr [cnt].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    else
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        r1 = RNDfromCI (0.0, leadIdGroupSize - 1);
        idBr [cnt].c [c] = leadIdeolGroup [(int)r1].c [c];
      }
    }

    cnt++;
  }
}

//----------------------------------------------------------------------------
for (int i = 0; i < alteIdGroupSize; i++)
{
  for (int b = 0; b < ideasBr; b++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      coord = alteIdeolGroup [i].c [c] + r1 * vect [c] * pow (r2, -2.0);
      idBr [cnt].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cnt++;
  }
}

Revisionメソッドは、イデオロギーの分岐を評価した結果に基づいてアイデアを修正し、グローバルな解決策の指標を更新するためのものです。コードは以下のステップを実行します。

1. cntとpos変数が初期化されます。

2.最高のアイデアを置き換えます。先行集団(leadIdeolGroup)の各リーダーのループの中で、グローバルなもの(idBr)から最適なイデオロギーの分岐の探索がおこなわれます。各分岐について、その適応度関数の値(f)が現在のリーダーの値より大きいかどうかを確認し、位置(pos)を現在のインデックス(cnt)と等しく設定します。より良いアイデアが見つかれば、機能値とリーダー座標はそのアイデアの値で更新されます。新しいアイデアの特徴量も現在の最良特徴量(fB)より大きい場合、fBと最良アイデアの座標(cB)も更新されます。

3.代替案の集団(alteIdeolGroup)も同様です。

4.アイデアの集団分け先行集団と代替集団は、適合度関数の値の降順に並べ替えられます。

5.最悪のアイデアを置き換えます。先行集団(leadIdeolGroup)の最悪のアイデアは、代替集団(alteIdeolGroup)の最良のアイデアと置き換えられます。

6.新しいアイデアの作成：代替集団(alteIdeolGroup)の各座標(c)に対して、支配集団(leadIdeolGroup)の要素に基づいて新しいアイデアが作成されます。座標は、リーダーの支配集団から無作為に選択されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MEC::Revision ()
{
  int cnt = 0;
  int pos = -1;

  //----------------------------------------------------------------------------
  //4. If there is a better ideological branch, replace the corresponding idea
  for (int i = 0; i < leadIdGroupSize; i++)
  {
    pos = -1;
    for (int b = 0; b < ideasBr; b++)
    {
      if (idBr [cnt].f > leadIdeolGroup [i].f) pos = cnt;

      cnt++;
    }

    if (pos != -1)
    {
      leadIdeolGroup [i].f = idBr [pos].f;
      ArrayCopy (leadIdeolGroup [i].c, idBr [pos].c, 0, 0, WHOLE_ARRAY);

      if (idBr [pos].f > fB)
      {
        fB = idBr [pos].f;
        ArrayCopy (cB, idBr [pos].c, 0, 0, WHOLE_ARRAY);
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < alteIdGroupSize; i++)
  {
    pos = -1;
    for (int b = 0; b < ideasBr; b++)
    {
      if (idBr [cnt].f > alteIdeolGroup [i].f) pos = cnt;

      cnt++;
    }

    if (pos != -1)
    {
      alteIdeolGroup [i].f = idBr [pos].f;
      ArrayCopy (alteIdeolGroup [i].c, idBr [pos].c, 0, 0, WHOLE_ARRAY);

      if (idBr [pos].f > fB)
      {
        fB = idBr [pos].f;
        ArrayCopy (cB, idBr [pos].c, 0, 0, WHOLE_ARRAY);
      }
    }
  }

  //----------------------------------------------------------------------------
  //5. Sort two groups of ideas.
  Sorting (leadIdeolGroup);
  Sorting (alteIdeolGroup);

  //----------------------------------------------------------------------------
  //6. Replace the worst idea of the first group with the best idea from the second group
  leadIdeolGroup [leadIdGroupSize - 1] = alteIdeolGroup [0];

  //----------------------------------------------------------------------------
  //7. Instead of an empty idea, create a new idea based on elements of the dominant group 
  double rnd   = 0.0;
  double coord = 0.0;
  for (int c = 0; c < coordinatesNumber; c++)
  {
    rnd = RNDfromCI (0.0, leadIdGroupSize - 2);
    alteIdeolGroup [0].c [c] = leadIdeolGroup [(int)rnd].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

テストベンチにおけるMind Evolutionaryアルゴリズムの動作の出力は次の通りです。

C_AO_MEC:50;10;0.3
=============================
5 Rastrigin's; Func runs 10000 result:78.73205273291103
Score:0.97553
25Rastrigin's;Funcruns10000result：58.554840607439516
Score:0.72553
500 Rastrigin's; Func runs 10000 result:42.32395504312925
Score:0.52442
=============================
5 Forest's; Func runs 10000 result:1.2024830541165685
Score:0.68018
25 Forest's; Func runs 10000 result:0.4588423143844061
Score:0.25954
500 Forest's; Func runs 10000 result:0.08756810826330522
Score:0.04953
=============================
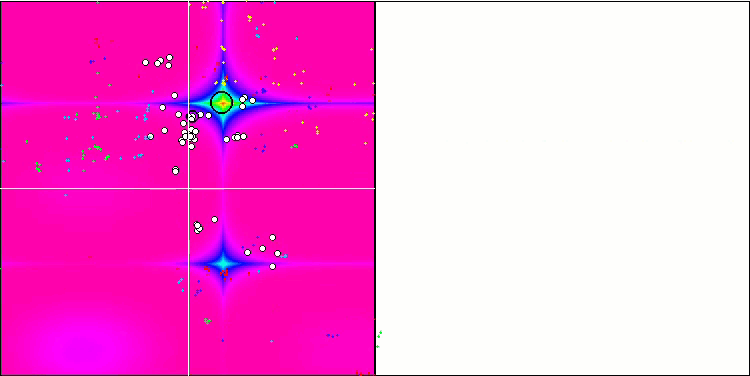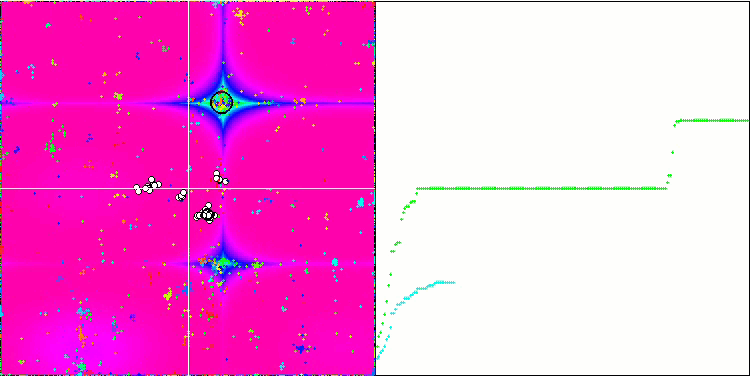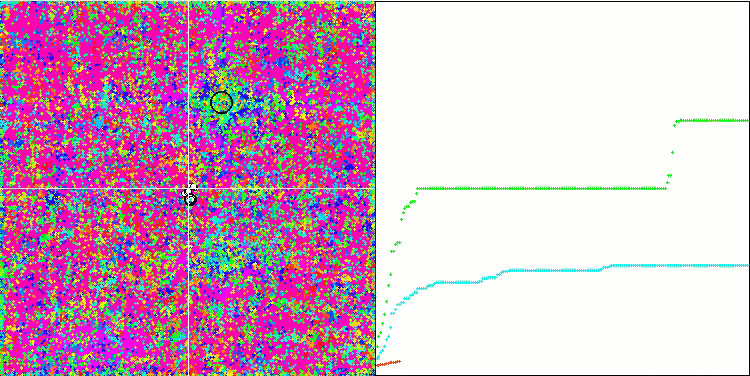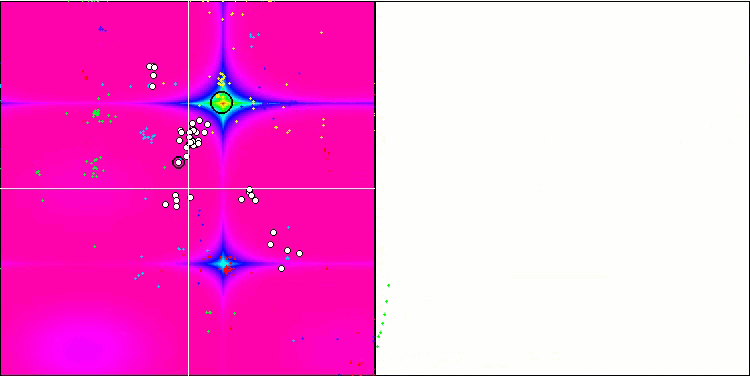
5 Megacity's; Func runs 10000 result:5.279999999999999
Score:0.44000
25 Megacity's; Func runs 10000 result:2.048
Score:0.17067
500 Megacity's; Func runs 10000 result:0.4364
Score:0.03637
=============================
All score:3.86178

MECアルゴリズムのアニメーションを観察すると、局所的な極端に集中したエージェントのクラスターが形成されているのがわかります。コンバージェンスの質は、格付け表で価値あるポジションを獲得する希望を与えてくれる。

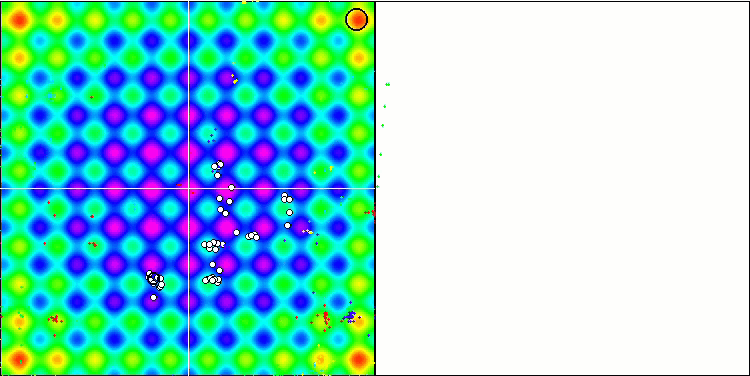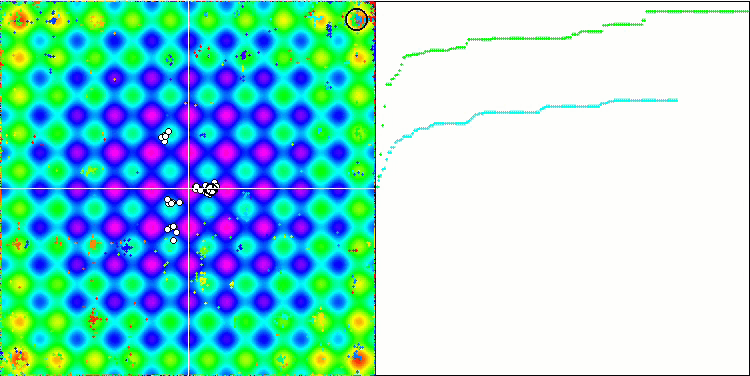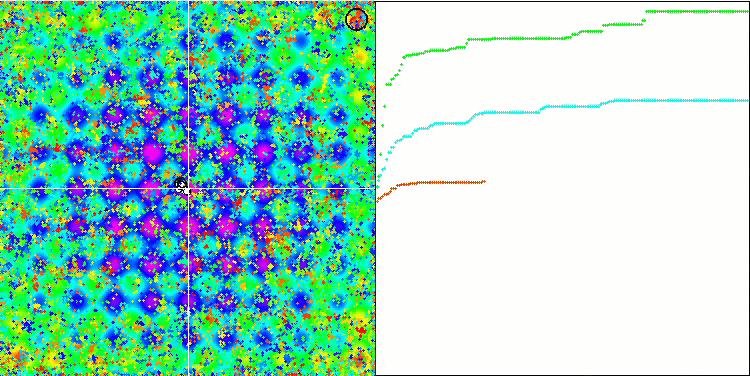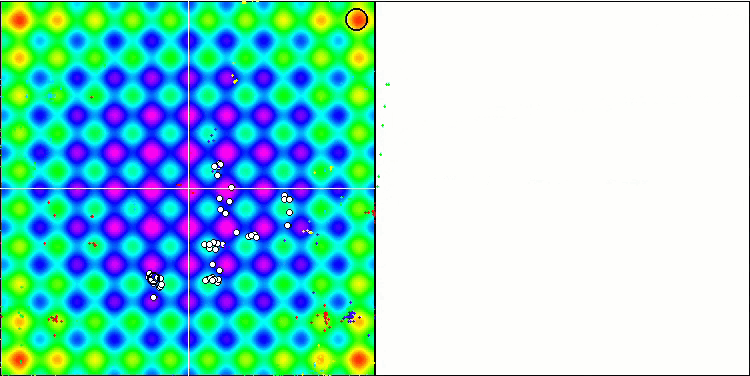
  ラストリギンテスト機能に関するMEC。

  フォレストテスト機能のMEC。

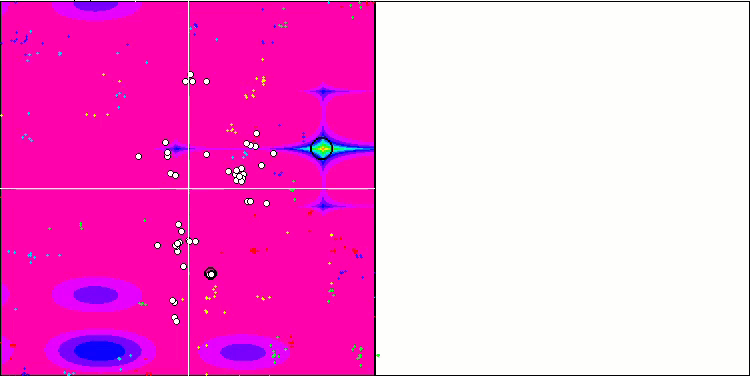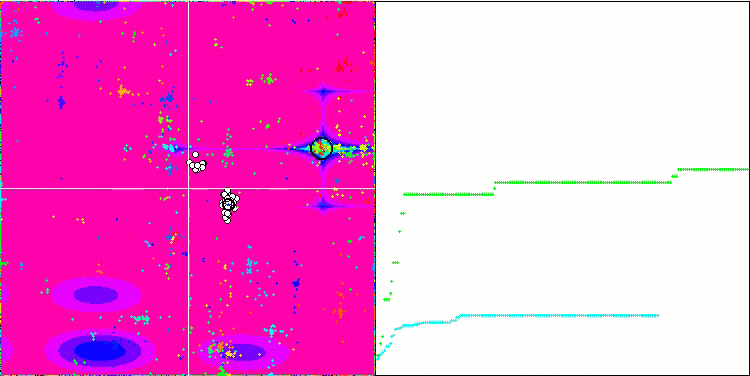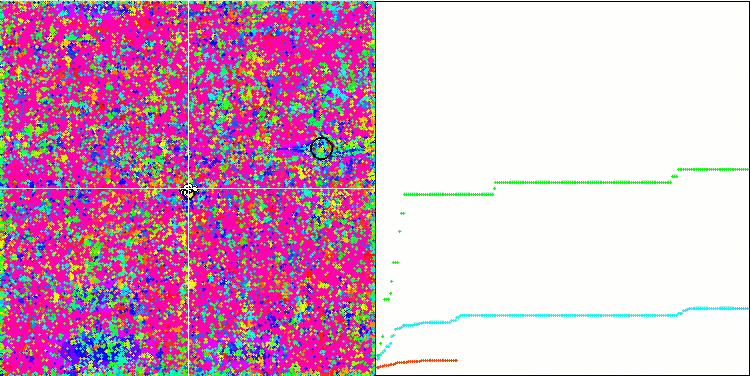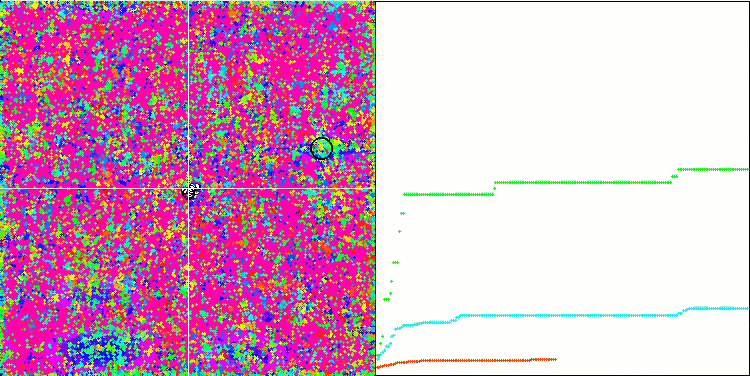
  メガシティテスト機能のMEC。

最適化アルゴリズムのテスト結果のランキング表を分析すると、MECアルゴリズムが非常に高いパフォーマンスを達成し、名誉ある第5位を獲得したことがわかります。MECは、Rastrigin関数、Forest関数、Megacity関数において、これらのテスト関数の表面は全く異なるにもかかわらず、優れた結果を示した。特に印象的な結果は、10個のパラメータを持つメガシティ機能で達成されます。しかし、MECは、比較分析の他の参加者と比べて、最適化されたパラメータがより少ない関数で、さらに高い効率を示したことは注目に値します。これはむしろデメリットだ。 

#	AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（個別）			Megacity最終	最終結果
			10ポンド（5金）	50p(25F)	1000p(500F)		10ポンド（5金）	50p(25F)	1000p(500F)		10ポンド（5金）	50p(25F)	1000p(500F)
1	SSG	苗木の播種と育成	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100000
2	HS	ハーモニー検索	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
3	ACOm	蟻コロニー最適化M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
4	IWO	侵入雑草最適化	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
5	メック	Mind Evolutionary Computation	0.99270	0.51040	0.22800	1.73110	0.60762	0.40658	0.25459	1.26880	0.93335	0.41328	0.26170	1.60833	56.227
6	COAm	カッコウ最適化アルゴリズムM	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
7	FAm	ホタルアルゴリズムM	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
8	ABC	人工蜂コロニー	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
9	GSA	重力探索法	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
10	BA	コウモリアルゴリズム	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
11	BFO	細菌採餌の最適化	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
12	ゆうようびせいぶつぐん	電磁気学的アルゴリズム	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
13	SFL	Shuffled Frog-Leaping	0.40072	0.23739	0.26548	0.90360	0.20153	0.04147	0.02652	0.26952	0.27273	0.05535	0.06639	0.39446	15.203
14	MA	モンキーアルゴリズム	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
15	FSS	魚群検索	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
16	PSO	粒子群最適化	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
17	RND	ランダム	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
18	GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

まとめ

Mind Evolutionary Computation (MEC)アルゴリズムは、生物進化の原理に基づいた効率的で強力な最適化手法です。複雑な最適化問題を解くのに魅力的な、多くの重要な利点があります。

Mindアルゴリズムの進化は、関数最適化、最適パラメータ値の探索、機械学習問題など、幅広い問題に適用できます。目的関数の解析形式の知識を必要とせず、連続、離散、組み合わせの解空間を扱うことができます。

MECは容易に並列化できるため、複数の計算資源を使用して最適化プロセスを高速化できます。これは、多くの計算や反復を必要とする問題を扱うときに特に便利です。

MECは局所極値で立ち往生する傾向がありますが、この欠点は主に離散関数やのこぎり状関数で現れます。適応度関数を設計する場合、この欠点は取るに足らないと考えることができます。

MECは、解空間の次元が高い問題で比較的良好な性能を発揮します。このアルゴリズムはあまり研究されておらず、改善の可能性があります。

一般的に、MECアルゴリズムは、柔軟性、多用途性、局所極限の精緻化を備えた強力な最適化ツールです。これらの利点により、様々な分野における複雑な最適化問題を解くための魅力的な選択肢となっています。アルゴリズムロジックがシンプルであることは、非標準のカスタムソフトウェアソリューションにおいて特に有用です。

個々のアルゴリズムの長所と短所をより視覚的に表現するために、上の表は図3のカラースケールを使って表すことができます。

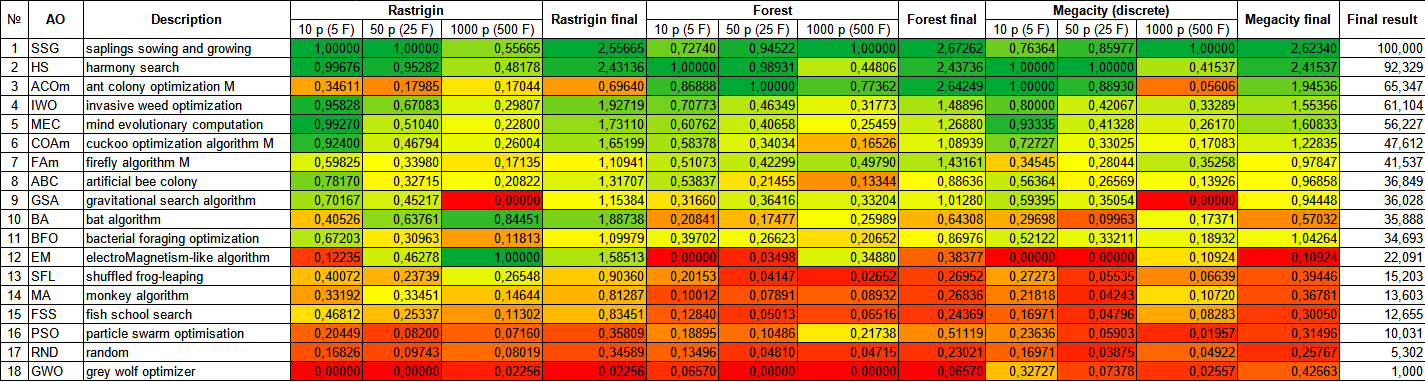
図3：関連テストによるアルゴリズムのカラーグラデーション

アルゴリズムのテスト結果のヒストグラムを以下に示します（0から100までのスケールで、多ければ多いほど良い。アーカイブには、この記事で説明した方法で格付け表を計算するスクリプトがある）。

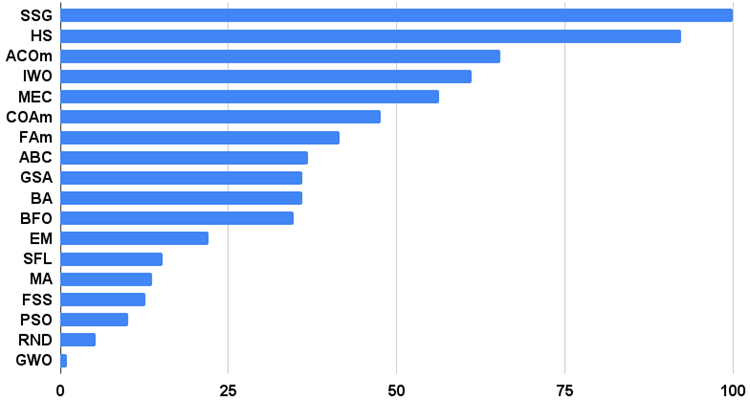
図4：テストアルゴリズムの最終結果のヒストグラム

MECの長所と短所は、次の通りです。

長所
1.外部パラメータが最小数
2.様々な問題を高い効率で解決
3.コンピューティングリソースへの負荷が低い
4.実装が容易

短所
1.水平に平らな「パッド」を持つ機能でスタックします。

各記事には、過去の記事のアルゴリズムコードを最新版に更新したアーカイブが用意されています。しかし、基準のアルゴリズムの記述における絶対的な正確さについては責任を負いませんのでご注意ください。私はしばしば、自分の経験や個人的な意見に基づいて、自分なりのアイデアや改良を加えます。記事に示された結論と判断は、実験結果に基づいています。