母集団最適化アルゴリズム：焼きなまし(SA)アルゴリズム（第１部）

MetaTrader 5 — 例 | 22 4月 2024, 11:30

209

Andrey Dik

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

焼きなましアルゴリズムは、1983年にScott Kirkpatrick、George Gelatt、Mario Vecchiによって開発されました。高温での液体と固体の特性を研究したところ、十分に高い初期温度と十分に長い冷却時間の条件下では、金属は液体状態に変化し、粒子は無作為に分布し、エネルギーは最小の状態に達することが判明した。この条件が満たされない場合、材料は最小ではないエネルギーを持つ準安定状態になります。これは硬化と呼ばれ、材料の急激な冷却を伴います。この場合、原子構造には対称性がありません（異方性状態、つまり結晶格子内の物質の特性が不均一になります）。

低速の焼きなまし過程では、材料も固体状態に変わりますが、原子が整然と並び対称性を持つため、この過程を使用して、複雑な問題で全体最適値を見つけることができる最適化アルゴリズムを開発することが提案されました。このアルゴリズムは、組み合わせ最適化問題を解く方法としても提案されています。

したがって、アルゴリズムの主なアイデアは、金属の焼きなまし過程の数学的類似物に基づいています。焼きなまし過程では、内部エネルギーを均等に分散させるために、金属を高温に加熱し、その後ゆっくり冷却します。これにより、金属分子がより安定した状態に移動し、金属の内部応力が緩和され、結晶間の欠陥が除去されます。「焼きなまし」という用語は、材料の属性であり、その状態に依存する熱力学的自由エネルギーにも関連しています。

焼きなまし最適化アルゴリズムでも同様の過程が使用されます。アルゴリズムは、材料の加熱と冷却に似た操作を適用します。このアルゴリズムは、初期解から作業を開始します。初期解は無作為でもよいし、以前の反復から得られたものでもいいです。そして、解の状態を変化させる操作を適用します。この操作は無作為でも制御されていてもよく、現在の状態より悪くても新しい状態を得ることができます。より悪い決定を下す確率は「冷却」機能によって決定されます。この機能は、時間の経過とともにより悪い決定を下す確率を減らし、アルゴリズムが一時的に局所的最適解から「抜け出して」、検索空間内の他の場所でより良い解決策を探すことを可能にします。

焼きなましアルゴリズムは、次の3つの主要な概念に基づいています。

無作為性の適用：アルゴリズムは無作為操作を使用して解の状態を変更し、次の状態を選択します。これにより、検索空間のさまざまな領域を探索し、局所的最適解に陥らないようにします。

より悪い決断を受け入れる：SAは、より良い決定よりも、ある程度の確率でより悪い決定を優先する数少ないアルゴリズムの1つです。

悪い決断を下す可能性を徐々に減らす：このアルゴリズムは、時間の経過とともに悪い決定を下す可能性を減らす「冷却」過程を使用します。これにより、まず検索空間をより広範囲に探索し、次に検索空間の探索と活用のバランスを取りながら解の改善に集中できるようになります。

焼きなまし最適化アルゴリズムは、メタヒューリスティックスで使用される方法の1つであり、複雑な最適化問題を解決するためのアルゴリズムのクラスを記述します。これらは、すべての可能なオプションを完全に検索する必要なく、検索空間内で近似解を検索できるヒューリスティックな方法に基づいています。無作為性は、メタヒューリスティックスにおける新しい有望な解決領域を発見することを可能にする重要な要素の1つです。このアルゴリズムは、「確率的最適化手法」と呼ばれるアルゴリズムのグループに属します。

SAアルゴリズムには欠点があり、それについては以下で説明します。SAに基づいて、適応型焼きなまし(ASA)や量子正規化（Quantum Normalization、QN）（別名量子焼きなまし法(QA)）などの他のアルゴリズムも開発されています。

2.アルゴリズム

著者が提案した焼きなましアルゴリズムの基本バージョンは非常にシンプルですが、温度変化過程のグラフと最悪の決定を下す確率のグラフを視覚的に表示せずにアルゴリズムがどのように機能するかを想像するのは簡単ではありません。

段階的に理解していきましょう。アルゴリズムは、冶金における材料の加熱に対応する特定の初期高温 (外部パラメータ) で動作を開始します。高温は、異なるエネルギー状態（低いまたは高い）から移動する分子のエネルギーが高いことを意味します。金属における高エネルギー運動のこの過程と同様に、システムはある程度の確率でより悪い決定を下す可能性があります。

山の頂上からのスキーヤーの動きを想像してみましょう。スキーヤーは自分が局地的な低地にいることに気づいたときに、山のふもとに到達したと判断するかもしれません。決定が正しいことを確認するには、位置を少し悪くして、ある程度の高さまで上昇し、さらに速い速度で急降下する必要があります。これが、ある程度の確率でより悪い決定を下すという点です。局所的な「罠」から抜け出すために、同時に2つの場所に存在する量子効果をシミュレートする量子焼きなましアルゴリズムが開発されました。このアルゴリズムでは、トンネル効果を使用して「壁」を飛び越えることになっていますが、いくつかの欠点を取り除こうとすると、量子焼きなましには他の欠点、特に量子遷移の強度を選択する問題が生じます。

焼きなましを説明するために、いくつかの簡単な方程式が使用されます。エネルギー計算式：

E = f (x)

つまり、Eはエージェントの現在の状態に対する適合度関数の値を表します。

エネルギー変化計算式：

ΔE = E_new - E_old

ここで

ΔE：現在の状態から新しい状態への移行中のエネルギーの変化（2回の連続した反復における適応度関数の値の差）
E_new：新しい状態のエネルギー値
E_old：前の状態のエネルギー値

より悪い決定を下す確率を計算する式：

P = exp (-ΔE / T)

ここで

P：より悪い決定を下す確率
T：現在の温度

P確率依存性を示す下のグラフから、ΔEが高いほど確率が低くなることがわかります。これは、温度が下がると、高エネルギーの下向き遷移の確率が、エネルギー差が小さい遷移よりも速く減少することを意味します。言い換えれば、アルゴリズムは「罠」から抜け出すために取るリスクをますます少なくし、解決策の改善のみを優先します。確率プロットは図1に示されています。アルゴリズムでは温度の非線形変化が使用されていますが、わかりやすくするために温度の線形減少が使用されています。

delta ch

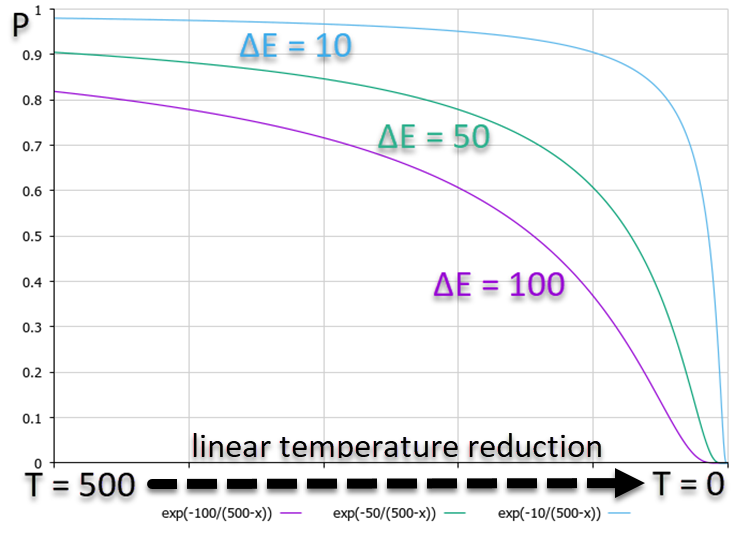
図1：エネルギーの変化に応じた意思決定確率のグラフは、温度の線形低下に伴って悪化する

温度更新方程式：

Tnew = α * Tprev

ここで

α：冷却比（通常0.8～0.99）
Tnew：新しい温度
Tprev：前の温度

開始温度 T = 500でα= 0.99、0.8、0.5、0.1の各反復における温度変化のグラフを図2に示します。温度は徐々に低下し、これは材料の冷却に相当します。各反復で温度を下げると、より悪い決定を下す可能性が減少します。これは、温度の低下に伴って分子がエネルギー状態を変える能力が低下することに対応します。

温度チャート

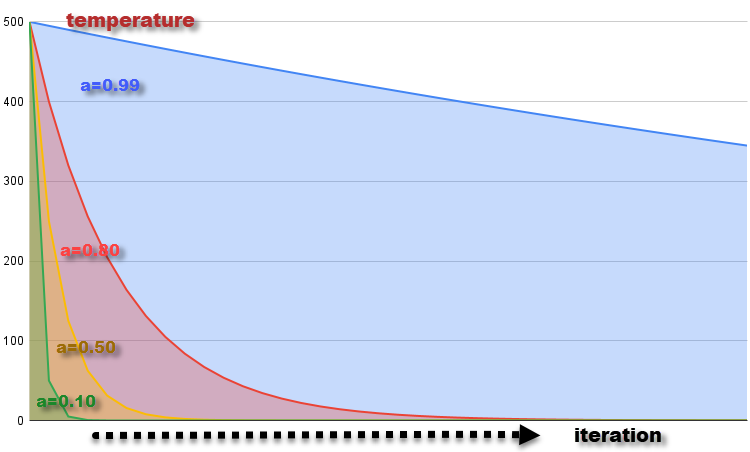
図2：α = 0.99、0.8、0.5、0.1の温度変化グラフ

新しいシステム状態を生成するための方程式：

x_new = GenerateNeighbor (x)

ここで

x_new：現在のxの状態に基づいて生成された新しい状態
GenerateNeighbor (x)：現在の状態に均一分布の無作為な変化を導入して新しい状態を生成する関数

焼きなましアルゴリズムの理論的基礎をすべて理解したので、SAコードを記述するのは難しくありません。エネルギー状態が変化する分子の動きを、最適化問題におけるエージェントに関する情報を含む構造体(S_Agent)の形で表現できます。フィールドと構造体メソッドは次の通りです。

Init (int coords)：エージェントを初期化し、coordsサイズのcおよびcPrev配列にメモリを割り当て、fとfPrevの初期値を「-DBL_MAX」（負の無限大）に設定します
c []：この配列は最適化空間におけるエージェントの座標を表します
cPrev []：エージェントの前の座標を表します
f：エージェントの現在の座標に対する適応度関数の値
fPrev：エージェントの適応度関数の前の値

//————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f     = -DBL_MAX;
    fPrev = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//————————————————————————————————————————

SAアルゴリズムクラスを記述し、C_AO_SAと呼びます。特定の熱変数と定数を除いて、これまで使用したことのない特別なものは何も含まれていないため、非常に単純であることがわかります。

クラスフィールドとメソッド：

cB []：現在の反復時に最適化アルゴリズムによって見つかった最適な座標の配列
fB：最適な座標の適合関数値
a []：エージェントを表します。最適化問題における各エージェントに関する情報を保存するために使用されます。配列の各要素はS_Agent構造体のインスタンスです。
rangeMax []：各エージェント座標の上限検索境界を決定するために使用される各座標の最大検索範囲値の配列
rangeMin []：各エージェント座標の下限検索境界を決定するために使用される各座標の最小検索範囲値の配列
rangeStep []：配列は各座標の検索ステップを表します
Init (const int coordsP, const int popSizeP, const double tP, const double aP, const double dP)：最適化アルゴリズムを初期化し、座標の数coordsP、集団サイズpopSizeP、初期温度tP、温度低下率aP、拡散係数dPをパラメータとして受け入れます。このメソッドはクラスとエージェントフィールドを初期化します
Moving()：最適化中にエージェントを移動し、アルゴリズムを使用してエージェントの新しい座標を決定します
Revision ()：エージェントの現在の値に基づいて、最適な座標と適合関数の修正と更新を実行します
SeInDiSp (double In、double InMin、double InMax、double Step)：Inの値をInMin～InMaxの範囲でStepステップで正規化するために使用されるprivateメソッド
RNDfromCI (double min, double max)：指定された範囲min～maxまでの乱数を生成するために使用されるprivateメソッド

dP拡散比は元のSAバージョンには存在しないことに注意してください。著者のアイデアは、システムの新しい状態を生成し、それに応じて各座標のmin～maxの全範囲にわたってエージェントの新しい座標を生成するというものでした。これは、焼きなましされた金属のvolume全体における分子の無秩序な動きに対応することになります。私の実験では、分子の振動の範囲を、許容される全区間の一部で表現される特定の区間のみに制限すると、結果が改善されることが示されました。拡散比パラメータの正確な目的は、分子の混合の可能性のある領域を制限することです。

元のSAと同等の結果を得るには、パラメータを1（デフォルトは0.2）に設定するだけです。

//————————————————————————————————————————
class C_AO_SA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double tP,           //temperature
                     const double aP,           //temperature reduction coefficient
                     const double dP);          //diffusion coefficient


  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double T;
  private: double α;
  private: double d;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//————————————————————————————————————————

Init関数は初期化メソッドとして機能し、クラスのすべてのフィールドを初期化し、最適化アルゴリズムが機能するために必要な配列のサイズを分散します。

//————————————————————————————————————————
void C_AO_SA::Init (const int    coordsP,      //coordinates number
                    const int    popSizeP,     //population size
                    const double tP,           //temperature
                    const double aP,           //temperature reduction coefficient
                    const double dP)           //diffusion coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords     = coordsP;
  popSize    = popSizeP;
  T          = tP;
  α          = aP;
  d          = dP;

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//————————————————————————————————————————

検索空間内でエージェントを移動するためのMovingメソッドを記述します。
最初の反復では、アルゴリズムが起動されたばかりのとき、変数revisionフラグはfalseに等しくなります。集団エージェントを、[min;max]座標の範囲内の初期値で均一分布で初期化する必要があります。必要な移動ステップを維持するために、エージェントの座標の取得値をSeInDiS関数で正規化します。次に、revisionフラグがtrueに設定され、焼きなましアルゴリズム演算子を次の反復で適用する必要があることを示します。

これが元のSAであれば、最初の反復で行ったことと同じこと、つまり、2回目以降の反復でも均一分布で指定された範囲内の乱数を生成し続けることになります。わずかに修正したバージョンでは、同じことをおこないますが、値の範囲を調整して、金属内の分子の拡散相互作用の領域を制限し、移動は前回の反復で分子があった場所から実行されます。必要な移動ステップを維持するために、エージェントの座標の取得値をSeInDiS関数で正規化します。

//————————————————————————————————————————
void C_AO_SA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (-0.1, 0.1);
      a [i].c [c] = a [i].cPrev [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
      a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//————————————————————————————————————————

Movingメソッドではシステムの新しい状態を生成し（つまり溶融金属内で分子を移動）、Revisionメソッドでは「熱バランス」と分子が新しい状態に遷移する確率を計算します。

メソッドの開始時に、エージェントのすべての適応度関数の値を確認します。グローバル値よりも優れた値が見つかった場合は、それを更新します。

次に、forループで、集団内の各エージェントに対して次のアクションを実行します。

値ΔEは、a[i].fとa[i].fPrevの差の絶対値、つまり現在の反復と前回の反復における適合関数の値の差として計算されます。

a[i].fの値がa[i].fPrevの値より大きい場合（つまり、現在の適応度が前回の適応度よりも優れている場合）、次のコードブロックが実行されます。

値a[i].fPrevはa[i].fに置き換えられる
a[i].cPrev配列の値はa[i].c配列からコピーされる

それ以外の場合は、次のコードブロックが実行されます (適合度関数の現在の値は、前の値よりも悪くなります)。

確率値Pは、ΔEとTの負の比率の指数として計算される
以前の状態よりも悪い新しい状態への遷移の確率をモデル化するrndの範囲[0.0;1.0]から乱数が生成される

rndの値がPの値より小さい場合（つまり、確率が満たされている場合）、次のようになります。

値a[i].fPrevはa[i].fに置き換えられる
a[i].cPrev配列の値はa[i].c配列からコピーされる

温度値Tにα熱比を掛けると、新しい反復ごとに温度が低下します。

//————————————————————————————————————————
void C_AO_SA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double ΔE;
  double P;

  for (int i = 0; i < popSize; i++)
  {
    ΔE = fabs (a [i].f - a [i].fPrev);

    if (a [i].f > a [i].fPrev)
    {
      a [i].fPrev = a [i].f;
      ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
    else
    {
      P = exp (-ΔE / T);
      rnd = RNDfromCI (0, 1.0);

      if (rnd < P)
      {
        a [i].fPrev = a [i].f;
        ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
      }

    }
  }

  T = α * T;
}
//————————————————————————————————————————

3.テスト結果

許容範囲全体の値で乱数を生成する元のアルゴリズムのテストスタンドの結果：

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result:61.3646399742684
Score:0.76034
25 Rastrigin's; Func runs 10000 result:47.454223750487884
Score:0.58798
500 Rastrigin's; Func runs 10000 result:39.06494648961887
Score:0.48404
=============================
5 Forest's; Func runs 10000 result:0.4708272303190655
Score:0.26632
25 Forest's; Func runs 10000 result:0.17553657864203864
Score:0.09929
500 Forest's; Func runs 10000 result:0.0538869772164491
Score:0.03048
=============================
5 Megacity's; Func runs 10000 result:2.6
Score:0.21667
25 Megacity's; Func runs 10000 result:1.0
Score:0.08333
500 Megacity's; Func runs 10000 result:0.3044
Score:0.02537
=============================
All score:2.55383

拡散率を追加したアルゴリズムのテストスタンド結果：

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result:65.78409729002105
Score:0.81510
25 Rastrigin's; Func runs 10000 result:52.25447043222567
Score:0.64746
500 Rastrigin's; Func runs 10000 result:40.40159931988021
Score:0.50060
=============================
5 Forest's; Func runs 10000 result:0.5814827554067439
Score:0.32892
25 Forest's; Func runs 10000 result:0.23156336186841173
Score:0.13098
500 Forest's; Func runs 10000 result:0.06760002887601002
Score:0.03824
=============================
5 Megacity's; Func runs 10000 result:2.92
Score:0.24333
25 Megacity's; Func runs 10000 result:1.256
Score:0.10467
500 Megacity's; Func runs 10000 result:0.33840000000000003
Score:0.02820
=============================
All score:2.83750

拡散率を適用することでアルゴリズムのパフォーマンスが著しく向上したことがわかります。元のアルゴリズムでは、表に含めるために改良が必要でした。このようなよく知られた人気の最適化手法が、特にニューラルネットワークの訓練に適用されているにもかかわらず、このように弱い結果をもたらしたことは予想外です。

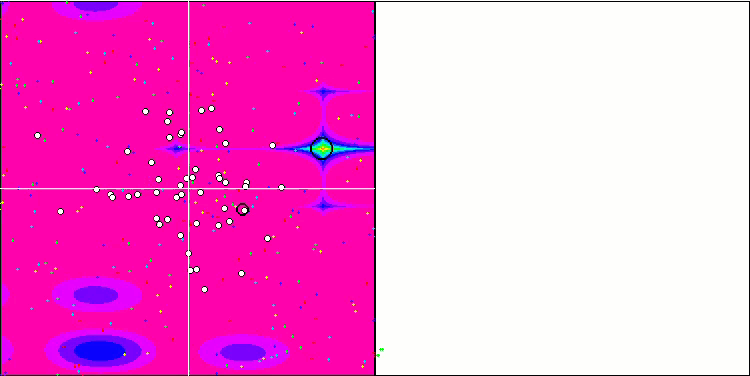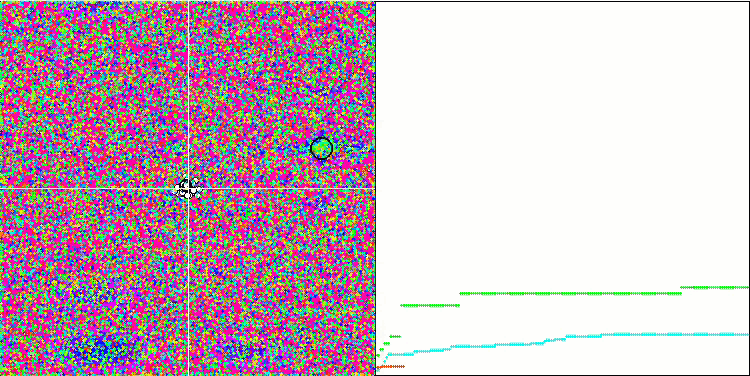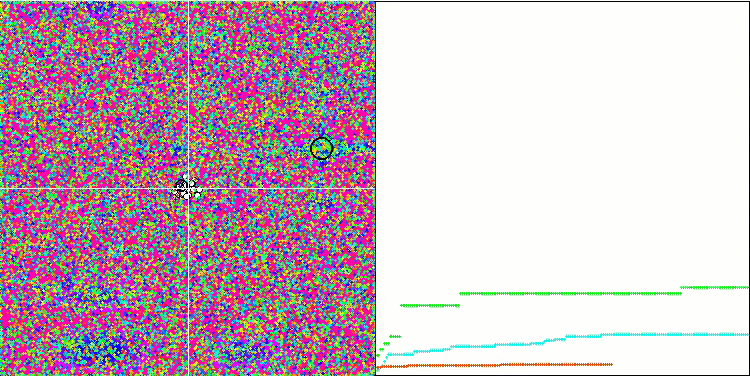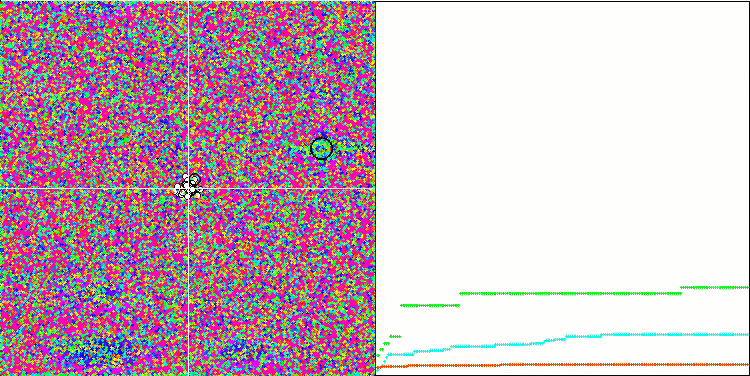
SAの視覚化では、検索空間内のエージェントの動作に目立った特徴は明らかにされませんでした。点は熱ブラウン運動に似た構造を形成せずに無秩序に動作します。さらに、集団の多様性が不足していない、つまり反復の最後に集団が枯渇していないにもかかわらず、アルゴリズムは局所的極値で行き詰まり、収束には多くの改善の余地があります。

rastrigin

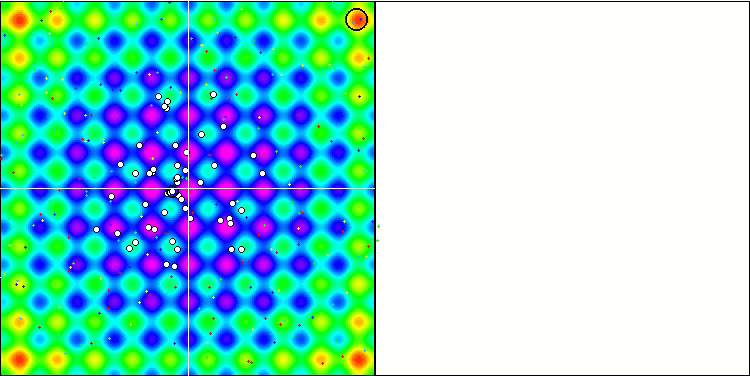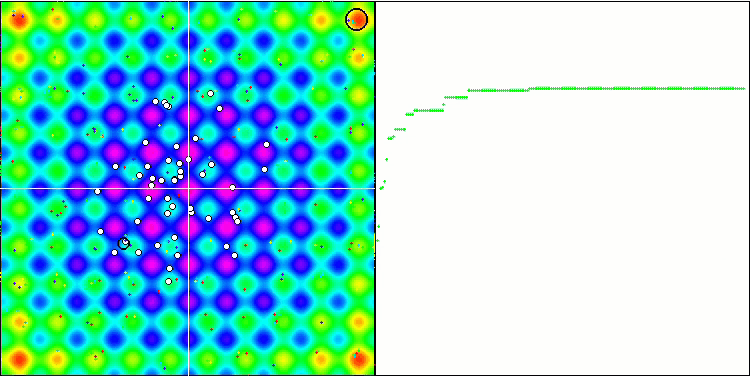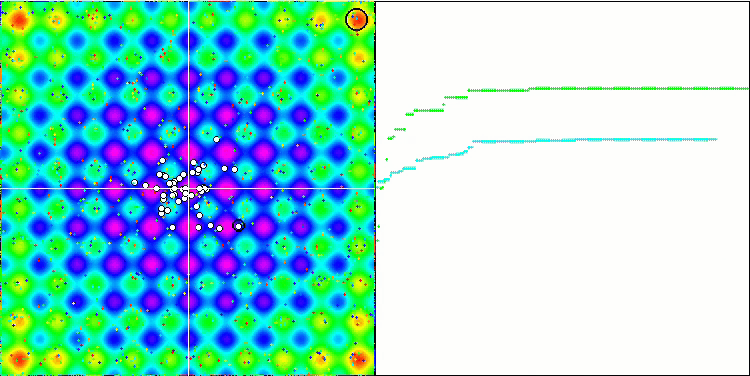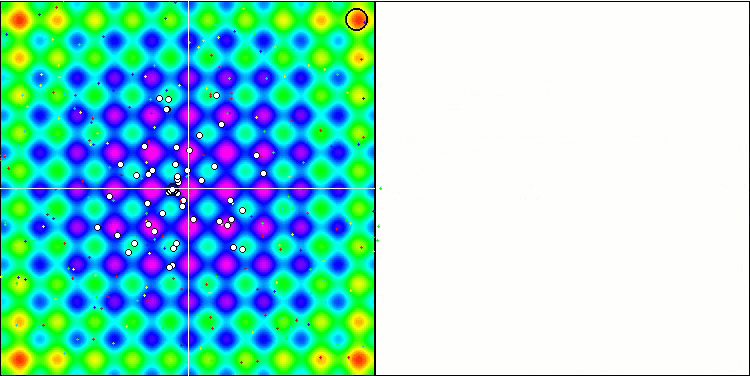
Rastriginテスト関数のSA

forest

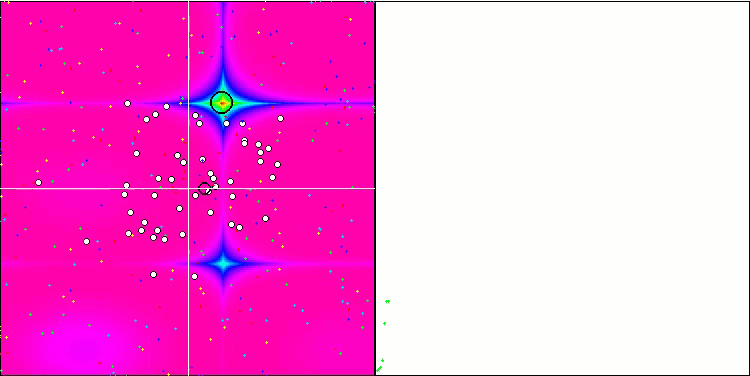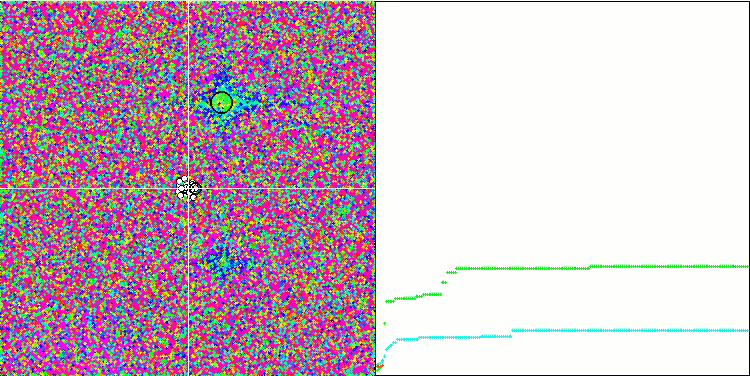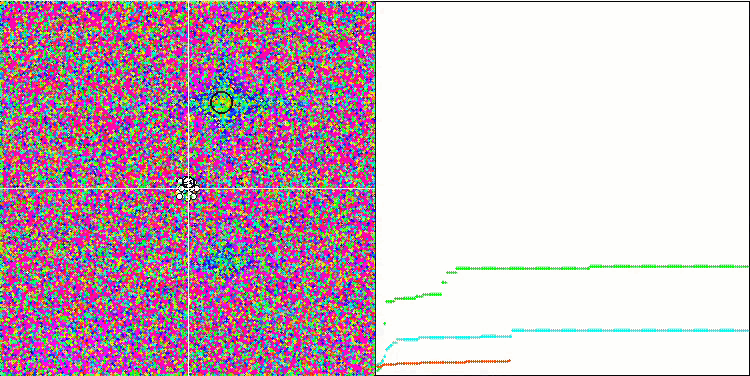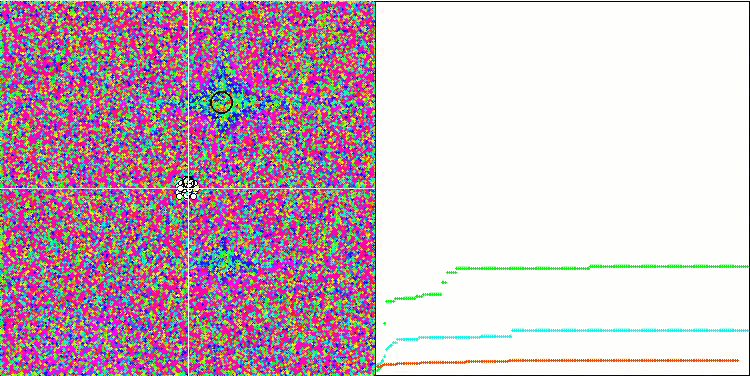
Forestテスト関数のSA

megacity

Megacityテスト関数のSA

焼きなましアルゴリズムは表の一番下にランクされました。比較表を見ると、アルゴリズムには個々のテストにおいて際立った特徴がないことがわかります。すべての結果は平均以下です。表の下部にはありますが、CSSなど、いくつかのテストで優れた結果を示すアルゴリズムも含まれています。残念ながら、SAアルゴリズムはそのうちの1つではありません。

#	AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Rastrigin最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果
1	SDSm	確率的拡散探索M	0.99809	1.00000	0.69149	2.68958	0.99265	1.00000	1.00000	2.99265	1.00000	1.00000	1.00000	3.00000	100.000
2	SSG	苗木の播種と育成	1.00000	0.92761	0.51630	2.44391	0.72120	0.65201	0.83760	2.21081	0.54782	0.61841	0.99522	2.16146	77.683
3	DE	差分進化	0.98295	0.89236	0.51375	2.38906	1.00000	0.84602	0.65510	2.50112	0.90000	0.52237	0.12031	1.54268	73.099
4	HS	ハーモニー検索	0.99676	0.88385	0.44686	2.32747	0.99148	0.68242	0.37529	2.04919	0.71739	0.71842	0.41338	1.84919	70.623
5	IWO	侵入雑草最適化	0.95828	0.62227	0.27647	1.85703	0.70170	0.31972	0.26613	1.28755	0.57391	0.30527	0.33130	1.21048	48.250
6	ACOm	蟻コロニー最適化M	0.34611	0.16683	0.15808	0.67103	0.86147	0.68980	0.64798	2.19925	0.71739	0.63947	0.05579	1.41265	47.387
7	MEC	MindEvolutionaryComputation	0.99270	0.47345	0.21148	1.67763	0.60244	0.28046	0.21324	1.09615	0.66957	0.30000	0.26045	1.23002	44.049
8	SDOm	螺旋ダイナミクス最適化M	0.69840	0.52988	0.33168	1.55996	0.59818	0.38766	0.37600	1.36183	0.35653	0.15262	0.25842	0.76758	40.289
9	NMm	ネルダー=ミード法M	0.88433	0.48306	0.45945	1.82685	0.46155	0.24379	0.21903	0.92437	0.46088	0.25658	0.16810	0.88555	39.660
10	COAm	カッコウ最適化アルゴリズムM	0.92400	0.43407	0.24120	1.59927	0.57881	0.23477	0.13842	0.95200	0.52174	0.24079	0.17001	0.93254	37.830
11	FAm	ホタルアルゴリズムM	0.59825	0.31520	0.15893	1.07239	0.50637	0.29178	0.41704	1.21519	0.24783	0.20526	0.35090	0.80398	33.139
12	ABC	人工蜂コロニー	0.78170	0.30347	0.19313	1.27829	0.53379	0.14799	0.11177	0.79355	0.40435	0.19474	0.13859	0.73768	29.766
13	BA	コウモリアルゴリズム	0.40526	0.59145	0.78330	1.78002	0.20664	0.12056	0.21769	0.54488	0.21305	0.07632	0.17288	0.46225	29.499
14	CSS	荷電系探索	0.56605	0.68683	1.00000	2.25289	0.13961	0.01853	0.13638	0.29452	0.07392	0.00000	0.03465	0.10856	27.930
15	GSA	重力探索法	0.70167	0.41944	0.00000	1.12111	0.31390	0.25120	0.27812	0.84322	0.42609	0.25525	0.00000	0.68134	27.807
16	BFO	細菌採餌の最適化	0.67203	0.28721	0.10957	1.06881	0.39364	0.18364	0.17298	0.75026	0.37392	0.24211	0.18841	0.80444	27.542
17	EM	電磁気学的アルゴリズム	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	19.002
18	SFL	ShuffledFrog-Leaping	0.40072	0.22021	0.24624	0.86717	0.19981	0.02861	0.02221	0.25063	0.19565	0.04474	0.06607	0.30646	13.200
19	SA	焼きなまし	0.36938	0.21640	0.10018	0.68595	0.20341	0.07832	0.09372	0.37545	0.16956	0.08422	0.10394	0.35772	13.138
20	MA	モンキーアルゴリズム	0.33192	0.31029	0.13582	0.77804	0.09927	0.05443	0.07482	0.22852	0.15652	0.03553	0.10669	0.29874	11.777
21	FSS	魚群検索	0.46812	0.23502	0.10483	0.80798	0.12730	0.03458	0.05458	0.21647	0.12175	0.03947	0.08244	0.24366	11.332
22	IWDm	インテリジェント水滴M	0.26459	0.13013	0.07500	0.46972	0.28358	0.05445	0.05112	0.38916	0.22609	0.05659	0.05054	0.33322	10.423
23	PSO	粒子群最適化	0.20449	0.07607	0.06641	0.34696	0.18734	0.07233	0.18207	0.44175	0.16956	0.04737	0.01947	0.23641	8.426
24	RND	無作為	0.16826	0.09038	0.07438	0.33302	0.13381	0.03318	0.03949	0.20648	0.12175	0.03290	0.04898	0.20363	5.054
25	GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02093	0.02093	0.06514	0.00000	0.00000	0.06514	0.23478	0.05789	0.02545	0.31812	1.000

まとめ

焼きなましアルゴリズムにはいくつかの弱点があり、一部の最適化問題を解決する際の有効性が制限される可能性があります。これらの弱点には次のようなものがあります。

初期解への依存性：他の多くの最適化方法と同様に、焼きなましアルゴリズムは、無作為に選択された初期解に依存する場合があります。初期解が不良である場合、アルゴリズムは局所的最適解で行き詰まり、グローバル最適値を見つけられない可能性があります。

アルゴリズムには、初期のtemperatureや温度変化のステップなどの調整パラメータが必要であり、これがより悪い決定を下す可能性に影響を与えることに注意することが重要です。これらのパラメータは解のパフォーマンスと品質に影響するため、焼きなましアルゴリズムを特定の最適化問題に適用する場合、パラメータの選択と調整は重要な側面となります。これらのパラメータを設定するのは難しい場合があります。設定を誤ると、結果が悪くなる可能性があります。テスト機能セットで最良の結果を得るために、デフォルト設定が選択されました。
焼きなましアルゴリズムのもう1つの弱点は、局所的極値で行き詰まってしまう可能性があることです。これは、アルゴリズムが局所的極値ではあるが全域的極値ではない最適解を見つけた場合に発生します。この場合、アルゴリズムはそれ以上進むことができず、局所的最適解で停止します。これは上の視覚化で非常に明確に確認できます。
収束速度が遅い：SAは、特に複雑な最適化問題の場合、最適解への収束が遅くなる可能性があります。これは、アルゴリズムが無作為性を使用し、より悪い決定を下す可能性があり、最適化の過程が遅くなる可能性があるためです。
多数の反復が必要：最適な解を実現するには、焼きなましアルゴリズムで多数の反復が必要になる場合があります。これは、実行時間が重要な要素となるタスクでは問題になる可能性があります。
変数の数が多い問題を解決する際の効率が低い：多数の変数を持つ問題を解決する場合、検索空間が大きすぎるため、SAは効果がない可能性があります。この場合、遺伝的アルゴリズムや勾配ベースの最適化方法などの他の最適化方法の方が効果的である可能性があります。このアルゴリズムは、単純な無作為なRNDを含むあらゆるアルゴリズムと同様に、少数（1～2）の変数にうまく対応します。

焼きなましアルゴリズムのパフォーマンスと効率を向上させるために適用できる改善点がいくつかあります。

1.冷却機能の変更：冷却機能は、システムの冷却速度と温度を制御するアルゴリズムの重要なパラメータです。

2.次の状態を選択するためのより効率的な方法の使用：SAは次の状態を無作為に選択します。ただし、突然変異法や交差法など、次の状態を選択するためのより効率的な方法があります。

3.適応パラメータの使用：初期温度や冷却率などのアルゴリズムパラメータは、最適化問題の特性に応じて適応的に調整できます。

4.アルゴリズムの組み合わせを使用：SAは、遺伝的アルゴリズムや勾配降下法などの他の最適化アルゴリズムと組み合わせて、最適化のパフォーマンスと効率を向上させることができます。

システムの新しい状態を生成するときに、均一な分布ではなく、異なる分布の無作為変数を使用しても、結果の改善には役立ちませんでした。しかし、この非常に有名で人気のあるアルゴリズムを、トップクラスのアルゴリズムと競争できるレベルまで根本的に変える方法があります。これはどのように可能でしょうか。この記事の後半でこの方法を紹介し、おこなわれた変更のすべての段階について説明します。しかし、ご存知のように、最適化アルゴリズムを改善するための普遍的な方法は存在せず、アルゴリズム自体の検索戦略にのみ依存します。したがって、改善は、古き良き（しかし実際には役に立たない）焼きなましアルゴリズムにのみ関係します。

評価表

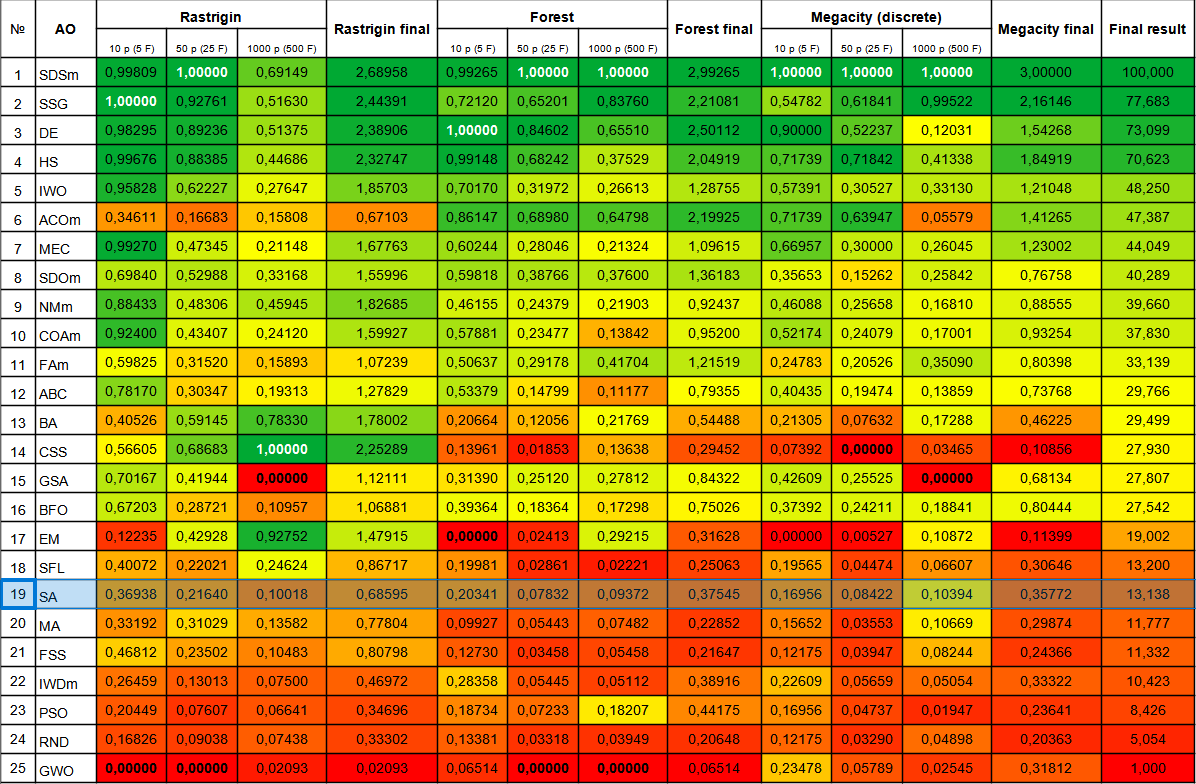
図3：関連テストによるアルゴリズムのカラーグラデーション

チャート

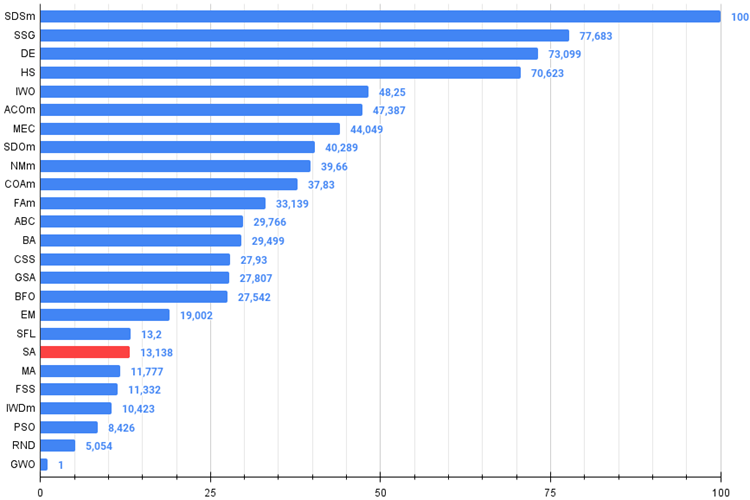
図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

アーカイブには、記事で適用された方法を使用して評価表を計算するためのスクリプトが含まれています。

SAの長所と短所

長所

外部パラメータが少ない
動作速度が高い
実装が非常にシンプル

短所

不明瞭な設定（温度が何にどのように影響するかが明確でない）
拡張性が非常に低い
結果のばらつきが大きい
極値で立ち往生する傾向
収束が悪い

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13851

添付されたファイル |

ZIPをダウンロード

25_The_world_of_AO_SA.zip (405.38 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークが簡単に（第67回）：過去の経験を活かした新しい課題の解決

この記事では、訓練セットにデータを収集する方法について引き続き説明します。明らかに、学習プロセスには環境との絶え間ない相互作用が必要です。しかし、状況はさまざまです。

PythonとMQL5を使用して初めてのグラスボックスモデルを作る

機械学習モデルの解釈は難しく、このような高度なテクニックを使用して何らかの価値を得たいのであれば、モデルが予想から外れる理由を理解することが重要です。モデルの内部構造に対する包括的な洞察がなければ、モデルのパフォーマンスを低下させるバグを発見できないことがあります。予測できない機能のエンジニアリングに時間を浪費し、長期的にはモデルのパワーを十分に活用できない危険性があります。幸いなことに、モデルの内部で何が起こっているかを正確に見ることができる、洗練され、よく整備されたオールインワンソリューションがあります。

MQL5での定量分析：有望なアルゴリズムの実装

定量分析とは何なのか、また、主要プレーヤーがどのように定量分析を使用しているのかを分析します。MQL5言語で定量分析アルゴリズムの1つを作成します。

母集団最適化アルゴリズム：ネルダー–ミード法、またはシンプレックス（NM）検索法

この記事では、ネルダー–ミード法の完全な探求を提示し、最適解を達成するために各反復でシンプレックス（関数パラメータ空間）がどのように修正され、再配置されるかを説明し、この方法がどのように改善されるかを説明します。