母集団最適化アルゴリズム：カッコウ最適化アルゴリズム(COA)
647
0
内容
1.はじめに2.アルゴリズムの説明、決定木、レヴィフライト
3.COAコード
4.テスト結果
1.はじめに
カッコウという鳥には興味をそそられます。その鳴き声によってだけではなく、他の鳥の巣に卵を産み付けるという、その強引な繁殖戦略によってもです。この鳥は子育ての責任を完全に他の種に転嫁するのです。それぞれの種のカッコウは、様々な里親の卵に最も合うように、色や大きさが決まっている卵を産みます。他の鳥の巣に投げ込まれたカッコウのヒナは、通常、巣の持ち主のヒナよりも大きくて強いので、より多くの餌を必要とします。ジュウイチ（カッコウの一種）のヒナは、発達の過程で翼にくちばしのような特殊な模様ができ、里親から多くの餌を受け取ることができるようになります。このような特徴を持つ鳥は、カッコウだけではありません。托卵は少なくとも80種の鳥で確認されています。また、マルハナバチ、ハチ、アリなどの社会性昆虫の一部の種では、雌が別のコロニーに侵入して女王を殺し、卵を産むという現象が広く見られます。口の中で卵を孵化させている他の魚に自らの卵を投げ入れるアフリカのタンガニーカ湖のナマズのように、托卵は一部の魚にも存在します。
カッコウ検索は、2009年にYangとDebによって開発された最新の自然界にヒントを得たヒューリスティックアルゴリズムの1つで、一部のカッコウ種の寄生が元になっています。このアルゴリズムは、単純な等方性ランダムウォーク法ではなく、いわゆるレヴィフライトによって、さらに改良されています。
2.アルゴリズムの説明
カッコウ最適化アルゴリズム(COA)は連続的な非線形最適化に使用されます。COAは、この鳥のライフスタイルにインスパイアされています。この最適化アルゴリズムは、その種の産卵・生殖の特徴に基づいています。他の進化的アプローチと同様に、COAも初期母集団からスタートします。アルゴリズムの基本は、生き残るための試みです。生き残りをかけて競争しているうちに、死んでしまう鳥もいます。生き残ったカッコウは、よりよい場所に移動して繁殖し、卵を産み始めます。最後に、生き残ったカッコウは、適合値が近いカッコウ社会が得られるように収束していきます。
この手法の最大の利点はそのシンプルさにあります。カッコウ検索に必要なパラメータは4つだけなので、チューニングは非常に簡単になります。
カッコウ探索アルゴリズムでは、巣の中の卵を最適化問題の解の候補として解釈し、カッコウの卵が新しい解を表します。この手法の究極の目標は、これらの新しい（そして潜在的に優れた）カッコウの寄生卵の解を使って、現在の巣の卵の解を置き換えることです。この置き換えを繰り返しおこなうことで、最終的に解を導き出します。
Yang教授とDeb教授は、このアルゴリズムの理想的な状態として、次の3つのセットを提案しました。
1.カッコウは1羽に1個の卵を産み、ランダムに選ばれた巣に落とします。
2.質の高い卵を持つ最高の巣は、次の世代に受け継がれます。
3.利用可能な巣の数は一定で、巣は「pa」の確率でよそ者の卵を検出できます。この場合、宿主の鳥は卵を捨てるか、巣から離れるかして、卵は死んでしまいます。
簡単にするために、3番目の仮定はn個の巣のpa分率で近似することができます。最大化問題では、解の質や適切さは、単純に目的関数に比例する場合があります。しかし、適合度関数は他の（より複雑な）式も定義できます。
各反復「g」に対して、カッコウ卵「i」がランダムに選択され、新しい解「xi (g + 1)」がレヴィフライトを用いて生成されます。これは、ある確率分布を持つステップ長の範囲内でステップが決定され、ステップの方向が等方的かつランダムであるランダムウォークの一種です。この手法の原案者によると、レヴィフライトを使う戦略は、他の単純なランダムウォークよりも全体的なパフォーマンスが高く、好ましくなります。一般的なレヴィフライト方程式は次のようになります。
xi(g + 1) = xi(g) + α ⊕ levy(λ)
ここで、gは現在の世代数を示し、α(> 0)はステップサイズを示しますが、これは研究中の特定の問題の規模に関係するはずです。「⊕」は要素ごとの乗算を表します。g + 1世代における次の位置は、g世代における現在の位置と、第1項と第2項でそれぞれ与えられる遷移確率にのみ依存するので、これは本質的にマルコフ連鎖であることにご注意ください。この遷移確率は、レヴィ分布によって次のように変調されます。
levy(λ) ∼ g−λ, (1 < λ ≤ 3)
無限平均で無限分散です。実践によって、2.0の固定度数で最も良い結果が得られることが示されています。ここで、ステップの長さは、基本的にべき乗の裾の重いステップ長分布のランダムウォーク過程を形成しています。計算の観点からは、レヴィフライトを用いた乱数生成は、まず一様分布に従ってランダムな方向を選び、次に選んだレヴィ分布に従ってステップを生成する2段階からなります。その後、アルゴリズムは新しい解の適合性を評価し、現在の解と比較します。新しい解がより良い適合性を提供する場合、それは現在のものを置き換えます。一方、より有望な解を求めて探索空間の探索回数を増やすために、巣を放棄する（巣の持ち主がカッコウの卵を捨てたり、巣を出て卵が死んだりする）ケースもあります。置き換え率は、性能向上のためにチューニングが必要なモデルパラメータであるpa確率で決定されます。このアルゴリズムは、停止基準に達するまで繰り返し適用されます。一般的な終了基準は、低い閾値を満たす解が見つかった場合、一定の世代数に達した場合、連続した反復でより良い結果が得られなくなった場合などです。
ここで、カッコウの産卵の過程をもう少し詳しく見てみましょう。すべての巣の中から、卵が産まれるはずの巣がランダムに選ばれます。卵は解なので、卵の質で表すことができます。カッコウの卵が巣主の卵より高品質であれば、置き換えられことになります。そうでなければ、巣主の卵が巣に残ってしまいます。実際、その後の進化は生き残ったヒナから続いていくことになります。つまり、巣主の卵のたヒナが生き残ったのであれば、同じところから進化が続くということです。カッコウの卵により生存能力があり、新たな場所から問題解決のための探索が続いてこそ、さらなる発展が可能となるのです。決定木は図1に模式的に示されています。
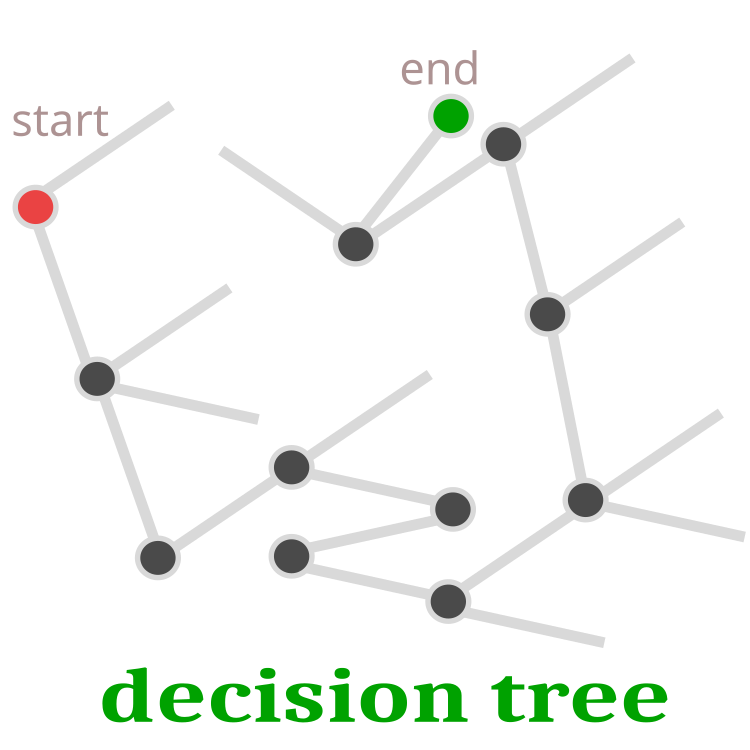
図1：決定木 - 赤い点が始まりで、緑の点が最終決定
決定木に続くアルゴリズムの基礎となる2つ目の要素は、レヴィフライトです。レヴィフライトは、ジャンプの長さがステップで変化し、ジャンプの方向がランダムに変化するランダムウォーク（マルコフ統計過程）であり、確率分布はパレート分布の特殊例で、裾が重いことが特徴です。空間におけるジャンプと定義され、ジャンプはランダムな方向に等方的です。レヴィフライトは、異常な確率過程を記述するためのツールです。分散は無限大（長いジャンプが可能）で、ジャンプの長さはどのレベルでも自己相似的（短いジャンプと長いフライトが混在）です。レヴィフライトという言葉は、連続空間ではなく、離散的なグリッド上で発生するランダムウォークを含むように拡張されることもあります。
パラメータが1つの最適化問題を考えてみると、カッコウアルゴリズムにおけるレヴィフライトの明確な応用例を想像できます。定義域の大部分で変化しない、すなわち水平線(y=x).である仮想の関数（図2の黒線）を考えてみましょう。狭い範囲でだけ、関数が変化して最大値が1つあります。図2のオレンジ色の点から最大値の探索を開始し、次にレヴィ分布のランダムな値xを得ると、関数の変化を得られないまま、開始点から遠ざかっていくことになります。ただし、分布の裾に強いジャンプがあると、元のオレンジの点よりも良い解である緑の点が得られ、その緑の点からだけ、関数の最大値に近づきながら、結果を改善することができるのです。この例では、レヴィフライトによってアルゴリズムの探索能力が飛躍的に向上しています。
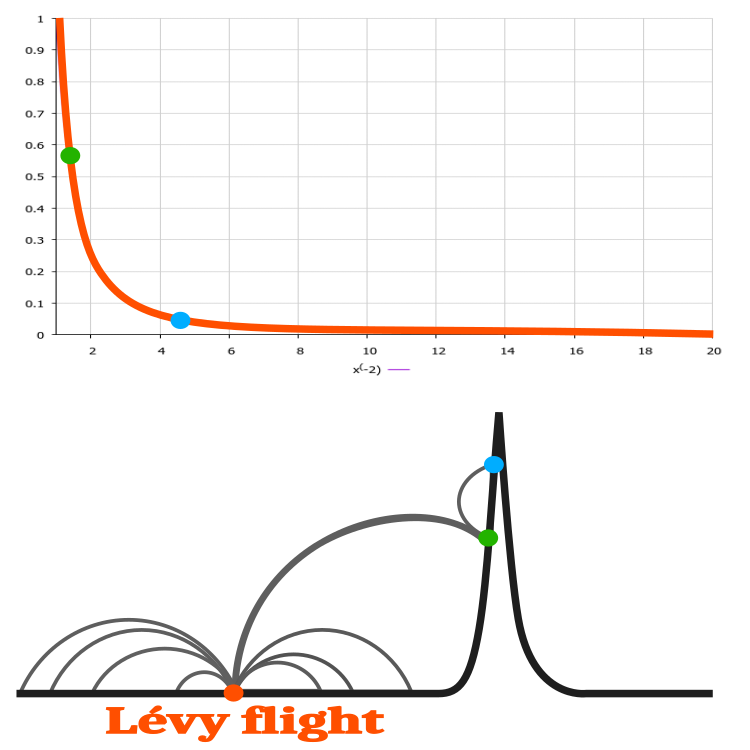
図2：レヴィフライトを使用して仮想的な1次元関数の解を見つける例
レヴィフライトの概念は、カオス理論において、ランダムあるいは擬似ランダムな自然現象（例：長い軌道と短い軌道を組み合わせるアホウドリの飛行）をモデル化する際に用いられます。地震データ解析、金融数学、暗号、信号解析、乱流運動などが例で、天文学、生物学、物理学などにも多くの応用があります。
COAアルゴリズムの擬似コード（図3）。
1.ランダムな値でカッコウを初期化する
2.適合を定義する
3.ランダムに巣に卵を産み付ける
4.所定の確率で巣を空にする
5.現在位置からレヴィフライト距離内のランダムな方向へカッコウを送る
6.適合を定義する
7.ランダムに巣に卵を産み付ける
8.所定の確率で巣を空にする
9.停止基準に達するまで5から繰り返す
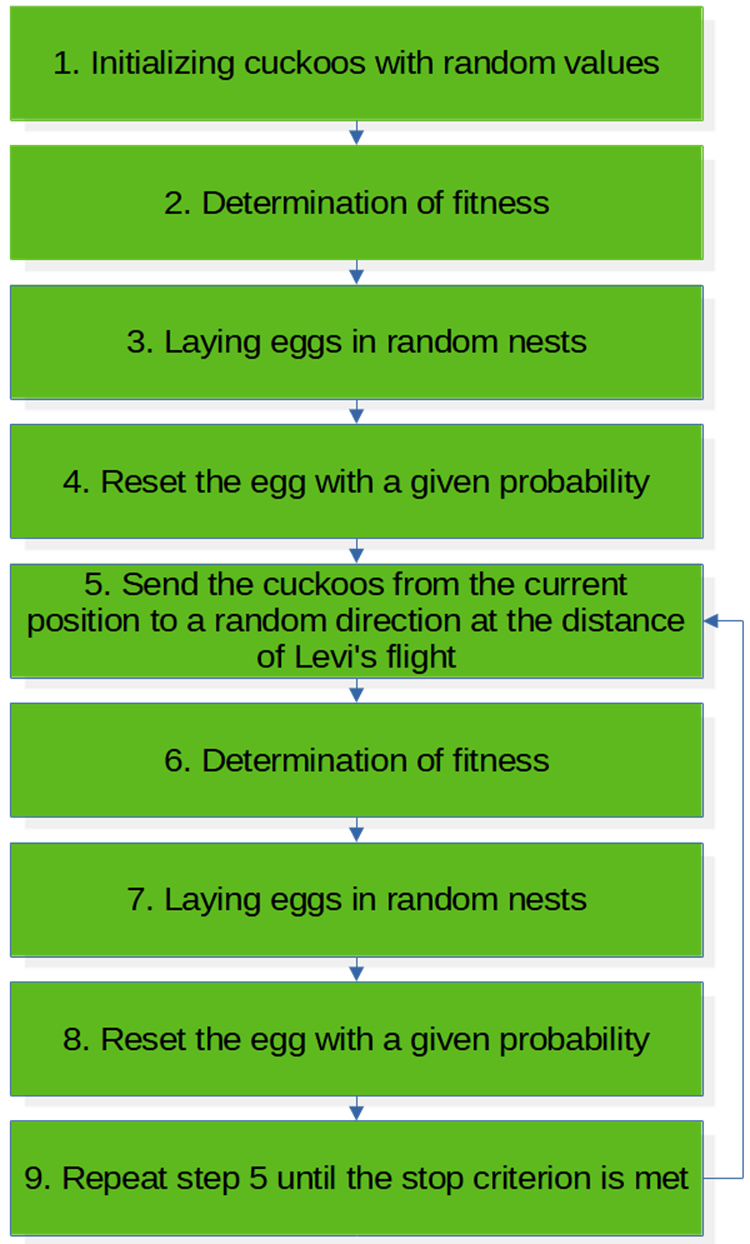
図3：COAアルゴリズムブロック図
3.COAコード
まず、アルゴリズムのコードから考えてみましょう。問題の解は、卵でもあるカッコウです。これは、探索空間内の座標と、適合度関数（卵の品質）の値を含むシンプルな構造です。
//—————————————————————————————————————————————————————————————————————————————— struct S_Cuckoo { double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
巣を構造体で表現してみましょう。ここでは、卵の構造と同じように、空間上の座標と、適合度関数の値があります。「巣に卵を産む」とは、基本的に、卵の構造体を巣の構造体に複製することです。確率パラメータpaを使用する場合、0.0からpaまでの乱数が[0.0;1.0]の範囲に落ち、eの値が-DBL_MAXに等しいとき卵が巣から排出されます。
//—————————————————————————————————————————————————————————————————————————————— struct S_Nest { void Init (int coordinates) { ArrayResize (c, coordinates); e = -DBL_MAX; } double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
アルゴリズムクラス：ここでは、public初期化メソッド、ユーザープログラムでの主な2つの呼び出しメソッド、最適化問題の引数の値の範囲、サービス関数を実行する追加のprivateメソッドが宣言されています。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Cuckoo cuckoos []; //all the cuckoos public: double cB []; //best coordinates (egg parameters) public: double eB; //best eggs quality public: void Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP); //step control value public: void CuckooFlight (); public: void LayEggs (); //============================================================================ private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: S_Nest nests []; //nests private: int cuckoosNumber; //number of cuckoos private: int nestsNumber; //number of cuckoo nests private: double koef_pa; //probability of detection of cuckoo eggs private: double koef_alpha; //step control value private: double v []; private: int coordinates; //coordinates number private: bool clutchEggs; //clutch of eggs }; //——————————————————————————————————————————————————————————————————————————————
Init() publicメソッド：ここでは、変数の値がリセットされ、配列のメモリが確保されます。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP) //step control value { MathSrand (GetTickCount ()); clutchEggs = false; eB = -DBL_MAX; coordinates = coordinatesP; cuckoosNumber = cuckoosP; nestsNumber = nestsP; koef_pa = koef_paP; koef_alpha = koef_alphaP; ArrayResize (nests, nestsNumber); for (int i = 0; i < nestsNumber; i++) { nests [i].Init (coordinates); } ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (v, coordinates); ArrayResize (cuckoos, cuckoosNumber); for (int i = 0; i < cuckoosNumber; i++) { ArrayResize (cuckoos [i].c, coordinates); } } //——————————————————————————————————————————————————————————————————————————————
「カッコウ飛行」の各反復で呼び出される最初のpublicメソッド：clutchEggsフラグがオフの場合は、対応する座標の範囲で乱数を発生させてランダムな方向にカッコウを送ります。このフラグが有効な場合、vベクトルの範囲内のレヴィフライトの分布に従って、カッコウの実際の飛行が実行されます。各座標は異なる値の範囲を持つ可能性があるため、vベクトルは各座標ごとにInit()で事前に計算されます。
式「cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0);」は、オフセット「r1 * v [c] * pow (r2, -2.0)」を加えることを意味します．ここで、r1は-1または1で元の位置からのオフセット方向、vは移動ベクトル，r2は 0.0 ～ 20.0を-2.0乗した範囲の乱数です。乱数をあるべき乗に上げるのがレヴィフライト機能です。そのグラフが図2です。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::CuckooFlight () { //---------------------------------------------------------------------------- if (!clutchEggs) { for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } clutchEggs = true; } else { double r1 = 0.0; double r2 = 0.0; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
これは、反復ごとに呼び出される2番目のpublicメソッドです。このメソッドでは、巣にカッコウの卵を産み付けるシミュレーションをアルゴリズムで再現しています。これは、既存のすべての巣からランダムに巣を選択することでおこなわれます。その後、カッコウの卵とすでに巣にある卵のの品質が比較されます。カッコウの卵の方が良ければ、置き換えがおこなわれます。このメソッドのアルゴリズムの面白いところは、カッコウの卵がより適合していたとしても、産卵後に卵が死ぬかどうかの確率を実行することです。つまり、自然界と同じように、どんな卵でも死んでしまう可能性koef_paがあるのです。もし卵が死んだり巣から捨てられたりした場合（実際、どちらでも同じです）、その巣は、あらゆる適合度の卵（適合度がもっと低い卵でも）を産卵するために自由に使えるようになります。アルゴリズムでいえばこれは新しい場所での研究を意味します。
こうすることで、托卵のような自然進化の手法の1つを、わずか数行のコードで記述することができるのです。多くの著者は、卵を取り除いた後の巣を新しいランダムな値で初期化することを論文で推奨しており、これは探索を最初から始めることを意味しています。多くの場合、アルゴリズムの探索能力を高めるという点では、これで望ましい結果を得ることはできません。私の研究によると、卵の質はともかく、巣を空にしておけばカッコウが卵を産んでくれるという都合のいいことが分かっています。これは単なるランダムな値よりも優れています。この研究の変動性は、現在の座標からランダムな方向にジャンプすることによってもたらされます。その結果、最適な解を探すための反復回数が減り、アルゴリズム全体の収束率が高まるのです。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::LayEggs () { int ind = 0; //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ for (int i = 0; i < cuckoosNumber; i++) { ind = (int)round (RNDfromCI (0.0, nestsNumber - 1)); if (cuckoos [i].e > nests [ind].e) { nests [ind].e = cuckoos [i].e; ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY); if (cuckoos [i].e > eB) { eB = cuckoos [i].e; ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY); } } else { ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY); } } //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv for (int n = 0; n < nestsNumber; n++) { if (RNDfromCI (0.0, 1.0) < koef_pa) { nests [ind].e = -DBL_MAX; } } } //——————————————————————————————————————————————————————————————————————————————
4.テスト結果
以下がテスト結果です。
2022.11.30 11:31:54.490 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 1 Skin's; Func runs 10000 result:4.918379100238852
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) Score:1.00000
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 20 Skin's; Func runs 10000 result:4.257477577760983
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) Score:0.84220
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 500 Skin's; Func runs 10000 result:1.3521208312080903
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) Score:0.14849
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 1 Forest's; Func runs 10000 result:1.7600394018343262
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) Score:0.99557
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 20 Forest's; Func runs 10000 result:0.4968964923017033
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) Score:0.28107
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 500 Forest's; Func runs 10000 result:0.07638950254648778
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) Score:0.04321
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 1 Megacity's; Func runs 10000 result:12.0
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) Score:1.00000
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 20 Megacity's; Func runs 10000 result:2.69
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) Score:0.22417
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 500 Megacity's; Func runs 10000 result:0.40800000000000003
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) Score:0.03400
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) All score for C_AO_COA:0.507633670637353
レヴィフライトカッコウ検索アルゴリズムは、印象的な結果を示しました。ほとんどのテストにおいて、他の最適化アルゴリズムよりも優れた結果を残しています。特に、2つの変数を持つ滑らかなSkin関数と、2つの変数を持つ離散的なMegacity関数に対して、100%の収束率を示しました。さらに驚くべきは、離散的な関数に対して優れたスケーラビリティを示したことです。他のテストでは、蟻コロニーアルゴリズムにわずかに劣る程度です。現時点では、評価表のリーダーであることは間違いありません。
すべてのアルゴリズムには、最終的な結果に影響を与えるチューニングパラメータがある程度存在するため、これらのアルゴリズムの中にはさらに最適なパラメータが存在し、評価表が異なるものになる可能性も十分にあることを明確にしておきたいとおもいます。私は、最良の結果を確保するためのパラメータを見つけて、テスト結果を示しただけです。もっと最適なパラメータを見つけ、より良い結果を得ることができれば、それに基づいて評価表を修正することができます。蟻アルゴリズムは現在のリーダーと首尾よく競合できるという前提があります。これは、一部の指標ではカッコウ検索アルゴリズムよりも進んでおり、最終的な指標に関してはわずかに遅れているためです。GWOは、1000個の変数を持つSkin関数では今でもリーダーです。いずれにせよ、プロジェクトで最適化問題を解決する際にアルゴリズムを使用する方は、表をナビゲートして、特定のニーズに合ったアルゴリズムを選択してください。
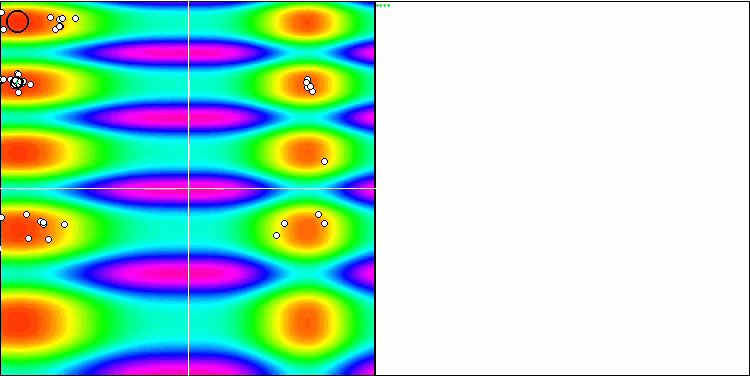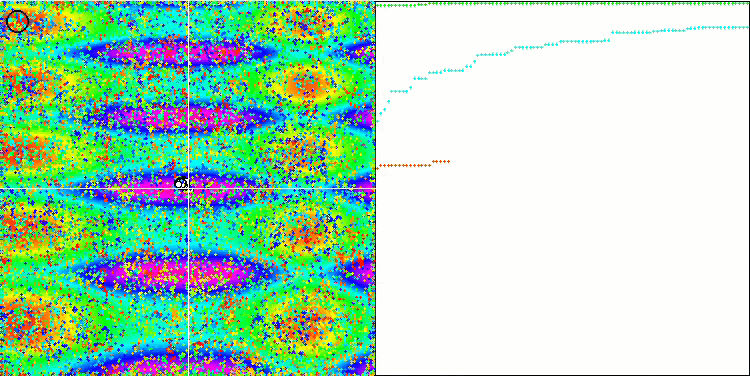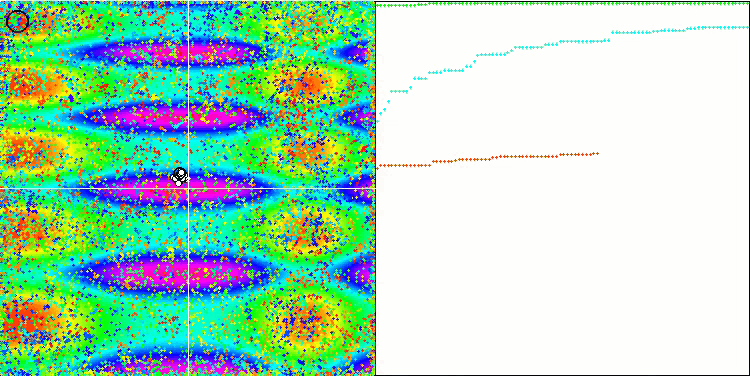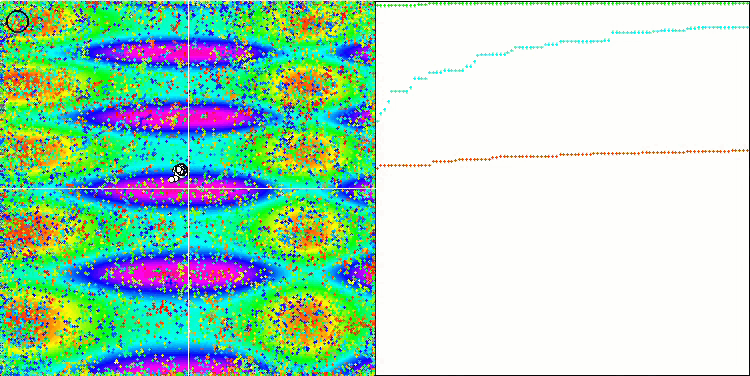
Skinテスト関数のCOA
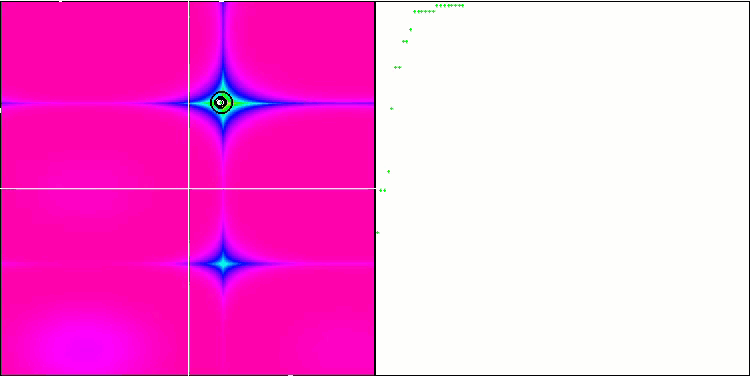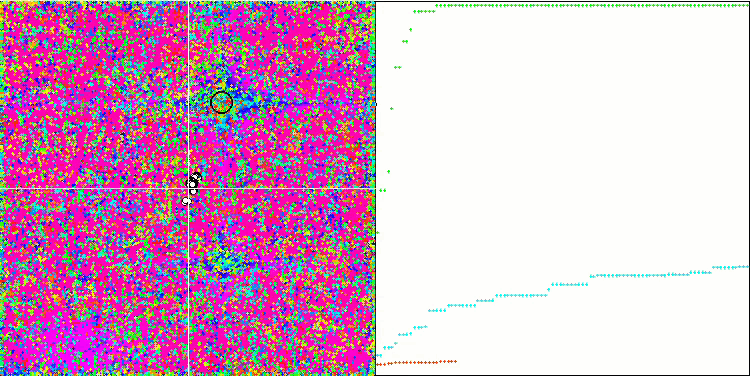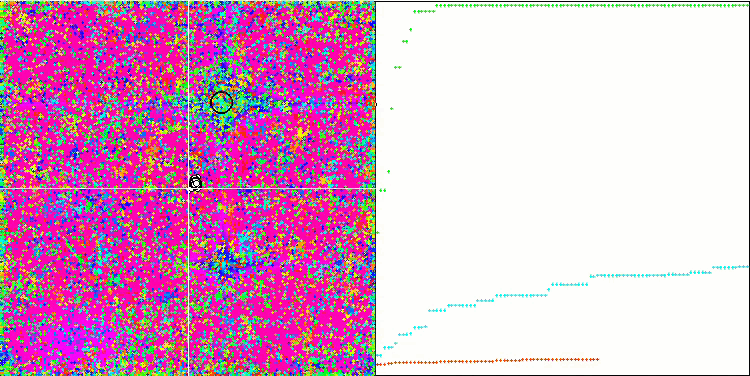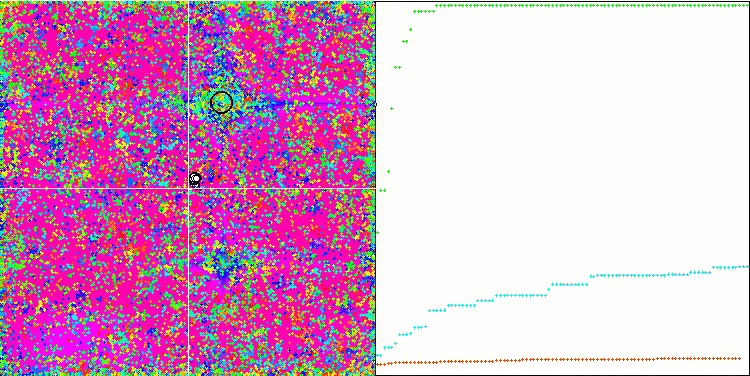
Forestテスト関数のCOA
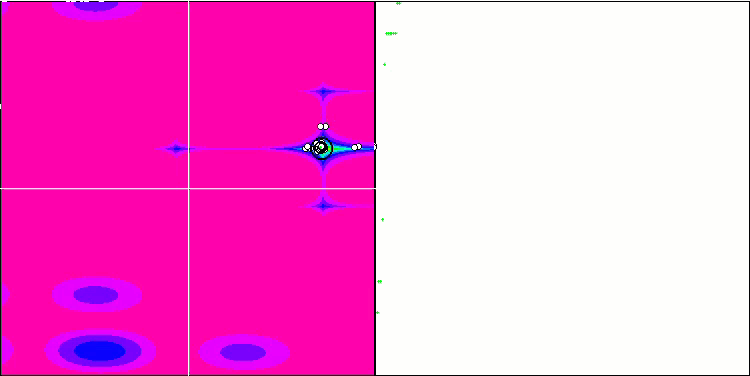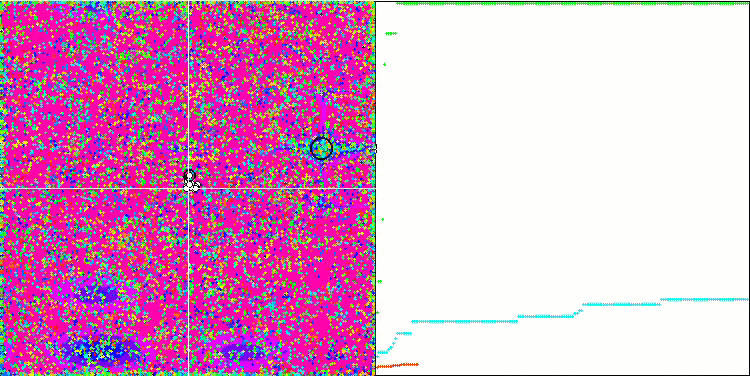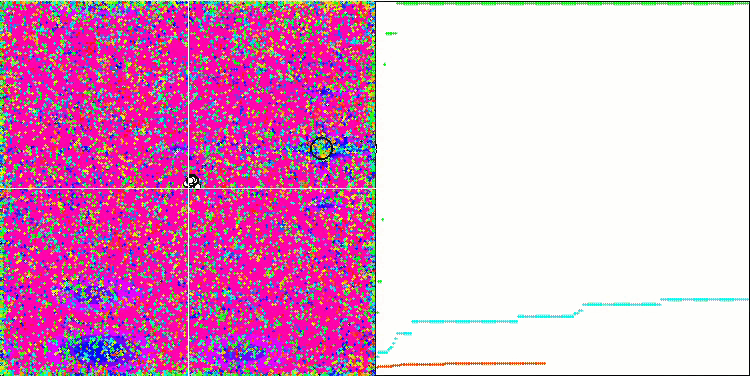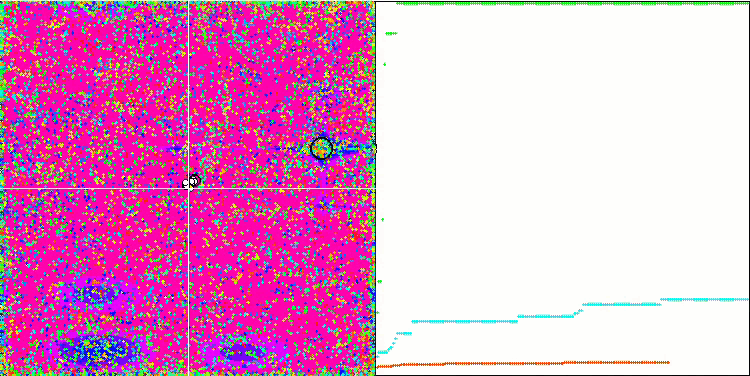
Megacityテスト関数のCOA
テストスタンドの可視化では、先に検討したアルゴリズムとは挙動が異なりますが、蜂コロニーアルゴリズムのようにタスクを学習領域に分割するアルゴリズムに特徴的なものがあります。これは、1つの極限に集中するのではなく、いくつかの有望な領域を探索することで、極限にはまりにくいアルゴリズムであることを特徴としています。この点については、巣を選別し、その中から品質に応じてカッコウが選択するというアルゴリズムの改良も可能かもしれません。これは、標準的なアルゴリズムのように、ランダムに選ばれた巣に卵を入れるのではなく、カッコウが巣を選ぶことを意味します。しかし、その結果、巣のランダムな選択の実用性を示す結果は改善されませんでした。これは、自然界で起こっていることと呼応しているのかもしれません。巣主がよりスマートな場合、卵を置き換えるのはより困難であり、無作為かつ統計的に正当化できません。
また、このアルゴリズムの特徴として、多変数を持つ関数に対してランダムウォークのような振る舞いをすることが挙げられます。視覚的には、ホワイトノイズや古いテレビ画面のように見えます。極値の場所に座標が集中するのは、繰り返しの終盤になってから顕著になります。蟻コロニーアルゴリズムのように、より明確なパラメータの「結晶化」を提供したいと思います。こうして、すべての最適化アルゴリズムに共通する、一般的な解のない問題に行き着きました。古典的なアルゴリズムからかなり新しいアルゴリズムまで、多くの作者がこの問題を解こうと試みてきました。
問題の本質は、対象となる関数の最適化されたパラメータのうち、どれに優先度や強度があるのかが確実にはわからない、それぞれのパラメータがどの程度、どのように結果に影響するのかがわからない、ということです。例えば、いくつかのパラメータがあり、アルゴリズムはすでに正しいものを見つけているが、具体的にどれがそうなのかは不明だということです。最大/小値に達するには、ほんの数個を変更すれば十分ですが、アルゴリズムは、それらすべてを変更しようとし続けるでしょう。何万、何千という変数を持つ関数になると、問題はさらに深刻になります。変数が多ければ多いほど、問題は深刻です。視覚的には、画面上のホワイトノイズのように見えます。
この問題を部分的にでも解決するための試みをおこないました。対象となる関数のパラメータのうち、どれを変えてどれを変えないかが先験的にわからない場合、確率的な方法でこれを解決しようとすることができます。すべてのパラメータのうち、一部だけを変更する必要があり、すべてを同時に変更する必要はないという前提に立っています。PSOアルゴリズムは、特徴的な振る舞いをします。最適化された関数のパラメータ（引数）の数が増えると、集中力のない雲のような振る舞いになります。そのために、アルゴリズムに新しいパラメータを導入し、座標が変更される確率を設定し、そうでなければ座標をそのままにするようにしました。
結果は...得られました。テスト結果が改善されました。実現したかった「結晶化」が、変数の多い関数に現れています。
テストスタンドの結果は以下のようになります。
2022.12.03 16:01:26.256 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 1 Skin's; Func runs 10000 result:4.918367945334852
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) Score:1.00000
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 20 Skin's; Func runs 10000 result:4.328327964103814
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) Score:0.85911
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) 500 Skin's; Func runs 10000 result:1.3297901702583084
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) Score:0.14316
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 1 Forest's; Func runs 10000 result:1.755200932219688
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) Score:0.99283
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 20 Forest's; Func runs 10000 result:0.5089243656052672
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) Score:0.28787
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 500 Forest's; Func runs 10000 result:0.08044934398920801
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) Score:0.04551
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 1 Megacity's; Func runs 10000 result:12.0
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) Score:1.00000
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 20 Megacity's; Func runs 10000 result:2.9899999999999998
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) Score:0.24917
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 500 Megacity's; Func runs 10000 result:0.4244
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) Score:0.03537
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) All score for C_AO_COAm:0.5125572342985216
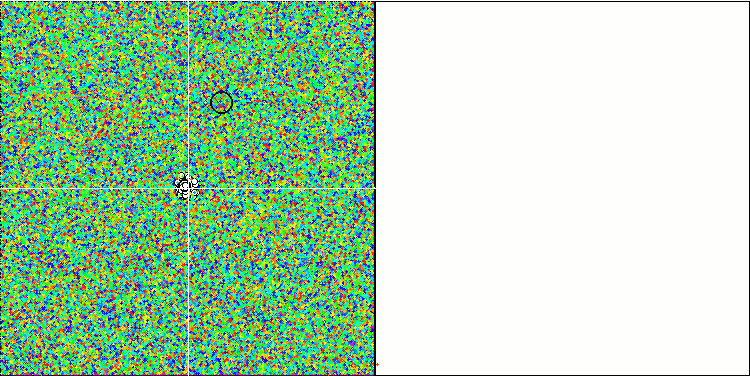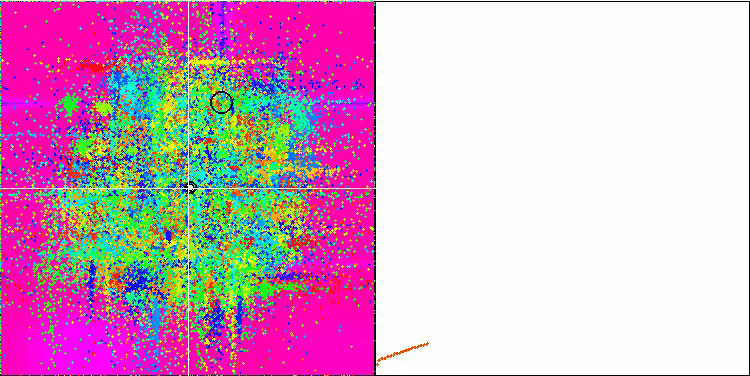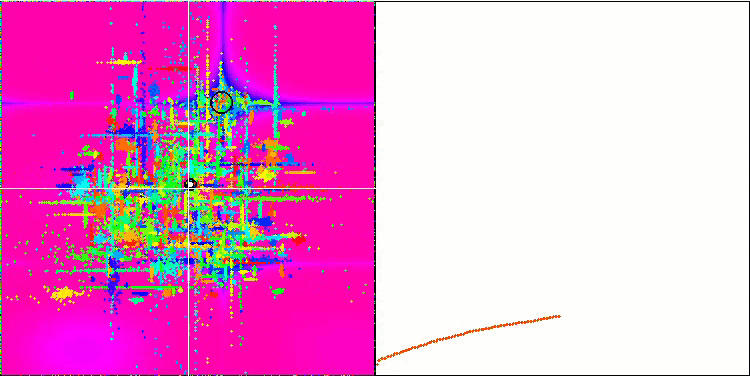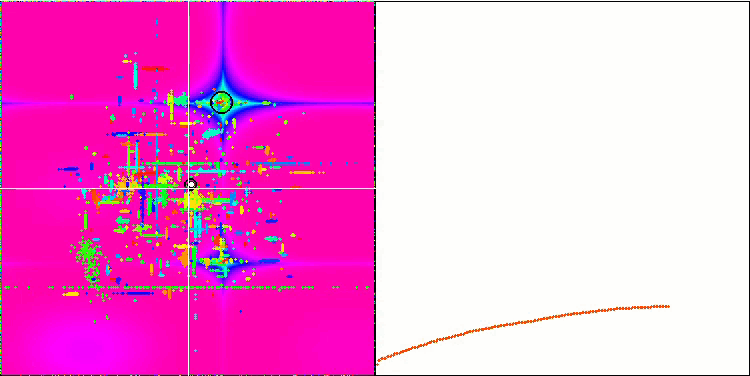
可視化では、「結晶化」をはっきりと確認することができます。最初はホワイトノイズのように見える画面がクリアになり、座標が集中し始め、集中の中心が可動します。
Megacityテスト関数のCOAm「結晶化」の効果をより実感できます。
一方では可変性、つまり新しい領域をダイナミックに探索する能力があり、他方では既に到達した極限の座標を明確にする能力があります。以下は、比較のために「結晶化」を顕著にした蟻コロニーアルゴリズムのアニメーションです。
テスト結果
| AO | 詳細 | Skin | Forest | Megacity（discrete） | 最終結果 | ||||||
| 2パラメータ（1F） | 40パラメータ（20F） | 1000パラメータ（500F） | 2パラメータ（1F） | 40パラメータ（20F） | 1000パラメータ（500F） | 2パラメータ（1F） | 40パラメータ（20F） | 1000パラメータ（500F） | |||
| カッコウ最適化アルゴリズム | 1.00000 | 0.85911 | 0.14316 | 0.99283 | 0.28787 | 0.04551 | 1.00000 | 0.24917 | 0.03537 | 0.51255778 | |
| 蟻コロニー最適化 | 0.98229 | 0.79108 | 0.12602 | 1.00000 | 0.62077 | 0.11521 | 0.38333 | 0.44000 | 0.02377 | 0.49805222 | |
| 人工蜂コロニーM | 1.00000 | 0.63922 | 0.08076 | 0.99908 | 0.20112 | 0.03785 | 1.00000 | 0.16333 | 0.02823 | 0.46106556 | |
| 人工蜂コロニー | 0.99339 | 0.73381 | 0.11118 | 0.99934 | 0.21437 | 0.04215 | 0.85000 | 0.16833 | 0.03130 | 0.46043000 | |
| 灰色オオカミオプティマイザ | 0.99900 | 0.48033 | 0.18924 | 0.83844 | 0.08755 | 0.02555 | 1.00000 | 0.10000 | 0.02187 | 0.41577556 | |
| 粒子群最適化 | 0.99627 | 0.38080 | 0.05089 | 0.93772 | 0.14540 | 0.04856 | 1.00000 | 0.09333 | 0.02233 | 0.40836667 | |
| ランダム | 0.99932 | 0.44276 | 0.06827 | 0.83126 | 0.11524 | 0.03048 | 0.83333 | 0.09000 | 0.02403 | 0.38163222 | |
カッコウ探索アルゴリズムの利点は、そのグローバル探索が標準的なランダムウォークではなく、フライトまたはレヴィ過程を用いることです。レヴィフライトは平均と分散が無限大なので、COAは標準的なガウス過程アルゴリズムよりも効率的に探索空間を探索することができます。レヴィフライト：冪乗則の尾を持つ確率密度関数から選択される一連の瞬間的なジャンプによって特徴付けられるランダムウォーク過程。
現在、このアルゴリズムは、個々のテストでは他のアルゴリズムを大きく上回り、他の「分野」でも遠く及ばないまま、表をリードしています。1000個の引数を持つMegacity離散関数に優れた結果があり、カッコウ検索はトレーダーのタスク（ほとんどの場合、離散的）に最適なツールとなっています。引数1000のSkin関数の結果が優れている（ベストではない）ことから、このアルゴリズムは特にニューラルネットワークや一般的な機械学習の学習に適していると断言することができます。
賛成：
1.高速。
2.汎用性がある。このアルゴリズムは、様々な最適化問題に利用することができます。
3.極値だけに注目しない能力。
4.滑らかな関数と離散的な関数の両方に対して、高い収束性を示す。
5.スケーラブルです。
反対：
1.複数設定可能。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11786
MQL5クックブック - サービス
母集団最適化アルゴリズム：魚群検索(FSS)
母集団最適化アルゴリズム：灰色オオカミオプティマイザー(GWO)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索