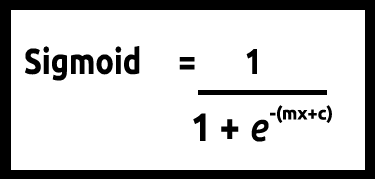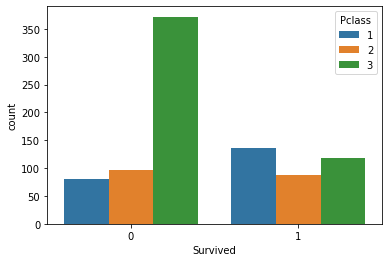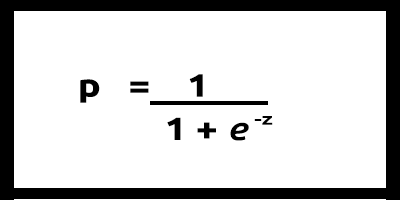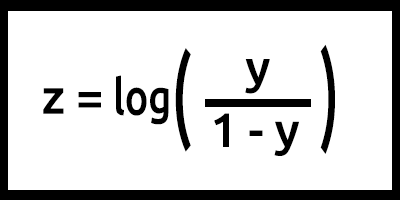
数据科学与机器学习(第 02 部分):逻辑回归
与我们在第 01 部分中讨论的线性回归不同,逻辑回归是一种基于线性回归的分类方法。
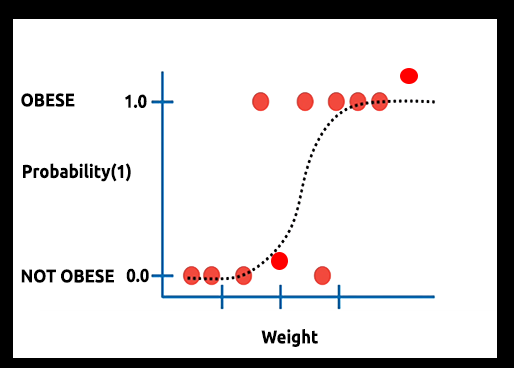
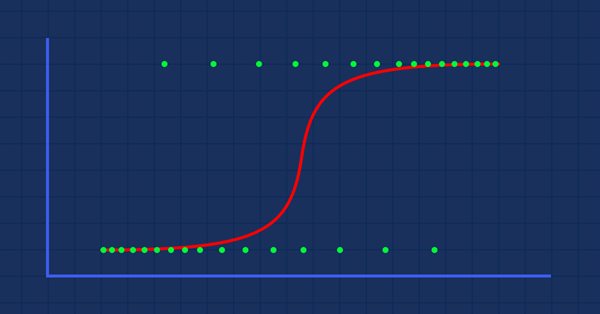
理论:假设我们绘制了一张肥胖概率与体重的关系图
在这种情况下,我们不能运用线性模型,我们会用另一种技术将这条线转换为称为“希格玛”的 “S-曲线”。
由于逻辑回归是以二元形式生成结果,可用来预测分类基于因变量的结果,因此结果应该是离散/分类的,例如:
- 0 或 1
- 确定 或 否定
- 真 或 假
- 高 或 低
- 做多 或 做空
在我们打算创建的函数库中,我们将忽略其它离散值。 我们只关注二元值 (0,1).
因为我们的 y 值应该在 0 和 1 之间,所以我们的指示线必须在 0 和 1 之间剪裁。 这可以通过以下公式实现:
这会为我们给出这个图形
将线性模型传递给逻辑函数 (sigmoid/p) =1/1+e^t ,其中 t 是线性模型,其结果是介于 0 和 1 之间的值。 这表示出的数据点的概率都属于一个等级。
替代用线性模型的 y 作为依赖项,其函数则显示为 “p” 作为依赖项
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn),多值的情况
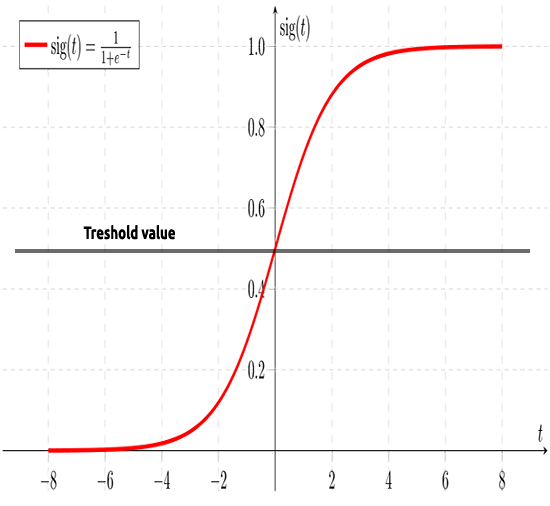
如早前所述,希格玛曲线旨在将无穷大的数值转换为二元形式的输出(0 或 1)。 但是,如果我有一个位于 0.8 的数据点,如何确定该值是零还是一? 这就是阈值发挥作用之处。
阈值表示获胜或失败的概率,它位于 0.5(0 和 1 的中心)。
任何大于或等于 0.5 的值将四舍五入为 1,因此被视为赢家,而任何低于 0.5 的值将四舍五入为 0,故因此被视为输家,现在是我们看到线性回归和逻辑回归之间差异的时候了。
线性对比逻辑回归
| 线性 | 逻辑回归 |
|---|---|
| 连续变量 | 分类变量 |
| 解决回归问题 | 解决分类问题 |
| 模型有一个直线方程 | 模型具有逻辑方程 |
在深入研究编码部分和数据分类算法之前,有几个步骤可以帮助我们理解数据,并令我们更容易建立模型:
- 收集 & 分析数据
- 清理您的数据
- 检查准确性
01: 收集 & 分析数据
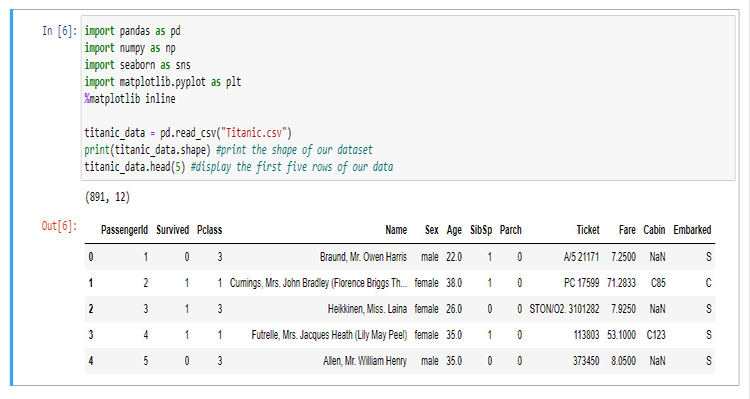
在本章节中,我们将编写大量 python 代码来可视化数据。 我们从函数库的导入开始,我们将要用这些函数库来提取和可视化 Jupyter 笔记本中的数据。
作为我们构建函数库的缘由,我们打算用泰坦尼克号的数据,对于那些不熟悉它的人来说,它是关于 1912 年 4 月 15 日泰坦尼克号撞上冰山后在北大西洋沉没的数据,维基百科。 所有 python 代码和数据集合都可以在本文末尾链接的 GitHub 上找到。
这些列代表
survival - 生存 (0 = No; 1 = Yes)
class - 乘客等级 (1 = 头等; 2 = 二等; 3 = 三等)
name - 姓名
sex - 性别
age - 年龄
sibsp - 登船兄弟姐妹/配偶人数
parch - 登船父母/子女人数
ticket - 船票号码
fare - 乘客票价
cabin - 客舱
embarked - 装货港口 (C = Cherbourg; Q = Queenstown; S = Southampton)
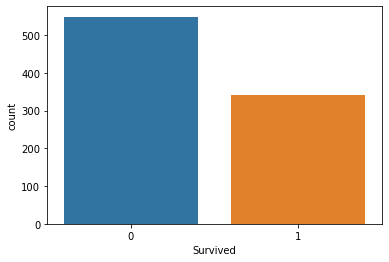
现在,我们已经收集到数据,并将数据存储到变量 titanic_data 当中,我们开始按列可视化数据,从 survival 列开始。
sns.countplot(x="Survived", data = titanic_data)
输出
这告诉我们,只有少数乘客在事故中幸存下来,大约一半的乘客在事故中幸存下来。
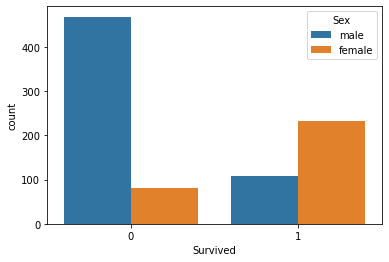
我们依据性别可视化幸存人数
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
我不知道那天男性发生了什么事,但女性存活下来的数量是男性的两倍多
我们依据等级分组来可视化存活数
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
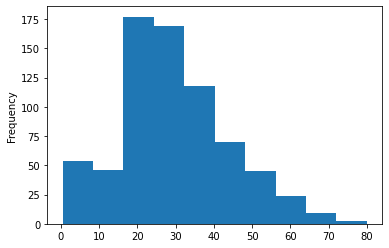
我们依据船上乘客年龄组绘制的直方图,在此我们不能用计数图来可视化我们的数据,因为我们的数据集合上有许多不同的年龄段无法组织。
titanic_data['Age'].plot.hist()输出:
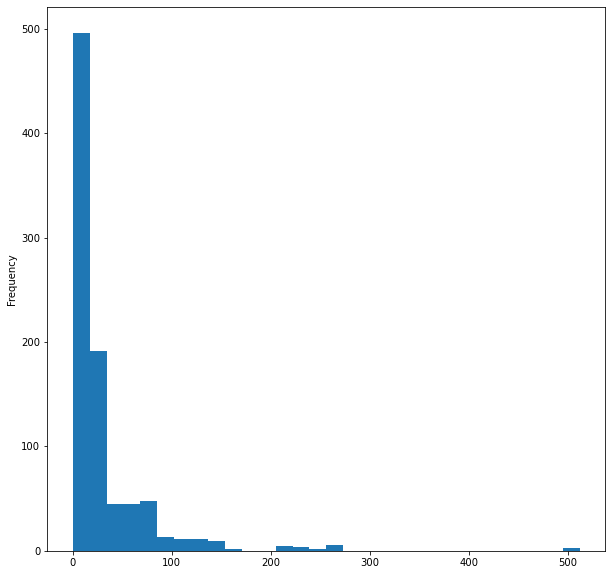
最后,我们可视化客船票价直方图
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
这是为了数据可视化,然而我们只把 12 列中的 5 列进行了可视化,因为我认为这些是比较重要的列,现在让我们清理数据。
02: 清理我们的数据
在此,我们通过删除 NaN(缺失)值来清理数据,同时避免/删除数据集合中不必要的列。
运用逻辑回归,您需要具有双精度和整数值,因此您必须避免无意义的字符串值。在这种情况下,我们将忽略以下列:
- Name 列 (它的信息没有任何有意义)
- Ticket 列 (对事故的幸存没有任何意义)
- Cabin 列 (它有太多的缺失值,即使前 5 行也表现如此)
- Embarked (我认为这无关紧要)
为此,我将在 WPS office 中打开 CSV 文件,并手动删除这些列,您可以用您所选的任何电子表格程序。
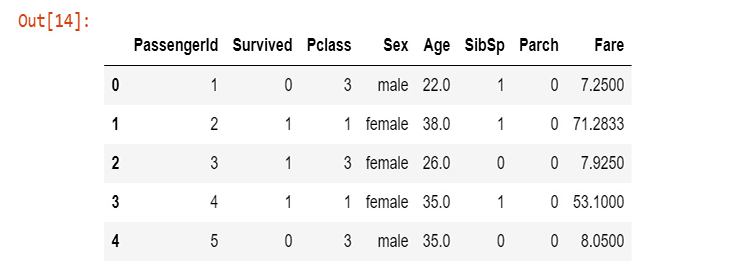
经由电子表格删除这些列后,我们就来可视化新数据。
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
输出:
我们现已清理数据完毕,但在年龄列中仍然有缺失的数值,更不用说在性别列中还有字符串值。 我们需通过一些代码来解决这个问题。 我们来创建一个标签编码器,将字符串男性和女性分别转换为 0 和 1。
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
为了得到名为 src[] 的源数组,我还编写了一个函数,从 CSV 文件中的特定列中提取数据,然后将其放入字符串值 MembersArray[] 数组中,以备后用:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
在我们的 testscript.mq5 中,此为如何正确调用函数和初始化函数库:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
成功运行脚本后打印输出,
male total =577 Encoded To = 0
female total =314 Encoded To = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
在您针对您的数值进行编码之前,请注意函数参数上的 members="male,female",字符串上出现的第一个值将被编码为 0,正如您在男性列上看到的那样,首先出现的是男性,因此所有男性将被编码为 0,女性将被编码为 1。 不过,该函数不限于两个值,只要字符串对数据有意义,就可以进行任意编码。
缺失数值
如果您注意年龄列,就会注意到有缺失值,缺失值可能主要是由于一个原因...死亡,在我们的数据集合中,无法识别个人的年龄,您可以通过查看数据集合来识别这些缺口,考虑到数据集合可能很耗时,尤其是大型数据集合,我们还使用 pandas 来可视化数据,我们来找出所有列中缺失的行
titanic_data.isnull().sum()
输出为:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
Out of 891, 177 rows in our Age column have missing values (NAN).
现在,我们打算用所有值的平均值替换列中缺少的值。
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
该函数找到所有非零值的平均值,然后用平均值替换数组中的所有零值。
成功运行该函数后的输出,如您所见,所有零值均已替换为 30.0,这是泰坦尼克号乘客的平均年龄。
mean 30.0 before Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
After Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
构建逻辑回归模型
首先,我们来构建逻辑回归,其中我们将有一个自变量和一个因变量。 然后,我们稍后会把它扩展到问题的完整解决方案模型。
我们根据存活率与年龄这两个变量构建模型,根据年龄找出一个人的存活几率。
到目前为止,我们知道在逻辑模型的深处有一个线性模型。 我们开始为函数编码,从而令线性模型成为可能。
Coefficient_of_X() 和 y_intercept() 这些并不是新函数,我们基于本系列第一篇文章来构建它们,参阅这些内容可以获取有关这些函数和一般线性回归的更多信息。
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
现在,我们据公式为逻辑模型编程。
注意,z 也被称为 log-odds,因为希格玛状态的逆表示 z 可以定义为标签 1 的概率对数(例如 “Survived”)除以标签 0(例如 “did not survive”)的概率:
在这种情况下,y = mx+c (记住线性模型)
将其转化为代码,结果将是,
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
注意这里针对 z 值完成的工作,基于公式 log(y/1-y), ,但代码编写为 log(y_)-log(1-y_); 。记住数学中的对数定律!! 具有相同底数的对数的除法会得到指数的减法,参阅。
当为公式编程时,这基本上是我们的模型,但在我们的 LogisticRegression() 函数中发生了很多事情,下面是函数中的所有内容:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
现在,我们运行 TestScript.mq5 训练和测试我们的模型。
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
成功运行脚本的输出则为:
Training starting..., train size=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
start testing...., test size=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
太棒了。 我们的模型现在正在运行,我们至少可以从中获得结果,但该模型是否做出了优良的预测?
我们需要验证它的准确性。
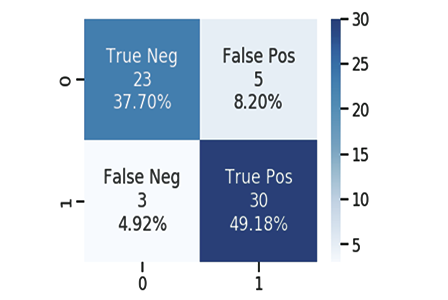
混淆矩阵
众所周知,每个优秀或糟糕的模型都能进行预测,我为我们的模型做出的预测创建了一个 CSV 文件,该文件与乘客生存测试数据的原始值一致,同样以 1 表示存活,0 表示未存活。
以下只是 10 列:
| 原始 | 预测 | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
我们用以下公式计算混淆矩阵:
- TP - 真阳性
- TN - 真阴性
- FP - 假阳性
- FN - 假阴性
现在,这些值是什么?
TP( True Positive )
当原始值为正(1),并且您的模型也预测为正(1)
TN( True Negative )
当原始值为负(0),并且您的模型也预测为负(0)
FP( False Positive )
初始值为负(0),但模型预测为正(1)
FN ( False Negative )
初始值为正(1),但模型预测为负(0)
现在您已经知道了这些值,我们来计算上述样本的混淆矩阵作为示例
| 原始 | 预测 | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
混淆矩阵可用于计算我们用该公式时的模型精度。
来自我们的表格:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Accuracy = 1 + 5 / 4 + 1 + 2 + 3
Accuracy = 0.5
在这种情况下,我们的精度为 50%(0.5*100% 换算成百分比)
现在,您了解了 1X1 混淆矩阵的工作原理。 现在需要将其转换为代码,并在整个数据集合上分析我们模型的准确性
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
现在我们回到类中的主函数,称为 LogisticRegression(),这次我们打算把它返回的模型准确性值转换成一个双精度,我还打算减少 Print() 方法的数量,但会把它们添加到 if 语句中,因为我们不想每次都打印数值,除非我们想调试我们的类。 所有修改均以蓝色高亮显示:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
成功运行脚本将输出以下内容:
Training starting..., train size=624
Confusion Matrix
[ 378 0 ]
[ 246 0 ]
Train Model Accuracy =0.60577
start testing...., test size=267
Confusion Matrix
[ 171 0 ]
[ 96 0 ]
Testing Model Accuracy =0.64045
好极了! 我们现在可以依据数字来识别我们的模型有多出色,尽管基于测试数据的 64.045 % 准确性还不足以确保该模型用于实际预测(在我看来),但至少目前,我们有一个函数库可以帮助我们运用逻辑回归针对数据进行分类。
进而,主要函数的说明:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
输入 train_size_split 用于将数据分割为训练和测试;默认情况下,分割为 0.7,这意味着 70% 的数据将用于训练,而其余的 30% 将用于测试,Predicted[] 引用数组将返回测试的预测数据。
二元交叉熵损失函数
正如均方误差是线性回归的误差函数一样,二元交叉熵是逻辑回归的成本函数。
理论:
我们看看它在逻辑回归的两个用例中是如何工作的,即:当实际输出为 0 和 1 时
01: 当实际输出值为 1 时
考虑两个输入样本 p1 = 0.4 和 p2 = 0.6 的模型。 预计 p1 相比 p2 处于更不利的位置,因为与 p1 相比,p1 远离 1。
从数学角度来看,小数字的负对数会得到大数字,反之亦然。
对于不利输入,我们将使用公式
penalty = -log(p)
在这两种情况下
- Penalty = -log(0.4)=0.4 即 p1 的 penalty 为 0.4
- Penalty = -log(0.6)=0.2 即 p2 的 penalty 为 is 0.2
02: 当实际输出值为 0 时
考虑模型针对两个输入样本的输出,p1 = 0.4 和 p2 = 0.6(与前一种情况相同)。由于 p2 远离 0,因此预计 p2 的不利值应该大于 p1,但请记住,逻辑模型的输出是样本为正的概率,为了不利值输入概率,我们需要找到样本为负的概率,此处的公式很简单
样本为负的概率 = 1 - 样本为正的概率
故此,在这种情况下,为了找到 penalty,其公式将是
penalty = -log(1-p)
在这两种情况下
- penalty = -log(1-p) = -log(1-0.4) =0.2 即 penalty 为 0.2
- penalty = -log(1-p) = -log(1-0.6) =0.4 即 penalty 为 0.4
p2 上的 penalty 大于 p1(符合预期),酷!
现在,对于模型输出为 p 且真实输出值为 y 的单个输入样本,可以按以下方式计算 penalty。
如果输入样本为正 y=1:
penalty = -log(p)
否则:
penalty = -log(1-p)
与上述 if-else 语句块等效的单行方程可以写成
penalty = -( y*log(p) + (1-y)*log(1-p) )
其中
y = 数据集合中的实际值
p = 模型的无修改预测概率(舍入前)
我们来证明这个方程等价于上面的 if-else 语句
01: 当输出值 y = 1
penalty = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) 故此证明
02: 当输出值 y = 0
penalty = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) 故此证明
最后,N 个输入样本的对数损失函数如下所示
Log-loss 表示预测概率与相应的实际/真(在二元分类的情况下为 0 或 1)值的接近程度。 预测概率与实际值的偏差越大,对数损失值越高。
Cost 函数(如对数损失等)可以用作衡量模型好坏的指标,但最大的用途是在使用梯度下降或其它算法优化模型时,从而可以获得最佳参数(我们将在后面的系列中讨论,敬请期待)。
如果您能测量它,您就能改进它。 这是成本函数的主要目的。
从我们的测试和训练数据集合来看,我们的对数损失在 0.64 - 0.68 之间,这并不理想(粗略地说)。
训练数据集合
Logloss =0.6858006105398738
测试数据集合
Logloss =0.6599503403665642
下面是如何将 log-loss 函数转换为代码
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
为了获得无修改原始预测输出,我们需要返回到主要的测试和训练循环,并在概率舍入过程之前将数据存储到无修改原始预测数组当中。
多重动态逻辑回归挑战
在本文和前一篇文章中,我在构建线性回归和逻辑回归函数库时面临的最大挑战就是多重动态回归函数,我们可以将它们用于多个数据列,而无需对添加到模型中的每个数据进行硬编码。在前一篇文章中,我硬编码了两个同名函数,它们之间唯一的区别就是每个模型可以处理的数据数量,一个能够处理两个自变量,另一个则可处理四个自变量:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
但是,这种方法很不方便,而且感觉像是一种不成熟的编码方式;它违反了简洁代码和 DRY(不要自我重复原则,OOP 尝试帮助我们来实现)的规则。
与 python 不同的是,python 拥有灵活的函数,可以在 *args 和 **kwargs 的帮助下接受大量函数参数,在 MQL5 中,迄今我能想到的只能通过使用字符串来实现,我相信这是我们的出发点。
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
输入 x_columns 表示我们将在函数库中使用的所有自变量列,这些列要求我们为每个列都分配独立的数组,但是,我们无法动态创建数组,故此在此使用数组没有任何意义。
我们可以动态创建多个 CSV 文件,并将其当作数组使用,但这肯定会令我们的程序占用计算机资源时比直接使用数组更昂贵,尤其是在处理多个数据时,更不用说我们打开文件时经常要用到的 while 循环会减慢整个过程;这一点我不是百分之百肯定,如果我错了,请纠正我。
尽管我们仍然可以使用上述方式。
我已发现了使用数组的方法,我们打算把所有列中的所有数据存储在一个数组当中,然后从单一数组中分别提取所需的数据。
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
在 for 循环中,我们可以操纵数组中的数据,并按所有列所需的方式执行模型的所有计算;我已经尝试过这种方法,但遗憾没有成功,究其原因我解释为这个假设是为了让所有阅读本文的人都理解这个挑战,我欢迎大家在评论部分针对如何编写这个多重动态逻辑回归函数发表意见。我创建这个函数库的全部尝试都可以在这个链接上找到 https://www.mql5.com/zh/code/38894。
这一尝试虽未成功,但仍有希望,我相信值得分享。
逻辑回归的优势
- 不必假设分类在特征空间中的分布
- 易于扩展到多个分类(多项式回归)
- 分类预测的自然概率观
- 快速训练
- 针对未知记录进行快速分类
- 针对许多简单数据集和拥有优良的准确性
- 抗过度匹配
- 可以将模型系数解释为特征重要性的指标
缺点
- 构造线性边界
最后的想法
这就是本文的全部内容,逻辑回归在现实生活中的多个领域中都有应用,例如将电子邮件分类为垃圾邮件和非垃圾邮件,手写识别,以及更有趣的事情。
我知道我们不会使用逻辑回归算法对泰坦尼克数据或任何提及的字段进行分类,但是,特别是在 MetaTrader 5 平台中,正如前面所说,使用数据集合只是为了拿所构建的函数库,与在此链接处 https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python 的 python 实现输出进行对比。 在下一篇文章中,我们将看到如何使用逻辑模型预测股市崩盘。
鉴于本文篇幅太长了,我把多重回归任务作为家庭作业留给所有读者。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/10626
 学习如何基于 ADX 设计交易系统
学习如何基于 ADX 设计交易系统
 从头开始开发智能交易系统(第 12 部分):时序与交易(I)
从头开始开发智能交易系统(第 12 部分):时序与交易(I)