
Data Science and Machine Learning (Part 17): Money in the Trees? The Art and Science of Random Forests in Forex Trading
Two heads are better than one, not because either is infallible, but because they are unlikely to go wrong in the same direction.
The Random Forest Algorithm
A Random Forest is an ensemble learning method that operates by constructing many decision trees during training and outputs the class, that is, the mode of the classes (classification) or mean prediction (regression) of the individual trees. Each tree in a Random Forest trains on a different subset of the data, and the randomness introduced during training helps improve the model's overall performance and generalization.
To understand this better, we must look at ensemble learning in Machine learning lingo.
Ensemble learning
Ensemble learning is an approach in which two or more machine learning models are fitted to the same data, and the predictions of each model are combined. Ensemble learning aims to perform better with ensemble models than with any individual model.
Random forest is an ensemble method that combines the predictions of multiple decision trees to improve the overall predictive capability of an individual/single model.
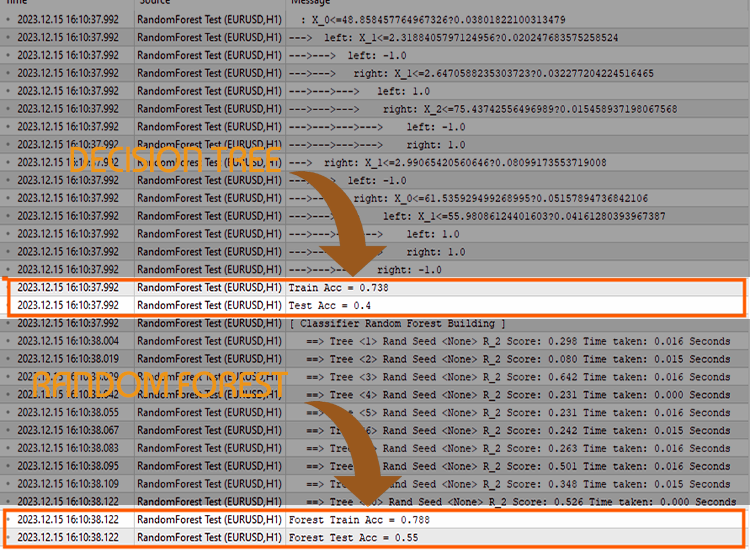
I created a decision tree and a random forest set for ten(10) trees to demonstrate this. Using the same dataset, I got better accuracy in the training and testing phases using the random forest AI.
Key Features of the Random Forest AI
01: Ensemble Learning
Random forest is an ensemble method that combines the predictions of multiple machine-learning models to improve overall performance.
for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees { temp_data = data; matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest preds = forest[i].predict(x_subset); }
02: Bootstrapping Aggregating (Bagging)
In Machine Learning, bootstrapping is a resampling technique that involves repeatedly drawing samples from the source data with replacement, often to estimate a population parameter.
Each tree in the Random Forest is trained on a different subset of the data, created through bootstrapping(sampling with replacement).
matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets
source:
template<typename T> void CMatrixutils::Randomize(matrix<T> &matrix_,int random_state=-1, bool replace=false)
replace = true parameter allows the same index to be chosen more than once, simulating the bootstrapping process.
03: Feature Randomness:
Random subsets of features are considered when splitting nodes during the construction of each tree.
This introduces further diversity among the trees, making the ensemble more robust.
04: Voting (or Averaging) Mechanism
For classification problems, the mode (most frequent class) of the predictions is taken.
For regression problems, the average of the predictions is considered.
The voting process is crucial for the classification Random-Forest, and there are various techniques one can choose from to use as a voting mechanism; some are soft voting and voting threshold:
Soft Voting
Each tree's prediction is associated with a confidence score (probability) in soft voting. The final prediction is then a weighted average of these probabilities.
Since our decision tree class cannot predict the probabilities yet, we can not use this voting mechanism. We will use custom voting.
Voting Threshold
The voting mechanism goes like this: if a certain percentage of trees predict a particular class, It is considered the final prediction. This can help deal with ties or ensure a minimum level of confidence.
Using the percentage of trees to determine which class to predict may be sophisticated for many classes to predict; we will customize the predict function to select the class that most of the trees predicted regardless of how many classes were predicted.
double CRandomForestClassifier::predict(vector &x) { vector predictions(m_ntrees); //predictions from all the trees for (uint i=0; i<this.m_ntrees; i++) //all trees make the predictions predictions[i] = forest[i].predict(x); vector uniques = matrix_utils.Unique(predictions); return uniques[matrix_utils.Unique_count(predictions).ArgMax()]; //select the majority decision }
Extending the Decision Tree Class
In the prior article, We discussed the Classification Decision Tree, which is suitable for classifying binary target variables; I had to extend the classes and code for a regression decision tree.
class CDecisionTreeRegressor: public CDecisionTreeClassifier { private: double calculate_leaf_value(vector &Y); split_info get_best_split(matrix &data, uint num_features); double variance_reduction(vector &parent, vector &l_child, vector &r_child); Node *build_tree(matrix &data, uint curr_depth = 0); public: CDecisionTreeRegressor(uint min_samples_split = 2, uint max_depth = 2); ~CDecisionTreeRegressor(void); void fit(matrix &x, vector &y); };
The two classes are similar in most cases, and they share the same Node Class and a lot of functions except the leaf value calculation, Information gain, build tree, and the fit function which calls the build tree function.
Leaf Value in Regressor Decision Trees
In regression problems, the leaf value of a given node is the mean of all its values.
double CDecisionTreeRegressor::calculate_leaf_value(vector &Y) { return Y.Mean();
Calculating Information Gain
As said in the prior article, Information gain measures the reduction in entropy or uncertainty after a dataset is split.
Instead of using Gini and entropy, which are probability-based, we use the variance reduction formula to measure impurity in a given node.
double CDecisionTreeRegressor::variance_reduction(vector &parent, vector &l_child, vector &r_child) { double weight_l = l_child.Size() / (double)parent.Size(), weight_r = r_child.Size() / (double)parent.Size(); return parent.Var() - ((weight_l * l_child.Var()) + (weight_r * r_child.Var())); }
The above function calculates the reduction in variance achieved by splitting a dataset into left and right child nodes at a particular node in the decision tree.
Build Tree & Fit Function
Build Tree
Node *CDecisionTreeRegressor::build_tree(matrix &data, uint curr_depth=0) { matrix X; vector Y; if (!matrix_utils.XandYSplitMatrices(data,X,Y)) //Split the input matrix into feature matrix X and target vector Y. { #ifdef DEBUG_MODE printf("%s Line %d Failed to build a tree Data Empty",__FUNCTION__,__LINE__); #endif return NULL; //Return a NULL pointer } ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset. ArrayResize(nodes, nodes.Size()+1); //Append the nodes to memory Node *left_child, *right_child; if (samples >= m_min_samples_split && curr_depth<=m_max_depth) { split_info best_split = this.get_best_split(data, (uint)features); #ifdef DEBUG_MODE Print(__FUNCTION__," | ",__LINE__,"\nbest_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold); #endif if (best_split.info_gain > 0) { left_child = this.build_tree(best_split.dataset_left, curr_depth+1); right_child = this.build_tree(best_split.dataset_right, curr_depth+1); nodes[nodes.Size()-1] = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain); return nodes[nodes.Size()-1]; } } nodes[nodes.Size()-1] = new Node(); nodes[nodes.Size()-1].leaf_value = this.calculate_leaf_value(Y); return nodes[nodes.Size()-1]; }
Fit function
void CDecisionTreeRegressor::fit(matrix &x, vector &y) { matrix data = matrix_utils.concatenate(x, y, 1); this.root = this.build_tree(data); is_fitted = true; }
The only difference between this build_tree function on the Regressor class and the Classifier class is the variance_reduction function.
I used the popular Airfoil noise data to test the Regression tree built.
matrix data = matrix_utils.ReadCsv("airfoil_noise_data.csv"); matrix x; vector y; if (!matrix_utils.XandYSplitMatrices(data, x, y)) return INIT_FAILED; regressor_tree = new CDecisionTreeRegressor(3,3); regressor_tree.fit(x, y); regressor_tree.print_tree(regressor_tree.root); vector preds = regressor_tree.predict(x); Print("r-squared: ",metrics.r_squared(y, preds));
outputs:
KS 0 00:04:11.402 RandomForest Test (EURUSD,H1) : X_0<=3150.0?7.6482714516406745 FI 0 00:04:11.402 RandomForest Test (EURUSD,H1) ---> left: X_4<=0.0150478?4.070223732531591 ME 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> left: X_2<=0.1016?2.453283788183441 RR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=630.0?2.3366165961173238 JR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 126.94465000000002 MF 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 130.51523904382472 II 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_0<=1600.0?4.999630155449349 HF 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 127.90983653846149 JM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 122.97036507936505 JR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> right: X_4<=0.0483159?6.040280153408631 FI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=1250.0?5.315257051142112 IG 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 125.68045918367342 GM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 120.69493181818189 NQ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_0<=1250.0?13.291165881821172 GK 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 117.69977777777775 GH 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 109.80075000000001 EL 0 00:04:11.402 RandomForest Test (EURUSD,H1) ---> right: X_4<=0.00152689?28.997059993530435 OL 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> left: X_0<=6300.0?11.053304033466667 HK 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_4<=0.000930789?9.067095683299033 FG 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 134.9866388888889 NO 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 128.59900000000002 QS 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_4<=0.000930789?9.783359845444707 NI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 128.05125581395347 GJ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 120.90806666666667 RM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> right: X_4<=0.0341183?5.715854852017056 LN 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=5000.0?5.190320913085316 GN 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 120.08625170068028 NE 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 115.52968965517242 MI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_4<=0.0483159?4.450134400476193 IS 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 109.44371428571428 GQ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 104.84033333333332 PH 0 00:04:11.403 RandomForest Test (EURUSD,H1) r-squared: 0.5937442611327515
The regression tree appears to have more branches for the same parameters, which causes fewer branches in the classification decision tree.
The accuracy of our regression model was 59% during training; this is a good indication we got it right? When the predictions were plotted on a graph, they looked something like below:
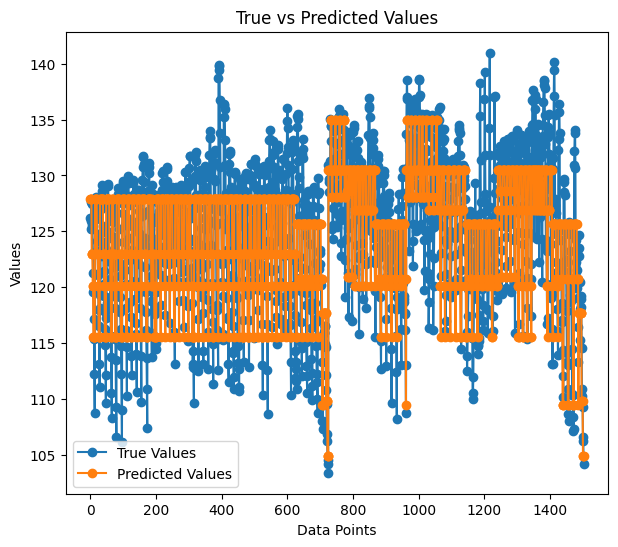
The way predictions are fitted to the actual values, they almost look like a tree.
Why Random Forest?
High Accuracy: Random Forests often provide increased accuracy in both classification and regression tasks.
Robustness: The ensemble nature of Random Forest makes it robust to overfitting and noisy data.
Feature Importance: Random Forests can provide information about the importance of features, helping in feature selection.
Reduced Variance: The diversity among trees minimizes the variance of the model, leading to better generalization.
No Need for Feature Scaling: Like the decision tree, Random Forests are less sensitive to feature scaling, making them suitable for datasets with different scales.
Versatility: Practical for various types of data, including categorical and numerical features.
Building the Random Forest Classifier
Now that we have seen why one should prefer the random forest algorithm to the decision tree, Let's see how to build the random forest model, starting with the classifier.
Including the CDecisionTreeClassifier class.
class CRandomForestClassifier { CMetrics metrics; protected: uint m_ntrees; uint m_maxdepth; uint m_minsplit; int m_random_state; CMatrixutils matrix_utils; CDecisionTreeClassifier *forest[]; string ConvertTime(double seconds); public: CRandomForestClassifier(uint n_trees=100, uint minsplit=NULL, uint max_depth=NULL, int random_state=-1); ~CRandomForestClassifier(void); void fit(matrix &x, vector &y, bool replace=true); double predict(vector &x); vector predict(matrix &x); };
Since the Random forest classifier is simply an x amount of classifier trees combined in one forest, The class is pointed into an array of CDecisionTreeClassifier objects named forest[].
n_trees = 100 (by default), which implies 100 trees will be in the Random forest classifier forest.
min_split and max_depth, are the parameters for each tree we discussed in the previous article. The min_split is the minimum number of branches the tree should have, while the max_depth is how long the tree should be in terms of those branches.
Fitting trees into a Random Forest
This is the most essential function in the CRandomForestClassifier class, where the forest comprises n_trees number of trees chosen in the class constructor.
void CRandomForestClassifier::fit(matrix &x, vector &y, bool replace=true) { matrix x_subset; vector y_subset; matrix data = this.matrix_utils.concatenate(x, y, 1); matrix temp_data = data; vector preds; datetime time_start = GetTickCount(), current_time; Print("[ Classifier Random Forest Building ]"); for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees { time_start = GetTickCount(); temp_data = data; matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets if (!this.matrix_utils.XandYSplitMatrices(temp_data, x_subset, y_subset)) //split the random subset into x and y subsets { ArrayRemove(forest,i,1); //Delete the invalid tree in a forest printf("%s %d Failed to split data for a tree ",__FUNCTION__,__LINE__); continue; } forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest preds = forest[i].predict(x_subset); current_time = GetTickCount(); printf(" ==> Tree <%d> Rand Seed <%s> Accuracy Score: %.3f Time taken: %s",i+1,m_random_state==-1?"None":string(m_random_state),metrics.accuracy_score(y_subset, preds), ConvertTime((current_time - time_start) / 1000.0)); } m_ntrees = ArraySize(forest); //The successfully build trees }
Decision Tree Classifier Vs. Random Forest Classifier
To prove a point about whether random classifiers do a better job at classification tasks than decision trees, I ran 5 tests.
Test 01:
| Train | Test | |
|---|---|---|
| Decision Tree | 73.8% | 40% |
| Random Forest | 78% | 45% |
Test 02:
| Decision Tree | 73.8% | 40% |
| Random Forest | 83% | 45% |
Test 03:
| Decision Tree | 73.8% | 40% |
| Random Forest | 80% | 45% |
Test 04:
| Decision Tree | 73.8% | 40% |
| Random Forest | 78.8% | 45% |
Test 05:
| Decision Tree | 73.8% | 40% |
| Random Forest | 78.8% | 45% |
In my experience, using the Random forest classifier on trading data may lead to confusion as you may encounter situations where the overall accuracy of the random forest is no bigger than that of a single decision tree; that happens due to one or more of the below factors:
Factors contributing to the Random Forest not providing better accuracy than a single decision tree:
Lack of Diversity in Trees
Random Forests benefit from the diversity of individual trees. If all trees are similar, the ensemble won't provide much improvement.
Ensure that you're introducing randomness properly during the training of each tree. Randomization can involve selecting random subsets of features and/or using different subsets of the training data.
Hyperparameter Tuning
Experiment with different hyperparameters, such as the number of features to consider for each split (m_max_features), the minimum samples required to split an internal node (m_minsplit), and the maximum depth of the trees (m_maxdepth).
Grid search or random search over a range of hyperparameter values can help identify better configurations.
Cross-Validation
Use cross-validation to evaluate the model's performance. This helps to get a more robust estimate of how well the model generalizes to new data.
Cross-validation can also help in detecting overfitting or underfitting issues.
Training on Entire Dataset
Ensure that the trees are not overfitting to the training data. If each tree in the forest is trained on the entire dataset, it might capture noise rather than signal.
Consider training each tree on a bootstrapped sample (bagging) of the data.
Feature Scaling
If your features have different scales, it might be beneficial to scale them. Decision trees are generally not sensitive to feature scales, but normalizing or standardizing features could help, especially if you compare a single tree's performance with an ensemble.
Evaluation Metric
Ensure that you are using an appropriate evaluation metric for a problem you are trying to solve with your models; the common evaluation metric for regression is the R-squared, while the common evaluation metric for classification is the accuracy score.
The last argument of a fit() function has an error argument, which allows you to choose an appropriate metric for measuring the accuracy of each tree in the forest.
enum errors_classifier { ERR_ACCURACY }; enum errors_regressor { ERR_R2_SCORE, ERR_ADJUSTED_R };
Ensemble Size
Experiment with the number of trees in the forest. Sometimes, increasing the number of trees can improve the ensemble's performance.
Beware that this adds complexity; the training and testing time could increase drastically after the change.
Data Quality
Ensure the quality of your data. If there are outliers or missing values, it might affect the performance of the Random Forest.
Random Seed
Ensure that the random seed is set consistently during each run for reproducibility.
Having the same random seed will cause all trees to produce the same accuracy, which will be no better than a single decision tree.
The Battle continues in the Strategy Tester
The random forest has won in the training and testing phase, but can it also become victorious in trading, where it takes more than the ability to predict to become profitable?
I ran tests on both algorithms with default settings from 2022.01.01 to 2023.02.01.
Other tester settings:
- Delays: Random delay
- Modelling: Open Prices only
- Deposit: 1000$
- Leverage: 1/100
Random Forest results graph:
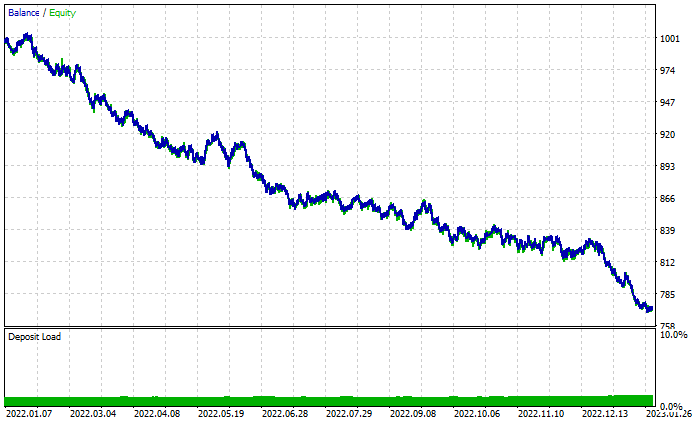
Despite the 46% profitable trades total, the graph looks terrible. Let's see what the decision tree does:
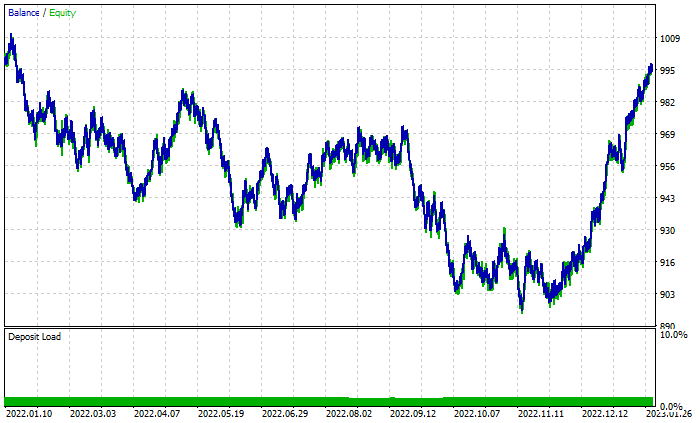
Better than the random forest comprised of 100 trees despite having 44% profitable trades.
A quick optimization was done to find the best stop-loss = 960 and take-profits = 1295 levels for both models, while the minimum split was set to 2. Below is the outcome of both models.
The decision tree classifier:
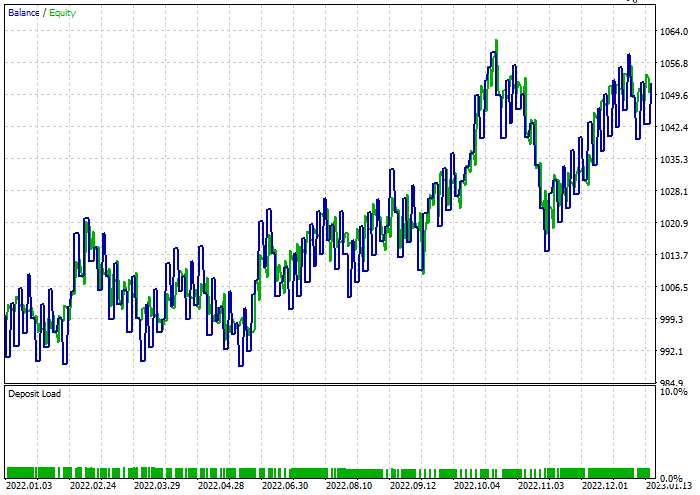
47.68% of the trades were profitable during the test. The model made 52$ profit during the test.
The random forest classifier:
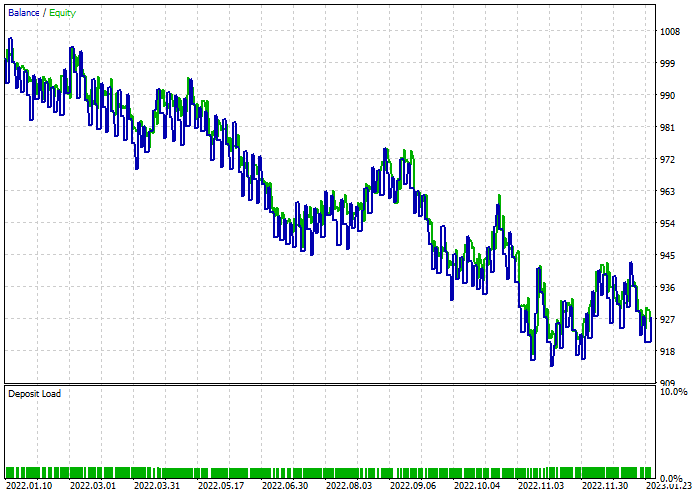
Final thoughts
Random forests have been used in various activities in many industries, such as finance, entertainment, and the medical sector. However, just like any model, they have some setbacks that one must understand before deciding to pick this model for their trading project.
Computational Complexity:
Random Forest models, especially with many trees, can be computationally expensive and require substantial resources.
Memory Usage:
As the number of trees increases, the Random Forest model's memory footprint also grows, potentially leading to high memory usage.
Interpretability:
The ensemble nature of Random Forests makes them less interpretable than individual decision trees, mainly when the forest consists of many trees.
Overfitting:
Although Random Forests are less prone to overfitting than individual decision trees, they can still overfit noisy data or data with outliers.
Biased Towards Dominant Classes:
In classification problems with imbalanced class distributions, Random Forests might be biased toward the dominant class, affecting the model's predictive performance on minority classes.
Parameter Sensitivity:
While Random Forests are robust to the choice of hyperparameters, the model's performance can still be sensitive to specific parameter values.
Black-Box Nature:
The ensemble nature of Random Forests, which combines multiple decision trees, can make interpreting the model's decision-making process challenging.
Training Time:
Training a Random Forest model can take longer than training a single decision tree, especially for large datasets.
The trading activity was delayed for 10 minutes, as they had to wait to train 100 trees.
Thanks for reading;
We discuss the track development of this machine learning model and much more discussed in this article series on this GitHub repo.
Attachments:
| File | Usage & Description |
|---|---|
| forest.mqh (Found under the include folder) | Contains the random forest classes, both CRandomForestClassifier and CRandomForestRegressor |
| matrix_utils.mqh (Include) | Contains additional functions for matrix manipulations. |
| metrics.mqh (Include) | Contains functions and code to measure the performance of ML models. |
| preprocessing.mqh (Include) | The library for pre-processing raw input data to make it suitable for Machine learning models usage. |
| tree.mqh (Include) | Contains the decision tree classes. |
| RandomForest Test.mq5(Experts) | The final Expert advisor for running and testing random forest models. |
 Design Patterns in software development and MQL5 (Part 4): Behavioral Patterns 2
Design Patterns in software development and MQL5 (Part 4): Behavioral Patterns 2
 Understanding Programming Paradigms (Part 1): A Procedural Approach to Developing a Price Action Expert Advisor
Understanding Programming Paradigms (Part 1): A Procedural Approach to Developing a Price Action Expert Advisor
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Very informative and interesting