
Ciência de dados e aprendizado de máquina (Parte 17): O dinheiro cresce em árvores? Florestas aleatórias no trading de forex
Duas cabeças pensam melhor do que uma, não porque cada uma seja infalível, mas porque é improvável que cometam o mesmo erro ao mesmo tempo.
Algoritmo de floresta aleatória
A floresta aleatória é um método de aprendizado de conjunto que cria várias árvores de decisão durante o treinamento e gera a classe durante a classificação ou a média da previsão durante a regressão. Cada árvore na floresta é treinada em um subconjunto diferente dos dados, e a aleatoriedade adicionada no treinamento ajuda a melhorar o desempenho geral do modelo e sua capacidade de generalização.
Primeiro, vamos entender o que é aprendizado de conjunto.
Aprendizado de conjunto
Aprendizado de conjunto é uma abordagem em que dois ou mais modelos de aprendizado de máquina são ajustados aos mesmos dados, e as previsões de cada modelo são combinadas. A ideia é que os modelos de conjunto funcionem melhor do que qualquer modelo isolado.
A floresta aleatória é um método de conjunto que combina previsões de várias árvores de decisão para melhorar as capacidades preditivas de um único modelo.
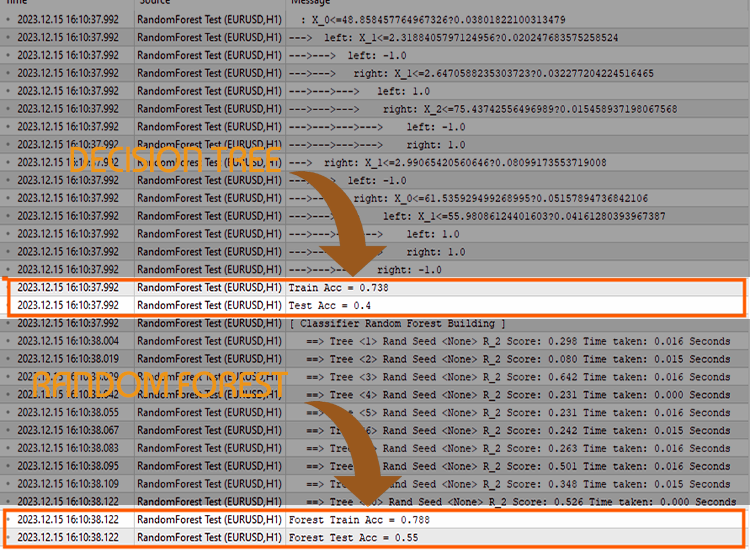
Para demonstrar isso, construí uma árvore de decisão e uma floresta aleatória com dez (10) árvores. No mesmo conjunto de dados, obtive maior precisão nas fases de treinamento e teste usando a floresta aleatória.
Características principais da floresta aleatória
01: Aprendizado de conjunto
A floresta aleatória é um método de conjunto que combina as previsões de vários modelos para obter um resultado melhor.
for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees { temp_data = data; matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest preds = forest[i].predict(x_subset); }
02: Bootstrapping — agregação inicial (empacotamento)
O bootstrapping em aprendizado de máquina é um método de reamostragem que envolve obter repetidamente amostras dos dados originais com substituição, geralmente para estimar um parâmetro populacional.
Cada árvore na floresta é treinada em um subconjunto diferente dos dados, criado através do bootstrapping (amostragem com substituição).
matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets
Código:
template<typename T> void CMatrixutils::Randomize(matrix<T> &matrix_,int random_state=-1, bool replace=false)
O parâmetro replace = true permite escolher o mesmo índice mais de uma vez, simulando o processo de bootstrapping.
03: Aleatoriedade dos atributos
Ao dividir os nós ao construir cada árvore, são considerados subconjuntos aleatórios de atributos.
Isso traz mais diversidade às árvores, tornando o conjunto mais robusto.
04: Mecanismo de votação (ou média)
Para tarefas de classificação, é usado o modo de previsões (classe mais frequente).
Em tarefas de regressão, é considerada a média das previsões.
Na classificação de florestas aleatórias, é usado o processo de votação. Existem diferentes técnicas que podem ser usadas como mecanismo de votação, como a votação ponderada ou por limiar:
Votação ponderada
Na votação ponderada, cada previsão de árvore vem com uma medida de confiança (probabilidade). A previsão final é a média ponderada dessas probabilidades.
Como nossa classe de árvore de decisão ainda não pode prever probabilidades, não dá pra usar esse mecanismo de votação. Vamos usar a votação personalizada.
Votação por limiar
Aqui, se uma certa porcentagem de árvores prevê uma determinada classe, essa é a previsão final. Isso garante um nível mínimo de confiança.
Usar a porcentagem de árvores para determinar qual classe prever pode ser complicado quando se tem várias classes. Então, configuramos uma função pra escolher a classe que a maioria das árvores previu, não importa quantas classes foram previstas.
double CRandomForestClassifier::predict(vector &x) { vector predictions(m_ntrees); //predictions from all the trees for (uint i=0; i<this.m_ntrees; i++) //all trees make the predictions predictions[i] = forest[i].predict(x); vector uniques = matrix_utils.Unique(predictions); return uniques[matrix_utils.Unique_count(predictions).ArgMax()]; //select the majority decision }
Expansão da classe de árvore de decisão
No artigo anterior, falamos sobre a classificação por árvores de decisão, que é ótima pra classificar variáveis-alvo binárias. Foi necessário expandir as classes e o código das árvores de decisão para tarefas de regressão.
class CDecisionTreeRegressor: public CDecisionTreeClassifier { private: double calculate_leaf_value(vector &Y); split_info get_best_split(matrix &data, uint num_features); double variance_reduction(vector &parent, vector &l_child, vector &r_child); Node *build_tree(matrix &data, uint curr_depth = 0); public: CDecisionTreeRegressor(uint min_samples_split = 2, uint max_depth = 2); ~CDecisionTreeRegressor(void); void fit(matrix &x, vector &y); };
Na maioria dos casos, essas duas classes são parecidas, usando a mesma classe de nó e muitas das mesmas funções, exceto as funções cálculo do valor da folha, ganho de informação, construção da árvore e treinamento.
Valores das folhas em árvores de decisão para tarefas de regressão
Em tarefas de regressão, o valor da folha de um determinado nó é a média de todos os seus valores.
double CDecisionTreeRegressor::calculate_leaf_value(vector &Y) { return Y.Mean();
Cálculo do ganho de informação
No artigo anterior, já mencionamos que o critério de ganho de informação mede a redução da entropia ou incerteza após a divisão do conjunto de dados.
Em vez de usar Gini e entropia, que são baseados em probabilidade, usamos a fórmula de redução da variância para medir as impurezas em um determinado nó.
double CDecisionTreeRegressor::variance_reduction(vector &parent, vector &l_child, vector &r_child) { double weight_l = l_child.Size() / (double)parent.Size(), weight_r = r_child.Size() / (double)parent.Size(); return parent.Var() - ((weight_l * l_child.Var()) + (weight_r * r_child.Var())); }
A função acima calcula a redução da variância alcançada dividindo o conjunto de dados em nós filhos esquerdo e direito em um determinado nó da árvore de decisão.
Construção da árvore e função de treinamento
Construção da árvore
Node *CDecisionTreeRegressor::build_tree(matrix &data, uint curr_depth=0) { matrix X; vector Y; if (!matrix_utils.XandYSplitMatrices(data,X,Y)) //Split the input matrix into feature matrix X and target vector Y. { #ifdef DEBUG_MODE printf("%s Line %d Failed to build a tree Data Empty",__FUNCTION__,__LINE__); #endif return NULL; //Return a NULL pointer } ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset. ArrayResize(nodes, nodes.Size()+1); //Append the nodes to memory Node *left_child, *right_child; if (samples >= m_min_samples_split && curr_depth<=m_max_depth) { split_info best_split = this.get_best_split(data, (uint)features); #ifdef DEBUG_MODE Print(__FUNCTION__," | ",__LINE__,"\nbest_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold); #endif if (best_split.info_gain > 0) { left_child = this.build_tree(best_split.dataset_left, curr_depth+1); right_child = this.build_tree(best_split.dataset_right, curr_depth+1); nodes[nodes.Size()-1] = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain); return nodes[nodes.Size()-1]; } } nodes[nodes.Size()-1] = new Node(); nodes[nodes.Size()-1].leaf_value = this.calculate_leaf_value(Y); return nodes[nodes.Size()-1]; }
Função Fit
void CDecisionTreeRegressor::fit(matrix &x, vector &y) { matrix data = matrix_utils.concatenate(x, y, 1); this.root = this.build_tree(data); is_fitted = true; }
A única diferença entre a função build_tree da classe Regressor e da classe Classifier é a função variance_reduction.
Para testar a regressão, usei dados prontos do conjunto Airfoil noise data.
matrix data = matrix_utils.ReadCsv("airfoil_noise_data.csv"); matrix x; vector y; if (!matrix_utils.XandYSplitMatrices(data, x, y)) return INIT_FAILED; regressor_tree = new CDecisionTreeRegressor(3,3); regressor_tree.fit(x, y); regressor_tree.print_tree(regressor_tree.root); vector preds = regressor_tree.predict(x); Print("r-squared: ",metrics.r_squared(y, preds));
Resultado
KS 0 00:04:11.402 RandomForest Test (EURUSD,H1) : X_0<=3150.0?7.6482714516406745 FI 0 00:04:11.402 RandomForest Test (EURUSD,H1) ---> left: X_4<=0.0150478?4.070223732531591 ME 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> left: X_2<=0.1016?2.453283788183441 RR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=630.0?2.3366165961173238 JR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 126.94465000000002 MF 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 130.51523904382472 II 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_0<=1600.0?4.999630155449349 HF 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 127.90983653846149 JM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 122.97036507936505 JR 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> right: X_4<=0.0483159?6.040280153408631 FI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=1250.0?5.315257051142112 IG 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 125.68045918367342 GM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 120.69493181818189 NQ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_0<=1250.0?13.291165881821172 GK 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 117.69977777777775 GH 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 109.80075000000001 EL 0 00:04:11.402 RandomForest Test (EURUSD,H1) ---> right: X_4<=0.00152689?28.997059993530435 OL 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> left: X_0<=6300.0?11.053304033466667 HK 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_4<=0.000930789?9.067095683299033 FG 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 134.9866388888889 NO 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 128.59900000000002 QS 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_4<=0.000930789?9.783359845444707 NI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 128.05125581395347 GJ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 120.90806666666667 RM 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->---> right: X_4<=0.0341183?5.715854852017056 LN 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> left: X_0<=5000.0?5.190320913085316 GN 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 120.08625170068028 NE 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 115.52968965517242 MI 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->---> right: X_4<=0.0483159?4.450134400476193 IS 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> left: 109.44371428571428 GQ 0 00:04:11.402 RandomForest Test (EURUSD,H1) --->--->--->---> right: 104.84033333333332 PH 0 00:04:11.403 RandomForest Test (EURUSD,H1) r-squared: 0.5937442611327515
Parece que a árvore de regressão tem mais ramos com os mesmos parâmetros.
A precisão do nosso modelo de regressão durante o treinamento foi de 59%. Isso é um bom sinal de que entendemos tudo corretamente. Veja como as previsões ficam quando plotadas em um gráfico:
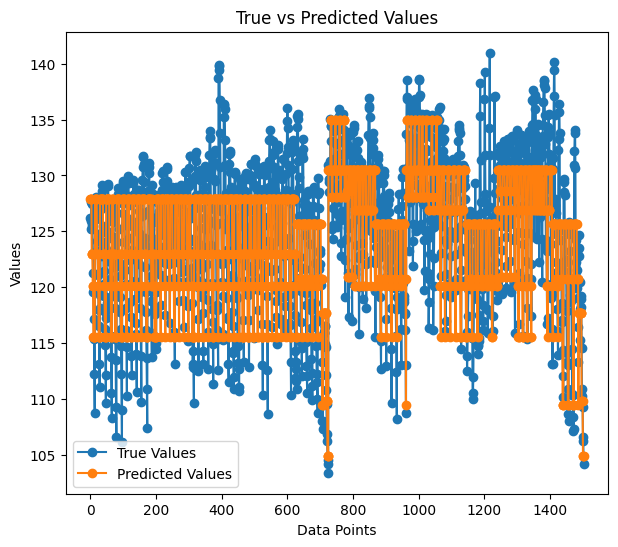
A forma como as previsões correspondem aos valores reais parece quase uma árvore.
Vantagens das florestas aleatórias
Alta precisão — as florestas aleatórias geralmente oferecem maior precisão tanto em tarefas de classificação quanto em tarefas de regressão.
Robustez — a natureza em conjunto da Random Forest a torna robusta contra sobreajuste e dados ruidosos.
Importância dos atributos — as florestas aleatórias podem fornecer informações sobre a importância dos atributos, ajudando na seleção dos mesmos.
Redução da variância — a diversidade das árvores minimiza a variância do modelo, resultando em uma melhor capacidade de generalização.
Não há necessidade de escalonamento dos atributos — assim como as árvores de decisão, as florestas aleatórias são menos sensíveis ao escalonamento dos atributos, o que as torna adequadas para amostras com diferentes escalas de dados.
Versatilidade — são adequadas para diferentes tipos de dados, incluindo características categóricas e numéricas.
Construção de um classificador de floresta aleatória
Exploramos as vantagens do algoritmo de floresta aleatória em comparação com a árvore de decisão. Agora, vamos ver como construir um modelo de floresta aleatória, começando com o classificador.
Incluímos a classe CDecisionTreeClassifier.
class CRandomForestClassifier { CMetrics metrics; protected: uint m_ntrees; uint m_maxdepth; uint m_minsplit; int m_random_state; CMatrixutils matrix_utils; CDecisionTreeClassifier *forest[]; string ConvertTime(double seconds); public: CRandomForestClassifier(uint n_trees=100, uint minsplit=NULL, uint max_depth=NULL, int random_state=-1); ~CRandomForestClassifier(void); void fit(matrix &x, vector &y, bool replace=true); double predict(vector &x); vector predict(matrix &x); };
Como o classificador de floresta aleatória consiste em várias árvores classificadoras combinadas em uma floresta, a classe recebe uma matriz forest[] de objetos CDecisionTreeClassifier.
n_trees = 100 (padrão), o que significa que a floresta do classificador de floresta aleatória terá 100 árvores.
min_split e max_depth são parâmetros para cada árvore, dos quais falamos no artigo anterior min_split é o número mínimo de ramos que a árvore deve ter, e max_depth é a profundidade máxima da árvore em termos desses ramos.
Incorporação de árvores na floresta aleatória
Esta é a função mais importante da classe CRandomForestClassifier, onde a floresta inclui n_trees árvores, selecionadas no construtor da classe.
void CRandomForestClassifier::fit(matrix &x, vector &y, bool replace=true) { matrix x_subset; vector y_subset; matrix data = this.matrix_utils.concatenate(x, y, 1); matrix temp_data = data; vector preds; datetime time_start = GetTickCount(), current_time; Print("[ Classifier Random Forest Building ]"); for (uint i=0; i<m_ntrees; i++) //Build a given x number of trees { time_start = GetTickCount(); temp_data = data; matrix_utils.Randomize(temp_data, m_random_state, replace); //Get randomized subsets if (!this.matrix_utils.XandYSplitMatrices(temp_data, x_subset, y_subset)) //split the random subset into x and y subsets { ArrayRemove(forest,i,1); //Delete the invalid tree in a forest printf("%s %d Failed to split data for a tree ",__FUNCTION__,__LINE__); continue; } forest[i] = new CDecisionTreeClassifier(this.m_minsplit, this.m_maxdepth); //Add the tree to the forest forest[i].fit(x_subset, y_subset); //Add the trained tree to the forest preds = forest[i].predict(x_subset); current_time = GetTickCount(); printf(" ==> Tree <%d> Rand Seed <%s> Accuracy Score: %.3f Time taken: %s",i+1,m_random_state==-1?"None":string(m_random_state),metrics.accuracy_score(y_subset, preds), ConvertTime((current_time - time_start) / 1000.0)); } m_ntrees = ArraySize(forest); //The successfully build trees }
Comparando o classificador de árvore de decisão e o classificador de floresta aleatória
Para provar que os classificadores de floresta aleatória lidam melhor com tarefas de classificação do que as árvores de decisão, realizei 5 testes.
Teste 01:
| Treinamento | Teste | |
|---|---|---|
| Árvore de decisão | 73,8% | 40% |
| Floresta aleatória | 78% | 45% |
Teste 02:
| Árvore de decisão | 73,8% | 40% |
| Floresta aleatória | 83% | 45% |
Teste 03:
| Árvore de decisão | 73,8% | 40% |
| Floresta aleatória | 80% | 45% |
Teste 04:
| Árvore de decisão | 73,8% | 40% |
| Floresta aleatória | 78,8% | 45% |
Teste 05:
| Árvore de decisão | 73,8% | 40% |
| Floresta aleatória | 78,8% | 45% |
Na minha experiência, descobri que usar o classificador de floresta aleatória para dados de negociação pode ser confuso, pois pode-se encontrar situações em que a precisão geral da floresta aleatória não excede a precisão de uma única árvore de decisão. Isso ocorre devido a um ou mais dos seguintes fatores.
Por que a floresta aleatória não proporciona maior precisão do que uma única árvore de decisão:
Falta de diversidade das árvores
Florestas aleatórias se beneficiam da diversidade das árvores individuais. Se todas as árvores forem iguais, o conjunto não trará uma melhoria significativa.
Certifique-se de introduzir a aleatoriedade corretamente durante o treinamento de cada árvore. A randomização pode incluir a escolha de subconjuntos aleatórios de atributos e/ou o uso de diferentes subconjuntos de dados de treinamento.
Ajuste de hiperparâmetros
Experimente diferentes hiperparâmetros, como o número de atributos a considerar para cada divisão (m_max_features), o número mínimo de amostras para dividir um nó interno (m_minsplit) e a profundidade máxima das árvores (m_maxdepth).
Tentar a busca em grade ou a busca aleatória dentro de uma faixa de valores de hiperparâmetros pode ajudar a encontrar as melhores configurações.
Validação cruzada
Use a validação cruzada para avaliar o desempenho do modelo. Isso ajuda a avaliar de forma mais confiável como o modelo se generaliza para novos dados.
A validação cruzada também ajuda a identificar problemas de sobreajuste ou subajuste.
Treinamento em todo o conjunto de dados
Certifique-se de que as árvores não se ajustem aos dados de treinamento. Se cada árvore na floresta for treinada em todo o conjunto de dados, ela pode captar o ruído em vez do sinal.
Talvez cada árvore deva ser treinada com dados de bootstrapping (reamostragem).
Escalonamento dos atributos
Se os seus atributos tiverem escalas diferentes, pode ser útil escaloná-los. As árvores de decisão geralmente não são sensíveis às escalas dos atributos. A normalização ou padronização dos atributos pode ajudar, especialmente se você estiver comparando o desempenho de uma árvore com um conjunto.
Métrica de avaliação
Certifique-se de usar a métrica de avaliação apropriada para o problema que você está tentando resolver com seus modelos. Uma métrica comum de avaliação para regressão é o R-quadrado, e uma métrica comum de avaliação para classificação é a precisão.
O último argumento da função fit() — error. Permite escolher a métrica adequada para medir a precisão de cada árvore na floresta.
enum errors_classifier { ERR_ACCURACY }; enum errors_regressor { ERR_R2_SCORE, ERR_ADJUSTED_R };
Tamanho do conjunto
Experimente com o número de árvores na floresta. Às vezes, aumentar o número de árvores pode melhorar o desempenho do conjunto.
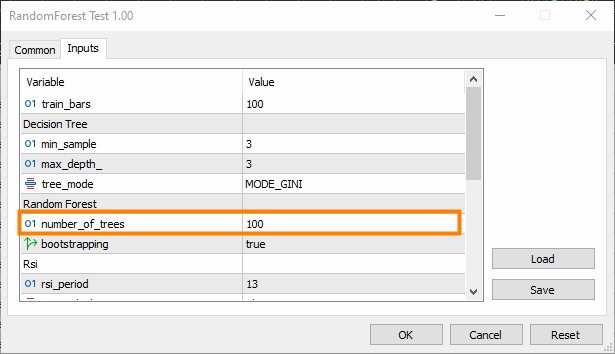
Mas, ao mesmo tempo, isso adiciona complexidade — o tempo de treinamento e teste pode aumentar significativamente após a alteração.
Qualidade dos dados
Assegure-se da qualidade dos seus dados. Se houver valores atípicos ou valores ausentes, isso pode afetar o desempenho da floresta aleatória.
Semente aleatória
Para garantir a reprodutibilidade, certifique-se de definir corretamente o valor da semente aleatória para cada execução.
Usar o mesmo número inicial aleatório (Random seed) fará com que todas as árvores forneçam a mesma precisão, o que não será melhor do que uma única árvore de decisão.
Verificação no testador de estratégias
A floresta aleatória venceu na fase de treinamento e teste, mas será que ela também se sairá bem no trading, onde é necessário mais do que a habilidade de prever para obter lucro?
Realizei testes com ambos os algoritmos com as configurações padrão de 2022.01.01 a 2023.02.01.
Configurações do testador:
- Atrasos: Atraso arbitrário
- Modelagem: Somente preços de abertura
- Depósito: $1000
- Alavancagem: 1/100
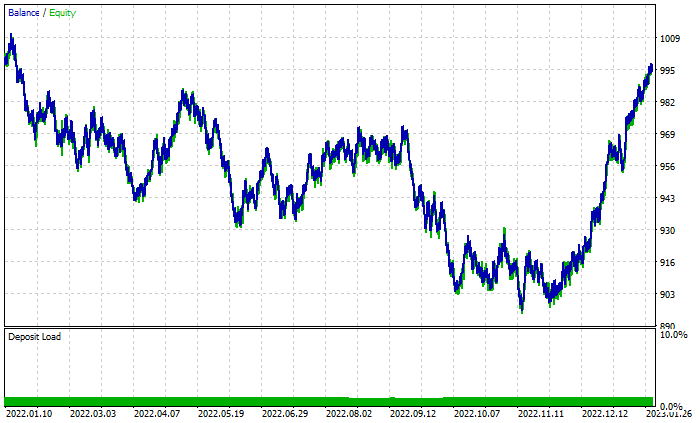
Gráfico dos resultados da floresta aleatória:
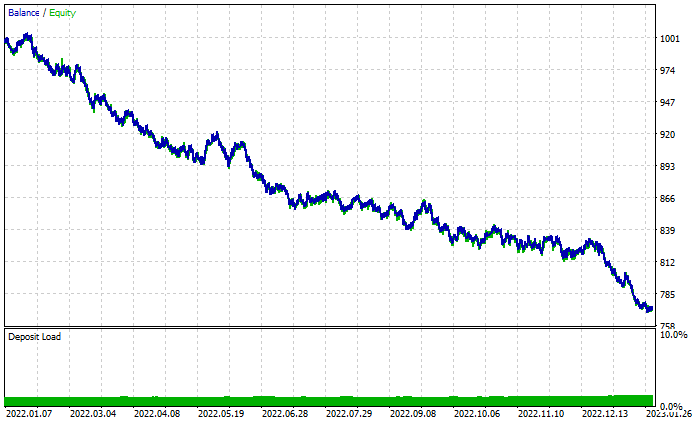
Apesar de ter 46% de negociações lucrativas, o gráfico parece horrível. Vamos ver o que faz a Árvore de decisão:
Melhor do que a floresta aleatória de 100 árvores, apesar de 44% de negociações lucrativas.
Realizei uma rápida otimização para encontrar os melhores níveis de stop-loss e take-profit. Os resultados foram stop-loss = 960 e take-profit = 1295 para ambos os modelos, com o split mínimo definido como 2. Abaixo estão os resultados de ambos os modelos.
Classificador de árvore de decisão:
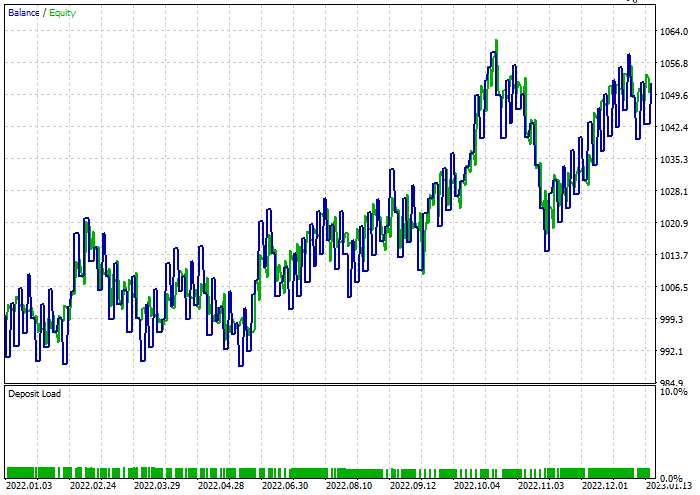
Durante o teste, 47,68% das negociações foram lucrativas. Durante o período de teste, o modelo gerou um lucro de 52 dólares.
Classificador de floresta aleatória:
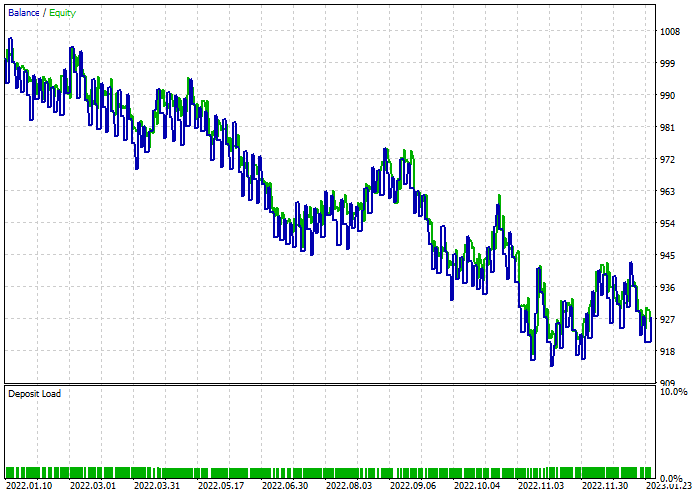
Considerações finais
As florestas aleatórias são usadas em várias áreas e indústrias, incluindo finanças, entretenimento e setor médico. No entanto, como qualquer modelo, elas têm algumas desvantagens que devem ser entendidas antes de decidir usar este modelo para seu projeto de negociação.
Complexidade computacional:
Modelos de floresta aleatória, especialmente com um grande número de árvores, podem ser caros em termos de computação e exigir recursos significativos.
Uso de memória:
À medida que o número de árvores aumenta, o uso de memória do modelo de floresta aleatória também aumenta, o que pode levar a um maior uso de memória.
Interpretabilidade:
A natureza de conjunto das florestas aleatórias as torna menos interpretáveis do que árvores de decisão individuais, especialmente quando a floresta é composta por muitas árvores.
Sobreajuste:
Embora florestas aleatórias sejam menos propensas ao sobreajuste do que árvores de decisão individuais, elas ainda podem se ajustar aos dados ruidosos ou com valores atípicos.
Tendência a classes dominantes:
Em tarefas de classificação com distribuição desequilibrada de classes, florestas aleatórias podem ser tendenciosas em relação à classe dominante, o que afeta a eficácia preditiva do modelo para classes minoritárias.
Sensibilidade aos parâmetros:
Embora florestas aleatórias sejam robustas em relação à escolha de hiperparâmetros, o desempenho do modelo ainda pode ser sensível a valores específicos dos parâmetros.
Caixa-preta:
A natureza de conjunto das florestas aleatórias, que combina várias árvores de decisão, pode dificultar a interpretação do processo de tomada de decisão do modelo.
Tempo de treinamento:
Treinar um modelo de floresta aleatória pode levar mais tempo do que treinar uma única árvore de decisão, especialmente para grandes conjuntos de dados.
A atividade de negociação atrasou 10 minutos, pois tive que esperar para treinar 100 árvores.
Obrigado por ler.
Você pode acompanhar o desenvolvimento deste modelo de aprendizado de máquina e muito mais desta série de artigos no meu repositório no GitHub.
Conteúdo do anexo:
| Arquivo | Uso e descrição |
|---|---|
| Forest.mqh (localizado na pasta include) | Contém classes de floresta aleatória, CRandomForestClassifier e CRandomForestRegressor. |
| matrix_utils.mqh (Include) | Funções adicionais para trabalhar com matrizes. |
| metrics.mqh (Include) | Funções e código para medir o desempenho dos modelos de aprendizado de máquina. |
| preprocessing.mqh (Include) | Biblioteca para pré-processamento de dados brutos, tornando-os adequados para uso em modelos de aprendizado de máquina. |
| tree.mqh (Include) | Contém classes de árvore de decisão. |
| RandomForest Test.mq5 (Experts) | EA para executar e testar modelos de floresta aleatória. |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/13765
 Padrões de projeto no MQL5 (Parte 4): Padrões comportamentais 2
Padrões de projeto no MQL5 (Parte 4): Padrões comportamentais 2
 Indicador de posições históricas no gráfico em forma de diagrama de lucro/prejuízo
Indicador de posições históricas no gráfico em forma de diagrama de lucro/prejuízo
 Algoritmos de otimização populacional: algoritmos de estratégias evolutivas (Evolution Strategies, (μ,λ)-ES e (μ+λ)-ES)
Algoritmos de otimização populacional: algoritmos de estratégias evolutivas (Evolution Strategies, (μ,λ)-ES e (μ+λ)-ES)
 Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 09): Combinação de agrupamento k-médias com ondas fractais
Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 09): Combinação de agrupamento k-médias com ondas fractais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso