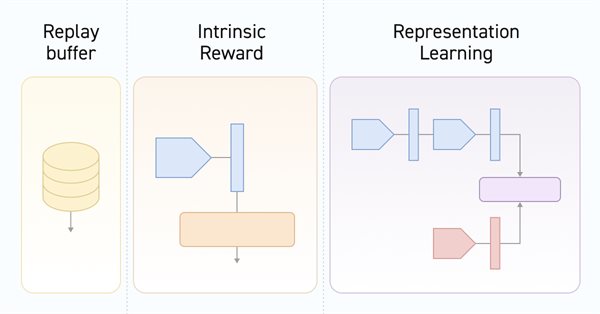
Neural networks made easy (Part 55): Contrastive intrinsic control (CIC)
4 245
0
Introduction
In previous articles, we have already discussed the benefits of using hierarchical models. We considered methods for training models that are capable of extracting and highlighting individual Agent skills. The acquired skills can be useful in achieving the ultimate goal of the task. The examples of such algorithms are DIAYN, DADS and EDL. These algorithms approach the skill training process in different ways, but all of them were used for discrete action space problems. Today we will talk about another approach to studying the Agent’s skills and look at its application in the field of solving continuous action space problems.
1. Main CIC components
Reinforcement learning actively uses algorithms for preliminary training of Agents using self-controlled internal rewards. Such algorithms can be divided into 3 categories: ones based on competencies, knowledge and data. Tests in Unsupervised Reinforcement Learning Benchmark demonstrate that competency-based algorithms are inferior to other categories.
Algorithms using competencies strive to maximize mutual information between observed states and a latent vector of skills. This mutual information is estimated through the Discriminator model. Typically, a classifier or regressor model is used as a Discriminator. However, achieving accuracy in classification and regression tasks requires a huge amount of diverse training data. In simple environments where the number of potential behaviors is limited, competency-based methods have demonstrated their efficiencies. But in environments with many potential behavioral options, their effectiveness is significantly reduced.
Complex environments require a wide variety of skills. To handle them, we need a Discriminator with high power. The contradiction between this requirement and the limited capabilities of existing Discriminators prompted the creation of the Contrastive Intrinsic Control (CIC) method.
Contrastive Intrinsic Control is a new approach to contrastive density estimation to approximate the conditional entropy of the Discriminator. The method handles transitions between states and skill vectors. This allows for powerful representation learning techniques from visual processing to skill detection. The proposed method makes it possible to increase the stability and efficiency of Agent training in a variety of environments.
The Contrastive Intrinsic Control algorithm begins with training the Agent in the environment using feedback and obtaining trajectories of states and actions. Representation training is then performed using Contrastive Predictive Coding (CPC), which motivates the Agent to retrieve key features from states and actions. Representations are formed that take into account the dependencies between successive states.
Intrinsic rewards play an important role in determining which behavioral strategies should be maximized. CIC maximizes the entropy of transitions between states, which promotes diversity in Agent behavior. This allows the Agent to explore and create a variety of behavioral strategies.
After generating a variety of skills and strategies, the CIC algorithm uses the Discriminator to instantiate the skill representations. The Discriminator aims to ensure that states are predictable and stable. In this way, the Agent learns to "use" skills in predictable situations.
The combination of exploration motivated by intrinsic rewards and the use of skills for predictable actions creates a balanced approach for creating varied and effective strategies.
As a result, the Contrastive Predictive Coding algorithm encourages the Agent to detect and learn a wide range of behavioral strategies, while ensuring stable learning. Below is the custom algorithm visualization.
We will get acquainted with the algorithm in more detail during the implementation.
2. Implementation using MQL5
Before implementing the Contrastive Predictive Coding algorithm using MQL5, we should determine some key points. Firstly, the model training algorithm is divided into two large stages:
- training skills without external rewards from the environment;
- training a policy for solving a given task based on external rewards.
Secondly, during the training process, the Discriminator learns the correspondence of transitions between states and skills. Keep in mind that we are operating precisely a state change, rather than an external reward for the transition to a new state or an action that led to this state. If we draw analogies with the previously discussed algorithms that operated with the same data, then DIAYN determined the skill based on the initial and new model states. On the contrary, in DADS, the Discriminator predicted the next state based on the initial state and skill. In this method, we determine the contrast error between the transition (initial and subsequent states) and the skill used by the Agent. At the same time, latent representations of states and skills are formed. It is the Discriminator that influences the training of the state encoder, which is subsequently used by the Agent and the scheduler. This is reflected in the architecture of the models we use. This is what prompted us to move the environmental state encoder into a separate model.
2.1 Model architecture
We gradually approach the CreateDescriptions method of describing the architectures of the models used. In the method parameters, we can see the pointers to architecture description arrays of six models. Their purpose will be described later.
bool CreateDescriptions(CArrayObj *state_encoder, CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution, CArrayObj *descriminator, CArrayObj *skill_project ) { //--- CLayerDescription *descr; //--- if(!state_encoder) { state_encoder = new CArrayObj(); if(!state_encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!convolution) { convolution = new CArrayObj(); if(!convolution) return false; } if(!descriminator) { descriminator = new CArrayObj(); if(!descriminator) return false; } if(!skill_project) { skill_project = new CArrayObj(); if(!skill_project) return false; }
First we have a model of the environmental state encoder. We have already started talking about the functionality of this model. As you know, our state of the environment consists of two blocks: historical data and account status. We will feed both of these tensors to the encoder input. The architecture of this model will remind you of the source data preprocessing block previously used in Actor models.
bool CreateDescriptions(CArrayObj *state_encoder, CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution, CArrayObj *descriminator, CArrayObj *skill_project ) { //--- CLayerDescription *descr; //--- if(!state_encoder) { state_encoder = new CArrayObj(); if(!state_encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!convolution) { convolution = new CArrayObj(); if(!convolution) return false; } if(!descriminator) { descriminator = new CArrayObj(); if(!descriminator) return false; } if(!skill_project) { skill_project = new CArrayObj(); if(!skill_project) return false; } //--- State Encoder state_encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count - 1; descr.window = 2; descr.step = 1; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = 8; descr.step = 8; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.optimization = ADAM; descr.activation = LReLU; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = 128; descr.activation = LReLU; descr.optimization = ADAM; if(!state_encoder.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = NSkills; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!state_encoder.Add(descr)) { delete descr; return false; }
Next, let's look at the Actor architecture. It is still the same model. However, we exclude the block of preliminary processing of the source data placed in a separate Encoder. But there is one detail. We add another input tensor that describes the skill being used.
Besides, we refuse to use stochastic policies so that the policies of the Actor’s behavior when using different skills can be clearly separated.
//--- Actor actor.Clear(); //--- layer 0 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NSkills; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NSkills; descr.optimization = ADAM; descr.activation = SIGMOID; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NActions; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
As usual, after the Actor, we describe the architecture of the Critic. It is time to think about its functionality. At first glance, the question is quite simple. The Critic estimates the expected reward for moving to a new state. The reward for a particular transition depends on the action performed, not the skill used. Of course, the action is chosen by the Actor based on the specified skill. But the environment does not care what motive the Agent was guided by. It reacts to the Agent influence.
On the other hand, the Critic evaluates the Actor's policy and predicts the expected reward for subsequent use of this policy. The Actor’s policies directly depend on the skill used. Therefore, in the initial data, the Critic does not need to convey the current state of the environment, the skill used and the selected action of the Actor. Here we will use a technique that has previously been used. We will take the latent state of the Actor, which already takes into account the description of the environment state and the skill used, and add the action selected by the Actor. Thus, the Critic architecture has remained unchanged. But the Actor's latent state ID has changed.
Besides, we abandoned the decomposition of the reward function. This is a necessary measure. As already mentioned, we will train the model in two stages. At each stage, we will use a different reward function. We face a choice. We may use reward decomposition and train 2 different Critics at each stage. Alternatively, we may abandon reward decomposition but use the same Critic at both stages. I decided to take the second path.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; }
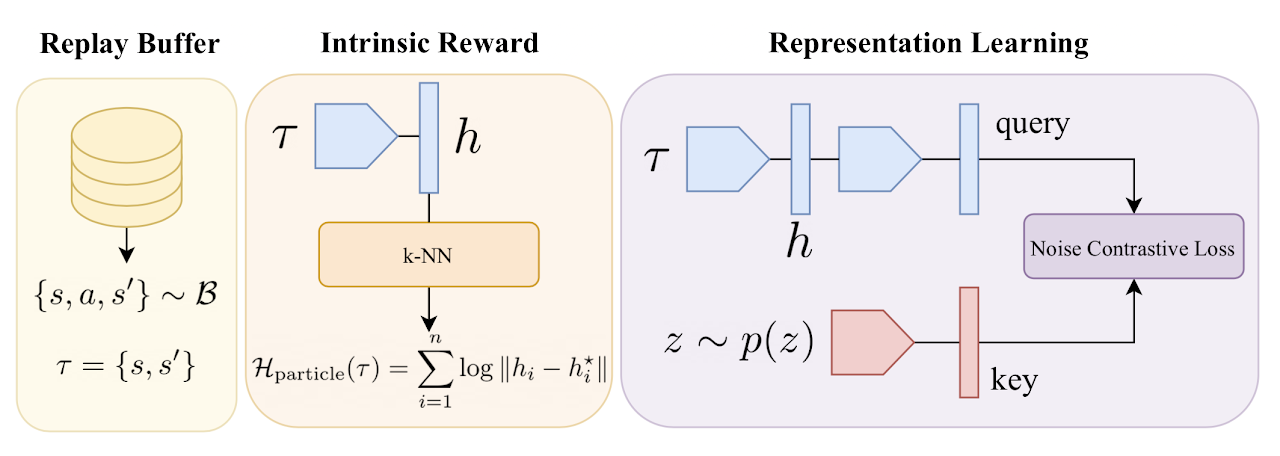
Next, we brought our vision to the algorithm optimization. The method authors propose to use the entropy of transitions as an internal reward using the method of particles from k nearest neighbors, as we did in the previous article. The only difference is that the authors used the transition distance from the mini-batch in the trained encoder representation. To achieve this, we will need to encode a certain package of transitions at each iteration of updating the parameters. We cannot code a mini-batch once and use this representation in training. After all, after each update of the encoder parameters, the space of its results will change.
But we know that even a random convolutional model can give us enough data to compare two states. Therefore, we will create a non-trainable convolutional model for the purpose of intrinsic reward. Before training, we will first create a compressed representation of all the transitions from the experience playback buffer. During training, we will only encode the analyzed transition.
Speaking about transition, we mean two subsequent environment states.
//--- Convolution convolution.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = 2 * (HistoryBars * BarDescr + AccountDescr); descr.activation = None; descr.optimization = ADAM; if(!convolution.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = SIGMOID; if(!convolution.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = 512 / 8; descr.window = 8; descr.step = 8; int prev_wout = descr.window_out = 2; descr.activation = LReLU; descr.optimization = ADAM; if(!convolution.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = (prev_count * prev_wout) / 4; descr.window = 4; descr.step = 4; prev_wout = descr.window_out = 2; descr.activation = LReLU; descr.optimization = ADAM; if(!convolution.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = (prev_count * prev_wout) / 4; descr.window = 4; descr.step = 4; prev_wout = descr.window_out = 2; descr.activation = LReLU; descr.optimization = ADAM; if(!convolution.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = EmbeddingSize; descr.activation = LReLU; descr.optimization = ADAM; if(!convolution.Add(descr)) { delete descr; return false; }
Let's move on to the Discriminator. In this case, the Discriminator will consist of two models. One model named Discriminator takes two consecutive environmental states as input and returns some latent representation of the transition. As mentioned above, the model encodes exactly the transition in the environment without taking into account the skill used and the action taken. Here, as initial data, we use the results of the encoder for two subsequent states.
At the model output, we use SoftMax to normalize the obtained results.
//--- Descriminator descriminator.Clear(); //--- layer 0 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NSkills; descr.activation = None; descr.optimization = ADAM; if(!descriminator.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NSkills; descr.optimization = ADAM; descr.activation = SIGMOID; if(!descriminator.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!descriminator.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!descriminator.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = EmbeddingSize; descr.activation = LReLU; descr.optimization = ADAM; if(!descriminator.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = 1; descr.optimization = ADAM; if(!descriminator.Add(descr)) { delete descr; return false; }
The second component of the Discriminator is a model for representing a latent representation of the skill being used. From the functionality of the model, it follows that it receives only the skill used as input returning its compressed representation in the form of a tensor similar to the latent representation of the transition (the result of the Discriminator model).
The results of these two models will be the data for contrasting intrinsic control. Accordingly, we also use SoftMax at the output of the model.
//--- Skills project skill_project.Clear(); //--- layer 0 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NSkills; descr.activation = None; descr.optimization = ADAM; if(!skill_project.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = SIGMOID; if(!skill_project.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!skill_project.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!skill_project.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = EmbeddingSize; descr.activation = LReLU; descr.optimization = ADAM; if(!skill_project.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = 1; descr.optimization = ADAM; if(!skill_project.Add(descr)) { delete descr; return false; } //--- return true; }
Although the last two models use different initial data, they have fairly similar functionality. This is why we used somewhat similar architectural solutions for them.
As you can see, we have completed the method of describing the architectural solutions of the models used. But it does not describe the scheduler architecture. We do not use the scheduler at the skill training stage. Looking ahead a little, I will say that we will randomly generate a representation of skills at the first training stage. This will allow our Actor to better learn different behavior policies. But we will use the scheduler to teach the policy of using skills to achieve the desired goal. Therefore, the scheduler model was moved to a separate SchedulerDescriptions method.
bool SchedulerDescriptions(CArrayObj *scheduler) { //--- Scheduller if(!scheduler) { scheduler = new CArrayObj(); if(!scheduler) return false; } scheduler.Clear(); //--- CLayerDescription *descr = NULL; //--- layer 0 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = NSkills; descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.window = prev_count; descr.optimization = ADAM; descr.activation = SIGMOID; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NSkills; descr.activation = LReLU; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = NSkills; descr.step = 1; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- return true; }
With this, we complete the work of describing the architectural solutions of the models used and move on to building an algorithm for their operation.
2.2 Training sample collection EA
As before, we will use several programs while training the model. We will use the first "...\CIC\Research.mq5" EA to collect a training sample. The data collection process itself has not changed. We need to consistently use several models to form the Actor action. But first we should create them in the OnInit EA initialization method.
In the method body, we, as usual, initialize all the necessary indicators.
int OnInit() { //--- if(!Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh(); //--- if(!RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice)) return INIT_FAILED; //--- if(!CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice)) return INIT_FAILED; //--- if(!ATR.Create(Symb.Name(), TimeFrame, ATRPeriod)) return INIT_FAILED; //--- if(!MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice)) return INIT_FAILED; if(!RSI.BufferResize(HistoryBars) || !CCI.BufferResize(HistoryBars) || !ATR.BufferResize(HistoryBars) || !MACD.BufferResize(HistoryBars)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); return INIT_FAILED; } //--- if(!Trade.SetTypeFillingBySymbol(Symb.Name())) return INIT_FAILED;
Next, load the Encoder and Actor models. If there are no pre-trained models, we will generate random ones.
//--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); CArrayObj *descr = new CArrayObj(); if(!CreateDescriptions(encoder,actor, descr,descr,descr,descr)) { delete encoder; delete actor; delete descr; return INIT_FAILED; } if(!Encoder.Create(encoder) || !Actor.Create(actor)) { delete encoder; delete actor; delete descr; return INIT_FAILED; } delete encoder; delete actor; delete descr; //--- }
The case is a bit different for the Scheduler. We will need to collect training sample data for both training stages. Using the Scheduler model at the first stage may somewhat limit the Actor's action space. Using a randomly generated skill tensor is in many ways similar to using a Scheduler with random parameters. At the same time, it is many times faster than the direct passage of the model.
At the same time, it is advisable to use a pre-trained Scheduler at the second stage of training. This will allow not only to collect data in the field of its policy action, but also to evaluate training results.
Therefore, we try to load the pre-trained scheduler model, and the result of the operation is written to the random skill vector usage flag.
bRandomSkills = (!Scheduler.Load(FileName + "Sch.nnw", temp, temp, temp, dtStudied, true));
Next, we transfer all used models into a single OpenCL context.
COpenCLMy *opcl = Encoder.GetOpenCL();
Actor.SetOpenCL(opcl);
if(!bRandomSkills)
Scheduler.SetOpenCL(opcl);
Check the conformity of the models.
Actor.getResults(ActorResult); if(ActorResult.Size() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; } //--- Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- vector<float> EncoderResults; Actor.GetLayerOutput(0,Result); Encoder.getResults(EncoderResults); if(Result.Total() != int(EncoderResults.Size())) { PrintFormat("Input size of Actor doesn't match Encoder outputs (%d <> %d)", Result.Total(), EncoderResults.Size()); return INIT_FAILED; } //--- if(!bRandomSkills) { Scheduler.GetLayerOutput(0,Result); if(Result.Total() != int(EncoderResults.Size())) { PrintFormat("Input size of Scheduler doesn't match Encoder outputs (%d <> %d)", Result.Total(), EncoderResults.Size()); return INIT_FAILED; } }
Initialize the variables.
//--- PrevBalance = AccountInfoDouble(ACCOUNT_BALANCE); PrevEquity = AccountInfoDouble(ACCOUNT_EQUITY); //--- return(INIT_SUCCEEDED); }
Collect data in the OnTick method. As before, all operations are carried out only when opening a new bar.
void OnTick() { //--- if(!IsNewBar()) return;
Here we first collect historical data and account data. This process has been transferred without changes from the previously discussed algorithms. I will not dwell on this here. Let’s immediately move on to arranging the direct passage of models. We call the Encoder first.
//--- Encoder if(!Encoder.feedForward(GetPointer(bState), 1, false, GetPointer(bAccount))) return;
We then check the random skill vector usage flag. If we previously managed to load the Scheduler model, then we make a sequential call of the Scheduler and Actor.
//--- Scheduler & Actor if(!bRandomSkills) { if(!Scheduler.feedForward((CNet *)GetPointer(Encoder),-1,NULL,-1) || !Actor.feedForward(GetPointer(Encoder),-1,GetPointer(Scheduler),-1)) return; }
Otherwise, we first generate a random skill tensor. Do not forget to normalize it with the SoftMax function since these are vectors of probabilities of using individual skills. Finally, call the Actor.
else { vector<float> skills = vector<float>::Zeros(NSkills); for(int i = 0; i < NSkills; i++) skills[i] = (float)((double)MathRand() / 32767.0); skills.Activation(skills,AF_SOFTMAX); bSkills.AssignArray(skills); if(bSkills.GetIndex() >= 0 && !bSkills.BufferWrite()) return; if(!Actor.feedForward(GetPointer(Encoder),-1,(CBufferFloat *)GetPointer(bSkills))) return; }
As a result of the direct passage of the models, we obtain a certain tensor of actions at the Actor output. The rejection of a stochastic policy leads to strict associations of the Actor between the initial data and the chosen action. We will add a little noise to the resulting action vector for environmental research purposes.
PrevBalance = sState.account[0]; PrevEquity = sState.account[1]; //--- vector<float> temp; Actor.getResults(temp); //--- for(ulong i = 0; i < temp.Size(); i++) { float rnd = ((float)MathRand() / 32767.0f - 0.5f) * 0.1f; temp[i] += rnd; } temp.Clip(0.0f,1.0f); ActorResult = temp;
After these operations, we carry out the Actor actions and save the result into the experience playback buffer.
Keep in mind that we save the same data set without the skill identifier. We need transitions and rewards from the environment for training models, while we are going to generate various skill identification vectors during training. This will allow us to expand the training set many times without additional interaction with the environment.
The remaining method code, as well as the EA as a whole, remained unchanged and was carried over from previously considered similar EAs. We will not analyze it in detail now. You can find it in the attachment.
2.3 Skills training
The first stage of model training - learning skills - is arranged in the "...\CIC\Pretrain.mq5" EA. In many ways, it is built by analogy with the previously discussed “Study.mq5” EAs, while taking into account the specifics of the Contrastive Intrinsic Control algorithm under consideration.
The algorithm for initializing the OnInit EA is no different from the methods of the same name of previously discussed similar EAs. Let us dwell only on the list of models used. Here we see Encoder, Actor, two Critics, random convolutional Encoder and Discriminator models. But only one Encoder model is a targeted one.
We need two Encoder models to encode the analyzed and subsequent environmental states, which are used by the Discriminator.
However, we do not use target models of the Actor and Critics, since at this stage we are teaching the Actor to perform separable actions under the influence of a particular skill in a specific state of the environment. We do not seek to accumulate intrinsic rewards for various skills. We maximize it in every single moment.
int OnInit() { //--- ....... ....... //--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) || !Descriminator.Load(FileName + "Des.nnw", temp, temp, temp, dtStudied, true) || !SkillProject.Load(FileName + "Skp.nnw", temp, temp, temp, dtStudied, true) || !Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true) || !TargetEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *encoder = new CArrayObj(); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *descrim = new CArrayObj(); CArrayObj *convolution = new CArrayObj(); CArrayObj *skill_poject = new CArrayObj(); if(!CreateDescriptions(encoder,actor, critic, convolution,descrim,skill_poject)) { delete encoder; delete actor; delete critic; delete descrim; delete convolution; delete skill_poject; return INIT_FAILED; } if(!Encoder.Create(encoder) || !Actor.Create(actor) || !Critic1.Create(critic) || !Critic2.Create(critic) || !Descriminator.Create(descrim) || !SkillProject.Create(skill_poject) || !Convolution.Create(convolution)) { delete encoder; delete actor; delete critic; delete descrim; delete convolution; delete skill_poject; return INIT_FAILED; } if(!TargetEncoder.Create(encoder)) { delete encoder; delete actor; delete critic; delete descrim; delete convolution; delete skill_poject; return INIT_FAILED; } delete encoder; delete actor; delete critic; delete descrim; delete convolution; delete skill_poject; //--- TargetEncoder.WeightsUpdate(GetPointer(Encoder), 1.0f); } //--- OpenCL = Actor.GetOpenCL(); Encoder.SetOpenCL(OpenCL); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); TargetEncoder.SetOpenCL(OpenCL); Descriminator.SetOpenCL(OpenCL); SkillProject.SetOpenCL(OpenCL); Convolution.SetOpenCL(OpenCL); //--- ........ ........ //--- return(INIT_SUCCEEDED); }
The actual process of training models is arranged in the Train method.
Similar to the previous article, we encode all transitions between states available in the experience playback buffer at the beginning of the method. The algorithm for constructing the process is identical. However, it has its own nuances. We code transitions. Therefore, we provide a tensor of two consecutive states as input to a random encoder, without taking into account the actions being performed.
Besides, we use only internal reward at this stage. This means we exclude the processing of external environmental rewards.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- int total_states = Buffer[0].Total - 1; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total - 1; vector<float> temp; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size()); int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total - 1; st++) { State.AssignArray(Buffer[tr].States[st].state); float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance); double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- State.AddArray(Buffer[tr].States[st + 1].state); State.Add((Buffer[tr].States[st + 1].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[1] / PrevBalance); State.Add((Buffer[tr].States[st + 1].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st + 1].account[2]); State.Add(Buffer[tr].States[st + 1].account[3]); State.Add(Buffer[tr].States[st + 1].account[4] / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[5] / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[6] / PrevBalance); x = (double)Buffer[tr].States[st + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } Convolution.getResults(temp); state_embedding.Row(temp,state); state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } } if(state != total_states) { state_embedding.Reshape(state,state_embedding.Cols()); total_states = state; }
Next, declare local variables.
vector<float> reward = vector<float>::Zeros(NRewards); vector<float> rewards1 = reward, rewards2 = reward; int bar = (HistoryBars - 1) * BarDescr;
Arrange a model training cycle. In the cycle body, we, as before, randomly select the trajectory and the analyzed state from the experience playback buffer.
for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
Using the sampled state data, we form the initial data tensors of our models.
//--- State State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
Here we form a random tensor of the skill used.
//--- Skills vector<float> skills = vector<float>::Zeros(NSkills); for(int sk = 0; sk < NSkills; sk++) skills[sk] = (float)((double)MathRand() / 32767.0); skills.Activation(skills,AF_SOFTMAX); Skills.AssignArray(skills); if(Skills.GetIndex() >= 0 && !Skills.BufferWrite()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We first submit the generated initial data to the Encoder input.
//--- Encoder State if(!Encoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Then we carry out a direct pass of the Actor.
//--- Actor if(!Actor.feedForward(GetPointer(Encoder), -1, GetPointer(Skills))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Based on the resulting action tensor, we form a predictive subsequent state. We have no problems with historical price movement data. We simply take them from the experience playback buffer. In order to calculate the forecast account status, we will create the ForecastAccount method, whose algorithm will be considered later.
//--- Next State TargetState.AssignArray(Buffer[tr].States[i + 1].state); double cl_op = Buffer[tr].States[i + 1].state[bar]; double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op / SymbolInfoDouble(_Symbol, SYMBOL_POINT); Actor.getResults(Result); vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,Result,prof_1l, Buffer[tr].States[i + 1].account[7]); TargetAccount.AssignArray(forecast); if(TargetAccount.GetIndex() >= 0 && !TargetAccount.BufferWrite()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Perform a direct pass through the target Encoder to obtain a latent representation of the subsequent state.
if(!TargetEncoder.feedForward(GetPointer(TargetState), 1, false, GetPointer(TargetAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
At this stage, we have a latent representation of the two subsequent environmental states. We are able to obtain the transition representation vector. We get the skill representation vector here.
//--- Descriminator if(!Descriminator.feedForward(GetPointer(Encoder),-1,GetPointer(TargetEncoder),-1) || !SkillProject.feedForward(GetPointer(Skills),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
The result of the contrastive comparison of the two resulting vectors serves as the first part of our internal reward. Maximizing this reward encourages the Actor to train easily separable and predictable skills that are easily mapped to individual state transitions in the environment.
Descriminator.getResults(rewards1); SkillProject.getResults(rewards2); float norm1 = rewards1.Norm(VECTOR_NORM_P,2); float norm2 = rewards2.Norm(VECTOR_NORM_P,2); reward[0] = (rewards1 / norm1).Dot(rewards2 / norm2);
We immediately update the parameters of the Discriminator models. Without further complicating the algorithm, we simply train the Discriminator model to approximate a compressed representation of a skill. The skill projection model is trained to approximate a compressed transition representation.
At the same time, we train the Encoder to represent the state of the environment in a way that could be identified with a certain skill. We train the Encoder based on the error gradients received from the Discriminator similar to Actor and Critic in a continuous space of actions.
Result.AssignArray(rewards2); if(!Descriminator.backProp(Result,GetPointer(TargetEncoder)) || !Encoder.backPropGradient(GetPointer(Account),GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Result.AssignArray(rewards1); if(!SkillProject.backProp(Result,(CNet *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
The second component of our internal reward function is a penalty for the lack of open positions at the current moment. We take information about the presence of transactions from the forecast state of the account.
if(forecast[3] == 0.0f && forecast[4] == 0.f) reward[0] -= Buffer[tr].States[i + 1].state[bar + 6] / PrevBalance;
The third component of our internal reward is the entropy of transition, which stimulates the Actor to study a variety of behaviors and master a large number of skills. To obtain the transition entropy, we first obtain a compressed representation of the transition in random encoder space and determine the k nearest neighbors in the KNNReward method.
State.AddArray(GetPointer(Account)); State.AddArray(GetPointer(TargetState)); State.AddArray(GetPointer(TargetAccount)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Convolution.getResults(rewards1); reward[0] += KNNReward(7,rewards1,state_embedding);
We add the resulting transition entropy result to our internal reward.
Now that we have established the full meaning of our complex intrinsic rewards, we can move on to training the Critics and the Actor. We have already carried out the forward passage of the Actor earlier. We now call the direct pass of both critics.
Result.AssignArray(reward); //--- if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor),-1) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor),-1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We will train the actor using a critic with minimal error. Check the Critics' moving average error. First, we carry out the reverse pass of the Critic with minimal error. This is followed by the Actor's reverse pass. The last stage is the reverse pass of the Critic with the largest average error in predicting the cost of the Actor’s actions.
if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError()) { if(!Critic1.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Skills), GetPointer(Gradient), -1) || !Critic2.backProp(Result, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } } else { if(!Critic2.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Skills), GetPointer(Gradient), -1) || !Critic1.backProp(Result, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
Next, we update the parameters of the target Encoder and inform a user about the state of the model training.
//--- Update Target Nets TargetEncoder.WeightsUpdate(GetPointer(Encoder), Tau); //--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-20s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-20s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
After completing all training cycle iterations, we clear the chart comment field and initiate the program closure process.
Comment(""); //--- PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
To get a general picture of training, let’s consider another method for generating the forecast state of the ForecastAccount account. In the parameters, the method receives a pointer to the previous account state, an action tensor, the profit value of 1 lot of a long position for the next bar, and the timestamp of the next bar. The profit size per 1 lot is determined before calling the method based on the subsequent candle data. This operation is only possible with offline training based on historical data on price movements.
We will first do a little preparatory work in the method body. Here we declare local variables and load some information about the tool. It should be noted that since we did not specify the instrument anywhere in the training data, we will use the data about the chart instrument. Therefore, for the correct training, it is necessary to launch the learning EA on the necessary instrument chart.
vector<float> ForecastAccount(float &prev_account[], CBufferFloat *actions,double prof_1l,float time_label) { vector<float> account; vector<float> act; double min_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); double step_lot = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP); double stops = MathMax(SymbolInfoInteger(_Symbol,SYMBOL_TRADE_STOPS_LEVEL), 1) * Point(); double margin_buy,margin_sell; if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_ASK),margin_buy) || !OrderCalcMargin(ORDER_TYPE_SELL,_Symbol,1.0,SymbolInfoDouble(_Symbol,SYMBOL_BID),margin_sell)) return vector<float>::Zeros(prev_account.Size());
For convenience, let’s transfer the data obtained in the parameters into vectors.
actions.GetData(act); account.Assign(prev_account);
After this, we will adjust the agent’s actions to open a position in only one direction to the difference in the declared volumes. After that, check the sufficiency of funds for operations. If there are insufficient funds on the account, reset the trade volume to zero.
if(act[0] >= act[3]) { act[0] -= act[3]; act[3] = 0; if(act[0]*margin_buy >= MathMin(account[0],account[1])) act[0] = 0; } else { act[3] -= act[0]; act[0] = 0; if(act[3]*margin_sell >= MathMin(account[0],account[1])) act[3] = 0; }
Next come the decoding operations of the received actions. The process is built by analogy with the algorithm for performing actions in the EA for collecting training data. Only instead of performing actions, we change the corresponding elements of the account state description. First, we look at the elements of a long position. If the volume of a trade is equal to "0" or the stop levels are less than the minimum margin for the instrument, then this set of parameters indicates the closure of a trade provided that one was open. We reset the size of the current position in this direction, while the accumulated profit/loss is added to the current balance.
//--- buy control if(act[0] < min_lot || (act[1] * MaxTP * Point()) <= stops || (act[2] * MaxSL * Point()) <= stops) { account[0] += account[4]; account[2] = 0; account[4] = 0; }
In case of opening or holding a position, we normalize the trade volume and check the resulting volume with the previously opened one. If the position was larger than the one offered by the Actor, then we divide the accumulated profit/loss in proportion to the offered and closed volumes. Add profit/ loss of the closed volume to the balance. Leave the difference in the accumulated profit field. Change the position volume to the one proposed by the Actor. Also, add profit/loss from the transition to the next environmental state to the accumulated volume.
else { double buy_lot = min_lot + MathRound((double)(act[0] - min_lot) / step_lot) * step_lot; if(account[2] > buy_lot) { float koef = (float)buy_lot / account[2]; account[0] += account[4] * (1 - koef); account[4] *= koef; } account[2] = (float)buy_lot; account[4] += float(buy_lot * prof_1l); }
The operations are repeated for short positions.
//--- sell control if(act[3] < min_lot || (act[4] * MaxTP * Point()) <= stops || (act[5] * MaxSL * Point()) <= stops) { account[0] += account[5]; account[3] = 0; account[5] = 0; } else { double sell_lot = min_lot + MathRound((double)(act[3] - min_lot) / step_lot) * step_lot; if(account[3] > sell_lot) { float koef = float(sell_lot / account[3]); account[0] += account[5] * (1 - koef); account[5] *= koef; } account[3] = float(sell_lot); account[5] -= float(sell_lot * prof_1l); }
The accumulated profits from long and short positions constitute the accumulated profit of the account. The sum of accumulated profit and balance gives the Equity parameter.
account[6] = account[4] + account[5]; account[1] = account[0] + account[6];
Use the obtained values to form a vector describing the state of the account and return it to the calling program.
vector<float> result = vector<float>::Zeros(AccountDescr); result[0] = (account[0] - prev_account[0]) / prev_account[0]; result[1] = account[1] / prev_account[0]; result[2] = (account[1] - prev_account[1]) / prev_account[1]; result[3] = account[2]; result[4] = account[3]; result[5] = account[4] / prev_account[0]; result[6] = account[5] / prev_account[0]; result[7] = account[6] / prev_account[0]; double x = (double)time_label / (double)(D'2024.01.01' - D'2023.01.01'); result[8] = (float)MathSin(2.0 * M_PI * x); x = (double)time_label / (double)PeriodSeconds(PERIOD_MN1); result[9] = (float)MathCos(2.0 * M_PI * x); x = (double)time_label / (double)PeriodSeconds(PERIOD_W1); result[10] = (float)MathSin(2.0 * M_PI * x); x = (double)time_label / (double)PeriodSeconds(PERIOD_D1); result[11] = (float)MathSin(2.0 * M_PI * x); //--- return result return result; }
After the training process is completed, all models are saved in the OnDeinit EA's deinitialization method.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- TargetEncoder.WeightsUpdate(GetPointer(Encoder), Tau); Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); TargetEncoder.Save(FileName + "Enc.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); Critic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); Critic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true); Convolution.Save(FileName + "CNN.nnw", 0, 0, 0, TimeCurrent(), true); Descriminator.Save(FileName + "Des.nnw", 0, 0, 0, TimeCurrent(), true); SkillProject.Save(FileName + "Skp.nnw", 0, 0, 0, TimeCurrent(), true); delete Result; }
This concludes our work on the EA for preliminary training of Actor skills without external reward. The full EA code can be found in the attachment. There you will also find the complete code of all programs used in the article.
2.4 Fine tuning EA
Model training ends with training the Scheduler, which generates a vector of skills used and thereby controls the actions of the Actor.
The Scheduler's policy is trained to maximize external rewards. We arrange the training in the "...\CIC\Finetune.mq5" EA. The EA is built similarly to the previous one, but there are some nuances. For the EA to work, we need pre-trained Encoder, Actor and Critic models. We will also use target copies of the specified models.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; } //--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) || !Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true) || !TargetEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !TargetActor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("No pretrained models found"); return INIT_FAILED; }
In addition, we load a random convolutional encoder model. But we do not load the Discriminator models. At this stage, we use only external rewards. The Actor's behavioral policies were studied at the previous stage. Now we have to learn the top-level policy of the Scheduler.
Therefore, after loading the pre-trained models, we try to load the Scheduler model. If one is not found, then this time we create a new model and initialize it with random parameters.
if(!Scheduler.Load(FileName + "Sch.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *descr = new CArrayObj(); if(!SchedulerDescriptions(descr) || !Scheduler.Create(descr)) { delete descr; return INIT_FAILED; } delete descr; }
Next, we transfer all models into a single OpenCL context and disable the Actor and Encoder training mode.
OpenCL = Actor.GetOpenCL(); Encoder.SetOpenCL(OpenCL); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); TargetEncoder.SetOpenCL(OpenCL); TargetActor.SetOpenCL(OpenCL); TargetCritic1.SetOpenCL(OpenCL); TargetCritic2.SetOpenCL(OpenCL); Scheduler.SetOpenCL(OpenCL); Convolution.SetOpenCL(OpenCL); //--- Actor.TrainMode(false); Encoder.TrainMode(false);
At the end of the initialization method, we check the consistency of the model architecture and generate the training start event.
vector<float> ActorResult; Actor.getResults(ActorResult); if(ActorResult.Size() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; } //--- Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- vector<float> EncoderResults; Actor.GetLayerOutput(0,Result); Encoder.getResults(EncoderResults); if(Result.Total() != int(EncoderResults.Size())) { PrintFormat("Input size of Actor doesn't match Encoder outputs (%d <> %d)", Result.Total(), EncoderResults.Size()); return INIT_FAILED; } //--- Actor.GetLayerOutput(LatentLayer, Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; } //--- Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
In the EA deinitialization method, we save only the Critics and Scheduler models.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau); TargetCritic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); TargetCritic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true); Scheduler.Save(FileName + "Sch.nnw", 0, 0, 0, TimeCurrent(), true); delete Result; }
I do not think anyone questions the need to train the Scheduler. But the issue of updating Critics parameters and fixing Actor parameters is probably worth explaining. In the previous step, we trained the Actor's policies depending on the skill used. At this stage, we learn to manage skills. Therefore, we fix the parameters of the Actor and train the Scheduler to control it.
Another question concerns Critics. At the skill training stage, we used only internal rewards, which were aimed at training various skills of the Actor. Of course, Critics have built dependencies between the Actor’s actions and their impact on internal rewards. But we use external rewards at this stage. Most likely, the Actor’s actions have a completely different impact on it. Therefore, we have to retrain Critics for new circumstances.
In addition, while we previously used our assumptions about the influence of the selected skill on the result, now we will pass the gradient of the reward error from the Critic through the Actor to the Scheduler. But let's go back to our EA and look at the algorithm for arranging the process.
The model training process is still arranged in the Train method. As in the skill training EA discussed above, we encode transitions at the beginning of the method. However, this time we add external reward loading from the environment. Note that we only take reward per a separate transition. We will predict the cumulative reward using target models.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); float loss = 0; //--- int total_states = Buffer[0].Total - 1; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total - 1; vector<float> temp; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size()); matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards); int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total - 1; st++) { State.AssignArray(Buffer[tr].States[st].state); float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance); double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- State.AddArray(Buffer[tr].States[st + 1].state); State.Add((Buffer[tr].States[st + 1].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[1] / PrevBalance); State.Add((Buffer[tr].States[st + 1].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st + 1].account[2]); State.Add(Buffer[tr].States[st + 1].account[3]); State.Add(Buffer[tr].States[st + 1].account[4] / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[5] / PrevBalance); State.Add(Buffer[tr].States[st + 1].account[6] / PrevBalance); x = (double)Buffer[tr].States[st + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } Convolution.getResults(temp); state_embedding.Row(temp,state); temp.Assign(Buffer[tr].States[st].rewards); for(ulong r = 0; r < temp.Size(); r++) temp[r] -= Buffer[tr].States[st + 1].rewards[r] * DiscFactor; rewards.Row(temp,state); state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } } if(state != total_states) { state_embedding.Reshape(state,state_embedding.Cols()); rewards.Reshape(state,NRewards); total_states = state; }
Next, we arrange a model training cycle. In the cycle body, we sample the state from the experience playback buffer.
vector<float> reward, rewards1, rewards2, target_reward; int bar = (HistoryBars - 1) * BarDescr; for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; } reward = vector<float>::Zeros(NRewards); rewards1 = reward; rewards2 = reward; target_reward = reward;
Prepare the source data buffers.
//--- State State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; if(PrevBalance == 0.0f || PrevEquity == 0.0f) continue; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
After generating a complete set of initial data of the selected state, we carry out a direct pass of the Encoder.
//--- Encoder State if(!Encoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Following the Encoder is a forward pass of the Scheduler, which evaluates the latent representation of the environment state and generates a skill vector for the Actor.
//--- Skills if(!Scheduler.feedForward(GetPointer(Encoder), -1, NULL,-1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
The Actor in turn uses the skill specified by the Scheduler and analyzes the latent representation of the environment state from the Encoder. Based on the totality of initial data, the Actor generates a vector of actions.
//--- Actor if(!Actor.feedForward(GetPointer(Encoder), -1, GetPointer(Scheduler),-1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We use the resulting action vector to predict the next state of the environment.
//--- Next State TargetState.AssignArray(Buffer[tr].States[i + 1].state); double cl_op = Buffer[tr].States[i + 1].state[bar]; double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op / SymbolInfoDouble(_Symbol, SYMBOL_POINT); Actor.getResults(Result); vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,Result,prof_1l, Buffer[tr].States[i + 1].account[7]); TargetAccount.AssignArray(forecast); if(TargetAccount.GetIndex() >= 0 && !TargetAccount.BufferWrite()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We repeat the actions for the subsequent state with target models. The Scheduler is excluded from this chain, since we assume the use of the same skill.
if(!TargetEncoder.feedForward(GetPointer(TargetState), 1, false, GetPointer(TargetAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } //--- Target if(!TargetActor.feedForward(GetPointer(TargetEncoder), -1, GetPointer(Scheduler),-1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
However, to evaluate the Actor's policies, we need the Critic to evaluate its actions. Here we will use the lower estimate as a prediction of a future reward.
//--- if(!TargetCritic1.feedForward(GetPointer(TargetActor), LatentLayer, GetPointer(TargetActor)) || !TargetCritic2.feedForward(GetPointer(TargetActor), LatentLayer, GetPointer(TargetActor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } TargetCritic1.getResults(rewards1); TargetCritic2.getResults(rewards2); if(rewards1.Sum() <= rewards2.Sum()) target_reward = rewards1; else target_reward = rewards2; target_reward *= DiscFactor;
We will evaluate the current action based on the k nearest neighbors of the predicted transition. To do this, we will use a random Encoder.
State.AddArray(GetPointer(TargetState)); State.AddArray(GetPointer(TargetAccount)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Convolution.getResults(rewards1); reward[0] += KNNReward(7,rewards1,state_embedding,rewards); reward += target_reward; Result.AssignArray(reward);
We combine the current and forecast rewards. We now have a target value to train the models. All that remains is to select the Critic model to update the Scheduler parameters. We carry out a direct pass of both Critics and select the minimum rating for the action chosen by the Actor.
if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor),-1) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor),-1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Critic1.getResults(rewards1); Critic2.getResults(rewards2);
As in the previous EA, we perform a reverse pass through the selected Critic, Actor and Scheduler. In the latter, we carry out a reverse pass of the Critic with the maximum assessment of the Actor’s actions.
if(rewards1.Sum() <= rewards2.Sum()) { loss = (loss * MathMin(iter,999) + (reward - rewards1).Sum()) / MathMin(iter + 1,1000); if(!Critic1.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Scheduler),-1,-1) || !Scheduler.backPropGradient() || !Critic2.backProp(Result, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } } else { loss = (loss * MathMin(iter,999) + (reward - rewards2).Sum()) / MathMin(iter + 1,1000); if(!Critic2.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Scheduler),-1,-1) || !Scheduler.backPropGradient() || !Critic1.backProp(Result, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
At the end of the iterations of the training cycle, all we have to do is update the target Critics' models and inform a user about the model training progress.
//--- Update Target Nets TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau); //--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-20s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-20s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); str += StringFormat("%-20s %5.2f%% -> Error %15.8f\n", "Scheduler", iter * 100.0 / (double)(Iterations), loss); Comment(str); ticks = GetTickCount(); } }
After completing all iterations of the model training cycle, we clear the comment block on the chart and initiate the process of terminating the EA.
Comment(""); //--- PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-20s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Scheduler", loss); ExpertRemove(); //--- }
This concludes our consideration of programs for implementing the presented algorithm. We have not looked at the EA for testing trained models yet. It has received the adjustments similar to the EA for collecting a training sample. However, I have not added random noise to the action vector in order to evaluate the real quality of the trained models. The full code of all programs used in the article is available in the attachment.
3. Test
Training and testing of models is carried out on the first 5 months of 2023 on EURUSD H1. As always, the parameters of all indicators were used by default. The model training process is quite lengthy. The method authors propose two million iterations on the first stage of training skills. Of course, the number of iterations can be increased for more complex environments. While training my model, I followed this path in several approaches with additional collection of training data.
After training the skills, it is time to fine-tune and train the Scheduler. This stage also has at least 100 thousand iterations. I also propose to carry out this stage in several approaches. We first initialize a random Scheduler model and train it on a wide dataset. After the first pass of the Scheduler training, we collect additional training sets, which will include examples of how Scheduler policies interact with the environment. This will allow to adjust its policy to the better.
During the training, I was able to train a model capable of generating profit. The graph shows a clear upward trend in the balance line. At the same time, I noticed some Equity drawdown zones, which may indicate the need for additional training of the model. We know that financial markets are quite stochastic and complex environments. So, it is to be expected that longer periods of training are required to obtain the desired results.
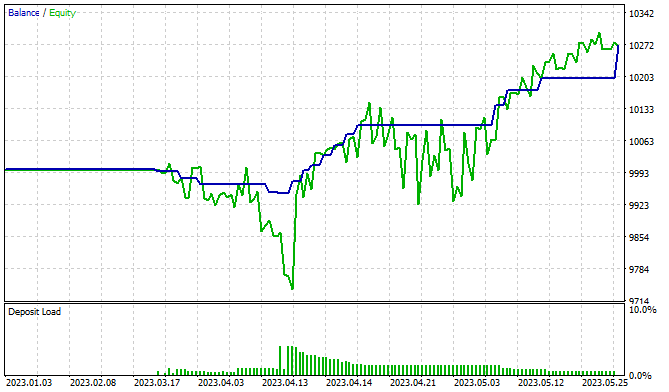
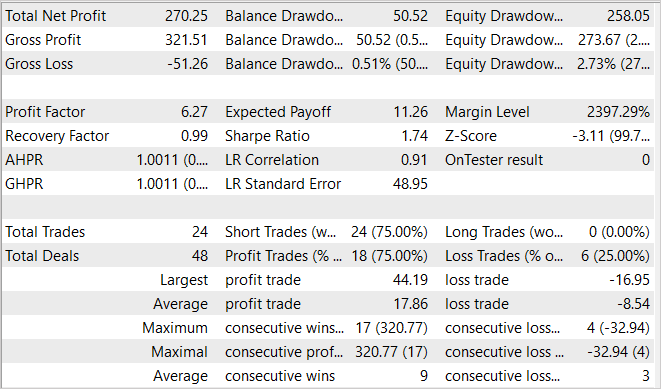
Conclusion
In this article, we introduced a promising method in the field of hierarchical reinforcement learning - Contrastive Internal Control (CIC). This method belongs to a family of algorithms based on self-controlled intrinsic rewards. Based on the principles of the DIAYN algorithm, it aims to improve the extraction of Agent hierarchical skills by introducing contrastive training.
One of the key features of CIC is its ability to learn a variety of skills in complex environments where the number of potential behaviors can be quite large. This property is especially useful in the field of solving problems with a continuous action space. Using contrastive training allows us to guide the Agent so that it can not only learn effectively in a variety of scenarios, but also extract valuable knowledge from these scenarios.
In the practical part of our article, we implemented the algorithm using MQL5. The model was trained and tested on real historical data. The obtained results suggest the potential efficiency of the method. Training a large number of skills also requires comparable costs for training the Agent.
Links
- CIC: Contrastive Intrinsic Control for Unsupervised Skill Discovery
- Representation Learning with Contrastive Predictive Coding
- Neural networks made easy (Part 43): Mastering skills without the reward function
- Neural networks made easy (Part 44): Learning skills with dynamics in mind
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Example collection EA |
| 2 | Pretrain.mq5 | Expert Advisor | Actor skills training EA |
| 3 | Finetune.mq5 | Expert Advisor | Scheduler fine tuning and training EA |
| 4 | Test.mq5 | Expert Advisor | Model testing EA |
| 5 | Trajectory.mqh | Class library | System state description structure |
| 6 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 7 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/13212
Data Science and Machine Learning (Part 17): Money in the Trees? The Art and Science of Random Forests in Forex Trading
Understanding Programming Paradigms (Part 1): A Procedural Approach to Developing a Price Action Expert Advisor
Design Patterns in software development and MQL5 (Part 4): Behavioral Patterns 2
Brute force approach to patterns search (Part VI): Cyclic optimization
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use