Datenwissenschaft und ML (Teil 28): Vorhersage mehrerer Futures für EURUSD mithilfe von KI
Inhalt
- Einführung
- Direkte mehrstufige Prognosen
- Stärke der mehrstufigen Direktprognose
- Schwächen der mehrstufigen Direktprognose
- Rekursive Mehrschrittprognose
- Vorteile der rekursiven Mehrschrittprognose
- Schwächen der rekursiven Mehrschrittprognose
- Mehrstufige Prognosen unter Verwendung von Modellen mit mehreren Ausgängen
- Vorteile der mehrstufigen Prognosen unter Verwendung von Modellen mit mehreren Ausgängen
- Nachteile der mehrstufigen Prognosen unter Verwendung von Modellen mit mehreren Ausgängen
- Wann und wo sollten mehrstufige Prognosen eingesetzt werden?
- Schlussfolgerung
Einführung
In der Welt der Finanzdatenanalyse mit Hilfe von maschinellem Lernen besteht das Ziel oft darin, zukünftige Werte auf der Grundlage historischer Daten vorherzusagen. Die Vorhersage des nächsten unmittelbaren Wertes ist zwar sehr nützlich, wie wir in vielen Artikeln dieser Serie besprochen haben. In realen Anwendungen gibt es viele Situationen, in denen wir möglicherweise mehrere zukünftige Werte anstelle von einem vorhersagen müssen. Der Versuch, verschiedene aufeinanderfolgende Werte vorherzusagen, wird als Mehrschritt- oder Mehrhorizontprognose bezeichnet.
Mehrstufige Prognosen sind in verschiedenen Bereichen von entscheidender Bedeutung, z. B. im Finanzwesen, bei der Wettervorhersage, im Lieferkettenmanagement und im Gesundheitswesen. Auf den Finanzmärkten beispielsweise müssen die Anleger Aktienkurse oder Wechselkurse für mehrere Tage, Wochen oder sogar Monate im Voraus vorhersagen. Bei der Wettervorhersage können genaue Prognosen für die kommenden Tage oder Wochen bei der Planung und beim Katastrophenmanagement helfen.
Dieser Artikel setzt voraus, dass Sie ein grundlegendes Verständnis von maschinellem Lernen und KI, ONNX, der Verwendung von ONNX-Modellen in MQL5, linearer Regression, LightGBM und neuronalen Netzen haben.
Der Prozess der mehrstufigen Prognosen umfasst mehrere Methoden, die jeweils ihre Stärken und Schwächen haben. Zu diesen Methoden gehören.
- Mehrstufige Direktprognose
- Rekursive mehrstufige Vorausberechnung
- Modelle mit mehreren Ausgängen
- Vektorielle Autoregression (VAR) (wird in den nächsten Artikeln behandelt)
In diesem Artikel werden wir diese Methoden, ihre Anwendungen und ihre Umsetzung mit Hilfe verschiedener maschineller Lern- und Statistikverfahren untersuchen. Wenn wir die mehrstufigen Prognosen verstehen und anwenden, können wir fundiertere Entscheidungen über die Zukunft von EURUSD treffen.
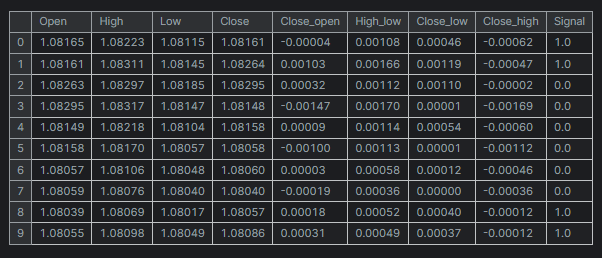
# Create target variables for multiple future steps def create_target(df, future_steps=10): target = pd.concat([df['Close'].shift(-i) for i in range(1, future_steps + 1)], axis=1) # using close prices for the next i bar target.columns = [f'target_close_{i}' for i in range(1, future_steps + 1)] # naming the columns return target # Combine features and targets new_df = pd.DataFrame({ 'Open': df['Open'], 'High': df['High'], 'Low': df['Low'], 'Close': df['Close'] }) future_steps = 5 target_columns = create_target(new_df, future_steps).dropna() combined_df = pd.concat([new_df, target_columns], axis=1) #concatenating the new pandas dataframe with the target columns combined_df = combined_df.dropna() #droping rows with NaN values caused by shifting values target_cols_names = [f'target_close_{i}' for i in range(1, future_steps + 1)] X = combined_df.drop(columns=target_cols_names).values #dropping all target columns from the x array y = combined_df[target_cols_names].values # creating the target variables print(f"x={X.shape} y={y.shape}") combined_df.head(10)
Direkte mehrstufige Prognosen
Die direkte mehrstufige Prognose ist eine Methode, bei der für jeden vorauszusagenden Zeitschritt separate Prognosemodelle trainiert werden. Wenn wir zum Beispiel die Werte für die nächsten 5 Zeitschritte vorhersagen wollen, müssen wir 5 verschiedene Modelle trainieren. Eine zur Vorhersage des ersten Schritts, eine weitere zur Vorhersage des zweiten Schritts und so weiter.
Bei der direkten mehrstufigen Vorhersage ist jedes Modell auf die Vorhersage eines bestimmten Horizonts ausgerichtet. Dieser Ansatz ermöglicht es jedem Modell, sich auf die spezifischen Muster und Beziehungen zu konzentrieren, die für den entsprechenden zukünftigen Zeitschritt relevant sind, wodurch die Genauigkeit jeder Vorhersage verbessert werden kann. Allerdings bedeutet dies auch, dass Sie mehrere Modelle trainieren und pflegen müssen, was ressourcenintensiv sein kann.
Versuchen wir eine mehrstufige Vorhersage mit dem maschinellen Lernmodell LightGBM.
Zunächst erstellen wir eine Funktion zur Verarbeitung von Daten aus mehreren Schritten.
Aufbereitung der Daten
Python-Code
def multi_steps_data_process(data, step, train_size=0.7, random_state=42): # Since we are using the OHLC values only data["next signal"] = data["Signal"].shift(-step) # The target variable from next n future values data = data.dropna() y = data["next signal"] X = data.drop(columns=["Signal", "next signal"]) return train_test_split(X, y, train_size=train_size, random_state=random_state)
Diese Funktion erstellt die neue Zielvariable unter Verwendung der Spalte „Signal“ aus dem Datensatz. Die Zielvariable wird aus dem Wert des Indexschritts+1 in der Signalspalte entnommen.
Angenommen, Sie haben.
| Signale |
|---|
1 |
2 |
3 |
4 |
5 |
Bei Schritt 1 wird das nächste Signal 2 sein, bei Schritt 2 wird das nächste Signal 3 sein und so weiter.
In diesem Artikel werden wir Daten aus dem stündlichen Zeitrahmen von EURUSD für 1000 Bars verwenden.
Python-Code
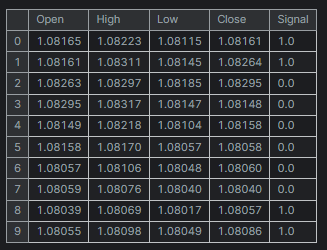
df = pd.read_csv("/kaggle/input/eurusd-period-h1/EURUSD.PERIOD_H1.csv") print(df.shape) df.head(10)
Ausgabe
Der Einfachheit halber habe ich einen Mini-Datensatz für nur fünf (5) Variablen erstellt.
Die Spalte „Signal“ steht für auf- oder abwärts gerichtete Kerzensignale. Sie wurde nach der Logik erstellt, dass immer dann, wenn der Schlusskurs größer als der Eröffnungskurs war, dem Signal der Wert 1 und für das Gegenteil der Wert 0 zugewiesen wurde.
Da wir nun eine Funktion zur Erstellung von Daten in mehreren Schritten haben, müssen wir unsere Modelle für die Verarbeitung der einzelnen Schritte deklarieren.
Training mehrerer Modelle für Vorhersagen
Die Modelle für jeden Zeitschritt manuell zu kodieren, könnte zeitaufwändig und ineffektiv sein. Die Kodierung innerhalb einer Schleife ist einfacher und effektiver. Innerhalb der Schleife führen wir alle notwendigen Schritte durch, wie z. B. das Trainieren, Validieren und Speichern des Modells für die externe Verwendung im MetaTrader 5.
Python-Code
for pred_step in range(1, 6): # We want to 5 future values lgbm_model = lgbm.LGBMClassifier(**params) X_train, X_test, y_train, y_test = multi_steps_data_process(new_df, pred_step) # preparing data for the current step lgbm_model.fit(X_train, y_train) # training the model for this step # Testing the trained mdoel test_pred = lgbm_model.predict(X_test) # Changes from bst to pipe # Ensuring the lengths are consistent if len(y_test) != len(test_pred): test_pred = test_pred[:len(y_test)] print(f"model for next_signal[{pred_step} accuracy={accuracy_score(y_test, test_pred)}") # Saving the model in ONNX format, Registering ONNX converter update_registered_converter( lgbm.LGBMClassifier, "GBMClassifier", calculate_linear_classifier_output_shapes, convert_lightgbm, options={"nocl": [False], "zipmap": [True, False, "columns"]}, ) # Final LightGBM conversion to ONNX model_onnx = convert_sklearn( lgbm_model, "lightgbm_model", [("input", FloatTensorType([None, X_train.shape[1]]))], target_opset={"": 12, "ai.onnx.ml": 2}, ) # And save. with open(f"lightgbm.EURUSD.h1.pred_close.step.{pred_step}.onnx", "wb") as f: f.write(model_onnx.SerializeToString())
Ausgabe
model for next_signal[1 accuracy=0.5033333333333333 model for next_signal[2 accuracy=0.5566666666666666 model for next_signal[3 accuracy=0.4866666666666667 model for next_signal[4 accuracy=0.4816053511705686 model for next_signal[5 accuracy=0.5317725752508361
Überraschenderweise war das Modell für die Vorhersage des nächsten zweiten Balkens das genaueste Modell mit einer Genauigkeit von 55 %, gefolgt von dem Modell für die Vorhersage des nächsten fünften Balkens mit einer Genauigkeit von 53 %.
Laden von Modellen für die Vorhersage in MetaTrader 5
Wir beginnen damit, dass wir alle LightGBM AI-Modelle, die im ONNX-Format gespeichert sind, als Ressourcendateien in unseren Expert Advisor integrieren.
MQL5-Code
#resource "\\Files\\lightgbm.EURUSD.h1.pred_close.step.1.onnx" as uchar model_step_1[] #resource "\\Files\\lightgbm.EURUSD.h1.pred_close.step.2.onnx" as uchar model_step_2[] #resource "\\Files\\lightgbm.EURUSD.h1.pred_close.step.3.onnx" as uchar model_step_3[] #resource "\\Files\\lightgbm.EURUSD.h1.pred_close.step.4.onnx" as uchar model_step_4[] #resource "\\Files\\lightgbm.EURUSD.h1.pred_close.step.5.onnx" as uchar model_step_5[] #include <MALE5\Gradient Boosted Decision Trees(GBDTs)\LightGBM\LightGBM.mqh> CLightGBM *light_gbm[5]; //for storing 5 different models MqlRates rates[];
Anschließend initialisieren wir unsere 5 verschiedenen Modelle.
MQL5-Code
int OnInit() { //--- for (int i=0; i<5; i++) light_gbm[i] = new CLightGBM(); //Creating LightGBM objects //--- if (!light_gbm[0].Init(model_step_1)) { Print("Failed to initialize model for step=1 predictions"); return INIT_FAILED; } if (!light_gbm[1].Init(model_step_2)) { Print("Failed to initialize model for step=2 predictions"); return INIT_FAILED; } if (!light_gbm[2].Init(model_step_3)) { Print("Failed to initialize model for step=3 predictions"); return INIT_FAILED; } if (!light_gbm[3].Init(model_step_4)) { Print("Failed to initialize model for step=4 predictions"); return INIT_FAILED; } if (!light_gbm[4].Init(model_step_5)) { Print("Failed to initialize model for step=5 predictions"); return INIT_FAILED; } return(INIT_SUCCEEDED); }
Schließlich können wir die Eröffnungs-, Höchst-, Tiefst- und Schlusskurse des vorherigen Balkens sammeln und sie verwenden, um Vorhersagen von allen 5 verschiedenen Modellen zu erhalten.
MQL5-Code
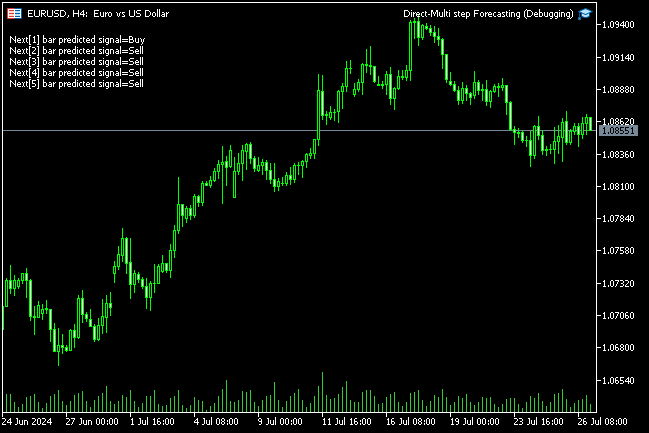
void OnTick() { //--- CopyRates(Symbol(), PERIOD_H1, 1, 1, rates); vector input_x = {rates[0].open, rates[0].high, rates[0].low, rates[0].close}; string comment_string = ""; int signal = -1; for (int i=0; i<5; i++) { signal = (int)light_gbm[i].predict_bin(input_x); comment_string += StringFormat("\n Next[%d] bar predicted signal=%s",i+1, signal==1?"Buy":"Sell"); } Comment(comment_string); }
Ergebnis:
Stärken der direkten mehrstufigen Vorausberechnung
- Jedes Modell ist auf einen bestimmten Prognosehorizont spezialisiert, was zu genaueren Vorhersagen für jeden Schritt führen kann.
- Das Trainieren separater Modelle kann einfach sein, insbesondere wenn Sie einfache Algorithmen für maschinelles Lernen verwenden.
- Sie können für jeden Schritt unterschiedliche Modelle oder Algorithmen wählen, was eine größere Flexibilität bei der Bewältigung verschiedener Prognoseaufgaben ermöglicht.
Schwachstellen der direkten Mehrschrittprognose
- Dazu müssen mehrere Modelle trainiert und gepflegt werden, was rechenintensiv und zeitaufwändig sein kann.
- Anders als bei rekursiven Methoden werden Fehler von einem Schritt nicht direkt auf den nächsten übertragen, was sowohl eine Stärke als auch eine Schwäche sein kann. Dies kann zu Inkonsistenzen zwischen den einzelnen Schritten führen.
- Jedes Modell ist unabhängig und erfasst die Abhängigkeiten zwischen den Prognosehorizonten möglicherweise nicht so effektiv wie ein einheitlicher Ansatz.
Rekursive mehrstufige Prognosen
Die rekursive Mehrschrittprognose, auch bekannt als iterative Prognose, ist eine Methode, bei der ein einziges Modell verwendet wird, um eine Vorhersage in einem Schritt zu treffen. Diese Vorhersage wird dann wieder in das Modell eingespeist, um die nächste Vorhersage zu treffen. Dieser Vorgang wird so lange wiederholt, bis die Vorhersagen für die gewünschte Anzahl zukünftiger Zeitschritte vorliegen.
Bei der rekursiven mehrstufigen Prognose wird das Modell so trainiert, dass es den nächsten unmittelbaren Wert vorhersagt. Sobald dieser Wert vorhergesagt ist, wird er zu den Eingabedaten hinzugefügt und zur Vorhersage des nächsten Wertes verwendet. Bei dieser Methode wird dasselbe Modell iterativ eingesetzt.
Um dies zu erreichen, werden wir das Modell der linearen Regression verwenden, um den nächsten Schlusskurs anhand des vorherigen Schlusskurses vorherzusagen. Auf diese Weise kann der vorhergesagte Schlusskurs als Input für die nächste Iteration verwendet werden und so weiter. Dieser Ansatz scheint auch mit einer einzigen unabhängigen Variable (Merkmal) gut zu funktionieren.
Python-Code
new_df = pd.DataFrame({
'Close': df['Close'],
'target close': df['Close'].shift(-1) # next bar closing price
})
Dann
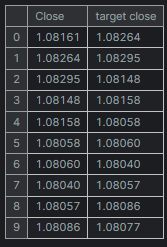
new_df = new_df.dropna() # after shifting we want to drop all NaN values X = new_df[["Close"]].values # Assigning close values into a 2D x array y = new_df["target close"].values print(new_df.shape) new_df.head(10)
Ausgabe
Training und Test eines linearen Regressionsmodells
Bevor wir das Modell trainieren, teilen wir die Daten auf, ohne sie zu randomisieren. Dies könnte dem Modell helfen, zeitliche Abhängigkeiten zwischen den Werten zu erfassen, da wir wissen, dass der nächste Schlusskurs durch den vorherigen Schlusskurs beeinflusst wird.
model = Pipeline([ ("scaler", StandardScaler()), ("linear_regression", LinearRegression()) ]) # Split the data into training and test sets train_size = int(len(new_df) * 0.7) X_train, X_test = X[:train_size], X[train_size:] y_train, y_test = y[:train_size], y[train_size:] # Train the model model.fit(X_train, y_train)
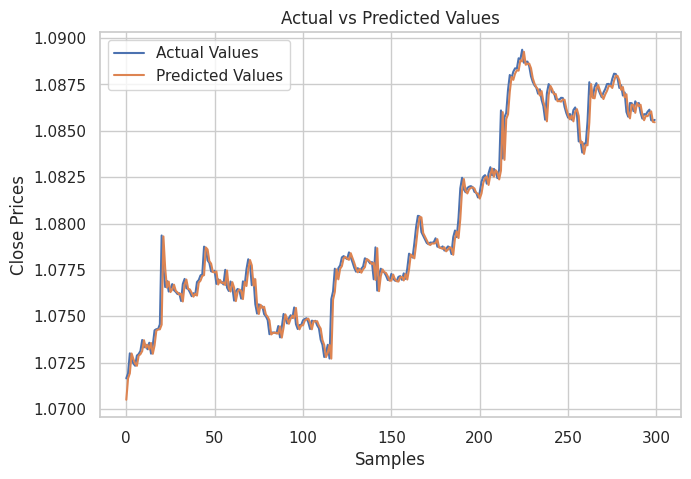
Anschließend habe ich ein Diagramm erstellt, in dem die tatsächlichen Werte der Teststichprobe und die vorhergesagten Werte dargestellt werden, um zu analysieren, wie effektiv das Modell bei der Erstellung von Vorhersagen war.
# Testing the Model
test_pred = model.predict(X_test) # Make predictions on the test set
# Plot the actual vs predicted values
plt.figure(figsize=(7.5, 5))
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('Close Prices')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()
Ergebnis:
Wie auf dem Bild oben zu sehen ist. Das Modell hat in der Tat ordentliche Vorhersagen gemacht, es war zu 98 % genau bei der Teststichprobe, aber die Vorhersagen aus dem Diagramm zeigen, wie das lineare Modell bei dem historischen Datensatz abgeschnitten hat, indem es Vorhersagen auf normale Weise und nicht in einem rekursiven Format gemacht hat. Um das Modell dazu zu bringen, rekursive Vorhersagen zu machen, müssen wir eine nutzerdefinierte Funktion für diese Arbeit erstellen.
Python-Code
# Function for recursive forecasting def recursive_forecast(model, initial_value, steps): predictions = [] current_input = np.array([[initial_value]]) for _ in range(steps): prediction = model.predict(current_input)[0] predictions.append(prediction) # Update the input for the next prediction current_input = np.array([[prediction]]) return predictions
Wir können dann Zukunftsprognosen für 10 Takte erhalten.
current_close = X[-1][0] # Use the last value in the array # Number of future steps to forecast steps = 10 # Forecast future values forecasted_values = recursive_forecast(model, current_close, steps) print("Forecasted Values:") print(forecasted_values)
Ausgabe
Forecasted Values: [1.0854623040804965, 1.0853751608200348, 1.0852885667357617, 1.0852025183667728, 1.0851170122739744, 1.085032045039946, 1.0849476132688034, 1.0848637135860637, 1.0847803426385094, 1.0846974970940555]
Um die Genauigkeit eines rekursiven Modells zu testen, können wir die obige Funktion recursive_forecast verwenden, um ausgehend vom aktuellen Index nach 10 Zeitschritten in einer Schleife Vorhersagen für die 10 nächsten Zeitschritte in der Historie zu machen.
predicted = [] for i in range(0, X_test.shape[0], steps): current_close = X_test[i][0] # Use the last value in the test array forecasted_values = recursive_forecast(model, current_close, steps) predicted.extend(forecasted_values) print(len(predicted))
Ausgabe
Die Genauigkeit des rekursiven Modells betrug 91 %.
Schließlich können wir das lineare Regressionsmodell im ONNX-Format speichern, das mit MQL5 kompatibel ist.
# Convert the trained pipeline to ONNX
initial_type = [('float_input', FloatTensorType([None, 1]))]
onnx_model = convert_sklearn(model, initial_types=initial_type)
# Save the ONNX model to a file
with open("Lr.EURUSD.h1.pred_close.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
print("Model saved to Lr.EURUSD.h1.pred_close.onnx") Rekursive Vorhersagen in MQL5 machen.
Wir beginnen mit dem Hinzufügen des ONNX-Modells mit linearer Regression in unserem Expert Advisor.
#resource "\\Files\\Lr.EURUSD.h1.pred_close.onnx" as uchar lr_model[]
Anschließend importieren wir die Klasse für die Behandlung von Linear Regression.
#include <MALE5\Linear Models\Linear Regression.mqh>
CLinearRegression lr; Nach der Initialisierung des Modells in der Funktion OnInit können wir den Preis des letzten geschlossenen Balkens abrufen und dann Prognosen für die nächsten 10 Balken erstellen.
int OnInit() { //--- if (!lr.Init(lr_model)) return INIT_FAILED; //--- ArraySetAsSeries(rates, true); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- CopyRates(Symbol(), PERIOD_H1, 1, 1, rates); vector input_x = {rates[0].close}; //get the previous closed bar close price vector predicted_close(10); //predicted values for the next 10 timestepps for (int i=0; i<10; i++) { predicted_close[i] = lr.predict(input_x); input_x[0] = predicted_close[i]; //The current predicted value is the next input } Print(predicted_close); }
Ausgabe
OR 0 16:39:37.018 Recursive-Multi step forecasting (EURUSD,H4) [1.084011435508728,1.083933353424072,1.083855748176575,1.083778619766235,1.083701968193054,1.083625793457031,1.083550095558167,1.08347487449646,1.083400130271912,1.083325862884521]
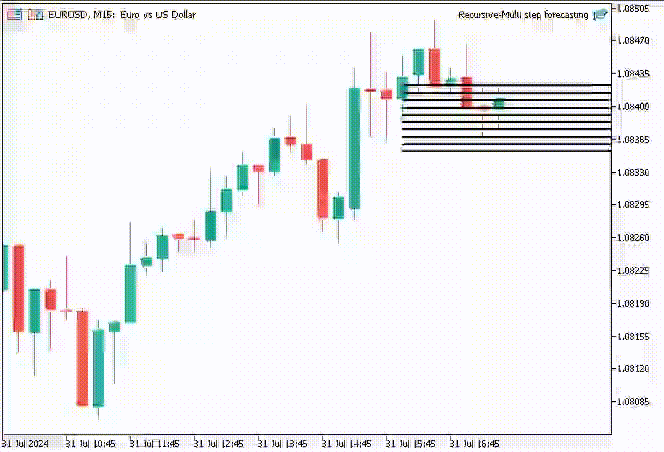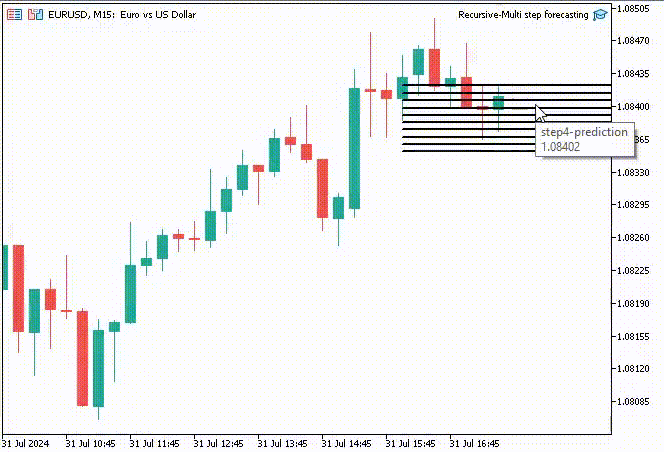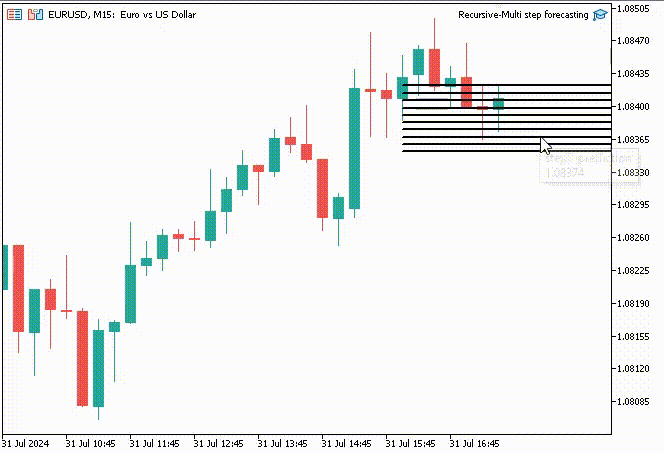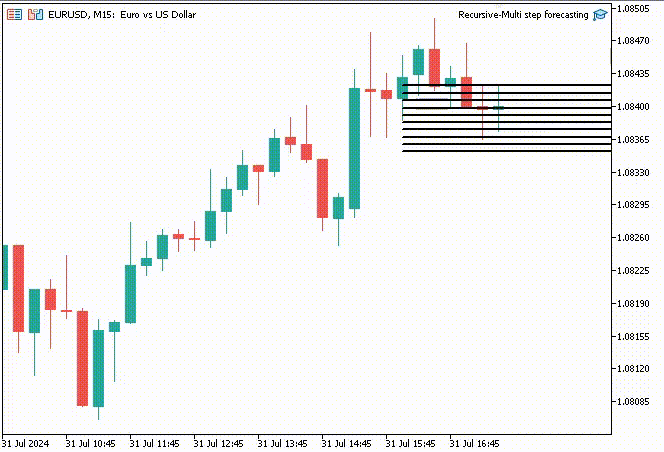
Um die Sache interessant zu machen, habe ich beschlossen, Trendlinienobjekte zu erstellen, um diese vorhergesagten Werte für 10 Zeitschritte im Hauptdiagramm anzuzeigen.
if (NewBar()) { for (int i=0; i<10; i++) { predicted_close[i] = lr.predict(input_x); input_x[0] = predicted_close[i]; //The current predicted value is the next input //--- ObjectDelete(0, "step"+string(i+1)+"-prediction"); //delete an object if it exists TrendCreate("step"+string(i+1)+"-prediction",rates[0].time, predicted_close[i], rates[0].time+(10*60*60), predicted_close[i], clrBlack); //draw a line starting from the previous candle to 10 hours forward } }
Die Funktion TrendCreate erstellt eine kurze horizontale Trendlinie, die vom letzten geschlossenen Balken bis zu 10 Balken weiter reicht.
Ergebnis:
Vorteile der rekursiven Mehrschrittprognose
- Da nur ein Modell trainiert und gepflegt wird, vereinfacht dies die Implementierung und reduziert die Rechenressourcen.
- Da das gleiche Modell iterativ verwendet wird, bleibt die Konsistenz über den gesamten Vorhersagehorizont erhalten.
Schwächen der rekursiven Mehrstufenprognose
- Fehler in frühen Vorhersagen können sich in späteren Vorhersagen ausbreiten und verstärken, was die Gesamtgenauigkeit verringern kann.
- Bei diesem Ansatz wird davon ausgegangen, dass die vom Modell erfassten Beziehungen über den Prognosehorizont hinweg stabil bleiben, was nicht immer der Fall sein muss.
Mehrstufige Prognosen unter Verwendung von Modellen mit mehreren Ausgängen
Multi-Output-Modelle sind so konzipiert, dass sie mehrere Werte gleichzeitig vorhersagen können. Wir können dies zu unserem Vorteil nutzen, indem wir die Modelle zukünftige Zeitschritte gleichzeitig vorhersagen lassen. Anstatt für jeden Prognosehorizont separate Modelle zu trainieren oder ein einziges Modell rekursiv zu verwenden, hat ein Multi-Ausgangsmodell mehrere Ausgänge, die jeweils einem zukünftigen Zeitschritt entsprechen.
Bei einem Modell mit mehreren Ausgängen wird das Modell so trainiert, dass es in einem einzigen Durchgang einen Vektor von Vorhersagen erzeugt. Das bedeutet, dass das Modell lernt, die Beziehungen und Abhängigkeiten zwischen verschiedenen zukünftigen Zeitschritten direkt zu verstehen. Dieser Ansatz lässt sich gut mit neuronalen Netzen umsetzen, da diese in der Lage sind, mehrere Ausgaben zu erzeugen.
Vorbereitung des Datensatzes für ein neuronales Netzmodell mit mehreren Ausgängen
Wir müssen die Zielvariablen für alle Zeitschritte vorbereiten, die unser trainiertes neuronales Netzmodell vorhersagen soll.
Python-Code
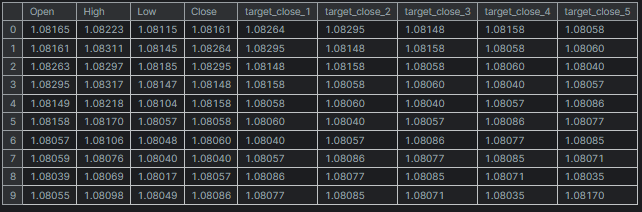
# Create target variables for multiple future steps def create_target(df, future_steps=10): target = pd.concat([df['Close'].shift(-i) for i in range(1, future_steps + 1)], axis=1) # using close prices for the next i bar target.columns = [f'target_close_{i}' for i in range(1, future_steps + 1)] # naming the columns return target # Combine features and targets new_df = pd.DataFrame({ 'Open': df['Open'], 'High': df['High'], 'Low': df['Low'], 'Close': df['Close'] }) future_steps = 5 target_columns = create_target(new_df, future_steps).dropna() combined_df = pd.concat([new_df, target_columns], axis=1) #concatenating the new pandas dataframe with the target columns combined_df = combined_df.dropna() #droping rows with NaN values caused by shifting values target_cols_names = [f'target_close_{i}' for i in range(1, future_steps + 1)] X = combined_df.drop(columns=target_cols_names).values #dropping all target columns from the x array y = combined_df[target_cols_names].values # creating the target variables print(f"x={X.shape} y={y.shape}") combined_df.head(10)
Ausgabe
x=(995, 4) y=(995, 5)
Training und Test eines neuronalen Netzes mit mehreren Ausgängen
Wir beginnen mit der Definition eines sequentiellen neuronalen Netzmodells.
Python-Code
# Defining the neural network model model = Sequential([ Input(shape=(X.shape[1],)), Dense(units = 256, activation='relu'), Dense(units = 128, activation='relu'), Dense(units = future_steps) ]) # Compiling the model adam = Adam(learning_rate=0.01) model.compile(optimizer=adam, loss='mse') # Mmodel summary model.summary()
Ausgabe
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense (Dense) │ (None, 256) │ 1,280 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 128) │ 32,896 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_2 (Dense) │ (None, 5) │ 645 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 34,821 (136.02 KB) Trainable params: 34,821 (136.02 KB) Non-trainable params: 0 (0.00 B)
Anschließend teilen wir die Daten in Trainings- und Teststichproben auf, anders als bei der rekursiven mehrstufigen Prognose. Diesmal teilen wir die Daten auf, nachdem wir sie mit einem 42-fachen Zufallswert randomisiert haben , da wir nicht wollen, dass das Modell sequentielle Muster versteht, da wir glauben, dass das neuronale Netz noch besser in der Lage ist, nicht-lineare Beziehungen aus diesen Daten zu verstehen.
Schließlich trainieren wir das NN-Modell anhand der Trainingsdaten.
# Split the data into training and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=42) scaler = MinMaxScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) # Training the model early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True) # stop training when 5 epochs doesn't improve history = model.fit(X_train, y_train, epochs=20, validation_split=0.2, batch_size=32, callbacks=[early_stopping])
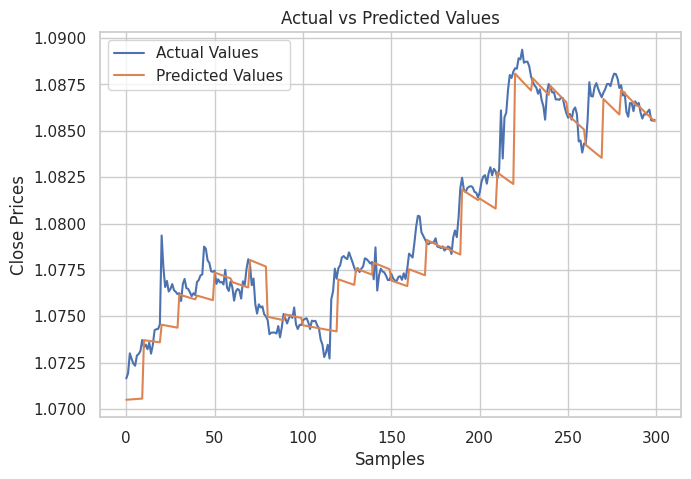
Nach dem Testen des Modells anhand eines Testdatensatzes.
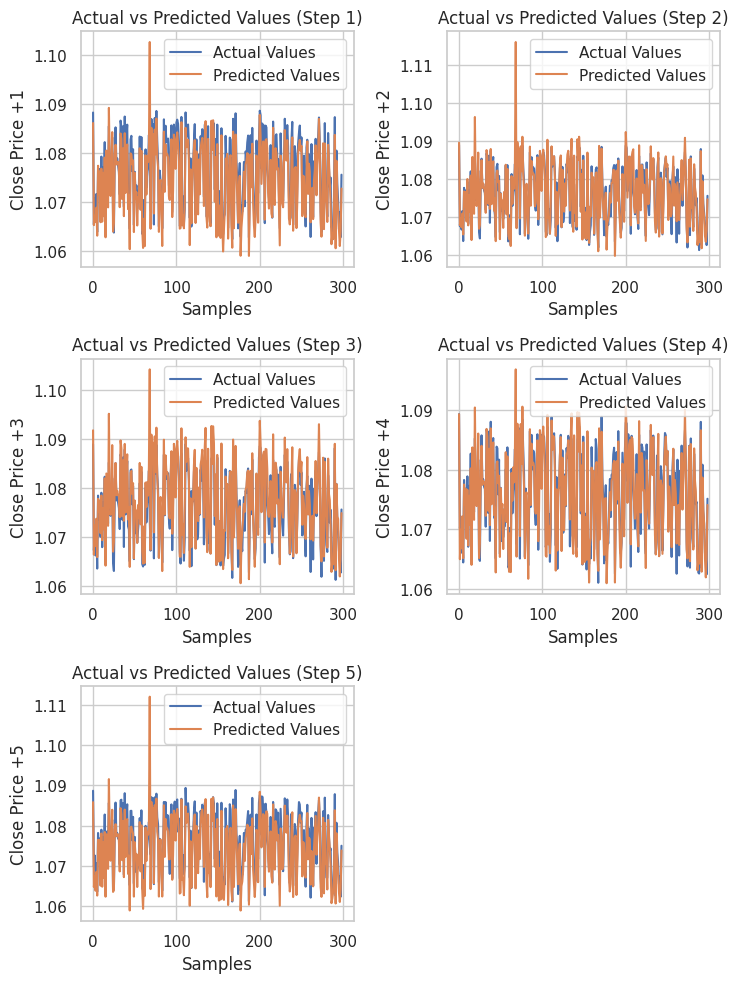
# Testing the Model test_pred = model.predict(X_test) # Make predictions on the test set # Plotting the actual vs predicted values for each future step plt.figure(figsize=(7.5, 10)) for i in range(future_steps): plt.subplot((future_steps + 1) // 2, 2, i + 1) # subplots grid plt.plot(y_test[:, i], label='Actual Values') plt.plot(test_pred[:, i], label='Predicted Values') plt.xlabel('Samples') plt.ylabel(f'Close Price +{i+1}') plt.title(f'Actual vs Predicted Values (Step {i+1})') plt.legend() plt.tight_layout() plt.show() # Evaluating the model for each future step for i in range(future_steps): accuracy = r2_score(y_test[:, i], test_pred[:, i]) print(f"Step {i+1} - R^2 Score: {accuracy}")
Nachstehend das Ergebnis.
Step 1 - R^2 Score: 0.8664635514027637 Step 2 - R^2 Score: 0.9375671150885528 Step 3 - R^2 Score: 0.9040736780305894 Step 4 - R^2 Score: 0.8491904738263638 Step 5 - R^2 Score: 0.8458062142647863
Das neuronale Netz lieferte beeindruckende Ergebnisse für dieses Regressionsproblem. Der folgende Code zeigt, wie man die Vorhersagen in Python erhält.
# Predicting multiple future values current_input = X_test[0].reshape(1, -1) # use the first row of the test set, reshape the data also predicted_values = model.predict(current_input)[0] # adding[0] ensures we get a 1D array instead of 2D print("Predicted Future Values:") print(predicted_values)
Ausgabe
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step Predicted Future Values: [1.0892788 1.0895394 1.0892794 1.0883198 1.0884078]
Dann können wir dieses neuronale Netzmodell im ONNX-Format und die Skalierungsdateien in binär formatierten Dateien speichern.
import tf2onnx
# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, X_train.shape[1]), tf.float16, name="input"),)
model.output_names=['output']
onnx_model, _ = tf2onnx.convert.from_keras(model, input_signature=spec, opset=13)
# Save the ONNX model to a file
with open("NN.EURUSD.h1.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
# Save the used scaler parameters to binary files
scaler.data_min_.tofile("NN.EURUSD.h1.min_max.min.bin")
scaler.data_max_.tofile("NN.EURUSD.h1.min_max.max.bin") Schließlich können wir das gespeicherte Modell und seine Daten-Skalierungsparameter in MQL5 verwenden.
Neuronales Netzwerk - mehrstufige Vorhersagen in MQL5
Zunächst fügen wir unserem Expert Advisor (EA) das Modell und die Parameter des Min-Max-Scalers hinzu.
#resource "\\Files\\NN.EURUSD.h1.onnx" as uchar onnx_model[]; //rnn model in onnx format #resource "\\Files\\NN.EURUSD.h1.min_max.max.bin" as double min_max_max[]; #resource "\\Files\\NN.EURUSD.h1.min_max.min.bin" as double min_max_min[];
Anschließend importieren wir die ONNX-Klasse des neuronalen Regressionsnetzwerks und den MinMax-Scaler-Bibliotheks-Handler.
#include <MALE5\Neural Networks\Regressor Neural Nets.mqh> #include <MALE5\preprocessing.mqh> CNeuralNets nn; MinMaxScaler *scaler;
Anschließend können wir das NN-Modell und den Skalierer initialisieren und die endgültigen Vorhersagen des Modells erhalten.
MqlRates rates[]; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if (!nn.Init(onnx_model)) return INIT_FAILED; scaler = new MinMaxScaler(min_max_min, min_max_max); //Initializing the scaler, populating it with trained values //--- ArraySetAsSeries(rates, true); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if (CheckPointer(scaler)!=POINTER_INVALID) delete (scaler); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- CopyRates(Symbol(), PERIOD_H1, 1, 1, rates); vector input_x = {rates[0].open, rates[0].high, rates[0].low, rates[0].close}; input_x = scaler.transform(input_x); // We normalize the input data vector preds = nn.predict(input_x); Print("predictions = ",preds); }
Ausgabe
2024.07.31 19:13:20.785 Multi-step forecasting using Multi-outputs model (EURUSD,H4) predictions = [1.080284595489502,1.082370758056641,1.083482265472412,1.081504583358765,1.079929828643799]
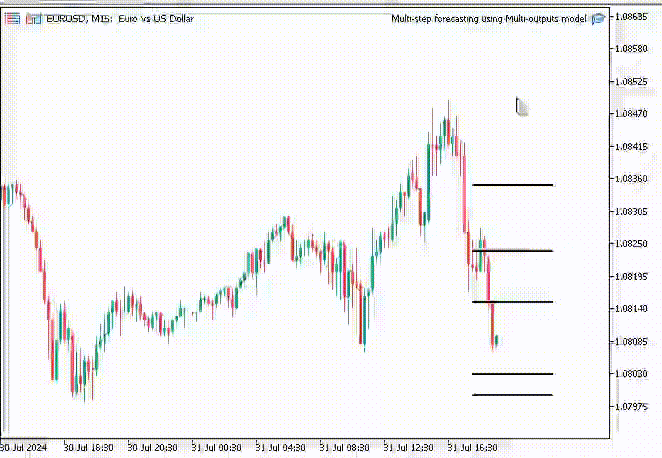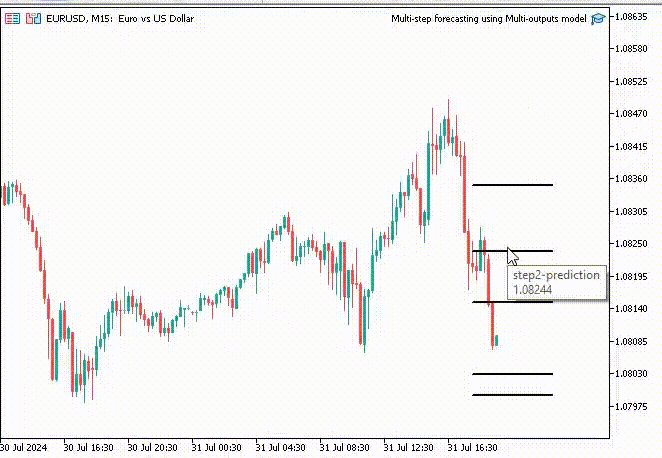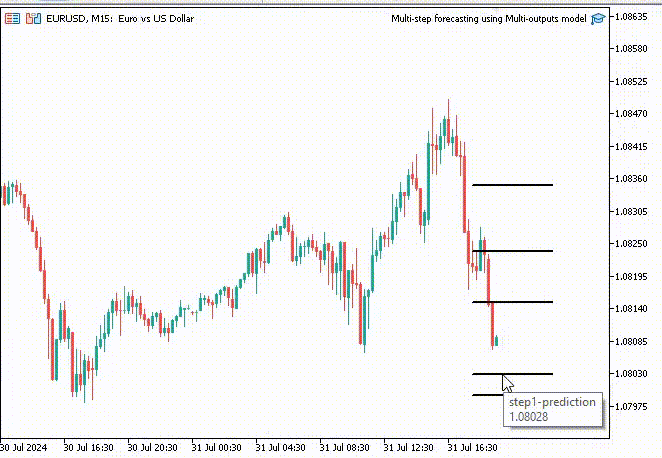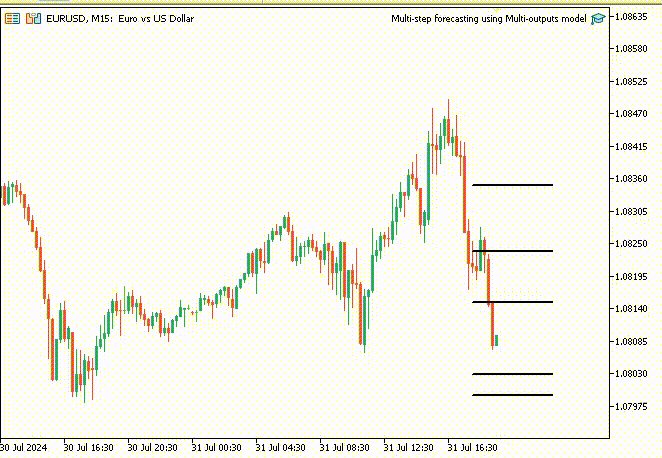
Um die Sache interessanter zu machen, habe ich Trendlinien in das Chart eingefügt, um alle Zukunftsprognosen des neuronalen Netzes zu markieren.
void OnTick() { //--- CopyRates(Symbol(), PERIOD_H1, 1, 1, rates); vector input_x = {rates[0].open, rates[0].high, rates[0].low, rates[0].close}; if (NewBar()) { input_x = scaler.transform(input_x); // We normalize the input data vector preds = nn.predict(input_x); for (int i=0; i<(int)preds.Size(); i++) { //--- ObjectDelete(0, "step"+string(i+1)+"-prediction"); //delete an object if it exists TrendCreate("step"+string(i+1)+"-prediction",rates[0].time, preds[i], rates[0].time+(5*60*60), preds[i], clrBlack); //draw a line starting from the previous candle to 5 hours forward } } }
Dieses Mal erhielten wir besser aussehende Prognoselinien als die, die wir mit dem rekursiven linearen Regressionsmodell erhielten.
Überblick über mehrstufige Prognosen unter Verwendung von Multi-Output-Modellen
Vorteile- Durch die gleichzeitige Vorhersage mehrerer Schritte kann das Modell die Beziehungen und Abhängigkeiten zwischen zukünftigen Zeitschritten erfassen.
- Es wird nur ein Modell benötigt, was die Implementierung und Wartung vereinfacht.
- Das Modell lernt, über den gesamten Prognosehorizont hinweg konsistente Vorhersagen zu treffen.
Benachteiligungen
- Das Trainieren eines Modells, das mehrere zukünftige Werte ausgibt, kann komplexer sein und erfordert unter Umständen ausgefeiltere Architekturen, insbesondere für neuronale Netze.
- Je nach Komplexität des Modells kann es mehr Rechenressourcen für das Training und die Inferenz erfordern.
- Es besteht die Gefahr der Überanpassung, insbesondere wenn der Prognosehorizont lang ist und das Modell zu sehr auf die Trainingsdaten spezialisiert wird.
Nutzung von Mehrschritt-Prognosen in Handelsstrategien
Mehrstufige Prognosen, insbesondere unter Verwendung von Modellen wie neuronalen Netzen und LightGBM, können verschiedene Handelsstrategien erheblich verbessern, indem sie dynamische Anpassungen auf der Grundlage der vorhergesagten Marktbewegungen ermöglichen. Im Netzhandel ermöglichen mehrstufige Prognosen anstelle von festen Aufträgen dynamische Eingaben, die sich an erwartete Preisänderungen anpassen und so die Reaktionsfähigkeit des Systems auf die Marktbedingungen verbessern.
Auch Hedging-Strategien profitieren davon, da die Prognosen Anhaltspunkte dafür liefern, wann Positionen zu eröffnen oder zu schließen sind, um sich vor möglichen Verlusten zu schützen, z. B. durch das Eingehen von Short-Positionen oder den Kauf von Verkaufsoptionen, wenn ein Abwärtstrend vorhergesagt wird. Bei der Trenderkennung hilft das Verständnis künftiger Marktrichtungen durch Prognosen den Händlern, ihre Strategien entsprechend auszurichten, indem sie entweder Short-Positionen bevorzugen oder Long-Positionen aufgeben, um Verluste zu vermeiden.
Im Hochfrequenzhandel (HFT) schließlich können Algorithmen durch schnelle mehrstufige Prognosen kurzfristige Kursbewegungen ausnutzen und so die Rentabilität steigern, indem sie rechtzeitig Kauf- und Verkaufsaufträge auf der Grundlage der vorhergesagten Kursänderungen in den nächsten Sekunden oder Minuten ausführen.
Die Quintessenz
In der Finanzanalyse und im Devisenhandel ist die Fähigkeit, mehrere Werte in die Zukunft vorauszusagen, sehr nützlich, wie im vorherigen Abschnitt dieses Artikels beschrieben. Dieser Beitrag soll Ihnen verschiedene Möglichkeiten aufzeigen, wie Sie sich dieser Herausforderung stellen können. In den nächsten Artikeln werden wir uns mit der Vektor-Autoregression beschäftigen, einer Technik, die für die Analyse mehrerer Werte entwickelt wurde und auch mehrere Werte vorhersagen kann.
Peace out.
Verfolgen Sie die Entwicklung von Modellen für maschinelles Lernen und vieles mehr in dieser Artikelserie auf diesem GitHub repo.
Tabelle der Anhänge
| Dateiname | Datei Typ | Beschreibungen & Verwendung |
|---|---|---|
Direct Muilti step Forecasting.mq5 Multi-step forecasting using multi-outputs model.mq5 Recursive-Multi step forecasting.mq5 | Expert Advisors | Dieser EA hat den Code, der mehrere LightGBM-Modelle für mehrstufige Prognosen verwendet. Dieser EA verfügt über ein neuronales Netzmodell, das mehrere Schritte unter Verwendung einer Multi-Ausgangsstruktur vorhersagt. Bei diesem EA wird die lineare Regression iterativ zur Vorhersage künftiger Zeitschritte eingesetzt. |
| LightGBM.mqh | MQL5-Bibliotheksdatei | Enthält den Code zum Laden des LightGBM-Modells im ONNX-Format und dessen Verwendung zur Erstellung von Vorhersagen. |
| Linear Regression.mqh | MQL5-Bibliotheksdatei | Enthält den Code zum Laden des linearen Regressionsmodells im ONNX-Format und zur Verwendung für Vorhersagen. |
| preprocessing.mqh | MQL5-Bibliotheksdatei | Diese Datei enthält den MInMax-Skalierer, eine Skalierungstechnik, die zur Normalisierung der Eingabedaten verwendet wird. |
| Regressor Neural Nets.mqh | MQL5-Bibliotheksdatei | Enthält den Code zum Laden und Bereitstellen des neuronalen Netzmodells aus dem ONNX-Format in MQL5. |
lightgbm.EURUSD.h1.pred_close.step.1.onnx lightgbm.EURUSD.h1.pred_close.step.2.onnx lightgbm.EURUSD.h1.pred_close.step.3.onnx lightgbm.EURUSD.h1.pred_close.step.4.onnx lightgbm.EURUSD.h1.pred_close.step.5.onnx Lr.EURUSD.h1.pred_close.onnx NN.EURUSD.h1.onnx | AI-Modelle im ONNX-Format | LightGBM-Modelle zur Vorhersage der nächsten Stufenwerte Ein einfaches lineares Regressionsmodell im ONNX-Format Neuronales Netz mit Vorwärtskopplung im ONNX-Format |
| NN.EURUSD.h1.min_max.max.bin NN.EURUSD.h1.min_max.min.bin | Binäre Dateien | Enthält Höchst- bzw. Mindestwerte für den Min-Max-Scaler |
| predicting-multiple-future-tutorials.ipynb | Jupyter-Notebook | Der gesamte Python-Code, der in diesem Artikel gezeigt wird, befindet sich in dieser Datei |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15465
 Implementierung des Deus EA: Automatisierter Handel mit RSI und gleitenden Durchschnitten in MQL5
Implementierung des Deus EA: Automatisierter Handel mit RSI und gleitenden Durchschnitten in MQL5
 Ihrer eigenes LLM in einen EA integrieren (Teil 5): Handelsstrategie mit LLMs(I) entwickeln und testen – Feinabstimmung
Ihrer eigenes LLM in einen EA integrieren (Teil 5): Handelsstrategie mit LLMs(I) entwickeln und testen – Feinabstimmung
 Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 1): Senden von Nachrichten von MQL5 an Telegram
Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 1): Senden von Nachrichten von MQL5 an Telegram
 Implementierung einer Handelsstrategie der Bollinger Bänder mit MQL5: Ein schrittweiser Leitfaden
Implementierung einer Handelsstrategie der Bollinger Bänder mit MQL5: Ein schrittweiser Leitfaden
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.