Datenwissenschaft und ML (Teil 29): Wichtige Tipps für die Auswahl der besten Forex-Daten für AI-Trainingszwecke
Inhalt
- Einführung
- Was ist Merkmalsauswahl?
- Warum ist die Auswahl von Merkmalen für KI-Modelle notwendig?
- Filter-Methoden
Korrelationsmatrix
Statistische Tests
- Chi-Quadrat-Test
- ANOVA-Test - Wrapper-Methoden
Rekursive Merkmalseliminierung (RFE)
Sequentielle Merkmalsauswahl (SFS) - Eingebettete Methoden
Lasso-Regression
Entscheidungsbaumbasierte Methoden - Techniken zur Dimensionenreduzierung
- Schlussfolgerung
Einführung
Mit allen Handelsdaten und Informationen wie Indikatoren (es gibt mehr als 36 integrierte Indikatoren in MetaTrader 5), Symbolpaaren (es gibt mehr als 100 Symbole), die auch als Daten für Korrelationsstrategien verwendet werden können, gibt es auch Nachrichten, die wertvolle Daten für Händler sind, usw. Was ich damit sagen will, ist, dass es für Händler eine Fülle von Informationen gibt, die sie beim manuellen Handel oder bei der Entwicklung von Modellen der künstlichen Intelligenz nutzen können, um intelligente Handelsentscheidungen für unsere Handelsroboter zu treffen.
Unter all den Informationen, die uns zur Verfügung stehen, muss es auch einige schlechte Informationen geben (das ist nur der gesunde Menschenverstand). Nicht alle Indikatoren, Daten, Strategien usw. sind für ein bestimmtes Handelssymbol, eine bestimmte Strategie oder eine bestimmte Situation nützlich. Wie ermitteln wir die richtigen Informationen für Handels- und maschinelle Lernmodelle, um maximale Effizienz und Rentabilität zu erzielen? Hier kommt die Merkmalsauswahl ins Spiel.
Was ist Merkmalsauswahl?
Die Merkmalsauswahl ist ein Prozess der Identifizierung und Auswahl einer Teilmenge relevanter Merkmale aus dem ursprünglichen Datensatz, die für die Modellbildung verwendet werden. Dies ist ein Prozess, bei dem die nützlichsten Informationen für ein maschinelles Lernmodell ermittelt werden und der Müll (weniger wichtige Merkmale/Informationen) weggelassen wird.
Die Auswahl von Merkmalen ist einer der wichtigsten Schritte beim Aufbau eines effektiven maschinellen Lernmodells.
Warum ist die Auswahl von Merkmalen für KI-Modelle notwendig?
- Reduziert die Dimensionen
Durch die Eliminierung irrelevanter oder redundanter Merkmale vereinfacht die Merkmalsauswahl das Modell und reduziert die Rechenkosten. - Erhöht die Leistung
Die Konzentration auf die informativsten Merkmale kann die Genauigkeit und Vorhersagekraft des Modells verbessern. - Verbessert die Interpretierbarkeit
Modelle mit weniger Merkmalen sind oft leichter zu verstehen und zu erklären. - Umgang mit Rauschen durch Entfernen verrauschter oder irrelevanter Daten
Durch das Entfernen weniger wichtiger Merkmale kann die Merkmalsauswahl dazu beitragen, eine Überanpassung zu verhindern, die häufig durch zu viele irrelevante Daten verursacht wird.
Da wir nun wissen, wie wichtig die Auswahl von Merkmalen ist, wollen wir verschiedene Techniken untersuchen, die häufig von Datenwissenschaftlern und Experten für maschinelles Lernen verwendet werden, um die besten Merkmale für ihre KI-Modelle zu finden.
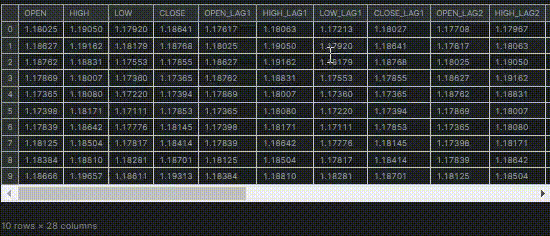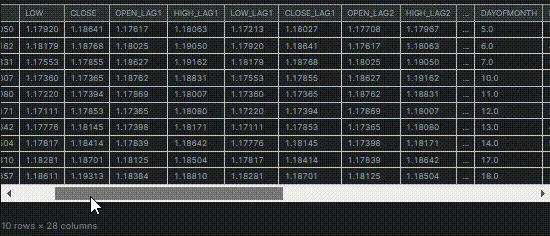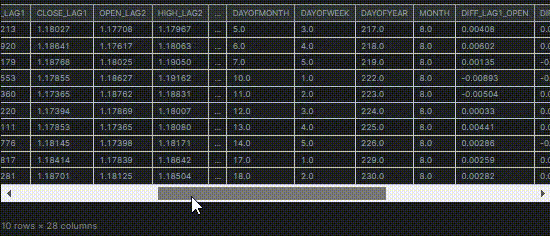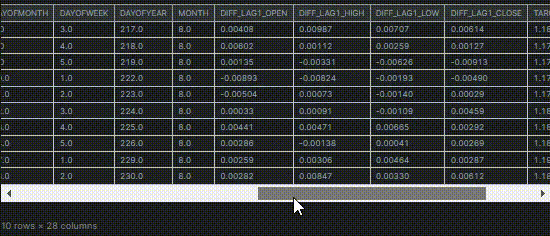
Unter Verwendung derselben Datensatzes, den wir in diesem Artikel verwendet haben (unbedingt lesen). Er umfasst 28 Variablen.
Von den 28 Variablen wollen wir die relevantesten Variablen für die Spalten „TARGET_OPEN“ (mit den Eröffnungskursen der nächsten Kerze) und „TARGET_CLOSE“ (mit den Schlusskursen der nächsten Kerze) finden und die weniger relevanten Daten zurücklassen.
Die Techniken und Methoden der Merkmalsauswahl lassen sich in drei Haupttypen einteilen: Filtermethoden, Wrapper-Methoden und eingebettete Methoden. Lassen Sie uns eine Methode nach der anderen analysieren, um zu sehen, worum es bei ihnen geht.
Filter-Methoden
Filtermethoden bewerten Merkmale unabhängig vom Modell oder Algorithmus des maschinellen Lernens. Zu diesen Methoden gehören die Verwendung der Korrelationsmatrix und die Durchführung statistischer Tests.
Korrelationsmatrix
Eine Korrelationsmatrix ist eine Tabelle, die die Korrelationskoeffizienten zwischen verschiedenen Variablen aufzeigt.
Ein Korrelationskoeffizient ist ein statistisches Maß, das die Stärke und Richtung der Beziehung zwischen zwei Variablen angibt. Er reicht von -1 bis 1.
Ein Wert von 1 bedeutet eine perfekte positive Korrelation (wenn eine Variable zunimmt, nimmt die andere proportional zu).
Ein Wert von 0 bedeutet, dass keine Korrelation besteht (keine Beziehung zwischen den beiden Variablen).-1
Ein Wert von -1 bedeutet eine perfekte negative Korrelation (wenn eine Variable zunimmt, nimmt die andere proportional ab).
Wir beginnen mit der Berechnung der Korrelationsmatrix mit Python.
Berechnung der Korrelationsmatrix
# Compute the correlation matrix corr_matrix = df.corr() # We generate a mask for the upper triangle mask = np.triu(np.ones_like(corr_matrix, dtype=bool)) cmap = sns.diverging_palette(220, 10, as_cmap=True) # Custom colormap plt.figure(figsize=(28, 28)) # 28 columns to fit better # Draw the heatmap with the mask and correct aspect ratio sns.heatmap(corr_matrix, mask=mask, cmap=cmap, vmax=1.0, center=0, annot=True, square=True, linewidths=1, cbar_kws={"shrink": .75}) plt.title('Correlation Matrix') plt.savefig("correlation matrix.png") plt.show()
Ausgabe
Die Matrix ist zu umfangreich, um sie hier zu zeigen, aber hier sind einige sehr nützliche Teile.
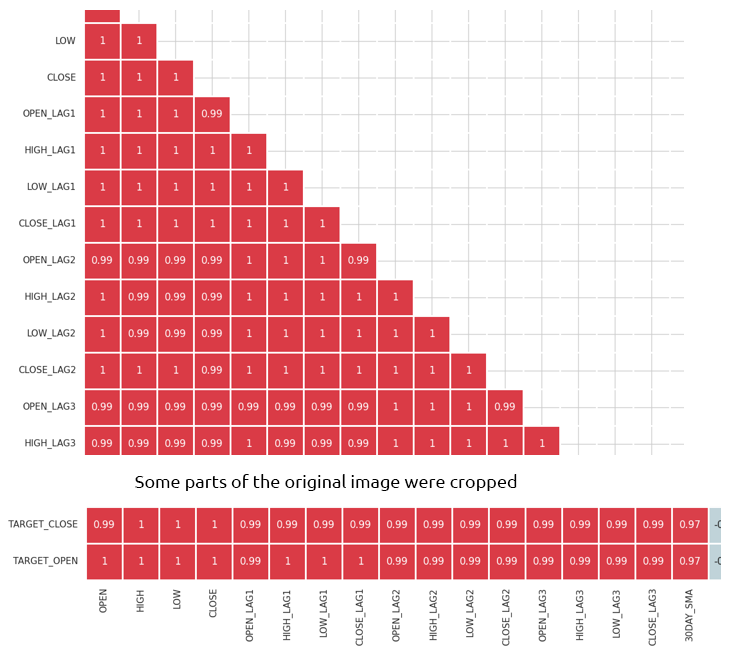
Identifizieren und Eliminieren stark korrelierter Merkmale
Eine hohe Multikollinearität liegt vor, wenn zwei oder mehr Merkmale stark miteinander korreliert sind. Dies kann bei vielen Algorithmen des maschinellen Lernens zu Problemen führen, insbesondere bei den linearen Modellen. Diese Situation führt zu instabilen Schätzungen der Koeffizienten.
Korrelation zwischen den unabhängigen Variablen selbst
Durch das Kombinieren oder Entfernen von stark korrelierten Merkmalen können Modelle vereinfacht werden, ohne viel Information zu verlieren. Ein Beispiel: In der obigen Korrelationsmatrix sind Open, High und Low zu 100 % korreliert. Sie korrelieren zu 99,0 % (diese endgültigen Werte sind gerundet). Wir können beschließen, diese Variablen zu entfernen und mit nur einer Variablen auszukommen, oder wir können Techniken anwenden, um die Dimension der Daten, die wir diskutieren wollen, zu reduzieren.
Korrelation zwischen unabhängigen Variablen (Merkmalen) und der Zielvariablen
Merkmale, die eine starke Korrelation mit der Zielvariable aufweisen, sind im Allgemeinen informativer und können die Vorhersageleistung des Modells verbessern.
Die Konfusionsmatrix ist nicht direkt auf kategorische Merkmale in unserem Datensatz wie „DAYOFWEEK“, „DAYOFYEAR“ und „MONTH“ anwendbar, da Korrelationskoeffizienten die linearen Beziehungen zwischen numerische Variablen messen.
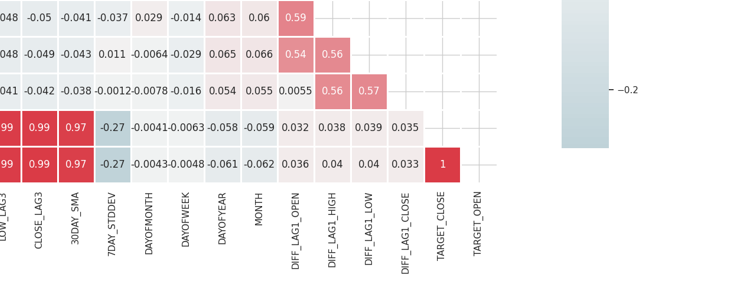
Statistische Tests
Wir können statistische Tests durchführen, um Merkmale mit signifikanten Beziehungen zur Zielvariablen auszuwählen.
Chi-Quadrat-Test
Der Chi-Quadrat-Test misst, wie die erwarteten Zahlen im Vergleich zu den beobachteten Zahlen in einer Kontingenztabelle aussehen. Sie hilft festzustellen, ob ein signifikanter Zusammenhang zwischen zwei kategorialen Variablen besteht.
Eine Kontingenztabelle ist eine Tabelle im Matrixformat, die die Häufigkeitsverteilung der Variablen anzeigt. Sie kann verwendet werden, um die Beziehung zwischen zwei kategorialen Variablen zu untersuchen. Im Rahmen des Chi-Quadrat-Tests wird eine Kontingenztabelle verwendet, um die beobachteten Häufigkeiten von kategorialen Variablen mit den erwarteten Häufigkeiten zu vergleichen.
Der Chi-Quadrat-Test ist nur auf kategoriale Variablen anwendbar.
In unserem Datensatz gibt es eine Reihe von kategorischen Variablen (DAYOFMONTH, DAYOFWEEK, DAYOFYEAR, und MONTH). Wir müssen auch eine Zielvariable erstellen, um die Beziehungen zwischen ihr und den Merkmalen zu messen.
Python-Codefrom sklearn.feature_selection import chi2 from sklearn.feature_selection import SelectKBest target = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: target.append(1) else: target.append(0) X = pd.DataFrame({ 'DAYOFMONTH': df['DAYOFMONTH'], 'DAYOFWEEK': df['DAYOFWEEK'], 'DAYOFYEAR': df['DAYOFYEAR'], 'MONTH': df['MONTH'] }) chi2_selector = SelectKBest(chi2, k='all') chi2_selector.fit(X, target) chi2_scores = chi2_selector.scores_ # Output scores for each feature feature_scores = pd.DataFrame({'Feature': X.columns, 'Chi2 Score': chi2_scores}) print(feature_scores)
Ausgabe
Feature Chi2 Score 0 DAYOFMONTH 0.622628 1 DAYOFWEEK 0.047481 2 DAYOFYEAR 14.618057 3 MONTH 0.489713
Aus den obigen Ergebnissen geht hervor, dass DAYOFYEAR den höchsten Chi2-Wert aufweist, was darauf hindeutet, dass diese Variable im Vergleich zu den anderen den größten Einfluss auf die Zielvariable hat. Dies ist sinnvoll, da die Daten in einem täglichen Zeitrahmen erhoben wurden und jeder Tag eindeutig einem Tag des Jahres entspricht. Das starke Vorhandensein der Variable DAYOFYEAR im Datensatz erhöht wahrscheinlich ihre Häufigkeit und Signifikanz und macht sie zu einem Schlüsselmerkmal bei der Vorhersage der Zielvariable.
ANOVA (Varianzanalyse) Test
Die ANOVA ist eine statistische Methode zum Vergleich der Mittelwerte von drei oder mehr Gruppen, um festzustellen, ob sich mindestens einer der Gruppenmittelwerte statistisch von den anderen unterscheidet. Sie hilft, die Stärke der Beziehung zwischen kontinuierlichen Merkmalen und der kategorialen Zielvariable zu bestimmen.
Dabei wird nicht nur die Varianz innerhalb jeder Gruppe und zwischen den Gruppen analysiert, sondern auch die Variabilität der Beobachtungen innerhalb jeder Gruppe und die Variabilität zwischen den Mittelwerten der verschiedenen Gruppen gemessen.
Mit diesem Test wird die F-Statistik berechnet, die das Verhältnis der Varianz zwischen den Gruppen zur Varianz innerhalb der Gruppen darstellt. Eine höhere F-Statistik zeigt an, dass die Gruppen unterschiedliche Mittelwerte haben.
Wir verwenden „f_classif“ von Scikit-learn, um einen ANOVA-Test für die Merkmalsauswahl durchzuführen.
Python-Code
from sklearn.feature_selection import f_classif
# We start by dropping the categorical variables in the dataset
X = df.drop(columns=[
"DAYOFMONTH",
"DAYOFWEEK",
"DAYOFYEAR",
"MONTH",
"TARGET_CLOSE",
"TARGET_OPEN"
])
# Perform ANOVA test
selector = SelectKBest(score_func=f_classif, k='all')
selector.fit(X, target)
# Get the F-scores and p-values
anova_scores = selector.scores_
anova_pvalues = selector.pvalues_
# Create a DataFrame to display results
anova_results = pd.DataFrame({'Feature': X.columns, 'F-Score': anova_scores, 'p-Value': anova_pvalues})
print(anova_results) Ausgabe
Feature F-Score p-Value 0 OPEN 3.483736 0.062268 1 HIGH 3.627995 0.057103 2 LOW 3.400320 0.065480 3 CLOSE 3.666813 0.055792 4 OPEN_LAG1 3.160177 0.075759 5 HIGH_LAG1 3.363306 0.066962 6 LOW_LAG1 3.309483 0.069181 7 CLOSE_LAG1 3.529789 0.060567 8 OPEN_LAG2 3.015757 0.082767 9 HIGH_LAG2 3.034694 0.081810 10 LOW_LAG2 3.259887 0.071295 11 CLOSE_LAG2 3.206956 0.073629 12 OPEN_LAG3 3.236211 0.072329 13 HIGH_LAG3 3.022234 0.082439 14 LOW_LAG3 3.020219 0.082541 15 CLOSE_LAG3 3.075698 0.079777 16 30DAY_SMA 2.665990 0.102829 17 7DAY_STDDEV 0.639071 0.424238 18 DIFF_LAG1_OPEN 1.237127 0.266293 19 DIFF_LAG1_HIGH 0.991862 0.319529 20 DIFF_LAG1_LOW 0.131002 0.717472 21 DIFF_LAG1_CLOSE 0.198001 0.656435
Höhere F-Werte zeigen an, dass das Merkmal einen starken Zusammenhang mit der Zielvariablen hat.
P-Werte, die unter dem Signifikanzniveau (z. B. 0,05) liegen, gelten als statistisch signifikant.
Wir können auch die Merkmale mit den höchsten F-Werten oder den niedrigsten P-Werten auswählen , die die wichtigsten Merkmale sind, und andere Merkmale ignorieren. Lassen Sie uns die 10 besten Funktionen auswählen.
Python-Code
selector = SelectKBest(score_func=f_classif, k=10) X_selected = selector.fit_transform(X, target) # print the selected feature names selected_features = X.columns[selector.get_support()] print("Selected Features:", selected_features)
Ausgabe
Selected Features: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
Wrapper-Methoden
Bei diesen Methoden wird die Leistung eines Modells anhand verschiedener Teilmengen oder Merkmale bewertet. Unter den Wrapper-Methoden werden wir die rekursive Merkmalseliminierung (RFE) und die sequentielle Merkmalsauswahl (SFS) diskutieren.
Rekursive Merkmaleliminierung (RFE)
Dabei handelt es sich um eine Technik zur Auswahl von Merkmalen, die darauf abzielt, die relevantesten Merkmale auszuwählen, indem rekursiv immer kleinere Merkmalsmengen berücksichtigt werden. Dabei wird ein Modell angepasst und die unwichtigsten Merkmale entfernt, bis die gewünschte Anzahl von Merkmalen erreicht ist.
Wie RFE funktioniert
Wir beginnen mit dem Training eines beliebigen maschinellen Lernmodells. In diesem Beispiel wollen wir die logistische Regression verwenden.
Python-Code
from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression # Prepare the target variable, again y = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: y.append(1) else: y.append(0) # Drop future variables from the feature set X = df.drop(columns=["TARGET_CLOSE", "TARGET_OPEN"]) # Initialize the model model = LogisticRegression(max_iter=10000)
Dann initialisieren wir den RFE mit dem Modell und der Anzahl der wichtigsten Merkmale, die wir aus den Daten auswählen wollen.
# Initialize RFE with the model and number of features to select rfe = RFE(estimator=model, n_features_to_select=10) # Fit RFE rfe.fit(X, y) selected_features_mask = rfe.support_
Schließlich bestimmen wir die unwichtigsten Merkmale und eliminieren sie.
Python-Code
# Getting the names of the selected features feature_names = X.columns selected_feature_names = feature_names[selected_features_mask] selected_features = pd.DataFrame({ "Name": feature_names, "Mask": selected_features_mask }) selected_features.head(-1)
Ausgabe
Name Mask 0 OPEN True 1 HIGH True 2 LOW True 3 CLOSE True 4 OPEN_LAG1 False 5 HIGH_LAG1 True 6 LOW_LAG1 True 7 CLOSE_LAG1 True 8 OPEN_LAG2 False 9 HIGH_LAG2 False 10 LOW_LAG2 True 11 CLOSE_LAG2 True 12 OPEN_LAG3 True 13 HIGH_LAG3 False 14 LOW_LAG3 False 15 CLOSE_LAG3 False 16 30DAY_SMA False 17 7DAY_STDDEV False 18 DAYOFMONTH False 19 DAYOFWEEK False 20 DAYOFYEAR False 21 MONTH False 22 DIFF_LAG1_OPEN False 23 DIFF_LAG1_HIGH False 24 DIFF_LAG1_LOW False
Alle Merkmale, denen der Wert True zugewiesen wurde, sind die wichtigsten Werte. Um sie zu erhalten, können wir sie aus der ursprünglichen X-Matrix herausschneiden.
# Filter the dataset to keep only the selected features X_selected = X.loc[:, selected_features_mask] #for better readability, we convert this into pandas dataframe X_selected_df = pd.DataFrame(X_selected, columns=selected_feature_names) print("Selected Features") X_selected_df.head()
Ausgabe
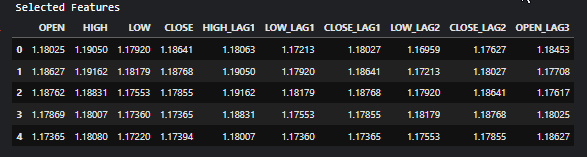
- RFE kann mit jedem Modell verwendet werden, das Merkmale nach Wichtigkeit einstufen kann.
- Durch die Eliminierung irrelevanter Merkmale kann RFE die Leistung des Modells verbessern.
- Durch das Entfernen unnötiger Merkmale kann die Überanpassung reduziert werden.
- Bei großen Datensätzen und komplexen Modellen wie neuronalen Netzen kann dies rechenintensiv sein, da das Modell mehrfach neu trainiert werden muss.
- RFE ist ein gieriger Algorithmus und findet möglicherweise nicht immer die optimale Teilmenge von Merkmalen.
Sequentielle Merkmalsauswahl (SFS)
Hierbei handelt es sich um eine Wrapper-Methode für die Merkmalsauswahl, die schrittweise einen Merkmalsatz aufbaut, indem sie Merkmale auf der Grundlage ihres Leistungsbeitrags zu einem Modell hinzufügt oder entfernt. Es gibt zwei Haupttypen der sequenziellen Merkmalsauswahl: Vorwärts- und Rückwärtselimination.
Bei der Vorwärtsselektion werden die Merkmale ausgehend von einer leeren Menge nacheinander hinzugefügt, bis die gewünschte Anzahl von Merkmalen erreicht ist oder das Hinzufügen weiterer Merkmale die Modellleistung nicht verbessert.
Bei der Rückwärtsauswahl funktioniert dies umgekehrt wie bei der Vorwärtsauswahl. Wir beginnen mit allen Merkmalen und entfernen sie eines nach dem anderen, wobei jedes Mal das am wenigsten signifikante Merkmal entfernt wird, bis die gewünschte Anzahl von Merkmalen übrig ist.
Auswahl vorwärts
from sklearn.feature_selection import SequentialFeatureSelector # Create a logistic regression model model = LogisticRegression(max_iter=10000) # Create a SequentialFeatureSelector object sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='forward') # Fit the SFS object to the training data sfs.fit(X, target) # Get the selected feature indices selected_features = sfs.get_support(indices=True) selected_features_names = X.columns[selected_features] # get the feature names # Print the selected features print("Selected feature indices:", selected_features) print("Selected feature names:", selected_feature_names)
Outputs
Selected feature indices: [ 1 7 8 12 17 19 22 23 24 25] Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
Auswahl rückwärts
# Create a logistic regression model model = LogisticRegression(max_iter=10000) # Create a SequentialFeatureSelector object sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='backward') # Fit the SFS object to the training data sfs.fit(X, target) # Get the selected feature indices selected_features = sfs.get_support(indices=True) selected_features_names = X.columns[selected_features] # get the feature names # Print the selected features print("Selected feature indices:", selected_features) print("Selected feature names:", selected_feature_names)
Ausgabe
Selected feature indices: [ 2 3 7 10 11 12 13 14 15 16] Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
Trotz der unterschiedlichen Herangehensweise konvergieren beide Methoden, die Rückwärts- und die Vorwärtsmethode, zur gleichen Lösung. Es wird die gleiche Anzahl von Merkmalen produziert.
- Leicht zu verstehen und umzusetzen.
- Es kann mit jedem maschinellen Lernalgorithmus verwendet werden.
- Dies führt häufig zu einer besseren Modellleistung, da die relevantesten Merkmale ausgewählt werden.
- Diese Methode ist bei großen Datensätzen oder vielen Merkmalen langsam.
- Findet möglicherweise nicht die optimale Merkmalsgruppe, da sie Entscheidungen auf der Grundlage lokaler Verbesserungen trifft.
Eingebettete Methoden
Bei diesen Methoden erfolgt die Auswahl der Merkmale während des Modelltrainings. Der Arbeitsablauf zur Auswahl eingebetteter Merkmale umfasst.
- Training eines maschinellen Lernmodells
- Ableitung der Bedeutung von Merkmalen
- Auswahl der ranghöchsten Prädiktorvariablen
Lasso-Regression
Lineare Regressionsmodelle sagen das Ergebnis auf der Grundlage einer linearen Kombination des Merkmalsraums voraus. Die Koeffizienten werden durch Minimierung der quadratischen Differenz zwischen dem tatsächlichen und dem vorhergesagten Wert des Ziels bestimmt. Es gibt drei wesentliche Regularisierungsverfahren: Ridge, Lasso und Elastic Net Regularisierung, die die beiden erstgenannten kombiniert. Bei der Lasso-Regression werden die Koeffizienten mit Hilfe der L1-Regularisierung um eine bestimmte Konstante verkleinert. Bei der Ridge-Regression wird das Quadrat der Koeffizienten durch eine Konstante bestraft, wobei die L2-Regularisierung verwendet wird. Ziel der Schrumpfung der Koeffizienten ist es, die Varianz zu verringern und eine Überanpassung zu verhindern. Die beste Konstante (Regularisierungsparameter) muss durch Hyperparameteroptimierung geschätzt werden.Die Lasso-Regularisierung kann einige der Koeffizienten genau auf Null setzen. Dies führt zu einer Merkmalsauswahl, die es uns ermöglicht, diese Merkmale sicher aus den Daten zu entfernen.
Python-Code
from sklearn.model_selection import train_test_split from sklearn.linear_model import Lasso from sklearn.metrics import r2_score from sklearn.preprocessing import MinMaxScaler y = df["TARGET_CLOSE"] # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # A scaling technique scaler = MinMaxScaler() # Initialize and fit the lasso model lasso = Lasso(alpha=0.001) # You need tune for the best penalty value # Train the scaler and transfrom data X_train = scaler.fit_transform(X_train) lasso.fit(X_train, y_train) print(f'Coefficients: {lasso.coef_}') #print coefficients # Predict on the test set X_test = scaler.transform(X_test) y_pred = lasso.predict(X_test) # Calculate mean squared error mse = r2_score(y_test, y_pred) print(f'Lasso regression test accuracy = {mse}') # select all features with coefficents not equal to zero selected_features = X.columns[lasso.coef_ != 0] print(f'Selected Features: {selected_features}')
Ausgabe
Coefficients: [ 0. 0.02575516 0.05720178 0.1453415 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.0228085 -0. 0. -0. 0. 0. 0. 0. 0. 0. ] Lasso regression test accuracy = 0.9894539761500866 Selected Features: Index(['HIGH', 'LOW', 'CLOSE', '30DAY_SMA'], dtype='object')
Das Modell war zu 98 % genau, da es nur 4 Merkmale auswählte.
- Lasso wählt automatisch die wichtigsten Merkmale aus, wodurch das Modell vereinfacht und die Interpretierbarkeit verbessert wird.
- Durch Hinzufügen eines Strafterms verringert Lasso das Risiko einer Überanpassung.
- Lasso kann Modelle erstellen, die aufgrund der Eliminierung irrelevanter Merkmale leichter zu interpretieren sind.
- Wenn die Merkmale stark korreliert sind, kann die Lasso-Regressionstechnik zu instabilen Koeffizientenschätzungen führen.
- In Fällen, in denen die Anzahl der Merkmale die Anzahl der Beobachtungen übersteigt, kann Lasso Probleme haben, gut zu funktionieren.
Entscheidungsbaumbasierte Methoden
Entscheidungsbaum-Algorithmen sagen die Ergebnisse durch rekursive Partitionierung der Daten voraus. An jedem Knotenpunkt wählt der Algorithmus ein Merkmal und einen Wert aus, um die Daten aufzuteilen, mit dem Ziel, den Rückgang der Verunreinigung zu maximieren.
Die Bedeutung eines Merkmals in Entscheidungsbäumen wird durch die Gesamtreduktion der Verunreinigung bestimmt, die jedes Merkmal im gesamten Baum erreicht. Wird ein Merkmal beispielsweise dazu verwendet, die Daten an mehreren Knoten aufzuteilen, wird seine Bedeutung als die Summe der Verunreinigungsreduzierung an all diesen Knoten berechnet.Im „Random Forest“ wachsen viele Entscheidungsbäume parallel. Die endgültige Vorhersage ist der Durchschnitt (oder das Mehrheitsvotum) der Vorhersagen der einzelnen Bäume. Die Merkmalsbedeutung in Random Forests ist die durchschnittliche Bedeutung jedes Merkmals in allen Bäumen.
Die Gradient-Boosting-Maschinen (GBMs), wie XGBoost, bauen Bäume sequentiell auf. Jeder Baum zielt darauf ab, die Fehler (Residuen) des vorherigen Baumes zu korrigieren. Bei GBMs ist die Merkmalsbedeutung die Summe der Bedeutung aller Bäume.
Durch die Analyse der von den Entscheidungsbäumen erzeugten Merkmalsbedeutungswerte können wir die wichtigsten Merkmale für unser Modell ermitteln und auswählen.
from sklearn.ensemble import RandomForestClassifier y = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: y.append(1) else: y.append(0) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) model = RandomForestClassifier(n_estimators=50, min_samples_split=10, max_depth=5, min_samples_leaf=5) model.fit(X_train, y_train) importances = model.feature_importances_ print(importances) selected_features = importances > 0.04 selected_feature_names = X.columns[selected_features] print("selected features\n",selected_feature_names)
Ausgabe
[0.02691807 0.05334113 0.03780997 0.0563491 0.03162462 0.03486413 0.02652285 0.0237652 0.03398946 0.02822157 0.01794172 0.02818283 0.04052433 0.02821834 0.0386661 0.03921218 0.04406372 0.06162133 0.03103843 0.02206782 0.05104613 0.01700301 0.05191551 0.07251801 0.0502405 0.05233394] selected features Index(['HIGH', 'CLOSE', 'OPEN_LAG3', '30DAY_SMA', '7DAY_STDDEV', 'DAYOFYEAR', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CLOSE'], dtype='object')
Bevor wir die ausgewählten Merkmale verwenden können, müssen wir die Genauigkeit des Random-Forest-Klassifikators messen, der diese Merkmale ausgewählt hat. Achten Sie darauf, dass Sie die Merkmale erhalten, die von einem Modell ausgewählt wurden, das bei den Testdaten gut abgeschnitten hat.
from sklearn.metrics import accuracy_score
test_pred = model.predict(X_test)
print(f"Random forest test accuracy = ",accuracy_score(y_test, test_pred)) - Zufällige Wälder erzeugen ein Ensemble von Bäumen, das das Risiko einer Überanpassung im Vergleich zu einzelnen Entscheidungsbäumen verringert. Diese Robustheit macht die Bewertungen der Merkmalsbedeutung zuverlässiger.
- Sie können Datensätze mit zahlreichen Merkmalen ohne signifikante Leistungseinbußen verwalten und sind daher für die Merkmalsauswahl in hochdimensionalen Räumen geeignet.
- Sie können komplexe, nicht-lineare Wechselwirkungen zwischen Merkmalen erfassen und ermöglichen so ein differenzierteres Verständnis der Bedeutung von Merkmalen.
- Das Training von Random Forests kann bei großen Datensätzen und einer hohen Anzahl von Merkmalen sehr rechenintensiv sein.
- Random Forests können korrelierten Merkmalen ähnliche Wichtigkeitswerte zuweisen, sodass es schwierig ist, zu unterscheiden, welche Merkmale wirklich wichtig sind.
- Random Forests können manchmal kontinuierliche Merkmale oder solche mit vielen Stufen gegenüber kategorialen Merkmalen mit weniger Stufen bevorzugen, wodurch die Bewertungen der Merkmalsbedeutung möglicherweise verzerrt werden.
Techniken zur Dimensionenreduktion
Techniken zur Dimensionenreduktion können ebenfalls in den Mix der Techniken zur Merkmalsauswahl aufgenommen werden. Techniken zur Dimensionenreduktion wie die Hauptkomponentenanalyse (PCA), die lineare Diskriminanzanalyse (LDA), die nichtnegative Matrixfaktorisierung (NMF), die verkürzte SVD usw. zielen darauf ab, die Daten in einen weniger dimensionalen Raum zu transformieren.
Wie aus der Korrelationsmatrix ersichtlich ist, sind die Merkmale OPEN, HIGH, LOW und CLOSE stark korreliert. Wir fassen diese Variablen zu einer einzigen zusammen, um die Merkmale für unsere Modelle zu vereinfachen und gleichzeitig die notwendigen Informationen in dieser einzigen, durch PCA erzeugten Variable zu erhalten. Anhand des linearen Regressionsmodells soll gemessen werden, wie effektiv die PCA die Genauigkeit der im Vergleich zu den ursprünglichen Daten reduzierten Daten beibehalten hat.
from sklearn.decomposition import PCA from sklearn.linear_model import LinearRegression pca = PCA(n_components=1) ohlc = pd.DataFrame({ "OPEN": df["OPEN"], "HIGH": df["HIGH"], "LOW": df["LOW"], "CLOSE": df["CLOSE"] }) y = df["TARGET_CLOSE"] # let us use the linear regression model model = LinearRegression() # for OHLC original data model.fit(ohlc, y) preds = model.predict(ohlc) print("ohlc_original data LR accuracy = ",r2_score(y, preds)) # For data reduced in dimension ohlc_reduced = pca.fit_transform(ohlc) print(ohlc_reduced[:10]) # print 10 rows of the reduced data model.fit(ohlc_reduced, y) preds = model.predict(ohlc_reduced) print("ohlc_reduced data LR accuracy = ",r2_score(y, preds))
Ausgabe
ohlc_original data LR accuracy = 0.9937597843724363 [[-0.14447016] [-0.14997874] [-0.14129409] [-0.1293209 ] [-0.12659902] [-0.12895961] [-0.13831287] [-0.14061213] [-0.14719862] [-0.15752861]] ohlc_reduced data LR accuracy = 0.9921387699876517
Beide Modelle ergaben in etwa den gleichen Genauigkeitswert von etwa 0,99. Bei der einen wurden die Originaldaten (mit 4 Merkmalen) und bei der anderen die in der Dimension reduzierten Daten (mit 1 Merkmal) verwendet.
Schließlich können wir die ursprünglichen Daten ändern, indem wir die Merkmale OPEN, HIGH, LOW und CLOSE weglassen und ein neues Merkmal namens OHLC hinzufügen, das die vorherigen vier (4) Merkmale kombiniert.
new_df = df.drop(columns=["OPEN", "HIGH", "LOW", "CLOSE"]) # new_df["OHLC"] = ohlc_reduced # Reorder the columns to make "ohlc" the first column cols = ["OHLC"] + [col for col in new_df.columns if col != "OHLC"] new_df = new_df[cols] new_df.head(10)
Ausgabe
Vorteile von Dimensionenreduktionstechniken bei der Merkmalsauswahl
- Die Reduzierung der Anzahl von Merkmalen kann die Leistung von Modellen des maschinellen Lernens verbessern, indem Rauschen und redundante Informationen eliminiert werden.
- Durch die Verkleinerung des Merkmalsraums helfen Techniken zur Dimensionenreduktion, die Überanpassung bei hochdimensionalen Daten, bei denen eine Überanpassung wahrscheinlicher ist, abzuschwächen.
- Diese Techniken können ein Rauschen aus dem Datensatz herausfiltern, was zu saubereren Daten führt, die die Genauigkeit und Zuverlässigkeit des Modells verbessern können.
- Modelle mit weniger Merkmalen sind einfacher und besser interpretierbar.
Nachteile von Dimensionenreduktionstechniken bei der Merkmalsauswahl
- Die Dimensionenreduktion führt häufig zum Verlust wichtiger Informationen, was sich negativ auf die Leistung des Modells auswirken kann.
- Techniken wie die PCA erfordern die Auswahl der Anzahl der beizubehaltenden Komponenten, was nicht immer einfach ist und mit Versuch und Irrtum oder Kreuzvalidierung verbunden sein kann.
- Die durch Dimensionenreduktionstechniken erzeugten neuen Merkmale können im Vergleich zu den ursprünglichen Merkmalen schwer zu interpretieren sein.
- Eine Verringerung der Dimensionen könnte die Daten zu sehr vereinfachen und zu Modellen führen, die subtile, aber wichtige Beziehungen zwischen den Merkmalen übersehen.
Abschließende Überlegungen
Das Wissen, wie man die wertvollsten Informationen extrahiert, ist entscheidend für die Optimierung von Modellen für maschinelles Lernen. Eine effektive Merkmalsauswahl kann die Trainingszeit erheblich reduzieren und die Modellgenauigkeit verbessern, was zu effizienteren KI-gestützten Handelsrobotern in MetaTrader 5 führt. Durch die sorgfältige Auswahl der wichtigsten Funktionen können Sie die Leistung sowohl im Live-Handel als auch beim Testen von Strategien verbessern und letztendlich bessere Ergebnisse mit Ihren Handelsalgorithmen erzielen.
Mit besten Grüßen
Tabelle der Anhänge
| Datei | Beschreibung und Verwendung |
|---|---|
| feature_selection.ipynb | Der gesamte Python-Code, der in diesem Artikel besprochen wird, ist in diesem Jupyter-Notizbuch zu finden |
| Timeseries OHLC.csv | Ein in diesem Artikel verwendeter Datensatz |
Quellen
- A Chi-Square Statistics-Based Feature Selection Method in Text Classification (https://www.researchgate.net/publication/331850396_A_Chi-Square_Statistics_Based_Feature_Selection_Method_in_Text_Classification)
- Auswahl der Merkmale (https://en.wikipedia.org/wiki/Feature_selection)
- Eingebettete Methoden (https://www.blog.trainindata.com/feature-selection-with-embedded-methods/)
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15482
 Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 2): Senden von Signalen von MQL5 an Telegram
Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 2): Senden von Signalen von MQL5 an Telegram
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 30): Spotlight auf Batch-Normalisierung beim maschinellen Lernen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 30): Spotlight auf Batch-Normalisierung beim maschinellen Lernen
 MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 31): Auswahl der Verlustfunktion
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 31): Auswahl der Verlustfunktion
 Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 1): Senden von Nachrichten von MQL5 an Telegram
Erstellen eines integrierten MQL5-Telegram Expert Advisors (Teil 1): Senden von Nachrichten von MQL5 an Telegram
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.