Datenwissenschaft und maschinelles Lernen (Teil 25): Forex-Zeitreihenvorhersage mit einem rekurrenten neuronalen Netzwerk (RNN)

MetaTrader 5 — Experten | 21 August 2024, 16:13

276

Omega J Msigwa

Inhalt

Was sind die rekurrenten neuronalen Netze (RNNs)?

Rekurrente neuronale Netze (RNN) sind künstliche neuronale Netze, die darauf ausgelegt sind, Muster in Datensequenzen zu erkennen, z. B. in Zeitreihen, Sprache oder Videos. Im Gegensatz zu herkömmlichen neuronalen Netzen, die davon ausgehen, dass die Eingaben unabhängig voneinander sind, können RNNs Muster aus einer Folge von Daten (Informationen) erkennen und verstehen.

Nicht zu verwechseln mit der Terminologie in diesem Artikel: Wenn ich von rekurrenten neuronalen Netzen spreche, beziehe ich mich auf einfache RNN als Modell. Wenn ich dagegen rekurrente neuronale Netze (RNNs) verwende, beziehe ich mich auf eine Familie von rekurrenten neuronalen Netzmodellen wie einfache RNN, Long Short Term Memory (LSTM) und Gated Recurrent Unit (GRU).

Ein grundlegendes Verständnis von Python, ONNX in MQL5, und Pythons maschinellem Lernen ist erforderlich, um den Inhalt dieses Artikels vollständig zu verstehen.

RNNs verstehen

RNNs verfügen über ein sogenanntes sequentielles Gedächtnis, das sich auf das Konzept der Beibehaltung und Nutzung von Informationen aus den vorherigen Zeitschritten in einer Sequenz bezieht, um die Verarbeitung der nachfolgenden Zeitschritte zu informieren.

Das sequenzielle Gedächtnis ähnelt dem des menschlichen Gehirns. Es ist die Art von Gedächtnis, die es Ihnen erleichtert, Muster in Sequenzen zu erkennen, z. B. beim Sprechen von Wörtern.

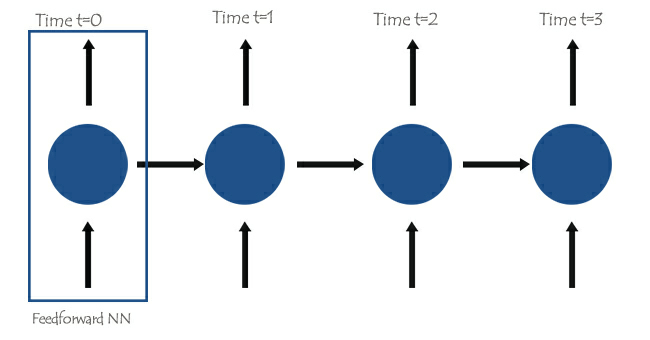
Das Herzstück rekurrenter neuronaler Netze (RNN) sind neuronale Netze mit Vorwärtskopplung, die so miteinander verbunden sind, dass das nächste Netz über die Informationen des vorherigen Netzes verfügt, was dem einfachen RNN die Fähigkeit verleiht, die aktuellen Informationen auf der Grundlage der vorherigen zu lernen und zu verstehen.

Um dies besser zu verstehen, betrachten wir ein Beispiel, bei dem wir das RNN-Modell für einen Chatbot einlernen wollen. Wir wollen, dass unser Chatbot die Wörter und Sätze eines Nutzers versteht, nehmen wir an, der empfangene Satz lautet: What time is it? (Wie spät ist es?)

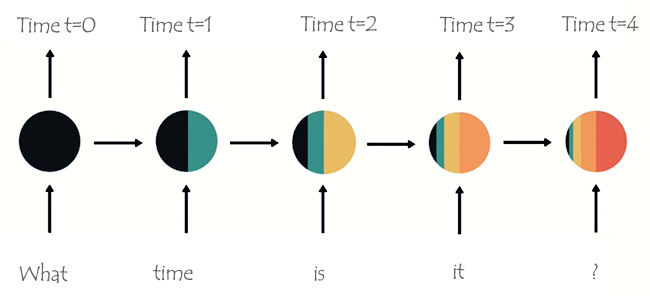
Die Wörter werden in ihre jeweiligen Timesteps aufgeteilt und nacheinander in das RNN eingespeist, wie in der folgenden Abbildung zu sehen ist.

Beim Betrachten des letzten Knotens im Netzwerk ist Ihnen vielleicht eine seltsame Anordnung von Farben aufgefallen, die die Informationen aus den vorherigen Netzwerken und dem aktuellen Netzwerk darstellen. Betrachtet man die Farben, so ist die Information des Netzes zum Zeitpunkt t=0 und zum Zeitpunkt t=1 in diesem letzten Knoten des RNN zu klein (fast nicht vorhanden).

Wenn das RNN mehr Schritte verarbeitet, hat es Schwierigkeiten, die Informationen aus den vorherigen Schritten zu behalten. Wie in der obigen Abbildung zu sehen ist, sind die Wörter what und time im letzten Knoten des Netzes fast nicht vorhanden.

Das ist das, was wir Kurzzeitgedächtnis nennen. Sie wird durch viele Faktoren verursacht, wobei Backpropagation einer der wichtigsten ist.

Rekurrente neuronale Netze (RNNs) haben ihren eigenen Backpropagation-Prozess, der als backpropagation through time bekannt ist. Bei der Backpropagation schrumpfen die Gradientenwerte exponentiell, wenn sich das Netz in jedem Zeitschritt rückwärts fortpflanzt. Gradienten werden verwendet, um Anpassungen an den Parametern des neuronalen Netzes (Gewichte und Bias) vorzunehmen, wodurch das neuronale Netz lernen kann. Kleine Steigungen bedeuten kleinere Anpassungen. Da die ersten Schichten nur kleine Gradienten erhalten, lernen sie nicht so effektiv, wie sie sollten. Dies wird als das Problem der verschwindenden Gradienten bezeichnet.

Aufgrund des Problems des verschwindenden Gradienten lernt das einfache RNN keine weitreichenden Abhängigkeiten über Zeitschritte hinweg. Im obigen Bildbeispiel besteht die große Möglichkeit, dass Wörter wie what und time überhaupt nicht berücksichtigt werden, wenn unser Chatbot-RNN-Modell versucht, einen Beispielsatz eines Nutzers zu verstehen. Dies macht das RNN weniger effektiv, da sein Speicher zu kurz ist, um lange Zeitreihendaten zu verstehen, wie sie in realen Anwendungen häufig vorkommen.

Zur Abschwächung des Kurzzeitgedächtnisses wurden zwei spezialisierte rekurrente neuronale Netze, Long Short Term Memory (LSTM) und Gated Recurrent Unit (GRU), eingeführt.

Sowohl LSTM als auch GRU arbeiten in vielerlei Hinsicht ähnlich wie RNN, sind jedoch in der Lage, langfristige Abhängigkeiten zu verstehen, indem sie einen Mechanismus namens Gates verwenden. Wir werden sie im nächsten Artikel ausführlich erörtern , bleiben Sie dran.

Die Mathematik hinter einem rekurrenten neuronalen Netz (RNN)

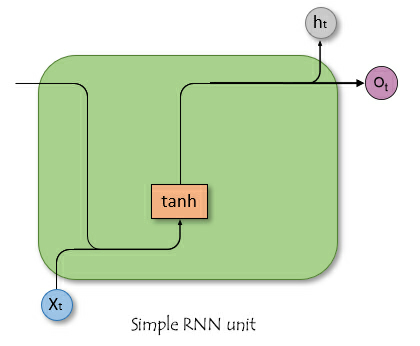
Im Gegensatz zu neuronalen Vorwärtsdurchgangs-Netzwerken haben RNNs Verbindungen, die Zyklen bilden, sodass die Informationen erhalten bleiben. Die folgende vereinfachte Abbildung zeigt, wie eine RNN-Einheit/Zelle aussieht, wenn sie zerlegt wird.

wobei:

ist die Eingabe zum Zeitpunkt t.

ist der verborgene Zustand zum Zeitpunkt t.

Verborgener Zustand

ist ein Vektor, der Informationen aus den vorangegangenen Zeitschritten speichert. Es fungiert als Gedächtnis des Netzes und ermöglicht es, zeitliche Abhängigkeiten und Muster in den Eingabedaten zu erfassen.

Die Rolle des verborgenen Zustands im Netz

Der verborgene Zustand erfüllt in einem RNN mehrere wichtige Funktionen, wie z. B.;

Es speichert Informationen aus früheren Eingaben. Dadurch kann das Netz aus der gesamten Sequenz lernen.
Sie liefert den Kontext für die aktuellen Eingaben, sodass das Netz auf der Grundlage früherer Daten fundierte Vorhersagen machen kann.
Sie bildet die Grundlage für die rekurrenten Verbindungen innerhalb des Netzes. Dadurch kann sich die verborgene Schicht über verschiedene Zeitschritte hinweg selbst beeinflussen.

Es ist nicht so wichtig, die Mathematik hinter RNN zu verstehen, sondern zu wissen, wie, wo und wann man sie einsetzt. Fühlen Sie sich frei, zum nächsten Abschnitt dieses Artikels zu springen, wenn Sie das möchten.

Mathematische Formel

Der verborgene Zustand im Zeitschritt wird anhand der Eingabe im Zeitschritt , des verborgenen Zustands aus dem vorhergehenden Zeitschritt und der entsprechenden Gewichtungsmatrizen und des Bias berechnet. Die Formel lautet wie folgt;

wobei:

ist die Gewichtsmatrix für die Eingabe in den verborgenen Zustand.

ist die Gewichtsmatrix für den verborgenen Zustand zum verborgenen Zustand.

ist der Bias-Term für den verborgenen Zustand.

σ ist die Aktivierungsfunktion (z. B. tanh oder ReLU).

Ausgangsschicht

Die Ausgabe im Zeitschritt wird aus dem verborgenen Zustand im Zeitschritt errechnet.

Wobei

ist die Ausgabe im Zeitschritt .

ist die Gewichtsmatrix vom verborgenen Zustand zum Ausgang.

Bias der Ausgabeschicht.

Verlustberechnung

Angenommen wird eine Verlustfunktion (dies kann eine beliebige Verlustfunktion sein, z. B. Mean Squared Error für Regression oder Cross-Entropy für Klassifikation).

Der Gesamtverlust über alle Zeitschritte beträgt;

Backpropagation durch Zeit (BPTT)

Um sowohl die Gewichte als auch das Bias zu aktualisieren, müssen wir die Gradienten des Verlusts in Bezug auf jedes Gewicht bzw. jedes Bias berechnen und dann die erhaltenen Gradienten verwenden, um Aktualisierungen vorzunehmen. Dazu gehören die unten beschriebenen Schritte.

Schritt	Für Gewichte	Für Bias
Berechnung des Gradienten der Ausgabeschicht	in Bezug auf die Gewichte: Dabei ist die Steigung des Verlustes in Bezug auf die Leistung.	in Bezug auf das Bias: Da sich das Bias des Ausgangs direkt auf die Ausgänge auswirkt, gilt Folgendes; Deshalb.
Berechnung der Gradienten des verborgenen Zustands in Bezug auf Gewichte und Bias	Der Gradient des Verlustes in Bezug auf den verborgenen Zustand beinhaltet sowohl den direkten Beitrag aus dem aktuellen Zeitschritt als auch den indirekten Beitrag durch die nachfolgenden Zeitschritte. 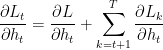Gradient des verborgenen Zustands im Vergleich zum vorherigen Zeitschritt. Gradient der verborgenen Zustandsaktivierung. Gradient der Gewichte der verborgenen Schicht. Der Gesamtgradient ist die Summe der Gradienten über alle Zeitschritte.	Die Steigung des Verlusts in Bezug auf des versteckten Bias ist durch die Summe der Steigungen des Verlusts in Bezug auf den versteckten Zustand über alle Zeitschritte gegeben. Da das versteckte Bias den versteckten Zustand durch die Aktivierungsfunktion beeinflusst, haben wir Folgendes; Wir verwenden die Kettenregel und stellen fest, dass; Dabei ist die Ableitung der Aktivierungsfunktion. Deshalb: Der Gesamtgradient für das versteckte Bias ist die Summe der Gradienten über alle Zeitschritte.
Aktualisierung von Gewichten und Bias. Mit Hilfe der oben berechneten Gradienten können wir die Gewichte mit Hilfe des Gradientenabstiegs oder einer seiner Varianten (z. B. Adam) aktualisieren .

Obwohl einfache RNN(RNN) nicht in der Lage sind, lange Zeitreihendaten zu lernen, sind sie dennoch gut in der Lage, zukünftige Werte anhand von Informationen aus der Vergangenheit, die nicht allzu lange zurückliegen, vorherzusagen. Wir können ein einfaches RNN bauen, das uns bei unseren Handelsentscheidungen hilft.

Aufbau eines rekurrenten neuronalen Netzes (RNN) in Python

Die Erstellung und Kompilierung eines RNN-Modells in Python ist einfach und erfordert nur ein paar Zeilen Code unter Verwendung der Bibliothek Keras.

Python

import tensorflow as tf
from tensorflow.keras.models import Sequential #import sequential neural network layer
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.layers import SimpleRNN, Dense, Input
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from keras.optimizers import Adam

reg_model = Sequential()

reg_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
reg_model.add(SimpleRNN(50, activation='sigmoid')) #first hidden layer
reg_model.add(Dense(50, activation='sigmoid')) #second hidden layer
reg_model.add(Dense(units=1, activation='relu'))  # final layer 

adam_optimizer = Adam(learning_rate = 0.001)

reg_model.compile(optimizer=adam_optimizer, loss='mean_squared_error') # Compile the model
reg_model.summary()

Der obige Code ist für ein regressiv-rekurrentes neuronales Netz, deshalb haben wir 1 Knoten in der Ausgabeschicht und eine Relu-Aktivierungsfunktion in der letzten Schicht, es gibt einen Grund dafür. Wie in dem Artikel Entmystifizierte Feed Forward Neurale Netzwerke beschrieben.

Anhand der Daten, die wir im vorangegangenen Artikel Zeitreihenprognose im Forex mit regulären AI-Modellen (ein Pflichtlektüre) gesammelt haben, wollen wir sehen, wie wir RNNs-Modelle verwenden können, da sie in der Lage sind, Zeitreihendaten zu verstehen, um uns zu helfen, worin sie gut sind.

Am Ende werden wir die Leistung von RNNs im Vergleich zu LightGBM, das im vorherigen Artikel entwickelt wurde, anhand der gleichen Daten bewerten. Wir hoffen, dass dies dazu beiträgt, Ihr Verständnis der Zeitreihenprognose im Allgemeinen zu festigen.

Sequentielle Daten erstellen

In unserem Datensatz haben wir 28 Spalten, die alle für ein Nicht-Zeitreihenmodell entwickelt wurden.

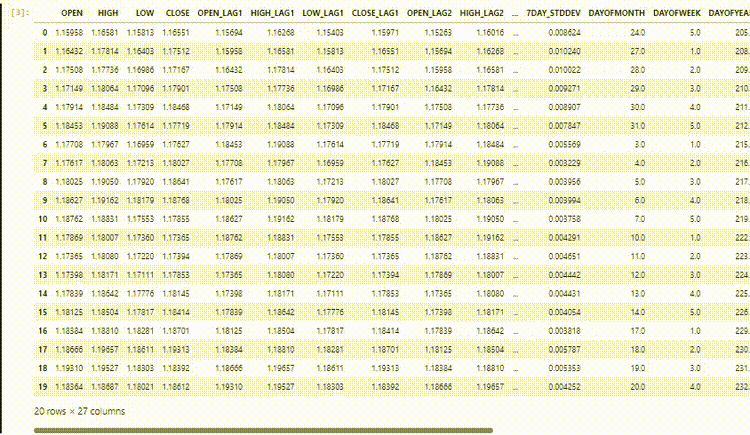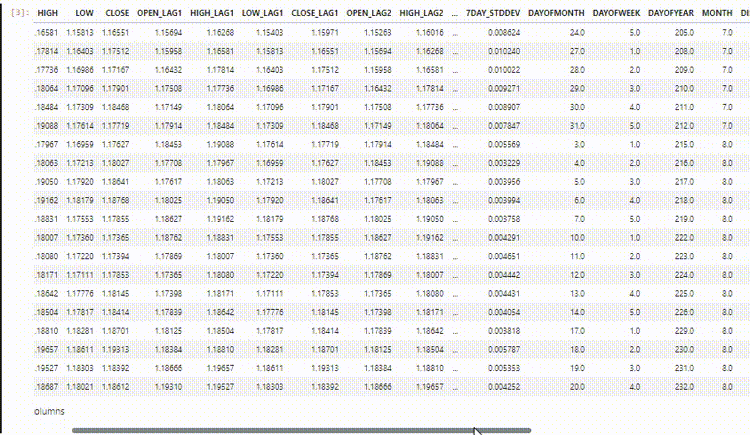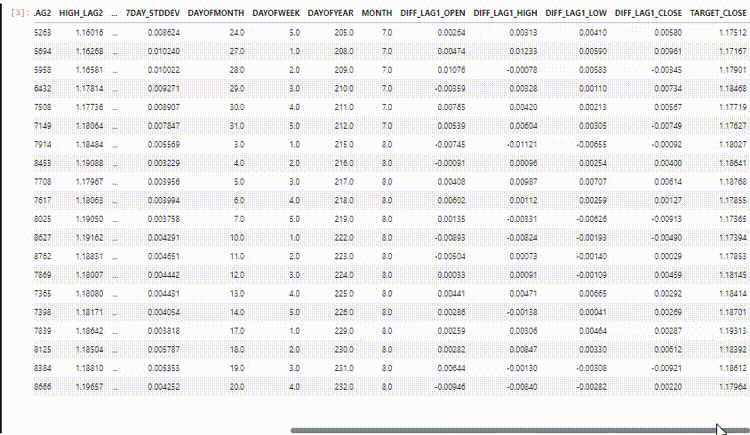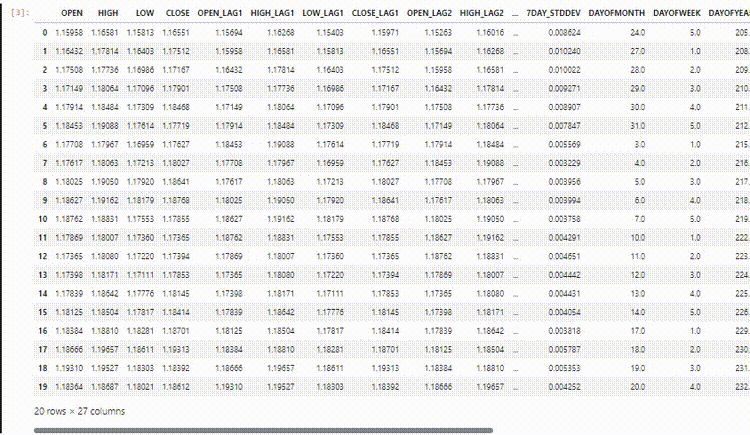
Datensatz für Zeitreihenprognosen

Die von uns gesammelten und aufbereiteten Daten enthalten jedoch viele verzögerte Variablen, die für das Nicht-Zeitreihenmodell nützlich waren, um zeitabhängige Muster zu erkennen. Wie wir wissen, können RNNs Muster innerhalb der vorgegebenen Zeitschritte erkennen.

Wir brauchen diese verzögerten Werte im Moment nicht, wir müssen sie weglassen.

Python

lagged_columns = [col for col in data.columns if "lag" in col.lower()] #let us obtain all the columns with the name lag

print("lagged columns: ",lagged_columns)

data = data.drop(columns=lagged_columns) #drop them

Ausgänge

lagged columns:  ['OPEN_LAG1', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'OPEN_LAG2', 'HIGH_LAG2', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3', 'HIGH_LAG3', 'LOW_LAG3', 'CLOSE_LAG3', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CL

Die neuen Daten haben jetzt 12 Spalten.

neuer gefilterter Datensatz

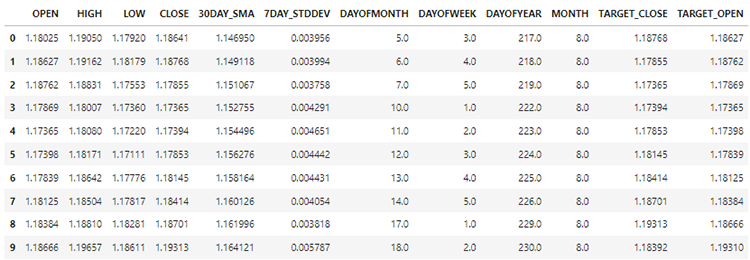
Wir können 70 % der Daten zum Trainieren und die restlichen 30 % zum Testen aufteilen. Wenn Sie train_test_split von Scikit-Learn verwenden, müssen Sie shuffle=False einstellen. Dadurch wird die Funktion das Original aufteilen, wobei die Reihenfolge der vorhandenen Informationen erhalten bleibt.

Erinnern Sie sich! Dies ist die Zeitreihenprognose.

# Split the data

X = data.drop(columns=["TARGET_CLOSE","TARGET_OPEN"]) #dropping the target variables
Y = data["TARGET_CLOSE"]

test_size = 0.3 #70% of the data should be used for training purpose while the rest 30% should be used for testing

x_train, x_test, y_train, y_test = train_test_split(X, Y, shuffle=False, test_size = test_size) # this is timeseries data so we don't shuffle

print(f"x_train {x_train.shape}\nx_test {x_test.shape}\ny_train{y_train.shape}\ny_test{y_test.shape}")

Nachdem wir auch die beiden Zielvariablen gestrichen haben, verbleiben nun 10 Merkmale in unseren Daten. Wir müssen diese 10 Merkmale in sequentielle Daten umwandeln, die von RNNs verarbeitet werden können.

def create_sequences(X, Y, time_step):
    if len(X) != len(Y):
        raise ValueError("X and y must have the same length")
    
    X = np.array(X)
    Y = np.array(Y)
    
    Xs, Ys = [], []
    
    for i in range(X.shape[0] - time_step):
        Xs.append(X[i:(i + time_step), :])  # Include all features with slicing
        Ys.append(Y[i + time_step])
        
    return np.array(Xs), np.array(Ys)

Die obige Funktion erzeugt eine Sequenz aus gegebenen x- und y-Arrays für einen bestimmten Zeitschritt. Um zu verstehen, wie diese Funktion funktioniert, lesen Sie das folgende Beispiel;

Angenommen, wir haben einen Datensatz mit 10 Stichproben und 2 Merkmalen und wollen Sequenzen mit einem Zeitschritt von 3 erstellen.

X, die eine Matrix der Form (10, 2) ist. Y ist ein Vektor der Länge 10.
Die Funktion erstellt Sequenzen wie folgt
Für i=0: Xs erhält [0:3, :] X[0:3, :], und Ys erhält Y[3]. Für i=1: Xs erhält 𝑋[1:4, :] X[1:4, :], und Ys erhält Y[4].

Und so weiter, bis i=6.

Die resultierenden Xs haben die Form (7, 3, 2), und Ys haben die Länge 7.

Nach der Standardisierung der unabhängigen Variablen, die wir aufgeteilt haben, können wir dann die Funktion create_sequences anwenden, um sequentielle Informationen zu erzeugen.

time_step = 7 # we consider the past 7 days

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train_seq, y_train_seq = create_sequences(x_train, y_train, time_step)
x_test_seq, y_test_seq = create_sequences(x_test, y_test, time_step)

print(f"Sequential data\n\nx_train {x_train_seq.shape}\nx_test {x_test_seq.shape}\ny_train{y_train_seq.shape}\ny_test{y_test_seq.shape}")

Ausgänge

Sequential data

x_train (693, 7, 10)
x_test (293, 7, 10)
y_train(693,)
y_test(293,)

Der Zeitschrittwert von 7 stellt sicher, dass das RNN in jeder Instanz mit den Informationen der letzten 7 Tage gefüllt wird, da wir alle Informationen im Datensatz aus dem täglichen Zeitrahmen gesammelt haben. Dies ist vergleichbar mit der manuellen Ermittlung der Verzögerung (lag) für die vorangegangenen 7 Tage aus dem aktuellen Balken, was wir im letzten Artikel dieser Serie getan haben.

Training des einfachen RNN für ein Regressionsproblem

early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = reg_model.fit(x_train_seq, y_train_seq, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_seq), callbacks=[early_stopping])

Ausgänge

Epoch 95/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4504e-05 - val_loss: 4.4433e-05
Epoch 96/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4380e-05 - val_loss: 4.4408e-05
Epoch 97/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4259e-05 - val_loss: 4.4386e-05
Epoch 98/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4140e-05 - val_loss: 4.4365e-05
Epoch 99/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.4024e-05 - val_loss: 4.4346e-05
Epoch 100/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.3910e-05 - val_loss: 4.4329e-05

Regressor RNN-Trainingsverlustkurve

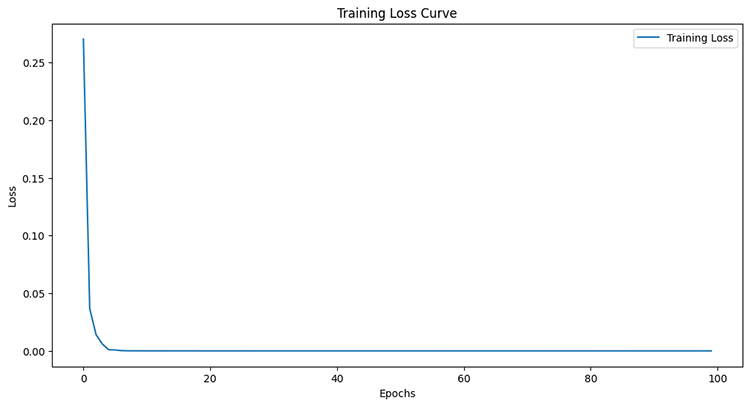
Nach der Messung der Leistung des Teststichprobe.

Python

from sklearn.metrics import r2_score

y_pred = reg_model.predict(x_test_seq) # Make predictions on the test set

# Plot the actual vs predicted values
plt.figure(figsize=(12, 6))
plt.plot(y_test_seq, label='Actual Values')
plt.plot(y_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('TARGET_CLOSE')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()

print("RNN accuracy =",r2_score(y_test_seq, y_pred))

Das Modell war zu 78 % genau.

Regressor rnn tatsächlich vs. vorhergesagt

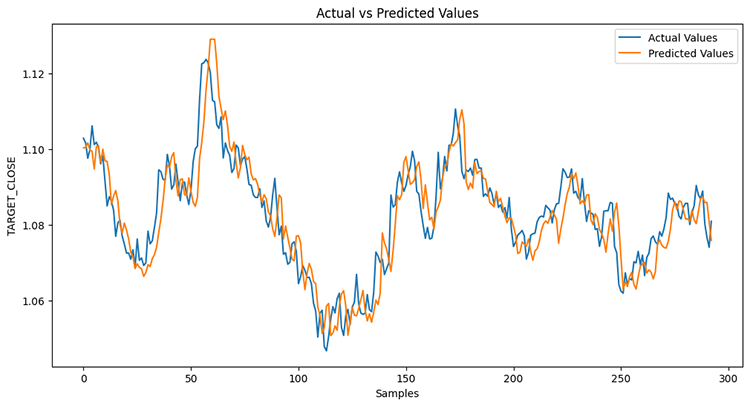
Wenn Sie sich an den vorigen Artikel erinnern, war das LightGBM-Modell bei einem Regressionsproblem zu 86,76 % genau, d. h. ein Nicht-Zeitreihenmodell hat ein Zeitreihenmodell übertroffen.

Das Merkmal Bedeutung

Ich habe einen Test durchgeführt, um zu prüfen, wie sich die Variablen auf den Entscheidungsprozess des RNN-Modells unter Verwendung von SHAP auswirken.

import shap

# Wrap the model prediction for KernelExplainer
def rnn_predict(data):
    data = data.reshape((data.shape[0], time_step, x_train.shape[1]))
    return reg_model.predict(data).flatten()

# Use SHAP to explain the model
sampled_idx = np.random.choice(len(x_train_seq), size=100, replace=False)
explainer = shap.KernelExplainer(rnn_predict, x_train_seq[sampled_idx].reshape(100, -1))
shap_values = explainer.shap_values(x_test_seq[:100].reshape(100, -1), nsamples=100)

Ich habe Code ausgeführt, um ein Diagramm für die Bedeutung der Merkmale zu zeichnen.

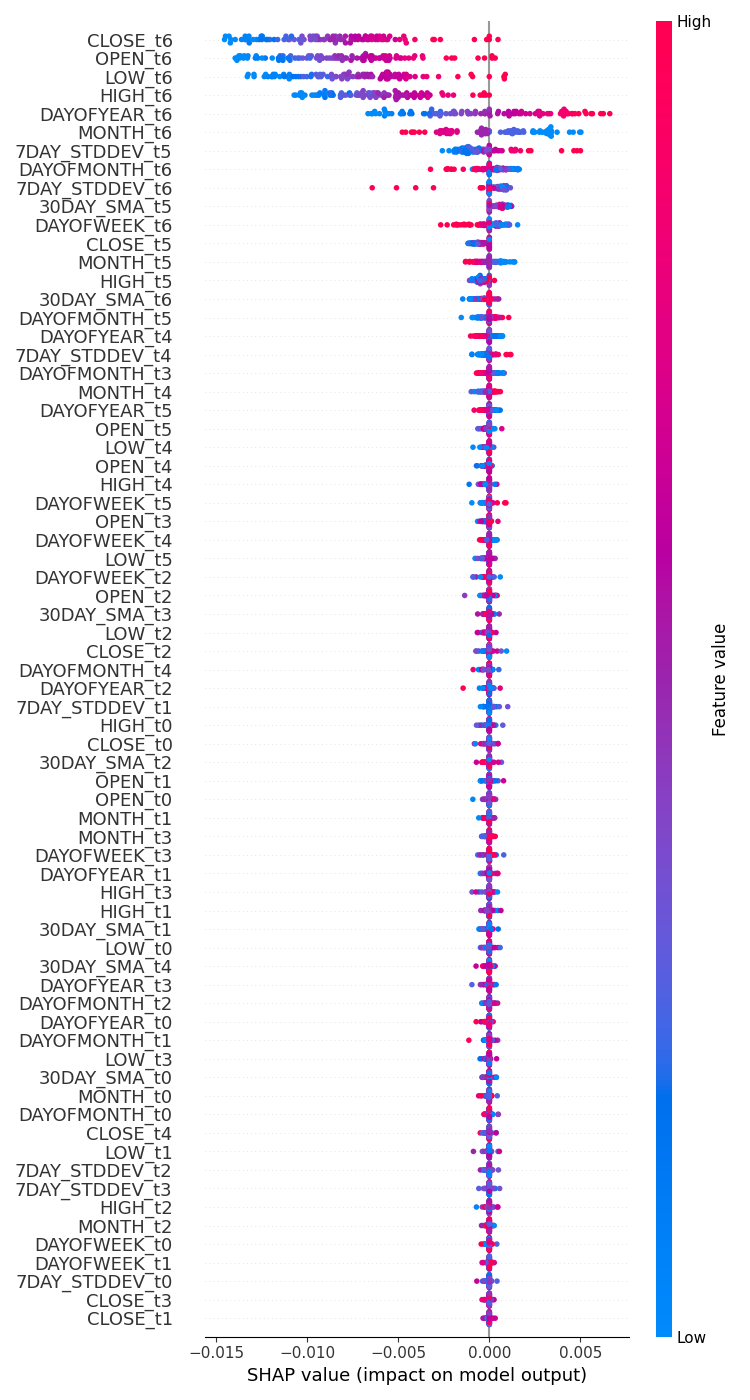
# Update feature names for SHAP
feature_names = [f'{original_feat}_t{t}' for t in range(time_step) for original_feat in X.columns]

# Plot the SHAP values
shap.summary_plot(shap_values, x_test_seq[:100].reshape(100, -1), feature_names=feature_names, max_display=len(feature_names), show=False)

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(7.5, 14) 
plt.tight_layout()

plt.savefig("regressor-rnn feature-importance.png")
plt.show()

Das Ergebnis ist nachstehend aufgeführt.

Die aussagekräftigsten Variablen sind die mit den jüngsten Informationen, während die weniger aussagekräftigen Variablen diejenigen mit den ältesten Informationen sind.

Das ist so, als würde man sagen, dass das letzte Wort, das in einem Satz gesprochen wird, die größte Bedeutung für den gesamten Satz hat.

Dies mag für ein maschinelles Lernmodell zutreffen, auch wenn es für uns Menschen nicht viel Sinn ergibt.

Wie bereits im vorigen Artikel erwähnt, können wir uns nicht allein auf die Darstellung der Bedeutung des Merkmals verlassen, da ich KernelExplainer anstelle des empfohlenen DeepExplainer verwendet habe und viele Fehler bei der Anwendung der Methode auftraten.

Wie im vorigen Artikel erwähnt, ist ein Regressionsmodell, das den nächsten Schluss- oder Eröffnungskurs vorhersagt, nicht so praktisch wie ein Klassifikator, der uns sagt, wohin sich der Markt seiner Meinung nach im nächsten Balken bewegen wird. Lassen Sie uns ein RNN-Klassifikatormodell erstellen, das uns bei dieser Aufgabe hilft.

Das Training des einfachen RNN für ein Klassifizierungsproblem

Wir können ein ähnliches Verfahren wie bei der Codierung eines Regressors anwenden, allerdings mit einigen Änderungen: Zunächst müssen wir die Zielvariable für das Klassifizierungsproblem erstellen.

Python

Y = []
target_open = data["TARGET_OPEN"]
target_close = data["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)
        
Y = np.array(Y) #converting this array to NumPy


classes_in_y = np.unique(Y) # obtaining classes present in the target variable for the sake of setting the number of outputs in the RNN

Dann müssen wir die Zielvariable, eine „Hot Encode Matrix“ gleich nach der Erstellung der Sequenz codieren, wie bei der Erstellung eines Regressionsmodells besprochen.

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train_seq)
y_test_encoded = to_categorical(y_test_seq)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

Ausgänge

One hot encoded

y_train (693, 2)
y_test (293, 2)

Schließlich können wir das RNN-Klassifikatormodell erstellen und trainieren.

cls_model = Sequential()

cls_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
cls_model.add(SimpleRNN(50, activation='relu'))
cls_model.add(Dense(50, activation='relu'))
cls_model.add(Dense(units=len(classes_in_y), activation='sigmoid', name='outputs')) 


adam_optimizer = Adam(learning_rate = 0.001)

cls_model.compile(optimizer=adam_optimizer, loss='binary_crossentropy') # Compile the model
cls_model.summary()


early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = cls_model.fit(x_train_seq, y_train_encoded, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_encoded), callbacks=[early_stopping])

Für den Klassifikator RNN-Modell habe ich Sigmoid für die letzte Schicht in das Netzwerk. Die Anzahl der Neuronen (Einheiten) in der letzten Schicht muss der Anzahl der Klassen in der Zielvariablen (Y) entsprechen, in diesem Fall werden wir zwei Einheiten haben.

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN)        │ (None, 50)             │         3,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 50)             │         2,550 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           102 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

6 Epochen reichten aus, damit das RNN-Klassifikatormodell beim Training konvergieren konnte.

Epoch 1/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 36ms/step - loss: 0.7242 - val_loss: 0.6872
Epoch 2/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.6883 - val_loss: 0.6891
Epoch 3/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6817 - val_loss: 0.6909
Epoch 4/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6780 - val_loss: 0.6940
Epoch 5/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6743 - val_loss: 0.6974
Epoch 6/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6707 - val_loss: 0.6998

Trotz einer geringeren Genauigkeit bei der Regressionsaufgabe im Vergleich zur Genauigkeit des LightGBM-Regressors war das RNN-Klassifizierungsmodell 3 % genauer als der LightGBM-Klassifizierer.

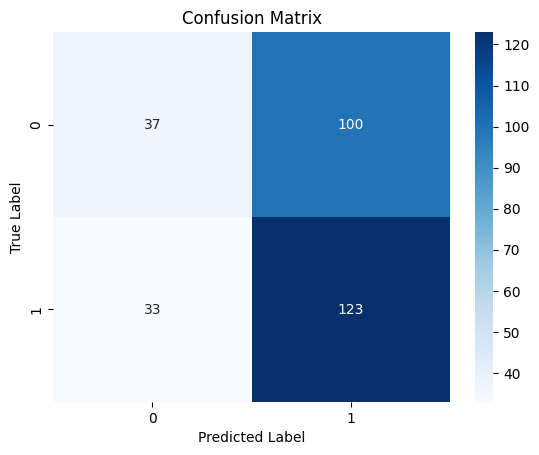
10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.27      0.36       137
           1       0.55      0.79      0.65       156

    accuracy                           0.55       293
   macro avg       0.54      0.53      0.50       293
weighted avg       0.54      0.55      0.51       293

Heatmap der Konfusionsmatrix

Speichern des rekurrenten neuronalen Netzmodells in ONNX

Da wir nun ein Klassifizierungs-RNN-Modell haben, können wir es im ONNX-Format speichern, das von MetaTrader 5 verstanden wird.

Im Gegensatz zu Scikit-Learn-Modellen ist das Speichern der Deep-Learning-Modelle von Keras wie RNNs nicht ganz einfach. ist auch für RNNs keine einfache Lösung.

Wie im Artikel „Überwindung der ONNX-Herausforderungen“ beschrieben, können wir entweder die Daten in MQL5 kurz nach der Erfassung skalieren oder wir können den Skalierer, den wir in Python haben, speichern und ihn in MQL5 laden, indem wir die Vorverarbeitungsbibliothek für MQL5 verwenden.

Speichern des Modells

import tf2onnx

# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, time_step, x_train.shape[1]), tf.float16, name="input"),)
cls_model.output_names=['output']

onnx_model, _ = tf2onnx.convert.from_keras(cls_model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open("rnn.EURUSD.D1.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

Speichern der Parameter des Standardisierungs-Skalierers

# Save the mean and scale parameters to binary files

scaler.mean_.tofile("standard_scaler_mean.bin")
scaler.scale_.tofile("standard_scaler_scale.bin")

Durch die Speicherung von Mittelwert und Standardabweichung, die die Hauptbestandteile des Standardskalierer sind, können wir sicher sein, dass wir den Standardskalierer erfolgreich gespeichert haben.

Rekurrentes Neuronales Netz (RNN) Expert Advisor

In unserem EA müssen wir als Erstes sowohl das RNN-Modell im ONNX-Format als auch die Binärdateien des Standardskalierers als Ressourcendateien zu unserem EA hinzufügen.

MQL5 | RNN Zeitreihenprognose.mq5

#resource "\\Files\\rnn.EURUSD.D1.onnx" as uchar onnx_model[]; //rnn model in onnx format
#resource "\\Files\\standard_scaler_mean.bin" as double standardization_mean[];
#resource "\\Files\\standard_scaler_scale.bin" as double standardization_std[];

Wir können dann die Bibliotheken für das Laden des RNN-Modells im ONNX-Format und den Standardskalierer laden.

MQL5

#include <MALE5\Recurrent Neural Networks(RNNs)\RNN.mqh>
CRNN rnn;

#include <MALE5\preprocessing.mqh>
StandardizationScaler *scaler;

Innerhalb der OnInit-Funktion.

vector classes_in_data_ = {0,1}; //we have to assign the classes manually | it is very important that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Initialize ONNX model
   
   if (!rnn.Init(onnx_model))
     return INIT_FAILED;
   
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(standardization_mean, standardization_std);
   
//--- Initializing the CTrade library for executing trades

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
           
   lotsize = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
//--- Initializing the indicators

   ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
   stddev_handle = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   

   return(INIT_SUCCEEDED);
  }

Bevor wir das Modell für den Live-Handel in der OnTick-Funktion einsetzen können, müssen wir Daten sammeln, ähnlich wie wir die Trainingsdaten gesammelt haben, aber dieses Mal müssen wir die Merkmale vermeiden, die wir beim Training weggelassen haben.

Erinnern Sie sich! Wir haben das Modell nur mit 10 Merkmalen (unabhängigen Variablen) trainiert.

neuer Datensatz: schattierte Zielvariablen

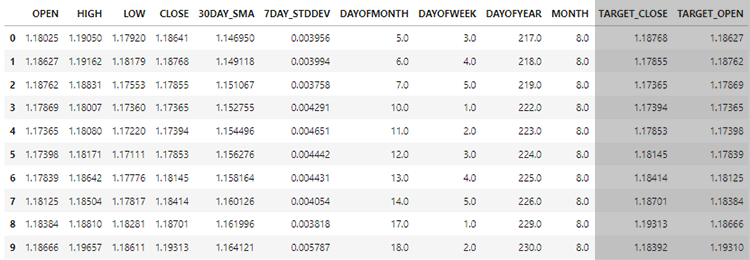
Mit der Funktion GetInputData sollen nur diese 10 unabhängigen Variablen erfasst werden.

matrix GetInputData(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars), 
          ma(bars), 
          stddev(bars), 
          dayofmonth(bars), 
          dayofweek(bars), 
          dayofyear(bars), 
          month(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
   vector time_vector;
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//---

   
   ma.CopyIndicatorBuffer(ma_handle, 0, start_bar, bars); //getting moving avg values 
   stddev.CopyIndicatorBuffer(stddev_handle, 0, start_bar, bars); //getting standard deviation values
   
   string time = "";
   for (int i=0; i<bars; i++) //Extracting time features 
     {
       time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
       TimeToStruct((datetime)StringToTime(time), date_time_struct); //convering the string time to date then assigning them to a structure
       
       dayofmonth[i] = date_time_struct.day;
       dayofweek[i] = date_time_struct.day_of_week;
       dayofyear[i] = date_time_struct.day_of_year;
       month[i] = date_time_struct.mon;
     }
   
   matrix data(bars, 10); //we have 10 inputs from rnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   data.Col(ma, 4);
   data.Col(stddev, 5);
   data.Col(dayofmonth, 6);
   data.Col(dayofweek, 7);
   data.Col(dayofyear, 8);
   data.Col(month, 9);
   
   return data;
 }

Schließlich können wir das RNN-Modell einsetzen, um uns Handelssignale für unsere einfache Strategie zu geben.

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetInputData(rnn_time_step);
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = rnn.predict_bin(input_data_matrix, classes_in_data_); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

Testen des rekurrenten neuronalen Netzwerks EA mit dem Strategie-Tester

Wenn wir eine Handelsstrategie entwickelt haben, können wir mit dem Strategietester Tests durchführen. Ich verwende dieselben Werte für Stop-Loss und Take-Profit, die wir für das LightGBM-Modell verwendet haben, einschließlich der Einstellungen des Testers.

input group "rnn";
input uint rnn_time_step = 7; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;
input int stoploss = 500;
input int takeprofit = 700;

Einstellungen des Strategietesters:

tester einstellungen rnn modell

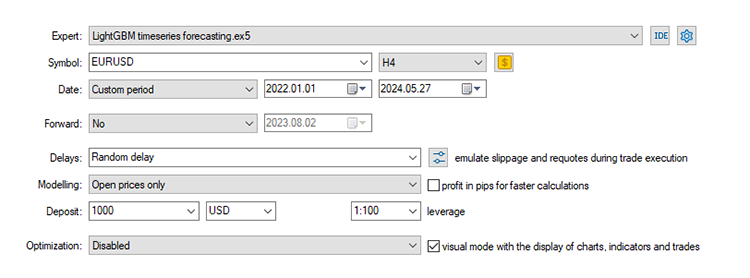
Der EA war in den 561 Handelsgeschäften, die er durchgeführt hat, zu 44,56 % profitabel.

rnn expert advisor bericht

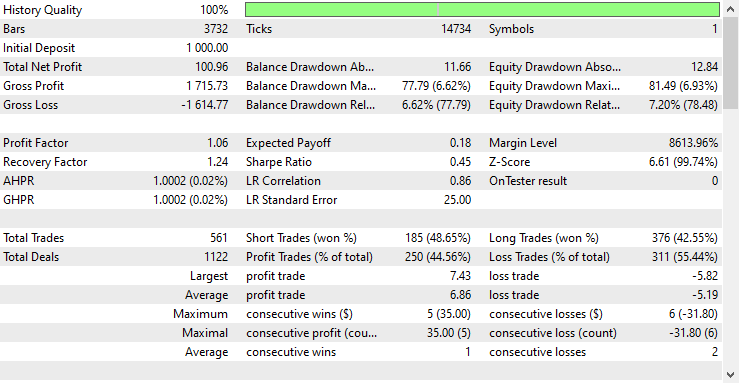
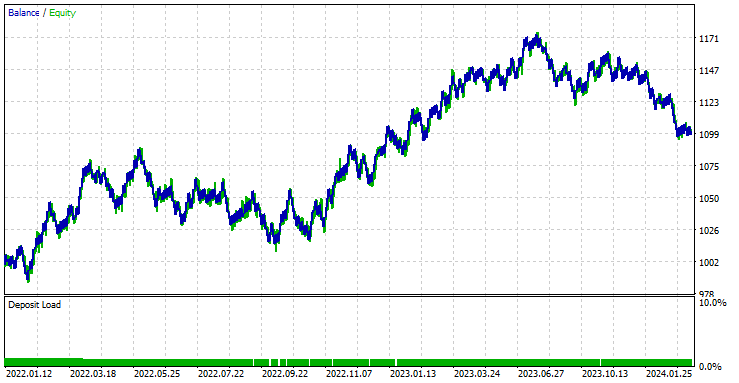
Mit den aktuellen Werten für Stop-Loss und Take-Profit kann man mit Fug und Recht behaupten, dass das LightGBM-Modell ein einfaches RNN-Modell für die Zeitreihenprognose übertroffen hat, da es einen Nettogewinn von 572 $ im Vergleich zu RNN erzielte, das einen Nettogewinn von 100 $ erzielte.

Ich habe eine Optimierung durchgeführt, um die besten Werte für Stop-Loss und Take-Profit zu finden, und einer der besten Werte war ein Stop-Loss von 1000 Punkten und ein Take-Profit von 700 Punkten.

optimierter rnn EA-Bericht

optimierte rnn EA-Aktien/Grafik-Kurve

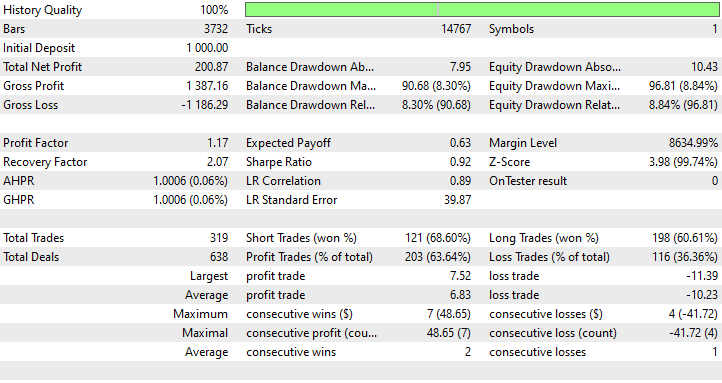
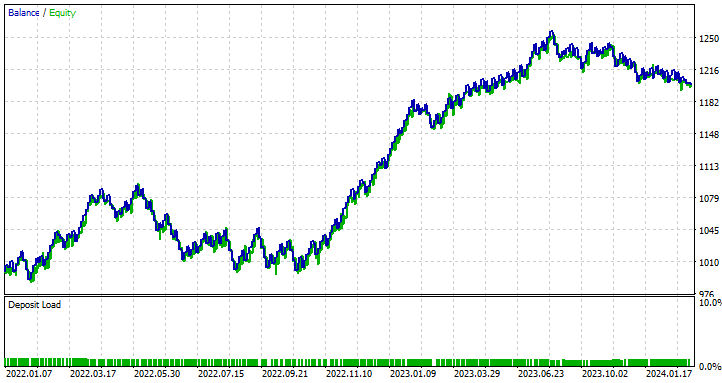
Vorteile der Verwendung eines einfachen RNN für die Zeitreihenprognose

Sie können sequenzielle Daten verarbeiten
Einfache RNNs sind für die Verarbeitung von Sequenzdaten konzipiert und eignen sich gut für Aufgaben, bei denen die Reihenfolge der Datenpunkte eine Rolle spielt, wie z. B. Zeitreihenvorhersage, Sprachmodellierung und Spracherkennung.
Sie teilen Parameter über verschiedene Zeitschritte hinweg
Dies hilft beim effektiven Erlernen zeitlicher Muster. Diese gemeinsame Nutzung von Parametern macht das Modell effizient in Bezug auf die Anzahl der Parameter, insbesondere im Vergleich zu Modellen, die jeden Zeitschritt unabhängig behandeln.
Sie sind in der Lage, zeitliche Abhängigkeiten zu erfassen
Sie können Abhängigkeiten im Zeitverlauf erfassen, was für das Verständnis von Zusammenhängen in sequenziellen Daten unerlässlich ist. Sie können kurzfristige zeitliche Abhängigkeiten effektiv modellieren.
Flexibel in der Sequenzlänge
Einfache RNNs können mit Sequenzen variabler Länge umgehen, was sie flexibel für verschiedene Arten von sequentiellen Dateneingaben macht.
Einfach zu verwenden und zu implementieren
Die Architektur eines einfachen RNN ist relativ einfach zu implementieren. Diese Einfachheit kann für das Verständnis der grundlegenden Konzepte der Sequenzmodellierung von Vorteil sein.

Abschließende Überlegungen

Dieser Artikel vermittelt Ihnen ein tiefes Verständnis eines einfachen rekurrenten neuronalen Netzes und wie es in der Programmiersprache MQL5 eingesetzt werden kann. Im Laufe des Artikels habe ich die Ergebnisse des RNN-Modells oft mit dem LightGBM-Modell verglichen, das wir im vorigen Artikel dieser Reihe erstellt haben, nur um Ihr Verständnis für die Zeitreihenprognose mit Hilfe von Zeitreihen- und nicht zeitreihenbasierten Modellen zu schärfen.

Der Vergleich ist in vielerlei Hinsicht unfair, da sich die beiden Modelle in ihrer Struktur und in der Art und Weise, wie sie Vorhersagen treffen, stark voneinander unterscheiden. Alle Schlussfolgerungen, die ich oder der Leser in diesem Artikel ziehen, sollten außer Acht gelassen werden.

Es ist erwähnenswert, dass das RNN-Modell im Vergleich zum LightGBM-Modell nicht mit ähnlichen Daten gefüttert wurde. In diesem Artikel haben wir die Verzögerung etwas reduziert, die differenzierte Werte zwischen OHLC-Kursen waren (DIFF_LAG1_OPEN, DIFF_LAG1_HIGH, DIFF_LAG1_LOW und DIFF_LAG1_CLOSE).

Wir könnten dafür nicht verzögerte Werte verwenden, deren Verzögerungen von RNN automatisch erkannt werden, aber wir haben uns dafür entschieden, sie nicht einzubeziehen, da sie im Datensatz nicht vorhanden waren.

Mit freundlichen Grüßen.

Verfolgen Sie die Entwicklung von Modellen für maschinelles Lernen und vieles mehr in dieser Artikelserie auf diesem GitHub repo.

Tabelle der Anhänge

Dateiname	Dateityp	Beschreibung und Verwendung
RNN timeseries forecasting.mq5	Expert Advisor	Handelsroboter zum Laden des RNN ONNX-Modells und Testen der endgültigen Handelsstrategie in MetaTrader 5.
rnn.EURUSD.D1.onnx	ONNX	RNN-Modell im ONNX-Format.
standard_scaler_mean.bin standard_scaler_scale.bin	Binäre Dateien	Binärdateien für den Normierungsscaler
preprocessing.mqh	Eine Include-Datei	Eine Bibliothek, die aus dem Standardskalierer besteht
RNN.mqh	Eine Include-Datei	Eine Bibliothek zum Laden und Bereitstellen des ONNX-Modells
rnns-for-forex-forecasting-tutorial.ipynb	Python-Skript/Jupyter-Notizbuch	Besteht aus dem gesamten Python-Code, der in diesem Artikel besprochen wird

Quellen und Referenzen

Illustrierter Leitfaden für rekurrente neuronale Netze: Zum Verständnis: https://www.youtube.com/watch?v=LHXXI4-IEns
Recurrent Neural Networks - Ep. 9 (Deep Learning SIMPLIFIED): https://youtu.be/_aCuOwF1ZjU
Rekurrente Neuronale Netze: https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#

Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15114

Beigefügte Dateien |

ZIP herunterladen

Attachments.zip (34.59 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Verwendung des Algorithmus PatchTST für maschinelles Lernen zur Vorhersage der Kursentwicklung in den nächsten 24 Stunden

In diesem Artikel wenden wir einen relativ komplexen Algorithmus eines neuronalen Netzes aus dem Jahr 2023 namens PatchTST zur Vorhersage der Kursentwicklung der nächsten 24 Stunden an. Wir werden das offizielle Repository verwenden, geringfügige Änderungen vornehmen, ein Modell für EURUSD trainieren und es zur Erstellung von Zukunftsprognosen sowohl in Python als auch in MQL5 anwenden.

Neuinterpretation klassischer Strategien in Python: Das Kreuzen von MAs

In diesem Artikel wird die klassische Kreuzungsstrategie von gleitenden Durchschnitten erneut untersucht, um ihre aktuelle Wirksamkeit zu bewerten. Angesichts der langen Zeit, die seit ihrer Einführung vergangen ist, untersuchen wir die potenziellen Verbesserungen, die KI für diese traditionelle Handelsstrategie bringen kann. Durch den Einsatz von KI-Techniken wollen wir fortschrittliche Vorhersagefähigkeiten nutzen, um Einstiegs- und Ausstiegspunkte für den Handel zu optimieren, sich an unterschiedliche Marktbedingungen anzupassen und die Gesamtperformance im Vergleich zu herkömmlichen Ansätzen zu verbessern.

MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 25): Multi-Timeframe-Tests und -Handel

Strategien, die auf mehreren Zeitrahmen (Multi-Timeframe) basieren, können aufgrund der in den Assembly-Klassen verwendeten MQL5-Code-Architektur standardmäßig nicht in den vom Assistenten zusammengestellten Expert Advisors getestet werden. In einer Fallstudie mit dem quadratischen gleitenden Durchschnitt untersuchen wir, wie sich diese Einschränkung bei Strategien, die mehrere Zeitrahmen nutzen wollen, umgehen lässt.

Algorithmen zur Optimierung mit Populationen: Der Boids-Algorithmus

Der Artikel befasst sich mit dem Boids Algorithmus, der auf einzigartigen Beispielen für das Verhalten von Tierschwärmen basiert. Der Boids-Algorithmus wiederum dient als Grundlage für die Schaffung einer ganzen Klasse von Algorithmen, die unter dem Namen „Schwarmintelligenz“ zusammengefasst werden.