データサイエンスと機械学習（第25回）：回帰型ニューラルネットワーク(RNN)を用いたFX時系列予測

MetaTrader 5 — エキスパートアドバイザー | 28 8月 2024, 11:06

Omega J Msigwa

内容

RNN（回帰型ニューラルネットワーク）とは？

RNN（回帰型ニューラルネットワーク）は、時系列、言語、動画など、一連のデータのパターンを認識するように設計された人工ニューラルネットワークです。入力が互いに独立していることを前提とする従来のニューラルネットワークとは異なり、RNNは一連のデータ（情報）からパターンを検出し、理解することができます。

この記事全体で使用される用語を混同しないでください。単純RNNと言った場合、私はモデルとしての単純RNNを指します。一方、私がRNNと言った場合、これには、単純RNN、Long Short Term Memory (LSTM)、Gated Recurrent Unit (GRU)などの回帰型ニューラルネットワークモデルのファミリを指します。

この記事の内容を完全に理解するためには、Python、MQL5のONNX、Python機械学習の理解が必要です。

RNNを理解する

RNNには逐次記憶と呼ばれるものがあり、これはシーケンスの前の時間ステップの情報を保持し、次の時間ステップの処理に役立てるという概念です。

逐次記憶とは、人間の脳にある記憶と似ているもので、話すための言葉を表現するときなど、連続したパターンを認識しやすくする記憶です。

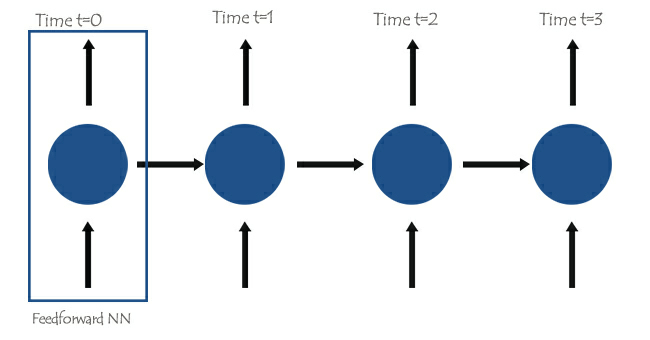
RNNの中核には、フィードフォワードニューラルネットワークが相互接続されており、次のネットワークが前のネットワークからの情報を持つため、単純RNNは以前の情報に基づいて現在の情報を学習して理解できるようになります。

このことをよりよく理解するために、チャットボットにRNNモデルを教える例を見てみましょう。チャットボットにユーザーの単語や文章を理解させたく、「What time is it?」という文章を受け取ったとします。

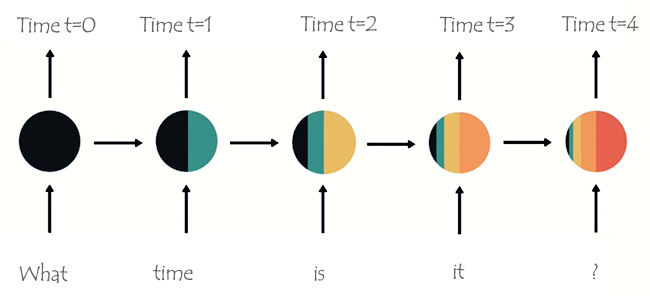
以下の画像のように、単語はそれぞれのタイムステップに分割され、RNNに次々と入力されます。

ネットワークの最後のノードを見ると、以前のネットワークと現在のネットワークからの情報を表す色が奇妙に配置されていることに気づいたかもしれません。色を見ると、時刻t=0とt=1のネットワークからの情報は、RNNのこの最後のノードでは小さすぎます（ほとんど存在しない）。

RNNの処理ステップが増えるにつれて、前のステップの情報を保持することが難しくなります。上の画像に見られるように、ネットワークの最終ノードにはwhatとtimeという単語はほとんど存在しません。

これが短期記憶と呼ばれるものです。バックプロパゲーションはその大きな要因の1つです。

RNNは、backpropagation through time (BPTT)として知られる独自のバックプロパゲーションプロセスを持っています。バックプロパゲーションでは、ネットワークが各時間ステップを後方に伝搬するにつれて、勾配値は指数関数的に縮小します。勾配はニューラルネットワークのパラメータ（重みとバイアス）の調整に使用され、この調整によってニューラルネットワークは学習することができます。勾配が小さいということは、調整も小さいということです。初期の層は勾配が小さいため、学習効率が悪くなります。これは消失勾配問題と呼ばれます。

勾配が消失するという問題があるため、単純RNNでは時間ステップをまたいだ長距離依存関係を学習することができません。上の画像の例では、チャットボットのRNNモデルがユーザーの例文を理解しようとする際に、whatやtimeといった単語が全く考慮されていない可能性が大きくなります。これは、RNNのメモリが短すぎて、実世界のアプリケーションでよく見られる長い時系列データを理解できないためです。

短期記憶を緩和するために、2つの特殊な回帰型ニューラルネットワーク、Long Short Term Memory(LSTM)とGated Recurrent Unit (GRU)が導入されました。

LSTMもGRUも、多くの点でRNNと似た働きをしますが、ゲートと呼ばれるメカニズムを用いて長期的な依存関係を理解することができます。次回はその詳細について説明します。

回帰型ニューラルネットワーク(RNN)を支える数学

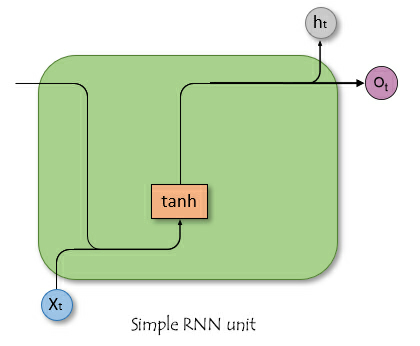
フィードフォワードニューラルネットワークとは異なり、RNNにはサイクルを形成する接続があり、情報を持続させることができます。下の単純化した画像は、RNNのユニット/セルを分解するとどのように見えるかを示しています。

ここで

は時刻tにおける入力です。

は時刻tにおける隠れた状態です。

隠された状態

とすると、これは前の時間ステップからの情報を格納するベクトルです。これはネットワークのメモリーとして機能し、入力データの時間的な依存関係やパターンを時系列で捉えることができます。

隠れ状態がネットワークに果たす役割

隠れ状態は、RNNにおいて以下のような重要な機能を果たします。

これは、以前の入力からの情報を保持し、ネットワークがシーケンス全体から学習することを可能にします。
これにより、ネットワークは過去のデータに基づいて情報に基づいた予測をおこなうことができます。
これにより、隠れ層は異なる時間ステップにまたがってそれ自体に影響を与えることができます。

RNNの背後にある数学を理解することは、それをいつ、どこで、どのように使うかを知ることほど重要ではない。

数式

時間ステップにおける隠れ状態は、時間ステップにおける入力、前の時間ステップにおける隠れ状態、および対応する重み行列とバイアスを用いて計算されます。計算式は以下の通り；

ここで

は隠れ状態への入力の重み行列です。

は隠れ状態に対する隠れ状態の重み行列です。

は隠れ状態のバイアス項です。

σは活性化関数（tanhやReLUなど）です。

出力層

時間ステップにおける出力は、時間ステップにおける隠れ状態から計算されます。

どこ

は時間ステップにおける出力です。

は隠れ状態から出力への重み行列です。

は出力層のバイアスです。

損失計算

損失関数を仮定します（これは回帰の平均2乗誤差や分類のクロスエントロピーなど、どのような損失関数でもよい）。

すべての時間ステップにおける総損失は以下の通りです。

バックプロパゲーションスルータイム(BPTT)

重みとバイアスの両方を更新するには、重みとバイアスそれぞれに対する損失の勾配を計算し、得られた勾配を使って更新をおこなう必要があります。これには以下のステップが含まれます。

手順	重み	バイアス
出力層の勾配を計算する	重みに関して：ここで、は出力に対する損失の勾配です。	バイアスに関して：出力バイアスは出力に直接影響するので、次のようになる；だから
重みとバイアスに関する隠れた状態の勾配を計算します。	隠れた状態に対する損失の勾配は、現在の時間ステップからの直接的な寄与と、その後の時間ステップを通じた間接的な寄与の両方を含みます。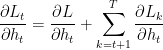前の時間ステップに対する隠れ状態の勾配。隠れ状態の活性化の勾配。隠れ層の重みの勾配。合計勾配は、すべての時間ステップの勾配の合計です。	隠れバイアスに対する損失の勾配は、すべての時間ステップにわたる隠れ状態に対する損失の勾配の和で与えられます。隠れバイアスは活性化関数を通して隠れ状態に影響を与えるので、次のようになります。連鎖法則を使い、こう記します。ここで、は活性化関数の導関数です。よって隠れバイアスの合計勾配は、すべての時間ステップの勾配の合計です。
重みとバイアスを更新します。上記で計算された勾配を使って、勾配降下法またはその亜種（例えばAdam）を使って重みを更新することができます（詳細）。

単純RNNは、長い時系列データをうまく学習する能力はないものの、それほど前の過去の情報を使って将来の値を予測することには長けています。単純RNNを構築することで、取引の意思決定に役立てることができます。

Pythonで回帰型ニューラルネットワーク(RNN)モデルを構築する

PythonでのRNNモデルの構築とコンパイルは簡単で、ライブラリを使用して数行のコードを実行するだけです。

Python

import tensorflow as tf
from tensorflow.keras.models import Sequential #import sequential neural network layer
from sklearn.preprocessing import StandardScaler
from tensorflow.keras.layers import SimpleRNN, Dense, Input
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from keras.optimizers import Adam

reg_model = Sequential()

reg_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
reg_model.add(SimpleRNN(50, activation='sigmoid')) #first hidden layer
reg_model.add(Dense(50, activation='sigmoid')) #second hidden layer
reg_model.add(Dense(units=1, activation='relu'))  # final layer 

adam_optimizer = Adam(learning_rate = 0.001)

reg_model.compile(optimizer=adam_optimizer, loss='mean_squared_error') # Compile the model
reg_model.summary()

上記のコードは回帰回帰型ニューラルネットワークのためのもので、出力層に1つのノードがあり、最終層にRelu活性化関数があるのはそのためです。記事「Feed Forward Neural Networks Demystified」で述べられているように。

前回の「通常のMLモデルを使ったFX時系列予測」稿（必読）で収集したデータを使って、時系列データを理解することができるRNNモデルが得意とすることを支援するために、RNNモデルをどのように使うことができるかを見てみたいです。

最後に、先行記事で構築したLightGBMと対比したRNNの性能を、同じデータで評価します。これで時系列予測全般の理解が深まることを願っています。

順次データの作成

データセットには、28列があり、すべて非時系列モデル用に設計されています。

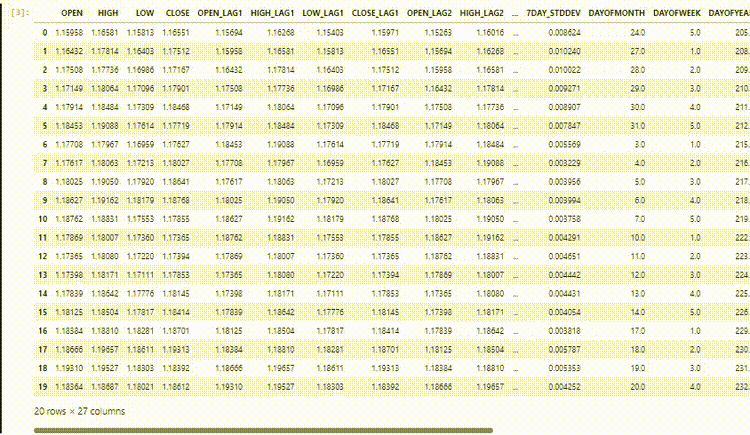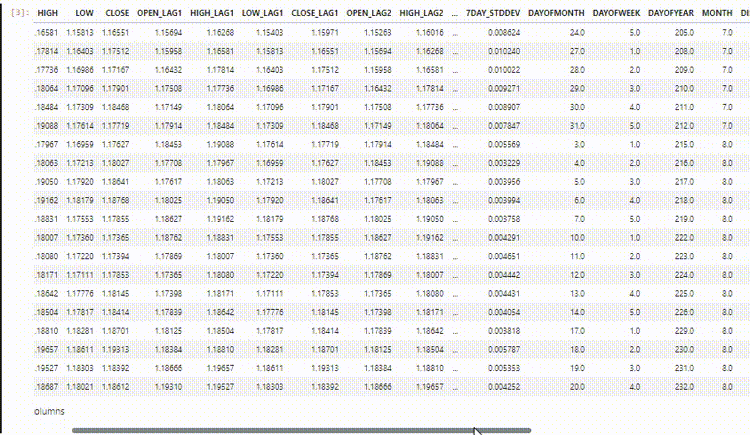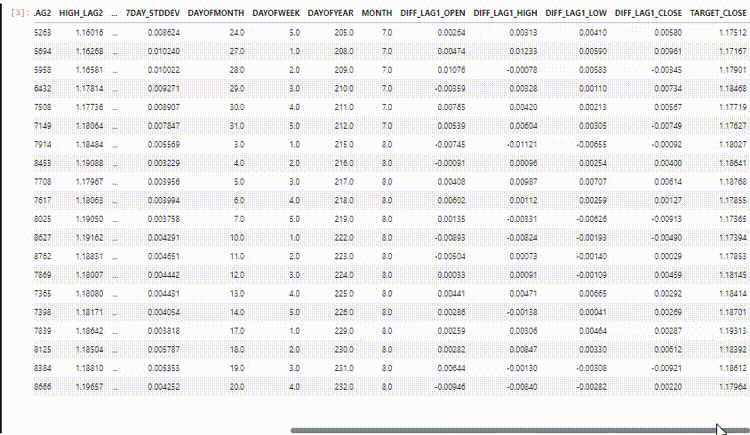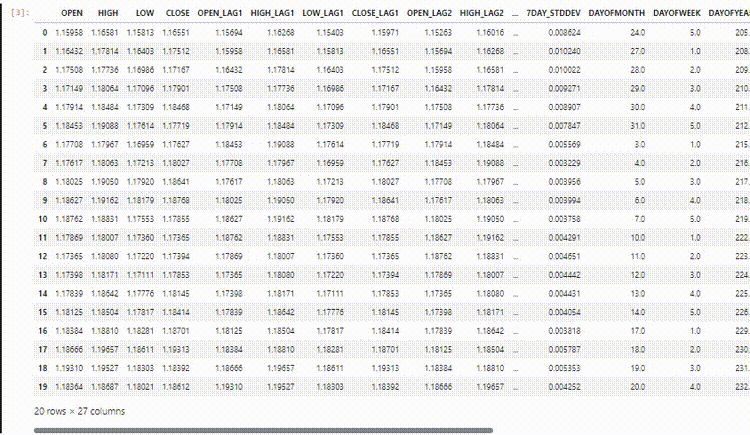
時系列予測データセット

しかし、収集し、設計したこのデータには多くのラグ付き変数があり、非時系列モデルが時間依存パターンを検出するのに便利でした。RNNは、与えられた時間ステップの中でパターンを理解することができます。

今のところ、これらのラグ値は必要ありません。

Python

lagged_columns = [col for col in data.columns if "lag" in col.lower()] #let us obtain all the columns with the name lag

print("lagged columns: ",lagged_columns)

data = data.drop(columns=lagged_columns) #drop them

出力

lagged columns:  ['OPEN_LAG1', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'OPEN_LAG2', 'HIGH_LAG2', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3', 'HIGH_LAG3', 'LOW_LAG3', 'CLOSE_LAG3', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CL

新しいデータは12列になりました。

新しいフィルターされたデータセット

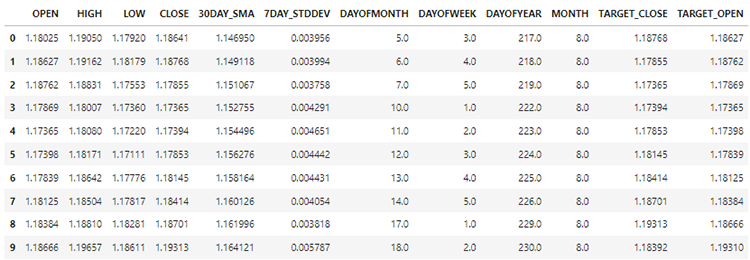
データの70%を訓練用に、残りの30%をテスト用に分けることができます。Scikit-Learnのtran_test_splitを使用している場合、shuffle=Falseに設定してください。これによって、情報の順序を保持したまま、オリジナルを分割することができます。

覚えておいてください。これは時系列予測です。

# Split the data

X = data.drop(columns=["TARGET_CLOSE","TARGET_OPEN"]) #dropping the target variables
Y = data["TARGET_CLOSE"]

test_size = 0.3 #70% of the data should be used for training purpose while the rest 30% should be used for testing

x_train, x_test, y_train, y_test = train_test_split(X, Y, shuffle=False, test_size = test_size) # this is timeseries data so we don't shuffle

print(f"x_train {x_train.shape}\nx_test {x_test.shape}\ny_train{y_train.shape}\ny_test{y_test.shape}")

2つの目標変数も削除した結果、データは10特徴量となりました。この10個の特徴量をRNNが消化できる逐次データに変換する必要があります。

def create_sequences(X, Y, time_step):
    if len(X) != len(Y):
        raise ValueError("X and y must have the same length")
    
    X = np.array(X)
    Y = np.array(Y)
    
    Xs, Ys = [], []
    
    for i in range(X.shape[0] - time_step):
        Xs.append(X[i:(i + time_step), :])  # Include all features with slicing
        Ys.append(Y[i + time_step])
        
    return np.array(Xs), np.array(Ys)

上記の関数は、指定されたx配列とy配列から、指定された時間ステップのシーケンスを生成します。この機能がどのように働くかを理解するには、次の例を読んでほしい；

10個のサンプルと2個の特徴量を持つデータセットがあり、時間ステップ3のシーケンスを作成したいとします。

Xは(10, 2)の行列です。Yは長さ10のベクトルです。
この関数は以下のようにシーケンスを作成します。
i=0の場合：Xsは[0:3, :]のX[0:3, :]を、YsはY[3]を得る。i=1：Xsは𝑋[1:4, :]X[1:4, :]を取得し、YsはY[4]を取得します。

そしてi=6まで続ける。

その結果、Xの形状は(7, 3, 2)となり、Yの長さは7となります。

分割した独立変数を標準化した後、関数create_sequencesを適用して逐次情報を生成することができます。

time_step = 7 # we consider the past 7 days

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)

x_train_seq, y_train_seq = create_sequences(x_train, y_train, time_step)
x_test_seq, y_test_seq = create_sequences(x_test, y_test, time_step)

print(f"Sequential data\n\nx_train {x_train_seq.shape}\nx_test {x_test_seq.shape}\ny_train{y_train_seq.shape}\ny_test{y_test_seq.shape}")

出力

Sequential data

x_train (693, 7, 10)
x_test (293, 7, 10)
y_train(693,)
y_test(293,)

時間ステップの値を7にすることで、データセットに存在するすべての情報を1日の時間枠から収集したことを考慮し、各インスタンスでRNNに過去7日間の情報が差し込まれるようにします。これは、現在のバーから過去7日間のラグを手動で取得するのと似ています。

回帰問題に対する単純RNNの訓練

early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = reg_model.fit(x_train_seq, y_train_seq, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_seq), callbacks=[early_stopping])

出力

Epoch 95/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4504e-05 - val_loss: 4.4433e-05
Epoch 96/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4380e-05 - val_loss: 4.4408e-05
Epoch 97/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4259e-05 - val_loss: 4.4386e-05
Epoch 98/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 6.4140e-05 - val_loss: 4.4365e-05
Epoch 99/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.4024e-05 - val_loss: 4.4346e-05
Epoch 100/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 6.3910e-05 - val_loss: 4.4329e-05

回帰器RNN学習損失曲線

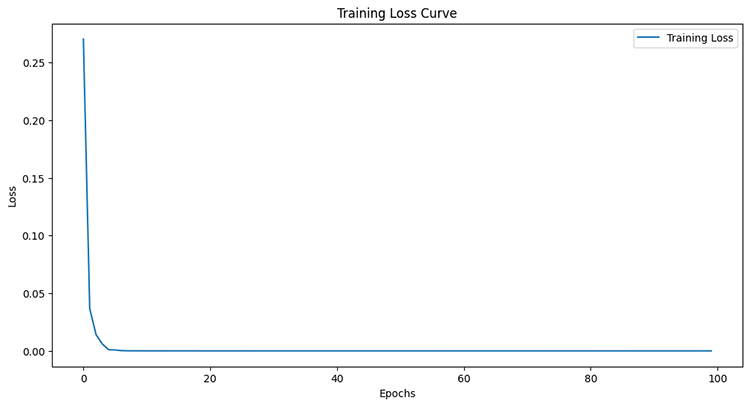
テストサンプルの性能を測定した後

Python

from sklearn.metrics import r2_score

y_pred = reg_model.predict(x_test_seq) # Make predictions on the test set

# Plot the actual vs predicted values
plt.figure(figsize=(12, 6))
plt.plot(y_test_seq, label='Actual Values')
plt.plot(y_pred, label='Predicted Values')
plt.xlabel('Samples')
plt.ylabel('TARGET_CLOSE')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.show()

print("RNN accuracy =",r2_score(y_test_seq, y_pred))

モデルの精度は78%でした。

回帰器RNNの実績vs予測

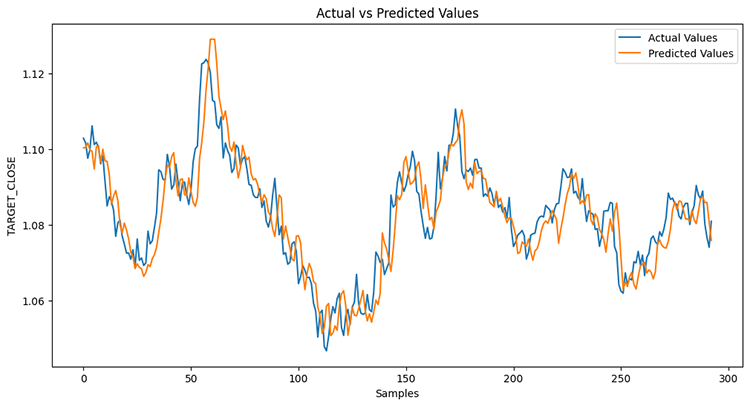
前回の記事で、LightGBMモデルは回帰問題で86.76%の精度を示したことを思い出してください。この時点で、非時系列モデルは時系列モデルを凌駕しています。

機能の重要性

SHAPを使用して、変数がRNNモデルの意思決定プロセスにどのような影響を与えるかをチェックするテストをおこないました。

import shap

# Wrap the model prediction for KernelExplainer
def rnn_predict(data):
    data = data.reshape((data.shape[0], time_step, x_train.shape[1]))
    return reg_model.predict(data).flatten()

# Use SHAP to explain the model
sampled_idx = np.random.choice(len(x_train_seq), size=100, replace=False)
explainer = shap.KernelExplainer(rnn_predict, x_train_seq[sampled_idx].reshape(100, -1))
shap_values = explainer.shap_values(x_test_seq[:100].reshape(100, -1), nsamples=100)

特徴量の重要度をプロットするコードを実行しました。

# Update feature names for SHAP
feature_names = [f'{original_feat}_t{t}' for t in range(time_step) for original_feat in X.columns]

# Plot the SHAP values
shap.summary_plot(shap_values, x_test_seq[:100].reshape(100, -1), feature_names=feature_names, max_display=len(feature_names), show=False)

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(7.5, 14) 
plt.tight_layout()

plt.savefig("regressor-rnn feature-importance.png")
plt.show()

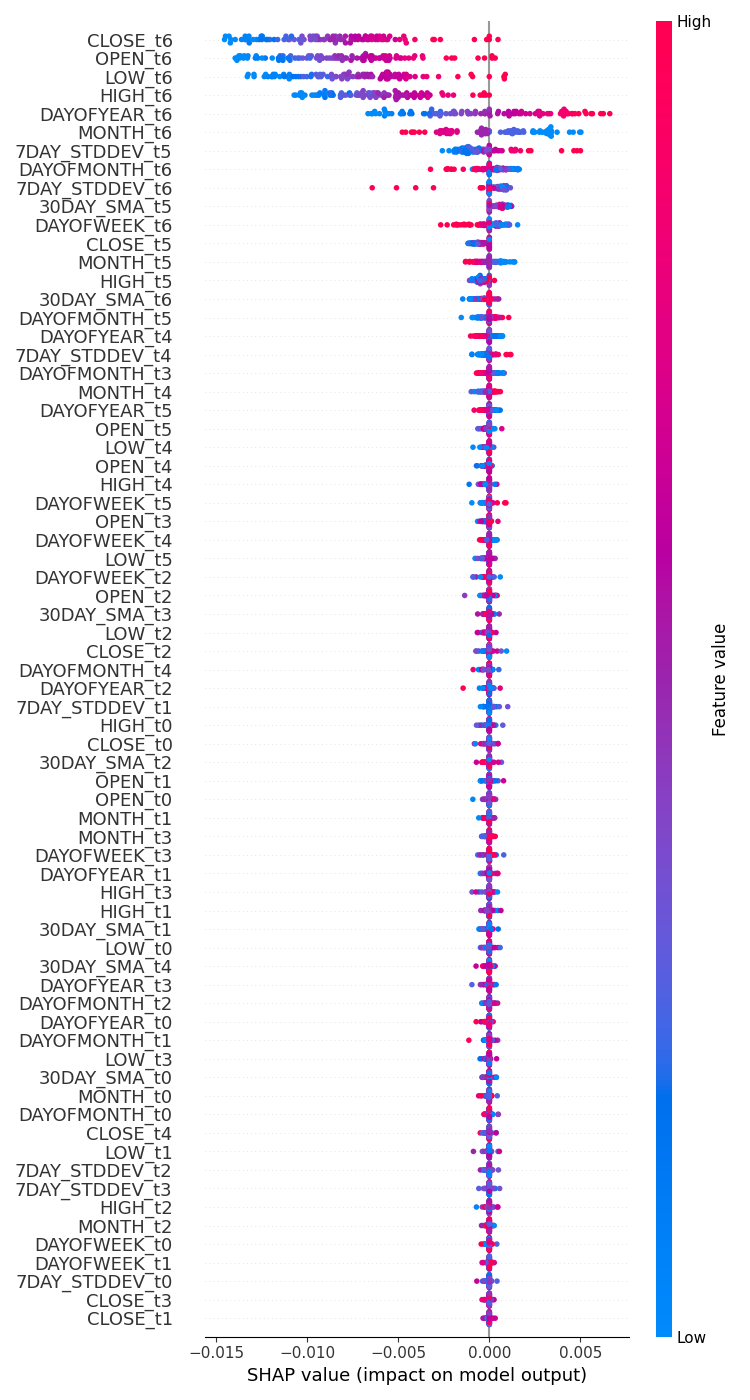
以下がその結果です。

最もインパクトのある変数は最近の情報であり、インパクトの少ない変数は古い情報です。

これはちょうど、文の中で最も新しく話された単語が、その文全体にとって最も大きな意味を持つと言うようなものです。

私たち人間にはあまり意味がないにもかかわらず、機械学習モデルには当てはまるかもしれません。

前の記事で述べたように、推奨されているDeepExplainerの代わりにKernelExplainerを使用したことを考えると、このメソッドを機能させる際に多くのエラーが発生したため、特徴量重要度プロットだけを信頼することはできません。

前回の記事で述べたように、次の終値や始値を推測する回帰モデルを持つことは、次のバーで市場がどこに向かうと考えるかを教えてくれる分類器を持つことほど実用的ではありません。RNN分類器モデルを作ってみましょう。

分類問題に対する単純RNNの訓練

いくつかの変更を加えて、回帰変数をコーディングしたときと同様のプロセスに従うことができます。まず、分類問題の目標変数を作成する必要があります。

Python

Y = []
target_open = data["TARGET_OPEN"]
target_close = data["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)
        
Y = np.array(Y) #converting this array to NumPy


classes_in_y = np.unique(Y) # obtaining classes present in the target variable for the sake of setting the number of outputs in the RNN

そして、回帰モデルの作成時に説明したように、シーケンスが作成された直後に目標変数をワンホットエンコードしなければなりません。

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train_seq)
y_test_encoded = to_categorical(y_test_seq)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

出力

One hot encoded

y_train (693, 2)
y_test (293, 2)

最後に、分類器RNNモデルを構築し、それを訓練します。

cls_model = Sequential()

cls_model.add(Input(shape=(time_step, x_train.shape[1]))) # input layer
cls_model.add(SimpleRNN(50, activation='relu'))
cls_model.add(Dense(50, activation='relu'))
cls_model.add(Dense(units=len(classes_in_y), activation='sigmoid', name='outputs')) 


adam_optimizer = Adam(learning_rate = 0.001)

cls_model.compile(optimizer=adam_optimizer, loss='binary_crossentropy') # Compile the model
cls_model.summary()


early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

history = cls_model.fit(x_train_seq, y_train_encoded, epochs=100, batch_size=64, verbose=1, validation_data=(x_test_seq, y_test_encoded), callbacks=[early_stopping])

分類器RNNモデルでは、ネットワークの最終層にシグモイドを使用しました。最終層のニューロン（ユニット）の数は、目標変数(Y)に存在するクラスの数と一致しなければなりません。この場合、ユニットは2つになります。

Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ simple_rnn_1 (SimpleRNN)        │ (None, 50)             │         3,050 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 50)             │         2,550 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ outputs (Dense)                 │ (None, 2)              │           102 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

RNN分類器モデルが訓練中に収束するには、6エポックで十分でした。

Epoch 1/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 36ms/step - loss: 0.7242 - val_loss: 0.6872
Epoch 2/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step - loss: 0.6883 - val_loss: 0.6891
Epoch 3/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6817 - val_loss: 0.6909
Epoch 4/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6780 - val_loss: 0.6940
Epoch 5/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6743 - val_loss: 0.6974
Epoch 6/100
11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6707 - val_loss: 0.6998

LightGBM回帰器が提供する精度に比べて、回帰タスクの精度は低かったものの、RNN分類器モデルはLightGBM分類器よりも3%精度が高かった。

10/10 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.27      0.36       137
           1       0.55      0.79      0.65       156

    accuracy                           0.55       293
   macro avg       0.54      0.53      0.50       293
weighted avg       0.54      0.55      0.51       293

混乱マトリックスのヒートマップ

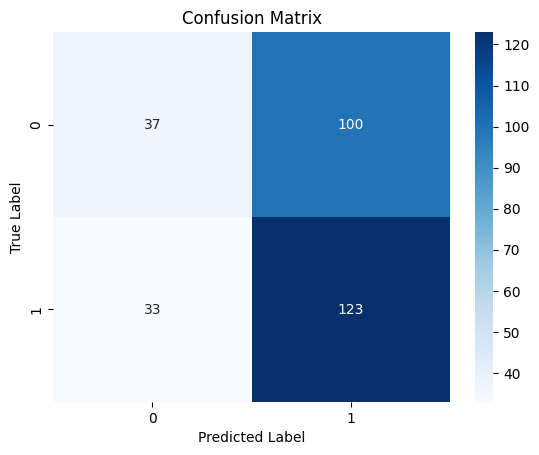
回帰型ニューラルネットワークモデルをONNXに保存する

分類器RNNモデルができたので、MetaTrader 5が理解できるONNXフォーマットに保存します。

Scikit-learnのモデルとは異なり、RNNのような深層学習モデルKerasの保存は簡単ではありません。、RNNにとっても簡単な解決策ではない。

ONNXの課題を克服するという記事で説明したように、データを収集した直後にMQL5でスケーリングするか、Pythonでスケーラーを保存し、MQL5用のライブラリ）を使ってMQL5にロードすることができる。

モデルの保存

import tf2onnx

# Convert the Keras model to ONNX
spec = (tf.TensorSpec((None, time_step, x_train.shape[1]), tf.float16, name="input"),)
cls_model.output_names=['output']

onnx_model, _ = tf2onnx.convert.from_keras(cls_model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open("rnn.EURUSD.D1.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

標準化スケーラーパラメータの保存

# Save the mean and scale parameters to binary files

scaler.mean_.tofile("standard_scaler_mean.bin")
scaler.scale_.tofile("standard_scaler_scale.bin")

スケーラーの主要な構成要素である平均と標準偏差を保存することで、私たちは標準スケーラーを保存することに成功したと確信できます。

回帰型ニューラルネットワーク(RNN) エキスパートアドバイザー(EA)

EAの内部では、まずONNX形式のRNNモデルとStandard ScalerのバイナリファイルをリソースファイルとしてEAに追加します。

MQL5｜RNN時系列予測.mq5

#resource "\\Files\\rnn.EURUSD.D1.onnx" as uchar onnx_model[]; //rnn model in onnx format
#resource "\\Files\\standard_scaler_mean.bin" as double standardization_mean[];
#resource "\\Files\\standard_scaler_scale.bin" as double standardization_std[];

次に、RNNモデルをONNX形式でロードするためのライブラリと、Standardスケーラーをロードするためのライブラリをロードすることができます。

MQL5

#include <MALE5\Recurrent Neural Networks(RNNs)\RNN.mqh>
CRNN rnn;

#include <MALE5\preprocessing.mqh>
StandardizationScaler *scaler;

OnInit関数の内部。

vector classes_in_data_ = {0,1}; //we have to assign the classes manually | it is very important that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Initialize ONNX model
   
   if (!rnn.Init(onnx_model))
     return INIT_FAILED;
   
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(standardization_mean, standardization_std);
   
//--- Initializing the CTrade library for executing trades

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
           
   lotsize = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
//--- Initializing the indicators

   ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
   stddev_handle = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   

   return(INIT_SUCCEEDED);
  }

OnTick関数内でモデルをライブ取引用にデプロイする前に、訓練データを収集した方法と同様にデータを収集する必要があります。

思い出してください。 10個の特徴量（独立変数）のみでモデルを訓練しました。

新しいデータセット陰影のついた目標変数

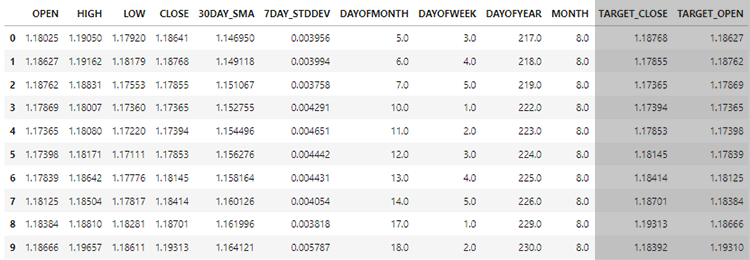
GetInputData関数を、これら10個の独立変数のみを収集するように作ってみましょう。

matrix GetInputData(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars), 
          ma(bars), 
          stddev(bars), 
          dayofmonth(bars), 
          dayofweek(bars), 
          dayofyear(bars), 
          month(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
   vector time_vector;
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//---

   
   ma.CopyIndicatorBuffer(ma_handle, 0, start_bar, bars); //getting moving avg values 
   stddev.CopyIndicatorBuffer(stddev_handle, 0, start_bar, bars); //getting standard deviation values
   
   string time = "";
   for (int i=0; i<bars; i++) //Extracting time features 
     {
       time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
       TimeToStruct((datetime)StringToTime(time), date_time_struct); //convering the string time to date then assigning them to a structure
       
       dayofmonth[i] = date_time_struct.day;
       dayofweek[i] = date_time_struct.day_of_week;
       dayofyear[i] = date_time_struct.day_of_year;
       month[i] = date_time_struct.mon;
     }
   
   matrix data(bars, 10); //we have 10 inputs from rnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   data.Col(ma, 4);
   data.Col(stddev, 5);
   data.Col(dayofmonth, 6);
   data.Col(dayofweek, 7);
   data.Col(dayofyear, 8);
   data.Col(month, 9);
   
   return data;
 }

最後に、RNNモデルを導入することで、シンプルな戦略の売買シグナルを得ることができます。

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetInputData(rnn_time_step);
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = rnn.predict_bin(input_data_matrix, classes_in_data_); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

ストラテジーテスターで回帰型ニューラルネットワークEAをテストする

ストラテジーテスターでテストしてみましょう。テスターの設定も含め、LightGBMモデルで使用したのと同じストップロスとテイクプロフィット値を使用しています。

input group "rnn";
input uint rnn_time_step = 7; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;
input int stoploss = 500;
input int takeprofit = 700;

ストラテジーテスターの設定：

テスター設定RNNモデル

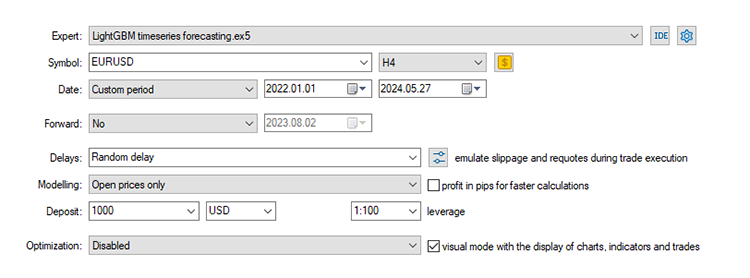
このEAは561回の取引で44.56%の利益を上げました。

RNN EAレポート

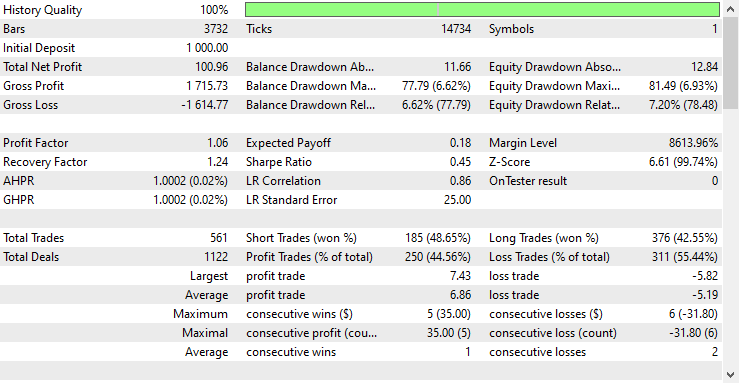
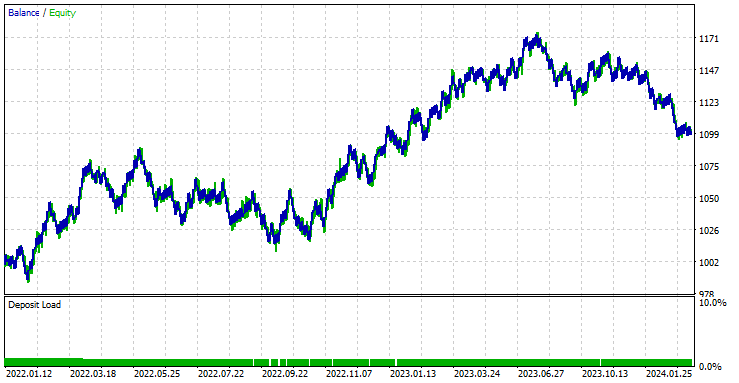
現在のストップロスとテイクプロフィットの値では、LightGBMモデルは、RNNが100ドルの純益を上げたのに対し、572ドルの純益を上げたので、時系列予測のための単純RNNモデルを上回ったと言うことができます。

最良のストップロスとテイクプロフィットの値を見つけるために最適化を実行したところ、最良の値の1つはストップロスが1000ポイント、テイクプロフィットが700ポイントでした。

最適化されたrnn EAレポート

最適化されたrnn EA 株式/グラフ曲線

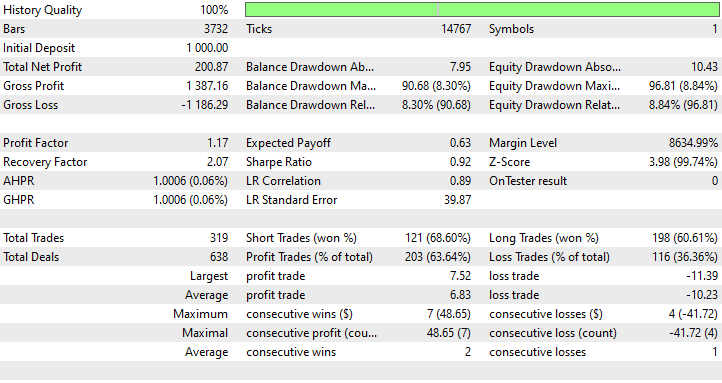
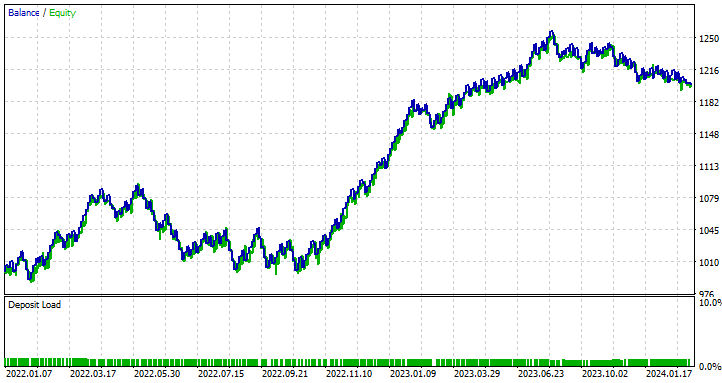
時系列予測に単純RNNを使用する利点

逐次データを扱うことができる
単純RNNは逐次データを扱うように設計されており、時系列予測、言語モデリング、音声認識など、データポイントの順序が重要なタスクに適しています。
異なる時間ステップでパラメータを共有する
これは、時間的パターンを効果的に学習するのに役立ちます。このようにパラメータを共有することで、各時間ステップを独立に扱うモデルと比較した場合、特にパラメータ数の点で効率的なモデルとなります。
時間的依存関係を捉えることができる
逐次データの文脈を理解するために不可欠な、時間経過に伴う依存関係を捉えることができます。短期的な時間依存関係を効果的にモデル化することができます。
シーケンスの長さに柔軟性がある
単純RNNは可変長のシーケンスを扱うことができるため、さまざまな種類の逐次データ入力に柔軟に対応できます。
簡単な操作と導入
単純RNNのアーキテクチャは比較的簡単に実装できます。この単純さは、シーケンスモデリングの基本概念を理解する上で有益です。

最後に

この記事では、シンプルな回帰型ニューラルネットワークと、それをMQL5プログラミング言語でどのように展開できるかについて詳しく説明しました。この記事を通して、しばしばRNNモデルの結果を、本連載の前回の記事で構築したLightGBMモデルと比較しましたが、その目的は時系列と非時系列ベースのモデルを使用した時系列予測の理解を深めるためです。

これら2つのモデルは構造も予測方法も大きく異なるため、多くの点で比較は不公平です。この記事で私または読者が導き出した結論は無視する必要があります。

この記事では、OHLCの価格値（DIFF_LAG1_OPEN、DIFF_LAG1_HIGH、DIFF_LAG1_LOW、DIFF_LAG1_CLOSE）間の差分値であるいくつかのラグを削除しました。

RNNがラグを自動検出するため、ラグを持たない値を持つこともできますが、データセットに存在しないため、まったく含めないことにしました。

ご精読ありがとうございました。

機械学習モデルの開発を追跡し、本連載で説明されている多くのことは、このGitHubレポに掲載されています。

添付ファイルの表

ファイル名	ファイルタイプ	説明と使用法
RNN timeseries forecasting.mq5	EA	RNN ONNXモデルを読み込み、MetaTrader 5で最終的な取引戦略をテストするための自動売買ロボット
rnn.EURUSD.D1.onnx	ONNX	ONNX形式のRNNモデル
standard_scaler_mean.bin standard_scaler_scale.bin	バイナリファイル	標準化スケーラー用バイナリファイル
preprocessing.mqh	インクルードファイル	標準化スケーラーで構成されるライブラリ
RNN.mqh	インクルードファイル	ONNXモデルの読み込みとデプロイのためのライブラリ
rnns-for-forex-forecasting-tutorial.ipynb	Pythonスクリプト/Jupyterノートブック	この記事で取り上げたすべてのpythonコードで構成される

情報源と参考文献

Illustrated Guide to Recurrent Neural Networks:Understanding the Intuition(https://www.youtube.com/watch?v=LHXXI4-IEns)
Recurrent Neural Networks - Ep.9 (Deep Learning SIMPLIFIED) (https://youtu.be/_aCuOwF1ZjU)
Recurrent Neural networks(https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#)

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15114

添付されたファイル |

ZIPをダウンロード

Attachments.zip (34.59 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

EAのサンプル

一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。

PatchTST機械学習アルゴリズムによる24時間の値動きの予測

この記事では、PatchTSTと呼ばれる2023年にリリースされた比較的複雑なニューラルネットワークアルゴリズムを適用し、今後24時間の値動きを予測します。公式リポジトリを使用し、若干の修正を加え、EURUSDのモデルを訓練し、PythonとMQL5の両方で将来の予測をおこなうために適用します。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

MQL5でインタラクティブなグラフィカルユーザーインターフェイスを作成する（第1回）：パネルの製作

この記事では、MetaQuotes Language 5 (MQL5)を使用して、グラフィカルユーザーインターフェイス(GUI)パネルを作成し、実装するための基本的な手順について説明します。カスタムユーティリティパネルは、一般的なタスクを簡素化し、重要な取引情報を可視化することで、取引におけるユーザーのインタラクションを向上させます。カスタムパネルを作成することで、トレーダーはワークフローを合理化し、取引操作の時間を節約することができます。