MetaTrader 5 / Handelssysteme
English Русский Español 日本語 Português
preview
Neuronale Netze leicht gemacht (Teil 60): Online Decision Transformer (ODT)

Neuronale Netze leicht gemacht (Teil 60): Online Decision Transformer (ODT)

MetaTrader 5 — Handelssysteme | 5 März 2024, 16:29
148 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Einführung

Die letzten beiden Artikel waren der Decision-Transformer-Methode gewidmet, die Handlungssequenzen im Rahmen eines autoregressiven Modells der gewünschten Belohnungen modelliert. Wie Sie sich vielleicht erinnern, haben die Ergebnisse der praktischen Tests in den zwei Artikeln gezeigt, dass zu Beginn des Testzeitraums die Rentabilität der Ergebnisse des trainierten Modells ziemlich gut war. Im weiteren Verlauf nimmt die Leistung des Modells ab, und es werden eine Reihe unrentabler Transaktionen beobachtet, die zu Verlusten führen. Die Höhe der erhaltenen Verluste kann die zuvor erhaltenen Gewinne übersteigen.

Das regelmäßige, zusätzliche Training des Modells kann hier wahrscheinlich helfen. Dieser Ansatz erschwert jedoch die Bedienung des Modells erheblich. Es ist also durchaus sinnvoll, die Möglichkeit des Online-Modelltrainings in Betracht zu ziehen. Hier sind wir mit einer Reihe von Problemen konfrontiert, die wir lösen müssen.

Eine der Möglichkeiten zur Implementierung der Online-Training von Decision Transformer wird in dem Artikel „Online Decision Transformer“ (Februar 2022) vorgestellt. Es ist erwähnenswert, dass die vorgeschlagene Methode das primäre Offline-Training der klassischen DT verwendet. Für die anschließende Feinabstimmung des Modells wird ein Online-Training durchgeführt. Die in dem Artikel des Autors vorgestellten experimentellen Ergebnisse zeigen, dass ODT in der Lage ist, mit den Besten in Bezug auf die absolute Leistung auf der Testprobe D4RL zu konkurrieren. Außerdem zeigt sich bei der Feinabstimmung eine viel deutlichere Verbesserung.

Schauen wir uns die vorgeschlagene Methode im Zusammenhang mit der Lösung unserer Probleme an.


1. ODT-Algorithmus

Bevor ich den Algorithmus Online Decision Transformer (ODT, Online-Entscheidungstransformator) bespreche, möchte ich kurz an den klassischen Entscheidungstransformator (Decision Transformer, DT) erinnern. DT verarbeitet die τ-Trajektorie als eine Folge von mehreren Eingabe-Token: Return-to-Go (RTG, Zurück auf Los), Zustände und Aktionen. Insbesondere ist der anfängliche RTG-Wert gleich der Rendite für die gesamte Trajektorie. Im Zeitschritt t verwendet DT die Token der K letzten Zeitschritte, um die Aktion At zu erzeugen. In diesem Fall ist K ein Hyperparameter, der die Kontextlänge für den Transformator angibt. Während der Operation kann die Kontextlänge kürzer sein als beim Training.

DT lernt die deterministische Politik π(At|St, RTGt), wobei St eine K-Sequenz der letzten Zustände von t-K+1 bis t ist. In ähnlicher Weise verkörpert RTGt den letzten Return-to-Go K. Es handelt sich um ein Autoregressionsmodell der Ordnung K. Die Agentenpolitik wird so trainiert, dass sie Aktionen mit Hilfe einer standardmäßigen MSE-Verlustfunktion (mean square error) vorhersagt.

Während des Betriebs geben wir die gewünschte Leistung von RTGinit und den Ausgangszustand S0 an. Dann erzeugt DT die Aktion A0. Nachdem wir die Aktion At erzeugt haben, führen wir sie aus und beobachten den nächsten Zustand St+1, der die Belohnung rt erhält. Daraus ergibt sich RTGt+1.

Wie zuvor erzeugt DT die Aktion A1 auf der Grundlage der Trajektorie mit A0, S0, S1 und RTG0, RTG1. Dieser Vorgang wird wiederholt, bis die Episode abgeschlossen ist.

Richtlinien, die nur auf Offline-Datensätzen trainiert werden, sind aufgrund der begrenzten Trainingsdaten in der Regel suboptimal. Offline-Trajektorien können einen geringen Ertrag haben und nur einen begrenzten Teil des Zustands- und Aktionsraums abdecken. Eine natürliche Strategie zur Verbesserung der Leistung besteht darin, RL-Agenten in der Online-Interaktion mit der Umwelt weiter zu schulen. Die Standardmethode des Decision Transformer ist jedoch für die Online-Schulung nicht ausreichend.

Der Online-Entscheidungstransformator-Algorithmus führt wichtige Änderungen am Entscheidungstransformator ein, um ein effektives Online-Training zu gewährleisten. Der erste Schritt ist ein verallgemeinertes, probabilistisches Trainingsziel. In diesem Zusammenhang besteht das Ziel darin, eine stochastische Strategie zu trainieren, die die Wahrscheinlichkeit der Wiederholung einer Trajektorie maximiert.

Die wichtigste Eigenschaft eines Online-RL-Algorithmus ist seine Fähigkeit, ein Gleichgewicht zwischen Erkundung und Ausbeutung herzustellen. Selbst bei stochastischen Strategien berücksichtigt die traditionelle DT-Formulierung die Exploration nicht. Um dieses Problem zu lösen, definieren die Autoren der ODT-Methode die Studie über die Entropie der Politik, die von der Verteilung der Daten in der Trajektorie abhängt. Diese Verteilung ist während des Offline-Pre-Trainings statisch, während der Online-Einrichtung jedoch dynamisch, da sie von neuen Daten abhängt, die während der Interaktion mit der Umgebung gewonnen werden.

Ähnlich wie bei vielen existierenden RL-Algorithmen mit maximaler Entropie, wie z.B. Soft Actor Critic, definieren die Autoren der ODT-Methode explizit eine untere Grenze für die Entropie der Politik, um die Exploration zu fördern.

Der Unterschied zwischen der ODT-Verlustfunktion und SAC und anderen klassischen RL-Methoden besteht darin, dass bei ODT die Verlustfunktion eine negative log Likelihood ist und nicht eine diskontierte Rendite. Im Grunde genommen konzentrieren wir uns nur auf das Training mit einem Muster von Handlungssequenzen, anstatt explizit den Ertrag zu maximieren. Und die Zielfunktion passt sich sowohl beim Offline- als auch beim Online-Training automatisch an die entsprechende Politik des Akteurs an. Während des Offline-Trainings steuert die Kreuzentropie den Grad der Divergenz der Verteilung, während sie beim Online-Training die Explorationsstrategie bestimmt.

Ein weiterer wichtiger Unterschied zu den klassischen RL-Methoden mit maximaler Entropie besteht darin, dass bei ODT die Entropie der Politik auf der Ebene von Sequenzen und nicht von Übergängen definiert ist. Während SAC die β-Untergrenze für die Politikentropie in allen Zeitschritten vorschreibt, begrenzt ODT die Entropie auf den Durchschnitt von K aufeinander folgenden Zeitschritten. Die Bedingung verlangt also nur, dass die über eine Folge von K Zeitschritten gemittelte Entropie höher als der angegebene β-Wert war. Daher erfüllt jede Strategie, die die Übergangsbeschränkung erfüllt, auch die Sequenzbeschränkung. Daher ist der durchführbare Politikraum größer, wenn K > 1 ist. Wenn K = 1 ist, wird die Bedingung auf Sequenzebene auf eine Bedingung auf Übergangsebene reduziert, ähnlich wie bei SAC.

Während des Modelltrainings wird ein Replay-Puffer verwendet, um frühere Erfahrungen mit regelmäßigen Aktualisierungen aufzuzeichnen. Bei den meisten bestehenden RL-Algorithmen besteht der Erfahrungswiedergabepuffer aus Übergängen. Nach jeder Phase der Online-Interaktion innerhalb einer Epoche werden die Strategie und die Q-Funktion des Agenten mittels Gradientenabstieg aktualisiert. Die Richtlinie wird dann ausgeführt, um neue Übergänge zu sammeln und sie dem Replay-Puffer der Erfahrungen hinzuzufügen. Im Falle von ODT besteht der Playback-Puffer für die Wiedergabe von Erfahrungen eher aus Trajektorien als aus Übergängen. Nach dem vorläufigen Offline-Training initialisieren wir den Playback-Puffer mit den Erfahrungen unter Verwendung von Trajektorien mit maximalen Ergebnissen aus dem Offline-Datensatz. Jedes Mal, wenn wir mit der Umgebung interagieren, führen wir die Episode mit der aktuellen Richtlinie vollständig aus. Dann aktualisieren wir den Playback-Puffer mit den Erfahrungen anhand der gesammelten Trajektorien in FIFO-Reihenfolge. Als Nächstes aktualisieren wir die Agentenrichtlinie und führen eine neue Episode aus. Die Bewertung von Maßnahmen anhand durchschnittlicher Aktionen führt in der Regel zu höheren Belohnungen, aber für die Online-Forschung ist es sinnvoll, zufällige Aktionen zu verwenden, da dadurch vielfältigere Trajektorien und Verhaltensmuster entstehen.

Darüber hinaus benötigt der ODT-Algorithmus einen Hyperparameter in Form eines anfänglichen RTG, um zusätzliche Online-Daten zu sammeln. Verschiedene Arbeiten zeigen, dass die tatsächlich geschätzte Rendite der Offline-DT empirisch stark mit dem ursprünglichen RTG korreliert und oft RTG-Werte über die im Offline-Datensatz beobachteten maximalen Renditen hinaus extrapoliert werden können. Die ODT-Autoren fanden heraus, dass es am besten ist, diesen Hyperparameter mit einer kleinen festen Skalierung aus den vorhandenen Expertenergebnissen festzulegen. Die Autoren der Methode verwenden in ihrer Arbeit eine zweifache Skalierung. In der Originalarbeit werden experimentelle Ergebnisse mit viel größeren Werten präsentiert, sowie solche, die sich während des Trainings ändern (zum Beispiel Quantile der besten geschätzten Rendite in Offline- und Online-Datensätzen). In der Praxis waren sie jedoch nicht so effektiv wie fest installierte RTG.

Wie DT verwendet der ODT-Algorithmus ein zweistufiges Abtastverfahren, um eine gleichmäßige Abtastung von Subtrajektorien der Länge K im Playback-Puffer zu gewährleisten. Zunächst wird eine Trajektorie mit einer Wahrscheinlichkeit proportional zu ihrer Länge ausgewählt. Wählen Sie dann die Subtrajektorie der Länge K mit gleicher Wahrscheinlichkeit.

Wir werden uns im nächsten Abschnitt des Artikels mit der praktischen Umsetzung der Methode vertraut machen.


2. Implementierung mit MQL5

Nachdem wir uns mit den theoretischen Aspekten der Methode vertraut gemacht haben, kommen wir nun zu ihrer praktischen Umsetzung. In diesem Abschnitt werden unsere eigenen Vorstellungen von der Umsetzung der vorgeschlagenen Ansätze vorgestellt und durch Entwicklungen aus früheren Artikeln ergänzt. Der ODT-Algorithmus umfasst insbesondere ein zweistufiges Modelltraining:

  1. Vorläufige Offline-Training.
  2. Feinabstimmung des Modells während der Online-Interaktion mit der Umwelt.

Für die Zwecke dieses Artikels verwenden wir das bereits trainierte Modell aus dem vorherigen Artikel. Daher überspringen wir die erste Stufe des Offline-Trainings, die bereits früher durchgeführt wurde, und gehen sofort zum zweiten Teil des Modelltrainings über.

An dieser Stelle sollte auch erwähnt werden, dass wir bei der Betrachtung der DoC-Methode im vorherigen Artikel zwei Modelle erstellt und offline trainiert haben:

  • RTG-Erzeugung;
  • Die Politik des Actors.

Die Verwendung der Modellgenerierung von RTG ist eine Abweichung vom ursprünglichen ODT-Algorithmus, der die Verwendung einer Expertenbewertungsskalierung für das anfängliche RTG mit anschließender Anpassung des Ziels an die tatsächlich erzielten Ergebnisse vorschlägt.

Außerdem können wir durch die Verwendung bereits trainierter Modelle die Architektur der Modelle nicht ändern. Aber sehen wir uns an, wie die Architektur der verwendeten Modelle mit dem ODT-Algorithmus übereinstimmt.

Die Autoren der Methode schlagen vor, die stochastische Akteurspolitik zu verwenden. Dies ist das Modell, das wir in früheren Artikeln verwendet haben.

ODT schlägt vor, anstelle einzelner Trajektorien einen Replay-Puffer der Erfahrungen zu verwenden. Das ist genau der Puffer, mit dem wir arbeiten.

Beim Training der Modelle haben wir die Entropiekomponente der Verlustfunktion nicht verwendet, um die Erkundung der Umgebung zu fördern. In diesem Stadium werden wir sie nicht hinzufügen und die möglichen Risiken in Kauf nehmen. Wir gehen davon aus, dass die stochastische Akteurspolitik und das RTG-Erzeugungsmodell eine ausreichende Erkundung im Prozess der Online-Interaktion mit der Umwelt ermöglichen.

Ein weiterer Punkt, den ich bei meiner Implementierung nicht berücksichtigt habe, betrifft den Playback-Puffer mit den Erfahrungen. Nach dem Offline-Training schlagen die Autoren der Methode vor, eine Reihe der profitabelsten Trajektorien auszuwählen, die in den ersten Phasen des Online-Trainings verwendet werden sollen. Wir haben zunächst die Anzahl der Trajektorien im Playback-Puffer mit den Erfahrungen begrenzt. Bei der Umstellung auf das Online-Training werden wir den gesamten vorhandenen Erfahrungswiedergabepuffer nutzen, dem wir im Laufe der Interaktion mit der Umgebung neue Bahnen hinzufügen werden. Gleichzeitig werden die ältesten Trajektorien nicht sofort gelöscht, wenn neue hinzugefügt werden. Wir begrenzen die Puffergröße mit zuvor erstellten Mitteln, wenn wir die Daten nach Abschluss des Durchlaufs in einer Datei speichern.

Unter Berücksichtigung möglicher Risiken können wir also problemlos die im vorigen Artikel trainierten Modelle verwenden. Dann werden wir versuchen, ihre Effizienz zu erhöhen, indem wir den Prozess des Online-Trainings von Modellen mit ODT-Ansätzen feinabstimmen.

Hier müssen wir einige konstruktive Fragen klären. Der Handelsprozess ist von Natur aus bedingt endlos. Ich sage „bedingt“, weil sie aus einer Reihe von Gründen immer noch begrenzt ist. Die Wahrscheinlichkeit, dass ein solches Ereignis in absehbarer Zeit eintritt, ist jedoch so gering, dass wir sie als unendlich hoch ansehen. Folglich führen wir den Prozess des zusätzlichen Trainings nicht nach dem Ende der Episode durch, wie von den Autoren der Methode vorgeschlagen, sondern in einer bestimmten Häufigkeit.

An dieser Stelle möchte ich Sie daran erinnern, dass in unserer DT-Implementierung nur die Daten des letzten Balkens an den Modelleingang geliefert werden. Der gesamte Kontext der historischen Daten wird im Ergebnispuffer der Einbettungsschicht gespeichert. Mit diesem Ansatz konnten wir den Ressourcenverbrauch für die redundante Wiederaufbereitung von Daten reduzieren. Dies wird jedoch zu einem der „Stolpersteine“ auf dem Weg des Online-Trainings. Die Daten im Einbettungspuffer werden nämlich in streng historischer Reihenfolge gespeichert. Die Verwendung des Modells im Rahmen des periodischen Zusatztrainings führt dazu, dass der Puffer mit historischen Daten aus anderen Trajektorien oder der gleichen Trajektorie, aber aus einem anderen Segment der Geschichte, aufgefüllt wird. Dies führt zu einer Verzerrung der Daten, wenn die Interaktion mit der Umwelt nach dem zusätzlichen Training der Modelle fortgesetzt wird.

Es gibt tatsächlich mehrere Möglichkeiten, dieses Problem zu lösen. Die Komplexität der Implementierung und der Ressourcenverbrauch während des Betriebs sind bei allen unterschiedlich. Auf den ersten Blick ist es am einfachsten, eine Kopie des Puffers zu erstellen und vor der Fortsetzung der Interaktion mit der Umwelt den Puffer wieder in den Zustand vor Beginn des Trainings zu versetzen. Bei näherer Betrachtung des Prozesses wird jedoch deutlich, dass auf der Seite des Hauptmodells nur mit der obersten Klasse des Modells gearbeitet wird, ohne Zugriff auf einzelne Puffer der neuronalen Schichten. In diesem Zusammenhang führt der einfache Vorgang des Kopierens der Daten eines Puffers aus dem Modell und zurück in das Modell zu einer Reihe von Designänderungen. Dies erschwert die Umsetzung dieser Methode erheblich.

Nach Abschluss des zusätzlichen Trainings können wir den gesamten Satz historischer Daten wiederholt auf das Modell übertragen, ohne konstruktive Änderungen am Modell vorzunehmen. Dies führt jedoch zu einer erheblichen Wiederholung von Vorwärtsmodell-Pass-Operationen. Der Umfang solcher Operationen wächst mit der Größe des Kontexts. Dies macht den Ansatz ineffizient. Der Zeit- und Rechenaufwand für die Wiederaufbereitung der Daten kann die Einsparungen übersteigen, die durch die Speicherung der Historie der Einbettungen im Puffer der neuronalen Schicht erzielt werden.

Eine andere Lösung für dieses Problem ist die Verwendung von duplizierten Modellen. Eine wird für die Interaktion mit der Umwelt benötigt. Die zweite wird im Zusatztraining verwendet. Dieser Ansatz ist zwar teurer in Bezug auf die Speicherressourcen, löst aber das Problem der Daten im Puffer der Einbettungsschicht vollständig. Es stellt sich jedoch die Frage des Datenaustauschs zwischen den Modellen. Schließlich sollte das Modell der Interaktion mit der Umwelt nach dem zusätzlichen Training die aktualisierte Agentenpolitik verwenden. Das Gleiche gilt für das RTG-Generationenmodell. Hier sei an die Soft Actor-Critic-Methode erinnert, die eine sanfte Aktualisierung der Zielmodelle vorsieht. So seltsam es klingen mag, dies ist der Mechanismus, der es uns ermöglicht, aktualisierte Gewichtungsverhältnisse zwischen Modellen zu übertragen, ohne die übrigen Puffer zu verändern, einschließlich der Puffer für die Ergebnisse der Einbettungsschicht.

Um diesen Ansatz zu verwenden, müssen wir der Einbettungsschicht eine Methode zum Austausch von Gewichten hinzufügen, die bisher in der SAC-Implementierung nicht verwendet wurde.

An dieser Stelle sei gesagt, dass wir bei der Hinzufügung einer Methode nur die Klasse CNeuronEmbeddingOCL direkt ergänzen, da alle für ihre Funktionsweise erforderlichen APIs bereits von uns festgelegt und in Form einer virtuellen Methode der Basisklasse der neuronalen Schicht CNeuronBaseOCL implementiert wurden. Es sollte auch beachtet werden, dass unser Modell ohne die angegebene Änderung keinen Fehler produziert. Schließlich wird standardmäßig die Methode der übergeordneten Klasse verwendet. Aber eine solche Arbeit wird in diesem Fall nicht vollständig und korrekt sein.

Um die Konsistenz und das korrekte Überschreiben virtueller Methoden zu gewährleisten, deklarieren wir eine Methode, die Parameter speichert. Im Methodenkörper rufen wir sofort eine ähnliche Methode der übergeordneten Klasse auf.

bool CNeuronEmbeddingOCL::WeightsUpdate(CNeuronBaseOCL *source, float tau)
  {
   if(!CNeuronBaseOCL::WeightsUpdate(source, tau))
      return false;

Wie wir bereits mehrfach erwähnt haben, ermöglicht uns dieser Ansatz, die übergeordnete Klasse aufzurufen, alle erforderlichen Steuerelemente in einer Aktion ohne unnötige Duplizierung zu implementieren und die erforderlichen Operationen mit geerbten Objekten durchzuführen.

Nachdem wir die Operationen der Methode der übergeordneten Klasse erfolgreich abgeschlossen haben, gehen wir dazu über, mit Objekten zu arbeiten, die direkt in unserer einbettenden Klasse deklariert sind. Um jedoch Zugang zu ähnlichen Objekten der Spenderklasse zu erhalten, sollten wir den Typ des resultierenden Objekts überschreiben.

//---
   CNeuronEmbeddingOCL *temp = source;

Als Nächstes müssen wir die Parameter des WeightsEmbedding-Puffers übertragen. Bevor wir jedoch mit den Operationen fortfahren, vergleichen wir die Puffergrößen des aktuellen und des Spenderobjekts.

   if(WeightsEmbedding.Total() != temp.WeightsEmbedding.Total())
      return false;

Dann müssen wir den Inhalt von einem Puffer in einen anderen übertragen. Aber wir erinnern uns, dass alle Operationen mit Puffern auf der OpenCL-Kontextseite durchgeführt werden. Daher werden wir den Datentransfer auf der Kontextseite durchführen. Ich verwende absichtlich den Ausdruck „Datenübertragung“ und nicht „Kopieren“. Ich lasse die Möglichkeit des „weichen Kopierens“ mit einem Verhältnis, wie es der SAC-Algorithmus für Zielmodelle vorsieht. OpenCL-Programmkernel wurden bereits früher erstellt. Jetzt müssen wir nur noch ihren Anruf arrangieren.

Wir definieren den Kernel-Task-Space anhand der Größe des Puffers für das Gewichtsverhältnis.

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {WeightsEmbedding.Total()};


Es folgt die Verzweigung des Algorithmus in Abhängigkeit von dem verwendeten Algorithmus zur Aktualisierung der Parameter. Die Verzweigung ist notwendig, weil wir mehr Puffer und Hyperparameter benötigen, wenn wir die Adam-Methode verwenden. Dies führt zur Verwendung unterschiedlicher Kernel.

Zuerst erstellen wir den Adam-Methodenzweig. Um ihn zu nutzen, müssen zwei Bedingungen erfüllt sein:

  • die Angabe der geeigneten Methode für die Aktualisierung der Parameter bei der Erstellung eines Objekts, da die Erstellung von Objekten der entsprechenden Datenpuffer davon abhängt;
  • das Aktualisierungsverhältnis sollte ungleich eins sein, da sonst eine vollständige Kopie der Daten erforderlich ist, unabhängig von der verwendeten Methode zur Aktualisierung der Parameter.
Im Hauptteil des bedingten Operators füllen wir die Parameter des aufgerufenen Kernels mit Zeigern auf die entsprechenden Datenpuffer und die erforderlichen Hyperparameter. 

   if(tau != 1.0f && optimization == ADAM)
     {
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_target, WeightsEmbedding.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_source, temp.WeightsEmbedding.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_m, FirstMomentumEmbed.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_v, SecondMomentumEmbed.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_tau, (float)tau))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b1, (float)b1))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b2, (float)b2))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.Execute(def_k_SoftUpdateAdam, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }

Dann senden wir den SoftUpdateAdam-Kernel an die Ausführungswarteschlange.

Im zweiten Zweig des Algorithmus führen wir ähnliche Operationen durch, allerdings für den SoftUpdate-Kernel.

   else
     {
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_target, WeightsEmbedding.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_source, temp.WeightsEmbedding.GetIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(def_k_SoftUpdate, def_k_su_tau, (float)tau))
        {
         printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.Execute(def_k_SoftUpdate, 1, global_work_offset, global_work_size))
        {
         printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
         return false;
        }
     }
//---
   return true;
  }

Das konstruktive Problem ist gelöst, und wir können uns nun der praktischen Umsetzung der Online-Trainingsmethode zuwenden. Den Prozess der Interaktion mit der Umwelt und des gleichzeitigen zusätzlichen Trainings der Modelle gestalten wir in der EA „...\DoC\OnlineStudy.mq5“. Dieser EA ist eine Art Symbiose aus den in den vorangegangenen Artikeln diskutierten EAs für die Sammlung von Daten für das Training und das direkte Offline-Training von Modellen. Sie enthält alle externen Parameter, die für die Interaktion mit der Umwelt erforderlich sind, insbesondere die Indikatorparameter. Gleichzeitig fügen wir aber auch Parameter hinzu, die die Häufigkeit und die Anzahl der Iterationen des Online-Trainings angeben. Der Standard-EA enthält subjektive Daten. Ich habe die Trainingshäufigkeit mit 120 Kerzen angegeben, was im H1-Zeitrahmen ungefähr einer Woche entspricht (5 Tage * 24 Stunden). Während der Optimierung können Sie Werte auswählen, die für Ihre Modelle optimaler sind.

//+------------------------------------------------------------------+
//| Input parameters                                                 |
//+------------------------------------------------------------------+
input ENUM_TIMEFRAMES      TimeFrame   =  PERIOD_H1;
//---
input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod=   9;            //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price
//---
input int                  StudyIters  =   5;            //Iterations to Study
input int                  StudyPeriod =  120;           //Bars between Studies

Bei der EA-Initialisierungsmethode laden wir zunächst den zuvor erstellten Playback-Puffer mit den Erfahrungen hoch. Wir haben ähnliche Aktionen in den Trainings-EAs „Study.mql5“ für verschiedene Offline-Trainingsmethoden durchgeführt. Nur jetzt beenden wir den EA nicht, wenn das Laden der Daten fehlschlägt. Im Gegensatz zum Offline-Modus können die Modelle nur auf neuen Daten trainiert werden, die bei der Interaktion mit der Umgebung gesammelt werden.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   LoadTotalBase();

Als Nächstes werden wir Indikatoren für die Interaktion mit der Umwelt vorbereiten, so wie wir es bereits bei den EAs getan haben.

   if(!Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();
//---
   if(!RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice))
      return INIT_FAILED;
//---
   if(!CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice))
      return INIT_FAILED;
//---
   if(!ATR.Create(Symb.Name(), TimeFrame, ATRPeriod))
      return INIT_FAILED;
//---
   if(!MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice))
      return INIT_FAILED;
   if(!RSI.BufferResize(NBarInPattern) || !CCI.BufferResize(NBarInPattern) ||
      !ATR.BufferResize(NBarInPattern) || !MACD.BufferResize(NBarInPattern))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      return INIT_FAILED;
     }
//---
   if(!Trade.SetTypeFillingBySymbol(Symb.Name()))
      return INIT_FAILED;

Laden wir die Modelle und prüfen wir, ob sie in Bezug auf die Größe der Quelldatenschichten und die Ergebnisse übereinstimmen. Falls erforderlich, erstellen wir neue Modelle mit einer vordefinierten Architektur. Dies geht ein wenig über den Rahmen einer zusätzlichen Ausbildung von Modellen hinaus. Aber wir lassen dem Nutzer die Möglichkeit, das Online-Training „von Grund auf“ durchzuführen.

//--- load models
   float temp;
   if(!Agent.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) ||
      !RTG.Load(FileName + "RTG.nnw", dtStudied, true) ||
      !AgentStudy.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) ||
      !RTGStudy.Load(FileName + "RTG.nnw", dtStudied, true))
     {
      PrintFormat("Can't load pretrained models");
      CArrayObj *agent = new CArrayObj();
      CArrayObj *rtg = new CArrayObj();
      if(!CreateDescriptions(agent, rtg))
        {
         delete agent;
         delete rtg;
         PrintFormat("Can't create description of models");
         return INIT_FAILED;
        }
      if(!Agent.Create(agent) ||
         !RTG.Create(rtg) ||
         !AgentStudy.Create(agent) ||
         !RTGStudy.Create(rtg))
        {
         delete agent;
         delete rtg;
         PrintFormat("Can't create models");
         return INIT_FAILED;
        }
      delete agent;
      delete rtg;
      //---
     }
//---
   Agent.getResults(Result);
   if(Result.Total() != NActions)
     {
      PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total());
      return INIT_FAILED;
     }
   AgentResult = vector<float>::Zeros(NActions);
//---
   Agent.GetLayerOutput(0, Result);
   if(Result.Total() != (NRewards + BarDescr * NBarInPattern + AccountDescr + TimeDescription + NActions))
     {
      PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", 
           Result.Total(), (NRewards + BarDescr * NBarInPattern + AccountDescr + TimeDescription + NActions));
      return INIT_FAILED;
     }
   Agent.Clear();
   RTG.Clear();

Bitte beachten Sie, dass wir zwei Kopien von jedem Modell laden (oder initialisieren). Eine wird für die Interaktion mit der Umwelt benötigt. Die zweite wird im Training verwendet. Die trainierten Modelle erhielten den Suffix Study.

Anschließend werden globale Variablen initialisiert und die Methode beendet.

   PrevBalance = AccountInfoDouble(ACCOUNT_BALANCE);
   PrevEquity = AccountInfoDouble(ACCOUNT_EQUITY);
//---
   return(INIT_SUCCEEDED);
  }

Bei der EA-Deinitialisierungsmethode speichern wir die trainierten Modelle und die gesammelten Erfahrungen im Reproduktionspuffer.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   AgentStudy.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true);
   RTGStudy.Save(FileName + "RTG.nnw", TimeCurrent(), true);
   delete Result;
   int total = ArraySize(Buffer);
   printf("Saving %d", MathMin(total + 1, MaxReplayBuffer));
   SaveTotalBase();
   Print("Saved");
  }

Bitte beachten Sie, dass wir die trainierten Modelle speichern, da ihre Puffer alle Informationen enthalten, die für das spätere Training und den Betrieb der Modelle notwendig sind.

Der Prozess der Interaktion mit der Umgebung ist in der OnTick-Tick-Verarbeitungsmethode geregelt. Zu Beginn der Methode wird geprüft, ob ein neues Bar Opening Event eingetreten ist, und ggf. werden die Indikatorparameter aktualisiert. Wir laden auch Daten zur Preisentwicklung herunter.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   if(!IsNewBar())
      return;
//---
   int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), NBarInPattern, Rates);
   if(!ArraySetAsSeries(Rates, true))
      return;
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();
   Symb.Refresh();
   Symb.RefreshRates();

Bereiten wir die vom Terminal empfangenen Daten für die Übertragung an das Modell der Interaktion mit der Umwelt als Eingangsdaten vor.

//--- History data
   float atr = 0;
   for(int b = 0; b < (int)NBarInPattern; b++)
     {
      float open = (float)Rates[b].open;
      float rsi = (float)RSI.Main(b);
      float cci = (float)CCI.Main(b);
      atr = (float)ATR.Main(b);
      float macd = (float)MACD.Main(b);
      float sign = (float)MACD.Signal(b);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      int shift = b * BarDescr;
      sState.state[shift] = (float)(Rates[b].close - open);
      sState.state[shift + 1] = (float)(Rates[b].high - open);
      sState.state[shift + 2] = (float)(Rates[b].low - open);
      sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f);
      sState.state[shift + 4] = rsi;
      sState.state[shift + 5] = cci;
      sState.state[shift + 6] = atr;
      sState.state[shift + 7] = macd;
      sState.state[shift + 8] = sign;
     }
   bState.AssignArray(sState.state);

Ergänzen wir den Datenpuffer mit Informationen über den Kontostatus.

//--- Account description
   sState.account[0] = (float)AccountInfoDouble(ACCOUNT_BALANCE);
   sState.account[1] = (float)AccountInfoDouble(ACCOUNT_EQUITY);
//---
   double buy_value = 0, sell_value = 0, buy_profit = 0, sell_profit = 0;
   double position_discount = 0;
   double multiplyer = 1.0 / (60.0 * 60.0 * 10.0);
   int total = PositionsTotal();
   datetime current = TimeCurrent();
   for(int i = 0; i < total; i++)
     {
      if(PositionGetSymbol(i) != Symb.Name())
         continue;
      double profit = PositionGetDouble(POSITION_PROFIT);
      switch((int)PositionGetInteger(POSITION_TYPE))
        {
         case POSITION_TYPE_BUY:
            buy_value += PositionGetDouble(POSITION_VOLUME);
            buy_profit += profit;
            break;
         case POSITION_TYPE_SELL:
            sell_value += PositionGetDouble(POSITION_VOLUME);
            sell_profit += profit;
            break;
        }
      position_discount += profit - (current - PositionGetInteger(POSITION_TIME)) * multiplyer * MathAbs(profit);
     }
   sState.account[2] = (float)buy_value;
   sState.account[3] = (float)sell_value;
   sState.account[4] = (float)buy_profit;
   sState.account[5] = (float)sell_profit;
   sState.account[6] = (float)position_discount;
   sState.account[7] = (float)Rates[0].time;
//---
   bState.Add((float)((sState.account[0] - PrevBalance) / PrevBalance));
   bState.Add((float)(sState.account[1] / PrevBalance));
   bState.Add((float)((sState.account[1] - PrevEquity) / PrevEquity));
   bState.Add(sState.account[2]);
   bState.Add(sState.account[3]);
   bState.Add((float)(sState.account[4] / PrevBalance));
   bState.Add((float)(sState.account[5] / PrevBalance));
   bState.Add((float)(sState.account[6] / PrevBalance));

Als Nächstes erstellen wir einen Zeitstempel.

//--- Time label
   double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01');
   bState.Add((float)MathSin(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1);
   bState.Add((float)MathCos(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1);
   bState.Add((float)MathSin(2.0 * M_PI * x));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1);
   bState.Add((float)MathSin(2.0 * M_PI * x));

Wir fügen den Vektor der letzten Aktionen des Agenten hinzu, die uns zum aktuellen Zustand geführt haben.

//--- Prev action
   bState.AddArray(AgentResult);

Die gesammelten Daten reichen aus, um einen Vorwärtsdurchlauf des RTG-Erzeugungsmodells durchzuführen.

//--- Return to go
   if(!RTG.feedForward(GetPointer(bState)))
      return;

Tatsächlich fehlen unserem Vektor der Ausgangsdaten nur diese Daten, um die optimalen Handlungen des Agenten in der aktuellen Zeitperiode vorherzusagen. Daher fügen wir nach einem erfolgreichen Vorwärtsdurchlauf des ersten Modells die erhaltenen Ergebnisse dem Quelldatenpuffer hinzu und rufen die Vorwärtsdurchlaufmethode unseres Akteurs auf. Achten Sie darauf, die Ergebnisse der Operationen zu überprüfen.

   RTG.getResults(Result);
   bState.AddArray(Result);
//---
   if(!Agent.feedForward(GetPointer(bState), 1, false, (CBufferFloat*)NULL))
      return;

Nachdem wir die Modelle erfolgreich durchlaufen haben, entschlüsseln wir die Ergebnisse ihrer Arbeit und führen die ausgewählte Aktion in der Umgebung aus. Dieser Prozess steht in vollem Einklang mit dem zuvor diskutierten Algorithmus in Modellen der Interaktion mit der Umwelt.

//---
   PrevBalance = sState.account[0];
   PrevEquity = sState.account[1];
//---
   vector<float> temp;
   Agent.getResults(temp);
//---
   double min_lot = Symb.LotsMin();
   double step_lot = Symb.LotsStep();
   double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point();
   if(temp[0] >= temp[3])
     {
      temp[0] -= temp[3];
      temp[3] = 0;
     }
   else
     {
      temp[3] -= temp[0];
      temp[0] = 0;
     }
   float delta = MathAbs(AgentResult - temp).Sum();
   AgentResult = temp;
//--- buy control
   if(temp[0] < min_lot || (temp[1] * MaxTP * Symb.Point()) <= stops || (temp[2] * MaxSL * Symb.Point()) <= stops)
     {
      if(buy_value > 0)
         CloseByDirection(POSITION_TYPE_BUY);
     }
   else
     {
      double buy_lot = min_lot + MathRound((double)(temp[0] - min_lot) / step_lot) * step_lot;
      double buy_tp = Symb.NormalizePrice(Symb.Ask() + temp[1] * MaxTP * Symb.Point());
      double buy_sl = Symb.NormalizePrice(Symb.Ask() - temp[2] * MaxSL * Symb.Point());
      if(buy_value > 0)
         TrailPosition(POSITION_TYPE_BUY, buy_sl, buy_tp);
      if(buy_value != buy_lot)
        {
         if(buy_value > buy_lot)
            ClosePartial(POSITION_TYPE_BUY, buy_value - buy_lot);
         else
            Trade.Buy(buy_lot - buy_value, Symb.Name(), Symb.Ask(), buy_sl, buy_tp);
        }
     }
//--- sell control
   if(temp[3] < min_lot || (temp[4] * MaxTP * Symb.Point()) <= stops || (temp[5] * MaxSL * Symb.Point()) <= stops)
     {
      if(sell_value > 0)
         CloseByDirection(POSITION_TYPE_SELL);
     }
   else
     {
      double sell_lot = min_lot + MathRound((double)(temp[3] - min_lot) / step_lot) * step_lot;;
      double sell_tp = Symb.NormalizePrice(Symb.Bid() - temp[4] * MaxTP * Symb.Point());
      double sell_sl = Symb.NormalizePrice(Symb.Bid() + temp[5] * MaxSL * Symb.Point());
      if(sell_value > 0)
         TrailPosition(POSITION_TYPE_SELL, sell_sl, sell_tp);
      if(sell_value != sell_lot)
        {
         if(sell_value > sell_lot)
            ClosePartial(POSITION_TYPE_SELL, sell_value - sell_lot);
         else
            Trade.Sell(sell_lot - sell_value, Symb.Name(), Symb.Bid(), sell_sl, sell_tp);
        }
     }

Bewertung der Belohnung aus der Umwelt für den Übergang in den aktuellen Zustand. Übertragen aller gesammelten Informationen, um die aktuelle Trajektorie zu erstellen.

//---
   int shift = BarDescr * (NBarInPattern - 1);
   sState.rewards[0] = bState[shift];
   sState.rewards[1] = bState[shift + 1] - 1.0f;
   if((buy_value + sell_value) == 0)
      sState.rewards[2] -= (float)(atr / PrevBalance);
   else
      sState.rewards[2] = 0;
   for(ulong i = 0; i < NActions; i++)
      sState.action[i] = AgentResult[i];
   if(!Base.Add(sState))
      ExpertRemove();

Damit ist der Prozess der Interaktion mit der Umwelt abgeschlossen. Bevor wir jedoch die Methode beenden, werden wir prüfen, ob es notwendig ist, den Prozess des zusätzlichen Trainings der Modelle zu starten. Ich habe wahrscheinlich die einfachste Kontrolle verwendet, um die Effizienz der Methode zu testen. Ich überprüfe einfach die Vielfachheit der Größe des Gesamtverlaufs für das Instrument in dem analysierten Zeitrahmen des Trainingszeitraums. In der täglichen Arbeit ist es ratsam, durchdachtere Ansätze zu verwenden, um das zusätzliche Training auf Zeiten zu verlagern, in denen der Markt geschlossen ist oder die Volatilität der Instrumente abnimmt. Darüber hinaus kann es sinnvoll sein, die Aktualisierung der Modellparameter zu verschieben, bis alle Positionen geschlossen sind. Generell würde ich für den Einsatz in realen Modellen einen ausgewogeneren und sinnvolleren Ansatz bei der Wahl der Häufigkeit und des Zeitpunkts für das zusätzliche Training von Modellen empfehlen.

//---
   if((Bars(_Symbol, TimeFrame) % StudyPeriod) == 0)
      Train();
  }

Als Nächstes wenden wir uns der Trainingsmethode des Models Train zu. Hier ist anzumerken, dass das zusätzliche Training unter Berücksichtigung der Erfahrungen erfolgt, die bei der aktuellen Interaktion mit der Umgebung gemacht werden. Bei der Tick-Processing-Methode haben wir alle von der Umgebung erhaltenen Informationen in einer separaten Trajektorie zusammengefasst. Diese Trajektorie wird jedoch nicht in den Puffer für den Playback-Puffer mit den Erfahrungen aufgenommen. Früher haben wir eine solche Operation erst nach dem Ende der Episode durchgeführt. Dieser Ansatz ist jedoch nicht akzeptabel, wenn die Parameter periodisch aktualisiert werden sollen. Dies bringt uns schließlich näher an das Offline-Training, bei dem die Strategie des Agenten nur auf festen Bahnen früherer Erfahrungen trainiert wird. Bevor wir mit dem Training beginnen, fügen wir daher die gesammelten Daten dem Replay-Puffer der Erfahrungen hinzu. 

Um die Aufzeichnung von zu kurzen und uninformativen Trajektorien zu vermeiden, wird die Mindestgröße der gespeicherten Trajektorie begrenzt. Im genannten Beispiel habe ich die Mindestgröße der Trajektorie während der Aktualisierungsperiode der Modellparameter begrenzt.

Wenn die Größe der akkumulierten Trajektorie die Mindestanforderungen erfüllt, fügen wir sie dem Playback-Puffer mit den Erfahrungen hinzu und berechnen den kumulierten Betrag der Belohnungen neu.

An dieser Stelle sei darauf hingewiesen, dass wir die kumulative Menge an Belohnungen nur für die in den Playback-Puffer mit den Erfahrungen übertragene Kopie der Trajektorie neu berechnen. In dem anfänglichen Puffer, in dem Informationen über die aktuelle Trajektorie gesammelt werden, sollte die Belohnung ungezählt bleiben. Bei der anschließenden Interaktion mit der Umgebung wird die Trajektorie ergänzt. Daher führt die wiederholte Neuberechnung der kumulativen Belohnung bei weiterer Hinzufügung der aktualisierten Trajektorie zu einer Verdoppelung der Daten. Um dies zu verhindern, behalten wir die nicht berechnete Belohnung immer im Trajektorien-Akkumulationspuffer.

//+------------------------------------------------------------------+
//| Train function                                                   |
//+------------------------------------------------------------------+
void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   if(Base.Total >= StudyPeriod)
      if(ArrayResize(Buffer, total_tr + 1) == (total_tr + 1))
        {
         Buffer[total_tr] = Base;
         Buffer[total_tr].CumRevards();
         total_tr++;
        }

Als Nächstes sollten wir uns daran erinnern, dass die Größe des Trajektorienakkumulationspuffers durch die Konstante Buffer_Size begrenzt ist. Um einen Fehler durch Überschreiten der Array-Grenzen zu vermeiden, stellen Sie sicher, dass genügend freie Zellen im Trajektorien-Akkumulationspuffer vorhanden sind, um Schritte bis zur nächsten Speicherung der Trajektorie aufzuzeichnen. Bei Bedarf könnten die einige der ältesten Schritte gelöscht werden.

Bitte beachten Sie, dass wir die Daten im primären Trajektorienakkumulationspuffer löschen. Gleichzeitig werden diese Informationen in der Kopie der Trajektorie gespeichert, die wir im Playback-Puffer mit den Erfahrungen abgelegt haben.

Bei der Festlegung von Modellkonstanten und -parametern sollte darauf geachtet werden, dass die Größe des Trajektorienpuffers es erlaubt, die Historie von mindestens einer Periode zwischen dem weiteren Training der Modelle zu speichern. 

   int clear = Base.Total + StudyPeriod - Buffer_Size;
   if(clear > 0)
      Base.ClearFirstN(clear);

Dann habe ich noch eine zusätzliche Kontrolle hinzugefügt, die vielleicht unnötig erscheint. Ich prüfe den Playback-Puffer mit den Erfahrungen auf kurze Trajektorien und lösche sie, wenn sie gefunden werden. Auf den ersten Blick ist das Vorhandensein solcher Trajektorien unwahrscheinlich, da vor dem Hinzufügen der Trajektorie zum Erfahrungswiedergabepuffer eine ähnliche Kontrolle stattfindet. Ich gebe jedoch zu, dass es beim Lesen und Schreiben von Trajektorien in eine Datei zu Fehlern kommen kann. Wir führen diese Prüfung durch, um spätere Fehler auszuschließen.

//---
   int count = 0;
   for(int i = 0; i < (total_tr + count); i++)
     {
      if(Buffer[i + count].Total < StudyPeriod)
        {
         count++;
         i--;
         continue;
        }
      if(count > 0)
         Buffer[i] = Buffer[i + count];
     }
   if(count > 0)
     {
      ArrayResize(Buffer, total_tr - count);
      total_tr = ArraySize(Buffer);
     }

Als Nächstes stellen wir ein System von Modell-Trainingszyklen auf. Dieser Prozess wiederholt sich weitgehend mit dem des vorherigen Artikels. Die externe Schleife ist entsprechend der in den externen EA-Parametern angegebenen Anzahl von Modelltrainingsiterationen organisiert.

Im Hauptteil der Schleife wählen wir nach dem Zufallsprinzip eine Trajektorie und ein Element dieser Trajektorie aus, von dem aus wir die nächste Iteration des Modelltrainings beginnen werden.

   uint ticks = GetTickCount();
//---
   bool StopFlag = false;
   for(int iter = 0; (iter < StudyIters && !IsStopped() && !StopFlag); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * MathMax(Buffer[tr].Total - 2 * HistoryBars,
                                                                            MathMin(Buffer[tr].Total, 20)));
      if(i < 0)
        {
         iter--;
         continue;
        }

Dann löschen wir die Puffer für die Modelleinbettung und den Vektor der vorangegangenen Aktionen des Akteurs.

      vector<float> Actions = vector<float>::Zeros(NActions);
      AgentStudy.Clear();
      RTGStudy.Clear();

In diesem Stadium haben wir die Vorbereitungsarbeiten abgeschlossen und können mit dem Training der Modelle beginnen. Wir arrangieren eine verschachtelte Lernschleife.

Im Hauptteil der Schleife wird der Prozess der Vorbereitung des Quelldatenpuffers wiederholt, ähnlich wie oben bei der Tick-Verarbeitungsmethode beschrieben. Die Reihenfolge des Schreibens von Daten in den Puffer wird vollständig wiederholt. Während wir jedoch zuvor Daten vom Terminal angefordert haben, entnehmen wir sie jetzt dem Playback-Puffer mit den Erfahrungen.

      for(int state = i; state < MathMin(Buffer[tr].Total - 2, int(i + HistoryBars * 1.5)); state++)
        {
         //--- History data
         bState.AssignArray(Buffer[tr].States[state].state);
         //--- Account description
         float prevBalance = (state == 0 ? Buffer[tr].States[state].account[0] : Buffer[tr].States[state - 1].account[0]);
         float prevEquity = (state == 0 ? Buffer[tr].States[state].account[1] : Buffer[tr].States[state - 1].account[1]);
         bState.Add((Buffer[tr].States[state].account[0] - prevBalance) / prevBalance);
         bState.Add(Buffer[tr].States[state].account[1] / prevBalance);
         bState.Add((Buffer[tr].States[state].account[1] - prevEquity) / prevEquity);
         bState.Add(Buffer[tr].States[state].account[2]);
         bState.Add(Buffer[tr].States[state].account[3]);
         bState.Add(Buffer[tr].States[state].account[4] / prevBalance);
         bState.Add(Buffer[tr].States[state].account[5] / prevBalance);
         bState.Add(Buffer[tr].States[state].account[6] / prevBalance);
         //--- Time label
         double x = (double)Buffer[tr].States[state].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
         bState.Add((float)MathSin(2.0 * M_PI * x));
         x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_MN1);
         bState.Add((float)MathCos(2.0 * M_PI * x));
         x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_W1);
         bState.Add((float)MathSin(2.0 * M_PI * x));
         x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_D1);
         bState.Add((float)MathSin(2.0 * M_PI * x));
         //--- Prev action
         bState.AddArray(Actions);

Nach der Erfassung des ersten Teils der Ausgangsdaten führen wir einen Vorwärtsdurchlauf des RTG-Erzeugungsmodells durch. Dann führen wir sofort einen direkten Durchlauf durch, um den Fehler gegenüber der tatsächlich erhaltenen Belohnung zu minimieren. Daher erstellen wir ein autoregressives Modell zur Vorhersage möglicher Belohnungen auf der Grundlage des vorherigen Verlaufs von Zustand und Aktionen.

         //--- Return to go
         if(!RTGStudy.feedForward(GetPointer(bState)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            StopFlag = true;
            break;
           }
         Result.AssignArray(Buffer[tr].States[state + 1].rewards);
         if(!RTGStudy.backProp(Result))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            StopFlag = true;
            break;
           }

Für das Training der Agentenpolitik geben wir die tatsächlich erhaltene Belohnung im Quelldatenpuffer anstelle des prädiktiven RTG an und führen einen direkten Durchlauf durch.

         //--- Policy Feed Forward
         bState.AddArray(Buffer[tr].States[state + 1].rewards);
         if(!AgentStudy.feedForward(GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            StopFlag = true;
            break;
           }

Die Strategie des Agenten wird so trainiert, dass der Fehler zwischen der vorhergesagten und der tatsächlich ausgeführten Aktion, die zum Erhalt der Belohnung führte, minimiert wird. 

         //--- Policy study
         Actions.Assign(Buffer[tr].States[state].action);
         vector<float> result;
         AgentStudy.getResults(result);
         Result.AssignArray(CAGrad(Actions - result) + result);
         if(!AgentStudy.backProp(Result, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            StopFlag = true;
            break;
           }

Dies ermöglicht es uns, ein autoregressives Modell für die Auswahl der optimalen Aktion zu erstellen, um die gewünschte Belohnung im Kontext der zuvor besuchten Zustände und abgeschlossenen Aktionen des Agenten zu erhalten.

Nach erfolgreichem Abschluss der Modelltrainingsiterationen informieren wir den Nutzer über den Fortschritt der Trainingsoperationen und gehen zur nächsten Iteration der Modelltrainingsschleife über.

Nach Abschluss aller Iterationen des Systems der verschachtelten Schleifen des Modelltrainings löschen wir das Kommentarfeld im Graphen und übertragen die Parameter der trainierten Modelle auf die Umweltinteraktionsmodelle. Im obigen Beispiel habe ich die Daten des Gewichtungskoeffizienten vollständig kopiert. So emuliere ich die Verwendung eines Modells für Training und Operation. Ich lasse aber auch Experimente mit unterschiedlichen Datenkopierverhältnissen zu.

   Comment("");
//---
   Agent.WeightsUpdate(GetPointer(AgentStudy), 1.0f);
   RTG.WeightsUpdate(GetPointer(RTGStudy), 1.0f);
//---
  }

Damit ist der EA-Algorithmus für das Online-Training des Lösungswandlers abgeschlossen. Den vollständigen EA-Code und alle seine Methoden finden Sie im Anhang.

Bitte beachten Sie, dass sich der EA „...\DoC\OnlineStudy.mq5“ im Unterverzeichnis „DoC“ mit den EAs aus dem vorherigen Artikel befindet. Ich habe es nicht in ein separates Unterverzeichnis aufgeteilt, da es funktionell ein zusätzliches Training von Modellen durchführt, die von Offline-EAs aus dem vorherigen Artikel trainiert wurden. Auf diese Weise wird die Integrität der Modell-Trainingsdateien gewahrt. 

Im Anhang finden Sie außerdem alle Programme, die im aktuellen und im vorherigen Artikel verwendet wurden.


3. Test

Wir haben die theoretischen Aspekte der Online Decision Transformer-Methode untersucht und unsere eigene Interpretation der vorgeschlagenen Methode entwickelt. Der nächste Schritt ist die Prüfung der geleisteten Arbeit. Wir nehmen eine Feinabstimmung der Modelle aus dem vorherigen Artikel vor. Zu diesem Zweck führen wir einen Zyklus von Einzelläufen unseres neuen EA auf der Historie der Trainingsdaten im Strategietester durch.


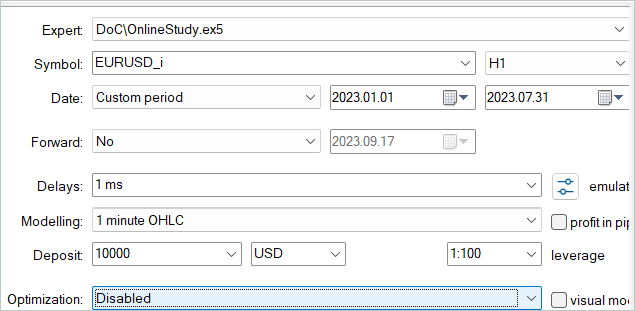
Im vorangegangenen Artikel haben wir ein Offline-Training der Modelle anhand historischer Daten für die ersten sieben Monate des Jahres 2023 durchgeführt. In diesem historischen Zeitraum nehmen wir auch die Feinabstimmung der Modelle vor.

Durch den Prozess der Feinabstimmung der Modelle verbesserte ODT die Gesamtrentabilität der Modelle. Bei dem Testmuster für August 2023 konnte das Modell einen Gewinn von etwa 10 % erzielen. Das Renditediagramm ist nicht perfekt, aber einige Tendenzen sind bereits zu erkennen.

Testgrafik

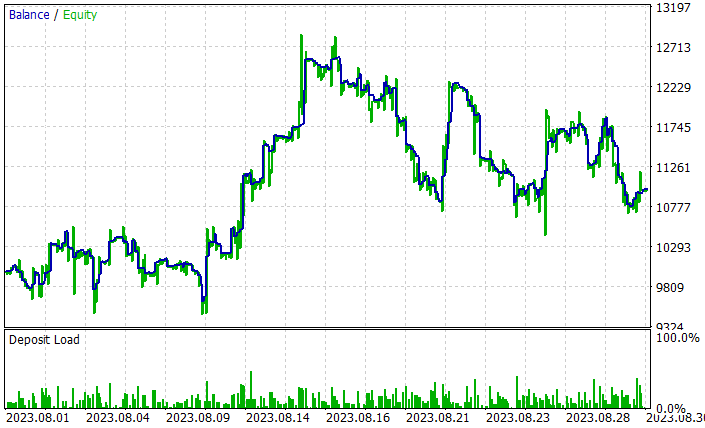
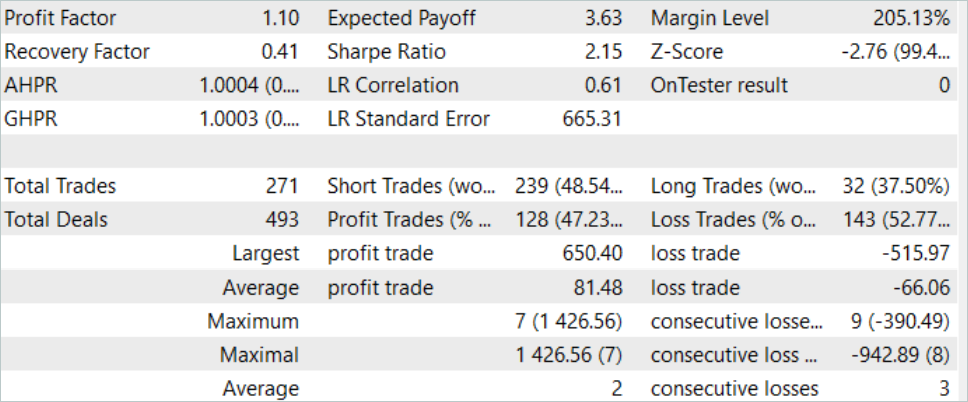
Die Ergebnisse des Tests des trainierten Modells sind oben dargestellt. Insgesamt wurden während des Testzeitraums 271 Transaktionen durchgeführt. 128 von ihnen wurden mit einem Gewinn abgeschlossen, der sich auf mehr als 47 % belief. Wie wir sehen können, ist der Anteil der gewinnbringenden Geschäfte etwas geringer als der Anteil der Verlustgeschäfte. Der maximale Gewinn ist jedoch 26 % höher als der maximale Verlust. Der durchschnittliche Gewinn liegt mehr als 20 % höher als der durchschnittliche Verlust. All dies ermöglichte eine Erhöhung des Gewinnfaktors des Modells auf 1,10.


Schlussfolgerung

In diesem Artikel haben wir die Überlegungen zur Steigerung der Effizienz der Decision-Transformer-Methode fortgesetzt und uns mit dem Algorithmus zur Feinabstimmung der Modelle im Online Decision Transformer (ODT)-Trainingsmodus vertraut gemacht. Diese Methode ermöglicht es, die Effizienz von offline trainierten Modellen zu steigern und die Agenten in die Lage zu versetzen, sich an eine sich verändernde Umgebung anzupassen und so ihre Strategien durch Interaktion mit der Umgebung zu verbessern.

Im praktischen Teil des Artikels haben wir die Methode mit MQL5 implementiert und ein Online-Training der Modelle aus dem vorherigen Artikel durchgeführt. Es sei an dieser Stelle darauf hingewiesen, dass die Optimierung der Modelle nur durch die Anwendung der betrachteten ODT-Methode erreicht wurde. Während des Online-Trainings haben wir Modelle verwendet, die im vorherigen Artikel offline trainiert wurden. Wir haben keine Änderungen an der Modellarchitektur vorgenommen. Es wurde lediglich ein zusätzliches Online-Training angeboten. Dadurch konnte die Effizienz der Modelle erhöht werden, was an sich schon die Effizienz der Online Decision Transformer-Methode bestätigt.

Ich möchte Sie noch einmal daran erinnern, dass alle in diesem Artikel vorgestellten Programme nur zur Demonstration der Technologie dienen und nicht für den realen Handel geeignet sind.


Links


Programme, die im diesem Artikel verwendet werden

# Name Typ Beschreibung
1 Research.mq5 Expert Advisor Beispielsammlung EA
2 Study.mq5  Expert Advisor Trainings-EA des Agenten
3 OnlineStudy.mq5  Expert Advisor
EA für das zusätzliche Online-Training von Agenten
4 Test.mq5 Expert Advisor Modeltraining-EA
5 Trajectory.mqh Klassenbibliothek Struktur der Systemzustandsbeschreibung
6 NeuroNet.mqh Klassenbibliothek Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7 NeuroNet.cl Code Base Die Bibliothek des Programmcodes von OpenCL

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13596

Beigefügte Dateien |
ZIP herunterladen
MQL5.zip (530.55 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Neuronale Netze sind einfach (Teil 59): Dichotomy of Control (DoC) Neuronale Netze sind einfach (Teil 59): Dichotomy of Control (DoC)
Im vorigen Artikel haben wir uns mit dem Decision Transformer vertraut gemacht. Das komplexe stochastische Umfeld des Devisenmarktes erlaubte es uns jedoch nicht, das Potenzial der vorgestellten Methode voll auszuschöpfen. In diesem Artikel werde ich einen Algorithmus vorstellen, der die Leistung von Algorithmen in stochastischen Umgebungen verbessern soll.
Entwicklung eines Replay Systems — Marktsimulation (Teil 22): FOREX (III) Entwicklung eines Replay Systems — Marktsimulation (Teil 22): FOREX (III)
Obwohl dies der dritte Artikel zu diesem Thema ist, muss ich für diejenigen, die den Unterschied zwischen dem Aktienmarkt und dem Devisenmarkt noch nicht verstanden haben, erklären: Der große Unterschied besteht darin, dass es auf dem Devisenmarkt keine Informationen über einige Punkte gibt, die im Laufe des Handels tatsächlich aufgetreten sind.
Entwicklung eines Replay Systems — Marktsimulation (Teil 23): FOREX (IV) Entwicklung eines Replay Systems — Marktsimulation (Teil 23): FOREX (IV)
Jetzt erfolgt die Erstellung an der gleichen Stelle, an der wir die Ticks in Balken umgewandelt haben. Wenn also bei der Konvertierung etwas schief geht, werden wir den Fehler sofort bemerken. Dies liegt daran, dass derselbe Code, der die 1-Minuten-Balken während des schnellen Vorlaufs auf dem Chart platziert, auch für das Positionierungssystem verwendet wird, um die Balken während der normalen Performance zu platzieren. Mit anderen Worten: Der Code, der für diese Aufgabe zuständig ist, wird nirgendwo anders dupliziert. Auf diese Weise erhalten wir ein viel besseres System sowohl für die Instandhaltung als auch für die Verbesserung.
Algorithmen zur Optimierung mit Populationen: Stochastische Diffusionssuche (SDS) Algorithmen zur Optimierung mit Populationen: Stochastische Diffusionssuche (SDS)
Der Artikel behandelt die stochastische Diffusionssuche (SDS), einen sehr leistungsfähigen und effizienten Optimierungsalgorithmus, der auf den Prinzipien des Random Walk basiert. Der Algorithmus ermöglicht es, optimale Lösungen in komplexen mehrdimensionalen Räumen zu finden, wobei er sich durch eine hohe Konvergenzgeschwindigkeit und die Fähigkeit auszeichnet, lokale Extrema zu vermeiden.