Datenwissenschaft und maschinelles Lernen (Teil 05): Entscheidungsbäume

MetaTrader 5 — Handel | 11 Juli 2022, 10:00

456

Omega J Msigwa

Was ist ein Entscheidungsbaum?

Bei einem Entscheidungsbaum handelt es sich um eine überwachte Technik des maschinellen Lernens, die zur Kategorisierung oder zur Erstellung von Vorhersagen auf der Grundlage der Antworten auf eine frühere Reihe von Fragen verwendet wird. Ein Modell ist eine Form des überwachten Lernens, d. h. das Modell wird anhand eines Datensatzes trainiert und getestet, der die gewünschte Kategorisierung enthält.

Der Entscheidungsbaum liefert nicht immer eindeutige Antworten oder Entscheidungen. Stattdessen kann er die Optionen so darstellen, dass der Datenwissenschaftler selbst eine fundierte Entscheidung treffen kann. Entscheidungsbäume imitieren die menschliche Denkweise, sodass es für Datenwissenschaftler im Allgemeinen einfach ist, die Ergebnisse zu verstehen und zu interpretieren.

Artikelbild Entscheidungsbäume

Terminologie-Alarm!!

In meinem ersten Artikel dieser Reihe habe ich vergessen, die Begriffe „überwachtes„ und „unüberwachtes„ Lernen zu beschreiben, hier ist sie

Überwachtes Lernen

Überwachtes Lernen ist ein Ansatz zur Entwicklung Künstlicher Intelligenz (KI), bei dem ein Computeralgorithmus auf Eingabedaten trainiert wird, die für eine bestimmte Ausgabe gekennzeichnet sind.

Im Gegensatz zum überwachten Lernen wird der Algorithmus bei diesem Ansatz mit unmarkierten Daten konfrontiert und soll selbständig Muster oder Ähnlichkeiten erkennen.

Zu den Algorithmen, die üblicherweise in Programmen für überwachtes Lernen verwendet werden, gehören die folgenden:

Lineare Regression
Logistische Regression
Entscheidungsbäume
Support-Vektor-Maschinen
Random Forests

Der Hauptunterschied zwischen überwachtem und unüberwachtem Lernen besteht darin, wie der Algorithmus lernt. Beim unüberwachten Lernen erhält der Algorithmus unmarkierte Daten als Trainingsmenge. Anders als beim überwachten Lernen gibt es keine korrekten Ausgabewerte; der Algorithmus ermittelt Muster und Ähnlichkeiten innerhalb der Daten, anstatt sie mit externen Messungen in Beziehung zu setzen. Mit anderen Worten: Algorithmen können frei arbeiten, um mehr über die Daten zu lernen und interessante oder unerwartete Dinge zu finden, nach denen der Mensch nicht gesucht hat.

Wir befassen uns derzeit mit überwachtem Lernen und werden in den nächsten Artikeln mehr über unüberwachtes Lernen erfahren.

Wie funktionieren die Entscheidungsbäume?

Entscheidungsbäume verwenden mehrere Algorithmen, um zu entscheiden, ob ein Knoten in zwei oder mehr Unterknoten aufgeteilt werden soll. Durch die Bildung von Unterknoten wird die Homogenität der entstehenden Unterknoten erhöht. Mit anderen Worten kann man sagen, dass die Reinheit des Knotens in Bezug auf die Zielvariable zunimmt. Der Entscheidungsbaum-Algorithmus teilt die Knoten anhand aller verfügbaren Variablen auf und wählt dann die Aufteilung aus, die zu den homogensten Unterknoten führt.

Beispiel für einen Entscheidungsbaum

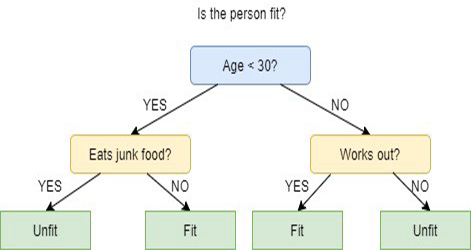
Die Auswahl des Algorithmus basiert auf der Art der Zielvariablen.

Die folgenden Algorithmen werden für den Entscheidungsbaum verwendet:

ID3 > Erweiterung von D3
C4.5 > Nachfolger von ID3
CART > Klassifizierungs- und Regressionsbaum
CHAID > Chi-Quadrat Automatic Interaction Detection, führt bei der Berechnung von Klassifikationsbäumen eine mehrstufige Aufteilung durch.
MARS > Multivariate adaptive Regressionssplines

In diesem Artikel werde ich einen Entscheidungsbaum erstellen, der auf dem ID3-Algorithmus basiert. Wir werden die anderen Algorithmen in den nächsten Artikeln dieser Serie diskutieren und verwenden.

Das Ziel des Entscheidungsbaums

Das Hauptziel des Entscheidungsbaum-Algorithmus ist es, die Daten mit Verunreinigungen und in reine oder in der Nähe von Knoten zu trennen, zum Beispiel gibt es einen Korb mit Äpfeln sind mit Orangen gemischt und der Entscheidungsbaum, wenn auf, wie Äpfel aussehen in Bezug auf ihre Farbe und Größe trainiert wird, wird Orangen in ihren eigenen Korb und Orangen in ihrem eigenen Korb zu trennen.

ID3-Algorithmus

ID3 steht für Iterative Dichotomiser 3 und wird so genannt, weil der Algorithmus bei jedem Schritt iterativ (wiederholt) Merkmale in zwei oder mehr Gruppen unterteilt.

ID3 wurde von Ross Quinlan erfunden und einen Top-Down-Greedy-Ansatz, um einen Entscheidungsbaum zu erstellen. In einfachen Worten bedeutet der greedy approach, dass der Baum von oben nach unten aufgebaut wird, und der gierige Ansatz (greedy approach) bedeutet, dass wir bei jeder Iteration das beste Merkmal zum aktuellen Zeitpunkt auswählen, um einen Knoten zu erstellen.

Im Allgemeinen wird ID3 nur für Klassifizierungsprobleme mit nominalen Daten verwendet (im Grunde Daten, die nicht gemessen werden können).

Abgesehen davon gibt es zwei Arten von Entscheidungsbäumen:

Klassifikationsbäume
Regressionsbäume

01: Klassifikationsbäume

Klassifizierungsbäume sind genau wie der Baum, den wir in diesem Artikel lernen werden, Merkmale ohne kontinuierliche numerische oder geordnete Werte, die wir klassifizieren wollen.

> Klassifikationsbäume ordnen Dinge in Kategorien ein.

02: Regressionsbäume

Diese werden mit geordneten Werten und mit kontinuierlichen Werten gebildet.

> Entscheidungsbaum sagt numerische Werte voraus.

Schritte im ID3-Algorithmus

01: Es beginnt mit dem Originaldatensatz als Wurzelknoten.

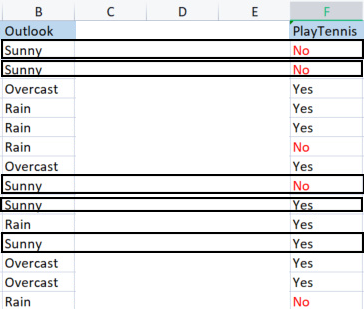
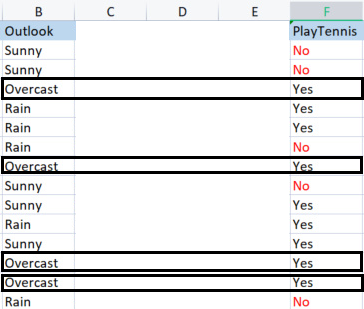
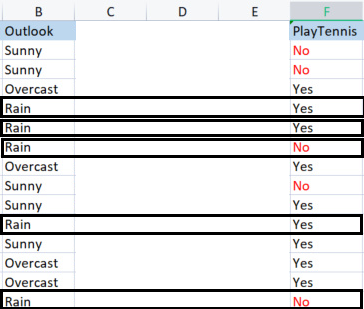
Um die Basisbibliothek zu erstellen, werden wir einen einfachen Datensatz über das Tennisspielen bei bestimmten Wetterbedingungen verwenden. Hier ist eine Übersicht über unseren Datensatz, es ist ein kleiner Datensatz (nur 14 Zeilen).

.

Um mit diesem Algorithmus einen Entscheidungsbaum zu erstellen, müssen wir verstehen, welche Attribute den größten Informationsgewinn von allen Attributen bieten, Lassen Sie mich das erklären.

Eines dieser Attribute (Spalten) muss zunächst ein Wurzelknoten sein , aber wie wird entschieden, welche Spalte ein Wurzelknoten sein soll? Hier nutzen wir den Informationsgewinn.

Informationsgewinn

Der Informationsgewinn berechnet die Verringerung der Entropie und misst, wie gut ein bestimmtes Merkmal die Zielklassen trennt oder klassifiziert. Das Merkmal mit dem höchsten Informationsgewinn wird als das beste Merkmal ausgewählt.

Entropie

Die Entropie ist das Maß für die Unsicherheit einer Zufallsvariablen, sie charakterisiert die Verunreinigung in der gegebenen Probe.

Die Formel für Entropie lautet:

Entropie-Formel eines EntscheidungsbaumstitlealtEntropie-Formel eines Entscheidungsbaumsalt

Als erstes müssen wir die Entropie des gesamten Datensatzes ermitteln, d. h. die Entropie der Zielvariablen, da alle diese Spalten auf die Zielspalte PlayTennis projiziert werden,

Spalte der Variablen PlayTennis

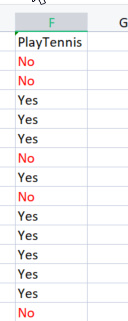
lassen Sie uns etwas Code schreiben,

Wir wissen mit Sicherheit, dass wir, bevor wir die Entropie unserer Zielvariablen ermitteln können, die Gesamtzahl der markierten negativen Werte haben müssen No und positiv markierte Werte Yes. Diese Werte könnten uns dabei helfen, die Wahrscheinlichkeiten der Elemente in unserer Spalte zu ermitteln, um solche Werte zu erhalten. Schreiben wir den entsprechenden Code in die Entropiefunktion.

double CDecisionTree::Entropy(int &SampleNumbers[],int total)
 {
    double Entropy = 0;
    double entropy_out =0; //the value of entropy that will be returned
     
     for (int i=0; i<ArraySize(SampleNumbers); i++)
        {                   
              double probability1 = Proba(SampleNumbers[i],total); 
              Entropy += probability1 * log2(probability1);
        }
     
    entropy_out = -Entropy;
    
    return(entropy_out);
 }

Die Funktion ist auf den ersten Blick leicht zu verstehen, vor allem, wenn Sie die Formel gelesen haben, aber achten Sie auf das Array SampleNumbers[]. Die Stichproben sind das Innere der Spalte. Wir können uns auch auf Stichproben beziehen, da die Klassifizierung zum Beispiel in diesem Zielspalte unsere Proben Yes und No sind.

Die erfolgreiche Ausführung der Funktion in der Spalte TargetArray führt zu:

12:37:48.394    TestScript      There are 5 No
12:37:48.394    TestScript      There are 9 Yes
12:37:48.394    TestScript      There are 2 classes
12:37:48.394    TestScript      "No"  "Yes"
12:37:48.394    TestScript      5     9
12:37:48.394    TestScript      Total contents = 14

Nachdem wir nun diese Zahlen haben, können wir die Entropie mit dieser Formel berechnen:

Wenn Sie sich die Formel anschauen, werden Sie feststellen, dass der Logarithmus, mit dem wir es hier zu tun haben, der zur Basis 2 ist, also Logarithmus zur Basis 2 (lesen Sie es, für weitere Informationen). Um den Logarithmus zur Basis 2 zu finden, teilen wir log2 durch den Logarithmus des Arguments:

double CDecisionTree::log2(double value)
 {
   return (log10(value)/log10(2));
 }

Da die Basis dieselbe ist, ist alles gut.

Ich habe auch eine Funktion Proba( ) geschrieben, mit der wir die Wahrscheinlichkeit einer Klasse von Werten ermitteln können, hier ist sie:

double CDecisionTree::Proba(int number,double total)
 {
    return(number/total);
 }

Der Elefant im Raum. Um die Wahrscheinlichkeit eines Elements in unserer Spalte zu ermitteln, müssen wir herausfinden, wie oft es in der Spalte vorkommt, und dies durch die Gesamtzahl aller Elemente in dieser Spalte teilen. Sie haben vielleicht bemerkt, dass es 5 Elemente mit No und 9 Elemente mit Yes.

Wahrscheinlichkeit von Nein = 5/14(Gesamtzahl der Elemente) = 0,357142..

Wahrscheinlichkeit von Ja = 9/14 (gleiche Geschichte) = 0,6428571...

Um schließlich die Entropie einer Attribut/Datensatzspalte zu ermitteln:

     for (int i=0; i<ArraySize(SampleNumbers); i++)
        {                   
              double probability1 = Proba(SampleNumbers[i],total); 
              Entropy += probability1 * log2(probability1);
        }
      entropy_out = -Entropy;

Wenn wir diese Funktion auf die Zielvariable anwenden, ist die Ausgabe:

13:37:54.273    TestScript      Proba1 0.35714285714285715
13:37:54.273    TestScript      Proba1 0.6428571428571429
13:37:54.273    TestScript      Entropy of the entire dataset = 0.9402859586706309

B A M!

Wir wissen, dass wir die Entropie des gesamten Datensatzes kennen, die im Grunde die Entropie der Werte von y ist, und wir haben die Funktion zur Ermittlung der Entropie zur Hand. Ermitteln wir die Entropie jeder einzelnen Spalte des Datensatzes.

Da wir nun die Entropie des gesamten Datensatzes haben, besteht der nächste Schritt darin, die Entropie der Mitglieder innerhalb jeder Spalte der unabhängigen Variablen zu ermitteln. Das Ziel der Ermittlung dieser Art von Entropie in den unabhängigen Variablen ist es, uns dabei zu helfen, den Informationsgewinn, für jede Datenspalte zu finden

Bevor wir unsere Bibliothek verwenden, um die Entropie der Outlook-Spalte zu ermitteln, lassen Sie uns diese von Hand berechnen, damit Sie ein klares Verständnis davon bekommen, was getan wird.

Wir nehmen die Spalte Ausblick im Vergleich zu ihrer Zielvariablen.

Outlook (Vorhersage) vs. PlayTennis-Spalte

Vorhersage vs. Playtennis

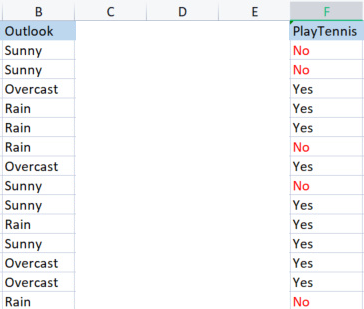
Anders als bei der Ermittlung der Entropie des gesamten Datensatzes, die auch als Entropie der Zielvariablen bezeichnet wird, müssen wir uns bei der Ermittlung der Entropie einer unabhängigen Variablen auf die Zielvariable beziehen, da dies unser Ziel ist,

Werte in Outlook (Vorhersage )

Wir haben 3 verschiedene Werte, nämlich Sunny (Sonne), Overcast (Wolken) und Rain (Regen). Wir müssen die Entropie jedes dieser Werte in Bezug auf ihre Zielvariable finden.

Samples(Sunny) (positive und negative Samples von Sunny) = [2 Positive (Yes), 3 Negative(No)]

Da wir nun die Anzahl der Positiven und Negativen haben, ist die Wahrscheinlichkeit für ein Ja beim Tennisspielen an einem sonnigen Tag

Wahrscheinlichkeit1= 2(Anzahl der Erscheinungen von Ja) / 5(Gesamtzahl der Sonnentage)

Also,

Im Kontrast dazu

Die Wahrscheinlichkeit, an einem sonnigen Tag nicht zu spielen, beträgt 0,6 , d. h. 3/5 = 0.6.

Schließlich wird die Entropie des Spielens an einem sonnigen Tag sein, siehe die Formel:

Entropie(Sunny) = - (P1*log2P1 +P2*log2P2)
Entropie(Sunny) = -(0,4*log2 0,4 + 0,6*log2 0,6)

Entropie(Sunny) = 0,97095

Nun wollen wir die Entropie von Overcast (bedeckt) ermitteln:

Stichproben bedeckter Himmel:

Positive Proben 4 (Proben mit Yes in der Zielspalte), Negative Proben 0 (Proben mit No in der Zielspalte), Diese Situation ist eine Ausnahme.

Ausnahmen im ID3-Algorithmus

Wenn es null (0) negative Stichproben gibt, während es positive Stichproben gibt, oder umgekehrt, wenn es null (0) positive Stichproben gibt, während es negative Stichproben gibt; in diesem Fall wird die Entropie auf null (0) gesetzt.

Wir sagen, dass es sich um einen reinen Knoten handelt, der nicht geteilt werden muss, da er homogene Proben hat. Sie werden besser verstehen, was ich damit meine, wenn wir einen Baum zeichnen.

Eine weitere Ausnahme ist,

wenn es eine gleiche Anzahl von positiven und negativen Proben gibt, dann ist die Entropie mathematisch gesehen Eins (1).

Die einzige Ausnahme, die wir effektiv behandeln müssen, ist, wenn der Wert Null in Proben auftaucht, weil Null kann dazu führen, dass zero divide (Teilen durch Null) hier ist die neue Funktion, mit der Fähigkeit, solche Ausnahmen zu behandeln.

double CDecisionTree::Entropy(int &SampleNumbers[],int total)
 {
    double Entropy = 0;
    double entropy_out =0; //the value of entropy that will be returned
     
     for (int i=0; i<ArraySize(SampleNumbers); i++)
        {       
            if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception
            
              double probability1 = Proba(SampleNumbers[i],total); 
              Entropy += probability1 * log2(probability1);
        }
     
     if (Entropy==0)     entropy_out = 0;  //handle the exception
     else                entropy_out = -Entropy;
    
    return(entropy_out);
 }

Abschließend wollen wir die Entropie des Regens bestimmen.

Regen-Proben;

Es gibt 3 positive Proben (Proben mit Ja in der Zielspalte).

Es gibt 2 negative Proben (Proben mit Nein in der Zielspalte).

Schlussendlich die Entropie des Tennisspiels an einem regnerischen Tag:

Entropy(Regen) = - (P1*log2P1 + P2*log2P2)
Entropy(Rain) = - (0.6*log2 0.6 + 0.4*log2 0.4)

Entropie(Rain) = 0,97095

Hier sind die Entropie-Werte, die wir aus der Outlook-Spalte erhalten haben:

Entropie aus der Outlook-Spalte
Entropie(Sunny) = 0,97095
Entropie(Overcast) = 0
Entropie(Rain) = 0,97095

So kann man also die Entropie von Proben manuell ermitteln. Wenn wir nun unser Programm verwenden, um diese Entropien zu ermitteln, wird die Ausgabe sein:

PD      0       13:47:20.571    TestScript      <<<<<<<<    Parent Entropy  0.94029  A = 0  >>>>>>>> 
FL      0       13:47:20.571    TestScript         <<<<<   C O L U M N  Outlook   >>>>>  
CL      0       13:47:20.571    TestScript           <<   Sunny   >> total > 5
MH      0       13:47:20.571    TestScript      "No"  "Yes"
DM      0       13:47:20.571    TestScript      3 2
CQ      0       13:47:20.571    TestScript      Entropy of Sunny = 0.97095
LD      0       13:47:20.571    TestScript           <<   Overcast   >> total > 4
OI      0       13:47:20.571    TestScript      "No"  "Yes"
MJ      0       13:47:20.571    TestScript      0 4
CM      0       13:47:20.571    TestScript      Entropy of Overcast = 0.00000
JD      0       13:47:20.571    TestScript           <<   Rain   >> total > 5
GN      0       13:47:20.571    TestScript      "No"  "Yes"
JH      0       13:47:20.571    TestScript      2 3
HR      0       13:47:20.571    TestScript      Entropy of Rain = 0.97095

Wir werden diese Werte verwenden, um den Informationsgewinn der gesamten Daten mit Hilfe der Formel zu ermitteln, die wir vorher besprochen haben.

Lassen Sie mich nun die Entropie manuell finden, damit Sie verstehen, was hinter verschlossenen Türen vor sich geht:

Informationsgewinn (IG) = Entropie des gesamten Datensatzes - Summe des Produkts aus der Wahrscheinlichkeit einer Stichprobe und ihrer Entropie

IG = E(dataset) - ( Prob(sunny) * E(sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain) )

IG = 0,9402 - ( 5/14 * (0,97095) + 4/14 * (0) + 5/14(0,97095) )

IG = 0,2467 (Dies ist ein Informationsgewinn der Outlook-Spalte)

Wenn wir die Formel in Code umwandeln, wird das zu:

double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_)
 {
    double IG = 0;
    
    for (int i=0; i<ArraySize(EntropyArr); i++)
      {  
        double prob = ClassNumbers[i]/double(rows_); 
        IG += prob * EntropyArr[i];
      }
     
     return(parent_entropy - IG);
 }

Funktionsaufruf:

    if (m_debug)  printf("<<<<<<  Column Information Gain %.5f >>>>>> \n",IGArr[i]);

Ausgabe:

PF      0       13:47:20.571    TestScript      <<<<<<  Column Information Gain 0.24675 >>>>>>

Nun müssen wir den Vorgang für alle Spalten wiederholen und ihre Informationsgewinne ermitteln. Das Ergebnis wird sein:

RH      0       13:47:20.571    TestScript (EURUSD,H1)  Default Parent Entropy 0.9402859586706309
PD      0       13:47:20.571    TestScript (EURUSD,H1)  <<<<<<<<    Parent Entropy  0.94029  A = 0  >>>>>>>> 
FL      0       13:47:20.571    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Outlook   >>>>>  
CL      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Sunny   >> total > 5
MH      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
DM      0       13:47:20.571    TestScript (EURUSD,H1)  3 2
CQ      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Sunny = 0.97095
LD      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Overcast   >> total > 4
OI      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
MJ      0       13:47:20.571    TestScript (EURUSD,H1)  0 4
CM      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Overcast = 0.00000
JD      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Rain   >> total > 5
GN      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
JH      0       13:47:20.571    TestScript (EURUSD,H1)  2 3
HR      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Rain = 0.97095
PF      0       13:47:20.571    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.24675 >>>>>> 
QP      0       13:47:20.571    TestScript (EURUSD,H1)  
KH      0       13:47:20.571    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Temp   >>>>>  
PR      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Hot   >> total > 4
QF      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
OS      0       13:47:20.571    TestScript (EURUSD,H1)  2 2
NK      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Hot = 1.00000
GO      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Mild   >> total > 6
OD      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
KQ      0       13:47:20.571    TestScript (EURUSD,H1)  2 4
GJ      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Mild = 0.91830
HQ      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Cool   >> total > 4
OJ      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
OO      0       13:47:20.571    TestScript (EURUSD,H1)  1 3
IH      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Cool = 0.81128
OR      0       13:47:20.571    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.02922 >>>>>> 
ID      0       13:47:20.571    TestScript (EURUSD,H1)  
HL      0       13:47:20.571    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Humidity   >>>>>  
FH      0       13:47:20.571    TestScript (EURUSD,H1)       <<   High   >> total > 7
KM      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
HF      0       13:47:20.571    TestScript (EURUSD,H1)  4 3
GQ      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of High = 0.98523
QK      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Normal   >> total > 7
GR      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
DD      0       13:47:20.571    TestScript (EURUSD,H1)  1 6
OF      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Normal = 0.59167
EJ      0       13:47:20.571    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.15184 >>>>>> 
EL      0       13:47:20.571    TestScript (EURUSD,H1)  
GE      0       13:47:20.571    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Wind   >>>>>  
IQ      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Weak   >> total > 8
GE      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
EO      0       13:47:20.571    TestScript (EURUSD,H1)  2 6
LI      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Weak = 0.81128
FS      0       13:47:20.571    TestScript (EURUSD,H1)       <<   Strong   >> total > 6
CK      0       13:47:20.571    TestScript (EURUSD,H1)  "No"  "Yes"
ML      0       13:47:20.571    TestScript (EURUSD,H1)  3 3
HO      0       13:47:20.571    TestScript (EURUSD,H1)  Entropy of Strong = 1.00000
LE      0       13:47:20.571    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.04813 >>>>>> 
IE      0       13:47:20.571    TestScript (EURUSD,H1)

Da wir nun den Informationsgewinn für alle Spalten haben, beginnen wir mit dem Zeichnen unseres Entscheidungsbaums, aber wie?

Das Ziel dieses anfänglichen Prozesses war es, die Informationsgewinne für alle Spalten zu finden, so dass wir entscheiden können, welche Spalte der Wurzelknoten sein soll. Die Spalte mit einer großen Anzahl von Informationsgewinnen als alle anderen wird der Wurzelknoten, in diesem Fall hat der Ausblick den höchsten Informationsgewinn, so dass er der Wurzelknoten unseres Entscheidungsbaums wird.

Entscheidungsbaum erste Aufteilung

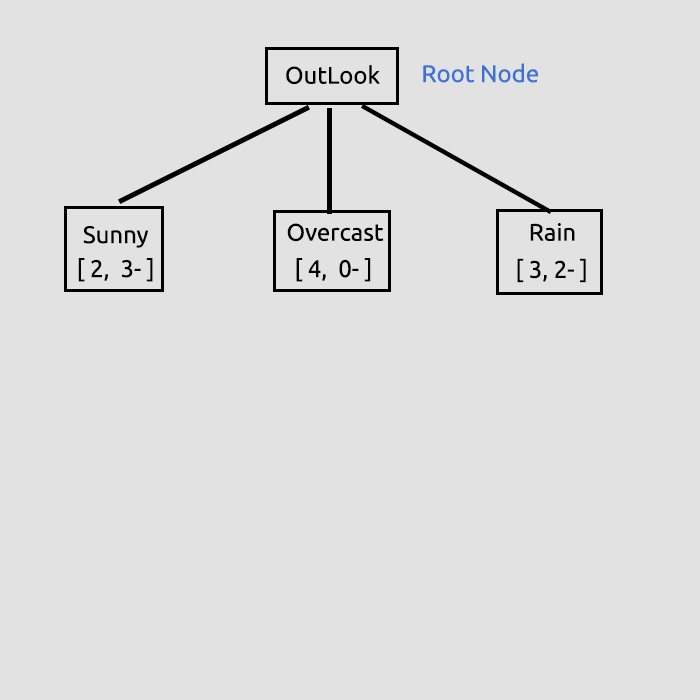
Wenn Sie das am Ende des Artikels verlinkte Skript Test-Skript ausführen, werden viele Informationen gedruckt, wenn Sie sich im Debug-Modus der Bibliothek befinden, das der Standard ist.

Der Informationsgewinn wurde von seiner Funktion erhalten und dann in einem Array von Doppelwerten gespeichert, das alle Informationsgewinne speichert. Der Maximalwert in einem Array wird schließlich unser Zielwert sein

         //--- Finding the Information Gain
                        
                        ArrayResize(IGArr,i+1); //information gains matches the columns number
                        
                        IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows);
                        
                        max_gain = ArrayMaximum(IGArr);

Der Ausdruck ist:

QR      0       13:47:20.571    TestScript (EURUSD,H1)  Parent Noce will be Outlook with IG = 0.24675
IK      0       13:47:20.574    TestScript (EURUSD,H1)  Parent Entropy Array and Class Numbers
NL      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny"    "Overcast" "Rain"    
NH      0       13:47:20.574    TestScript (EURUSD,H1)  0.9710 0.0000 0.9710
FR      0       13:47:20.574    TestScript (EURUSD,H1)  5 4 5

Weitere Erläuterungen zum Baum, den wir bis zu diesem Punkt gezogen haben:

Erklärungen zum Entscheidungsbaum

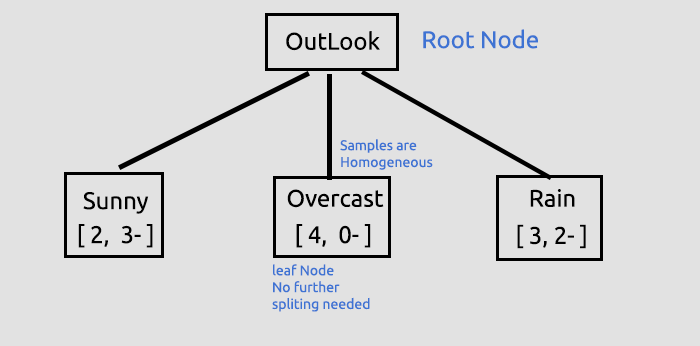
Dies war der erste, aber entscheidende Schritt, bei dem wir den Wurzelknoten gefunden und diesen Wurzelknoten in Zweige und Blätter aufgeteilt haben. Wir werden die Daten so lange aufteilen, bis es nichts mehr aufzuteilen gibt, hier werden wir den Prozess fortsetzen, indem wir den Zweig mit den Einträgen Sunny (sonnig) und den Zweig mit den Einträgen Rain (Regen) aufteilen.

Overcast (bedeckt) besteht aus homogenen Elementen (es ist sauber), so dass wir sagen, dass es vollständig klassifiziert wurde, wenn es um einen Entscheidungsbaum geht, nennen wir es ein Blatt. Es werden keine Zweige erzeugt.

Doch bevor wir die Daten weiter aufteilen, müssen wir einige wichtige Schritte mit dem aktuellen Datensatz durchführen,

KLASSIFIZIERUNG DER VERBLEIBENDEN MATRIX DES DATENSATZES

Wir müssen die verbleibende Matrix des Datensatzes so klassifizieren, dass die Zeilen mit den gleichen Werten in aufsteigender Reihenfolge angeordnet werden; dies wird bei der Erstellung von Zweigen und Blättern mit homogenem Inhalt hilfreich sein (etwas, das wir unbedingt erreichen wollen)

void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols)
 {
   string ClassifiedArr[];
   ArrayResize(ClassifiedArr,ArraySize(dataArr));
   
   int fill_start = 0, fill_ends = 0;
   int index = 0;
   for (int i = 0; i<ArraySize(Classes); i++)
     {
      int start = 0;  int curr_col = 0;
      for (int j = 0; j<ArraySize(dataArr); j++)
        { 
          curr_col++;
          
            if (Classes[i] == dataArr[j])
              {
                //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]);
                
                 if (curr_col == 1) 
                     fill_start =  j;
                 else
                   {
                      if (j>curr_col)
                        fill_start = j - (curr_col-1);
                      else fill_start = (curr_col-1) - j;
                          
                      fill_start  = fill_start;
                      //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start );
                      
                   }
                 
                 fill_ends = fill_start + cols; 
                 
                 //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i);
//---
                  //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break;
                  //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i);
                  
                  
                  for (int k=fill_start; k<fill_ends; k++)
                    {
                      index++;
                      //printf(" k %d index %d",k,index);
                      //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1);
                      ClassifiedArr[index-1] = dataArr[k];
                    }
                    
                if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs
              }
              
          if (curr_col == cols) curr_col = 0;
        } 
         
      if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs
     }
     
    ArrayCopy(dataArr,ClassifiedArr);
    ArrayFree(ClassifiedArr);
 }

Warum ist zu viel Code auskommentiert? Unsere Bibliothek muss noch verbessert werden, und die Kommentare dienen der Fehlersuche, und ich hoffe, Sie spielen damit.

Wenn wir diese Funktion aufrufen und die Ausgabe drucken, erhalten wir:

JG      0       13:47:20.574    TestScript (EURUSD,H1)  Classified matrix dataset
KL      0       13:47:20.574    TestScript (EURUSD,H1)  "Outlook"     "Temp"        "Humidity"    "Wind"        "PlayTennis "
GS      0       13:47:20.574    TestScript (EURUSD,H1)  [ 
QF      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny" "Hot"   "High"  "Weak"  "No"   
DN      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny"  "Hot"    "High"   "Strong" "No"    
JF      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny" "Mild"  "High"  "Weak"  "No"   
ND      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny"  "Cool"   "Normal" "Weak"   "Yes"   
PN      0       13:47:20.574    TestScript (EURUSD,H1)  "Sunny"  "Mild"   "Normal" "Strong" "Yes"   
EH      0       13:47:20.574    TestScript (EURUSD,H1)  "Overcast" "Hot"      "High"     "Weak"     "Yes"     
MH      0       13:47:20.574    TestScript (EURUSD,H1)  "Overcast" "Cool"     "Normal"   "Strong"   "Yes"     
MN      0       13:47:20.574    TestScript (EURUSD,H1)  "Overcast" "Mild"     "High"     "Strong"   "Yes"     
DN      0       13:47:20.574    TestScript (EURUSD,H1)  "Overcast" "Hot"      "Normal"   "Weak"     "Yes"     
MG      0       13:47:20.574    TestScript (EURUSD,H1)  "Rain" "Mild" "High" "Weak" "Yes" 
QO      0       13:47:20.574    TestScript (EURUSD,H1)  "Rain"   "Cool"   "Normal" "Weak"   "Yes"   
LN      0       13:47:20.574    TestScript (EURUSD,H1)  "Rain"   "Cool"   "Normal" "Strong" "No"    
LE      0       13:47:20.574    TestScript (EURUSD,H1)  "Rain"   "Mild"   "Normal" "Weak"   "Yes"   
FE      0       13:47:20.574    TestScript (EURUSD,H1)  "Rain"   "Mild"   "High"   "Strong" "No"    
GS      0       13:47:20.574    TestScript (EURUSD,H1)  ] 
DH      0       13:47:20.574    TestScript (EURUSD,H1)  columns = 5 rows = 70

B A M! Die Funktion funktioniert wie von Zauberhand

Okay, der nächste entscheidende Schritt ist

ENTFERNEN VON BLATTKNOTEN AUS DEM DATENSATZ

Vor der nächsten Iteration des gesamten Prozesses, den wir bis zu diesem Punkt durchgeführt haben, ist es sehr wichtig, die Blattknoten zu entfernen, da sie keine Verzweigungen bilden werden, was ja auch Sinn macht.

Wir entfernen alle Zeilen, die den Wert des Blattknotens haben. In diesem Fall entfernen wir alle Zeilen mit Overcast:

    //--- Search if there is zero entropy in the Array
         
            int zero_entropy_index = 0;
            bool zero_entropy = false;
            for (int e=0; e<ArraySize(P_EntropyArr); e++)
              if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; }
            
            if (zero_entropy) //if there is zero in the Entropy Array 
              {
                MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols);    
               
                rows_total = ArraySize(m_dataset); //New number of total rows from Array   
                 if (m_debug)
                  {
                    printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]);
                    ArrayPrint(DataColumnNames);
                    MatrixPrint(m_dataset,cols,rows_total);
                  }
                
                //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next
                
                ArrayRemove(P_EntropyArr,zero_entropy_index,1);
                ArrayRemove(p_Classes,zero_entropy_index,1);
                ArrayRemove(p_ClassNumbers,zero_entropy_index,1);
              }
            
            if (m_debug)  
             Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);

Die Ausgabe nach Ausführung dieses Code-Blocks ist,

NQ      0       13:47:20.574    TestScript (EURUSD,H1)  Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..
GP      0       13:47:20.574    TestScript (EURUSD,H1)  "Outlook"     "Temp"        "Humidity"    "Wind"        "PlayTennis "
KG      0       13:47:20.574    TestScript (EURUSD,H1)  [ 
FS      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny" "Hot"   "High"  "Weak"  "No"   
GK      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny"  "Hot"    "High"   "Strong" "No"    
EI      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny" "Mild"  "High"  "Weak"  "No"   
IP      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny"  "Cool"   "Normal" "Weak"   "Yes"   
KK      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny"  "Mild"   "Normal" "Strong" "Yes"   
JK      0       13:47:20.575    TestScript (EURUSD,H1)  "Rain" "Mild" "High" "Weak" "Yes" 
FL      0       13:47:20.575    TestScript (EURUSD,H1)  "Rain"   "Cool"   "Normal" "Weak"   "Yes"   
GK      0       13:47:20.575    TestScript (EURUSD,H1)  "Rain"   "Cool"   "Normal" "Strong" "No"    
OI      0       13:47:20.575    TestScript (EURUSD,H1)  "Rain"   "Mild"   "Normal" "Weak"   "Yes"   
IQ      0       13:47:20.575    TestScript (EURUSD,H1)  "Rain"   "Mild"   "High"   "Strong" "No"    
LG      0       13:47:20.575    TestScript (EURUSD,H1)  ] 
IL      0       13:47:20.575    TestScript (EURUSD,H1)  columns = 5 rows = 50
HE      0       13:47:20.575    TestScript (EURUSD,H1)  rows total 50 Rain 5

B A M!

Der letzte, aber nicht minder wichtige Prozess an dieser Stelle ist:

ENTFERNEN DER ÜBERGEORDNETEN SPALTE ODER DES WURZELKNOTENS AUS DEM DATENSATZ

Da wir ihn bereits als Wurzelknoten erkannt und in unseren Baum eingezeichnet haben, brauchen wir ihn nicht mehr in unserem Datensatz, unser Datensatz muss mit unklassifizierten Werten bleiben.

//---    REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET

            MatrixRemoveColumn(m_dataset,max_gain,cols);
         
         // After removing the columns assign the new values to these global variables
         
            cols = cols-1;   // remove that one column that has been removed
            rows_total = rows_total - single_rowstotal; //remove the size of one column rows
            
         // we also remove the column from column names Array 
            ArrayRemove(DataColumnNames,max_gain,1);

//---

            printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1);
            ArrayPrint(DataColumnNames);
            MatrixPrint(m_dataset,cols,rows_total);

Die Ausgabe dieses Code-Blocks schaut so aus:

OM      0       13:47:20.575    TestScript (EURUSD,H1)  Column 1 removed from the Matrix, The remaining dataset is
ON      0       13:47:20.575    TestScript (EURUSD,H1)  "Temp"        "Humidity"    "Wind"        "PlayTennis "
HF      0       13:47:20.575    TestScript (EURUSD,H1)  [ 
CR      0       13:47:20.575    TestScript (EURUSD,H1)  "Hot"  "High" "Weak" "No"  
JE      0       13:47:20.575    TestScript (EURUSD,H1)  "Hot"    "High"   "Strong" "No"    
JR      0       13:47:20.575    TestScript (EURUSD,H1)  "Mild" "High" "Weak" "No"  
NG      0       13:47:20.575    TestScript (EURUSD,H1)  "Cool"   "Normal" "Weak"   "Yes"   
JI      0       13:47:20.575    TestScript (EURUSD,H1)  "Mild"   "Normal" "Strong" "Yes"   
PR      0       13:47:20.575    TestScript (EURUSD,H1)  "Mild" "High" "Weak" "Yes" 
JJ      0       13:47:20.575    TestScript (EURUSD,H1)  "Cool"   "Normal" "Weak"   "Yes"   
QQ      0       13:47:20.575    TestScript (EURUSD,H1)  "Cool"   "Normal" "Strong" "No"    
OG      0       13:47:20.575    TestScript (EURUSD,H1)  "Mild"   "Normal" "Weak"   "Yes"   
KD      0       13:47:20.575    TestScript (EURUSD,H1)  "Mild"   "High"   "Strong" "No"    
DR      0       13:47:20.575    TestScript (EURUSD,H1)  ]

B A M!

Der Grund, warum wir in der Lage waren, einige Teile des Datensatzes sicher zu verlassen, liegt darin, dass die Bibliothek einen Baum zeichnet, der Hinweise darauf gibt, wohin der Datensatz geht, hier ist ein Baum, den wir bis zu diesem Punkt gezeichnet haben.

Entscheidungsbaum-Textdatei

Sieht hässlich aus, aber es ist gut genug für Demonstrationszwecke. Wir werden versuchen, es mit HTML in den nächsten Artikel-Serie. Helfen Sie mir das in meinem GitHub-Repository zu erreichen, unten, über den Link dorthin. Lassen Sie mich jetzt durch die Beschreibung der verbleibenden Prozess in den Aufbau eines Baumes zu beenden, Die Protokolle dieses Iterationsprozesses, bis es nichts mehr zu teilen gibt, ist wie folgt:

HI      0       13:47:20.575    TestScript (EURUSD,H1)  Final Parent Entropy Array and Class Numbers
RK      0       13:47:20.575    TestScript (EURUSD,H1)  "Sunny" "Rain" 
CL      0       13:47:20.575    TestScript (EURUSD,H1)  0.9710 0.9710
CE      0       13:47:20.575    TestScript (EURUSD,H1)  5 5
EH      0       13:47:20.575    TestScript (EURUSD,H1)  <<<<<<<<    Parent Entropy  0.97095  A = 1  >>>>>>>> 
OF      0       13:47:20.575    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Temp   >>>>>  
RP      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Hot   >> total > 2
MD      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
MQ      0       13:47:20.575    TestScript (EURUSD,H1)  2 0
QE      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Hot = 0.00000
FQ      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Mild   >> total > 5
KJ      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
NO      0       13:47:20.575    TestScript (EURUSD,H1)  2 3
DH      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Mild = 0.97095
IS      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Cool   >> total > 3
KH      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
LM      0       13:47:20.575    TestScript (EURUSD,H1)  1 2
FN      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Cool = 0.91830
KD      0       13:47:20.575    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.20999 >>>>>> 
EF      0       13:47:20.575    TestScript (EURUSD,H1)  
DJ      0       13:47:20.575    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Humidity   >>>>>  
HJ      0       13:47:20.575    TestScript (EURUSD,H1)       <<   High   >> total > 5
OS      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
FD      0       13:47:20.575    TestScript (EURUSD,H1)  4 1
NG      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of High = 0.72193
KM      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Normal   >> total > 5
CP      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
JR      0       13:47:20.575    TestScript (EURUSD,H1)  1 4
MD      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Normal = 0.72193
EL      0       13:47:20.575    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.24902 >>>>>> 
IN      0       13:47:20.575    TestScript (EURUSD,H1)  
CS      0       13:47:20.575    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Wind   >>>>>  
OS      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Weak   >> total > 6
CK      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
GM      0       13:47:20.575    TestScript (EURUSD,H1)  2 4
OO      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Weak = 0.91830
HE      0       13:47:20.575    TestScript (EURUSD,H1)       <<   Strong   >> total > 4
GI      0       13:47:20.575    TestScript (EURUSD,H1)  "No"  "Yes"
OJ      0       13:47:20.575    TestScript (EURUSD,H1)  3 1
EM      0       13:47:20.575    TestScript (EURUSD,H1)  Entropy of Strong = 0.81128
PG      0       13:47:20.575    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.09546 >>>>>> 
EG      0       13:47:20.575    TestScript (EURUSD,H1)  
HK      0       13:47:20.575    TestScript (EURUSD,H1)  Parent Noce will be Humidity with IG = 0.24902
OI      0       13:47:20.578    TestScript (EURUSD,H1)  Parent Entropy Array and Class Numbers
JO      0       13:47:20.578    TestScript (EURUSD,H1)  "High"   "Normal" "Cool"  
QJ      0       13:47:20.578    TestScript (EURUSD,H1)  0.7219 0.7219 0.9183
QO      0       13:47:20.578    TestScript (EURUSD,H1)  5 5 3
PJ      0       13:47:20.578    TestScript (EURUSD,H1)  Classified matrix dataset
NM      0       13:47:20.578    TestScript (EURUSD,H1)  "Temp"        "Humidity"    "Wind"        "PlayTennis "
EF      0       13:47:20.578    TestScript (EURUSD,H1)  [ 
FM      0       13:47:20.578    TestScript (EURUSD,H1)  "Hot"  "High" "Weak" "No"  
OD      0       13:47:20.578    TestScript (EURUSD,H1)  "Hot"    "High"   "Strong" "No"    
GR      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild" "High" "Weak" "No"  
QG      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild" "High" "Weak" "Yes" 
JD      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild"   "High"   "Strong" "No"    
KS      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool"   "Normal" "Weak"   "Yes"   
OJ      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild"   "Normal" "Strong" "Yes"   
CL      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool"   "Normal" "Weak"   "Yes"   
LJ      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool"   "Normal" "Strong" "No"    
NH      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild"   "Normal" "Weak"   "Yes"   
ER      0       13:47:20.578    TestScript (EURUSD,H1)  ] 
LI      0       13:47:20.578    TestScript (EURUSD,H1)  columns = 4 rows = 40
CQ      0       13:47:20.578    TestScript (EURUSD,H1)  rows total 36 High 5
GH      0       13:47:20.578    TestScript (EURUSD,H1)  Column 2 removed from the Matrix, The remaining dataset is
MP      0       13:47:20.578    TestScript (EURUSD,H1)  "Temp"        "Wind"        "PlayTennis "
QG      0       13:47:20.578    TestScript (EURUSD,H1)  [ 
LL      0       13:47:20.578    TestScript (EURUSD,H1)  "Hot"  "Weak" "No"  
OE      0       13:47:20.578    TestScript (EURUSD,H1)  "Hot"    "Strong" "No"    
QQ      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild" "Weak" "No"  
QE      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
LQ      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild"   "Strong" "No"    
HE      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
RM      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild"   "Strong" "Yes"   
PF      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
MR      0       13:47:20.578    TestScript (EURUSD,H1)  "Cool"   "Strong" "No"    
IF      0       13:47:20.578    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
EN      0       13:47:20.578    TestScript (EURUSD,H1)  ] 
ME      0       13:47:20.578    TestScript (EURUSD,H1)  columns = 3 rows = 22
ER      0       13:47:20.578    TestScript (EURUSD,H1)  Final Parent Entropy Array and Class Numbers
HK      0       13:47:20.578    TestScript (EURUSD,H1)  "High"   "Normal" "Cool"  
CQ      0       13:47:20.578    TestScript (EURUSD,H1)  0.7219 0.7219 0.9183
OK      0       13:47:20.578    TestScript (EURUSD,H1)  5 5 3
NS      0       13:47:20.578    TestScript (EURUSD,H1)  <<<<<<<<    Parent Entropy  0.91830  A = 2  >>>>>>>> 
JM      0       13:47:20.578    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Temp   >>>>>  
CG      0       13:47:20.578    TestScript (EURUSD,H1)       <<   Hot   >> total > 2
DM      0       13:47:20.578    TestScript (EURUSD,H1)  "No"  "Yes"
LF      0       13:47:20.578    TestScript (EURUSD,H1)  2 0
HN      0       13:47:20.578    TestScript (EURUSD,H1)  Entropy of Hot = 0.00000
OJ      0       13:47:20.578    TestScript (EURUSD,H1)       <<   Mild   >> total > 5
JS      0       13:47:20.578    TestScript (EURUSD,H1)  "No"  "Yes"
GD      0       13:47:20.578    TestScript (EURUSD,H1)  2 3
QG      0       13:47:20.578    TestScript (EURUSD,H1)  Entropy of Mild = 0.97095
LL      0       13:47:20.578    TestScript (EURUSD,H1)       <<   Cool   >> total > 3
JQ      0       13:47:20.578    TestScript (EURUSD,H1)  "No"  "Yes"
IR      0       13:47:20.578    TestScript (EURUSD,H1)  1 2
OE      0       13:47:20.578    TestScript (EURUSD,H1)  Entropy of Cool = 0.91830
RO      0       13:47:20.578    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.15733 >>>>>> 
PO      0       13:47:20.578    TestScript (EURUSD,H1)  
JS      0       13:47:20.578    TestScript (EURUSD,H1)     <<<<<   C O L U M N  Wind   >>>>>  
JR      0       13:47:20.578    TestScript (EURUSD,H1)       <<   Weak   >> total > 6
NH      0       13:47:20.578    TestScript (EURUSD,H1)  "No"  "Yes"
JM      0       13:47:20.578    TestScript (EURUSD,H1)  2 4
JL      0       13:47:20.578    TestScript (EURUSD,H1)  Entropy of Weak = 0.91830
QD      0       13:47:20.578    TestScript (EURUSD,H1)       <<   Strong   >> total > 4
JN      0       13:47:20.578    TestScript (EURUSD,H1)  "No"  "Yes"
JK      0       13:47:20.578    TestScript (EURUSD,H1)  3 1
DM      0       13:47:20.578    TestScript (EURUSD,H1)  Entropy of Strong = 0.81128
JF      0       13:47:20.578    TestScript (EURUSD,H1)  <<<<<<  Column Information Gain 0.04281 >>>>>> 
DG      0       13:47:20.578    TestScript (EURUSD,H1)  
LI      0       13:47:20.578    TestScript (EURUSD,H1)  Parent Noce will be Temp with IG = 0.15733
LH      0       13:47:20.584    TestScript (EURUSD,H1)  Parent Entropy Array and Class Numbers
GR      0       13:47:20.584    TestScript (EURUSD,H1)  "Hot"  "Mild" "Cool"
CD      0       13:47:20.584    TestScript (EURUSD,H1)  0.0000 0.9710 0.9183
GN      0       13:47:20.584    TestScript (EURUSD,H1)  2 5 3
CK      0       13:47:20.584    TestScript (EURUSD,H1)  Classified matrix dataset
RL      0       13:47:20.584    TestScript (EURUSD,H1)  "Temp"        "Wind"        "PlayTennis "
NK      0       13:47:20.584    TestScript (EURUSD,H1)  [ 
CQ      0       13:47:20.584    TestScript (EURUSD,H1)  "Hot"  "Weak" "No"  
LI      0       13:47:20.584    TestScript (EURUSD,H1)  "Hot"    "Strong" "No"    
JM      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "No"  
NI      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
CL      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild"   "Strong" "No"    
KI      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild"   "Strong" "Yes"   
LR      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
KJ      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
IQ      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
DE      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool"   "Strong" "No"    
NR      0       13:47:20.584    TestScript (EURUSD,H1)  ] 
OI      0       13:47:20.584    TestScript (EURUSD,H1)  columns = 3 rows = 30
OO      0       13:47:20.584    TestScript (EURUSD,H1)  Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..
HL      0       13:47:20.584    TestScript (EURUSD,H1)  "Temp"        "Wind"        "PlayTennis "
DJ      0       13:47:20.584    TestScript (EURUSD,H1)  [ 
DL      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "No"  
LH      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
QL      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild"   "Strong" "No"    
MH      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild"   "Strong" "Yes"   
RQ      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Weak" "Yes" 
MI      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
KQ      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool" "Weak" "Yes" 
FD      0       13:47:20.584    TestScript (EURUSD,H1)  "Cool"   "Strong" "No"    
HQ      0       13:47:20.584    TestScript (EURUSD,H1)  ] 
NN      0       13:47:20.584    TestScript (EURUSD,H1)  columns = 3 rows = 24
IF      0       13:47:20.584    TestScript (EURUSD,H1)  rows total 24 Mild 5
CO      0       13:47:20.584    TestScript (EURUSD,H1)  Column 1 removed from the Matrix, The remaining dataset is
DM      0       13:47:20.584    TestScript (EURUSD,H1)  "Wind"        "PlayTennis "
PD      0       13:47:20.584    TestScript (EURUSD,H1)  [ 
LN      0       13:47:20.584    TestScript (EURUSD,H1)  "Weak" "No"  
JI      0       13:47:20.584    TestScript (EURUSD,H1)  "Weak" "Yes" 
EL      0       13:47:20.584    TestScript (EURUSD,H1)  "Strong" "No"    
GO      0       13:47:20.584    TestScript (EURUSD,H1)  "Strong" "Yes"   
JG      0       13:47:20.584    TestScript (EURUSD,H1)  "Weak" "Yes" 
JN      0       13:47:20.584    TestScript (EURUSD,H1)  "Weak" "Yes" 
JE      0       13:47:20.584    TestScript (EURUSD,H1)  "Weak" "Yes" 
EP      0       13:47:20.584    TestScript (EURUSD,H1)  "Strong" "No"    
HK      0       13:47:20.584    TestScript (EURUSD,H1)  ] 
PP      0       13:47:20.584    TestScript (EURUSD,H1)  columns = 2 rows = 10
HG      0       13:47:20.584    TestScript (EURUSD,H1)  Final Parent Entropy Array and Class Numbers
FQ      0       13:47:20.584    TestScript (EURUSD,H1)  "Mild" "Cool"
OF      0       13:47:20.584    TestScript (EURUSD,H1)  0.9710 0.9183
IO      0       13:47:20.584    TestScript (EURUSD,H1)  5 3

HIER IST EIN ÜBERBLICK ÜBER DIE FUNKTION BUILD TREE. Ich fand dieses Stück Code schwer und verwirrend zu lesen, dass trotz des Prozesses scheint einfach, wenn die Werte manuell zu berechnen, so habe ich beschlossen, es im Detail auf diesem Abschnitt zu erklären.

void CDecisionTree::BuildTree(void)
 {   
    int ClassNumbers[];
    
    int max_gain = 0;
    double IGArr[]; 
    //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal);
    
    string p_Classes[];     //parent classes
    double P_EntropyArr[];  //Parent Entropy
    int p_ClassNumbers[]; //parent/ Target variable class numbers
    
    GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers);
    
    ArrayResize(P_EntropyArr,1);
    P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal);

//--- temporary disposable arrays for parent node information

   string TempP_Classes[];
   double TempP_EntropyArr[];
   int    TempP_ClassNumbers[];
   
//---

    if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]);
   
    int cols = m_colschosen; 
     
        
      for (int A =0; A<ArraySize(P_EntropyArr); A++)  
        {
           printf("<<<<<<<<    Parent Entropy  %.5f  A = %d  >>>>>>>> ",P_EntropyArr[A],A);
           
           
             for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn
               {
                  int rows = ArraySize(m_dataset)/cols;
                    
                    string Arr[]; //ArrayFor the current column
                    string ArrTarg[]; //Array for the current target
                    
                    ArrayResize(Arr,rows);
                    ArrayResize(ArrTarg,rows);
                    
                       printf("   <<<<<   C O L U M N  %s   >>>>>  ",DataColumnNames[i]);
                       int index_target=cols-1;
                       for (int j=0; j<rows; j++) //get column data and its target column
                          {
                              int index = i+j * cols;
                              //Print("index ",index);
                              Arr[j] = m_dataset[index];
         
                              //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]);
                              ArrTarg[j] = m_dataset[index_target];
                              
                              //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); 
                              
                              index_target += cols; //the last index of all the columns
                          }  
           
         //--- Finding the Entropy
                        
                     //The function to find the Entropy of samples in a given column inside its loop
                        //then restores all the entropy into one array
                
                        
         //--- Finding the Information Gain
                  
                        //The Function to find the information gain from the entropy array above

         //---

                        if (i == max_gain)
                         { 
                          //Get the maximum information gain of all the information gain in all columns then 
                        //store it to the parent information gain
                         }
                  
         //---
                  
                  ZeroMemory(ClassNumbers);
                  ZeroMemory(SamplesNumbers);
                  
               }
               
         //---- Get the parent Entropy, class and class numbers
               // here we store the obtained parent class from the information gain metric then we store them into a parent array
                  ArrayCopy(p_Classes,TempP_Classes);
                  ArrayCopy(P_EntropyArr,TempP_EntropyArr);
                  ArrayCopy(p_ClassNumbers,TempP_ClassNumbers);
               
         //---
         
            string Node[1]; 
            Node[0] = DataColumnNames[max_gain];
            
            if (m_debug)
            printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]);
            
            if (A == 0)
             DrawTree(Node,"parent",A);

             DrawTree(p_Classes,"child",A);
            
       
            
         //---  CLASSIFY THE MATRIX
         MatrixClassify(m_dataset,p_Classes,cols);
         
          
         //--- Search if there is zero entropy in Array if there is any remove its data from the dataset
                 

            if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; }
            
            if (zero_entropy) //if there is zero in the Entropy Array 
              {
                MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols);    
               
                rows_total = ArraySize(m_dataset); //New number of total rows from Array   
           
                
                //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next
                
                ArrayRemove(P_EntropyArr,zero_entropy_index,1);
                ArrayRemove(p_Classes,zero_entropy_index,1);
                ArrayRemove(p_ClassNumbers,zero_entropy_index,1);
              }
            
            if (m_debug)  
             Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
            
//---    REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET

            MatrixRemoveColumn(m_dataset,max_gain,cols);
         
         // After removing the columns assing the new values to these global variables
         
            cols = cols-1;   // remove that one column that has been removed
            rows_total = rows_total - single_rowstotal; //remove the size of one column rows
            
         // we also remove the column from column names Array 
            ArrayRemove(DataColumnNames,max_gain,1);

            
//---

         
      }

      
 }

Die Quintessenz

Sie verstehen nun die grundlegenden Berechnungen, die mit Klassifizierungsbäumen verbunden sind. Dies ist ein schwieriges und langes Thema, das in einem Artikel zu behandeln ist, und ich hoffe, dass ich es in den nächsten ein oder zwei Artikeln vervollständigen kann,

Danke fürs Lesen! Mein GitHub-Repository finden Sie hier: https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5

Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11061

Beigefügte Dateien |

ZIP herunterladen

decisiontree_2.zip (42.95 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 14): Hinzufügen des Volumens zum Preis (II)

Heute werden wir unserem EA weitere Ressourcen hinzufügen. Dieser interessante Artikel kann einige neue Ideen und Methoden zur Präsentation von Informationen liefern. Gleichzeitig kann es Ihnen helfen, kleinere Fehler in Ihren Projekten zu beheben.

Neuronale Netze leicht gemacht (Teil 14): Datenclustering

Es ist mehr als ein Jahr her, dass ich meinen letzten Artikel veröffentlicht habe. Das ist eine ganze Menge Zeit, um Ideen zu überarbeiten und neue Ansätze zu entwickeln. In dem neuen Artikel möchte ich von der bisher verwendeten Methode des überwachten Lernens abweichen. Diesmal werden wir uns mit Algorithmen des unüberwachten Lernens beschäftigen. Wir werden insbesondere einen der Clustering-Algorithmen - K-Means - betrachten.

DoEasy. Steuerung (Teil 6): Paneel-Steuerung, automatische Größenanpassung des Containers an den inneren Inhalt

In diesem Artikel werde ich meine Arbeit an dem WinForms-Objekt Panel fortsetzen und seine automatische Größenanpassung an die allgemeine Größe der Dock-Objekte, die sich innerhalb des Paneels befinden, implementieren. Außerdem werde ich die neuen Eigenschaften zum Objekt der Symbolbibliothek hinzufügen.

Lernen Sie, wie man ein Handelssystem mit Williams PR entwirft

Ein neuer Artikel in unserer Serie über das Lernen, wie man ein Handelssystem durch die beliebtesten technischen Indikatoren von MQL5 zu entwerfen, um in den MetaTrader 5 verwendet werden. In diesem Artikel lernen wir, wie man ein Handelssystem mit Hilfe des Indikators Williams' %R entwickelt.