Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 5) : Arbres de Décision
Qu'est-ce qu'un Arbre de Décision ?
Un arbre de décision est un type de technique de Machine Learning (Apprentissage Automatique) supervisé utilisé pour catégoriser ou faire des prédictions sur la base des réponses données à une série de questions précédentes. Un modèle est une forme d'apprentissage supervisé, ce qui signifie que le modèle est formé et testé sur un ensemble de données contenant la catégorisation souhaitée.
L'arbre de décision ne fournit pas toujours des réponses ou des décisions claires. Il présente plutôt les options de manière à ce que le data scientist puisse prendre sa propre décision en connaissance de cause. Les arbres de décision imitent la façon dont nous pensons, de sorte qu'il est généralement facile pour les data scientists de comprendre et d'interpréter les résultats.

Alerte sur la terminologie !
J'ai oublié de décrire la terminologie de l'apprentissage supervisé et non supervisé dans le premier article de cette série.
Apprentissage Supervisé
L'apprentissage supervisé est une approche de la création de l'intelligence artificielle (IA), dans laquelle un algorithme informatique est formé sur des données d'entrée pour un résultat particulier. Le modèle est formé jusqu'à ce qu'il puisse détecter les modèles et les relations sous-jacents entre les données d'entrée et les étiquettes de sortie, ce qui lui permet de produire des résultats précis lorsqu'il est confronté à des données inédites.
Contrairement à l'apprentissage supervisé, l'algorithme est ici présenté avec des données non étiquetées et est conçu pour détecter des modèles ou des similitudes par lui-même.
Les algorithmes couramment utilisés dans les programmes d'apprentissages supervisés sont les suivants :
- Régression linéaire
- Régression logistique
- Arbres de Décision
- Machines à Vecteurs de Support
- Forêts aléatoires
La principale différence entre l'apprentissage supervisé et l’apprentissage non supervisé réside dans la manière dont l'algorithme apprend. Dans l'apprentissage non supervisé, l'algorithme reçoit des données non étiquetées comme ensemble d'apprentissage. Contrairement à l'apprentissage supervisé, il n'y a pas de valeurs de sortie correctes ; l'algorithme détermine des modèles et des similitudes dans les données plutôt que de les relier à des mesures externes. Dit autrement, les algorithmes peuvent fonctionner librement pour en apprendre davantage sur les données et trouver des éléments intéressants ou inattendus que les êtres humains ne recherchaient pas.
Nous en sommes actuellement à l'apprentissage supervisé, mais nous aborderons l'apprentissage non supervisé dans de prochains articles.
Comment fonctionnent les Arbres de Décision ?
Les Arbres de Décision utilisent plusieurs algorithmes pour décider de diviser un nœud en deux ou plusieurs sous-ensembles de nœuds. La création de sous-nœuds augmente l'homogénéité des sous-nœuds résultants. En d'autres termes, nous pouvons dire que la pureté du nœud augmente, en ce qui concerne la variable cible. L'algorithme d’un arbre de décision divise les nœuds en fonction de toutes les variables disponibles et sélectionne ensuite la division qui donne les sous-nœuds les plus homogènes.
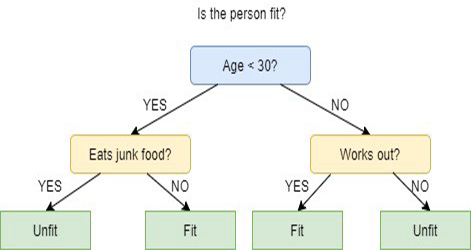
La sélection de l'algorithme est basée sur le type des variables cibles.
Les algorithmes utilisés dans les arbres de décision sont les suivants :
- ID3 > Extension de D3
- C4.5 > Successeur de ID3
- CART > Arbre de Classification et de Régression
- CHAID > Chi-square Automatic Interaction Detection (Détection Automatique des Interactions Chi-carré), effectue des divisions à plusieurs niveaux lors du calcul des arbres de classification.
- MARS > Splines de Régression Adaptatives Multivariées
Dans cet article, je vais créer un arbre de décision basé sur l'algorithme ID3. Nous discuterons et utiliserons des autres algorithmes dans les prochains articles de cette série.
Objectif d'un Arbre de Décision
L'objectif principal de l'algorithme des arbres de décision est de séparer les données impures, les données pures ou celles proches des nœuds. Par exemple, un panier contient des pommes mélangées à des oranges et l'arbre de décision, lorsqu'il est entraîné sur l'aspect des pommes en termes de couleur et de taille, séparera les oranges dans leur propre panier et les oranges dans leur propre panier également.
Algorithme ID3
ID3 signifie Iterative Dichotomiser 3 et est nommé ainsi parce que l'algorithme effectue des dichotomies successives (i.e. divise de façon répétée) les caractéristiques en deux groupes ou plus à chaque étape.
Inventé par Ross Quinlan, l’ID3 utilise une approche gourmande descendante pour construire un arbre de décision. En d'autres termes, l'approche gourmande descendante signifie qu'elle commence à construire l'arbre à partir du sommet et l'approche gourmande signifie qu'à chaque itération, la meilleure caractéristique au moment présent est sélectionnée pour créer un nœud.
En général, ID3 n'est utilisé que pour les problèmes de classification avec des données nominales (des données qui ne peuvent pas être mesurées).
Ceci étant dit, il existe 2 types d'Arbres de Décision :
- Arbres de Classification
- Arbres de Régression
1 - Arbres de Classification
Les Arbres de Classification sont exactement comme l'arbre que nous sommes sur le point de voir dans cet article, avec des caractéristiques sans valeurs numériques continues ou ordonnées, et que nous voulons classer.
Les Arbres de Classification classent les éléments en catégories.
2 - Arbres de Régression
Les Arbres de Régression sont construits avec des valeurs ordonnées et des valeurs continues.
L’Arbre de Décision prédit des valeurs numériques.
Étapes de l'algorithme ID3
1 - Le Nœud racine comprend l'ensemble de données original.
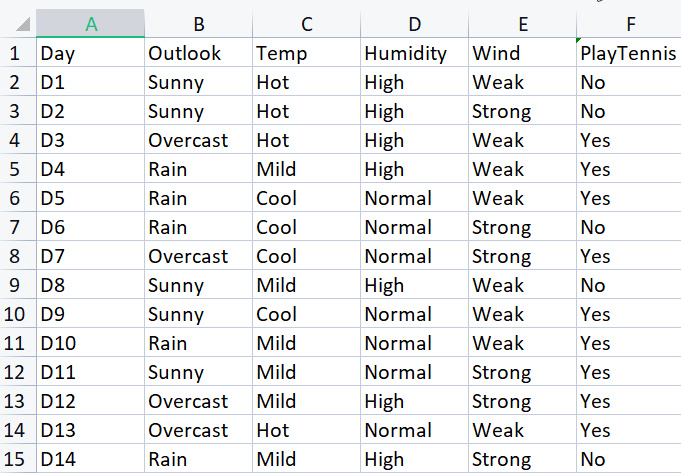
Pour construire la bibliothèque de base, nous utiliserons un jeu de données simple sur la pratique du tennis dans certaines conditions météorologiques. Voici l'aperçu de notre jeu de données (il s'agit d'un petit jeu de données de seulement 14 lignes).
Pour dessiner un arbre de décision à l'aide de cet algorithme, nous devons comprendre quels sont les attributs qui fournissent le plus de gains d'informations. Je m'explique.
L'un de ces attributs (colonnes) doit devenir le nœud racine pour commencer, mais comment décider quelle colonne doit être le nœud racine ? C'est ici que nous utilisons le Gain d'information.
Gain d'Information
Le gain d'information calcule la réduction de l'entropie et mesure à quel point une caractéristique donnée sépare ou classifie les classes cibles. La caractéristique présentant le gain d'information le plus élevé est considérée comme étant la meilleure.
![]()
Entropie
L'entropie est la mesure de l'incertitude d'une variable aléatoire. Elle caractérise l'impureté de l'échantillon donné.
La formule de l'entropie est la suivante :
![]()
La première chose à faire est de trouver l'entropie de l'ensemble des données, c'est-à-dire l'entropie des variables cibles, puisque toutes ces colonnes sont projetées vers la colonne cible PlayTennis.
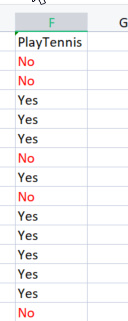
Ecrivons un peu de code,
Nous savons avec certitude qu'avant de pouvoir trouver l'entropie de nos variables cibles, nous devons avoir le nombre total de valeurs négatives marquées No et de valeurs positives marquées Yes. Ces valeurs pourraient nous aider à obtenir les probabilités des éléments à l'intérieur de notre colonne. Pour obtenir ces valeurs, écrivons le code dans la Fonction Entropie.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
La fonction est facile à comprendre au premier coup d'œil, surtout si vous avez lu la formule. Mais faites attention au tableau SampleNumbers[]. Les échantillons correspondent au contenu de la colonne. Nous pouvons également nous référer aux échantillons en tant que classes, par exemple dans cette colonne cible, nos échantillons sont Yes et No.
Si la fonction est exécutée avec succès sur la colonne TargetArray, le résultat sera le suivant :
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
Maintenant que nous avons ces chiffres, nous allons trouver l'entropie à l'aide de la formule suivante :
![]()
Si vous prêtez attention à la formule, vous remarquerez que le logarithme dont il est question ici est celui de base 2, c'est-à-dire le logarithme binaire(lire pour plus d'informations). Pour trouver le logarithme de base 2, nous divisons le log2 par le logarithme de la valeur de l'argument.
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
La base étant la même, tout va bien.
J'ai également codé une fonction Proba() pour nous aider à obtenir la probabilité d'une classe de valeurs :
double CDecisionTree::Proba(int number,double total) { return(number/total); }
Un éléphant dans la pièce. Pour déterminer la probabilité d'un élément dans notre colonne, il faut diviser le nombre de fois où il est apparu par le nombre total d'éléments dans cette colonne. Vous avez peut-être remarqué qu'il y a 5 éléments No et 9 éléments Yes :
probabilité de No = 5/14 (nombre total d'éléments) = 0,357142...
probabilité de Yes = 9/14 (même histoire) = 0,6428571...
Enfin, pour trouver l'entropie d'une colonne d'attributs / d'un ensemble de données :
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
Si nous exécutons cette fonction sur la variable Cible, le résultat sera le suivant :
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
B A M
Nous connaissons maintenant l'entropie de l'ensemble des données, qui est essentiellement l'entropie des valeurs de y, et nous disposons de la fonction permettant de trouver l'entropie. Déterminons l'entropie de chaque colonne de l'ensemble de données.
Maintenant que nous disposons de l'entropie de l'ensemble des données, l'étape suivante consiste à trouver l'entropie des membres de chaque colonne de variables indépendantes. L'objectif de ce type d'entropie dans les variables indépendantes est de nous aider à trouver le gain d'information pour chaque colonne de données.
Avant d'utiliser notre bibliothèque pour trouver l'entropie de la colonne Outlook, calculons-la à la main afin de bien comprendre ce que nous faisons.
Nous prenons la colonne Outlook par rapport à sa variable cible.
Colonne Outlook vs PlayTennis
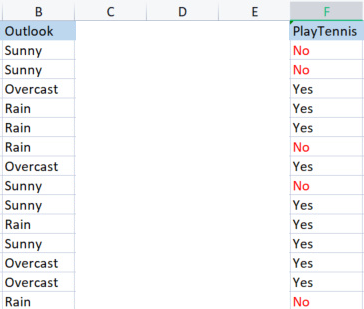
Contrairement à la façon dont nous avons trouvé l'entropie de l'ensemble des données, également appelée entropie de la variable cible, pour trouver l'entropie d'une variable indépendante, nous devons la référer à la variable cible.
Valeurs dans Outlook
Nous disposons de 3 valeurs différentes : Sunny (soleil), Overcast (ciel couvert) et Rain (pluie). Nous devons trouver l'entropie de chacune de ces valeurs par rapport à leur variable cible.
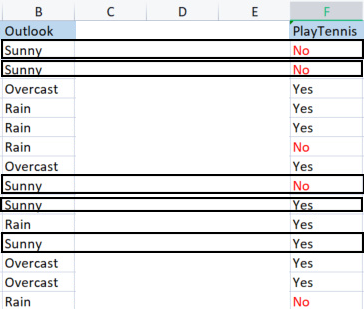
Echantillons (Sunny) (échantillons positifs et négatifs de Sunny) = [2 Positifs (Les Yes), 3 Négatifs(Les No)].
Maintenant que nous avons le nombre de positifs et de négatifs, la probabilité que Yes jouer au tennis par une journée ensoleillée sera de :
probabilité 1 = 2 (nombre de fois où Yes est apparu) / 5 (nombre total de jours ensoleillés)
soit 2/5 = 0,4
Par comparaison
La probabilité de ne pas jouer lors d'une journée ensoleillée sera de 0,6, c'est-à-dire 3/5 = 0,6
Enfin, l'entropie d'un jeu par temps ensoleillé sera, selon la formule :
Entropie (Sunny) = - (P1*log2P1 + P2*log2P2)
Entropie (Sunny) = -(0,4*log2 0,4 + 0,6*log2 0,6)
Entropie (Sunny) = 0,97095
Trouvons maintenant l'entropie de Overcast :
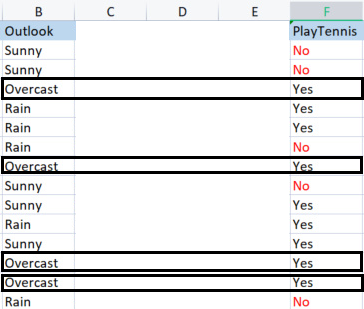
Échantillons de Overcast.
Échantillons positifs 4 (échantillons avec Yes dans la colonne Cible), échantillons négatifs 0 (échantillons avec No dans la colonne Cible). Cette situation est une exception.
Exceptions dans l'Algorithme ID3
Lorsqu'il n’y a aucun échantillon négatif alors qu'il y a des échantillons positifs (ou inversement), l'entropie est liée à 0.
On dit que c'est un nœud pur, il n'y a pas besoin de le diviser puisqu'il a des échantillons homogènes. Vous comprendrez mieux ce que j'entends par là lorsque nous dessinerons un arbre.
Il existe une autre exception :
Lorsqu'il y a un nombre égal d'échantillons positifs et d'échantillons négatifs, l'entropie est mathématiquement égale à 1.
La seule exception que nous devons gérer efficacement est lorsqu'il y a une valeur 0 dans les échantillons. La valeur 0 peut mener à une erreur fatale de division par 0. Voici donc la nouvelle fonction qui gère ce genre d’exceptions :
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
Nous pouvons maintenant trouver l'entropie de la Pluie (Rain) :
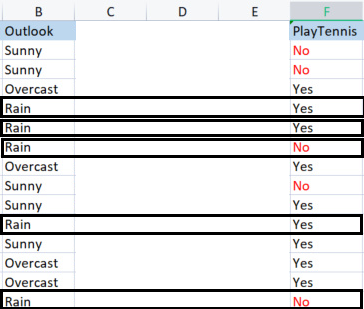
Échantillons pour Rain :
Il y a 3 échantillons positifs (échantillons avec Yes dans la colonne Cible).
Il y a 2 échantillons négatifs (échantillons avec No dans la colonne Cible).
Enfin, l'entropie de Jouer au tennis par temps de Pluie (Rain):
Entropie (Rain) = - (P1*log2P1 + P2*log2P2)
Entropie (Rain) = -(0.6*log2 0.6 + 0.4*log2 0.4)
Entropy(Rain) = 0,97095
Voici les valeurs d'entropie que nous avons obtenues pour la colonne Outlook :
| Entropie de la colonne Outlook |
|---|
| Entropie (Sunny) = 0,97095 |
| Entropie (Overcast) = 0 |
| Entropie (Rain) = 0,97095 |
Voilà donc comment trouver manuellement l'entropie des échantillons. Si nous utilisons notre programme pour trouver ces entropies, le résultat sera le suivant :
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
Nous allons utiliser ces valeurs pour trouver le gain d'information de l'ensemble des données à l'aide de la formule présentée précédemment :
![]()
Maintenant, laissez-moi trouver l'entropie manuellement pour que vous compreniez ce qui est fait derrière :
Gain d'information (IG) = Entropie de l'ensemble des données existantes - Somme du produit de la probabilité d'un échantillon et de son entropie.
IG = E(ensemble des données) - ( Prob(sunny) * E(sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain) )
IG = 0,9402 - ( 5/14 * (0,97095) + 4/14 * (0) + 5/14(0,97095) )
IG = 0,2467 (Il s'agit du gain d'information de la colonne Outlook)
Conversion de la formule en code :
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
Appel de la fonction :
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
Sortie :
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
Nous devons maintenant répéter le processus pour toutes les colonnes et trouver leurs gains d'information. La sortie sera :
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
Maintenant que nous avons le(s) gain(s) d'information pour toutes les colonnes, nous allons pouvoir commencer à dessiner notre arbre de décision. Voici comment.
Le but de ce processus initial était de trouver les gains d'information pour toutes les colonnes pour décider quelle colonne sera le Nœud Racine. La colonne avec un plus grand nombre de gains d'information par rapport à toutes les autres deviendra le nœud racine. Ici, la colonne Outlook a le gain d'information le plus élevé, il deviendra donc le Nœud Racine de notre arbre de décision. Dessinons l'arbre maintenant :
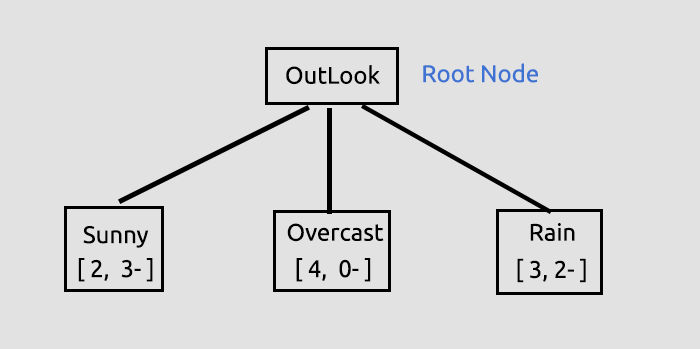
Ces informations sur Outlook sont fournies par la bibliothèque, lorsque vous exécutez le script de test lié à la fin de l'article. De nombreuses informations sont affichées lorsque vous êtes en mode de débogage de la bibliothèque, ce qui est le cas par défaut.
Le gain d'information a été obtenu, à partir de la fonction, puis stocké dans un tableau de valeurs doubles stockant tous les gains d'information. Finalement la valeur maximale à l'intérieur d'un tableau sera notre valeur cible.
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);La sortie sera la suivante :
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
Plus d'explications sur l'arbre que nous avons dessiné jusqu'à présent.
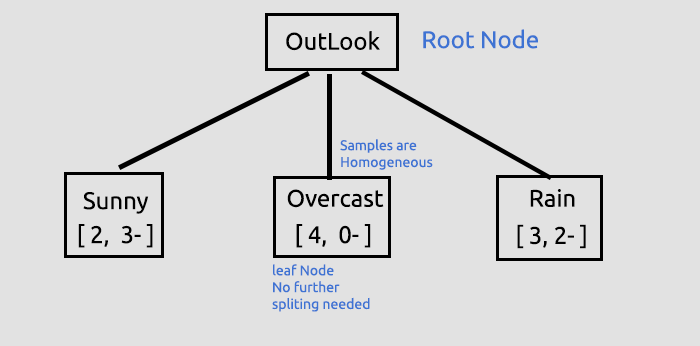
Il s'agit de la première étape, encore cruciale, au cours de laquelle nous avons trouvé le nœud racine et l’avons divisé en branches et en feuilles. Nous allons continuer à diviser les données jusqu'à ce qu'il n'y ait plus rien à diviser. Ici nous allons poursuivre le processus en divisant la branche avec les éléments Sunny et la branche avec les éléments Rain.
La valeur Overcast se compose d'éléments homogènes (il est pur) et nous disons donc qu'il a été complètement classé. Lorsqu'il s'agit d'un arbre de décision, nous l'appelons une feuille. Il ne générera pas de branche supplémentaire.
Mais avant d'aller plus loin dans la division des données, il y a des étapes cruciales à franchir avec l'ensemble de données dont nous disposons actuellement.
CLASSIFICATION DE LA MATRICE DE L'ENSEMBLE DE DONNÉES RESTANT
Nous devons classer la matrice de l'ensemble de données restant afin de placer les lignes ayant les mêmes valeurs dans un ordre croissant, ce qui permettra de créer des branches et des feuilles au contenu homogène (ce que nous souhaitons par dessus tout).
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
Pourquoi y a-t-il beaucoup de code commenté ? Notre bibliothèque a encore besoin d'être améliorée et les commentaires sont destinés à faciliter le débogage. N’hésitez pas à jouer avec.
Lorsque nous appelons cette fonction, nous obtenons les informations suivantes :
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
B A M, la fonction fonctionne comme par magie
Ok. La prochaine étape cruciale est la suivante.
SUPPRESSION DES NŒUDS FEUILLES DE L'ENSEMBLE DE DONNÉES
Avant la prochaine itération de tout le processus, il est très important de supprimer les nœuds feuilles puisqu'ils ne vont pas créer de branches, ce qui est logique, non ? D'ailleurs, ce sont des nœuds de valeurs pures.
Nous supprimons toutes les lignes qui correspondent à des nœuds feuilles. Dans ce cas, nous supprimons toutes les lignes avec Overcast.
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
Le résultat de l'exécution de ce bloc de code sera le suivant :
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
B A M
Le dernier processus crucial à ce stade, mais non le moindre, est le suivant.
SUPPRESSION DE LA COLONNE DU NŒUD PARENT OU DU NŒUD RACINE DE L'ENSEMBLE DE DONNÉES
Puisque nous l'avons déjà détecté en tant que nœud racine et que nous l'avons intégré à notre arbre, nous n'avons plus besoin de l'intégrer à notre ensemble de données, qui doit rester composé uniquement de valeurs non classées.
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
Le résultat de l'exécution de ce bloc de code sera le suivant :
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
B A M
La raison pour laquelle nous avons pu laisser en toute confiance certaines parties de l'ensemble de données est que la bibliothèque dessine un arbre qui laisse des indices sur la destination de l'ensemble de données. Voici l’arbre que nous avons dessiné jusqu'à présent :
Cela a l'air moche, mais c'est suffisant pour la démonstration. Nous allons essayer de le créer en HTML dans la prochaine série d'articles. Vous pouvez m’aider à le faire dans mon dépôt GitHub. Le lien est ci-dessous. Pour l'instant, laissez-moi terminer en décrivant le processus restant dans la construction d'un arbre. Après avoir itéré ce processus jusqu'à ce qu'il n'y ait plus rien à diviser, les logs sont les suivantes :
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
VOICI UN APERCU DE LA CONSTRUCTION DE L’ARBRE. J'ai trouvé ce morceau de code difficile et déroutant à lire malgré le fait que le processus semble facile lorsque l'on calcule les valeurs manuellement. J'ai donc décidé de l'expliquer en détail dans cette section.
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
Conclusion
Vous comprenez maintenant les calculs de base impliqués dans les arbres de classification. Il s'agit d'un sujet difficile et long à couvrir en un seul article. J'espère le terminer dans les deux prochains articles. La bibliothèque contient presque tout ce dont vous avez besoin pour commencer à construire des algorithmes d'arbres de décision pour vous aider à résoudre les problèmes de trading qui vous intéressent.
Merci de m’avoir lu. Mon dépôt GitHub est ici : https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5.
Traduit de l’anglais par MetaQuotes Ltd.
Article original : https://www.mql5.com/en/articles/11061
 Data Science et Apprentissage Automatique (partie 6) : Descente de Gradient
Data Science et Apprentissage Automatique (partie 6) : Descente de Gradient
 Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 4) : Prévoir le Krach Boursier Actuel
Data Science des Données et Apprentissage Automatique (Machine Learning) (partie 4) : Prévoir le Krach Boursier Actuel
 Développer un Expert Advisor de trading à partir de zéro (Partie 16) : Accès aux données sur le web (2)
Développer un Expert Advisor de trading à partir de zéro (Partie 16) : Accès aux données sur le web (2)
 Indicateur CCI Mise à jour et nouvelles fonctionnalités
Indicateur CCI Mise à jour et nouvelles fonctionnalités
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation