Scienza dei Dati e Apprendimento Automatico (Parte 05): Alberi Decisionali
545
0
Cos'è un Albero Decisionale?
Un albero decisionale è un tipo di tecnica di Apprendimento Automatico supervisionata utilizzata per classificare o fare previsioni in base a come è stato risposto ad una precedente serie di domande. Un modello è una forma di apprendimento supervisionato, il che significa che il modello viene addestrato e testato su un set di dati che contiene la categorizzazione desiderata.
L'albero decisionale potrebbe non fornire sempre risposte o decisioni chiare, invece potrebbe presentare le opzioni in modo che un analista esperto possa prendere una decisione informata per conto proprio. Gli alberi decisionali imitano il modo in cui noi umani pensiamo, quindi è generalmente facile per il data scientist comprendere e interpretare i risultati.
Avviso sulla terminologia!
Ho dimenticato di descrivere la terminologia dell'apprendimento supervisionato e non supervisionato nel mio primo articolo di questa serie, quindi eccolo qui.
Apprendimento Supervisionato
L'apprendimento supervisionato è un approccio alla creazione di intelligenza artificiale (AI), in cui un algoritmo informatico viene addestrato sui dati di input etichettati per un particolare output. Il modello viene addestrato fino a quando non è in grado di rilevare gli schemi e le relazioni sottostanti tra i dati di input e le etichette di output, consentendogli di produrre risultati accurati se presentati con dati mai visti prima.
Contrariamente all'apprendimento supervisionato, in questo approccio l'algoritmo viene presentato con dati non etichettati e progettato per rilevare modelli o somiglianze da solo.
Gli algoritmi comunemente usati nei programmi di apprendimento supervisionato includono quanto segue:
- Regressione lineare
- Regressione logistica
- Alberi Decisionali
- Supporto Macchine Vettoriali
- Foreste casuali
La principale differenza tra apprendimento supervisionato e non supervisionato sta nel modo in cui l'algoritmo apprende. Nell'apprendimento non supervisionato, all'algoritmo vengono forniti dati non etichettati come set di addestramento. A differenza dell'apprendimento supervisionato, non ci sono valori di output corretti; l'algoritmo determina modelli e somiglianze all'interno dei dati anziché metterli in relazione con alcune misurazioni esterne, in altre parole, gli algoritmi possono funzionare liberamente per apprendere di più sui dati e trovare cose interessanti o inaspettate che gli esseri umani non stavano cercando.
Attualmente siamo sull'apprendimento supervisionato , impareremo a conoscere l'apprendimento non supervisionato nei prossimi articoli.
Come funzionano gli alberi decisionali?
Gli alberi decisionali utilizzano molteplici algoritmi per decidere di dividere un nodo in due o più sottogruppi di nodi. La creazione di sottonodi aumenta l'omogeneità dei sottonodi risultanti. In altre parole, possiamo dire che la purezza del nodo aumenta rispetto alla variabile target. L'algoritmo dell'albero decisionale suddivide i nodi su tutte le variabili disponibili e poi seleziona la suddivisione che risulta nei sottonodi più omogenei.
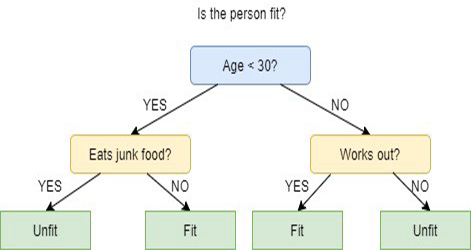esempio di albero decisionale
La selezione dell'algoritmo si basa sul tipo di variabili target.
Di seguito sono riportati gli Algoritmi utilizzati nell'Albero Decisionale:
- ID3 > Estensione di D3
- C4.5 > Successore di ID3
- CART > Albero di classificazione e regressione
- CHAID > Rilevamento Automatico dell'Interazione Chi-quadrato, esegue divisioni multi livello durante il calcolo degli alberi di classificazione
- MARS > Spline di Regressione Adattiva Multivariata
In questo articolo creerò un albero decisionale basato sull'algoritmo ID3, discuteremo e utilizzeremo gli altri algoritmi nei prossimi articoli di questa serie.
L'obiettivo dell'albero decisionale
L'obiettivo principale dell'algoritmo degli alberi decisionali è separare i dati con impurità in nodi puri o vicini, ad esempio, c'è un cesto con le mele mescolate con le arance e l'albero decisionale quando viene addestrato su come appaiono le mele in termini del loro colore e dimensione, separerà le mele e le arance nei propri panieri.
Algoritmo ID3
ID3 sta per Iterative Dichotomiser 3 ed è chiamato così perché l'algoritmo iterativamente (ripetutamente) dicotomizza (divide) le caratteristiche in due o più gruppi ad ogni passaggio.
Inventato da Ross Quinlan, ID3 utilizza un approccio top-down greedy per costruire un albero decisionale. In parole semplici, l'approccio top-down greedy significa che inizia a costruire l'albero dall'alto e l'approccio greedy significa che ad ogni iterazione selezioniamo la caratteristica migliore in questo momento per creare un nodo.
Generalmente, ID3 viene utilizzato solo per problemi di classificazione con dati nominali (in pratica, dati che non possono essere misurati).
Detto questo, esistono due tipi di alberi decisionali.
- Alberi di Classificazione
- Alberi di Regressione
01: Alberi di Classificazione
Gli alberi di classificazione sono proprio come l'albero che stiamo per imparare in questo articolo, dove abbiamo caratteristiche senza valori numerici continui o ordinati, che vogliamo classificare.
Gli alberi di classificazione classificano le cose in categorie.
02: Alberi di Regressione
Questi sono costruiti con valori ordinati e con valori continui.
L’Albero Decisionale prevede valori numerici.
Passaggi nell'algoritmo ID3
01: Inizia con il set di dati originale come nodo radice.
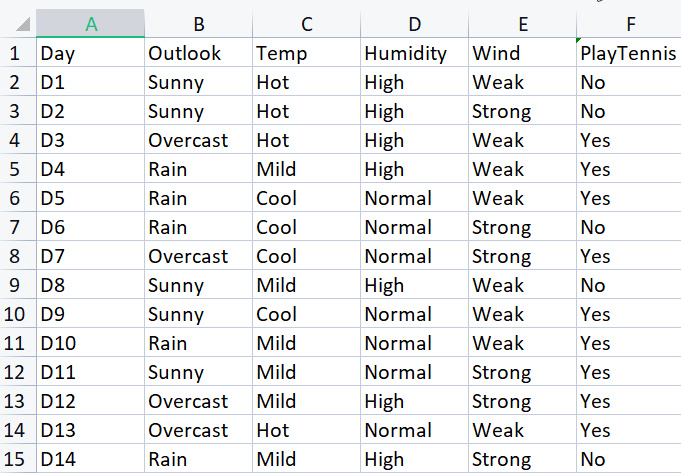
Per costruire la libreria di base, utilizzeremo il semplice set di dati per giocare a tennis in determinate condizioni meteorologiche, ecco la nostra panoramica del set di dati, questo è un piccolo set di dati (solo 14 righe).
Per disegnare un albero decisionale utilizzando questo algoritmo dobbiamo capire quali attributi forniscono il maggior guadagno di informazioni tra tutti gli attributi, lasciami spiegare.
Uno di questi attributi (colonne) deve essere un nodo radice per cominciare , ma come si decide quale colonna deve essere un nodo radice? Qui è dove usiamo il guadagno di informazioni.
Guadagno di informazioni
Il guadagno di informazioni calcola la riduzione dell'entropia e misura la capacità di una determinata caratteristica di separare o classificare le classi target. La funzione con il maggior guadagno di informazioni viene selezionata come la migliore.
Entropia
L’entropia è la misura dell'incertezza di una variabile casuale, caratterizza l'impurità nel campione dato.
La formula dell'entropia è:
La prima cosa che dobbiamo fare è trovare l'entropia dell'intero set di dati, con ciò significa trovare l'entropia delle variabili target poiché tutte queste colonne sono proiettate sulla colonna target PlayTennis.
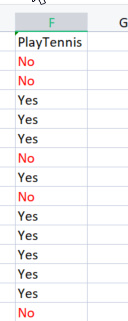
Scriviamo un po' di codice,
sappiamo per certo che prima di poter trovare l'entropia delle nostre variabili target dobbiamo avere il numero totale di valori negativi contrassegnati con No e valori positivi contrassegnati con Sì, questi valori potrebbero aiutarci a ottenere le probabilità degli elementi all'interno della nostra colonna per ottenere tale valori scriviamo il codice per fare una cosa del genere all'interno di Entropy Function
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
La funzione è facile da capire a colpo d'occhio soprattutto se hai letto la formula, ma presta attenzione all'Array SampleNumbers[]. I campioni sono ciò che è l'interno della colonna, possiamo anche fare riferimento a campioni come classi per esempio in questa colonna target i nostri campioni sono Sì e NO.
L'esecuzione corretta della funzione sulla colonna TargetArray risulterà in
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
Ora che abbiamo questi numeri procediamo a trovare l'entropia utilizzando questa nostra formula
se presti attenzione alla formula, noterai che il logaritmo con cui abbiamo a che fare qui è quello della base 2, che è il logaritmo binario (leggi per maggiori informazioni) per trovare il log in base 2 dividiamo il log2 per il log del valore dell'argomento.
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
Poiché la base è la stessa, va tutto bene.
Ho anche codificato una funzione Proba() in modo da aiutarci a ottenere la probabilità di una classe di valori, eccola qui.
double CDecisionTree::Proba(int number,double total) { return(number/total); }
Elefante nella stanza. Per trovare la probabilità di un elemento nella nostra colonna troviamo quante volte è apparso diviso per il numero totale di tutti gli elementi in quella colonna, potresti aver notato che ci sono 5 elementi che sono No e 9 elementi che sono Sì quindi,
le probabilità di no = 5/14(numero totale di elementi) = 0.357142..
le probabilità di sì = 9/14 (stessa storia) = 0,6428571...
Infine, per trovare l'entropia di una colonna attributo/set di dati
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
Se eseguiamo questa funzione sulla variabile Target, l'output sarà
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
B A M
Ora conosciamo l'entropia dell'intero set di dati che è fondamentalmente l'entropia dei valori di y, e abbiamo la funzione per trovare l'entropia in mano. Troviamo l'entropia di ogni singola colonna nel set di dati.
Ora che abbiamo l'entropia dell'intero set di dati, il passo successivo è trovare l'entropia dei membri all'interno di ogni colonna della variabile indipendente, lo scopo di trovare questo tipo di entropia nelle variabili indipendenti è quello di aiutarci a trovare il guadagno di informazioni, per ogni colonna di dati.
Prima di utilizzare la nostra libreria per trovare l'entropia della colonna Outlook, calcoliamola a mano così che tu possa comprendere chiaramente ciò che viene fatto.
Prendiamo in confronto la colonna outlook con la sua variabile target.
Colonna Outlook vs PlayTennis
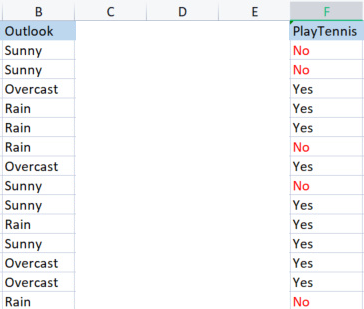
A differenza di come abbiamo trovato l'entropia dell'intero set di dati che è anche indicata come l'entropia della variabile target, per trovare l'entropia di una variabile indipendente dobbiamo riferirla alla variabile target poiché questo è il nostro obiettivo.
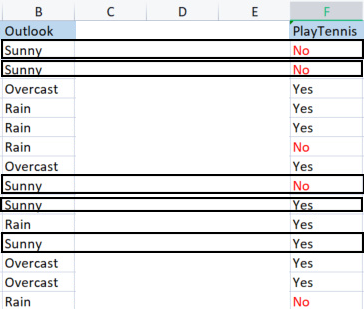
Valori in Outlook
Abbiamo 3 diversi valori che sono Sunny, Overcast e Rain. Dobbiamo trovare l'entropia di ognuno di questi valori rispetto alla loro variabile target
Campioni (Sunny) (campioni positivi e negativi di Sunny) = [2 Positivi (i Sì), 3 Negativi (i No)]
Ora che abbiamo il numero di positivi e negativi, la probabilità di si di giocare a tennis in una giornata soleggiata sarà:
probabilità1= 2(numero di volte in cui è apparso Sì) / 5(numero totale di giorni di sole)
Quindi 2/5 = 0.4
In Contrasto
La probabilità di non giocare in una giornata soleggiata sarà 0,6 cioè 3/5 = 0.6
Infine, l'entropia di giocare in una giornata soleggiata sarà, fare riferimento alla formula
Entropy(Sunny) = - (P1*log2P1 + P2*log2P2)
Entropy(Sunny) = -(0.4*log2 0.4 + 0.6*log2 0.6)
Entropy(Sunny) = 0,97095
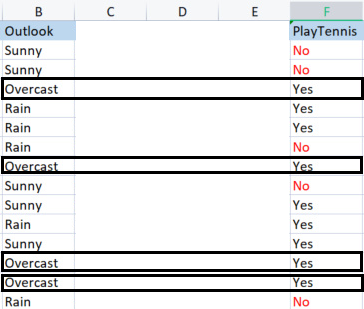
Ora troviamo l'entropia di Overcast
Campioni in overcast.
Campioni positivi 4 (campioni con Sì nella colonna Target), Campioni negativi 0 (campioni con No nella colonna Target). Questa situazione è un'eccezione.
Eccezioni nell'algoritmo ID3
Quando accade che ci sono zero (0) campioni negativi mentre ci sono campioni positivi o viceversa, ci sono zero (0) campioni positivi mentre ci sono campioni negativi, ogni volta che questo accade l'entropia è vincolata a zero (0).
Diciamo che è un nodo puro, non c'è bisogno di dividerlo poiché ha campioni omogenei capirai di più cosa intendo con questo quando disegniamo un albero.
Un'altra eccezione è:
quando succede che c’è un numero uguale di campioni positivi e campioni negativi, matematicamente l'entropia sarà uno (1).
L'unica eccezione che dobbiamo gestire in modo efficace è quando c'è un valore zero nei campioni perché zero può portare a una divisione per zero qui c’è la nuova funzione, con la capacità di gestire tali eccezioni.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
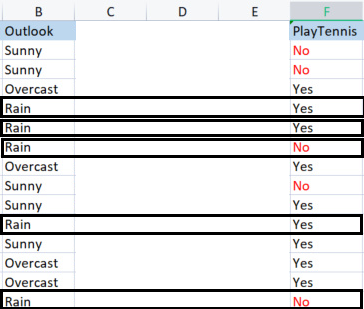
Infine, troviamo l'entropia di Rain
Campioni di Rain;
Ci sono 3 campioni positivi (campioni con Sì nella colonna Target).
Ci sono 2 campioni negativi (campioni con No nella colonna Target).
Finalmente l'entropia di giocare a tennis in un giorno di pioggia.
Entropy(Rain) = - (P1*log2P1 + P2*log2P2)
Entropy(Rain) = -(0.6*log2 0,6 + 0,4*log2 0.4)
Entropy(Rain) = 0.97095
Ecco i valori dell’entropia che abbiamo ottenuto dalla colonna Outlook
| Entropia dalla colonna Outlook |
|---|
| Entropy(Sunny) = 0,97095 |
| Entropy(Overcast) = 0 |
| Entropy(Rain) = 0.97095 |
Quindi, ecco come trovare manualmente l'entropia dei campioni, ora se usiamo il nostro programma per trovare quelle entropie, l'output sarà:
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
Utilizzeremo questi valori per trovare il guadagno di informazioni di tutti i dati utilizzando la formula discussa in precedenza.
Ora, fammi trovare manualmente l'entropia in modo che tu capisca cosa sta succedendo a porte chiuse.
Guadagno Informazioni(IG) = Entropia intero set dati - Somma del prodotto della probabilità di un campione e della sua entropia.
IG = E(dataset) - ( Prob(sunny) * E(sunny) + Prob(overcast)*E(overcast) + Prob(rain)*E(rain) )
IG = 0.9402 - ( 5/14 * (0.97095) + 4/14 * (0) + 5/14 * (0.97095) )
IG = 0,2467 (questo è un guadagno di informazioni della colonna Outlook)
Quando convertiamo la formula in codice sarà:
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
Chiamando la funzione
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
Output
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
Ora, dobbiamo ripetere il processo per tutte le colonne e trovare il loro Guadagno di Informazioni . L'output sarà:
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
Ora che abbiamo i Guadagni di Informazioni per tutte le colonne, inizieremo a disegnare il nostro albero decisionale, come?
Lo scopo di questo processo iniziale era trovare i guadagni di informazioni per tutte le colonne in modo da poter decidere quale colonna dovrebbe essere il Nodo Radice. La colonna con un alto numero di guadagno di informazioni rispetto a tutte le altre diventerà il nodo radice, in questo caso Outlook ha il più alto guadagno di informazioni, quindi diventerà il Nodo Radice del nostro albero decisionale, disegniamo ora l'albero.
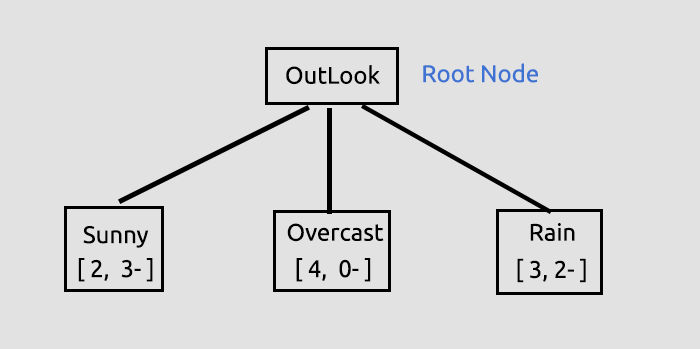
Queste informazioni su Outlook sono fornite dalla Libreria, quando si esegue lo Script Test linkato alla fine dell'articolo, molte informazioni vengono stampate quando si è in modalità di debug della libreria che è l'impostazione predefinita.
Il guadagno di informazioni è stato ottenuto dalla sua funzione, poi memorizzato all'interno di un Array di valori double che memorizza tutti i guadagni d’informazione, quindi finalmente il valore massimo all'interno di un array sarà il nostro valore target.
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);L'output sarà:
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
Ulteriori spiegazioni sull'Albero le abbiamo tratte a questo punto.
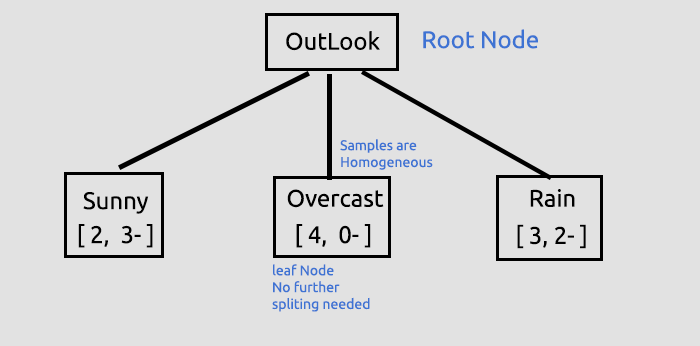
Questo è stato il primo passaggio cruciale in cui stavamo trovando il nodo radice e dividendo quel nodo radice in rami e foglie, continueremo a dividere i dati fino a quando non ci sarà nulla da dividere, qui continueremo il processo suddividendo il ramo con gli elementi Sunny e il ramo con gli elementi Rain .
Overcast è costituito da elementi omogenei (è puro), quindi diciamo che è stato completamente classificato, quando si tratta di albero decisionale lo chiamiamo foglia. Non genererà rami.
Ma prima di andare oltre nella suddivisione dei dati, ci sono passaggi cruciali che dobbiamo fare con l'attuale set di dati che abbiamo.
CLASSIFICAZIONE DELLA MATRICE DI DATASET RIMANENTE
Dobbiamo classificare la matrice del set di dati rimanente per mettere le righe con gli stessi valori in ordine crescente, questo sarà utile per creare rami e foglie con contenuti omogenei (qualcosa che siamo ansiosi di ottenere).
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
Perché ci sono troppi codici commentati? La nostra libreria ha ancora bisogno di miglioramenti e i commenti servono per il debug, se tutto va bene giocherai con loro.
Quando chiamiamo questa funzione e stampiamo l'output otterremo:
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
B A M, La funzione funziona come per magia
Ok, il prossimo passo cruciale è
RIMOZIONE DEI NODI FOGLIA DAL DATASET
Prima della prossima iterazione di tutto il processo che abbiamo fatto fino a questo punto, è molto importante rimuovere i nodi foglia poiché non creeranno rami, ha senso giusto? Tra l'altro sono un nodo di valori puri.
Rimuoviamo tutte le righe che hanno il valore del nodo foglia. In questo caso rimuoviamo tutte le righe con Overcast.
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
L'output dopo aver eseguito questo blocco di codice sarà:
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
B A M
L'ultimo ma non meno importante processo a questo punto è:
RIMOZIONE DELLA COLONNA PARENT O NODO RADICE DAL DATASET
Poiché lo abbiamo già rilevato come nodo radice e lo abbiamo disegnato nel nostro albero, non ne abbiamo più necessità nel nostro set di dati, il nostro set di dati deve rimanere con valori non classificati
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
L'output di questo blocco di codice sarà:
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
B A M
Ora il motivo per cui siamo stati in grado di lasciare con sicurezza alcune parti del set di dati è perché la libreria sta disegnando un albero che lascia indizi su dove va il set di dati, ecco l’albero che abbiamo disegnato fino a questo punto.
Sembra brutto, ma è abbastanza buono per scopi dimostrativi, proveremo a crearlo con HTML nella prossima serie di articoli, aiutami a farlo nel mio repository GitHub per questo linkato di seguito.Ora fammi finire descrivendo il processo rimanente nella costruzione dell’albero. I log dopo l'iterazione di questo processo fino a quando non c'è nulla da dividere sono i seguenti:
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
ECCO UNA PANORAMICA DELLA funzione BUILD TREE, ho trovato questo pezzo di codice difficile e confuso da leggere nonostante il processo sembri facile quando si calcolano i valori manualmente, quindi ho deciso di spiegarlo in dettaglio in questa sezione.
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
La Linea Inferiore
Ora capisci i calcoli di base coinvolti negli alberi di classificazione, questo è un argomento difficile e lungo da trattare in un articolo, spero di completarlo nel prossimo articolo o due, anche se la libreria ha quasi tutto ciò di cui hai bisogno per iniziare a costruire algoritmi di alberi decisionali per aiutarti a risolvere i problemi di trading che ti stanno a cuore.
Grazie per la lettura, il mio repository GitHub è linkato qui https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5.
Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/11061
Sviluppare un Expert Advisor per il trading da zero (Parte 14): Aggiunta dei Volumi al Prezzo (II)
Scienza dei Dati e Apprendimento Automatico (Parte 04): Predire l'Attuale Crollo del Mercato Azionario
Sviluppare un Expert Advisor per il trading da zero (Parte 15): Accesso ai dati sul web (I)
Matrici e vettori in MQL5
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso