
Машинное обучение и Data Science (Часть 05): Деревья решений на примере погодных условий для игры в теннис
Что такое дерево решений?
Дерево решений — это метод машинного обучения с учителем, используемый для категоризации или прогнозирования на основе ответов на предыдущий набор вопросов. Модель — форма обучения с учителем, т.е. модель обучается и тестируется на наборе данных, который содержит желаемую категоризацию.
Дерево решений не всегда дает четкие ответы или решения. Вместо этого оно может выдавать варианты, а специалист по данным на их основе может принять собственное обоснованное решение. Деревья решений имитируют то, как люди думают. Поэтому специалистам по данным обычно легко понять и интерпретировать результаты.

Терминология!
В первой статье этой серии я забыл описать терминологию обучения с учителем и без. Исправляюсь.
Обучение с учителем
Обучение с учителем — это подход к созданию искусственного интеллекта (ИИ), при котором компьютерный алгоритм обучается на входных данных и размеченных выходных данных. Модель обучается до тех пор, пока не сможет обнаруживать основные закономерности и взаимосвязи между входными и размеченными выходными данными. Это позволяет получать более точные результаты при встрече с ранее не виденными данными.
В отличие от обучения с учителем, обучение без учителя использует неразмеченные данные и предназначено для самостоятельного обнаружения закономерностей или сходств.
Алгоритмы, обычно используемые в программах обучения с учителем, включают в себя следующие:
- Линейная регрессия
- Логистическая регрессия
- Деревья решений
- Метод опорных векторов
- Случайные леса
Главное отличие между обучением с учителем и без учителя заключается в том, как обучается алгоритм. При обучении без учителя алгоритму предоставляются неразмеченные данные в качестве обучающего набора. В отличие от обучения с учителем, здесь нет правильных выходных значений. Алгоритм определяет закономерности и сходства в данных, а не связывает их с какими-либо внешними измерениями. Другими словами, алгоритмы могут свободно работать, чтобы узнать больше информации о данных и найти интересные или неожиданные вещи, которые мы не искали.
Сейчас мы с вами работает с обучением с учителем, а об обучении без учителя узнаем в следующих статьях.
Как работают деревья решений?
Деревья решений используют набор алгоритмов, чтобы принимать решения о разделении узла на два или более узлов подмножества. Создание подузлов увеличивает однородность полученных подузлов. Другими словами, можно сказать, что чистота узла увеличивается относительно целевой переменной. Алгоритм дерева решений разбивает узлы по всем доступным переменным, а затем выбирает разбиение, которое приводит к наиболее однородным подузлам.
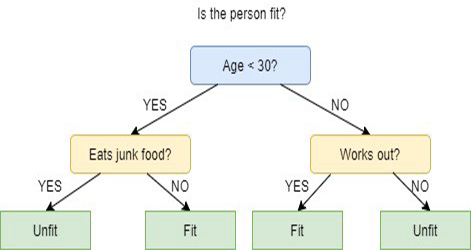
Выбор алгоритма основан на типе целевых переменных.
Ниже приведены алгоритмы, используемые в дереве решений:
- ID3 — расширение D3
- C4.5 — преемник ID3
- CART — дерево классификации и регрессии
- CHAID — автоматическое обнаружение взаимодействия по хи-квадрат (ЧЭЙД), выполняет многоуровневое разбиение при вычислении деревьев классификации
- MARS — сплайны многомерной адаптивной регрессии
В этой статье мы будем создавать дерево решений на основе алгоритма ID3, а другие алгоритмы мы обсудим и применим в следующих статьях этой серии.
Цель дерева решений
Основная цель алгоритма деревьев решений состоит в том, чтобы разделить данные на данные "с примесью" и "чистые" или близкие к узлам. Например, есть корзина с яблоками вперемешку с апельсинами. Когда дерево решений обучится на том, как выглядят яблоки в плане цвета и размера, он поделит фрукты — яблоки в одну корзину, а апельсины в другую.
Алгоритм ID3
ID3 (Iterative Dichotomiser 3) — алгоритм, которые итеративно (повторно) дихотомизирует (делит) объекты на две или более группы на каждом шаге.
Он был разработан Джоном Р. Квинланом. Алгоритм ID3 использует "жадный" подход сверху вниз для построения дерева решений. Подход сверху вниз означает, что он начинает строить дерево сверху, а "жадный" означает, что на каждой итерации мы выбираем лучшую функцию в настоящий момент для создания узла.
Как правило, ID3 используется только для задач классификации с номинальными данными (в основном, данные, которые невозможно измерить).
При этом существует два типа деревьев решений.
- Деревья классификации
- Деревья регрессии
1. Деревья классификации
Деревья классификации похожи на дерево, которое мы будем изучать в этой статье — у нас есть признаки без непрерывных числовых или упорядоченных значений, которые мы хотим классифицировать.
Деревья классификации классифицируют вещи по категориям.
2. Деревья регрессии
Они строятся с упорядоченными значениями и с непрерывными значениями.
Дерево решений прогнозирует числовые значения.
Шаги алгоритма ID3
1. Начинается с исходного набора данных в качестве корневого узла.
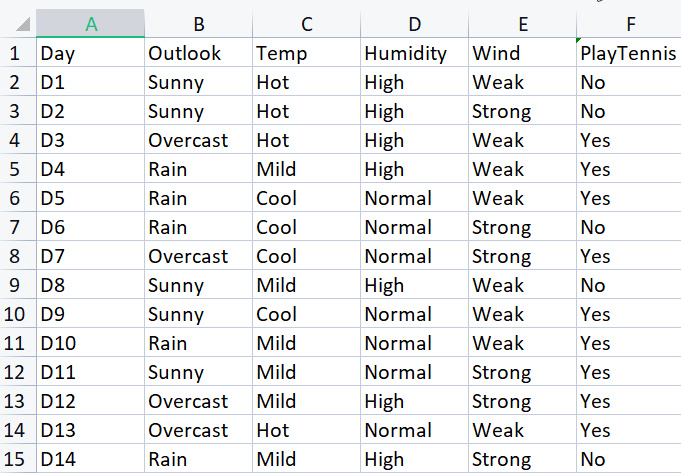
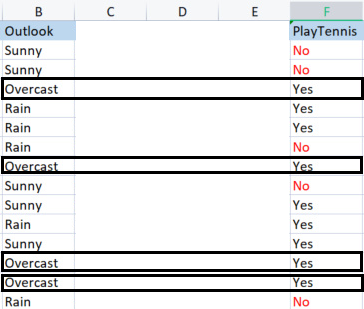
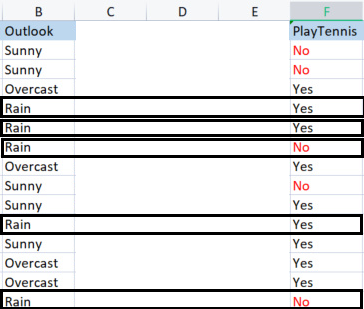
При создании базовой библиотеки мы будем использовать простой набор данных об игре в теннис при определенных погодных условиях. Вот обзор нашего небольшого набора данных (всего 14 строк).
Чтобы нарисовать дерево решений с помощью этого алгоритма, нам нужно понять, какие атрибуты обеспечивают максимальную информационную выгоду из всех атрибутов. Я объясню.
Один из этих атрибутов (столбцов) должен быть корневым узлом для начала. Но как решить, какой столбец будет корневым узлом? Здесь мы используем информационную выгоду.
Информационная выгода
Информационная выгода рассчитывает снижение энтропии и измеряет, насколько хорошо данная функция разделяет / классифицирует целевые классы. Признак с наибольшей информационной выгодой выбирается как лучший.
![]()
Энтропия
Энтропия — мера неопределенности случайной величины, характеризующая примесь в данной выборке.
Формула энтропии:
![]()
Первое, что нам нужно сделать, это найти энтропию всего набора данных, то есть найти энтропию целевых переменных, поскольку все эти столбцы проецируются в целевой столбец PlayTennis.
Напишем немного кода.
Мы точно знаем, что прежде, чем искать энтропию целевых переменных, нам нужно отметить общее количество размеченных отрицательных значений No и размеченных положительные значения Yes. Эти значения помогут найти вероятности элементов внутри нашего столбца. Чтобы получить такие значения, давайте напишем код — что будет происходить внутри функции энтропии.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //значение энтропии, которое вернет функция for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
Функцию легко понять с первого взгляда, особенно если вы изучили формулу. Но обратите внимание на массив SampleNumbers[]. Образцы — это то, что находится внутри столбца. Образцы могут служить классами. К примеру, в этом целевом столбце наши образцы это Yes и No.
Успешное выполнение функции по столбцу TargetArray даст такой результат:
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
У нас есть эти значения, и мы можем продолжить поиск энтропии, используя следующую формулу.
![]()
Если внимательно посмотреть на формулу, можно заметить, что логарифм, с которым мы имеем дело, является логарифмом по основанию 2, то есть двоичным логарифмом (посмотрите по ссылке дополнительную информацию). Чтобы найти логарифм по основанию 2, поделим log2 на логарифм значения аргумента.
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
Так как база одинаковая, то все хорошо.
Я также написал код функции Proba( ), которая позволяет получить вероятность класса значений. Вот она:
double CDecisionTree::Proba(int number,double total) { return(number/total); }
Слон в комнате. Чтобы найти вероятность элемента в столбце, мы определяем, сколько раз он появился, и делим на общее количество всех элементов в этом столбце. Вы наверняка заметили, что есть 5 элементов со значением No и 9 элементов со значением Yes, поэтому получается так:
вероятность No = 5/14 (общее количество элементов) = 0.357142..
вероятность Yes = 9/14 = 0.6428571...
Наконец, чтобы найти энтропию столбца атрибута/набора данных
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
Если запустить эту функцию для переменной Target, получим следующее:
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
Та-дам!
Теперь мы знаем энтропию всего набора данных, которая в основном представляет собой энтропию значений y, а также у нас есть функция для нахождения энтропии. Давайте найдем энтропию каждого столбца в наборе данных.
Итак, теперь у нас есть энтропия всего набора данных. Следующий шаг — найти энтропию членов внутри каждого столбца независимой переменной. Цель нахождения такого рода энтропии в независимых переменных — найти информационную выгоду для каждого столбца данных.
Прежде чем использовать нашу библиотеку для определения энтропии столбца Outlook, давайте посчитаем ее вручную, чтобы получить более четкое представление о том, что делается.
Мы сравниваем столбец Outlook с его целевой переменной.
Столбцы Outlook vs PlayTennis
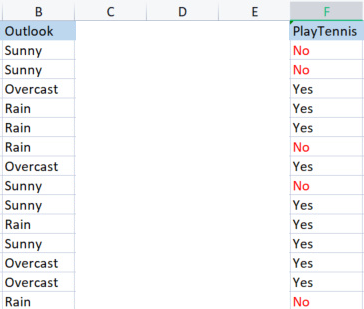
В отличие от того, как мы искали энтропию всего набора данных, которая также называется энтропией целевой переменной, чтобы найти энтропию независимой переменной, нужно обратиться к переменной Target, поскольку это наша цель.
Значения в солбце прогноза Outlook
У нас есть три разных значения: Sunny (солнечно), Overcast (пасмурно) и Rain (дождь). Нужно найти энтропию каждого из этих значений по отношению к их целевой переменной.
Выборка Sunny (положительные и отрицательные выборки Sunny) = [2 положительных (Yes), 3 отрицательных (No)]
Мы нашли количество положительных и отрицательных результатов. Получается, вероятность положительного решения Yes для игры в теннис в солнечный день будет:
вероятность1 = 2(количество раз, когда появилось Yes) / 5 (общее количество солнечных дней)
то есть 2/5 = 0.4
И наоборот
Вероятность того, что тенниса не будет в солнечный день, будет равна 0,6 то есть 3/5 = 0,6
И наконец, энтропия игры в солнечный день будет такой (посмотрим на формулу)
Entropy(Sunny) = - (P1*log2P1 + P2*log2P2)
Entropy(Sunny) = -(0.4*log2 0.4 + 0.6*log2 0.6)
Entropy(Sunny) = 0.97095
Теперь найдем энтропию пасмурной погоды Overcast
Выборки в пасмурную погоду.
Положительны[ выборок 4( со значением Yes в столбце target). Отрицательных выборок 0 (со значением No в столбце Target). Эта ситуация является исключением.
Исключения в алгоритме ID3
Когда случается, что есть ноль (0) отрицательных выборок, в то время как есть положительные выборки или наоборот, ноль (0) положительных выборок, и при этом есть отрицательные, энтропия привязана к нулю (0).
Тогда можно считать, что это чистый узел, его не нужно дальше разбивать, так как он имеет гомогенные выборки. Чтобы лучше понять это, мы нарисуем дерево.
Еще одно исключение:
Когда случается, что найдено равное количество положительных и отрицательных выборок, математически энтропия будет равна единице (1).
Единственное исключение, с которым мы должны эффективно справляться, — это когда в выборках есть нулевое значение, потому что ноль может привести к ошибке деления на ноль. Вот новая функция с возможностью обработки таких исключений.
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //значение энтропии, которое вернет функция for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Исключение double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //Обработка исключения else entropy_out = -Entropy; return(entropy_out); }
Наконец, давайте найдем энтропию дождя.
Выборки дождя
Есть 3 положительные выборки (со значением Yes в столбце Target).
Есть 2 отрицательные выборки (со значением No в столбце Target).
Вот такой будет энтропия игры в теннис в дождливый день.
Entropy(Rain) = - (P1*log2P1 + P2*log2P2)
Entropy(Rain) = -(0.6*log2 0.6 + 0.4*log2 0.4)
Entropy(Rain) = 0.97095
Вот значения энтропии, которые мы получили из столбца Outlook.
| Энтропия из столбца Outlook |
|---|
| Entropy(Sunny) = 0.97095 |
| Entropy(Overcast) = 0 |
| Entropy(Rain) = 0.97095 |
Итак, мы посчитали энтропию выборок вручную. Если запустить нашу программу для поиска этих энтропий, результат будет таким:
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
Мы будем использовать эти значения для поиска информационной выгоды, используя формулу, которую мы обсуждали ранее.
![]()
Теперь давайте посмотрим, как найти энтропию вручную, чтобы стало понятнее, что же происходит за закрытыми дверями.
Информационная выгода (Information Gainб IG) = Энтропия всего набора данных - Сумма произведений вероятности выборки и ее энтропии.
IG = E(dataset) - ( Prob(sunny) * E(sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain) )
IG = 0.9402 - ( 5/14 * (0.97095) + 4/14 * (0) + 5/14(0.97095) )
IG = 0.2467 (это информационная выгода столбца прогноза Outlook)
Когда мы преобразуем формулу в код, получим следующее:
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
Вызов функции
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
Результат
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
Теперь нужно повторить процесс для всех столбцов и найти их информационную выгоду. Результат будет таким:
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
После того, как мы получили информационную выгоду для всех столбцов, перейдем к построению дерева решений. Но как?
Цель этого начального процесса состояла в том, чтобы найти информационную выгоду для всех столбцов, чтобы можно было решить, какой столбец будет корневым узлом. Столбец с информационной выгодой больше, чем во всех других, станет корневым узлом. В этом случае столбец прогноза Outlook имеет максимальную информационную выгоду, поэтому он и станет корневым узлом нашего дерева решений. Давайте теперь построим это дерево.
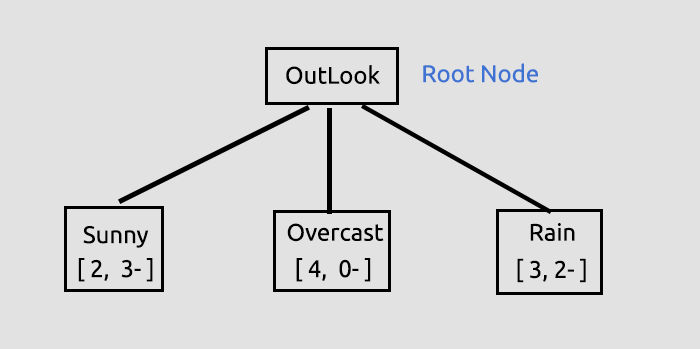
Эту информацию о прогнозе дает библиотека при запуске тестового скрипта. Скрипт прикреплен в конце статьи, много информации выводится в режиме отладки библиотеки, который используется по умолчанию.
Мы получили информационную выгоду, затем сохранили в массиве значений double, в котором хранятся все данные о выгоде. В конечном итоге максимальное значение внутри массива и будет целевым значением.
//--- Поиск информационной выгоды ArrayResize(IGArr,i+1); //информационная выгода по количеству столбцов IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);Результат вызова будет таким
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
Немного дополнительный пояснений к дереву, который мы создали к данному моменту.
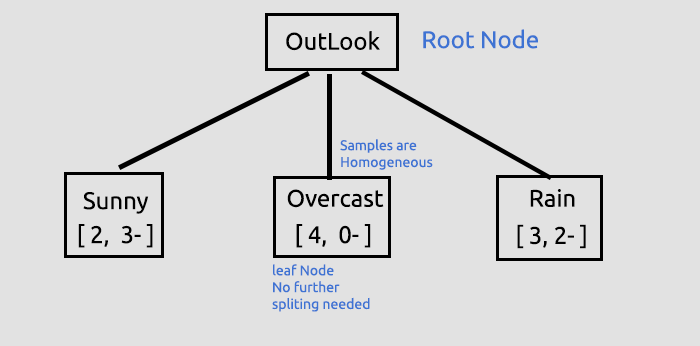
Это был первый, но очень важный шаг, на котором мы находили корневой узел и разбивали этот корневой узел на ветви и листья. Мы будем продолжать разбивать данные до тех пор, пока не останется ничего для разбивания. Здесь продолжим процесс разделения ветки со значением Sunny и ветки со значением Rain.
Столбец Overcast состоит из однородных значений (он чистый), поэтому мы говорим, что он полностью классифицирован. В дереве решений такое состояние называется листом. Оно не будет генерировать ветки.
Но прежде, чем пойдем дальше с разделением данных, нужно сделать несколько важных шагов с текущим набором данных, который у нас есть.
КЛАССИФИКАЦИЯ ОСТАВШЕЙСЯ МАТРИЦЫ НАБОРА ДАННЫХ
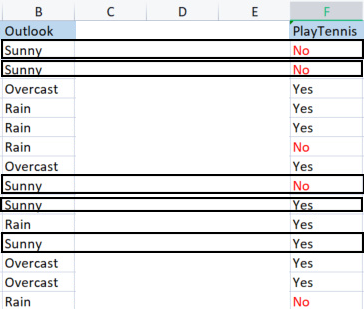
Нам нужно классифицировать оставшуюся матрицу набора данных, чтобы расположить строки с одинаковыми значениями в порядке возрастания. Это будет полезно для создания ветвей и листьев с однородным содержимым (как раз то, к чему мы стремимся).
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //если случится, можем получить бесконечный цикл } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //если случится, можем получить бесконечный цикл } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
Почему так много кода закомментировано? Библиотека все еще нуждается в доработках, а комментарии нужны для отладки. Поиграйтесь с ними.
Вызываем функцию, выводим результат, получаем следующее:
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
Функция работает как по волшебству.
Переходим к следующему важному шагу.
УДАЛЕНИЕ КОНЕЧНЫХ УЗЛОВ (ЛИСТЬЕВ) ИЗ НАБОРА ДАННЫХ
Перед следующей итерацией всего процесса очень важно удалить конечные узлы (листья), поскольку они не будут создавать никаких ветвей. Логично, не так ли? Кстати, они являются узлами "чистых" значений.
Удаляем все строки со значением листа Leaf Node. В нашем случае удаляем все строки с пасмурной погодой Overcast.
//--- ищем, есть ли в массиве нулевая энтропия int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //если найден ноль в массиве энтропий { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //новое общее количество строк из массива if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //также удаляем энтропию из массива и ее информацию везде из родительского узла, который будем строить далее ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
После выполнения этого кода получим такой результат:
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
Та-дам!
Последний, но не менее важный процесс на этом этапе:
УДАЛЕНИЕ РОДИТЕЛЬСКОГО ИЛИ КОРНЕВОГО УЗЛА ИЗ НАБОРА ДАННЫХ
Поскольку мы уже определили его как корневой узел и нарисовали его в нашем дереве, больше он не нужен для нашего набора данных. В наборе данных должны остаться только неклассифицированные значения.
//--- УДАЛЕНИЕ РОДИТЕЛЬСКОГО/КОРНЕВОГО УЗЛА ИЗ НАБОРА ДАННЫХ MatrixRemoveColumn(m_dataset,max_gain,cols); // После удаления столбцов присваиваем новые значения этим глобальным переменным cols = cols-1; // удаляем столбец, который был удален rows_total = rows_total - single_rowstotal; //убираем размер строк в один столбец // также удаляем столбец из массива с именами столбцов ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
Результат этого блока кода будет таким:
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
Та-дам!
Причина, по которой мы смогли с такой уверенностью оставить некоторые части набора данных, заключается в том, что библиотека рисует дерево, которое оставляет подсказки относительно того, куда идет набор данных. К текущему моменту у нас получилось вот такое дерево.
Выглядит некрасиво, но этого достаточно для демонстрации. Мы попробуем создать его с помощью HTML в следующей серии статей — помогите мне с этим. Ссылка на мой репозиторий GitHub ниже. Сейчас же закончим начатое, опишем оставшийся процесс сборки дерева. Вот что будет выводиться в лог, когда мы будем повторять процесс снова и снова до тех пор, пока не останется ничего для разбивки.
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
Ниже показана функция, строящая дерево. Эта часть кода мне показалась довольно сложной и непонятной, несмотря на то, что при расчете вручную процесс казался довольно простым. Поэтому я решил подробно разобрать его в деталях.
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //родительские классы double P_EntropyArr[]; //родительская энтропия int p_ClassNumbers[]; //номера классов родителя / переменной Target GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- временные одноразовые массивы для информации о родительском узле string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //вычитаем единицу, чтобы удалить независимую переменную { int rows = ArraySize(m_dataset)/cols; string Arr[]; //массив для текущего столбца string ArrTarg[]; //массив для текущего target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //получаем данные столбца и целевого столбца { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //последний индекс всех столбцов } //--- найдем энтропию //Функция для нахождения энтропии выборок в заданном столбце внутри цикла //затем сохраняем все энтропии водном массиве //--- Поиск информационной выгоды //Функция для нахождения информационной выгоды на основе массива энтропии выше //--- if (i == max_gain) { //Получаем максимальную информационную выгоду из всех выгод во всех столбцах, затем //сохраняем ее в родительской информационной выгоде } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- получим родительскую Энтропию, класс и номера классов // здесь мы сохраняем полученный родительский класс из значений информационной выгоды, затем сохраняем их в родительском массиве ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Ищем, есть ли нулевая энтропия в массиве, если есть удаляем ее данные из набора данных if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //если найден ноль в массиве энтропий { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //новое общее количество строк из массива //также удаляем энтропию из массива и ее информацию везде из родительского узла, который будем строить далее ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- УДАЛЕНИЕ РОДИТЕЛЬСКОГО/КОРНЕВОГО УЗЛА ИЗ НАБОРА ДАННЫХ MatrixRemoveColumn(m_dataset,max_gain,cols); // После удаления столбцов присваиваем новые значения этим глобальным переменным cols = cols-1; // удаляем столбец, который был удален rows_total = rows_total - single_rowstotal; //убираем размер строк в один столбец // также удаляем столбец из массива с именами столбцов ArrayRemove(DataColumnNames,max_gain,1); //--- } }
Заключение
Мы с вами разобрали основные вычисления, связанные с деревьями классификации. Это слишком сложная и длинная тема, чтобы ее можно было описать в одной статье. Надеюсь, я закончу ее в следующей статье или двух. Хотя в библиотеке уже есть почти все, что нужно, чтобы начать строить алгоритмы дерева решений и на их основе решать торговые задачи.
Спасибо за чтение! Вот ссылка на мой гитхаб: https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11061
 Разработка торговой системы на основе индикатора Ишимоку
Разработка торговой системы на основе индикатора Ишимоку
 Возможности Мастера MQL5, которые вам нужно знать (Часть 1): Регрессионный анализ
Возможности Мастера MQL5, которые вам нужно знать (Часть 1): Регрессионный анализ
 Нейросети — это просто (Часть 25): Практикум Transfer Learning
Нейросети — это просто (Часть 25): Практикум Transfer Learning
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
А кстати вот да, чего все упёрлись в MO, АИ и DeepLearning.. Есть же хорошо забытое старое, про которое напомнил топик-стартер. Есть же экспертные системы и всякие взвешенные оценки. Конечно методам лет по 30-50, не модно, но они придерживаются физичной модели и причинно-следственных связей и их результаты интерпретируемы. НАДО КОПНУТЬ ТУДА
это единственная штука которая потенциально может быть фильтром уже рассчитанных сигналов. Прочие методы в этом направлении обо@$лись
А кстати вот да, чего все упёрлись в MO, АИ и DeepLearning.. Есть же хорошо забытое старое, про которое напомнил топик-стартер. Есть же экспертные системы и всякие взвешенные оценки. Конечно методам лет по 30-50, не модно, но они придерживаются физичной модели и причинно-следственных связей и их результаты интерпретируемы. НАДО КОПНУТЬ ТУДА
это единственная штука которая потенциально может быть фильтром уже рассчитанных сигналов. Прочие методы в этом направлении обо@$лись