租用者 - 页 16 1...91011121314151617181920212223...31 新评论 [删除] 2011.02.26 07:34 #151 看看这些参数是如何影响结果的,这很有意思。 [删除] 2011.02.26 07:46 #152 例如,对于我们的基线条件,在不同的阀门位置,我们得到这些有趣的图片 . . . 这是为大局着想...... 我们对最后一个依赖关系感兴趣 ("a-da "相位图--最后一个图是它的一个特例) [删除] 2011.02.26 08:12 #153 Mathemat: 结果不是很好。我不会在这里公布计算结果。他们没有任何美丽之处。 我试图使用以下观察:1+q-k=1+epsilon,epsilon是一个小值。然后我用泰勒数列中的k来扩展导数,首先保持三阶以下的小项。然后,经过简化,我们得到了立方体方程。我舍弃了三阶最小项,并试图解决所产生的二次项。我失败了:判别式只有在小t时才是正数。 恐怕我在拒绝立方体项方面犯了一个错误:虽然它是一个在epsilon中属于第三阶小的项,但它并不小。我的方法是:epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3)。可以看出,对于大t来说,它可能相当小(即使epsilon~0.01是相当现实的假设)。而人们并不希望解决立方体的问题。 让我们看看奥列格 得到了什么。 P.S. 假设epsilon*t=O(1)(或q*t=O(1)),你可以通过指数来近似幂函数。让我们试一试吧。 还有一种方法--没有泰勒级数,而是简单地用正切法(我想是牛顿法)。而且,人们也可以得到一个相当精确的分析解。 问题是,最初的条件不包含连续时间,而是一个格子函数--即必须首先进行适当的转换。只有这样,引入一个小的伊普西龙才是有效的。这些都是格子函数的特性。 顺便说一下,我在解决问题的第一步中处理的正是向连续时间区域的转换,在离散--频率--时间链中使用拉普拉斯变换。更确切地说:也是通过这个... [删除] 2011.02.26 08:24 #154 因此,我们进一步分析的对象是函数 . Neutron 2011.02.26 09:08 #155 Mathemat:而我不想解决立方体的问题。阿列克谢,我从未见过立方体方程的根的分析表达式(除了部分简化的情况)。你没有这样的表情吗?就像一元二次方程:x1=b/2+SQRT()...等。如果你知道的话,请张贴出来。我在互联网上没有发现任何东西。我记得在学校里,甚至有一种通过谐波函数来表示根的方法! 还有一种方法--没有泰勒级数,而是简单地用正切法(我想是牛顿)。而且,人们也可以得到一个相当精确的分析解。 用这种方式真的可以得到分析形式的近似解吗?从未听说过。非常有趣,我想看看这个方法的例子。 我们去演播室吧! 是的,你说的是在大t 下得到的解。 作为一个 "无法杀死 "的存款案例,这也是具有实际意义的。你设法得到了一个近似值,是什么 t?也许t->inf 的极限转换是可能的。然后,我们可以得到最佳支付百分比的分析性表达,k,作为只有一个参数q 的函数--应计利息的价值。这将是一个很好的结果。 avtomat: 关键是初始条件不包含连续时间,而是一个格子函数--即必须首先进行转换。只有这样,引入一个小的ε才是有效的。这些都是格子函数的特性。顺便说一下,我在解决问题的第一步中处理的正是向连续时间区域的转换,在离散--频率--时间链中使用拉普拉斯变换。更确切地说:包括这个...奥列格,为什么你认为上面得到的可派生手段之和的分析表达式,对于连续时间来说不是边际的?毕竟,我们没有规定原始时间序列 的最小间隔(步长)限制(话题第一帖中的迭代形式写法)。如果是这样,那么在 dt->0 的极限转换处,我们有一定的df(t) 就足够了,而且 不存在矛盾......。 Renter MQL5 中的统计分布 - 充分利用 [删除] 2011.02.26 10:09 #156 Neutron: 奥列格,为什么你认为上述导数之和的分析表达式不是连续时间的极限?毕竟,我们没有特别规定对原始时间序列的最小间隔(步长)的限制(该主题第一帖中的迭代形式的符号)。如果是这样,那么在 dt->0 的极限转换处,我们有一个确定的df(t )就足够了, 不存在矛盾......。 不是这样的...尝试在这里引入一个小的ε... 是的,我们没有在任何地方具体规定,但问题本身的措辞隐含着使用格子函数的意思。 这意味着匹配将在格子的节点中进行。此外,对于格子函数来说,没有中间点--只有格子的节点。所以所有试图构建中间值的做法都会导致错误的结果(顺便说一下,这些问题属于信号量化领域)。中间值可以通过提高采样率来构建,即再次引入一个有更多节点的网格函数,这不会从根本上改变现象的本质。这尤其意味着,用第一、第二等导数来代替第一、第二等差值。而不是积分--和。等。-- 这是一个完整的研究领域。 但是有一些方法可以从一个领域转移到另一个领域,然后再回来。 在我们问题的这种特殊情况下,这种方法并不适合我们。因此,我们要做的第一件事就是从离散时间转向连续时间。 Alexey Subbotin 2011.02.26 10:21 #157 avtomat: 问题是,初始条件不是连续时间,而是一个网格函数--即必须首先进行转换。 ...或者不使用,而是使用拉普拉斯变换的离散版的现有仪器,即Z-变换。你不觉得这样会更简单吗? Ilnur Iksanov 2011.02.26 10:27 #158 Neutron: 我从来没有见过立方体方程的根的分析表达式(除了部分简化)。你没有吗?就像一元二次方程:x1=b/2+SQRT()...等。如果你知道的话,请张贴出来。我在互联网上找不到任何东西。 卡达诺的公式。 我记得在学校的时候,甚至还有通过谐波函数来表示根的方法!这是我在学校时的印象。 维茨的三角公式 [删除] 2011.02.26 10:31 #159 alsu: ...或者不生产,而是使用拉普拉斯变换的离散版本的现有仪器,即Z-变换。你不觉得这样会更简单吗? 这不是问题所在。在一开始就有一个 "增长%-收益%-收益率 "的三维画面--一切都已经计算好了,而且是在离散的领域。 现在的运动任务是以分析的形式呈现这一切;) Neutron 2011.02.26 14:02 #160 Ilnur: 卡达诺公式 维埃特的三角公式 谢谢你,伊尔努尔。 1...91011121314151617181920212223...31 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
看看这些参数是如何影响结果的,这很有意思。
例如,对于我们的基线条件,在不同的阀门位置,我们得到这些有趣的图片
.
.
.
这是为大局着想......
我们对最后一个依赖关系感兴趣
("a-da "相位图--最后一个图是它的一个特例)
结果不是很好。我不会在这里公布计算结果。他们没有任何美丽之处。
我试图使用以下观察:1+q-k=1+epsilon,epsilon是一个小值。然后我用泰勒数列中的k来扩展导数,首先保持三阶以下的小项。然后,经过简化,我们得到了立方体方程。我舍弃了三阶最小项,并试图解决所产生的二次项。我失败了:判别式只有在小t时才是正数。
恐怕我在拒绝立方体项方面犯了一个错误:虽然它是一个在epsilon中属于第三阶小的项,但它并不小。我的方法是:epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3)。可以看出,对于大t来说,它可能相当小(即使epsilon~0.01是相当现实的假设)。而人们并不希望解决立方体的问题。
让我们看看奥列格 得到了什么。
P.S. 假设epsilon*t=O(1)(或q*t=O(1)),你可以通过指数来近似幂函数。让我们试一试吧。
还有一种方法--没有泰勒级数,而是简单地用正切法(我想是牛顿法)。而且,人们也可以得到一个相当精确的分析解。
问题是,最初的条件不包含连续时间,而是一个格子函数--即必须首先进行适当的转换。只有这样,引入一个小的伊普西龙才是有效的。这些都是格子函数的特性。
顺便说一下,我在解决问题的第一步中处理的正是向连续时间区域的转换,在离散--频率--时间链中使用拉普拉斯变换。更确切地说:也是通过这个...
因此,我们进一步分析的对象是函数
.
而我不想解决立方体的问题。
阿列克谢,我从未见过立方体方程的根的分析表达式(除了部分简化的情况)。你没有这样的表情吗?就像一元二次方程:x1=b/2+SQRT()...等。如果你知道的话,请张贴出来。我在互联网上没有发现任何东西。我记得在学校里,甚至有一种通过谐波函数来表示根的方法!
还有一种方法--没有泰勒级数,而是简单地用正切法(我想是牛顿)。而且,人们也可以得到一个相当精确的分析解。
用这种方式真的可以得到分析形式的近似解吗?从未听说过。非常有趣,我想看看这个方法的例子。
我们去演播室吧!
是的,你说的是在大t 下得到的解。 作为一个 "无法杀死 "的存款案例,这也是具有实际意义的。你设法得到了一个近似值,是什么 t?也许t->inf 的极限转换是可能的。然后,我们可以得到最佳支付百分比的分析性表达,k,作为只有一个参数q 的函数--应计利息的价值。这将是一个很好的结果。
avtomat:
关键是初始条件不包含连续时间,而是一个格子函数--即必须首先进行转换。只有这样,引入一个小的ε才是有效的。这些都是格子函数的特性。
顺便说一下,我在解决问题的第一步中处理的正是向连续时间区域的转换,在离散--频率--时间链中使用拉普拉斯变换。更确切地说:包括这个...
奥列格,为什么你认为上面得到的可派生手段之和的分析表达式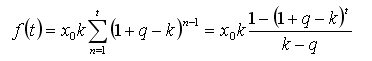 ,对于连续时间来说不是边际的?毕竟,我们没有规定原始时间序列 的最小间隔(步长)限制(话题第一帖中的迭代形式写法)。如果是这样,那么在 dt->0 的极限转换处,我们有一定的df(t) 就足够了,而且 不存在矛盾......。
,对于连续时间来说不是边际的?毕竟,我们没有规定原始时间序列 的最小间隔(步长)限制(话题第一帖中的迭代形式写法)。如果是这样,那么在 dt->0 的极限转换处,我们有一定的df(t) 就足够了,而且 不存在矛盾......。
奥列格,为什么你认为上述导数之和的分析表达式不是连续时间的极限?毕竟,我们没有特别规定对原始时间序列的最小间隔(步长)的限制(该主题第一帖中的迭代形式的符号)。如果是这样,那么在 dt->0 的极限转换处,我们有一个确定的df(t )就足够了, 不存在矛盾......。
不是这样的...尝试在这里引入一个小的ε...
是的,我们没有在任何地方具体规定,但问题本身的措辞隐含着使用格子函数的意思。
这意味着匹配将在格子的节点中进行。此外,对于格子函数来说,没有中间点--只有格子的节点。所以所有试图构建中间值的做法都会导致错误的结果(顺便说一下,这些问题属于信号量化领域)。中间值可以通过提高采样率来构建,即再次引入一个有更多节点的网格函数,这不会从根本上改变现象的本质。这尤其意味着,用第一、第二等导数来代替第一、第二等差值。而不是积分--和。等。-- 这是一个完整的研究领域。
但是有一些方法可以从一个领域转移到另一个领域,然后再回来。
在我们问题的这种特殊情况下,这种方法并不适合我们。因此,我们要做的第一件事就是从离散时间转向连续时间。
问题是,初始条件不是连续时间,而是一个网格函数--即必须首先进行转换。
我从来没有见过立方体方程的根的分析表达式(除了部分简化)。你没有吗?就像一元二次方程:x1=b/2+SQRT()...等。如果你知道的话,请张贴出来。我在互联网上找不到任何东西。
卡达诺的公式。
我记得在学校的时候,甚至还有通过谐波函数来表示根的方法!这是我在学校时的印象。
维茨的三角公式
...或者不生产,而是使用拉普拉斯变换的离散版本的现有仪器,即Z-变换。你不觉得这样会更简单吗?
这不是问题所在。在一开始就有一个 "增长%-收益%-收益率 "的三维画面--一切都已经计算好了,而且是在离散的领域。
现在的运动任务是以分析的形式呈现这一切;)
卡达诺公式
维埃特的三角公式