Redes neurais de maneira fácil (Parte 83): Transformador espaciotemporal de atenção contínua (Conformer)
Introdução
A imprevisibilidade do comportamento dos mercados financeiros pode ser comparada, de certa forma, à variabilidade do clima. No entanto, quando se trata de prever eventos climáticos, a humanidade avançou consideravelmente. Hoje em dia, confiamos bastante nas previsões meteorológicas feitas pelos especialistas. Mas podemos utilizar esses avanços para prever o "clima" dos mercados financeiros? Neste artigo, pretendo apresentar a você um algoritmo complexo, o transformador espaciotemporal de atenção contínua Conformer, desenvolvido para prever o tempo e apresentado no artigo "Conformer: Embedding Continuous Attention in Vision Transformer for Weather Forecasting". Neste trabalho, os autores propõem o algoritmo Continuous Attention, combinando-o com as Neural ODE discutidas no artigo anterior.
1. Algoritmo Conformer
O Conformer analisa as mudanças climáticas ao longo do tempo, mantendo a continuidade no mecanismo de atenção de várias cabeças. O mecanismo de atenção é codificado como uma função diferenciável na arquitetura do transformador para modelar a complexa dinâmica do clima.
Inicialmente, os autores têm a tarefa de construir um modelo que recebe dados climáticos como entrada na forma de (XN*W*H, T). Aqui, N é o número de variáveis climáticas, como temperatura, velocidade do vento, pressão, etc. W*H refere-se à resolução espacial da variável. T é o tempo durante o qual o sistema evolui. O modelo recebe as variáveis climáticas no tempo t, estuda a evolução do sistema espaciotemporal e prevê o clima no próximo passo de tempo t+1.
![]()
Como o clima muda constantemente ao longo do tempo, também é importante capturar as mudanças contínuas dentro dos dados fornecidos por um tempo fixo. A ideia é estudar a representação oculta contínua dos dados climáticos usando solucionadores de equações diferenciais. Assim, o modelo não só prevê o valor da variável climática no momento "T", mas também estuda a integral definida que acompanha as mudanças da variável climática, como a temperatura, do momento inicial ao momento "T". O sistema pode ser representado como:
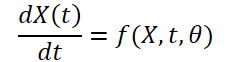
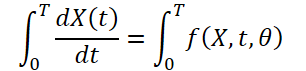
![]()
A informação climática é altamente variável e difícil de prever, tanto no nível temporal quanto no espacial. As derivadas temporais de cada variável climática são calculadas para preservar a dinâmica do clima e garantir uma melhor extração de características a partir de dados discretos. Os autores do método realizam diferenciação seletiva no nível de píxeis para capturar as mudanças contínuas dos fenômenos climáticos ao longo do tempo.
A normalização das derivadas é uma das etapas mais importantes para garantir a estabilidade do comportamento de modelos de aprendizado profundo. Os autores do método expandem a ideia de normalização como elementos individuais da arquitetura do modelo. Eles investigam o papel da normalização quando aplicada diretamente às derivadas. O trabalho dos autores explora o impacto de dois dos métodos de normalização mais comuns e da camada de pré-diferenciação nos resultados da modelagem, para demonstrar suas vantagens em sistemas contínuos.
A atenção é um dos componentes chave da arquitetura Transformer. Ela se baseia na ideia de identificar os blocos mais importantes dos dados de entrada na etapa final da previsão. Apesar do sucesso em resolver várias tarefas, o Transformer ainda é limitado em sua capacidade de aprender a incorporar informações para sistemas altamente dinâmicos, como a previsão do tempo. Os autores do método Conformer desenvolvem o mecanismo Continuous Attention para modelar a mudança contínua das variáveis climáticas. Primeiramente, os autores substituem a análise das dependências entre os elementos do estado inicial pela atenção entre os parâmetros correspondentes de diferentes estados ambientais. Isso permite calcular o espaço contextual de incorporação para cada variável climática que muda ao longo do tempo. Esse passo garante que o modelo processe a mesma variável em diferentes estados no lote, em vez de se referir a blocos no mesmo estado ambiental. O mapeamento das variáveis é realizado atribuindo a cada variável seu próprio Query, Key e Value para cada amostra dos dados de entrada, similar ao que é feito em um estado ambiental. O mecanismo de atenção calcula as pontuações de dependência entre variáveis de diferentes amostras (nas mesmas posições das variáveis). Similarmente aos mecanismos de atenção tradicionais, os pesos das dependências obtidos para diferentes lotes podem ser usados para agregar ou ponderar informações relacionadas a essas variáveis.
Essa modificação permite que o modelo capture as interrelações ou dependências entre as mesmas variáveis climáticas em diferentes estados ambientais. Isso se mostrou útil no cenário de previsão do tempo, onde o modelo é capaz de representar as características em contínua evolução de cada variável climática. Para garantir o aprendizado contínuo, os autores introduzem derivadas no mecanismo Continuous Attention. As equações diferenciais representam a dinâmica do sistema físico ao longo do tempo e consideram os valores de dados ausentes. Os autores combinaram o mecanismo de atenção com a abordagem de aprendizado baseada em equações diferenciais para modelar as mudanças na atmosfera tanto nas características espaciais quanto temporais. Além disso, essa abordagem elimina a limitação de modelar equações físicas complexas em modelos. E, em vez de fazer previsões apenas para um ponto específico no tempo, o Conformer estuda as mudanças transitórias de um passo de tempo para outro, o que é importante para capturar mudanças climáticas sem precedentes.
Para calcular a Continuous Attention, os autores do método propõem calcular as derivadas de similaridade para as mesmas variáveis em cada amostra de dados. Suponha que temos 2 amostras de dados de entrada de tamanho (N*W*H). Vamos denominá-las como X0 e X1 para os tempos t0 e t1, respectivamente. Cada variável possui seus próprios tensores Q, K e V em ambas as amostras. A Continuous Attention é calculada da seguinte forma:
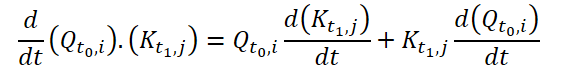
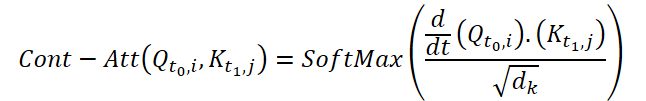
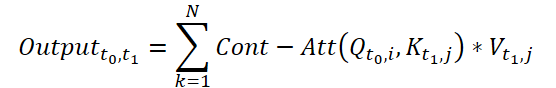
O resultado obtido é uma soma ponderada por atenção dos valores de variáveis semelhantes nos dados de entrada em um determinado momento t0 e t1. Esse processo calcula a atenção entre variáveis semelhantes nos dados de entrada em todos os passos temporais, permitindo que o modelo capture as interrelações ou interações entre as variáveis em toda a sequência das amostras de entrada.
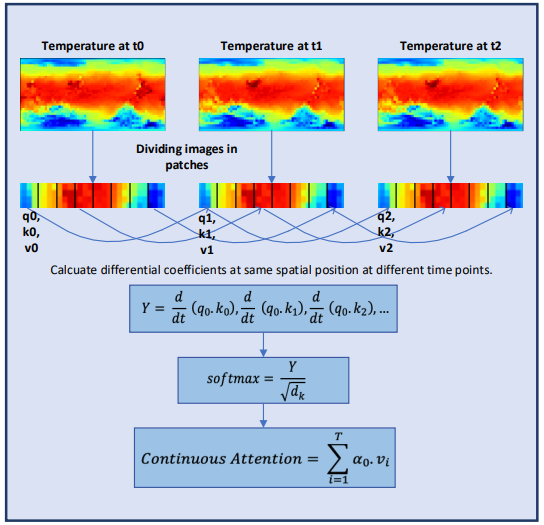
Para melhorar ainda mais o estudo das características contínuas das informações meteorológicas, os autores do Conformer adicionam à modelagem camadas Neural ODE. Como os solucionadores com tamanho adaptativo possuem maior precisão do que aqueles com tamanho fixo, os autores escolheram o método Dormand-Prince (Dopri5). Isso permite estudar as menores mudanças possíveis no clima ao longo do tempo. O fluxo de trabalho completo do Conformer e a colocação das camadas Neural ODE são mostrados na visualização do método fornecida pelos autores abaixo.
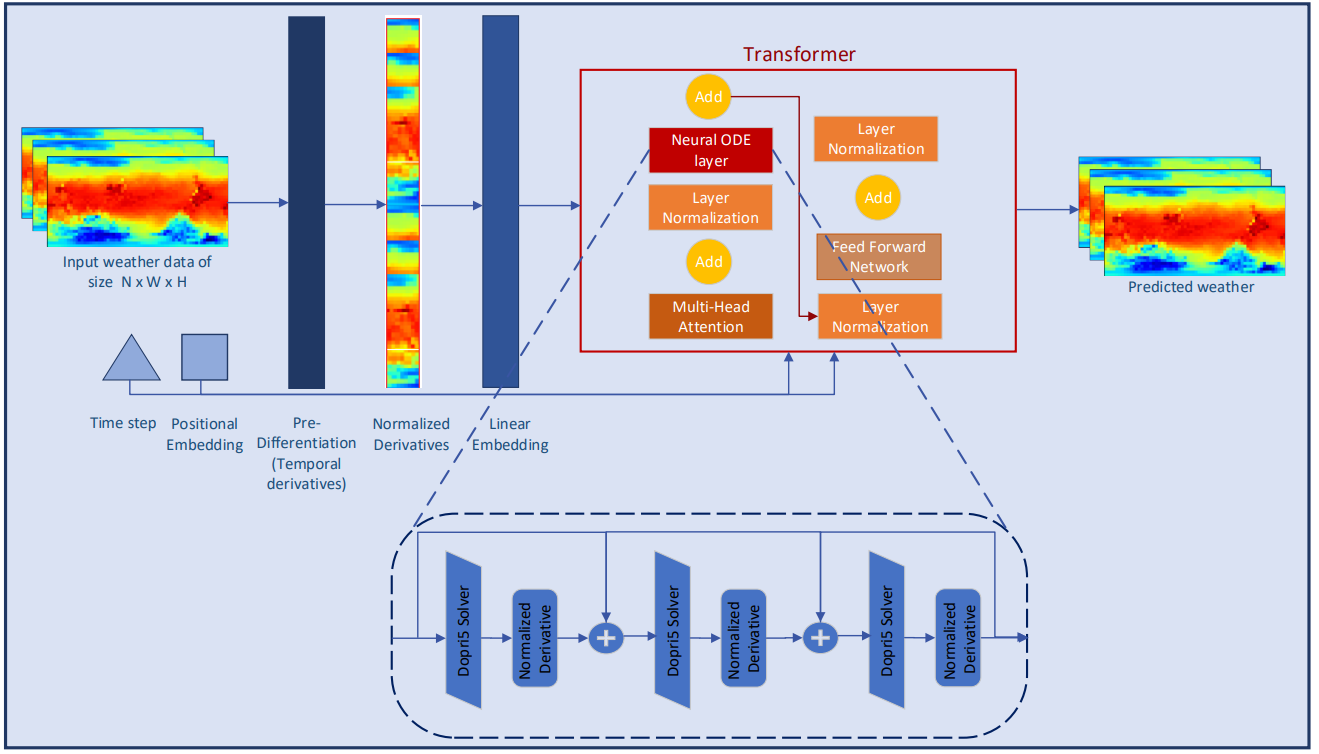
2. Implementação usando MQL5
Após a análise dos aspectos teóricos dos métodos Conformer, passamos à implementação prática das abordagens propostas utilizando MQL5. Implementaremos a funcionalidade principal em uma nova classe chamada CNeuronConformer, que será criada como herdeira da classe base de camada neural CNeuronBaseOCL.
2.1 Arquitetura da classe CNeuronConformer
Na estrutura da classe CNeuronConformer, observamos métodos já familiares, sobrescritos em todas as classes de implementação dos métodos de atenção. No entanto, a Continuous Attention é tão distinta dos métodos de atenção analisados anteriormente que foi decidido implementar completamente o algoritmo "do zero". Ainda assim, nesta implementação, utilizaremos desenvolvimentos de trabalhos anteriores.
Para registrar os principais parâmetros da arquitetura da camada, introduzimos 5 variáveis:
- iWindow — tamanho do vetor que descreve um parâmetro no tensor de dados de entrada;
- iDimension — dimensionalidade do vetor de uma entidade Query, Key, Value;
- iHeads — número de cabeças de atenção;
- iVariables — número de parâmetros que descrevem um estado ambiental;
- iCount — número de estados ambientais analisados (comprimento da sequência de dados de entrada).
Para gerar as entidades Query, Key e Value, utilizaremos, como em casos anteriores, a camada convolucional cQKV. Esse método nos permite realizar o processamento paralelo de todas as 3 entidades. As derivadas das entidades em relação ao tempo serão registradas na camada neural base cdQKV.
Os coeficientes de dependência, de forma semelhante ao algoritmo nativo do Transformer, serão armazenados na matriz Score. No entanto, nesta implementação, não criaremos uma cópia da matriz no lado do programa principal. Criaremos apenas um buffer no contexto do OpenCL. E na variável local iScore da classe CNeuronConformer, armazenaremos um ponteiro para o buffer.
Os resultados da atenção multicabeça serão armazenados nos buffers da camada neural base cAttentionOut. E reduziremos a dimensionalidade dos dados obtidos utilizando a camada convolucional cW0.
Segundo o algoritmo Conformer, após o bloco de atenção, há um bloco de camadas neurais de equações diferenciais ordinárias. Para eles, criaremos um array chamado cNODE. Da mesma forma, para o bloco FeedForward criaremos um array cFF.
class CNeuronConformer : public CNeuronBaseOCL { protected: //--- int iWindow; int iDimension; int iHeads; int iVariables; int iCount; //--- CNeuronConvOCL cQKV; CNeuronBaseOCL cdQKV; int iScore; CNeuronBaseOCL cAttentionOut; CNeuronConvOCL cW0; CNeuronNODEOCL cNODE[3]; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool attentionOut(void); //--- virtual bool AttentionInsideGradients(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConformer(void) {}; ~CNeuronConformer(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint variables, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronConformerOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual void SetOpenCL(COpenCLMy *obj); virtual CLayerDescription* GetLayerInfo(void); };
Todos os objetos internos da classe serão declarados como estáticos. Isso nos permite deixar o construtor e o destrutor da classe "vazios". A inicialização do objeto da classe, consoante os requisitos do usuário, será realizada no método Init. Nos parâmetros deste método, passaremos os principais parâmetros da arquitetura do objeto.
bool CNeuronConformer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint variables, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * variables * units_count, optimization_type, batch)) return false;
No corpo do método, chamaremos imediatamente o método de mesmo nome da classe pai, no qual é realizado o controle mínimo necessário dos parâmetros recebidos e a inicialização dos objetos herdados. Os resultados desse controle e inicialização serão conhecidos através do valor lógico retornado pelo método.
Em seguida, inicializamos a camada interna cQKV, que serve para gerar as entidades Query, Key e Value. Note que o método Conformer prevê a criação de entidades para cada variável individual. Portanto, o tamanho da janela e o passo da convolução são iguais ao comprimento do vetor de incorporação de uma variável. O número de elementos da convolução é igual ao produto do número de variáveis que descrevem um estado ambiental pelo número de tais estados analisados. O número de filtros de convolução é igual a 3 vezes o produto do comprimento de uma entidade pelo número de cabeças de atenção.
if(!cQKV.Init(0, 0, OpenCL, window, window, 3 * window_key * heads, variables * units_count, optimization, iBatch)) return false;
Após a conclusão bem-sucedida dos dois métodos acima mencionados, armazenaremos os parâmetros obtidos nas variáveis internas.
iWindow = int(fmax(window, 1)); iDimension = int(fmax(window_key, 1)); iHeads = int(fmax(heads, 1)); iVariables = int(fmax(variables, 1)); iCount = int(fmax(units_count, 1));
Inicializamos a camada interna para registrar as derivadas parciais em relação ao tempo.
if(!cdQKV.Init(0, 1, OpenCL, 3 * iDimension * iHeads * iVariables * iCount, optimization, iBatch)) return false;
E criaremos um buffer para os coeficientes de atenção.
iScore = OpenCL.AddBuffer(sizeof(float) * iCount * iHeads * iVariables * iCount, CL_MEM_READ_WRITE); if(iScore < 0) return false;
A inicialização das camadas internas cAttentionOut e cW0 conclui o trabalho de preparação dos objetos do bloco de atenção.
if(!cAttentionOut.Init(0, 2, OpenCL, iDimension * iHeads * iVariables * iCount, optimization, iBatch)) return false; if(!cW0.Init(0, 3, OpenCL, iDimension * iHeads, iDimension * iHeads, iWindow, iVariables * iCount, optimization, iBatch)) return false;
Aqui, é importante observar que a dimensionalidade dos dados na saída do bloco de atenção deve corresponder à dimensionalidade dos dados de entrada recebidos. Como o algoritmo Conformer prevê a análise das dependências dentro de uma única variável, mas em diferentes estados ambientais, a redução da dimensionalidade será realizada dentro de variáveis individuais.
Todas as camadas neurais usadas nas equações diferenciais ordinárias têm a mesma arquitetura. Isso nos permite inicializá-las em um loop.
for(int i = 0; i < 3; i++) if(!cNODE[i].Init(0, 4 + i, OpenCL, iWindow, iVariables, iCount, optimization, iBatch)) return false;
Por fim, resta-nos inicializar os objetos do bloco FeedForward.
if(!cFF[0].Init(0, 7, OpenCL, iWindow, iWindow, 4 * iWindow, iVariables * iCount, optimization, iBatch)) return false; if(!cFF[1].Init(0, 8, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iVariables * iCount, optimization, iBatch)) return false;
Antes de concluir o trabalho do método, configuramos a substituição do ponteiro do buffer de gradientes da nossa classe pelo buffer de gradientes da última camada do bloco FeedForward. Esse truque nos permite evitar a cópia desnecessária de dados, algo que já utilizamos em muitas implementações anteriores.
if(getGradientIndex() != cFF[1].getGradientIndex()) SetGradientIndex(cFF[1].getGradientIndex()); //--- return true; }
2.2 Implementação da propagação para frente
Após a inicialização da instância da classe, passamos à implementação do algoritmo de propagação para frente. Aqui, vale destacar o algoritmo Continuous Attention proposto pelos autores do método Conformer. Nele, são utilizadas as derivadas parciais das entidades Query e Key em relação ao tempo.
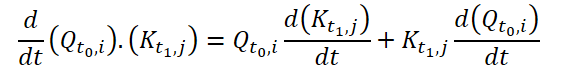
É evidente que, na fase de treinamento do modelo, não temos uma aproximação exata da função de dependência dessas entidades em relação ao tempo. Portanto, abordaremos a questão da definição das derivadas de outra maneira. Primeiro, vamos relembrar o significado geométrico da derivada de uma função. Ele afirma que a derivada de uma função em relação ao argumento em um ponto específico é o ângulo de inclinação da tangente ao gráfico da função nesse ponto e indica a variação aproximada (ou exata para funções lineares) do valor da função ao alterar o argumento em 1.
Nos nossos dados de entrada, recebemos os estados do ambiente com um passo de tempo fixo, que é igual ao time frame analisado. Para simplificar nossa implementação, vamos desconsiderar o time frame específico e igualar o passo de tempo entre dois estados subsequentes a "1". Assim, podemos obter uma aproximação da derivada da função de forma analítica, considerando a média da variação do valor da função nas duas transições subsequentes entre os estados, do anterior ao atual e do atual ao subsequente.
Implementaremos o mecanismo proposto no contexto OpenCL no kernel TimeDerivative. Nos parâmetros do kernel, passaremos os ponteiros de dois buffers: o de dados de entrada e o de resultados. Além disso, a dimensão de uma entidade.
__kernel void TimeDerivative(__global float *qkv, __global float *dqkv, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Planejamos executar o kernel em três dimensões:
- O número de estados do ambiente analisados;
- O número de variáveis que descrevem um estado do ambiente;
- O número de cabeças de atenção.
No corpo do kernel, identificamos imediatamente o fluxo atual em todas as três dimensões. Em seguida, determinamos os deslocamentos nos buffers até as entidades a serem processadas. Para conveniência, usaremos buffers de dados de entrada e de resultados de mesmo tamanho. Portanto, os deslocamentos serão idênticos.
const int shift = 3 * heads * variables * dimension; const int shift_query = pos * shift + (3 * variable * heads + head) * dimension; const int shift_key = shift_query + heads * dimension;
Em seguida, organizamos o cálculo das variações em um loop que percorre todos os elementos de uma entidade. Primeiro, determinamos a derivada para Query de forma analítica.
for(int i = 0; i < dimension; i++) { //--- dQ/dt { int count = 0; float delta = 0; float value = qkv[shift_query + i]; if(pos > 0) { delta = value - qkv[shift_query + i - shift]; count++; } if(pos < (total - 1)) { delta += qkv[shift_query + i + shift] - value; count++; } if(count > 0) dqkv[shift_query + i] = delta / count; }
Aqui, é importante prestar atenção aos casos particulares do primeiro e do último elementos da sequência. Nesses estados, temos apenas uma transição. Não complicaremos o algoritmo e utilizaremos apenas os dados disponíveis.
Da mesma forma, calculamos as derivadas para Key.
//--- dK/dt { int count = 0; float delta = 0; float value = qkv[shift_key + i]; if(pos > 0) { delta = value - qkv[shift_key + i - shift]; count++; } if(pos < (total - 1)) { delta += qkv[shift_key + i + shift] - value; count++; } if(count > 0) dqkv[shift_key + i] = delta / count; } } }
Após determinar as derivadas parciais em relação ao tempo, temos todos os dados necessários para executar o Continuous Attention. No contexto OpenCL, implementamos o algoritmo proposto no kernel FeedForwardContAtt. Nos parâmetros do kernel, passaremos os ponteiros de quatro buffers de dados: Dois buffers de dados de entrada (das entidades e suas derivadas), o buffer da matriz de coeficientes de dependência e o buffer dos resultados de atenção multicabeça. Além disso, passaremos dois parâmetros constantes: a dimensão do vetor de uma entidade e o número de cabeças de atenção.
__kernel void FeedForwardContAtt(__global float *qkv, __global float *dqkv, __global float *score, __global float *out, int dimension, int heads) { const size_t query = get_global_id(0); const size_t key = get_global_id(1); const size_t variable = get_global_id(2); const size_t queris = get_global_size(0); const size_t keis = get_global_size(1); const size_t variables = get_global_size(2);
No corpo do kernel, como de costume, identificamos primeiro o fluxo atual em todas as dimensões do espaço de tarefas. Neste caso, é utilizado um espaço de tarefas tridimensional, com a criação de grupos locais dentro de uma única solicitação para uma variável.
Aqui, declaramos um array local para os dados intermediários.
const uint ls_score = min((uint)keis, (uint)LOCAL_ARRAY_SIZE); __local float local_score[LOCAL_ARRAY_SIZE];
Em seguida, criamos um loop com iterações baseadas no número de cabeças de atenção. No corpo do loop, executamos a análise dos dados para todas as cabeças de atenção de forma sequencial.
for(int head = 0; head < heads; head++) { const int shift = 3 * heads * variables * dimension; const int shift_query = query * shift + (3 * variable * heads + head) * dimension; const int shift_key = key * shift + (3 * variable * heads + heads + head) * dimension; const int shift_out = dimension * (heads * (query * variables + variable) + head); int shift_score = keis * (heads * (query * variables + variable) + head) + key;
Primeiro, determinamos o deslocamento nos buffers de dados até os elementos a serem analisados. Depois disso, calculamos os coeficientes de dependência. A determinação desses coeficientes ocorre em três etapas. Primeiro, calculamos os valores exponenciais d/dt(Q.K) e os armazenamos no elemento correspondente do buffer de coeficientes de dependência. Os cálculos são realizados em fluxos paralelos de um grupo de trabalho.
//--- Score float scr = 0; for(int d = 0; d < dimension; d++) scr += qkv[shift_query + d] * dqkv[shift_key + d] + qkv[shift_key + d] * dqkv[shift_query + d]; scr = exp(min(scr / sqrt((float)dimension), 30.0f)); score[shift_score] = scr; barrier(CLK_LOCAL_MEM_FENCE);
Na segunda etapa, somamos todos os valores obtidos.
if(key < ls_score) { local_score[key] = scr; for(int k = ls_score + key; k < keis; k += ls_score) local_score[key] += score[shift_score + k]; } barrier(CLK_LOCAL_MEM_FENCE); //--- int count = ls_score; do { count = (count + 1) / 2; if(key < count) { if((key + count) < keis) { local_score[key] += local_score[key + count]; local_score[key + count] = 0; } } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Na terceira etapa, normalizamos os coeficientes de dependência.
score[shift_score] /= local_score[0];
barrier(CLK_LOCAL_MEM_FENCE);
E, ao finalizar as iterações do loop, calculamos o valor dos resultados do bloco de atenção consoante os coeficientes de dependência definidos acima.
shift_score -= key; for(int d = key; d < dimension; d += keis) { float sum = 0; int shift_value = (3 * variable * heads + 2 * heads + head) * dimension + d; for(int v = 0; v < keis; v++) sum += qkv[shift_value + v * shift] * score[shift_score + v]; out[shift_out + d] = sum; } barrier(CLK_LOCAL_MEM_FENCE); } //--- }
Após criar os kernels para a implementação do algoritmo Continuous Attention no contexto OpenCL, precisamos implementar a chamada dos kernels criados a partir do programa principal. Para isso, adicionaremos o método attentionOut à nossa classe CNeuronConformer.
Não dividimos a chamada dos kernels em métodos separados, pois a chamada deles é feita de forma sequencial. A divisão do algoritmo no lado do programa OpenCL é causada pela diferença no espaço de tarefas.
Como esse método foi criado apenas para chamadas internas da classe, seu algoritmo foi construído inteiramente com base no uso de objetos e variáveis internas. Isso permitiu eliminar completamente os parâmetros do método.
bool CNeuronConformer::attentionOut(void) { if(!OpenCL) return false;
No corpo do método, verificamos a validade do ponteiro para o contexto OpenCL. Em seguida, preparamos a chamada do primeiro kernel para determinar as derivadas das entidades.
Primeiro, definimos o espaço de tarefas.
bool CNeuronConformer::attentionOut(void) { if(!OpenCL) return false; //--- Time Derivative { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
Depois, passamos os parâmetros para o kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tdqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tddqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_TimeDerivative, def_k_tddimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_TimeDerivative, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } }
O algoritmo geral para colocar o segundo kernel na fila de execução é semelhante. Apenas adicionamos o espaço de tarefas do grupo de trabalho.
//--- MH Attention Out { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iCount, iVariables}; uint local_work_size[3] = {1, iCount, 1};
Além disso, aumenta o número de parâmetros passados.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cadqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cascore, iScore)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caout, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_cadimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_caheads, int(iHeads))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Após realizar o trabalho preparatório, colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_FeedForwardContAtt, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
No entanto, a chamada de dois kernels implementa apenas parte do método Conformer, especificamente a parte principal do Continuous Attention. O algoritmo completo de propagação para frente da nossa classe será descrito no método CNeuronConformer::feedForward. De forma semelhante aos métodos homônimos das classes criadas anteriormente, o método feedForward recebe, em seus parâmetros, um ponteiro para o objeto da camada anterior, que contém os dados de entrada para nossa classe.
bool CNeuronConformer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Generate Query, Key, Value if(!cQKV.FeedForward(NeuronOCL)) return false;
No corpo do método, primeiro chamamos o método de propagação para frente da camada interna cQKV para formar os tensores das entidades Query, Key e Value. Em seguida, chamamos o método criado anteriormente para invocar os kernels do mecanismo Continuous Attention.
//--- MH Continuas Attention if(!attentionOut()) return false;
Depois, reduzimos a dimensionalidade dos resultados obtidos da atenção multicabeça. O tensor resultante é somado aos dados de entrada e, em seguida, normalizado dentro dos limites das variáveis individuais.
if(!cW0.FeedForward(GetPointer(cAttentionOut))) return false; if(!SumAndNormilize(NeuronOCL.getOutput(), cW0.getOutput(), cW0.getOutput(), iDimension, true, 0, 0, 0, 1)) return false;
Após o bloco Continuous Attention, o algoritmo Conformer prevê um bloco de solucionadores de equações diferenciais ordinárias. Vamos chamá-los em um loop. Depois, somamos os tensores na entrada e saída do bloco, e normalizamos o resultado.
//--- Neural ODE CNeuronBaseOCL *prev = GetPointer(cW0); for(int i = 0; i < 3; i++) { if(!cNODE[i].FeedForward(prev)) return false; prev = GetPointer(cNODE[i]); } if(!SumAndNormilize(prev.getOutput(), cW0.getOutput(), prev.getOutput(), iDimension, true, 0, 0, 0, 1)) return false;
No final do método de propagação para frente, realizamos a propagação para frente do bloco FeedForward, seguida de somação e normalização dos resultados.
//--- Feed Forward for(int i = 0; i < 2; i++) { if(!cFF[i].FeedForward(prev)) return false; prev = GetPointer(cFF[i]); } if(!SumAndNormilize(prev.getOutput(), cNODE[2].getOutput(), getOutput(), iDimension, true, 0, 0, 0, 1)) return false; //--- return true; }
Com isso, concluímos a implementação do algoritmo de propagação para frente. Mas, para o treinamento dos modelos, também precisamos implementar a propagação reversa, distribuindo o gradiente de erro para todos os elementos de acordo com sua influência no resultado final e ajustando os parâmetros do modelo para reduzir o erro total.
2.3 Configuração da propagação reversa
A implementação do algoritmo de propagação reversa também exigirá a criação de novos kernels. E, antes de tudo, precisamos criar o kernel para distribuir os gradientes de erro através do bloco Continuous Attention — HiddenGradientContAtt. Nos parâmetros do kernel, passaremos os ponteiros de seis buffers de dados e uma constante.
__kernel void HiddenGradientContAtt(__global float *qkv, __global float *qkv_g, __global float *dqkv, __global float *dqkv_g, __global float *score, __global float *out_g, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Semelhante ao kernel de propagação para frente, a propagação reversa será implementada em um espaço de tarefas tridimensional, mas sem agrupamento em grupos de trabalho. No corpo do kernel, identificamos imediatamente o fluxo em todas as dimensões do espaço de tarefas.
O algoritmo do kernel pode ser dividido em três partes, dependendo do objeto de alocação do gradiente de erro. No primeiro bloco, distribuímos o gradiente de erro para a entidade Value.
//--- Value gradient { const int shift_value = dimension * (heads * (3 * variables * pos + 3 * variable + 2) + head); const int shift_out = dimension * (head + variable * heads); const int shift_score = total * (variable * heads + head); const int step_out = variables * heads * dimension; const int step_score = variables * heads * total; //--- for(int d = 0; d < dimension; d++) { float sum = 0; for(int g = 0; g < total; g++) sum += out_g[shift_out + g * step_out + d] * score[shift_score + g * step_score]; qkv_g[shift_value + d] = sum; } }
Primeiro, determinamos o deslocamento nos buffers de dados até os elementos a serem analisados. Em seguida, no sistema de loops, coletamos os gradientes de erro em todos os elementos dependentes e em todos os elementos do vetor da entidade.
No segundo bloco, distribuímos os gradientes de erro para Query. No entanto, aqui o algoritmo é um pouco mais complexo.
//--- Query gradient { const int shift_out = dimension * (heads * (pos * variables + variable) + head); const int step = 3 * variables * heads * dimension; const int shift_query = dimension * (3 * heads * variable + head) + pos * step; const int shift_key = dimension * (heads * (3 * variable + 1) + head); const int shift_value = dimension * (heads * (3 * variable + 2) + head); const int shift_score = total * (heads * (pos * variables + variable) + head);
Como no primeiro bloco, primeiro determinamos o deslocamento para os elementos a serem analisados nos buffers de dados. Em seguida, precisamos distribuir o gradiente na matriz de coeficientes de dependência e ajustá-lo com base na derivada da função SoftMax.
//--- Score gradient for(int k = 0; k < total; k++) { float score_grad = 0; float scr = score[shift_score + k]; for(int v = 0; v < total; v++) { float grad = 0; for(int d = 0; d < dimension; d++) grad += qkv[shift_value + v * step + d] * out_g[shift_out + d]; score_grad += score[shift_score + v] * grad * ((float)(pos == v) - scr); } score_grad /= sqrt((float)dimension);
Somente então podemos distribuir o gradiente de erro para a entidade Query. No entanto, ao contrário do algoritmo do Transformer nativo, neste caso, também distribuímos o gradiente de erro para as derivadas correspondentes da entidade Query em relação ao tempo.
//--- Query gradient for(int d = 0; d < dimension; d++) { if(k == 0) { dqkv_g[shift_query + d] = score_grad * qkv[shift_key + k * step + d]; qkv_g[shift_query + d] = score_grad * dqkv[shift_key + k * step + d]; } else { dqkv_g[shift_query + d] += score_grad * qkv[shift_key + k * step + d]; qkv_g[shift_query + d] += score_grad * dqkv[shift_key + k * step + d]; } } } }
De maneira semelhante, distribuímos o gradiente de erro para a entidade Key e sua derivada parcial. A única diferença é que percorremos outra dimensão na matriz de coeficientes de dependência.
//--- Key gradient { const int shift_key = dimension * (heads * (3 * variables * pos + 3 * variable + 1) + head); const int shift_out = dimension * (heads * variable + head); const int step_out = variables * heads * dimension; const int step = 3 * variables * heads * dimension; const int shift_query = dimension * (3 * heads * variable + head); const int shift_value = dimension * (heads * (3 * variable + 2) + head) + pos * step; const int shift_score = total * (heads * variable + head); const int step_score = variables * heads * total; //--- Score gradient for(int q = 0; q < total; q++) { float score_grad = 0; float scr = score[shift_score + q * step_score]; for(int g = 0; g < total; g++) { float grad = 0; for(int d = 0; d < dimension; d++) grad += qkv[shift_value + d] * out_g[shift_out + d + g * step_out]; score_grad += score[shift_score + q * step_score + g] * grad * ((float)(q == pos) - scr); } score_grad /= sqrt((float)dimension); //--- Key gradient for(int d = 0; d < dimension; d++) { if(q == 0) { dqkv_g[shift_key + d] = score_grad * qkv[shift_query + q * step + d]; qkv_g[shift_key + d] = score_grad * dqkv[shift_query + q * step + d]; } else { qkv_g[shift_key + d] += score_grad * dqkv[shift_query + q * step + d]; dqkv_g[shift_key + d] += score_grad * qkv[shift_query + q * step + d]; } } } } }
Como se pode notar, no kernel anterior, distribuímos o gradiente de erro tanto para as entidades quanto para suas derivadas. Lembro que as derivadas parciais em relação ao tempo foram calculadas de forma analítica com base nos valores das próprias entidades para diferentes estados do ambiente. É lógico que o gradiente de erro também pode ser transmitido de forma semelhante. Implementaremos esse algoritmo no kernel HiddenGradientTimeDerivative.
__kernel void HiddenGradientTimeDerivative(__global float *qkv_g, __global float *dqkv_g, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Os parâmetros do kernel e o espaço de tarefas são semelhantes à propagação para frente. Porém, em vez dos buffers de resultados, utilizamos os buffers de gradientes de erro.
No corpo do método, identificamos imediatamente o fluxo em todas as dimensões do espaço de tarefas utilizado. Em seguida, determinamos o deslocamento nos buffers de dados.
const int shift = 3 * heads * variables * dimension; const int shift_query = pos * shift + (3 * variable * heads + head) * dimension; const int shift_key = shift_query + heads * dimension;
De forma semelhante ao cálculo das derivadas, realizamos a distribuição dos gradientes de erro.
for(int i = 0; i < dimension; i++) { //--- dQ/dt { int count = 0; float grad = 0; float current = dqkv_g[shift_query + i]; if(pos > 0) { grad += current - dqkv_g[shift_query + i - shift]; count++; } if(pos < (total - 1)) { grad += dqkv_g[shift_query + i + shift] - current; count++; } if(count > 0) grad /= count; qkv_g[shift_query + i] += grad; }
//--- dK/dt { int count = 0; float grad = 0; float current = dqkv_g[shift_key + i]; if(pos > 0) { grad += current - dqkv_g[shift_key + i - shift]; count++; } if(pos < (total - 1)) { grad += dqkv_g[shift_key + i + shift] - current; count++; } if(count > 0) grad /= count; qkv_g[shift_key + i] += dqkv_g[shift_key + i] + grad; } } }
A chamada desses kernels no lado do programa principal é feita no método CNeuronConformer::AttentionInsideGradients. A construção do algoritmo é semelhante ao método correspondente de propagação para frente, com a diferença de que os kernels são chamados na ordem inversa. Primeiro, colocamos na fila de execução o kernel de distribuição do gradiente através do bloco Continuous Attention.
bool CNeuronConformer::AttentionInsideGradients(void) { if(!OpenCL) return false; //--- MH Attention Out Gradient { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv_g, cQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv_g, cdQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcascore, iScore)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaout_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientContAtt, def_k_hgcadimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.Execute(def_k_HiddenGradientContAtt, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } }
Depois, adicionamos o gradiente de erro das derivadas parciais.
//--- Time Derivative Gradient { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tdqkv, cQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tddqkv, cdQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGTimeDerivative, def_k_tddimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.Execute(def_k_HGTimeDerivative, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
Após concluir o trabalho preparatório, reunimos todo o algoritmo de distribuição do gradiente de erro no método CNeuronConformer::calcInputGradients, cujos parâmetros recebem um ponteiro para o objeto da camada anterior. É para este objeto que devemos transmitir o gradiente de erro.
bool CNeuronConformer::calcInputGradients(CNeuronBaseOCL *prevLayer) { //--- Feed Forward Gradient if(!cFF[1].calcInputGradients(GetPointer(cFF[0]))) return false; if(!cFF[0].calcInputGradients(GetPointer(cNODE[2]))) return false; if(!SumAndNormilize(Gradient, cNODE[2].getGradient(), cNODE[2].getGradient(), iDimension, false)) return false;
Graças à substituição dos buffers de gradientes que realizamos, a camada subsequente nos transmitiu o gradiente de erro diretamente no buffer da última camada interna do bloco FeedForward. Agora, sem operações de cópia desnecessárias, chamamos sequencialmente os métodos de propagação reversa dos objetos do bloco FeedForward.
Lembro que, durante a propagação para frente, somamos os valores dos buffers na entrada e saída do bloco FeedForward. Da mesma forma, somamos os gradientes de erro e passamos o resultado obtido para a saída do bloco de equações diferenciais ordinárias. Em seguida, realizamos um ciclo com iteração reversa sobre as camadas internas do bloco Neural ODE, distribuindo nelas o gradiente de erro.
//--- Neural ODE Gradient CNeuronBaseOCL *prev = GetPointer(cNODE[1]); for(int i = 2; i > 0; i--) { if(!cNODE[i].calcInputGradients(prev)) return false; prev = GetPointer(cNODE[i - 1]); } if(!cNODE[0].calcInputGradients(GetPointer(cW0))) return false; if(!SumAndNormilize(cW0.getGradient(), cNODE[2].getGradient(), cW0.getGradient(), iDimension, false)) return false;
Aqui, também somamos os gradientes de erro na entrada e saída do bloco.
Primeiro, durante a propagação para frente, e por último, durante a propagação reversa no bloco Continuous Attention, distribuímos o gradiente de erro entre as cabeças de atenção.
//--- MH Attention Gradient if(!cW0.calcInputGradients(GetPointer(cAttentionOut))) return false;
Em seguida, distribuímos o gradiente de erro através do bloco de atenção.
if(!AttentionInsideGradients()) return false;
E transferimos o gradiente de erro para o nível da camada anterior.
//--- Query, Key, Value Graddients if(!cQKV.calcInputGradients(prevLayer)) return false;
Ao final do método, somamos o gradiente de erro na entrada e saída do bloco de atenção.
if(!SumAndNormilize(cW0.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(), iDimension, false)) return false; //--- return true; }
Após distribuir o gradiente de erro entre todos os objetos de acordo com sua influência no resultado, passamos à otimização dos parâmetros para reduzir o erro total dos modelos.
Vale mencionar que todos os parâmetros treináveis da nossa classe CNeuronConformer estão contidos nas camadas neurais internas. Portanto, para atualizar os parâmetros do modelo, basta chamar sequencialmente os métodos homônimos dos objetos internos.
bool CNeuronConformer::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { //--- MH Attention if(!cQKV.UpdateInputWeights(NeuronOCL)) return false; if(!cW0.UpdateInputWeights(GetPointer(cAttentionOut))) return false;
//--- Neural ODE CNeuronBaseOCL *prev = GetPointer(cW0); for(int i = 0; i < 3; i++) { if(!cNODE[i].UpdateInputWeights(prev)) return false; prev = GetPointer(cNODE[i]); }
//--- Feed Forward for(int i = 0; i < 2; i++) { if(!cFF[i].UpdateInputWeights(prev)) return false; prev = GetPointer(cFF[i]); } //--- return true; }
Com isso, concluímos a análise dos métodos da nova classe CNeuronConformer, na qual implementamos as abordagens principais propostas pelos autores do método Conformer. Infelizmente, o formato do artigo não permite uma análise mais detalhada dos métodos auxiliares da classe. Sugiro que você se familiarize com eles no anexo. Você também encontrará o código completo de todos os programas usados na preparação do artigo. E agora, vamos prosseguir.
2.4 Arquitetura dos Modelos Treináveis
E, antes de prosseguir para a análise da arquitetura dos modelos treináveis, gostaria de lembrar que o método Conformer prevê a análise com base em parâmetros individuais que descrevem o ambiente. Consequentemente, ao processar os dados iniciais, precisamos criar embeddings para cada parâmetro analisado.
Primeiro, vamos examinar a estrutura dos dados analisados.
......... ......... sState.state[shift] = (float)(Rates[b].close - open); sState.state[shift + 1] = (float)(Rates[b].high - open); sState.state[shift + 2] = (float)(Rates[b].low - open); sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f); sState.state[shift + 4] = rsi; sState.state[shift + 5] = cci; sState.state[shift + 6] = atr; sState.state[shift + 7] = macd; sState.state[shift + 8] = sign; ........ ........
Na minha implementação, dividi os dados iniciais da seguinte forma:
- Descrição da última vela (4 elementos)
- RSI (1 elemento)
- CCI (1 elemento)
- ATF (1 elemento)
- MACD (2 elementos)
Essa divisão é apenas a minha visão. Em seu trabalho, você pode usar uma divisão diferente. No entanto, essa divisão deve ser refletida na arquitetura dos modelos treináveis.
Assim, a arquitetura dos modelos treináveis é descrita no método CreateDescriptions. Nos parâmetros, o método recebe 3 ponteiros para arrays dinâmicos, para transmitir a arquitetura de 3 modelos.
No corpo do método, primeiro verificamos os ponteiros recebidos e, se necessário, criamos novos objetos de arrays dinâmicos.
bool CreateDescriptions(CArrayObj *encoder, CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
Os dados não processados que descrevem o estado atual do ambiente são enviados como entrada para o modelo Codificador.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Os dados recebidos passam por um processamento inicial na camada de normalização em lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, criamos os embeddings dos parâmetros do estado atual de acordo com a estrutura apresentada acima.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {4, 1, 1, 1, 2}; ArrayCopy(descr.windows, temp); }
Observe que nas arquiteturas discutidas anteriormente, especificamos o tamanho da janela para o embedding igual ao tamanho dos dados iniciais. Assim, criamos um embedding de um estado individual. No entanto, neste caso, estamos partindo da análise da descrição do último candle, dividindo os parâmetros nos blocos mencionados acima. No caso de análise de mais de um candle ou de outra configuração de dados, isso deve ser refletido no tamanho das janelas dos dados analisados.
prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize / 2; if(!encoder.Add(descr)) { delete descr; return false; }
A camada convolucional subsequente conclui o processo de geração dos embeddings dos dados iniciais.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count * 5; descr.step = descr.window = prev_wout; prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
Adicionamos aos embeddings as harmônicas de codificação posicional.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout * 5; if(!encoder.Add(descr)) { delete descr; return false; }
E, ao final do modelo Codificador, criamos um bloco de 5 camadas sequenciais do Conformer. Os parâmetros da camada são especificados de maneira semelhante às outras camadas de atenção. E o número de variáveis analisadas é especificado em descr.layers.
for(int i = 0; i < 5; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConformerOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = EmbeddingSize; descr.layers = 5; if(!encoder.Add(descr)) { delete descr; return false; } }
Na base do modelo Ator, como anteriormente, está uma camada de cross-attention, que avalia as dependências entre o estado atual da conta e a representação comprimida do estado atual do ambiente, obtida a partir do Codificador.
Como entrada para o modelo, primeiro fornecemos a descrição do estado da conta.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Transformamos isso em um embedding.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
E adicionamos um bloco de 3 camadas de cross-attention.
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, GPTBars * 5}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, EmbeddingSize}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } }
Com base nos dados obtidos do bloco de cross-attention, formamos a política estocástica do Ator.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
O modelo Crítico é construído de maneira semelhante. Apenas em vez do estado da conta, ele correlaciona as ações do Ator com o estado do ambiente.
Como entrada para o modelo, fornecemos as ações geradas pelo Ator.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Essas ações são transformadas em um embedding.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
E, em seguida, vem um bloco de cross-attention de 3 camadas.
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, GPTBars * 5}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, EmbeddingSize}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } }
A avaliação direta das ações é realizada no bloco perceptron.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
2.5 Treinamento dos Modelos
As mudanças que fizemos não afetaram o processo de interação com o ambiente. Isso nos permitiu usar o EA "...\Conformer\Research.mq5" sem alterações para coletar dados iniciais de treinamento e atualizar o conjunto de dados de treinamento subsequente. Além disso, apesar das alterações na abordagem de análise dos dados iniciais, mantivemos sua estrutura inalterada. Isso nos permite utilizar os conjuntos de dados de treinamento coletados anteriormente no processo de treinamento do modelo.
No entanto, fizemos algumas modificações no processo de treinamento dos modelos, que foram refletidas no algoritmo do EA "...\Conformer\Study.mq5". Neste artigo, discutiremos apenas o método de treinamento direto dos modelos Train.
Como antes, no início do método, geramos um vetor de probabilidades para a escolha de trajetórias dependendo de sua rentabilidade. As passagens mais lucrativas recebem maior probabilidade durante a amostragem no processo de treinamento dos modelos.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Em seguida, inicializamos variáveis locais.
vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
E criamos um sistema de loops aninhados para o treinamento dos modelos. No corpo do loop externo, amostramos uma trajetória do buffer de reprodução de experiências e o estado inicial de treinamento nela.
int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
Depois disso, limpamos os buffers recorrentes do Codificador e determinamos o estado final do lote de treinamento.
Encoder.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
Após a preparação, realizamos o loop aninhado para a iteração direta dos estados de treinamento.
for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
No corpo do loop, primeiro carregamos o estado do ambiente do buffer de reprodução de experiências e o analisamos em nosso Codificador, chamando o método de propagação para frente.
Em seguida, carregamos as ações do Ator do buffer de reprodução de experiências e as avaliamos com nosso Crítico.
//--- Critic bActions.AssignArray(Buffer[tr].States[i].action); if(bActions.GetIndex() >= 0) bActions.BufferWrite(); if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Imediatamente após, ajustamos a avaliação do Crítico em direção à recompensa real do buffer de reprodução de experiências.
result.Assign(Buffer[tr].States[i + 1].rewards); target.Assign(Buffer[tr].States[i + 2].rewards); result = result - target * DiscFactor; Result.AssignArray(result); Critic.TrainMode(true); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
O gradiente do erro do Crítico também é passado para o Codificador, para otimizar a análise do estado do ambiente.
O próximo passo é carregar do buffer de reprodução de experiências a descrição do estado da conta, correspondente ao estado do ambiente analisado.
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Com esses dados, geramos a ação do Ator de acordo com sua política atual.
//--- Actor if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
E avaliamos essas ações com nosso Crítico.
if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
A correção da política do Ator é realizada em 2 etapas. Primeiro, ajustamos a política para minimizar o desvio das ações reais do Agente. Isso nos permite manter a política do Ator em uma distribuição próxima ao nosso conjunto de dados de treinamento.
if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Na segunda etapa, ajustamos a política do Ator de acordo com a avaliação de suas ações pelo Crítico. Para isso, desativamos o modo de treinamento do Crítico e propagamos o gradiente do erro até o Ator. Depois, ajustamos a política na direção do gradiente de erro obtido.
Critic.TrainMode(false); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Actor.backPropGradient((CNet *)GetPointer(Encoder), -1, -1, false) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Observe que, em ambos os casos de correção da política do Ator, passamos o gradiente de erro para o nosso Codificador e ajustamos a "representação dele" sobre o ambiente. Dessa forma, buscamos tornar a análise do ambiente o mais informativa possível.
Após atualizar os parâmetros de todos os modelos, resta apenas informar o usuário sobre o progresso do treinamento e passar para a próxima iteração do sistema de loops.
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
O processo de treinamento é repetido até a conclusão de todas as iterações do sistema de loops. E, após a conclusão bem-sucedida do processo de treinamento, limpamos o campo de comentários no gráfico.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
Registramos no log os resultados do processo de treinamento dos modelos e iniciamos a finalização do EA de treinamento.
Com isso, encerramos a análise dos algoritmos utilizados nos programas discutidos no artigo. O código completo pode ser encontrado no anexo.
3. Teste
Nesta parte do artigo, exploramos o método Conformer e implementamos as abordagens propostas usando MQL5. Agora, temos a oportunidade de treinar o modelo utilizando o método proposto e realizar testes com dados reais.
Como de costume, realizaremos o treinamento e o teste do modelo utilizando o Strategy Tester do MetaTrader 5 com dados históricos reais do instrumento EURUSD no time frame H1. Para o treinamento dos modelos, usaremos dados históricos dos primeiros 7 meses de 2023. O teste do modelo treinado foi realizado com dados históricos de agosto de 2023.
Na preparação deste artigo, treinei o modelo utilizando o conjunto de dados coletado para o treinamento dos modelos das séries de artigos anteriores.
Devo dizer que a alteração na arquitetura dos modelos e no algoritmo do processo de treinamento aumentou um pouco o custo de cada iteração. No entanto, as abordagens propostas demonstram estabilidade no processo de treinamento, o que, a meu ver, reduz a quantidade de repetições necessárias para treinar o modelo.
Durante o treinamento, consegui obter um modelo capaz de gerar lucro tanto nos dados de treinamento quanto nos dados de teste.
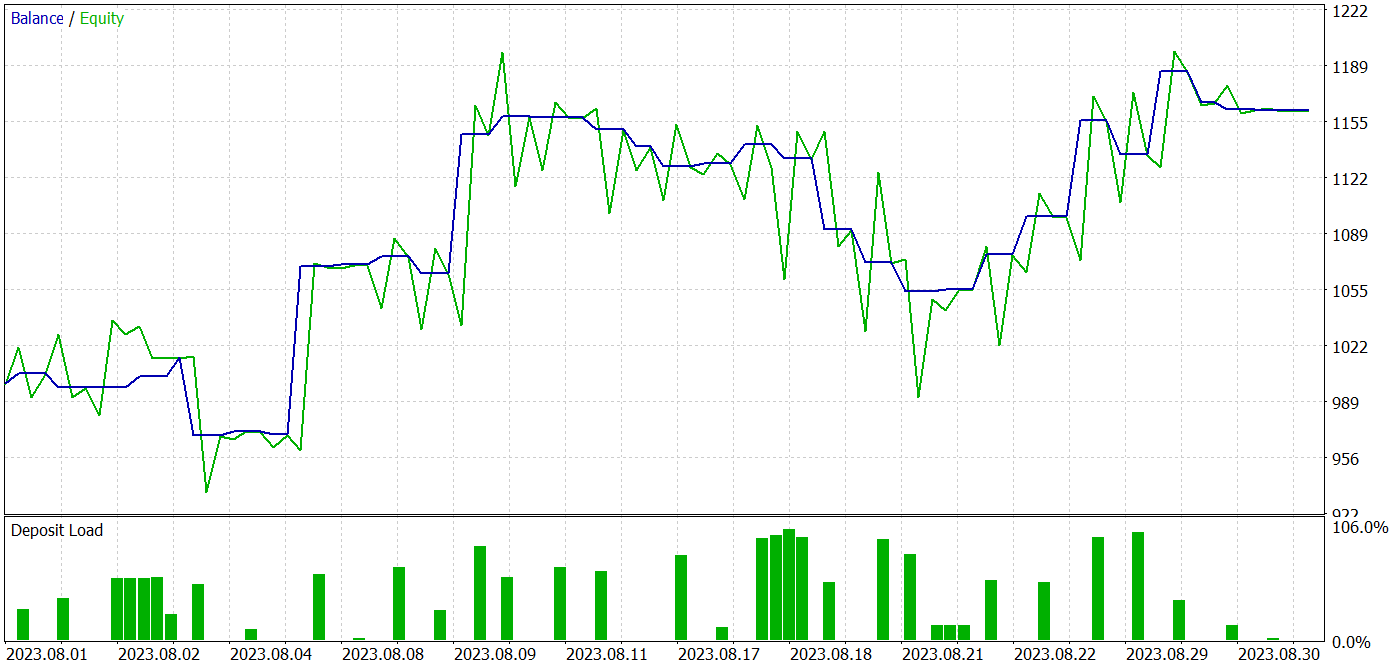
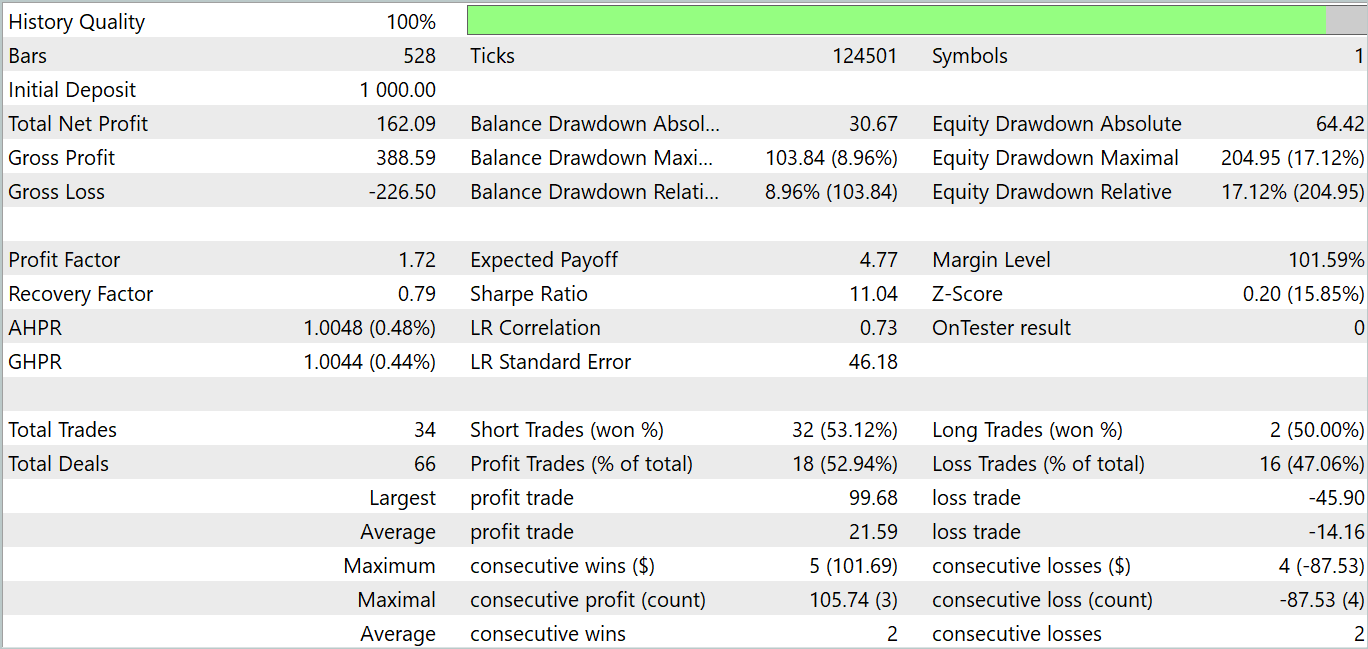
Durante o período de teste, o modelo realizou 34 operações, das quais 18 foram lucrativas. Isso representa 52,94% de operações lucrativas. Além disso, a operação média lucrativa superou em 52,47% a operação média com prejuízo. A operação mais lucrativa foi mais de duas vezes superior ao prejuízo máximo. No geral, o modelo apresentou um profit fAtor de 1,72 e uma tendência de crescimento no gráfico de saldo. O drawdown máximo no Equity foi de 17,12%, enquanto no saldo foi de 8,96%.
Considerações finais
Neste artigo, exploramos o algoritmo complexo do Transformador Espaciotemporal de Atenção Contínua Conformer, desenvolvido para prever o tempo e apresentado no artigo "Conformer: Embedding Continuous Attention in Vision Transformer for Weather Forecasting". Os autores propõem o algoritmo Continuous Attention e o combinam com Neural ODE.
Na parte prática do artigo, implementamos as abordagens propostas utilizando MQL5. Realizamos o treinamento e teste dos modelos criados. Os resultados dos testes são bastante promissores. O modelo conseguiu gerar lucro tanto no conjunto de dados de treinamento quanto no de teste.
No entanto, gostaria de lembrar que todos os programas apresentados no artigo são apenas de caráter informativo e destinados a demonstrar as abordagens propostas.
Links
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento dos Modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criar uma rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14615
 Uma Formulação Genérica de Otimização (GOF) para Implementar Max Personalizado com Restrições
Uma Formulação Genérica de Otimização (GOF) para Implementar Max Personalizado com Restrições
 Desenvolvendo um cliente MQTT para MetaTrader 5: uma abordagem TDD — Final
Desenvolvendo um cliente MQTT para MetaTrader 5: uma abordagem TDD — Final
 Desenvolvendo um EA multimoeda (Parte 7): Seleção de grupos considerando o período forward
Desenvolvendo um EA multimoeda (Parte 7): Seleção de grupos considerando o período forward
 Rede neural na prática: O primeiro neurônio
Rede neural na prática: O primeiro neurônio
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso