Técnicas do MQL5 Wizard que você deve conhecer (Parte 35): Regressão por Vetores de Suporte

Introdução

Regressão por Vetores de Suporte (SVR) é uma forma de regressão derivada de Máquinas de Vetores de Suporte. Em sua essência, o SVR usa métodos de núcleo para mapear os dados de entrada em espaços de dimensão superior, permitindo que relações mais complexas sejam capturadas, o que contrasta com a redução de dimensionalidade. Para este artigo, estamos explorando estritamente o papel de sua função de perda quando usada com um perceptron multicamada. Uma forma relacionada, mas diferente, de regressão que analisamos em um artigo anterior foi a Regressão por Processo Gaussiano. Então, talvez seja fundamental começarmos fazendo distinções entre as duas.

Diferenças entre SVR & GPR

Para destacar as diferenças entre esses dois, vamos dar uma pausa na linguagem de aprendizado de máquina e usar exemplos cotidianos para mostrar por que cada um é importante. Considere um cenário em que você está gerenciando uma start-up que desenvolveu um sorvete de baixo açúcar muito saudável que tem uma boa demanda em sua cidade natal. Como você está apenas começando e só vendeu o sorvete em sua cidade natal, você ainda realiza a maior parte da fabricação manualmente. Portanto, você precisa começar a aumentar sua produtividade, pois isso, além do controle de custos, traz benefícios como controle de qualidade e implementação de alguns padrões de produção.

Tal expansão exigiria capital, o que você não pode pegar emprestado de forma institucional, pois não possui a garantia necessária (ou recursos) para apresentar isso aos Bancos; ou você poderia fazer uma parceria com uma grande marca de sorvetes já estabelecida, no entanto, funcionários de grandes marcas estabelecidas costumam ser burocratas e dirão não independentemente do que pensam sobre seu produto.

Portanto, você se vê com a única opção de levantar capital por uma rota privada e semi-formal, e isso vem com a condição de que você tenha que escalar ou expandir seu produto. No entanto, ao expandir para fora de sua cidade natal, quais clientes vão olhar ou até considerar seu produto em comparação com as marcas estabelecidas? Por ser um território desconhecido, você não pode abordá-lo da mesma forma que fez na cidade natal. Isso levanta então a questão que você pode ter negligenciado em sua corrida inicial para atender à demanda local, que é qual é o seu segmento de cliente primário?

Segmentação de clientes, um aspecto comercial que alguns podem escolher ignorar, tem vários tipos. Ela inclui (mas não se limita a) segmentação por código postal (ou endereço), segmentação por idade, nível de educação, ocupação/profissão e segmentação por nível de renda; e outro segmento 'novo' e crescente, graças às mídias sociais, pode ser a segmentação por grupos de estilo de vida/interesses. Ao aumentar os dados de vendas por esses segmentos, podemos criar alguns conjuntos de dados interessantes que, quando reunidos mesmo sobre nossa cidade natal, podem fornecer uma janela para o que pode acontecer fora de nossa localização primária.

A Regressão por Processo Gaussiano, como introduzida em um artigo anterior, não apenas fornece uma projeção média, mas também anexa uma faixa indicativa a essa média junto com um nível de confiança. Isso tende a significar que é adequada para fazer projeções em situações onde a demanda por um produto é amplamente influenciada por fatores externos (não é consistente) e, portanto, é um produto de luxo ou caro para compensar as flutuações inconsistentes na demanda. Se não for um produto de luxo, pode ser altamente sazonal ou um produto de nicho com um preço alto e demanda flutuante. Isso significaria que nosso sorvete teria que ter um preço mais alto que a concorrência para se adequar ao nicho/produto de luxo mais indicado para uso com GPR.

Além disso, o tipo de produto e a segmentação do cliente apresentam uma confluência de escolhas ao selecionar um conjunto de dados para projetar a demanda futura, o que exige consideração cuidadosa, conforme ilustrado na tabela abaixo.

Tipo de Segmentação	Melhor com SVR	Melhor com GPR
Código Postal	Produtos de consumo diários	Não ideal, a menos que combinado com outros dados dinâmicos
Idade	Roupas, bens de consumo, ferramentas educacionais	Não ideal, a menos que combinado com outros dados dinâmicos
Nível de Educação	Produtos educacionais, produtos de tecnologia	Não ideal, a menos que fatores complexos estejam em jogo
Nível de Renda	Produtos básicos em mercados estáveis	Bens de luxo, eletrônicos de alta qualidade, itens premium
Ocupação	Produtos ligados a ocupações estáveis	Produtos sazonais, itens influenciados por fatores externos (por exemplo, clima)
Grupos de Estilo de Vida/Interesses	Grupos de interesse previsíveis (por exemplo, roupas de ginástica)	Produtos especializados ou de nicho, demanda altamente variável

Embora nossa tabela acima não seja necessariamente uma representação factual da relação entre segmentos de clientes e tipos de produtos, ela enfatiza o ponto importante de considerar esses aspectos antes de selecionar um conjunto de dados apropriado para fazer previsões. O GPR, para resumir, é mais adequado para empresas que frequentemente enfrentam incertezas e padrões de crescimento complexos, o que exige a necessidade de fazer previsões com intervalos de confiança.

A Regressão por Vetores de Suporte, por outro lado, é boa para fazer projeções onde a certeza e o crescimento estável estão em jogo. Elas são ideais para quando decisões podem ser baseadas em tendências lineares ou moderadamente lineares. Por quê? Porque o SVR é robusto ao ruído. Ele foca em obter a fronteira de decisão que maximiza a margem de erro enquanto minimiza a influência de outliers. Ao ter a margem de erro (epsilon) atuando como um classificador, o SVR deve ser eficaz com conjuntos de dados que não possuem muitos outliers.

E como podemos ver na recomendação da tabela cruzada acima, o SVR é mais adequado para fazer projeções de bens essenciais ou produtos de consumo diários, para os quais a demanda é quase constante e, exceto por um evento como o surto de COVID (que pode aumentar e derrubar a demanda), o nível de demanda pelo produto não deve flutuar muito, se é que flutua. Então, para considerar nossa situação de expandir as vendas de sorvete para fora da cidade natal, o SVR seria uma ferramenta adequada, desde que não tenha um preço excessivamente alto (como havia sido recomendado para o GPR acima), mas seja vendido a preços mais acessíveis e exposto nas prateleiras de supermercados onde os consumidores pegam seus mantimentos diários e produtos essenciais para a semana.

Portanto, se usarmos a tabela cruzada como guia, se nosso sorvete for um produto premium que vendemos principalmente em feriados ou apenas no verão, ou for oferecido a restaurantes de alto nível, por exemplo, então estaremos procurando usar o SVR com dados de vendas agregados por nível de renda. Além disso, a tabela cruzada recomenda considerar a ocupação do consumidor e os grupos de estilo de vida / interesses especiais, e esses também podem ser considerados. Por outro lado, o SVR funcionaria melhor se nosso produto fosse vendido predominantemente em grandes lojas de varejo, onde os preços baixos são importantes, como argumentado acima, e o segmento de consumidores relevante para isso seria o endereço (ou código postal). Portanto, os dados de vendas agregados por endereço serviriam melhor para fazer previsões com SVR sobre quão rápido ou devagar devemos expandir as vendas de nosso sorvete, já que isso é algo que precisaríamos acertar, pois agora estamos usando o dinheiro de outras pessoas.

Portanto, o SVR é mais adequado para situações de previsão onde um alto grau de incerteza é aceitável, enquanto o SVR, que estamos focando neste artigo, está quase no outro extremo do espectro, pois ignora os outliers que caem fora de um limite designado ao definir o hiperplano dos conjuntos de dados.

Definição do SVR

O SVR pode ser formulado como uma função objetivo e como uma função de decisão. Se começarmos com a fórmula da função objetivo, ela é a seguinte:

Onde

• w é o vetor de pesos (parâmetros do modelo), no nosso caso, estamos interessados na norma L2 das matrizes de pesos,
• C é o parâmetro de regularização que controla o equilíbrio entre a complexidade do modelo e a tolerância à classificação incorreta,
• L ϵ é a função de perda insensível ϵ definida por:

Onde

• f(xi ) é o valor previsto,
• yi é o valor real,
• ϵ define uma margem de tolerância dentro da qual nenhum penalidade é dada para erros.

A função de decisão, por outro lado, que é principalmente usada para previsões, tem a seguinte fórmula:

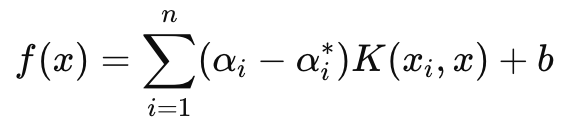
Onde

• αi e αi^∗ são os multiplicadores de Lagrange,
• K (xi , x) é a função de kernel (por exemplo, linear, polinomial, RBF),
• b é o termo de viés.

Como mencionado acima, o SVR introduz um parâmetro insensível à perda, epsilon, que garante que erros com uma magnitude menor que epsilon sejam ignorados e não resultem em ajustes nos pesos ou parâmetros do modelo que está sendo treinado. Isso torna o SVR mais robusto para lidar com pequenos ruídos e variações nos dados, permitindo que ele se concentre na visão geral ou nas grandes tendências.

Além disso, em nossa função objetivo, o parâmetro C gerencia o equilíbrio entre minimizar o erro de treinamento e minimizar a complexidade do modelo. Um valor maior de C minimiza o erro de treinamento, mas corre o risco de sobreajuste, enquanto um valor menor de C, teoricamente, levaria a mais generalização e melhor flexibilidade ao fazer previsões em diferentes cenários.

Nós vamos nos concentrar estritamente em usar a função de perda do SVR ao treinar um MLP simples para esta rede. Não faremos projeções com seus kernels, como seria o caso com a função de decisão. No entanto, vale mencionar que o SVR usa funções de kernel para transformar dados de entrada em um espaço de maior dimensão, onde relações que podem não ser lineares no espaço original podem ser identificadas. Os kernels comuns para isso incluem: o kernel linear, o kernel polinomial e o RBF.

A função de perda do SVR pode ser implementada em MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| SVR Loss                                                         |
//+------------------------------------------------------------------+
vector Cmlp::SVR_Loss()
{  vector _loss = fabs(output - label);
   for(int i = 0; i < int(_loss.Size()); i++)
   {  if(_loss[i] <= THIS.svr_epsilon)
      {  _loss[i] = 0.0;
      }
   }
   vector _l = THIS.svr_c*_loss;
   double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2);
   vector _weight_norms;
   _weight_norms.Init(_loss.Size());
   _weight_norms.Fill(_w);
   return(_weight_norms + _l);
}

Normalmente, este valor de perda é um escalar, no entanto, como essa função de perda está sendo usada agora na retropropagação e certas redes possuem mais de uma saída final, foi importante manter a estrutura da perda em uma forma vetorial, embora o SVR a condense para um escalar. E é isso que fizemos. Além disso, dentro da função de retropropagação, verificamos se a perda SVR está sendo usada. Isso é indicado abaixo:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
   
   ...


   if(EpochIndex < 0)
   {  printf(__FUNCSIG__ + " Epoch Index Should start from 1. ");
      return;
   }


    ...


   vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss));

    ....
}

Conseguimos adicionar essa modificação de uma linha porque os parâmetros do nosso construtor estão em uma estrutura e facilmente modificamos essa estrutura, (já que essa classe foi introduzida em artigos anteriores) da seguinte maneira:

//+------------------------------------------------------------------+
//| Multi-Layer-Perceptron Struct for Constructor Parameters         |
//+------------------------------------------------------------------+
struct Smlp
{  //arch array must be defined with at least 2 non zero values
   //that represent the size of the input layer and output layer
   //If more values than this are provided in the array then the
   //middle values will define the size(s) of the hidden layer(s)
   //first value (index zero) is size of input layer
   //last value (index size-1) is size of output layer
   int               arch[];


  ...


   bool              svr_loss;
   double            svr_c;
   double            svr_epsilon;

                     Smlp()
   {                 ArrayFree(arch);

     ...

      svr_loss = false;
      svr_c = 1.0;
      svr_epsilon = __EPSILON * 5.0;
   };
                    ~Smlp() {};
};

Implementando uma Classe de Sinal

Para ter uma classe de sinal com um MLP cuja função de perda usa o SVR, usaríamos nossa classe já codificada para um MLP que foi compartilhada em artigos anteriores. As mudanças necessárias para esta classe para usarmos a perda SVR já estão destacadas acima, então o que falta é como essa classe é chamada e usada dentro de uma instância personalizada de uma classe de sinal. Nossos MLPs cobertos recentemente nessas séries estão todos tentando prever a próxima mudança no preço de fechamento a cada nova barra. Isso significa que com base em um cronômetro (a cada nova barra), novos cálculos são feitos para qual será a próxima mudança no preço de fechamento.

As entradas para calcular isso também são as mudanças no preço de fechamento anterior, com a principal variável nisso sendo o número dessas mudanças. (Essa variável estabelece o tamanho da camada de entrada). Alternativas são possíveis para definir não apenas quais entradas devem ser alimentadas no MLP ao projetar a próxima mudança no preço de fechamento da barra, mas também como a previsão deve ser de longo alcance. O último ponto é importante porque, para nossos testes, estamos usando uma visão de uma única barra de preço para frente. Além disso, antes de fazer cada previsão, realizamos uma retropropagação em cada nova barra para treinar nossa rede sobre um conjunto de treinamento de tamanho definido por um número de épocas.

Esses dois parâmetros de entrada 'tamanho do conjunto de treinamento' e 'épocas' também são otimizáveis e isso exige um equilíbrio entre obter os pesos ideais da rede e a generalização. Isso porque, embora um conjunto de treinamento maior e mais épocas possam indicar um bom desempenho nos dados amostrados, uma validação cruzada provavelmente não será tão positiva, a menos que a rede tenha alguma generalização e não esteja excessivamente ajustada aos seus dados de treinamento. A função Get Output lida com a previsão através do MLP e seu código fonte é compartilhado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old;
         if
         (
            _in_new.Init(__MLP_SIGN_INPUTS) &&
            _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_new.Size() == __MLP_SIGN_INPUTS &&
            _in_old.Init(__MLP_SIGN_INPUTS) &&
            _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_old.Size() == __MLP_SIGN_INPUTS
         )
         {  _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new, _target_old;
               if
               (
                  _target_new.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) &&
                  _target_new.Size() == __MLP_SIGN_OUTPUTS &&
                  _target_old.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) &&
                  _target_old.Size() == __MLP_SIGN_OUTPUTS
               )
               {  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Não difere significativamente das implementações que tivemos em artigos anteriores. A retropropagação é realizada para cada ponto de dados do conjunto de treinamento que possui um rótulo (ou valor alvo). Normalmente, todos os dados de treinamento possuem um valor alvo, mas, como em nosso caso estamos mesclando com previsão, o "ponto de dados de treinamento" final é atual e sua eventual mudança no preço de fechamento é o que estamos buscando. Portanto, quando chegamos aos dados de entrada atuais que devem nos dar nossa previsão, não realizamos nenhum treinamento. Além disso, é por isso que estamos fazendo o contador regressivo em cada conjunto de treinamento, ou seja, primeiro treinamos com dados muito antigos e depois vamos reduzindo até os dados atuais.

Implementando uma Classe de Stop Trailing

Já faz algum tempo nesta série que não consideramos nada além de uma classe de sinal personalizada, mas leitores que viram meus artigos anteriores se lembrarão que eu frequentemente compartilhava ideias de trade, não apenas como uma classe de sinal, mas também classes de stop trailing e até classes de gerenciamento de dinheiro. Portanto, retornamos a esses caminhos considerando uma classe de stop trailing personalizada que pode ser anexada a um Expert Advisor via o MQL5 wizard. Orientações, para novos leitores, sobre como o código compartilhado abaixo pode ser usado no MQL5 wizard para criar um Expert Advisor podem ser encontradas aqui e aqui.

Então, para implementar uma classe de trailing personalizada, vamos verificar se para qualquer posição aberta que não tenha um stop loss e precise que um seja introduzido, ou uma que já tenha um stop loss mas precise ser ajustado para bloquear melhor os lucros. Stops loss são um pouco controversos porque nunca são garantidos. Apenas os preços de ordens limitadas são. Se por qualquer razão, o mercado se mover mais do que a maioria das pessoas antecipou, o corretor só poderá fechar seu pedido no próximo "preço disponível", não no seu stop loss. Não obstante, vamos tomar a decisão de definir ou mover o stop loss com base na magnitude da mudança no alcance da barra de preço prevista. Implementamos isso em outra função Get Output, similar, mas diferente, do que tivemos com a classe de sinal personalizada. Ele é compartilhado abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo;
         if
         (
            _in_new_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_hi.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_hi.Size() == __MLP_TRAIL_INPUTS
            &&
            _in_new_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_lo.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_lo.Size() == __MLP_TRAIL_INPUTS
         )
         {  vector _in_new = _in_new_hi - _in_new_lo;
            vector _in_old = _in_old_hi - _in_old_lo;
            _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo;
               if
               (
                  _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS
                  &&
                  _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS
               )
               {  vector _target_new = _target_new_hi - _target_new_lo;
                  vector _target_old = _target_old_hi - _target_old_lo;
                  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Nosso código acima, embora quase idêntico ao que tivemos no sinal, é diferente principalmente pelo tipo de dados de entrada que recebe e sua saída esperada. Estamos tentando determinar se precisamos mover nosso stop loss e nossa suposição pré-requisito para isso é um aumento na volatilidade. Portanto, precisamos descobrir qual será a próxima mudança no alcance da barra de preço. Esse tipo de dado tende a ser muito volátil (ou ruidoso), o que é o motivo de, se tivéssemos usado buffers de média móvel como nossos dados de entrada e valores alvo, poderia ter sido mais prudente. Isso pode ser modificado, pois o código completo está anexado abaixo, no entanto, estamos usando mudanças nos máximos menos os mínimos de cada barra de preço como entradas e estamos procurando que a saída seja a próxima mudança nesses valores de entrada, assim como tivemos com os preços de fechamento para o sinal acima.

Portanto, se a mudança projetada no alcance da barra de preço for positiva, implicando que a volatilidade está aumentando, tomamos medidas para mover nosso stop loss em proporção ao aumento projetado. Isso pode parecer imprudente porque, como mencionado acima, os corretores nunca garantem um preço de stop loss, razão pela qual a opção contra de mover um stop loss apenas em uma diminuição projetada na volatilidade poderia ser "mais certa", já que em tempos de menor volatilidade os corretores são mais propensos a honrar os stops loss do que quando há volatilidade. Sim, é um pouco de debate e deixo isso para o leitor explorar e fazer os ajustes apropriados no código dependendo de suas descobertas.

Resultados do Testador de Estratégia

Realizamos testes no par USDJPY, no período diário de 01.01.2023 a 01.01.2024 Esses testes foram realizados com algumas das melhores configurações obtidas por meio de otimizações rápidas, para as quais não foram feitos caminhamentos à frente ou validação cruzada. Eles são exibidos aqui para simplesmente demonstrar a capacidade de realizar trades e usar o Expert Advisor montado com o wizard. A diligência extra nos testes durante períodos históricos mais longos, enquanto também se fazem caminhamentos à frente, se a otimização estiver envolvida, é deixada para o leitor. Vale ressaltar também que os Expert Advisors montados com o wizard podem combinar múltiplos sinais ao desenvolver um sistema de trading, então o teste ou otimização não precisa ser apenas com os sinais personalizados usados aqui.

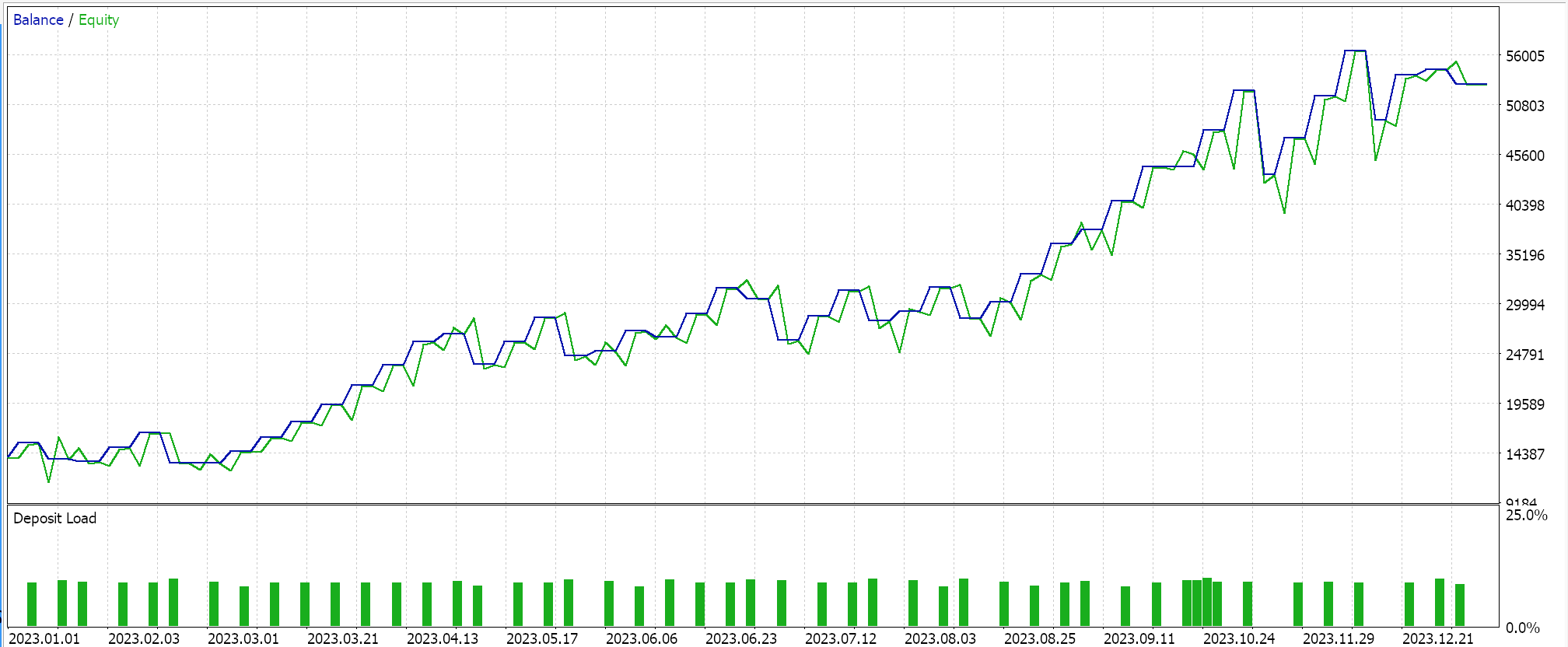
Desenvolvemos um sinal personalizado com SVR e uma classe de trailing personalizada com um MLP similar. Os testes apresentados abaixo são, portanto, para dois Expert Advisors cujo código de interface está anexado abaixo. O primeiro usa apenas o sinal personalizado sem o stop trailing. Seus resultados são apresentados abaixo:

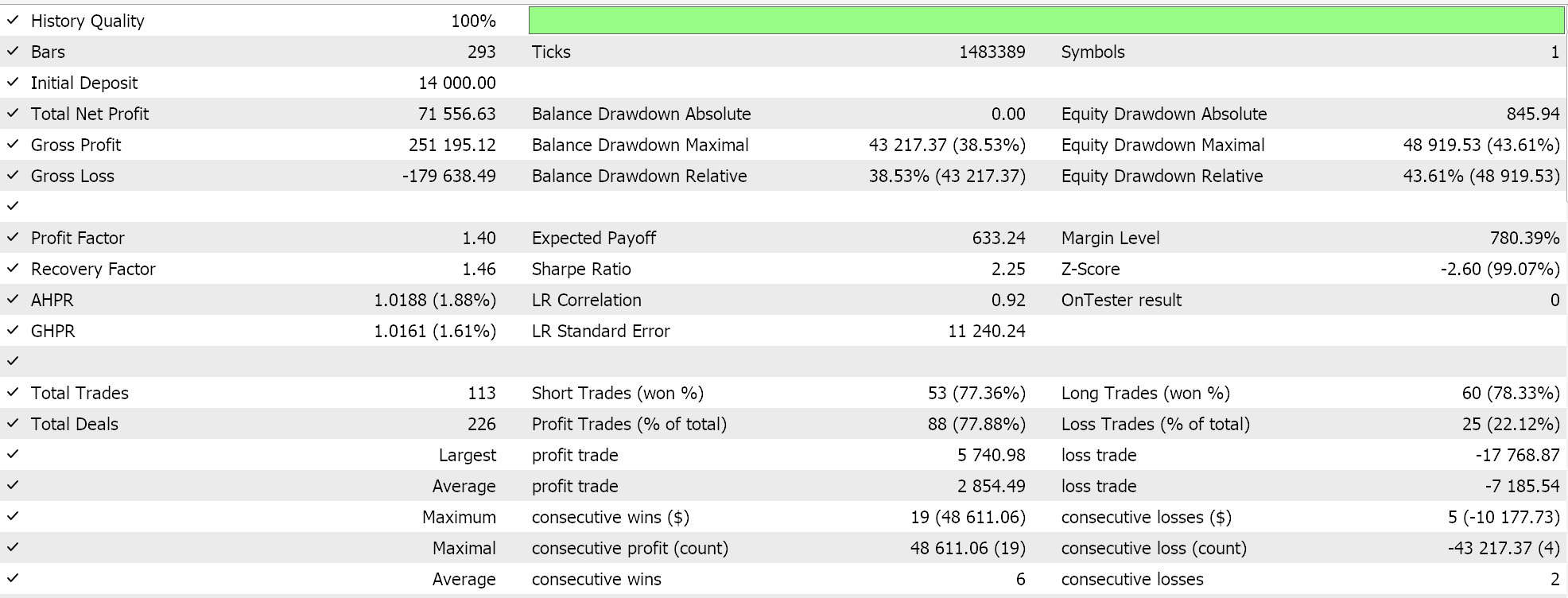
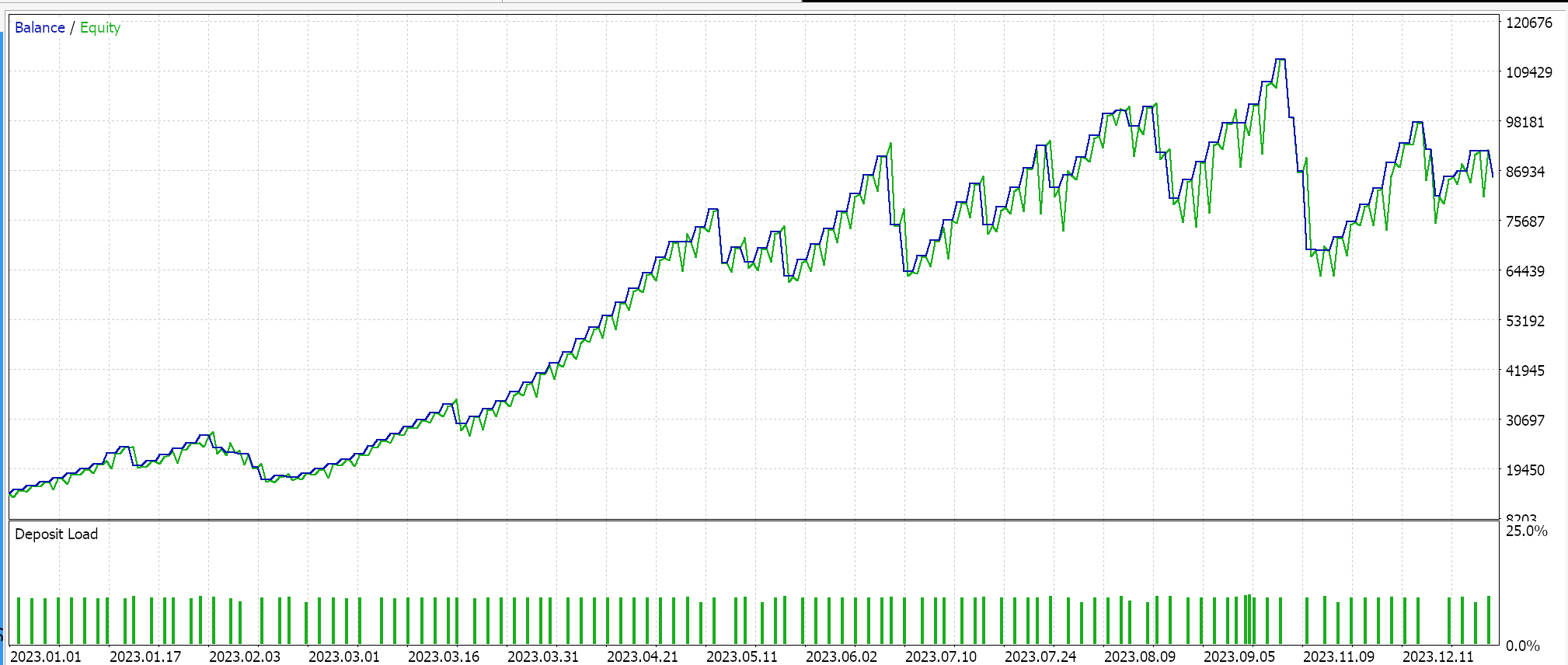
O segundo usa o sinal personalizado e a classe de trailing personalizada que implementamos acima. Seus resultados também são mostrados abaixo.

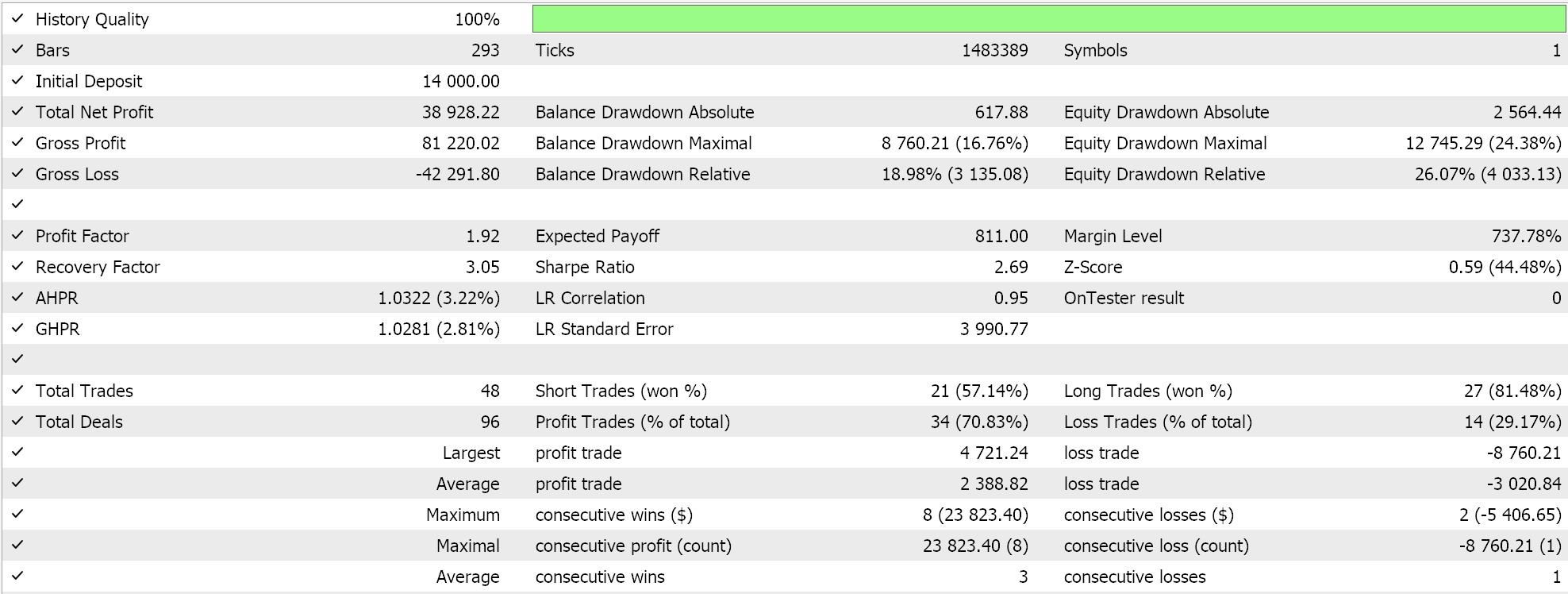
Conclusão

Para concluir, olhamos a Regressão por Vetores de Suporte, que segue outra forma de regressão que consideramos quando analisamos os Kernels de Processos Gaussianos. Essas duas regressões, Regressão por Vetores de Suporte e Regressão por Processo Gaussiano, são quase opostas em sua aplicação, já que o SVR tende a ser mais adequado para conjuntos de dados menos voláteis e em tendência, enquanto o GPR se destaca em ambientes mais voláteis e menos certos. A Regressão por Vetores de Suporte possui uma função objetivo e uma função de decisão. Buscamos explorar a primeira, a função objetivo, como uma função de perda em um perceptron multicamada em uma classe de sinal e em uma classe personalizada de stop trailing.

O uso da função de decisão, para atuar como um previsor, exigiria o uso adicional de kernels, algo que exploramos no artigo sobre Kernels de Processos Gaussianos, mas que nos abstivemos neste artigo, pois nosso previsor foi puramente um MLP. Em um futuro artigo(s), poderíamos considerar isso, dado que existem diferentes formas de kernels que podem ser usados para isso, no entanto, a função de perda SVR foi nosso alvo neste artigo. Usando um parâmetro insensível à perda epsilon, ele também, juntamente com uma lista crescente de implementações de funções de perda, algumas das quais cobrimos aqui, pode introduzir uma maneira diferente de treinar redes neurais.

Este parâmetro insensível à perda, epsilon, age mais como um classificador do que como um regressor e pode-se argumentar que isso faz o caso para essa função de perda ser usada mais em redes classificadoras do que em redes regredidoras, como fizemos neste artigo, e isso poderia ser verdade. No entanto, o SVR ainda lida com saídas contínuas (conjuntos de dados decimais) e prevê valores numéricos em um formato semelhante. Ele simplesmente usa a margem epsilon para decidir se um erro deve ser penalizado, mas seu objetivo continua sendo regressão, e não classificação.