データサイエンスと機械学習（第12回）：自己学習型ニューラルネットワークは株式市場を凌駕することができるのか？

MetaTrader 5 — トレーディング | 25 5月 2023, 10:49

348

「ニューラルネットワークが簡単だと言っているわけではありません。それを機能させるには、専門家でなければなりません。ただし、その専門知識は、幅広いアプリケーションにわたって役に立ちます。ある意味では、以前は機能の設計に費やされていたすべての労力が、アーキテクチャの設計、損失関数の設計、および最適化スキームの設計に費やされるようになります。手作業が抽象度を高めているのです。」

Stefano Soatto

はじめに

アルゴリズムトレーダーの方なら、多分ニューラルネットワークについてお聞きになったことがあるでしょう。というのも、収益性の高いシステムを完成させるには、自動売買ロボットにニューラルネットワークを追加するだけでは不十分なのです。ニューラルネットワークを使用する際にその内容を理解する必要があるのは言うまでもありません。なぜなら、小さなことでも成功か失敗か、つまり利益か損失かを意味するからです。

自己訓練型NN

正直なところ、ニューラルネットは誰にでも使えるものではないと思います。特に自分の手を汚したくない人にとってはです。なぜなら、モデルによって生じる誤差の分析、入力データの前処理とスケーリングなど、この記事でお話しするようなことに時間を費やす必要があることが非常に多いからです。

まず、人工ニューラルネットワークの定義から説明します。

人工ニューラルネットワークとは？

人工ニューラルネットワークとは、簡単に言うと、通常ニューラルネットワークと呼ばれるもので、動物の脳を構成する神経回路網にヒントを得たコンピューティングシステムです。ニューラルネットワークの基本的な構成要素については、本連載の前回の記事を参照してください。

これまでのニューラルネットワークに関する記事で、フィードフォワードニューラルネットワークに関する基本的なことを説明しました。今回は、ニューラルネットワークのフォワードパスとバックワードパスの両方、ニューラルネットワークの訓練とテストについて解説します。また、最後に説明したすべてをもとに自動売買ロボットを作成し、自動売買ロボットのパフォーマンスを確認する予定です。

多層パーセプトロンのニューラルネットワークでは、現在の層のすべてのニューロン/ノードは、2番目の層のノードに相互接続されており、入力から出力までのすべての層がそのように相互接続されています。これが、ニューラルネットワークがデータセットの複雑な関係を把握することができる理由です。層が多ければ多いほど、データセットの複雑な関係を理解することができるモデルになります。これは高い計算量を必要とし、特に問題が単純であるにもかかわらずモデルが複雑になりすぎている場合、必ずしもモデルの正確性を保証できない可能性があります。

ほとんどの場合、このような空想的なニューラルネットワークを使って解決しようとする問題の大半は、隠れ層が1つあれば十分です。そのため、単層のニューラルネットワークを使用することになりました。

フォワードパス

フォワードパスに関わる操作はシンプルで、数行のコードで実現可能です。しかし、ニューラルネットワークを柔軟にするためには、行列とベクトルの演算がニューラルネットワークや本連載で取り上げる多くの機械学習アルゴリズムの構成要素であるため、しっかりと理解する必要があります。

なぜなら、問題が異なれば、異なる構成と異なる出力を持つ異なるタイプのニューラルネットワークが必要になるからです。

ご存じない方のために、問題の種類は以下の通りです。

回帰の問題
分類の問題

01：回帰の問題

回帰の問題とは、連続的な変数を予測しようとする問題です。例えば取引では、市場が次に向かう価格帯を予測しようとすることがよくあります。まだの方は「線形回帰」をお読みになることをお勧めします。

この種の問題には、回帰型ニューラルネットワークが対応します。

02：分類の問題

分類の問題とは、離散的・非連続的な変数を予測しようとする問題のことです。例えば、取引では、シグナルが0であれば相場が下がり、1であれば相場が上がるというように、シグナルを予測することができます。

このような問題は、分類ニューラルネットワークやパターン認識ニューラルネットワークによって取り組まれますが、MATLABではパターンネットと呼ばれています。

今回は、市場が次に動く価格を予測する回帰の問題を解いてみたいと思います。

matrix CRegNeuralNets::ForwardPass(vector &input_v)
 {
   matrix INPUT = this.matrix_utils.VectorToMatrix(input_v);
   matrix OUTPUT;
   
   OUTPUT = W.MatMul(INPUT); //Weight X Inputs
   
   OUTPUT = OUTPUT + B;  //Outputs + Bias
   
   OUTPUT.Activation(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX)); //Activation Function
   
   return (OUTPUT);
 }

このフォワードパス関数は読みやすいのですが、すべてをスムーズにおこなうために最も注意しなければならないのは、各ステップの行列サイズです。

matrix INPUT = this.matrix_utils.VectorToMatrix(input_v);

この部分は説明のしがいがあります。このVectorToMatrix関数は、入力をベクトルで受け取るので、これからおこなわれる行列演算のために、これらの入力は行列形式である必要があります。

常に覚えておいてください。

最初のNNINPUT行列はnx1行列
重み行列はHN×n（HNは現在の隠れ層のノード数、nは前の層からの入力数または入力行列の行数）
バイアス行列は層の出力と同じ大きさ

これは非常に重要なことです。いつか自分で解決しようとしたときに、不安に溺れることがないようにするためです。

私たちが取り組んでいるニューラルネットワークのアーキテクチャをお見せして、私たちが何をしようとしているのか、明確にイメージしていただきましょう。

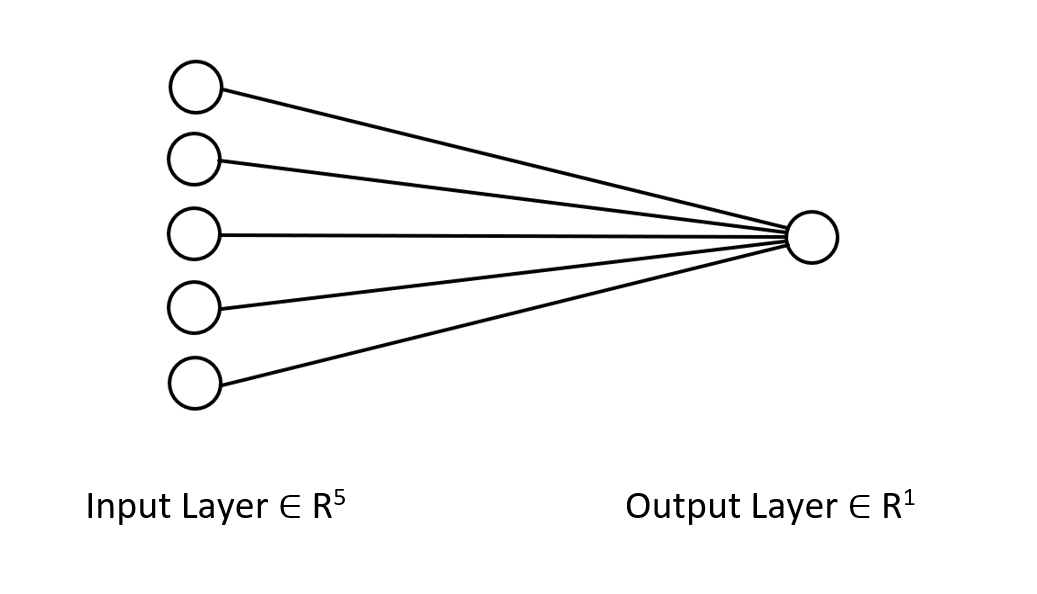
これは単なる単層のニューラルネットワークです。今示した関数でフォワードパスのループがないのはこのためです。しかし、先ほど説明したような次元を確保した上で、同じ行列アプローチに従えば、どんな複雑なアーキテクチャでも実装することができます。

W行列を使ったフォワードパスを見ていただきましたが、モデルの重みをどのように生成するか見てみましょう。

重みを生成する

ニューラルネットワークに適した重みを生成するのは、単にランダムな値を初期化すればいいというわけではありません。苦い経験から学んだのですが、これを間違えると、バックプロパゲーションで様々なトラブルが発生し、ハードコーディングされた既に複雑なコードを疑い、デバッグし始めることになるのです。

不適切な重みの初期化は、学習プロセス全体を退屈で時間のかかるものにしてしまいます。ネットワークが極値にはまり、収束が非常に遅くなることがあります。

まず、ランダムな値を選択するのですが、私は42のランダムな状態を使用するのが好きです。

   this.W = matrix_utils.Random(0.0, 1.0,1,m_inputs, RANDOM_STATE);

多くの人はこのステップで、重みを生成し、それで終わりと考えるでしょう。乱数変数を選択した後、GlorotまたはHeInitializationを使用して重みを初期化する必要があります。

Xavier/Glorot初期化はシグモイドとtanh活性化関数に最適で、He初期化はRELUとその変形に有効です。

Heの初期化

Xavier初期化メソッドは、一様正規分布（U）の乱数として計算されます。その式は以下の通りです。

ここで、nはノードへの入力数です。

そこで、重みを初期化した後、重みの正規化をおこないました。

   this.W = matrix_utils.Random(0.0, 1.0,1,m_inputs, RANDOM_STATE);
   this.W = this.W * 1/sqrt(m_inputs); //He initialization

このニューラルネットワークは1層なので、重みを乗せる行列は1つだけです。

活性化関数

これは回帰型ニューラルネットワークなので、このネットワークの活性化関数は回帰活性化関数の変形に過ぎません。RELU：

enum activation
  {
   AF_ELU_ = AF_ELU,
   AF_EXP_ = AF_EXP,
   AF_GELU_ = AF_GELU,
   AF_LINEAR_ = AF_LINEAR,
   AF_LRELU_ = AF_LRELU,
   AF_RELU_ = AF_RELU,
   AF_SELU_ = AF_SELU,
   AF_TRELU_ = AF_TRELU,
   AF_SOFTPLUS_ = AF_SOFTPLUS
  };

これらの赤で示した活性化関数やその他多くの関数は、行列の標準ライブラリで提供されているデフォルトのものです（詳細）。

損失関数

この回帰型ニューラルネットワークの損失関数は、以下の通りです：

enum loss
  {
    LOSS_MSE_ = LOSS_MSE,
    LOSS_MAE_ = LOSS_MAE,
    LOSS_MSLE_ = LOSS_MSLE,
    LOSS_HUBER_ = LOSS_HUBER
  };

標準ライブラリで提供される活性化関数はまだまだあります（詳細）。

デルタルールによるバックプロパゲーション

デルタルールとは、単層ニューラルネットワークの人工ニューロンへの入力の重みを更新するための勾配降下学習ルールです。これは、より一般的なバックプロパゲーションアルゴリズムの特殊なケースです。活性化関数g(x)を持つニューロンjに対して、デルタルールでjのi番目の重みWjiは、次のように与えられます。

ここで

は学習率と呼ばれる小さな定数、

はgの微分値、

g(x)はニューロンの活性化関数、

は目標出力、

は実際の出力、

はi番目の入力です。

素晴らしいです。数式ができたので、あとはそれを実行するだけですね。いいえ、違います。

この式の問題は、見た目がシンプルですが、コードにすると非常に複雑でいくつかのforループをコーディングする必要があることです。ニューラルネットワークのこの種の練習はすごく面倒です。ここで必要とする適切な数式は、行列の演算を示すものです。工作しましょう。

ここで、

=重み行列の変化、

=損失関数の微分、

=要素ごとの行列の乗算/ハダマード積、

=ニューロン活性化行列の微分値、

=入力行列です。

常にL行列はO行列と同じ大きさであり、結果として右辺の行列はW行列と同じ大きさである必要があります。そうでなければ終わりです。

これをコードに変換するとどのようになるのか見てみましょう。

for (ulong iter=0; iter<m_rows; iter++)
   {
        OUTPUT = ForwardPass(m_x_matrix.Row(iter)); //forward pass
        pred = matrix_utils.MatrixToVector(OUTPUT);
              
        actual[0] = m_y_vector[iter];
              
        preds[iter] = pred[0];
        actuals[iter] = actual[0];
              
//---
              
        INPUT = matrix_utils.VectorToMatrix(m_x_matrix.Row(iter));
              
        vector loss_v = pred.LossGradient(actual, ENUM_LOSS_FUNCTION(L_FX));
              
        LOSS_DX.Col(loss_v, 0);
              
        OUTPUT.Derivative(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX));
              
        OUTPUT = LOSS_DX * OUTPUT;
              
        INPUT = INPUT.Transpose();
        DX_W = OUTPUT.MatMul(INPUT);
               
        this.W -= (alpha * DX_W); //Weights update by gradient descent
 }

機械学習で配列の代わりにMQL5が提供する行列ライブラリを使うことの良い点は、微積分を気にする必要がないことです。つまり、損失関数の導関数や活性化関数の導関数を求める心配がありません。

モデルを訓練するためには、少なくとも今のところ、エポックとαと呼ばれる学習率の2つを考慮する必要があります。この連載の前回の記事で、勾配降下法について読まれた方は、私が何を言っているのかご存知だと思います。

エポック：1つのエポックは、データセット全体がネットワークを通じて完全に順方向と逆方向のサイクルを回した時です。簡単に言うと、ネットワークがすべてのデータを見たときです。エポック数が多いほど、ニューラルネットワークの訓練にかかる時間が長くなり、より良い学習ができる可能性があります。

αは、勾配降下アルゴリズムが最小値および極小値に行くときに取らせたいステップのサイズです。αは通常、0.1～0.00001の間の小さな値です。この値を大きくすると、ネットワークの収束が速くなりますが、極小値をスキップするリスクが高くなります。

以下は、このデルタルールの完全なコードです：

   for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++)
      {
         for (ulong iter=0; iter<m_rows; iter++)
            {
              OUTPUT = ForwardPass(m_x_matrix.Row(iter));
              pred = matrix_utils.MatrixToVector(OUTPUT);
              
              actual[0] = m_y_vector[iter];
              
              preds[iter] = pred[0];
              actuals[iter] = actual[0];
              
           //---
              
              INPUT = matrix_utils.VectorToMatrix(m_x_matrix.Row(iter));
              
              vector loss_v = pred.LossGradient(actual, ENUM_LOSS_FUNCTION(L_FX));
              
              LOSS_DX.Col(loss_v, 0);
              
              OUTPUT.Derivative(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX));
              
              OUTPUT = LOSS_DX * OUTPUT;
              
              INPUT = INPUT.Transpose();
              DX_W = OUTPUT.MatMul(INPUT);
               
              this.W -= (alpha * DX_W);
            }
         
         printf("[ %d/%d ] Loss = %.8f | accuracy %.3f ",epoch+1,epochs,preds.Loss(actuals,ENUM_LOSS_FUNCTION(L_FX)),metrics.r_squared(actuals, preds));
      }

これですべてが設定されました。データセットの中のほんの小さなパターンを理解するために、ニューラルネットワークを訓練する時間です。

#include <MALE5\Neural Networks\selftrain NN.mqh>
#include <MALE5\matrix_utils.mqh>

CRegNeuralNets *nn;
CMatrixutils matrix_utils;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
    matrix Matrix = {
                     {1,2,3},
                     {2,3,5},
                     {3,4,7},
                     {4,5,9},
                     {5,6,11}
                   };
   
   matrix x_matrix; vector y_vector;
   
   matrix_utils.XandYSplitMatrices(Matrix,x_matrix,y_vector);
   
   nn = new CRegNeuralNets(x_matrix,y_vector,0.01,100, AF_RELU_, LOSS_MSE_); //Training the Network
   
   
//---
   return(INIT_SUCCEEDED);
  }

機能XandYSplitMatricesは，行列をx行列とyベクトルに分割します．

X行列	Yベクトル
{{1,2}, {2,3}, {3,4}, {4,5}, {5,6}}	{3}, {5}, {7}, {9}, {11}

訓練の出力：

CS      0       20:30:00.878    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [1/100] Loss = 56.22401001 | accuracy -6.028 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [2/100] Loss = 2.81560904 | accuracy 0.648 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [3/100] Loss = 0.11757813 | accuracy 0.985 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [4/100] Loss = 0.01186759 | accuracy 0.999 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [5/100] Loss = 0.00127888 | accuracy 1.000 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [6/100] Loss = 0.00197030 | accuracy 1.000 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [7/100] Loss = 0.00173890 | accuracy 1.000 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [8/100] Loss = 0.00178597 | accuracy 1.000 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [9/100] Loss = 0.00177543 | accuracy 1.000 
CS      0       20:30:00.879    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [10/100] Loss = 0.00177774 | accuracy 1.000 
…
…
…
CS      0       20:30:00.883    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [100/100] Loss = 0.00177732 | accuracy 1.000

5回のエポックのみで、ニューラルネットワークの精度は100%になりました。この問題はとても簡単で早く習得できると思っていたので、これは良いニュースです。

さて、このニューラルネットワークの訓練が終わったので、新しい値{7,8}を使ってテストしてみましょう。あなたも私も、結果が15であることは分かっているはずです。

   vector new_data = {7,8};
   
   Print("Test ");
   Print(new_data," pred = ",nn.ForwardPass(new_data));

出力：

CS      0       20:37:36.331    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      Test 
CS      0       20:37:36.331    Self Trained NN EA (Apple_Inc_(AAPL.O),H1)      [7,8] pred = [[14.96557787153696]]

結果は約14.97となりました。15は単なるdoubleであり、そのためにこのような追加値が出たのですが、有効数字1桁で四捨五入すると15と出力されるのです。これは、私たちのニューラルネットワークが今、自ら学習することができるようになったことを示しています。最高です。

このモデルに実世界のデータセットを与えて、その動きを観察してみましょう。

NASDAQ(NAS100)指数を予測しようとしたとき、テスラ株とアップル株を独立変数として使用しました。以前、CNBCのネット記事で、NASDAQの価値の半分を占める6つのハイテク株のうち2つは、アップル株とテスラ株だと読んだことがあります。今回の例では、この2つの銘柄を独立変数としてニューラルネットワークを訓練することにします。

input string symbol_x = "Apple_Inc_(AAPL.O)"; 
input string symbol_x2 = "Tesco_(TSCO.L)";

input ENUM_COPY_RATES copy_rates_x = COPY_RATES_OPEN; 
input int n_samples = 100; 

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {

   matrix x_matrix(n_samples,2); vector y_vector;

   vector x_vector; 
  //---
   x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples);
   x_matrix.Col(x_vector, 0); 
   x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples);
   x_matrix.Col(x_vector, 1); 
   
   y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples);
    
   nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_);

私の証券会社によるこれらの銘柄の名前の付け方（symbol_xとsymbol_x2）は、読者の証券会社と違うかもしれません。テストEAを使用する前に、それらを変更し、それらの銘柄を気配値表示に追加することを忘れないでください。y銘柄は、チャート上の現在の銘柄です。このEAをNASDAQのチャートに必ず接続してください。

スクリプトを実行すると、次のような出力ログが表示されます：

CS      0       21:29:20.698    Self Trained NN EA (NAS100,M30) [ 1/1000 ] Loss = 353809311769.08959961 | accuracy -27061631.733 
CS      0       21:29:20.698    Self Trained NN EA (NAS100,M30) [ 2/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 
CS      0       21:29:20.699    Self Trained NN EA (NAS100,M30) [ 3/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 
CS      0       21:29:20.699    Self Trained NN EA (NAS100,M30) [ 4/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 
CS      0       21:29:20.699    Self Trained NN EA (NAS100,M30) [ 5/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 
CS      0       21:29:20.699    Self Trained NN EA (NAS100,M30) [ 6/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 
....
....
CS      0       21:29:20.886    Self Trained NN EA (NAS100,M30) [ 1000/1000 ] Loss = 149221473.48209998 | accuracy -11412.427

残念です。あれだけのことをした結果、得られたのはこれです。このようなことはニューラルネットワークではよくあることで、どんなフレームワークやPythonライブラリを使っても、このようなことはよく起こるので、NNをしっかり理解することはとても重要です。

データの正規化とスケーリング

すべてのデータセットが正規化されると最良の結果が得られるわけではありませんが、例えば、このNNがうまく機能しているかどうかをテストするために最初に使用したシンプルなデータセットを正規化すると、ひどい結果が得られます。ネットワークはそれらの値と同じかもっとひどい値を返します。試してみました。

正規化の手法はたくさんあります。その中でも特に広く使われているのが、この3つです。

これの詳細については、私のGitHub wiki https://github.com/MegaJoctan/MALE5/wiki/Pre-processing#pre-processing-libraryでご覧ください。とりあえず、この例では、欲しい結果が得られるMin-max Scalerテクニックを使っているとだけ説明しておこうと思います。

Min-Max Scaler

数値特徴の値を[0,1]の固定範囲にスケーリングする正規化手法です。その式は、

x_norm = (x -x_min) / (x_max - x_min)

となります。ここで、

xは元の特徴量、

x_minは特徴量の最小値、

x_maxは特徴量の最大値、

x_normは新たに正規化された特徴量です。

正規化手法を選択し、データを正規化するには、ライブラリをインポートする必要があります。記事末尾にファイルを添付します。

ニューラルネットのライブラリに、データを正規化する機能を追加することにしました。

CRegNeuralNets::CRegNeuralNets(matrix &xmatrix, vector &yvector,double alpha, uint epochs, activation ACTIVATION_FUNCTION, loss LOSS_FUNCTION, norm_technique NORM_METHOD)

これらの中からnorm_technique正規化メソッドを選択します。

enum norm_technique
 {
   NORM_MIN_MAX_SCALER, //Min max scaler
   NORM_MEAN_NORM,  //Mean normalization
   NORM_STANDARDIZATION, //standardization
   NORM_NONE    //Do not normalize.
 };

正規化技術を加えたクラスを呼び出したら、それなりの精度が出るようになりました。

   nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER);

出力：

CS      0       22:40:56.457    Self Trained NN EA (NAS100,M30) [ 1/1000 ] Loss = 0.19379434 | accuracy -0.581 
CS      0       22:40:56.457    Self Trained NN EA (NAS100,M30) [ 2/1000 ] Loss = 0.07735744 | accuracy 0.369 
CS      0       22:40:56.458    Self Trained NN EA (NAS100,M30) [ 3/1000 ] Loss = 0.04761891 | accuracy 0.611 
CS      0       22:40:56.458    Self Trained NN EA (NAS100,M30) [ 4/1000 ] Loss = 0.03559318 | accuracy 0.710 
CS      0       22:40:56.458    Self Trained NN EA (NAS100,M30) [ 5/1000 ] Loss = 0.02937830 | accuracy 0.760 
CS      0       22:40:56.458    Self Trained NN EA (NAS100,M30) [ 6/1000 ] Loss = 0.02582918 | accuracy 0.789 
CS      0       22:40:56.459    Self Trained NN EA (NAS100,M30) [ 7/1000 ] Loss = 0.02372224 | accuracy 0.806 
CS      0       22:40:56.459    Self Trained NN EA (NAS100,M30) [ 8/1000 ] Loss = 0.02245222 | accuracy 0.817 
CS      0       22:40:56.460    Self Trained NN EA (NAS100,M30) [ 9/1000 ] Loss = 0.02168207 | accuracy 0.823 
CS      0       22:40:56.460    Self Trained NN EA (NAS100,M30


CS      0       22:40:56.623    Self Trained NN EA (NAS100,M30) [ 1000/1000 ] Loss = 0.02046533 | accuracy 0.833

また、1時間の時間枠では期待した結果が得られず、ニューラルネットワークは30MINSのチャートの方が精度が高いようで、この時点では何が理由なのかをわざわざ理解することはありませんでした。

訓練データでの精度は82.3％です。精度は高いです。このネットワークが取引を開始するために使用する簡単な取引戦略を作ってみましょう。

現在私がおこなっているOnInit関数でデータを収集する方法には、信頼性がありません。ネットワークを訓練する関数を作り、Init関数に配置することにします。私たちのネットワークは、一生に一度しか訓練されません。ただし、読者はこの方法に限定されるわけではありません。

void OnTick()
  {
//---
     if (!train_nn)
       TrainNetwork(); //Train the network only once
     train_nn = true; 
      
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void TrainNetwork()
 {
   matrix x_matrix(n_samples,2); vector y_vector;
   vector x_vector; 
   
   x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples);
   x_matrix.Col(x_vector, 0); 
   x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples);
   x_matrix.Col(x_vector, 1); 
   
   y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples);
   
   nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER);
 }

このTraining関数には、私たちが市場から脱却するために必要なものがすべて詰まっているように見えますが、それでも信頼できるものではありません。日足でテストしたところ、精度は-77％、H4時間枠では-11234とかいう精度が返ってきました。データを増やし、さまざまな訓練サンプルを行使すると、ニューラルネットワークが与える訓練精度に矛盾が生じました。

その理由はいろいろありますが、そのうちのひとつは、問題によって必要なアーキテクチャが異なることです。デルタルールは単層ニューラルネットワークのためのものなので、異なる時間枠の市場パターンの中には、この単層ニューラルネットワークには複雑すぎるものもあるのでしょう。今のところ修正できないので、良いアウトプットができそうな時間枠で進めようと思っています。しかし、結果を改善し、この一貫性のない動作に少しでも取り組むために、できることがあります。ランダムな状態でデータを分割することです。

データ分割は思った以上に重要

機械学習のpython出身者であれば、sklearnのtrain_test_split関数を見たことがあるかもしれません。

データを訓練データとテストデータに分割する目的は、単にデータを分割するだけでなく、データセットを元の順序と異なるようにランダム化することです。説明します。ニューラルネットワークなどの機械学習アルゴリズムは、データのパターンを理解しようとするため、データを抽出した順番で持っていると、データがどのように整理・配置されているかによるパターンも理解してしまい、モデルにとって不利になる場合があります。配列は変数にあるパターンほど重要ではないので、これはモデルに学習させる賢い方法とは言えません。

void TrainNetwork()
 {
//--- collecting the data

   matrix Matrix(n_samples,3); vector y_vector;
   vector x_vector; 
   
   x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples);
   Matrix.Col(x_vector, 0); 
   x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples);
   Matrix.Col(x_vector, 1); 
   
   y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples);
   Matrix.Col(y_vector, 2);
   
//---

   matrix x_train, x_test; vector y_train, y_test;
   
   matrix_utils.TrainTestSplitMatrices(Matrix, x_train, y_train, x_test, y_test, 0.7, 42);
   
   nn = new CRegNeuralNets(x_train,y_train,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER);
   
   vector test_pred = nn.ForwardPass(x_test);
    
   printf("Testing Accuracy =%.3f",metrics.r_squared(y_test, test_pred));
 }

学習データを収集した後、ランダムな状態42を与えて、関数TrainTestSplitMatricesを導入しました。

void TrainTestSplitMatrices(matrix &matrix_,matrix &x_train,vector &y_train,matrix &x_test, vector &y_test,double train_size=0.7,int random_state=-1)

リアルタイムで市場を予測する

Ontick関数をリアルタイムで予測するためには、データを収集し、ニューラルネットワークのフォワードパス関数の入力ベクトルの中に入れるコードが必要です。

void OnTick()
  {
//---
     if (!train_nn)
       TrainNetwork(); //Train the network only once
     train_nn = true; 
     
     vector x1, x2;
     
     x1.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,1); //only the current candle
     x2.CopyRates(symbol_x2,PERIOD_CURRENT,copy_rates_x,0,1); //only the current candle
     
     vector inputs = {x1[0], x2[0]}; //current values of x1 and x2 instruments | Apple & Tesla
     
     matrix OUT = nn.ForwardPass(inputs); //Predicted Nasdaq value
     
     double pred = OUT[0][0];
     
     Comment("pred ",OUT);
 }

これで、ニューラルネットワークは予測をすることができるようになりました。取引で使ってみましょう。そのために戦略を立てます。

取引ロジック

取引ロジックはシンプルです：ニューラルネットワークが予測した価格が現在の価格を上回っている場合、予測価格に一定の入力値市場を乗じた値を利益確定として買い取引をおこない、逆に売り取引をおこないます。各取引において、ストップロスとしてマークされた特定の入力値に対して、いくつかのテイクプロフィットポイント値でストップロスが設定されます。以下は、MetaEditorでの様子です。

     stops_level = (int)SymbolInfoInteger(Symbol(),SYMBOL_TRADE_STOPS_LEVEL);
     Lots = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
     spread = (double)SymbolInfoInteger(Symbol(), SYMBOL_SPREAD);
     
     MqlTick ticks;
     SymbolInfoTick(Symbol(), ticks);
     
     if (MathAbs(pred - ticks.ask) + spread > stops_level)
        {
          if (pred > ticks.ask && !PosExist(POSITION_TYPE_BUY))
            {
               target_gap  = pred - ticks.bid;
               
               m_trade.Buy(Lots, Symbol(), ticks.ask, ticks.bid - ((target_gap*stop_loss) * Point()) , ticks.bid + ((target_gap*take_profit) * Point()),"Self Train NN | Buy");
            }
         
          if (pred < ticks.bid && !PosExist(POSITION_TYPE_SELL))
            {
               target_gap = ticks.ask - pred;
               
               m_trade.Sell(Lots, Symbol(), ticks.bid, ticks.ask + ((target_gap*stop_loss) * Point()), ticks.ask - ((target_gap*take_profit) * Point()), "Self Train NN | Sell");
            } 
        }

それが私たちのロジックです。このEAがMT5でどのように動作するか見てみましょう。

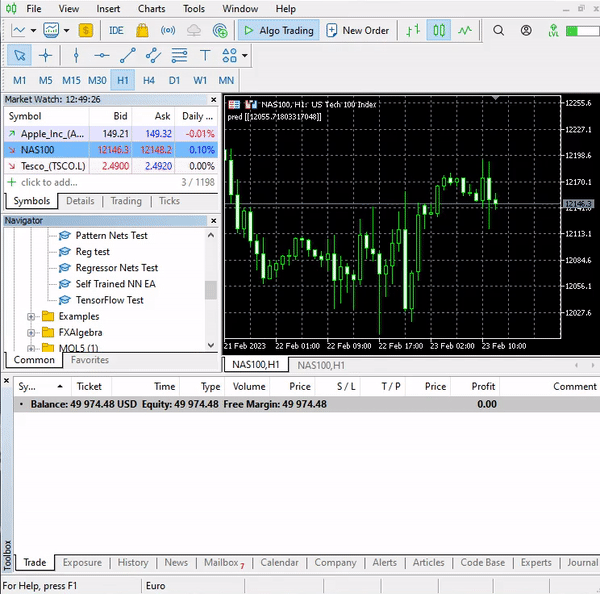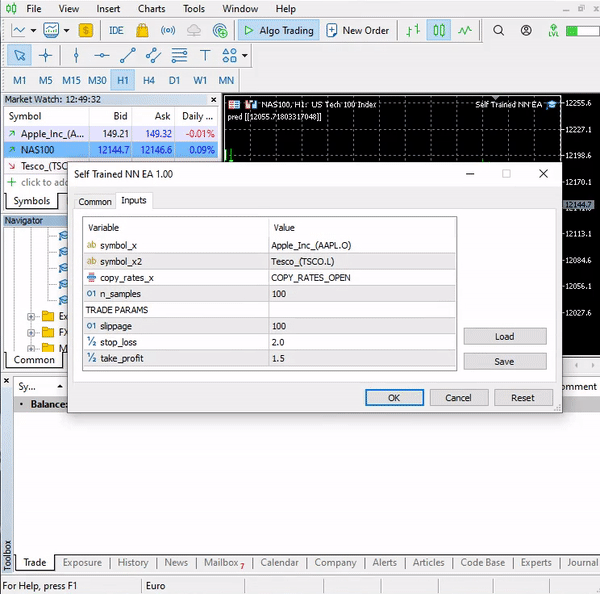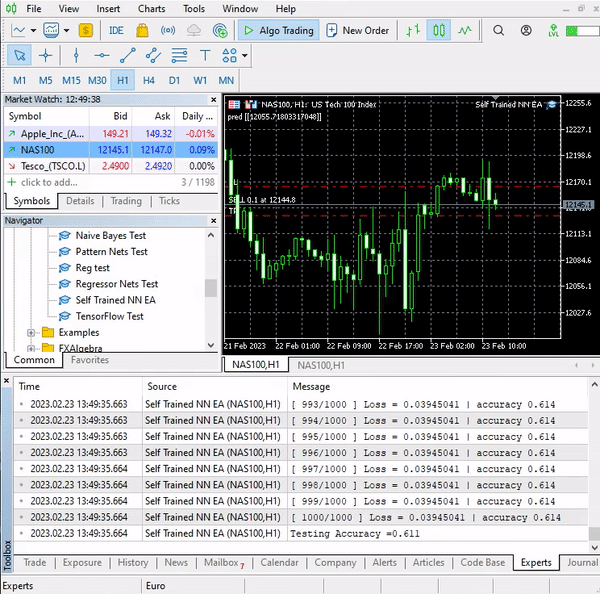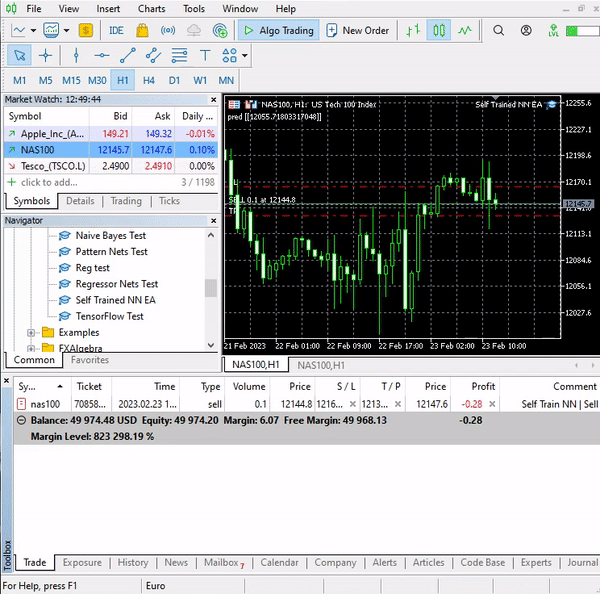
このシンプルなEAが単独で取引できるようになりました。今のところ、その性能を評価することはできません、あまりにも早すぎます。ストラテジーテスターを使用しましょう。

ストラテジーテスターの結果

ストラテジーテスターから機械学習アルゴリズムを実行する際には、アルゴリズムがスムーズかつ高速に動作することを確認しながら、最終的に利益も得られるようにしなければならないので、常に課題があります。

2023.01.01から2023.02.23まで4時間チャートで実ティックに基づいてテストを実行しました。何年も何ヶ月も前のティックを実行することに比べて、はるかに良い品質であると思われるので、最近のティックをテスト実行しました。

モデルを訓練する関数を、テストライフサイクルの最初のティックで実行するように設定したので、モデルの訓練とテストのプロセスが即座におこなわれたのです。チャートとストラテジーテスターが提供するすべてのものを見る前に、モデルがどのようなパフォーマンスを示したかを見てみましょう。

CS      0       15:50:47.676    Tester  NAS100,H4 (Pepperstone-Demo): generating based on real ticks
CS      0       15:50:47.677    Tester  NAS100,H4: testing of Experts\Advisors\Self Trained NN EA.ex5 from 2023.01.01 00:00 to 2023.02.23 00:00 started with inputs:
CS      0       15:50:47.677    Tester    symbol_x=Apple_Inc_(AAPL.O)
CS      0       15:50:47.677    Tester    symbol_x2=Tesco_(TSCO.L)
CS      0       15:50:47.677    Tester    copy_rates_x=1
CS      0       15:50:47.677    Tester    n_samples=200
CS      0       15:50:47.677    Tester    =
CS      0       15:50:47.677    Tester    slippage=100
CS      0       15:50:47.677    Tester    stop_loss=2.0
CS      0       15:50:47.677    Tester    take_profit=2.0
CS      3       15:50:49.209    Ticks   NAS100 : 2023.02.21 23:59 - real ticks absent for 2 minutes out of 1379 total minute bars within a day

CS      0       15:50:51.466    History Tesco_(TSCO.L),H4: history begins from 2022.01.04 08:00
CS      0       15:50:51.467    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 1/1000 ] Loss = 0.14025037 | accuracy -1.524 
CS      0       15:50:51.468    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 2/1000 ] Loss = 0.05244676 | accuracy 0.056 
CS      0       15:50:51.468    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 3/1000 ] Loss = 0.04488896 | accuracy 0.192 
CS      0       15:50:51.468    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 4/1000 ] Loss = 0.04114715 | accuracy 0.259 
CS      0       15:50:51.468    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 5/1000 ] Loss = 0.03877407 | accuracy 0.302 
CS      0       15:50:51.469    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 6/1000 ] Loss = 0.03725228 | accuracy 0.329 
CS      0       15:50:51.469    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 7/1000 ] Loss = 0.03627591 | accuracy 0.347 
CS      0       15:50:51.469    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 8/1000 ] Loss = 0.03564933 | accuracy 0.358 
CS      0       15:50:51.470    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 9/1000 ] Loss = 0.03524708 | accuracy 0.366 
CS      0       15:50:51.470    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 10/1000 ] Loss = 0.03498872 | accuracy 0.370 


CS      0       15:50:51.662    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 1000/1000 ] Loss = 0.03452066 | accuracy 0.379 
CS      0       15:50:51.662    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   Testing Accuracy =0.717

訓練の精度は37.9%でしたが、テストの精度は71.7%になりました。またもや失望です。

具体的に何が問題なのかは定かではありませんが、私は訓練の質を疑っています。訓練データとテストデータの品質が適切であることを常に確認します。データに穴があると、異なるモデルになる可能性があります。ストラテジーテスターでも良い結果を求めているのですから、バックテストの結果は、私たちが手間暇をかけて作った良いモデルから出ていることを確認する必要があります。

ストラテジーテスターの最後には、このEAが開いた取引の大半が78.27%の損失に終わったという驚くべき結果が出たのです。

ストップロスやテイクプロフィットターゲットについては最適化されていないので、これらの値や他のパラメータについて最適化するのが良いと思います。

短い最適化を実行し、copy_rates_x：COPY_Rates_LOW、n_samples：2950、スリッページ：1、ストップロス7.4、テイクプロフィット：5.0を選びました。

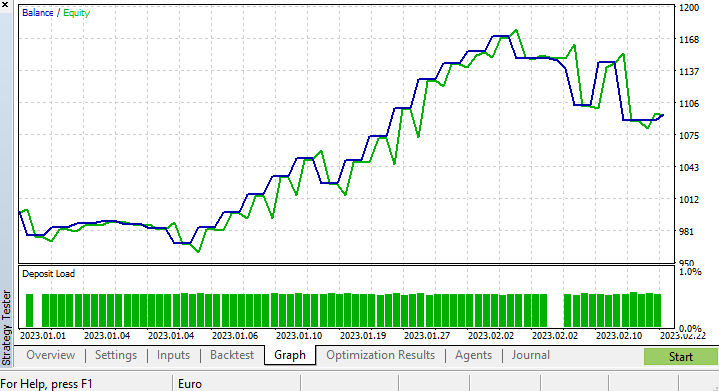
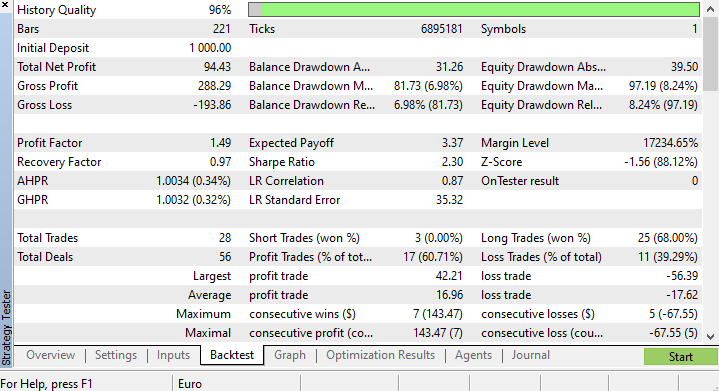
今回のモデルは、ストラテジーテスターの開始時に訓練精度が61.5％、テスト精度が63.5％という結果でした。合理的だと思います。

CS      0       17:11:52.100    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   [ 1000/1000 ] Loss = 0.05890808 | accuracy 0.615 
CS      0       17:11:52.101    Self Trained NN EA (NAS100,H4)  2023.01.03 01:00:00   Testing Accuracy =0.635

最後に

デルタルールは単層回帰型ニューラルネットワークのためのものです。単層のニューラルネットワークを使用しているにもかかわらず、うまくいかないときに構築し、改善することができることを確認しました。単層ニューラルネットワークは、与えられた問題を解決するために、チームとして協力する線形回帰モデルの組み合わせに過ぎません。次は例です。

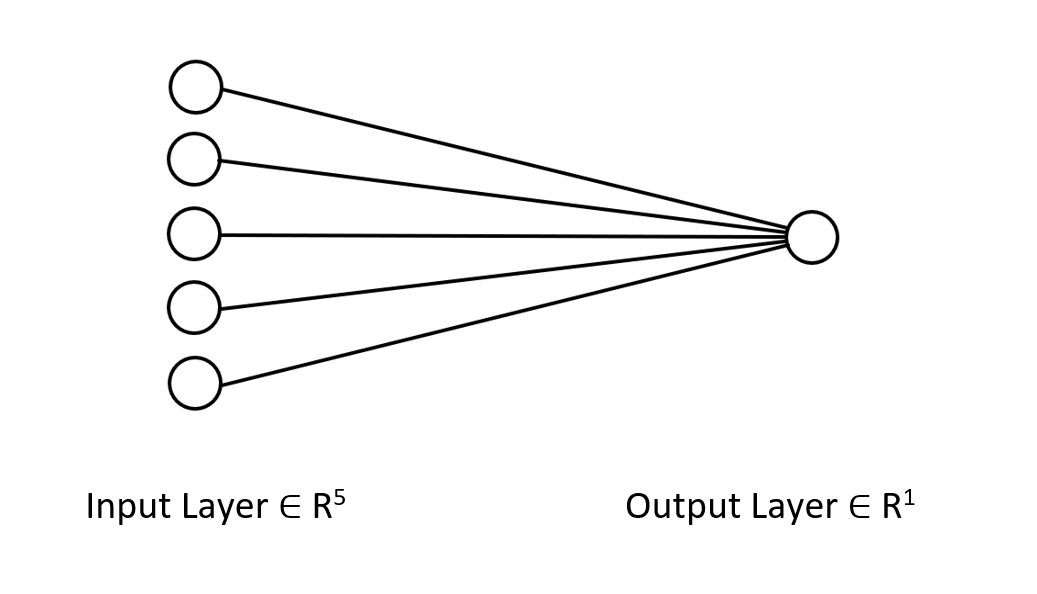
5つの線形回帰モデルが同じ問題に取り組んでいるようなものだと見ることができます。ただし、このニューラルネットワークは、変数の複雑なパターンを理解する能力はないので、できなくても驚かないでください。先に述べたように、デルタルールは、深層学習ではるかに複雑なニューラルネットワークに使用される一般的なバックプロパゲーションアルゴリズムの構成要素です。

エラーになりやすい状態でニューラルネットワークを構築したのは、ニューラルネットワークがパターンを学習する能力があっても、細部にまで気を配り、多くのことを正しく理解しないとうまくいかないということを説明するためです。

ありがとうございました。

このライブラリやその他多くのMLモデルの開発をこのレポジトリで追跡してください：https://github.com/MegaJoctan/MALE5

以下は添付ファイルの表です。

ファイル	内容・使用方法
metrics.mqh	ニューラルネットワークモデルの精度を測定するための関数が含まれています
preprocessing.mqh	NeuralNetworksモデル用のデータをスケーリングし、準備するための関数が含まれています
matrix_utils.mqh	追加の行列操作の関数
selftrain NN.mqh	自己学習型ニューラルネットワークを含むメインインクルードファイル
Self Train NN EA.mq5	自己学習したニューラルネットワークをテストするためのEA

参考記事：

免責事項：この記事は教育目的のみです。取引はリスクの高いゲームであるため、それに伴うリスクを理解する必要があります。本記事で取り上げたこのような方法を使用することにより発生した損失や損害について、著者は一切の責任を負いません。リスクにさらすのは失ってもいい資金だけにしてください。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/12209

添付されたファイル |

ZIPをダウンロード

Attachments.zip (13.98 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

データサイエンスと機械学習（第13回）：主成分分析(PCA)で金融市場分析を改善する

主成分分析（Principal component analysis、PCA）で金融市場分析に革命を起こしましょう。この強力な手法がどのようにデータの隠れたパターンを解き放ち、潜在的な市場動向を明らかにし、投資戦略を最適化するかをご覧ください。この記事では、PCAが複雑な金融データを分析するための新しいレンズをどのように提供できるかを探り、従来のアプローチでは見逃されていた洞察を明らかにします。金融市場データにPCAを適用することで競争力を高め、時代を先取りする方法をご覧ください。

キャンバスベースのインジケーター：チャネル内を透明にする

この記事では、標準ライブラリのCCanvasクラスを使用して描画されるカスタムインジケーターを作成して、座標変換のチャートプロパティを確認する方法を紹介します。特に、2本の線の間の領域を透明にする必要があるインジケーターに取り組みます。

自動で動くEAを作る（第11回）：自動化(III)

自動化されたシステムは、適切なセキュリティなしでは成功しません。ただし、いくつかのことをよく理解していなければ、セキュリティは保証されません。この記事では、自動化されたシステムで最大のセキュリティを達成することがなぜそれほど難しいのかを探ります。

母集団最適化アルゴリズム：SSG（Saplings Sowing and Growing up、苗木の播種と育成）

SSG（Saplings Sowing and Growing up、苗木の播種と育成）アルゴリズムは、様々な条件下で優れた生存能力を発揮する、地球上で最も回復力のある生物の1つからインスピレーションを得ています。