MetaTrader 5 / トレーディング
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
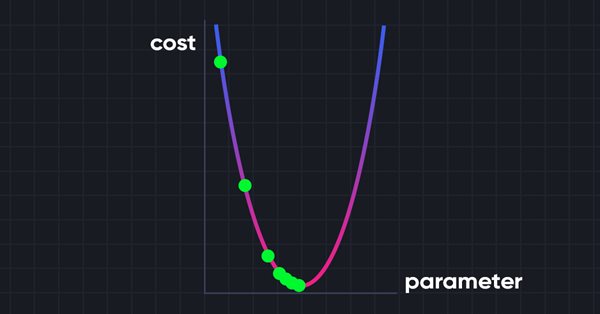
データサイエンスと機械学習（第06回）：勾配降下法

データサイエンスと機械学習（第06回）：勾配降下法

MetaTrader 5 — トレーディング | 2 11月 2022, 08:57
531 0
Omega J Msigwa
Omega J Msigwa

時期尚早の最適化は、プログラミングにおける諸悪の根源である

- ドナルド・クヌース 

はじめに

ウィキペディアによると、勾配降下法（最急降下法とも呼ばれる)は、微分可能な関数の局所的最小値を見つけるための一次反復最適化アルゴリズムです。その考え方は、現在の点での関数の勾配（または近似勾配)の反対方向に手順を繰り返すことです。これは最急降下の方向であるためです。逆に、勾配の方向に進むと、その関数の極大値が得られます。この手順は勾配上昇として知られています。


基本的に、勾配降下法は関数の最小値を見つけるために使用される最適化アルゴリズムです。

勾配降下法の記事gif

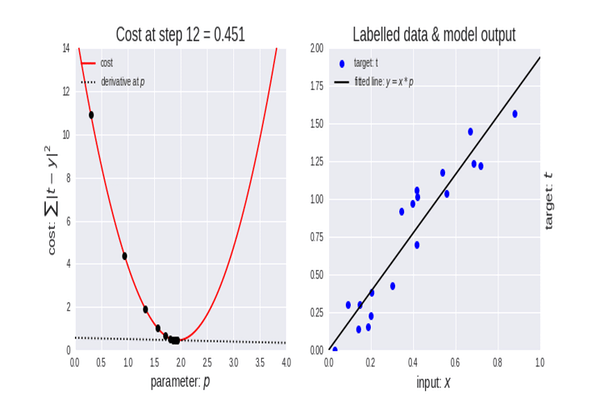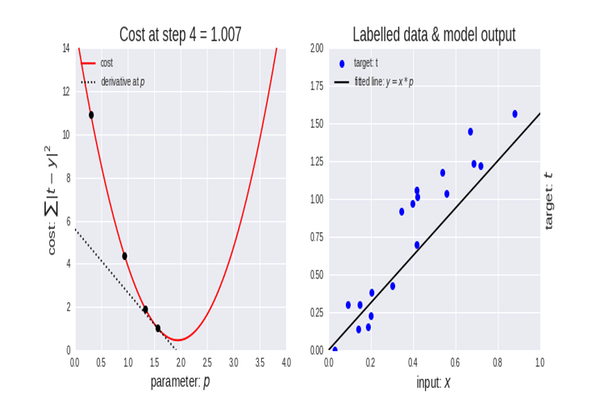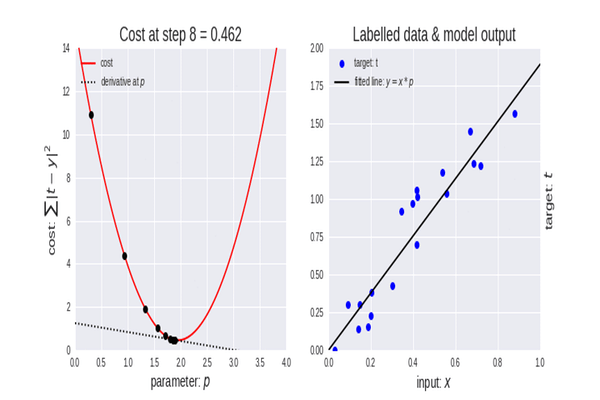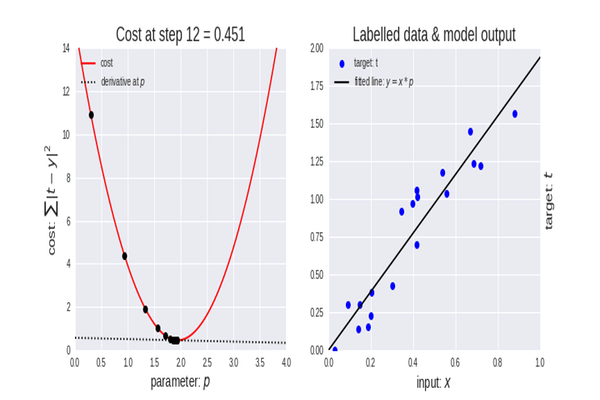
勾配降下法は、データセットに最適なモデルのパラメータを見つけるのに役立つため、機械学習において非常に重要なアルゴリズムです。まず、コスト関数という用語について説明します。


コスト関数

一部の人には損失関数と呼ばれます。これは、モデルがxとyの値の間の関係を予測する際にどれだけ良いか悪いかを計算するための指標です。

モデルがどのように予測しているかを判断するために使用できるメトリクスはたくさんありますが、それらすべてとは異なり、コスト関数はデータセット全体の平均損失を見つけます。コスト関数が大きいほど、モデルがデータセット内の関係を見つけるのが困難になります。

コスト関数が最小のモデルが最適なモデルであるため、勾配降下法はコスト関数を最小化することを目的としています。今説明したことを理解するために、次の例を見てみましょう。

コスト関数が次の式であるとします。 

この関数のグラフをPythonでプロットすると、次のようになります。

pyplot

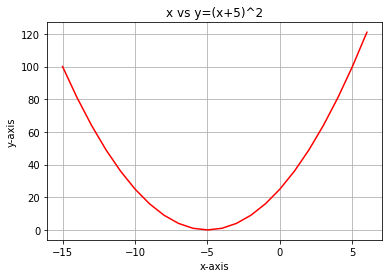
コスト関数に必要な最初の手順は、連鎖律を使用してコスト関数を微分することです。

方程式y=(x+5)^2は合成関数です（1つの関数が別の関数の中にあります）。 外側の関数は(x+5)^2で、内側の関数は(x+5)です。微分するために連鎖律を適用してみましょう。画像を参照してください。

連鎖律

理解するのが難しいと感じた場合は、手動で計算をおこなうビデオの最後にリンクされています。さて、取得したばかりのこの関数が勾配です。方程式の勾配を見つけるプロセスは、それらすべての中で最も重要な手順です。数学の先生が、関数を微分する目的は関数の勾配を取得することであると教えてくれたら良かったのですが。

これが最初で最も重要な手順です。以下は2番目の手順です。

手順02：

勾配の負の方向に移動します。ここで、どのくらい移動する必要があるかという疑問が生じます。学習率の出番です。


学習率

定義上、これは損失関数の最小値に向かって移動する間の各反復のステップサイズです。山を降りる人を例にとると、そのステップは学習率であり、ステップが小さいほど、ふもとにに到達するのに時間がかかります。その逆も同様です。

アルゴリズムの学習率を小さい値に保ちますが、0.0001のように小さくしないでください。そうすると、アルゴリズムが最小値に達するまでに時間がかかる可能性があるため、プログラムの実行時間が長くなります。対照的に、学習率に大きな数値を使用すると、アルゴリズムが最小値をスキップし、最終的に目標の最小値を見逃す可能性があります。

デフォルトの学習率は0.01です。

反復を実行して、アルゴリズムがどのように機能するかを確認しましょう。

最初の反復： アルゴリズムの開始点として任意のランダムポイントを選択します。xの値を更新するために、xの最初の値として0を選択しました。これが式です。

新しい値の勾配降下法

 反復ごとに、関数の最小値に向かって下降し、勾配降下法という名前も同様です。これでおわかりでしょうか。

わかる

これがどのように機能するかを詳しく見てみましょう。次に、何が起こっているのかをしっかりと理解できるように、2回の繰り返しで値を手動で計算しましょう。

1回目の反復

式：x1=x0 - 学習率*(2*(x+5))

x1 = 0 - 0.01 * 0.01 * 2*(0+5)

x1 = -0.01 * 10

x1=-0.1（最終的に） 

最後に、新しい値を古い値に代入して値を更新し、関数の最小値に達するまで同じ手順を繰り返します。

x0 = x1

2回目の反復

x1 = -0.1 - 0.01 * 2*(-0.1+5)

x1 = -0.198

Then: x0 =  x1

この手順を数回繰り返すと、最初の10回の反復の出力は次のようになります。

RS      0       17:15:16.793    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction CUSTOM
QQ      0       17:15:16.793    gradient-descent test (EURUSD,M1)       1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000
ES      0       17:15:16.793    gradient-descent test (EURUSD,M1)       2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000
PR      0       17:15:16.793    gradient-descent test (EURUSD,M1)       3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000
LE      0       17:15:16.793    gradient-descent test (EURUSD,M1)       4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000
JD      0       17:15:16.793    gradient-descent test (EURUSD,M1)       5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086
JF      0       17:15:16.793    gradient-descent test (EURUSD,M1)       8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325
NI      0       17:15:16.793    gradient-descent test (EURUSD,M1)       9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258
CK      0       17:15:16.793    gradient-descent test (EURUSD,M1)       10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213

関数の最小値に非常に近いときのアルゴリズムの他の10個の値も見てみましょう。

GK      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060
IH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059
NH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058
QI      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057
II      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055
RN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054
KN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049
HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

1062回反復した後、アルゴリズムはこの関数の極小値に到達することができました。

このアルゴリズムから気づいたこと

コスト関数の値を見ると、最初は値が大きく変化しているが、コスト関数の最後の値には非常に小さな変化が見られることがわかるでしょう。

勾配降下法は、関数の最小値に近くない場合はより大きなステップを使いますが、関数の最小値に近い場合は小さなステップを使います。山のふもとに近づいたときに行うのと同じことです。勾配降下法がかなり賢いことを知っておいてください。

結局、局所最小値は次になります。 

HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

この関数の最小値は-5.0であるため、これは正確な値です。

本当の質問

勾配はいつ停止するかをどのように知っているのでしょうか。無限に、または少なくともコンピュータの計算能力が尽きるまで、アルゴリズムを反復させ続けることができることは確かです。

コスト関数がゼロのときは、勾配降下法が機能したことがわかっているときです。

MQL5でこの操作全体をコーディングしましょう。

       while (true)
        {
           iterations++;
           
           x1 = x0 - m_learning_rate * CustomCostFunction(x0);
           
           printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); 
           
           if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0);  break;  }
              
           x0 = x1;
        }   

上記のコードブロックは、必要な結果を得ることができたものですが、クラスCGradientDescentの唯一なものではありません。微分方程式が保持され計算されていたのは、次の関数CustomCostFunctionです。

double CGradientDescent::CustomCostFunction(double x)
 {
   return(2 * ( x + 5 ));
 }


目的

この連載で説明した以前のライブラリによって作成された既定の線形モデルをそのまま使用できる場合、これらすべての計算の目的は何なのかを自問する人もいるかもしれません。デフォルト値を使用して作成されたモデルが必ずしも最適なモデルであるとは限らないため、コンピュータにエラーの少ないモデル（最適なモデル）の最適なパラメータを学習させる必要があります。

人工ニューラルネットワークの構築に近づいた記事がいくつかあります。バックプロパゲーションやその他の手法の過程でニューラルネットワークがどのように学習するか（パターンを学習するか）を誰もが理解できるように、勾配降下法はそれは可能にした最も人気のあるアルゴリズムです。物事が複雑になりつつあるため、それをしっかりと理解していないと、プロセスを理解できない可能性があります.


回帰モデルの勾配降下

給与のデータセットを使用して、勾配降下法を使用して最適なモデルを構築しましょう。

データセットの概要

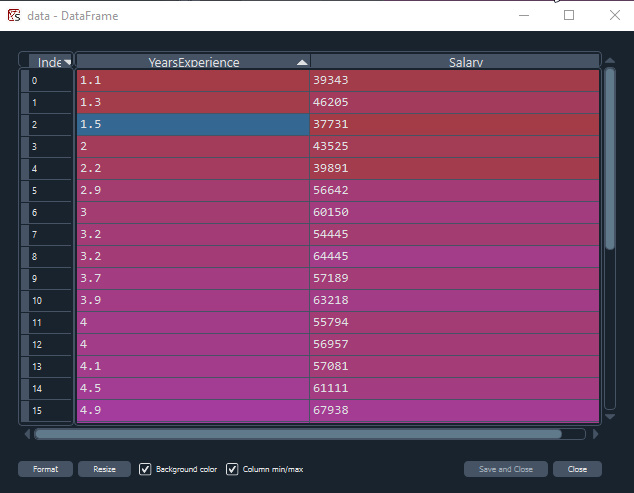
Pythonでのデータの視覚化:

import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt


data  = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv")

print(data.head(10))

x = data["YearsExperience"]
y = data["Salary"]

plt.figure(figsize=(16,9))
plt.title("Experience vs Salary")
plt.scatter(x,y,c="green")
plt.xlabel(xlabel="Years of Experience")
plt.ylabel(ylabel="Salary")
plt.show()

これがグラフになります。

と給与経験年数 v.s. 給与

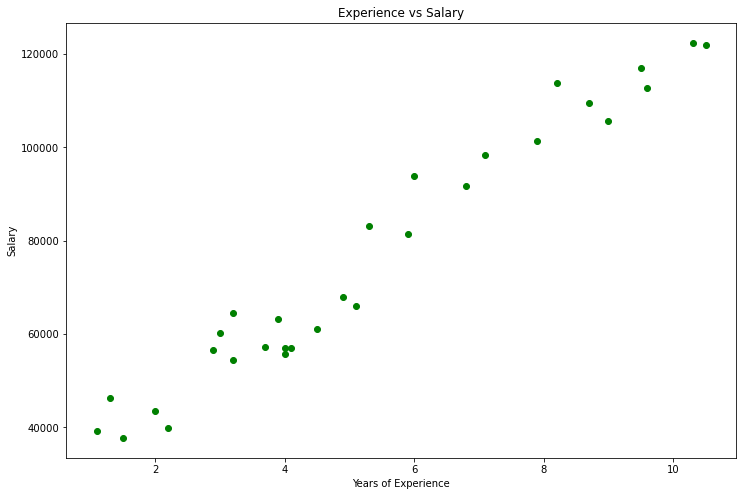
データセットを見ると、このデータセットが回帰問題用であることに気付かずにはいられませんが、予測や達成しようとしているものを作成するのに役立つモデルが100万個もある可能性があります。

複数のモード

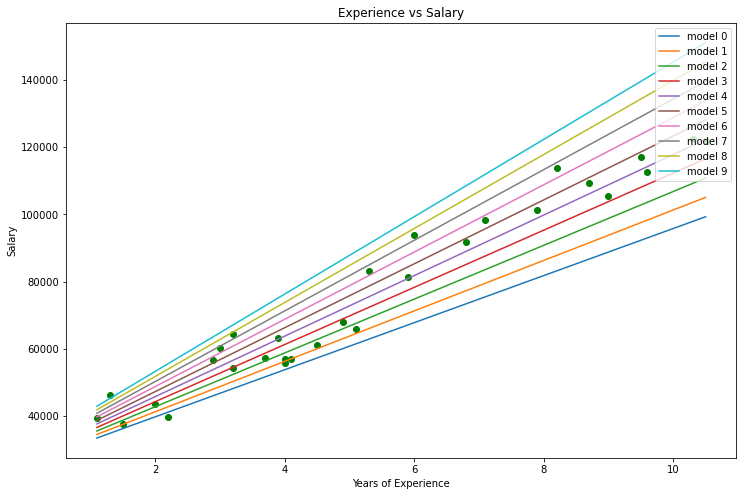
個人の経験と給与を予測するために使用する最適なモデルは何かをこれから調べていきますが、まず、回帰モデルのコスト関数を導出しましょう。

理論

線形回帰に戻りましょう。

すべての線形モデルにはそれに関連するエラーがあることがわかっています。また、このグラフでは100万本の線を作成でき、最適な線は常に誤差が最も少ない線であることもわかっています。

コスト関数は、実際の値と予測値の間の誤差を表します。コスト関数は

誤差=Y実績値-Y予測値

として書くことができます。誤差の大きさを見ているので、二乗すると、式は次のようになります。

データセット全体の誤差を探しているので、合計します。 

最後に、誤差の合計をデータセット内の項目数であるmで割ります。

線形回帰コスト関数

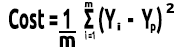
これは、手作業でおこなわれる数学的手順全体のビデオです。

コスト関数ができたので、勾配降下法をコーディングして、両方に最適なパラメータを見つけてみましょう。Boとして示されるX（スロープ）の係数とB1として示されるY切片 

   
   double cost_B0=0, cost_B1=0;
   
   if (costFunction == MSE)
    {
      int iterations=0;
      for (int i=0; i<m_iterations; i++, iterations++)
        {
        
           cost_B0 = Mse(b0,b1,Intercept);
           cost_B1 = Mse(b0,b1,Slope);
           
           b0 = b0 - m_learning_rate * cost_B0; 
           b1 = b1 - m_learning_rate * cost_B1;
           
           printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1);
           
           DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1);
           
           if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0)  break; 
           
        }
      printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f  ||  B1(Coefficient) = %.5f",iterations,b0,b1);    
    }

勾配降下法コードからいくつかのことに注意してください。

  • プロセスは以前に実行したプロセスと同じですが、今回はBoとB1の値を一度に2回見つけて更新しています。
  • 反復回数には制限があります。無限ループを作成する最善の方法はwhileループを使用することだと誰かが言っていましたが、今回はwhileループを使用せず、代わりにアルゴリズムが最適なモデルの係数を見つするために機能する回数を制限したいと考えています。
  • DBL_MAX_MINには、デバッグ目的の関数で、コンピュータの数学的限界に達したかどうかを確認して通知する責任があります。

これは、アルゴリズムの操作の出力です。学習率=0.01、反復回数=10000です。

PD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       [20]  91738.0000  98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000
JS      0       17:29:17.999    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
RF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000
OP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667
LP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770
QN      0       17:29:17.999    gradient-descent test (EURUSD,M1)       3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357
LO      0       17:29:17.999    gradient-descent test (EURUSD,M1)       4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058
GH      0       17:29:17.999    gradient-descent test (EURUSD,M1)       5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134
CJ      0       17:29:17.999    gradient-descent test (EURUSD,M1)       6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060
DD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310
HF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

EI      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
NG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GD      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PR      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IS      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RQ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
KN      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
DL      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RM      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IK      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PH      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GF      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
MG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000
LE      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 Iterations Local Minima are
OJ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       B0(Intercept) = 25792.20020  ||  B1(Coefficient) = 9449.96232

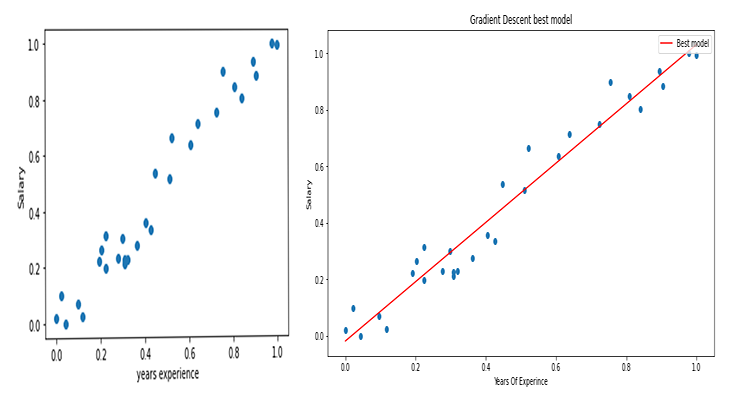
matplotlibを使用してグラフをプロットした場合 

最適モデル勾配降下法

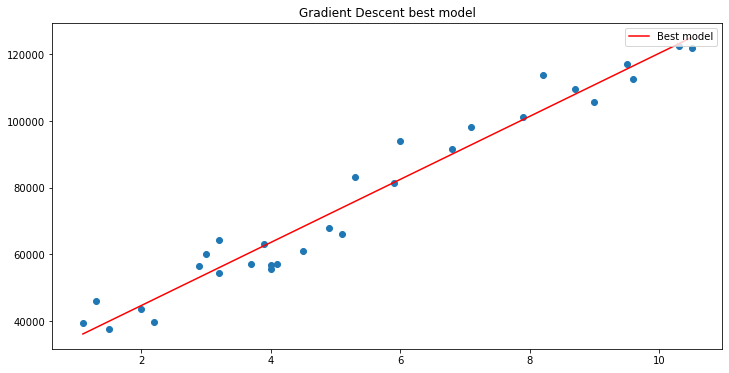
できました。勾配降下法は、私たちが試した10000個のモデルの中から最適なモデルをうまく取得することができました。素晴らしいですが、重要な手順が1つ欠けているため、モデルが奇妙な動作をして、得られない結果が得られる可能性があります。


線形回帰入力変数データの正規化

異なるデータセットでは異なる反復の後に最適なモデルを見つけることができることがわかっています。最良のモデルに到達するまでに100回の反復が必要な場合もあれば、コスト関数がゼロになるまでに10000回または最大100万回の反復が必要な場合もあります。学習率の間違った値は、極小値を逃してしまう可能性があり、その目標を逃すと、コンピュータの数学的限界に達することになります。これを実際に見てみましょう。

学習率=0.1.、反復回数1000


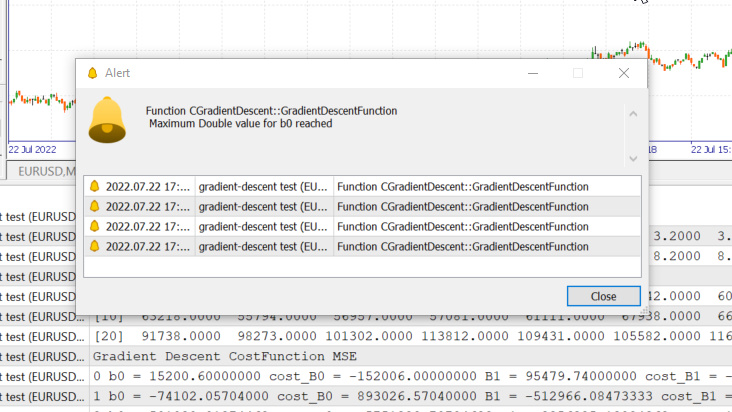
システムで許可されている最大double値に到達しました。次がログです。

GM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
OP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000
GR      0       17:28:14.819    gradient-descent test (EURUSD,M1)       1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333
NM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952
LH      0       17:28:14.819    gradient-descent test (EURUSD,M1)       3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822
KD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084
OQ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984
FM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615
JJ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730
MP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422
MM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625
HD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500
DP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000

つまり、学習率が間違っていた場合、最適なモデルを見つける可能性がほとんどないかまったくなく、警告で見たようにコンピュータの数学的限界に達する可能性が高いということです。

ただし、このデータセットの学習率を0.01にしようとすると、訓練プロセスは非常に遅くなりますが、問題は発生しなくなります。このデータセットの学習率を使用すると、数学的な限界に達してしまいます。すべてのデータセットに学習率があることはわかりましたが、複数の変数を持つデータセットでは学習率を最適化する機会がない場合があります。これはまた、このプロセス全体をおこなう効率の悪い方法です。

これらすべてに対する解決策は、データセット全体を正規化して同じスケールにできるようにすることです。これにより、値を同じ軸にプロットするときの読みやすさが向上し、正規化された値は通常0から1の範囲にあるため、訓練時間が改善されます。また、学習率パラメータが1つだけになると、学習率を0.01の学習率など、直面するあらゆるデータセットに使用できるため、学習率について心配する必要がなくなります。学習率について詳しくは、こちらでご覧ください。

最後に大事なこと

また、給与データの値が39,343～121,782であることもわかっています。平均経験年数は1.1～10.5です。このようにデータを保持すると、給与の値が非常に大きくなり、モデルがどの値よりも重要であると考える可能性があるため、経験年数と比較して大きな影響を与える可能性があります。すべての独立変数が必要です。 他の変数と同じ影響を与えるには、値を正規化することがいかに重要かがわかります。


(正規化）Min-Max Scalar

このアプローチでは、データを0～1の範囲内になるように正規化します。式は次のとおりです。

正規化Min-Max Scalar

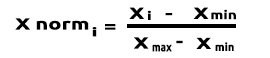
この式をMQL5のコード行に変換すると、次のようになります。

void CGradientDescent::MinMaxScaler(double &Array[])
 {
   double mean = Mean(Array);
   double max,min;
   double Norm[];
   
   ArrayResize(Norm,ArraySize(Array));
   
   max = Array[ArrayMaximum(Array)];   min = Array[ArrayMinimum(Array)];
   
    for (int i=0; i<ArraySize(Array); i++)
         Norm[i] = (Array[i] - min) / (max - min); 
   
   printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm));
   
   ArrayFree(Array);
   ArrayCopy(Array,Norm);
 }

関数std()は、データが正規化された後に標準偏差を知らせるためのものです。そのコードは次のとおりです。

double CGradientDescent::std(double &data[])
 {
   double mean =  Mean(data);
   double sum = 0;
   
    for (int i=0; i<ArraySize(data); i++)
       sum += MathPow(data[i] - mean,2);
    
    return(MathSqrt(sum/ArraySize(data)));  
 }

これをすべて呼び出して出力し、何が起こるか見てみましょう。

void OnStart()
  {
//---
      string filename = "Salary_Data.csv";

      double XMatrix[];
      double YMatrix[];
      
      
      grad = new CGradientDescent(1, 0.01,1000);
      
      grad.ReadCsvCol(filename,1,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
       
      grad.MinMaxScaler(XMatrix);
      grad.MinMaxScaler(YMatrix);
      
      ArrayPrint("Normalized X",XMatrix);
      ArrayPrint("Normalized Y",YMatrix);
      
      
      grad.GradientDescentFunction(XMatrix,YMatrix,MSE);
      
      delete (grad);
  }

出力

OK      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.44823 Std = 0.29683
MG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.45207 Std = 0.31838
MP      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized X
JG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617
ER      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000
NQ      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized Y
IF      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762
IS      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939

グラフは次のようになります。

の正規化価格グラフの正規化

ロジスティック回帰の勾配降下法

勾配降下法の直線的な側面を見てきましたが、今度はロジスティックな側面を見てみましょう。

ここでは、線形回帰部分でおこなったのと同じプロセスを実行します。これは、関係するプロセスがまったく同じであるためです。ロジスティック回帰を微分するプロセスが線形モデルのプロセスよりも複雑になるだけです。最初にコスト関数を見てみましょう。

ロジスティック回帰に関する連載の2番目の記事で説明したように、ロジスティック回帰モデルのコスト関数は、以下に示すバイナリクロスエントロピー（別名log loss）です。

バイナリクロスエントロピーまたはlog loss

それでは、最初に難しい部分を実行しましょう。この関数を微分して勾配を取得します。

導関数を見つけた後 

コスト関数の導関数

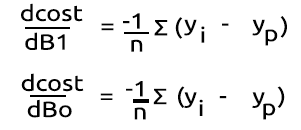
Binary Cross Entropyを表すBCE関数内で式をMQL5コードに変換しましょう。

double CGradientDescent::Bce(double Bo,double B1,Beta wrt)
 {
   double sum_sqr=0;
   double m = ArraySize(Y);
   double x[];
   
   MatrixColumn(m_XMatrix,x,2);
   
    if (wrt == Slope)
      for (int i=0; i<ArraySize(Y); i++)
        { 
          double Yp = Sigmoid(Bo+B1*x[i]);
          
          sum_sqr += (Y[i] - Yp) * x[i];
        }
        
    if (wrt == Intercept)
      for (int i=0; i<ArraySize(Y); i++)
         {
            double Yp = Sigmoid(Bo+B1*x[i]);
            sum_sqr += (Y[i] - Yp);
         } 
    return((-1/m)*sum_sqr);
 }

分類モデルを扱っているため、選択したデータセットはロジスティック回帰で使用したタイタニックデータセットです。独立変数はPclass（乗客クラス）であり、従属変数はSurvivedです。

クラスvs生存：タイタニックデータセット

分類された散布図

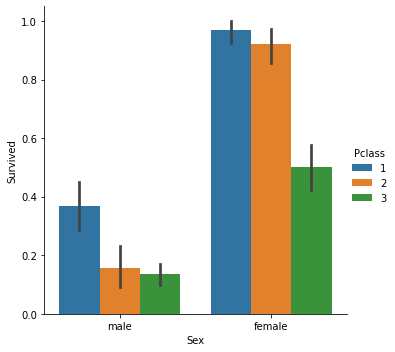
生存者とクラスの散布図

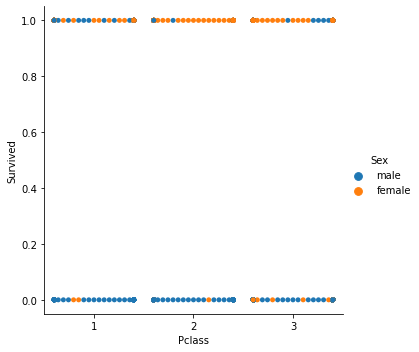
ここで、クラスをGradient Descentと呼びますが、今回はコスト関数としてBCE (Binary Cross Entropy)を使用します。

      filename = "titanic.csv";
      
      ZeroMemory(XMatrix);
      ZeroMemory(YMatrix);
      
      grad.ReadCsvCol(filename,3,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
      
      grad.GradientDescentFunction(XMatrix,YMatrix,BCE);
      
      delete (grad);
      

結果を見てみましょう。

CP      0       07:19:08.906    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction BCE
KD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391
FD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541
KE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898
QE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566
EE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123
CF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108
MF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329
JG      0       07:19:08.907    gradient-descent test (EURUSD,M1)       7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146
HE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129
ME      0       07:19:08.907    gradient-descent test (EURUSD,M1)       9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065
JQ      0       07:19:08.907    gradient-descent test (EURUSD,M1)       10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600
        <<<<<<  Last  10 iterations >>>>>>

FN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
NM      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
KL      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
RK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MJ      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
HI      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
CH      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MH      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
QG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000
NG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 Iterations Local Minima are
MJ      0       07:19:09.727    gradient-descent test (EURUSD,M1)       B0(Intercept) = 1.44679  ||  B1(Coefficient) = -0.85011

ロジスティック回帰の分類データは線形回帰でおこなったように正規化またはスケーリングしません。

これで、最も重要な2つの機械学習モデルの勾配降下法がわかりました。この記事で使用されているPythonコードが理解しやすく、役立つことを願っています。データセットは、このGitHubリポジトリにリンクされています。


結論

1つの独立変数と1つの従属変数の勾配降下法を見てきました。複数の独立変数の場合、ベクトル/行列形式の方程式を使用する必要があります。MQL5によって最近リリースされた行列のライブラリがあるので、今回は誰でも簡単に試して自分で見つけることができると思います。行列に関するヘルプがあれば、遠慮なく私に連絡してください。

よろしくお願いします。

微積分の詳細:


MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/11200

添付されたファイル |
ZIPをダウンロード
Gradient_Descent.zip (41.03 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ニューラルネットワークが簡単に（第22部）：回帰モデルの教師なし学習 ニューラルネットワークが簡単に（第22部）：回帰モデルの教師なし学習
モデルと教師なし学習アルゴリズムの研究を続けます。今回は、回帰モデルの学習に適用した場合のオートエンコーダの特徴について提案します。
一からの取引エキスパートアドバイザーの開発（第25部）：システムの堅牢性の提供(II) 一からの取引エキスパートアドバイザーの開発（第25部）：システムの堅牢性の提供(II)
この記事では、エキスパートアドバイザー(EA)のパフォーマンスを仕上げます。長くなるのでご準備ください。EAを信頼できるものにするために、まず取引システムの一部でないコードをすべて削除します。
チャイキンオシレーター(Chaikin Oscillator)による取引システムの設計方法を学ぶ チャイキンオシレーター(Chaikin Oscillator)による取引システムの設計方法を学ぶ
最も人気のあるテクニカル指標に基づいて取引システムを設計する方法を学ぶための連載の新しい記事にようこそ。この新しい記事を通して、チャイキンオシレーター指標による取引システムを設計する方法を学びます。
ニューラルネットワークが簡単に（第21部）：変分オートエンコーダ(Variational autoencoder、VAE) ニューラルネットワークが簡単に（第21部）：変分オートエンコーダ(Variational autoencoder、VAE)
前回の記事で、オートエンコーダアルゴリズムについて学びました。他のアルゴリズム同様、このアルゴリズムには長所と短所があります。元の実装では、オートエンコーダは、訓練標本からオブジェクトを可能な限り分離するために使用されます。今回はその短所への対処法についてお話します。