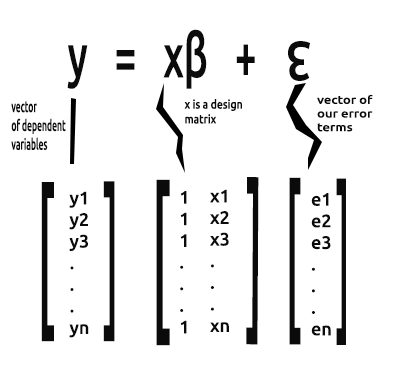
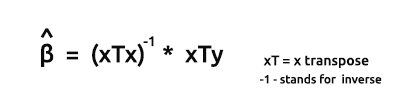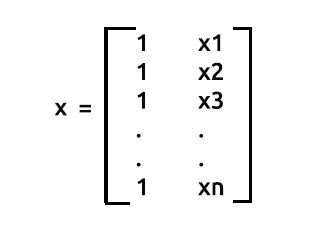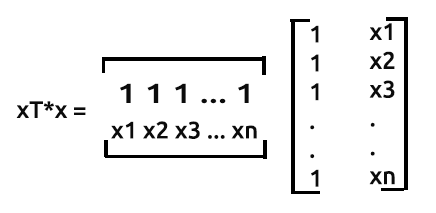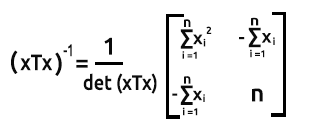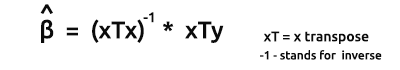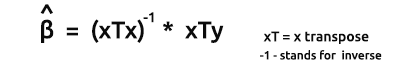データサイエンスと機械学習(第03回):行列回帰
長い試行錯誤の末、ようやく動的重回帰のパズルが解けました。続きをお読みください。
前の2つの記事に注目していただければ、私が抱えていた大きな問題は、より多くの独立変数を扱えるモデルのプログラミングであることにお気づきでしょう。つまり、より多くの入力を動的に扱うということです。戦略の作成に関しては、何百ものデータを処理することになるため、モデルがこの需要に確実に対応できるようにしたいからです。
行列
数学の授業をスキップした人のために説明すると、行列とは、数値やその他の数学的対象を行と列に並べた長方形の配列または表で、数学的対象やその対象の特性を表すために使用されます。
次は例です。
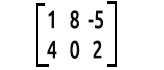
見て見ぬ振りをする
行列の読み方は行x列です。上の行列は、2行3列を意味する2x3行列です。
現代のコンピュータが情報を処理し、大きな数字を計算する上で、行列が大きな役割を果たしていることは間違いありません。そのようなことが実現できる大きな要因は、行列のデータがコンピュータが読み取り、操作できる配列形式で格納されていることです。機械学習への応用を見てみましょう。
線形回帰
線形代数の計算は行列によって可能になります。したがって、行列の学習は線形代数の大きな部分を占めております。行列を使って線形回帰モデルを作ることができるのです。
ご存知のように、直線の方程式は
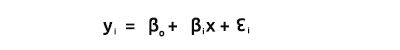
です。ここで、∈は誤差項、BoとBiはそれぞれ係数のy切片と傾き係数です。
この連載で今後興味を持つのは、方程式のベクトル形式です。こちらです。
これは単回帰を行列形式にしたものです。
単回帰モデル(および他の回帰モデル)の場合、通常,勾配係数や最小二乗推定量を求めることに興味があります.
ベクトルBetaは、ベータを含むベクトルです。
式から説明するとβoとβ1です。
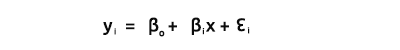
係数はモデルを構築する上で非常に重要な要素であるため、係数を求めることに興味があります。
ベクトル形式のモデルの推定量の公式は次の通りです。
これは、オタクの皆さんにはぜひとも覚えておいていただきたい大切な公式です。数式上の要素の求め方については、近日中に説明します。
xTの列数とxの行数が同じなので、xTxの積は対称行列になりますが、これは後で実際に見てみましょう。
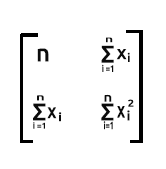
先に述べたように、xは計画行列とも呼ばれ、その行列は次のようになります。
計画行列
ご覧のとおり、最初の列では、Matrix配列の行の最後まで1の値だけを配置しています。これは、行列回帰のためのデータを準備する最初の手順です。このようなことをすることの利点は、さらに計算を進めるとわかります。
この処理は、ライブラリのInit()関数でおこなっています。
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
ここで、計画行列の値を出力してみると、ちょうど1の入力値が終わる行があり、そこからxの値が始まることがわかります。
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
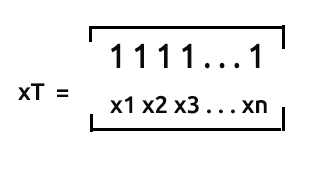
xT(x転置)は、行列の行と列を入れ替える処理です。
つまり、この2つの行列を乗算すると
になります。データを収集した時点で既に転置されているため、行列の転置は省略します。ただし、転置されているx行列と乗算するために、x値の転置を元に戻す必要があります。
一応付け加えますが、転置配列でない行列nx2は[1 x1 1 x2 1 ...1 xn]のようになります。実際に見てみましょう。
X行列の転置を元に戻す
csvファイルから取得した行列を転置して出力すると次のようになります。
転置行列
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
転置を元に戻すには、行列の行と列を入れ替えるだけで、転置と同じ逆方向の処理ができます。
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
厄介なのはここからです。
転置行列の列を行の位置に置き、行を列の位置に置くと、このコード片を実行したときの出力は次のようになります。
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xTは2xnの行列、xはnx2です。結果として得られる行列は,2x2の行列となります。
その乗算の積がどうなるのか計算してみましょう。
注意:行列を乗算するには、最初の行列の列数が2番目の行列の行数と等しくなければなりません。
このリンクhttps://ja.wikipedia.org/wiki/%E8%A1%8C%E5%88%97%E3%81%AE%E4%B9%97%E6%B3%95で行列の乗算規則を参照してください。
この行列での乗算のやり方は
- 行1×列1
- 行1×列2
- 行2×列1
- 行2×列2
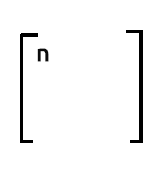
行列の行1 x 列1から、出力は行1の積(1の値を含む)と列1の積(1の値を含む)の和になります。これは、各反復で1の値を1ずつ増加させるのと同じです。
注意:
データセット中のオブザベーションの数を知りたい場合は、xTxの出力の最初の行の最初の列の数字に頼ることができます。
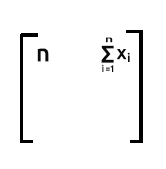
行1×列2行1(1の値)と列2(xの値)の積を合計すると、行1には1の値が含まれます。1は乗算の結果に影響を与えないため、出力はx項目の合計になります。 .
行2×列1。行2の1の値は列1のxの値に乗じても効果がないので、出力はxの総和となります。
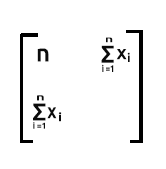
最後の部分は、xの値を2乗したときの総和になります。
x値を含む行2と同じくx値を含む列2の積の総和なので
ご覧のように、この場合の行列の出力は2x2行列です。
線形回帰の最初の記事https://www.mql5.com/ja/articles/10459で紹介したデータセットを使って、これが実際の世界でどのように機能するかを見てみましょう。データを抽出して、独立変数がx、従属変数がyの配列に入れてみましょう。
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
ここで第1回で作成したCsimpleLinearRegressionライブラリをインポートしました。
CSimpleLinearRegression lr;
データを配列に取り込むなど、使いたい関数があるからです。
xTxを求める
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? the output of the matrix will be the row1 and col2 marked in red
配列xT[]に注目すると、xの値をコピーしてこのxT[]配列に格納しただけであることがわかります。前述したように、GetDataToArray()という関数を使ってcsvファイルから配列にデータを収集すると、すでに転置されたデータが得られます。
次に、配列xT[]を転置されていないm_xvalues[]と乗算します。m_xvaluesは、このライブラリのx値のためにグローバルに定義されている配列です。これはMatrixMultiply()関数の内部です。
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
正直なところ、この乗算は紛らわしく、
k + (i*row2); j + (k*col2);
のようなものが使用されている場合には特に醜くなります。落ち着いてください。これらのインデックスを操作することで、特定の行と列でのインデックスを得ることができるようにしました。2次元の配列、例えばMatrix[行][列](ここではMatrix[i][k])を使えば簡単に理解できるのでしょうが、多次元の配列には限界があるので、使わないことにしたのです。記事の最後に簡単なc++のコードをリンクしているので、ご覧になれば私がどうやったか理解できると思いますし、このブログまで読めばもっと理解できると思います。https://www.programiz.com/cpp-programming/examples/matrix-multiplication。
MatrixPrint()関数を用いたxTxの出力は次のようになります。
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
xTx配列の最初の要素は、データセットの各データのオブザベーションの数を持っていることがわかります。これが、計画行列の最初の列に1の値を最初に入力することが非常に重要である理由です。
次に、xTx行列の逆行列を求めましょう。
xTx行列の逆行列
2×2行列の逆行列を求めるには、まず対角線上の最初と最後の要素を入れ替え、残りの2つの値に負の符号を付けます。
式は下図の通りです。
行列の行列式を求めると、det(xTx) =第1対角の積 - 第2対角の積になります。
以下は、mql5のコードで逆数を求める方法です。
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
このブロックのコードを実行すると、出力は次のようになります。
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375
行列の逆行列を出力して、どのようになるか見てみましょう。
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
必ずや次が出力されることでしょう。
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
さて、xTxの逆行列ができたので次に進みましょう。
xTyを見つける
ここでは、xT[]とy[]の値を乗算します。
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
必ずや次が出力されることでしょう。
xTy
[
10550016.7000000 46241904488.2699585
]
計算式参照
さて、xTxの逆行列とxTyができたので、最後にまとめましょう。
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
関数を呼び出す方法の詳細を説明します。
このコード片の出力は次のようになります。
coefficients
[
-5524.40278 4.49996
]
できました。 これは、本連載の第01回で紹介したスカラー形式のモデルで得られた係数と同じ結果です。
配列Betasの最初のインデックスの数値は、常に定数/Y切片になります。最初に得られるのは、計画行列の1列目を1の値で埋めたからで、ここでもそのプロセスがいかに重要かを示しています。その列の中にy切片のスペースが残ります。
これで、単回帰は終了です。重回帰がどのようなものになるか見てみましょう。物事が複雑になることもあるので、よく注意してください。
重動態回帰のパズルの解決
行列に基づいてモデルを構築することの良い点は、モデルを構築する際に、コードを大きく変更することなく、簡単にスケールアップできることです。重回帰で気付く重要な変更点は、行列の逆行列を見つける方法です。これは、私が長い間理解しようとしてきた最も難しい部分であるためです。後でそのセクションに到達したときに詳細を説明しますが、今のところは、MultipleMatrixRegressionライブラリで必要になる可能性のあるものをコーディングしましょう。
関数の引数を入力するだけで、単回帰と重回帰をすべて扱えるライブラリを1つだけ用意することもできますが、先ほど説明した単回帰の項で行った計算を理解していれば、ほぼ同じ処理になるので、物事を明確にするために別のファイルを作成することにしました。
まず最初に、ライブラリで必要になるような基本的なものをコーディングしてみましょう。
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
これは、Init()関数の内部で起こっていることです。
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
おこなわれたことの詳細
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
ここでは、TestScriptのInit関数を呼び出したときに選択したx列(独立変数)を取得し、それらの列をグローバル配列m_XColsArrayに格納します。列を配列にすると利点があります。それらを適切な順序ですべてのx値(独立変数行列)/計画行列の配列に格納できるようになります。
また、データセットの行がすべて同じであることを確認する必要があります。1行または1列に違いがあるだけで、すべての計算が失敗してしまうからです。
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
そして、すべてのx列のデータを、すべての独立変数の1つの行列/計画行列/配列に格納します(これらの名称のうち、どれを呼ぶかは自由です)。
GetAllDataToArray(m_allxvalues);
また、すべての従属変数をその行列に格納します。
GetColumnDatatoArray(y_column,m_yvalues);
これは、計画行列を計算できるようにするための重要な手順です。ここで先に述べたように、xの値の行列の1列目に1の値を追加します。
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
}
今回は、ライブラリの初期化時に転置されていない行列を表示します。
Init関数に必要なものは以上です。multipleMatRegTestScript.mq5(記事の最後にリンク)で呼び出してみましょう。
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
スクリプトが正常に実行されると、次のような出力が得られます(あくまで概要です)。
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
xTxの検索
単回帰の時と同じように、生データであるxTの値をcsvファイルから取り出し、未転置の行列と乗算します。
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
xTx行列を印刷したときの出力は次のようになります。
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
期待通りです。
xTx逆行列
これは重回帰の最も重要な部分であり、細心の注意を払う必要があります。 これから数学の奥深くに入り込み、物事が複雑になっていきます。
前の部分でxTxの逆行列を見つけていたとき、2x2行列の逆行列を探していましたが、今は違います。今回は、独立変数として3つの列を選択したため、4x4行列の逆行列を見つけています。1列の値を追加すると、逆行列を探すときに4x4行列につながる4つの列ができます。
今回は以前使った方法で逆行列を求めることはできませんが、本当の疑問はなぜです。
行列法を使った行列の逆行列の求め方は、行列が巨大になるとうまくいきません。3x3の行列の逆行列を求めるのにも使えません。
行列の逆行列を求める方法として、様々な数学者によっていくつかの方法が考案されましたが、そのうちの1つが古典的な余因子行列です。しかし,私の調査では,これらの方法のほとんどはコーディングが難しく,時には分かりにくいこともありました。https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/。
すべての手法の中で、私はガウス・ジョルダン消去法を選びました。信頼性が高く、コーディングが簡単で、簡単に拡張できることがわかったからです。https://www.youtube.com/watch?v=YcP_KOB6KpQガウス・ジョルダン法についてよく説明している素晴らしいビデオがあるので、概念を把握するのに役立つと思います。
では、ガウス・ジョルダン法のコードを書いてみましょう。コードがわかりにくい場合は、以下にリンクされているコードと以下にリンクされている私のGitHubのC++コードがあります。
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
では、関数を呼び出して、行列の逆行列を出力してみましょう。
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
次が必ずや出力されることでしょう。
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
行列の逆行列を求めるには,正方行列でなければありません。そのため,関数の引数には,行と列の数に等しいmat_orderという引数があります.
xTyを見つける
次に、xの転置とYの行列積を求めましょう。先ほどと同じ作業です。
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
出力されると次のようになります。
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
予期された通り1x4行列です。
式を参照してください。
さて、これで係数を求めるのに必要なものはすべて揃ったので、最後にまとめておきましょう。
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); 出力は次のようになります(係数/ベータ行列の最初の要素は定数、言い換えればy切片であることを再度思い出してください)。
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
すばらしいです。では、私が間違っていることを証明するためにpythonを使わせてください。
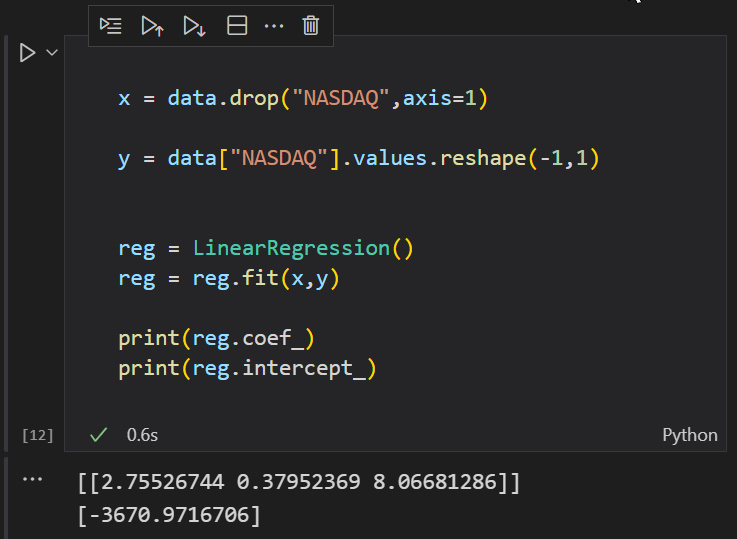
またやりました。
これでようやくmql5で重回帰モデルが可能になったわけですが、その原点を見てみましょう。
すべてはここから始まりました。
matreg.Init(2,"1,3,4",filename);
このアイデアは、無制限の数の独立変数を置くのに役立つ文字列入力を持つことでした。mql5では、pythonのように、あまりにも多くの引数を入力できる可能性がある言語から*argsと*kwargsを持つことができないようです。したがって、これをおこなう唯一の方法は、文字列を使用し、配列を操作して単一の配列だけにすべてのデータを格納できるようにする方法を見つけることでした。その後、それらを操作する方法を見つけることができます。詳しくは、私の最初の失敗例をご覧ください(https://www.mql5.com/ja/code/38894)。私がこれらのことを言う理由は、誰かがこのプロジェクトや他のプロジェクトで同じ道を歩むかもしれないと思うからです。私はただ、私にとって何がうまくいき、何がうまくいかなかったのかを説明しています。
最後に
独立変数がいくつあってもいいと思うかもしれませんが、独立変数が多すぎたり、データセットが大きすぎたりすると、コンピュータによる計算の限界につながる可能性があります。先ほど見たように、行列計算でも計算中に大きな数が発生する可能性があります。
重回帰モデルに独立変数を追加すると、一般的にr2乗として表される従属変数の分散量が常に増加するため、理論的な正当性なしに独立変数を追加しすぎると、モデルが過剰適合してしまう可能性があります。
たとえば、連載の最初の記事のように、NASDAQが依存しており、S&P500が独立している2つの変数だけに基づいてモデルを構築した場合、95%以上の精度が得られた可能性があります。しかし、今回は3つの独立した変数があるため、これはそうではないかもしれません。
モデルの構築後にモデルの精度を確認することは常に良い考えです。また、モデルを構築する前に、各独立変数とターゲットとの間に相関関係があるかどうかを確認する必要があります。
常に、ターゲット変数と強い線形関係を持つことが証明されているデータに基づいてモデルを構築します。
ご精読ありがとうございました。私のGitHubのリポジトリはこちらです。https://github.com/MegaJoctan/MatrixRegressionMQL5.git。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/10928
 一からの取引エキスパートアドバイザーの開発(第15部):Web上のデータにアクセスする(I)
一からの取引エキスパートアドバイザーの開発(第15部):Web上のデータにアクセスする(I)
 パラボリックSARによる取引システムの設計方法を学ぶ
パラボリックSARによる取引システムの設計方法を学ぶ
 ニューラルネットワークが簡単に(第14部):データクラスタリング
ニューラルネットワークが簡単に(第14部):データクラスタリング
 一からの取引エキスパートアドバイザーの開発(第14部):価格別出来高の追加((II)
一からの取引エキスパートアドバイザーの開発(第14部):価格別出来高の追加((II)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索