知っておくべきMQL5ウィザードのテクニック（第51回）：SACによる強化学習

はじめに

Soft Actor Criticは、私たちがこれまでに検討してきた近似方策最適化、ディープQネットワーク、SARSAなどに続く、もう一つの注目すべき強化学習アルゴリズムです。この手法もニューラルネットワークを活用しますが、重要な違いとして合計3つのネットワークを使用する点が挙げられます。それが、2つのCriticネットワークと1つのActorネットワークです。2つのCriticネットワークは、環境の状態と行動を入力として報酬予測（Q値）をおこない、その2つの出力のうち最小値を、Actorネットワークの損失関数の計算に使用します。

Actorネットワークへの入力は環境状態座標であり、出力は平均ベクトルと対数標準偏差ベクトルの2つになります。ガウス過程（英語）を使用することで、これら2つのベクトルを使用して、Actorに可能な行動の確率分布を導出します。したがって、2つのCriticネットワークは従来の方法で訓練できますが、Actorネットワークは明らかに別の話です。ここでは説明すべきことがたくさんあるので、先に進む前にまず基本をもう一度確認しましょう。入力用の2つのCriticネットワークは、環境の現在の状態と行動を受け取ります。出力は、その状態でその行動を実行する場合の期待収益（Q値）の推定値です。2つのCriticを使用することは、Q学習でよく見られる問題である過大評価バイアスを軽減するのに役立ちます。

Actorネットワークは、現在の環境状態を入力として持ちます。その出力は、実質的には可能な行動の確率分布であり、この分布は探索を促すように確率的です。私が「実質的に」というフレーズを使用するのは、Actorネットワークの実際の出力が、各行動の重みを取得するためにガウス確率分布に入力する必要がある2つのベクトルであるためです。MQL5では、これを次のように実現します。

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

SACの仕組み

とはいえ、SACの基本的な流れは他の多くの強化学習アルゴリズムと似ています。最初に行動選択がおこなわれ、Actorネットワークの出力から得られる確率分布に基づいて、Actorが行動をサンプリングします。次に「環境とのインタラクション」がおこなわれ、エージェントはその行動を環境内で実行し、次の状態と報酬を観測します。その後、Criticの更新がおこなわれます。ここでは、2つのCriticネットワークが、予測されたQ値と目標Q値の比較に基づく損失関数によって更新されます。ただし、前述のとおり、Actorネットワークの更新には独自の点があります。方策分布のエントロピー（不確実性）を考慮しつつ、期待される報酬を最大化する方策勾配法が用いられる点です。これは、探索を促進し、最適でない方策への早期の収束を防ぐための工夫です。

SACにおける方策分布のエントロピーは、行動のランダム性や不確実性の度合いを測定します。エントロピーが高いほど探索的な行動が選ばれやすくなり、逆にエントロピーが低ければ、より決定論的な行動選択がなされます。SACのActorネットワークは、確率分布（この記事ではガウス分布（英語）によってパラメータ化された確率的方策を出力します。この分布のエントロピーは、特定の状態（入力）が与えられたときに、エージェントがどのような行動をとる可能性があるかを示します。

この方策分布のエントロピーが重要である理由は、他の多くの強化学習アルゴリズムと同様に、エージェントに探索を促すことで、サブ最適な方策に早期に収束してしまうリスクを低減するためです。これにより、探索と活用のバランスが取られます。SACでは、方策最適化の目的関数にエントロピー項を組み込むことで、期待報酬とエントロピーの両方を最大化しようとします。目的関数は次のようになります。

ここで

• α：エントロピー温度（報酬最大化と探索のバランス）
• logπ(a∣s)：行動の対数確率（上記でコードを共有したLogProbability関数の出力）。これはμとlog(σ)の両方に依存します。
• Q(s,a)：Criticネットワークの2つの出力の最小Q値

エントロピーが高いほど、特定のシナリオへの過剰適合を防ぐことができるため、情報が不完全な環境においては、より堅牢な意思決定につながる傾向があります。したがって、SACにおいてエントロピーを最大化することは理にかなっています。これは、エージェントにより幅広い行動を試みさせて探索を促進するだけでなく、局所的な最適解にとらわれるようなサブ最適な方策を避ける助けにもなります。さらに、過度に決定論的な方策を防ぐことで、未知のシナリオにおいて失敗しにくくするという点でも、正則化の一種として機能します。加えて、エントロピーを段階的に調整することにより、方策の更新がより滑らかになり、学習の安定性や収束の向上にもつながります。

温度制御パラメータは、Actorネットワークのエントロピーや学習プロセスに強く影響するため、その重要性について触れておく価値があります。今回のケースでは、先に紹介したMQL5コードの対数確率関数に示されているように、この値を0.5に固定しています。ただし、温度パラメータ(α)は、目的関数においてエネルギー項にどの程度の重みを与えるかを決定します。αの値が高ければ探索が促進され、低ければより決定論的な方策、つまり活用が強調される傾向にあります。したがって、今回αを0.5に設定しているのは、探索と活用のちょうど良いバランスを取るための判断です。

ただし、SACでは、目標とするエントロピー水準を維持するために、αを動的に調整する自動エントロピー調整メカニズムが用いられることがよくあります。これにより、探索と活用のバランスが自動的に保たれるようになります。この仕組みの実用的な意義としては、さまざまなタスクに対して堅牢な学習が可能になること、不完全な情報下でも有効な一般化された方策（確率的方策）が形成されること、そして継続学習の基盤を提供できることなどが挙げられます。一方で、これには大きく2つのトレードオフが存在します。それは「過度な探索」と「計算コストの増加」です。

エントロピーが過剰になると、既に知られている高報酬の戦略を活用する代わりに、探索的な行動に偏りすぎることにより、学習が非効率になる可能性があります。また、エントロピー項の計算および最適化が必要になるため、報酬最大化だけを目的とするアルゴリズムと比べて、計算負荷が大きくなるというデメリットもあります。SACのActorネットワークは、前述のとおり、μとLog-STDという2つのベクトルを出力しますが、これらはエントロピーにどのように関係しているのでしょうか。

μは、方策がとる行動の分布の中心的な傾向を示すもので、エントロピーには直接影響しません。ただし、方策の「平均的な行動パターン」を定義する役割があります。一方、Log-STDは、行動分布の広がり（分散）や不確実性を制御するもので、エントロピーに直接影響を与えます。Log-STDの値が高いほど、行動の分布は広がり、より不確実性が高くなります。逆に、Log-STDが低いと、行動は狭い範囲に集中し、より決定論的になります。では、Log-STDにおける特定の行動の「大きさ」は、その行動が選択される確率の高さとどのような関係があるのでしょうか。

すでに述べたように、その具体的な挙動はガウス過程によって決定されますが、Log-STDが低いということは、Actorネットワークがその行動μを最適だと強く確信していることを意味する場合が多いです。これは、サンプリングされる行動のばらつきが少ないことを示しています。Log-STDの値が低いと、対応するμの周囲に行動が集中しやすくなるため、結果としてその周辺の方策がより活用される傾向になります。つまり、Log-STDの値が低いからといって、ある行動そのものの選択確率が直接高くなるわけではありませんが、行動の候補範囲が狭まることで、μ付近の行動が選ばれる可能性は相対的に高まるということになります。

エントロピーに関しては、実用上の調整もいくつかおこなわれます。まず、Log-STDはエントロピーに直接影響するため、安定した学習のためにSACでは通常、log(σ)の値を一定の範囲内に制限します。極端に高すぎたり低すぎたりするエントロピーは学習を不安定にするためです。この制限には、上記のLogProbabilities関数で使用されているzパラメータが使われます。次に、エントロピーの重み付けに関わるαの調整も、探索と活用のバランスを取るうえで極めて重要です（本稿では0.5fに固定）。このバランスをより柔軟に保つために、実際には自動α調整が用いられるケースも多く見られます。

この自動調整は、目標とするエントロピーHを基準にして実現されます。以下の式がその関係を定義します。

ここで

• αₜ：現在の温度パラメータであり、目的関数内のエントロピー項にどれだけ重みを与えるかを制御します。値が大きいほど探索が促進され、小さいほど活用が強調されます。

• αₜ₊₁：現在のエントロピーが目標と比較されたうえで更新された温度パラメータの新しい値です。

• λ：エントロピー目標からのズレに応じてαをどれだけ迅速に適応させるかを決定する、α調整プロセスにおける学習率です。

• 𝔼ₐ∼π：現在の方策からサンプリングされた行動に基づく期待値です。

• log(π(a|s))： 現在の方策において、状態sにおける行動aの対数確率です。方策がどれだけその行動に対して不確実であるか（あるいは確信しているか）を定量化します。

• Hₜₐᵣ₉ₑₜ ：方策の目標エントロピー値です。離散的な行動空間（たとえば「買い」「売り」「保持」といった、これまでに扱ったもの）の場合は、行動の数や範囲に基づいて設定されます。一方、連続的な行動空間の場合（たとえば、0.01〜0.10の範囲でスケーリングされた2つの銘柄のポジションサイズを、余剰証拠金の一定割合として同時に決定するような成行注文など）では、ターゲットエントロピーはそのスケーリングに応じて調整されることがあります。

したがって、この記事の実装では採用していないものの、自動α調整を使用することで、エージェントが環境の変化に動的に適応し、αの手動調整が不要になるとともに、あらかじめ定められた探索と活用のトレードオフを維持することで、効率的な学習が促進されます。

SACとDQNの比較

これまで、単一のニューラルネットワークを使用する別の強化学習アルゴリズム、すなわちDeep-Q-Networksを取り上げてきました。では、複数のネットワークを用いるSACを使用することで、どのような利点が得られるのでしょうか。SACの優位性を説明するために、ロボット操作タスクのユースケースを考えてみましょう。ここでのタスクは、ロボットアームが物体を把持し、指定された目標位置まで正確に移動させるというものです。アームの関節には、必要なトルクや角度調整を定量化するため、連続的な行動空間が割り当てられます。

このような状況においてDQNを使用する際の課題は、まずDQNが本質的に離散的な行動空間向けに設計されている点です。連続空間に対応させるためには行動空間を離散化する必要がありますが、高次元になるほど離散化によって必要な行動数が指数関数的に増加し、学習が極めて非効率になります。また、DQNはEpsilon-Greedy戦略によって探索と活用のバランスを取りますが、これも高次元の離散空間では十分に機能しない可能性があります。さらに、DQNは過大評価バイアスを持ちやすく、報酬のばらつきが大きい複雑な環境下では学習が不安定になる傾向があります。

一方、SACは連続行動空間のサポートを備えているため、このケースにおいてはより適しています。SACは、連続行動空間上で確率的方策を最適化するため、行動を離散化（あるいは分類）する必要がなくなり、ロボットアームの滑らかで正確な制御が可能になります。SACにおける3つのネットワークは協調して動作します。Actorネットワークは確率的方策を生成し、連続的な行動の分布（確率的な重み付け）を設定します。これにより効率的な学習が促されると同時に、過早な探索も回避されます。

一方で、CriticネットワークはツインQ値推定手法を採用しており、これにより過大評価バイアスを回避します。2つのQ関数のうち最小の値を用いてActorに誤差を逆伝播させることで、学習が安定し、より正確な結果が得られます。まとめると、エントロピー項を組み込んだ目的関数（特に、先に述べたαによる自動温度調整と組み合わせた場合）が探索を促進し、さらにSACが高次元な連続行動空間に対応できることによって得られる堅牢性と安定性は、DQNよりも明確な優位性を示します。このため、OpenAIのGymのReacherやFetchタスクにおける公開された性能結果を見ると、DQNは離散的な行動出力と探索の弱さにより、滑らかなアームの動作を実現できず、方策が次善の戦略に収束する傾向が強く見られます。一方、SACは確率的方策によって滑らかで精密な行動を生成し、タスクの完了速度を高め、衝突を減らし、オブジェクトの位置や目標地点の変化にも優れた適応力を発揮します。これも確率的方策アプローチによる効果といえるでしょう。

PythonとTensorFlow

この記事では、これまでの機械学習の記事とは異なり、PythonのTensorFlowについて詳しく説明します。MetaQuotesの親言語であるMQL5は、ウィザードによって組み立てられたEAがこれに大きく依存しているため、明らかに関連性を保ち続けています。新しい読者のために、この記事の最後に添付されているコードを使用してEAを組み立てる方法については、こちらとこちらにガイドがあります。しかし、Pythonは現在、金融モデルの開発においてMQL5の支配的地位を脅かしつつあります。簡単な調査でわかるのは、MetaQuotesがイノベーションのペースに追いつき、優位性を維持するためには、Python向けのライブラリをさらに増やす必要があるということです。 

とはいえ、私は2009年にMetaTrader 5が登場した当時をよく覚えています。その多くの利点にもかかわらず、顧客の導入は驚くほど遅かったのです。このため、Pythonのライブラリを積極的に展開し維持することに対して、MetaQuotesが慎重になる理由も理解できます。しかし、ここで進められているイノベーションの多くは、MetaQuotesではなく「顧客」—つまり、Pythonコミュニティから生まれたものです。MetaTrader 5では、注文システムではなくポジション管理が導入された事例を考えれば、MetaQuotesもこの点に急速に対応する必要があるのではないでしょうか。時間が経過すれば結果がわかるでしょうが、その間に、TensorFlowやPyTorchを使ったネットワークの開発・訓練の効率化がもたらす利点は非常に大きいのです。

私の意見では、MetaQuotesは企業スポンサーシップの検討や、貢献者として参加したり、Pandas、NumPy、Sci-Kitなどの主要なPythonライブラリのフォークプロジェクトを立ち上げたりすることができると思います。また、*.hccや.*tkcといった高度に圧縮されたファイル形式の読み取りを可能にすることも考えられます。しかし、これらは一般的な提案に過ぎません。さて、TensorFlowに話を戻すと、まず、TensorFlowは主に2つの高度なディープラーニング機能を提供します。それは、ソフトウェア面とGPU/ハードウェア面における機能です。  

MQL5はOpenCLをサポートしているため、両者が互角に渡り合えるとも言えますが、ディープラーニングモデルの構築、訓練、最適化におけるPythonの高度なライブラリやツールについては、同じことは言えません。これらのライブラリは、TensorFlow Agentsを介したSACのような複雑なアーキテクチャのサポートを提供しています。

また、強化学習を促進するための構築済みツール（テンソルエージェント以外のstable-baselineなど）を備えた豊富なエコシステムも提供しています。これにより、さまざまなモデル実装を迅速にプロトタイプ化し、テストすることができ、柔軟性と実験性が大いに向上します。再現性が高く、特にTensor-Boardなどのツールを使用してマトリックスやカーネルを視覚化・訓練することで、デバッグも容易になります。また、ONNXなどのエクスポート可能な形式との相互運用性があり、非常に広範かつ成長を続けるコミュニティサポートと定期的な更新が提供されます。

SACは、Pythonでさまざまな方法で実装できますが、ここではその中でも2つのアプローチに焦点を当てて、基本的な原則を説明します。最初の方法では、SACの3つの主要ネットワークを手動で定義し、forループの反復処理を使ってSACモデルを訓練およびテストします。2番目の方法では、先に述べたテンソルエージェントを使用し、これらは強化学習を支援するためにPythonライブラリに付属しており、特に役立ちます。

手動の反復アプローチの手順は次の通りです。TensorFlow/Kerasを用いてSACのコンポーネントを設計します。まず、Actorネットワークでは、ガウスサンプリングに基づく確率的方策を出力するニューラルネットワークを定義します。次に、Criticネットワークでは、過剰推定バイアスを管理するためにツインQ学習用の2つのQ値ネットワークを構築し、効率的な探索のためにエントロピー正規化を定義します。前述の通り、私たちの目的では、エントロピーに固定値のα(0.5)を使用しています。これらの手順をカバーする冒頭のソースコードは以下の通りです。

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

この後、TensorFlow/KerasでSACモデルを訓練する必要があります。通常、これには古いMetaTrader 5ライブラリを使用してMetaTrader端末からMetaTrader 5のデータをインポートし、そのデータをテストデータと訓練データに分割する作業が含まれます。私たちは訓練データの3分の2を使用し、残りの3分の1をテスト用データとして取っています。エポック数と訓練データのサイズに合わせて設定された、面倒で非常に非効率的なforループ内で、MetaTrader 5のトレードセットアップをシミュレートします。さらに、エントロピー項を含むSC目的関数を用いて、ActorネットワークとCriticネットワークを最適化することを目指します。これに関係するコードは以下に共有されています。

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

訓練後には、3つのネットワークで構成されたモデルをONNX形式でエクスポートすることができます。ONNX（Open Neural Network Exchangeの略）は、機械学習の相互運用性に関するオープンスタンダードを提供します。これにより、PyTorchやSciKit-Learnなど、Pythonで訓練されたモデルをこの形式にエクスポートして、より多くのプラットフォームやMQL5などのプログラミング言語で使用できるようになります。この互換性により、複雑な機械学習ロジックを再現する必要がなくなり、時間を節約でき、エラーも減少します。

ONNXをリソースとしてインポートすることで、ONNX機械学習モデルとMQL5の取引実行ロジックを含む単一のex5ファイルをコンパイルすることができ、トレーダーは複数のファイルを扱う必要がなくなります。PythonからONNXへのエクスポートプロセスにはいくつかの選択肢があり、その一つがtf2onnxですが、onnxmltools、skl2onnx、transformers.onnx（hugging face用）、mxnet.contrib.onnxなどもあります。  エクスポート段階で重要なのは、各ネットワークの入力層と出力層の形状が適切にログに記録されていることを確認することです。これは、MQL5ではこの情報が各ネットワークのONNXハンドルを正確に初期化するために重要だからです。このようにしておこないます。

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

上記のようにforループを使用するこの実装によるPythonコードのパフォーマンスは効率的とは言えず、実際にはテンソルやグラフの使用が十分に活用されていないため、MQL5と非常に似ています。しかし、バックプロパゲーションにおいて、2つのCriticネットワーク（Q値）の出力を使用してActorネットワークを訓練するという点を考慮すると、通常、TensorFlowの訓練効率を活用するために使用されるTensorFlowのfit関数は、この場合適用できません。この点が必要である理由です。というのも、Actorネットワークには、Criticネットワークや一般的なニューラルネットワークのように目標ベクトルや目標データセットが存在しないからです。

2番目のアプローチでは、TensorFlowとPythonで強化学習を処理するための組み込みライブラリであるtensor-agentsを使用します。これについては今後の記事で詳しく取り上げますが、初期化では構成されるネットワークだけでなく、環境やエージェントも考慮することが重要です。ネットワーク訓練の効率に過度に焦点を当てると、強化学習における重要な側面を見落としてしまう可能性があります。

MQL5との組み合わせ

エクスポートしたONNXモデルをMQL5のリソースにインポートすると、カスタムシグナルクラスファイルに次のヘッダーが表示されます。

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

Pythonにエクスポートしたデータは、2023年12月12日から2024年12月12日までの期間のEURUSDの1時間足データです。訓練はそのうちの3分の2、つまり8ヶ月間行い、2023年12月12日から2024年8月12日まで訓練しました。したがって、2024年8月12日以降にテストを実行できます。この期間はわずか4ヶ月強で、実際にはそれほど長くはありませんが、1時間足のデータを再利用しているため、重要な意味を持つ可能性があります。

バックプロパゲーションはすでにPythonでおこなっているため、今回のフォワードウォークテストには最適化のための特別な入力パラメータは含めていません。したがって、クラスインターフェイスは次のようになります。

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

次のように、各ONNXモデルの入力層と出力層のサイズを初期化して検証します。

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

レイヤーシェイプに関しては、SACの基本ロジックに反する変更を加えて、ONNXへのエクスポートを容易にした点に注目する必要があります。まず、Actorネットワークは、平均ベクトルと対数標準偏差ベクトルの2つのベクトルをエクスポートすることを目的としていますが、これらをONNXのレイヤーシェイプで定義するとエラーが発生しやすいため、Python内でこれらを単一のベクトルとして結合しました（上記のforループコードに示されているように）。また、Criticネットワークへの入力は、環境状態とActorネットワークによって提供される行動確率分布の2つです。これも通常は2つのテンソルとして定義できますが、簡潔にするために、これらを1つの4要素のベクトルにまとめました。出力取得関数は次の通りです。

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

これまで使用してきた9つの環境状態と3つの可能な行動というモデルを引き続き使用します。行動の確率分布を処理するためには、この記事の冒頭でコードを共有したLogProbabilities関数が必要です。  ウィザードを使用してコンパイルし、データウィンドウの残りの4か月間のテスト実行を行うと、次のレポートが表示されます。

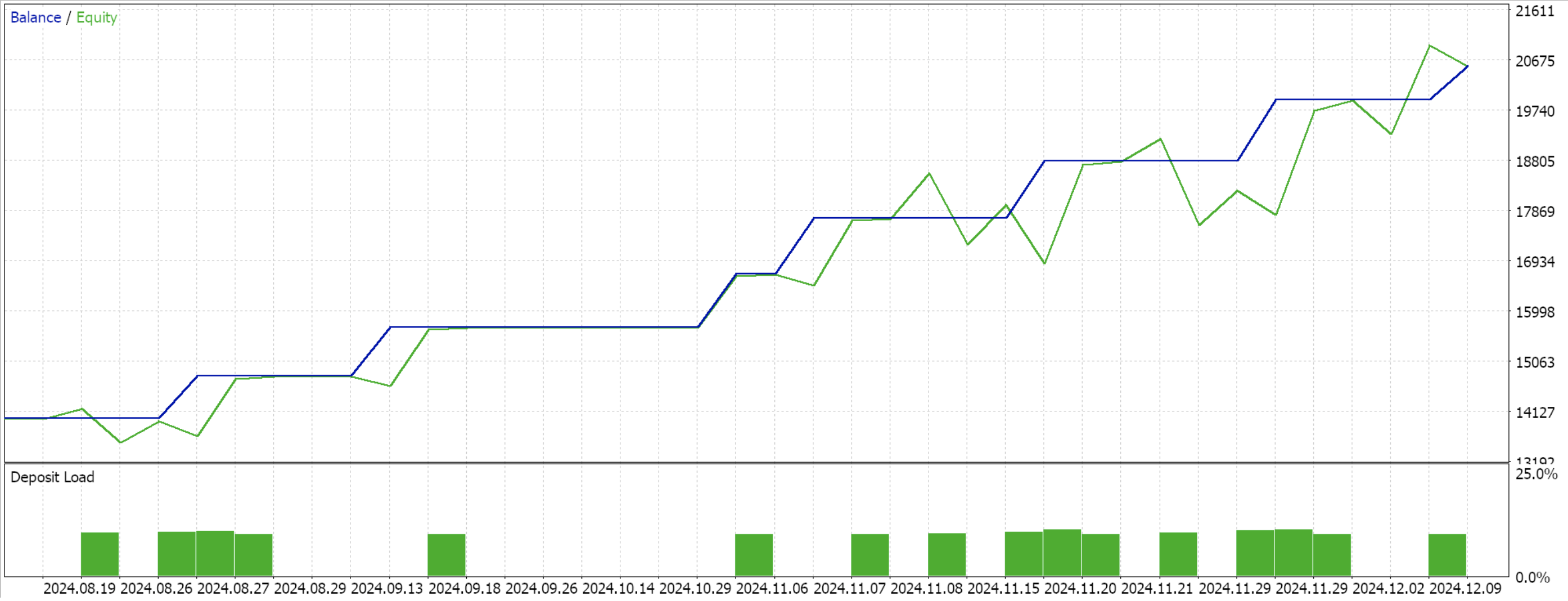
結論

テンソルエージェントライブラリを使用せず、その効率性を活用しない形で、Pythonでの強化学習SACの非常に基本的な実装シナリオを検討しました。このアプローチではSACの基本概念を説明し、複数のネットワークをペアリングする必要があり、そのうちの1つに一般的な訓練データセットがないため、バックプロパゲーションが少し時間を要する理由を強調しています。SACは、αパラメータ（ガウス分布で適用）によって調整されるエントロピーを通じて、安全に探索を促進することを目的としています。したがって、読者は目標エントロピー値を持つ自動調整などの固定されていないαを考慮し、さらに深く探求することが推奨されます。今後の記事では、これらの例についても詳しく取り上げる予定です。

ファイル名	詳細
WZ_51.mq5	ウィザードで組み立てられたEA。ヘッダーには使用されているファイルが表示されます。
SignalWZ_51.mqh	カスタムシグナルクラスファイル
EURUSD_H1_D1_critic2.onnx	Critic2ONNXネットワーク
EURUSD_H1_D1_critic1.onnx	Critic1ONNXネットワーク
EURUSD_H1_D1_actor.onnx	Actorネットワーク