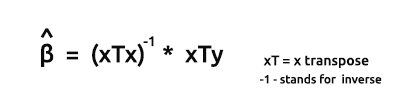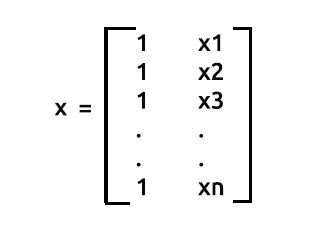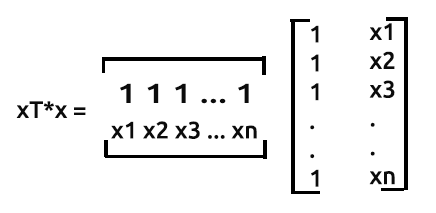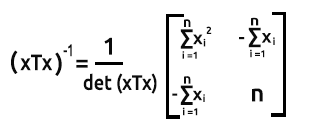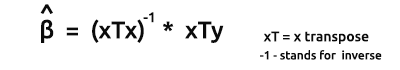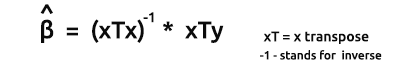Scienza dei dati e apprendimento automatico (Parte 03): Regressioni a matrice
Dopo un lungo periodo di prove ed errori, finalmente, il puzzle della regressione dinamica multipla è risolto... continua a leggere.
Se prestaste attenzione ai due articoli precedenti noterete che il problema più grande che ho avuto è programmando i modelli che potrebbero gestire più variabili indipendenti, con questo intendo gestire dinamicamente più input perché quando si tratta di creare strategie ci accingiamo a trattare con centinaia di dati, quindi vogliamo essere sicuri che i nostri modelli riescano far fronte a questa esigenza.
Matrice
Per coloro che hanno saltato le lezioni di matematica, una matrice è un array rettangolare o una tabella di numeri o altri oggetti matematici disposti in righe e colonne che viene utilizzata per rappresentare un oggetto matematico o una proprietà di tale oggetto.
Per esempio:
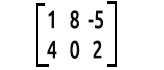
Elefante nella stanza.
Il modo in cui leggiamo le matrici è righe x colonne. La matrice di cui sopra è una matrice 2x3 che significa 2 righe, 3 colonne.
Non c'è dubbio che le matrici giocano un ruolo enorme nel modo in cui i computer moderni elaborano informazioni e calcolano grandi numeri, la ragione principale per cui sono in grado di ottenere una cosa del genere è perché i dati nella matrice sono memorizzati sotto forma di array che i computer possono leggere e manipolare. Quindi vediamo la loro applicazione nell'apprendimento automatico.
Regressione Lineare
Le matrici consentono calcoli in algebra lineare. Pertanto, lo studio delle matrici è una larga parte dell'algebra lineare, quindi possiamo usare le matrici per fare i nostri modelli di regressione lineare.
Come tutti sappiamo, l'equazione di una linea retta è
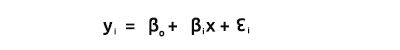
dove, ∈ sono i termini di errore, Bo e Bi sono rispettivamente i coefficienti intercetta-y e il coefficiente di pendenza
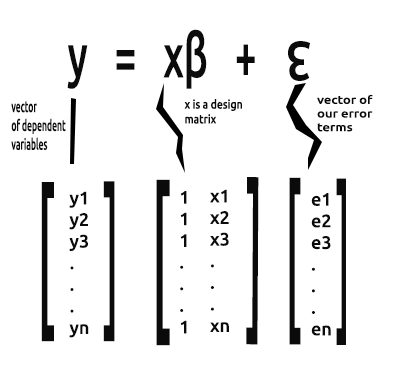
Ciò che ci interessa in questa serie di articoli d'ora in poi è la forma vettoriale di un'equazione. Eccola qui
Questa è la formulazione di una semplice regressione lineare in forma di matrice.
Per un modello lineare semplice( e altri modelli di regressione)siamo solitamente interessati a trovare i coefficienti di pendenza/ gli stimatori dei minimi quadrati.
Il vettore Beta è un vettore contenente beta.
Bo e Bi, come spiegato dalla forma scalare
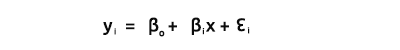
Siamo interessati a trovare i coefficienti in quanto sono molto essenziali nella costruzione di un modello.
La formula per gli stimatori dei modelli in forma vettoriale è
Questa è una formula molto importante per tutti i nerd là fuori da memorizzare. Discuteremo come trovare gli elementi sulla formula a breve.
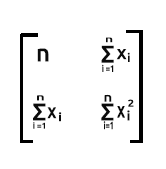
Il Prodotto di xTx darà la matrice simmetrica poiché il numero di colonne in xT è uguale al numero di righe in x, lo vedremo in azione più avanti.
Come detto precedentemente, x viene chiamata anche matrice di progettazione, ecco come apparirà la sua matrice.
Matrice di Progettazione
Come puoi vedere sulla prima colonna abbiamo messo solo i valori di 1 fino alla fine delle nostre righe in un array di Matrice. Questo è il primo passo per preparare i nostri dati per la regressione a Matrice vedrete i vantaggi di fare una cosa del genere mentre procediamo nei calcoli.
Gestiamo questo processo nella funzione Init() della nostra libreria.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //poiché è semplice regressione lineare abbiamo solo due variabili x e y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //aggiunge uno spazio della dimensione della riga per i valori occupati ArrayFill(m_xvalues,0,m_rowsize,1); //riempire la prima riga con una (s) qui è dove viene eseguita l'operazione ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //aggiunge x valori all'array iniziando dove terminavano i valori riempiti ArrayCopy(m_yvalues,y); m_debug=debugmode; }
A questo punto stampiamo i valori della matrice di progettazione, qui è il nostro output, come si può vedere solo dove terminano i valori riempiti con uno nella riga, la è dove iniziano i valori x .
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
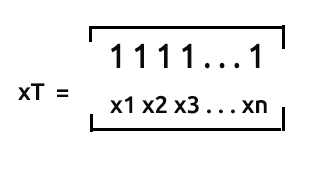
xT o x trasposta è il processo di matrice con il quale, scambiamo le righe con le colonne.
Questo significa che se moltiplichiamo queste due matrici
Salteremo il processo di trasposizione di una matrice perché il modo in cui abbiamo raccolto i nostri dati è già in forma trasposta, mentre non dobbiamo trasporre i valori x d'altra parte in modo da poterli moltiplicare con la matrice x già trasposta.
Solo uno shoutout, la matrice nx2 che non è l'array trasposto apparirà come [1 x1 1 x2 1 ... 1 xn]. Vediamolo in azione.
Annullare la trasposizione della Matrice X
La nostra matrice in forma trasposta, ottenuta da un file csv, si presenta così, quando stampata:
Matrice Trasposta
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
Il Processo di annullamento della trasposizione, dobbiamo solo scambiare le righe con le colonne, lo stesso processo opposto alla trasposizione della matrice.
int tr_rows = m_rowsize, tr_cols = 1+1; //poiché abbiamo una variabile indipendente, ne aggiungiamo una per lo spazio creato da quei valori di uno MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Le cose si complicano qui.
Mettiamo le colonne da una matrice trasposta in un posto dove si suppone siano righe e righe in un posto in cui sono necessarie colonne, l'output all'esecuzione di questo frammento di codice sarà:
Matrice Non Trasposta [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT è una matrice2xn, x è una nx2. La matrice risultante sarà una matrice 2x2
Quindi cerchiamo di capire come sarà il prodotto della loro moltiplicazione.
Attenzione: per rendere possibile la moltiplicazione matriciale, il numero di colonne nella prima matrice deve essere uguale al numero di righe nella seconda matrice.
Vedi le regole della moltiplicazione delle matrici a questo link https://it.wikipedia.org/wiki/Moltiplicazione_di_matrici
Il modo in cui la moltiplicazione viene eseguita in questa matrice è:
- Riga 1 per colonna 1
- Riga 1 per colonna 2
- Riga 2 per colonna 1
- Riga 2 per colonna 2
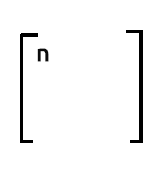
Dalle nostre matrici riga 1 per colonna1, l'output sarà la somma del prodotto di riga1 che contiene il valore di uno e il prodotto di colonna1 che contiene anche il valore di uno questo non è diverso dall'aumentare il valore di uno per uno ad ogni iterazione.
Nota:
Se si desidera conoscere il numero di osservazioni nel set di dati si può fare affidamento sul numero della prima colonna prima riga nell'output di xTx.
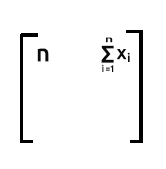
Riga 1 per colonna 2 Poiché la riga 1 contiene il valore di uno quando sommiamo il prodotto di riga1 (che ha valore di uno) e colonna2(che ha valore di x), l'output sarà la somma di x elementi poiché uno non avrà alcun effetto sulla moltiplicazione.
Riga 2 per colonna 1. L'output sarà la somma di x poiché il valore di uno di riga2 non ha effetto quando si moltiplica il valore di x che si trova sulla colonna 1.
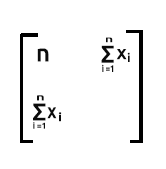
L'ultima parte sarà la somma dei valori x al quadrato.
Poiché è la somma del prodotto di riga2 che contiene valore x e colonna2 che contiene anch'essa valore x
Come potete vedere, l'output della matrice è una matrice 2x2 in questo caso.
Vediamo come funziona nel mondo reale, utilizzando il set di dati dal nostro primo articolo in regressione lineare https://www.mql5.com/it/articles/10459. Estraiamo i dati e inseriamoli in un array x per la variabile indipendente e y per le variabili dipendenti.
//dentro MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //sta per le vendite //double y[] = {23,26,30,34,43,48,52,57,58}; //soldi spesi per gli annunci //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
Ho importato la libreria CsimpleLinearRegression che abbiamo creato nel primo articolo qui
CSimpleLinearRegression lr;
perché ci sono alcune funzioni che potremmo voler usare, come quella di ottenere dati sugli array.
Cerchiamo di trovare xTx
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //ricordi?? l'output della matrice sarà riga 1 e col 2 contrassegnati in rosso
Se presti attenzione all'array xT[], puoi vedere che abbiamo appena copiato i valori x e li abbiamo memorizzati in questo array xT[], solo per chiarimento, come ho detto in precedenza il modo in cui abbiamo raccolto i dati dal nostro file csv in un array utilizzando la funzione GetDataToArray() ci fornisce dati già trasposti.
Abbiamo poi moltiplicato l'array xT[] con m_xvalues[] , i quali sono ora non trasposti, m_xvalues è l'array globale definito per i nostri valori x in questa libreria. Questo è all'interno della nostra funzione MatrixMultiply().
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //dove le moltiplicazioni verranno memorizzate if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplicazione per 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //se la matrice ha più di 2 dimensioni for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Ad essere onesti questa moltiplicazione sembra confusa e brutta soprattutto quando le cose come
k + (i*row2); j + (k*col2);
vengono utilizzate. Relax, bro! Il modo in cui ho manipolato quegli indici è per far si che possano darci l'indice di una riga e colonna specifica. Questo potrebbe essere facilmente comprensibile se avessi potuto utilizzare array bidimensionali, ad esempio Matrix[righe][colonne] che in questo caso sarebbe Matrix[i][k] ma ho scelto di non farlo perché gli array multidimensionali hanno dei limiti, quindi ho dovuto trovare una via d'uscita. Ho un semplice codice c++ linkato alla fine dell'articolo che penso possa aiutarti a capire come ho fatto oppure puoi leggere questo blog per saperne di più https://www .programiz.com/cpp-programming/examples/matrix-moltiplication.
L'output della funzione xTx utilizzando la funzione MatrixPrint() sarà
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Come si può vedere il primo elemento nel nostro array xTx ha il numero di osservazioni per ogni dato nel nostro set di dati, questo è il motivo per cui riempire la matrice di progettazione con valori di uno inizialmente sulla prima colonna è molto importante.
Ora troviamo la matrice Inversa xTx.
Matrice inversa xTx
Per trovare una Matrice inversa 2x2, per prima cosa scambiamo il primo e l'ultimo elemento della diagonale, quindi aggiungiamo segni negativi agli altri due valori.
La formula è quella riportata nell'immagine seguente:
Per trovare il determinante di una matrice det(xTx) = Prodotto della prima diagonale - Prodotto della seconda diagonale.
Ecco come possiamo trovare l'inversa nel codice mql5
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // Secondo le regole della matrice, una matrice inversa può essere trovata solo quando la //Matrice è identica a partire da una matrice 2x2, quindi questo è il nostro punto di partenza int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //il primo passo è scambiare il primo e l'ultimo valore della matrice //finora sappiamo che l'ultimo valore è uguale a arraysize meno uno int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); //prima diagonale output_mat[0] = Matrix[last_mat]; //scambiamo il primo array con l'ultimo output_mat[last_mat] = Matrix[0]; //scambiamo l'ultimo array con il primo double first_diagonal = output_mat[0]*output_mat[last_mat]; // seconda diagonale //Aggiunta dei segni negativi >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //la formula per l'inversa è 1/det(xTx) * (xtx)-1 //Il Determinante è uguale al prodotto della prima diagonale meno il prodotto della seconda diagonale double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
L'output dell'esecuzione di questo blocco di codice sarà
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 Stampiamo la matrice inversa per vedere come appare
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //l'inversa di una lr semplice sarà sempre una matrice 2x2
L'output sarà sicuramente
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Ora abbiamo l'inversa xTx andiamo avanti.
Cercando xTy
Qui moltiplichiamo xT[] con i valori y[]
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 alla fine è perché la matrice dei valori y avrà sempre una colonna Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //ricordi ancora??? come troviamo l'output della nostra matrice riga1 x colonna2 </S6>
L'output sarà sicuramente
xTy
[
10550016.7000000 46241904488.2699585
]
Fà riferimento alla formula
Ora che abbiamo xTx inversa e xTy concludiamo le cose.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //l'inversa è una matrice quadrata 2x2 mentre xty è un 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // per regressione lineare semplice la nostra matrice beta sarà 2x1
Maggiori dettagli su come abbiamo chiamato la funzione.
L'output di questo frammento di codice sarà
coefficenti
[
-5524.40278 4.49996
]
B A M !!! Questo è lo stesso risultato sui coefficienti che siamo stati in grado di ottenere con il nostro modello in forma scalare, nella parte 01 di queste serie di articoli.
Il numero al primo indice dell'array Beta sarà sempre la Costante/ Intercetta - Y. La ragione per cui siamo in grado di ottenerlo inizialmente è perché abbiamo riempito la matrice di progettazione con i valori di uno alla prima colonna, ancora una volta questo sta mostrando quanto sia importante quel processo. Lascia lo spazio per l'intercetta - y di rimanere in quella colonna.
Ora, abbiamo finito con la Regressione Lineare Semplice. Vediamo come sarà la regressione multipla. Prestate molta attenzione perché le cose possono diventare difficili e complicate a volte.
Risolto il Puzzle di Regressione Dinamica Multipla
La cosa buona di costruire i nostri modelli basati sulla matrice è che è facile scalarli senza dover cambiare molto il codice quando vengono realizzati. Il cambiamento più significativo che noterai sulla regressione multipla è come viene trovata una matrice inversa perché questa è la parte più difficile dove ho passato molto tempo a cercare di capire, lo farò nei dettagli più avanti quando raggiungeremo quella sezione, ma per ora , codifichiamo le cose di cui potremmo aver bisogno nella nostra libreria MultipleMatrixRegression.
Potremmo avere solo una libreria in grado di gestire la regressione semplice e multipla lasciandoci semplicemente inserire gli argomenti della funzione, ma ho deciso di creare un altro file in modo da rendere le cose chiare, poiché il processo sarà quasi lo stesso, affinché tu capisca i calcoli che abbiamo eseguito nella nostra sezione di regressione lineare semplice che ho appena spiegato.
Per prima cosa, codifichiamo le cose basilari che potrebbero servirci nella nostra libreria.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //memorizzare i nomi delle colonne dal file csv int rows_total; int x_columns_chosen; //Numero di x colonne scelte bool m_debug; double m_yvalues[]; //valori y o matrice di valori dipendenti double m_allxvalues[]; //tutti i valori x della Matrice di progettazione string m_XColsArray[]; //memorizzare le colonne x scelte nell'Init string m_delimiter; double Betas[]; //Array per memorizzare i coefficenti protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Questo è ciò che accade all'interno della funzione Init()
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- passare alcuni input agli input globali poiché sono riutilizzabili m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // verifica la varianza nei dati impostati dividendo la dimensione totale delle righe per il numero di colonne x selezionate, non dovrebbe esserci un richiamo if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Riempire la prima riga di una matrice di progettazione con i valori di 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Array x temporaneo ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //dopo aver riempito i valori di uno riempire lo spazio rimanente con valori di x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //non abbiamo più bisogno di questo array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //memorizzare i valori trasposti nel loro array globale prima di annularne la trasposizione MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //ne aggiungiamo uno per lasciare spazio ai valori di uno if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Maggiori dettagli su ciò che è stato fatto
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Qui otteniamo, le colonne x che uno ha selezionato (le variabili indipendenti) quando chiamiamo la funzione Init nel TestScript, quindi memorizziamo quelle colonne in un Array globale m_XColsArray , avere le colonne in un array ha dei vantaggi poiché presto le leggeremo in modo da poterle memorizzare nell'ordine corretto nell'array di tutti i valori x (matrice di variabili indipendenti)/matrice di progettazione.
Dobbiamo anche assicurarci che tutte le righe nei nostri set di dati siano le stesse perché una volta che c'è una differenza solo in una riga o colonna, tutti i calcoli falliranno.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Quindi otteniamo tutti i dati delle colonne x in una Matrice / Matrice di Progettazione / Array di tutte le variabili indipendenti (puoi scegliere di chiamarlo tra uno di questi nomi).
GetAllDataToArray(m_allxvalues);
Vogliamo anche memorizzare tutte le variabili dipendenti alla sua matrice.
GetColumnDatatoArray(y_column,m_yvalues);
Questo è il passo cruciale per preparare la matrice di progettazione per i calcoli. Aggiungendo i valori di uno alla prima colonna della nostra matrice di valori x, come detto in precedenza qui.
{
//--- Riempire la prima riga di una matrice di progettazione con i valori di 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Array x temporaneo
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //dopo aver riempito i valori di uno riempire lo spazio rimanente con valori di x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //non abbiamo più bisogno di questo array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //ne aggiungiamo uno per lasciare spazio ai valori di uno
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} Questa volta stampiamo la matrice non trasposta dopo aver inizializzato la libreria.
Questo è tutto ciò di cui abbiamo bisogno nella funzione Init per ora chiamiamolo nel nostro multipleMatRegTestScript.mq5 (linkato a fine articolo)
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
L'output dopo aver eseguito correttamente lo script sarà (questa è solo una panoramica):
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Cercando xTx
Proprio come quello che abbiamo fatto con la regressione semplice. Qui è lo stesso processo, prendiamo i valori di xT che sono i dati grezzi da un file CSV, quindi li moltiplichiamo per la matrice non trasposta.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
L'output quando la Matrice xTx viene stampata sarà
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
xTx Inversa
Questa è la parte più importante della regressione multipla, si dovrebbe prestare molta attenzione perché le cose stanno per complicarsi, stiamo per approfondire la matematica.
Quando stavamo trovando l'inversa della nostra xTx nella parte precedente, stavamo trovando l'inversa di una matrice 2x2, ma ora non ci siamo più questa volta dobbiamo trovare l'inversa di una matrice 4x4 perchè abbiamo selezionato 3 colonne come nostre variabili indipendenti, quando aggiungiamo i valori di una colonna avremo 4 colonne che ci porteranno a una matrice 4x4 quando proveremo a trovare l'inversa.
Questa volta non possiamo più usare il metodo che usavamo in precedenza per trovare l'inversa, la vera domanda è perché?
Vedi trovare matrice inversa usando il metodo del determinante che abbiamo usato in precedenza, non funziona quando le matrici sono enormi, non pouoi nemmeno usarlo per trovare l'inversa di una matrice 3x3.
Diversi metodi sono stati inventati da differenti matematici dopo aver trovato una matrice inversa, uno dei quali è il classico Metodo della Matrice trasposta coniugata ma alla mia ricerca , la maggior parte di questi metodi è difficile da codificare e a volte può creare confusione, se vuoi avere maggiori dettagli sui metodi e su come possono essere codificati dai un'occhiata a questo post del blog-https ://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/.
Di tutti i metodi ho optato per l'eliminazione di Gauss-Jordan perché ho scoperto che è affidabile, facile da codificare ed è facilmente scalabile, c'è un ottimo video https://www.youtube.com/watch?v=YcP_KOB6KpQ che spiega bene Gauss Jordan, spero possa aiutarti a cogliere il concetto.
Ok, quindi codifichiamo la Gauss-Jordan, se trovate il codice difficile da capire ho un codice c++ per lo stesso codice, nel link sotto e sul mio GitHub di cui troverete il link più giù, potrebbe aiutarci a capire come sono state fatte le cose.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //poiché l'array deve essere un quadrato // Crea una matrice identità moltiplicativa int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //matrice originale affiancata da matrice identità start = 0; for (int i=0; i<rowsCols; i++) //operazione per aggiungere una matrice identica a una originale { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //aggiunge la matrice identità alla fine ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //se non siamo sulla diagonale { /*i sta per righe mentre j per colonne, nel trovare il rapporto manteniamo le righe costanti mentre incrementando le colonne che non sono sulla diagonale dell'istruzione if sopra, questo ci aiuta a farlo accedere al valore dell'array in base a righe e colonne */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //numero righe + (numero colonne) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //primo elemento per colonna secondo per riga j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Operazione per riga per rendere la diagonale Principale a 1 /*tornando alla MatrixandIdentical Matrix Array poi eseguiremo operazioni per rendere la sua diagonale principale a 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //memorizzare la matrice inversa nell'array di output counter++; } } //--- }
Grande, quindi chiamiamo la funzione e stampiamo la matrice inversa
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
L'output sarà sicuramente,
xtx Inverso [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Ricorda che per trovare una matrice inversa deve essere una matrice quadrata, quindi ecco il motivo per cui sugli argomenti delle funzioni abbiamo l'argomento mat_order che è uguale al numero di righe e colonne.
Cercando xTy
Ora troviamo il prodotto Matrice di x trasposta e Y. Stesso processo che abbiamo fatto prima.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //ricordi!! il valore di 1 alla fine è perché abbiamo solo una variabile dipendente y
Quando l'output viene stampato, sembra così
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Cool, una matrice 1x4 come previsto.
Fare riferimento alla formula,
Ora che abbiamo tutto quello che ci serve per trovare i coefficienti, concludiamo.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); L'output sarà (ricordate ancora, il primo elemento dei nostri coefficienti/ matrice Beta è la costante o in altre parole l'intercetta-y):
Matrice dei coefficenti [ -3670.97167 2.75527 0.37952 8.06681 ]
Grande! Ora lascia che python mi dimostri che sbaglio.
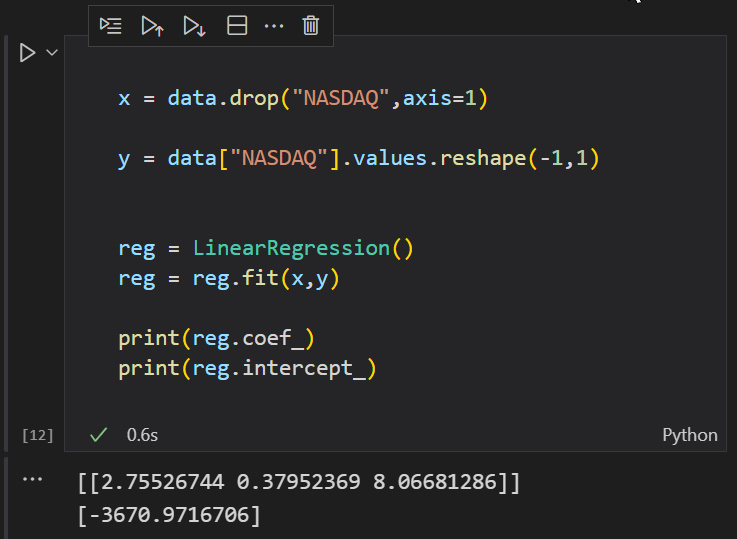
Doppio B A M ! ! ! questa volta
Ora l'avete, più modelli di regressione dinamica sono finalmente possibili in mql5, vediamo da dove tutto è iniziato.
Tutto è cominciato qui
matreg.Init(2,"1,3,4",filename);
L'idea era quella di avere una stringa di input che potesse aiutarci a mettere un numero illimitato di variabili indipendenti, e sembra che in mql5 non ci sia modo di avere *args e *kwargs da linguaggi come python che potrebbero farci inserire tanti argomenti. Quindi il nostro unico modo per farlo era usare la stringa, poi trovare una via d'uscita che ci permettesse di manipolare l'array per lasciare che solo un singolo array avesse tutti i nostri dati, poi in seguito possiamo trovare un modo per manipolarli. Vedi il mio primo infruttuoso tentativo per maggiori informazioni https://www.mql5.com/en/code/38894, il motivo per cui sto dicendo tutto questo è perché credo che qualcuno potrebbe seguire lo stesso percorso in questo o in un'altro progetto, sto solo spiegando cosa ha funzionato per me e cosa no.
Considerazioni Finali
Per quanto possa sembrare interessante che ora si possano avere tutte le variabili indipendenti che si vogliono, ricordate che c'è un limite a tutto ciò che ha troppe variabili indipendenti o colonne di dataset molto lunghe che potrebbero portare a limiti di calcolo da parte di un computer, come hai appena visto anche i calcoli della matrice potrebbero generare un numero elevato durante i calcoli ...
L'aggiunta di variabili indipendenti a un modello di regressione lineare multipla aumenterà sempre la quantità di varianza nella variabile dipendente tipicamente espressa come r-quadrato, perciò l'aggiunta di troppe variabili indipendenti senza alcuna giustificazione teorica può comportare un modello sovradimensionato.
Ad esempio, se avessimo costruito un modello come abbiamo fatto sul primo articolo di queste serie, basato su due sole variabili, essendo NASDAQ dipendente e S&P500 indipendente, la nostra precisione sarebbe potuta essere superiore al 95%, ma potrebbe non essere così su questo perché ora ne abbiamo 3 indipendenti.
È sempre una buona idea verificare l'accuratezza del tuo modello dopo che è stato realizzato, prima di costruire un modello è necessario verificare se esiste anche una correlazione tra ogni variabile indipendente e l'obiettivo.
Realizza sempre il modello su dati che hanno dimostrato di avere una forte relazione lineare con la variabile target.
Grazie per la lettura! Il mio repository GitHub è linkato qui https://github.com/MegaJoctan/MatrixRegressionMQL5.git.
Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/10928
 Sviluppare un Expert Advisor per il trading da zero (Parte 7): Aggiunta dei Volumi al Prezzo (I)
Sviluppare un Expert Advisor per il trading da zero (Parte 7): Aggiunta dei Volumi al Prezzo (I)
 Imparare come progettare un sistema di trading con ATR
Imparare come progettare un sistema di trading con ATR
 Sviluppare un Expert Advisor per il trading da zero (Parte 8): Un salto concettuale
Sviluppare un Expert Advisor per il trading da zero (Parte 8): Un salto concettuale
 Impara a progettare un sistema di trading tramite ADX
Impara a progettare un sistema di trading tramite ADX
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso