Algoritmi di ottimizzazione della popolazione: Semina e Crescita degli Alberelli (Saplings Sowing and Growing up - SSG)

Contenuti:

1. Introduzione
2. L’Algoritmo
3. Risultati del test

1. Introduzione

Tutti gli organismi viventi in natura sono soggetti a precise leggi. Questo li aiuta a sopravvivere in condizioni ambientali mutevoli. Esistono diverse opzioni per l'adattabilità delle piante all'ambiente. Alcune di loro sono in grado di tollerare i cambiamenti stagionali, altre si adattano alla mancanza di umidità, alle temperature alte o basse e all'assenza di impollinatori. Uno degli organismi più stabili tra le piante sono gli alberi, alcuni dei quali sono in grado di vivere per più di 50 mila anni formando colonie.

La natura è un campo di ispirazione inesauribile per molte idee efficaci nello sviluppo e nell'invenzione di metodi computazionali. In effetti, l'evoluzione computazionale è una proiezione dell'evoluzione in simulazioni al computer. Esistono molti metodi di ottimizzazione ispirati ai processi che avvengono in natura, come il calcolo evolutivo, l'immunologia artificiale, i metodi di popolazione e altri. La SSG è fondamentalmente definita come un processo iterativo di generazione e combinazione che lavora con un giardino di soluzioni potenziali chiamate piantine. L'algoritmo Saplings Sowing and Growing (SSG) è stato proposto da A. Karci e coautori nel 2002. L'algoritmo si ispira all'evoluzione degli alberi in crescita e modella la crescita e la ramificazione degli alberi.

2. L’Algoritmo

L'algoritmo è uno dei pochi a non avere una chiara descrizione da parte degli autori (vengono fornite solo disposizioni e idee generali). Anche gli operatori dell'algoritmo presentati dagli autori non sono istruzioni pronte per l'implementazione algoritmica del programma. Non ci sono istruzioni chiare sugli alberi figli e dei genitori e sulla loro interazione. Non ci sono requisiti per l'ordine di esecuzione degli operatori e ogni utente può modificare l'ordine per ottenere una piantina migliore.

In senso lato, SSG non è un algoritmo di ottimizzazione, ma un insieme generale di regole progettate per integrare altri algoritmi e migliorare la qualità dell'ottimizzazione. In altre parole, SSG è un componente aggiuntivo per qualsiasi algoritmo evolutivo di popolazione, quindi ho spazio per l'immaginazione e l'opportunità di sperimentare un'implementazione specifica dell'algoritmo di ottimizzazione. Ho applicato alcuni dei miei pensieri e delle mie esperienze durante la scrittura di algoritmi precedenti e li ho utilizzati per lavorare con SSG. I risultati degli esperimenti sono presentati di seguito per il giudizio del lettore.

Per iniziare a comprendere l'algoritmo, dobbiamo pensare ad un albero come ad un agente di ottimizzazione. Un albero è una soluzione a un problema di ottimizzazione, in cui ogni ramo rappresenta un parametro ottimizzato del problema. Nella Figura 1 è riportata un'illustrazione astratta e artistica degli alberi figlio e genitore. Il tronco dell'albero è un insieme di parametri da ottimizzare. Ogni ramo è un parametro ottimizzato separato, la cui lunghezza è limitata dall’intervallo di valori consentiti del parametro corrispondente. La direzione dei rami non ha importanza e viene mostrata nella figura solo per evidenziare la loro differenza.

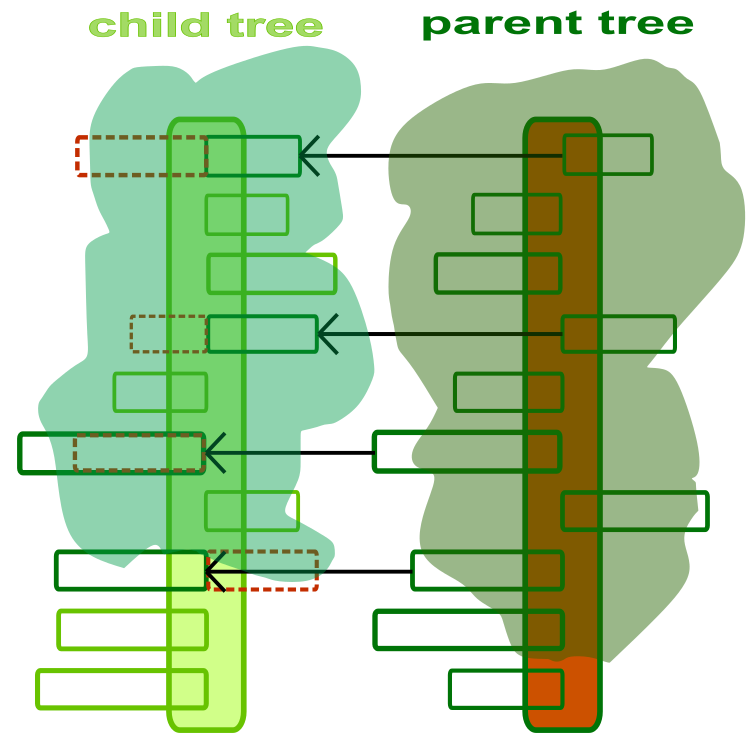
Figura 1. Albero figlio e genitore. La linea tratteggiata indica i rami figlio sostituiti da quelli genitore.

Pertanto, i rami dell’albero sono le coordinate degli alberi nello spazio di ricerca.

L'algoritmo SSG è composto da operatori di variazione che generano nuove soluzioni - candidati per il bacino comune delle soluzioni. I principali operatori di variazione sono l'incrocio, la ramificazione e la vaccinazione. La piantatura delle piantine deve essere effettuata ad una distanza equidistante in ogni direzione (ovest, est, nord, sud), e questa è la fase iniziale del metodo. Quando le coordinate (parametri ottimizzati) sono molto più di tre, la piantatura "uniforme" è una semplice distribuzione casuale di piantine nello spazio di ricerca. Poi le piantine crescono, si incrociano, si ramificano e il processo di vaccinazione ha luogo.

Consideriamo le fasi e gli operatori dell'algoritmo SSG:

1) Piantare le piantine.

Lo spazio di ricerca può essere considerato come un giardino di piantine e quindi tutte le piantine devono essere distribuite uniformemente nel giardino. Quando si seminano le piantine, l'agricoltore si limita a seminarle ad una distanza uguale l'una dall'altra, in modo che le piantine crescano più velocemente senza interferire l'una con l'altra. Per risolvere il problema simulando la coltivazione delle piantine, le soluzioni arbitrarie da generare inizialmente devono essere distribuite uniformemente nello spazio di ricerca valido.

Quando ci sono due o tre coordinate, non c'è problema a distribuire uniformemente le piantine, ma quando le coordinate sono molto più di tre, è più facile usare una distribuzione casuale. In pratica, con un numero ridotto di coordinate, non è necessario occuparsi della distribuzione uniforme delle piantine, poiché il compito non rappresenta un grosso problema e si sa che la soluzione sarà ottenuta con un'elevata precisione. Pertanto, indipendentemente dal numero di coordinate dell'algoritmo, utilizzeremo una distribuzione casuale delle piantine nel giardino.

2) Crescita delle piantine (alberi), tre operatori eseguiti in sequenza.

2.1) Incrocio (Crossing).

Lo scopo dell'operatore "crossing" è quello di creare una nuova piantina a partire da piantine già esistenti, scambiando informazioni tra di loro. L'incrocio è essenzialmente un trapianto di una copia di un ramo dall'albero genitore a quello figlio (Figura 1). Per ogni coppia di piantine viene utilizzato un coefficiente di incrocio diverso, che rappresenta la probabilità di incrocio. La probabilità di incrocio dipende dalla distanza tra le piantine in una coppia: maggiore è la distanza, minore è la probabilità di incrocio. L'operatore crossing è un metodo molto importante dell'algoritmo che fornisce meccanismi combinatori. La combinazione di informazioni tra gli agenti può migliorare significativamente la qualità complessiva dell'algoritmo di ottimizzazione.

2.2) Ramificazione.

L'operatore modella la crescita dei rami. La crescita può essere positiva (allungamento) o negativa (essiccamento). "Per far crescere un ramo in un punto qualsiasi del corpo dell’alberello, non deve esserci un ramo vicino che sia germogliato in precedenza". Si tratta di una descrizione approssimativa dell'operatore da parte degli autori dell'algoritmo. In realtà, questo processo è più semplice e chiaro di quanto possa sembrare a prima vista e consiste nella modifica dei rami esistenti dell'albero figlio (il metodo specifico di modifica non è specificato).

La modifica di ogni singolo ramo è tanto più probabile quante più iterazioni sono trascorse tra l'iterazione corrente e quella in cui è stata effettuata l'ultima modifica del ramo. I miei esperimenti hanno dimostrato l'inefficienza di questo operatore. Inoltre, non ci sono indicazioni dirette sull'uso del metodo di modifica, e ho preso l'iniziativa in questa materia e ho applicato la modifica della lunghezza del ramo secondo la legge di distribuzione del volo di Levy. La modifica verrà eseguita con la probabilità e l'intensità specificate come parametri esterni dell'algoritmo.

2.3) Vaccinazione.

Il processo di vaccinazione avviene tra due piantine differenti in caso di somiglianza tra le piantine. La somiglianza tra le piantine influisce sul successo del processo di vaccinazione ed è proporzionale alla media aritmetica della distanza ponderata. L'operatore è simile all'operatore di incrocio (crossing) e consiste nello scambio dei rami, fornendo all'algoritmo un ulteriore modo per combinare le informazioni tra gli agenti. L'operatore sarà evidenziato nell'articolo, ma questo operatore è commentato nei codici sorgente e i risultati dei test sono presentati senza la sua partecipazione, poiché la vaccinazione peggiora i risultati.

3) Calcolo della fitness degli alberi.

4) Piantare nuove piantine nel giardino.

Le piantine ottenute con l'aiuto degli operatori dell'incrocio, della ramificazione e della vaccinazione sono soluzioni temporanee (giardino filiale). In questa fase, è necessario selezionare le n migliori piantine (un parametro esterno dell'algoritmo) e collocarle nel giardino, sostituendo gli n alberi peggiori del giardino. Va notato che la sostituzione con piantine avverrà in ogni caso, anche se sono peggiori dei peggiori alberi del giardino.

Questo è un buon momento per dare un'occhiata al codice dell'algoritmo dell'albero crescente, avvicinandoci sempre di più all'emozionante culmine di questo studio - la revisione dei risultati dei test.

Pertanto, è conveniente rappresentare ogni albero come una struttura Garden, che servirà come base per la creazione di un giardino fiorito. In questo algoritmo non c'è niente di più semplice dell'entità "albero", che ha bisogno di due soli componenti: le coordinate con c[] e il valore di fitness f.

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

La classe C_AO_SSG dell'algoritmo SG non è nulla di speciale. Tutto questo è molto familiare grazie agli algoritmi considerati in precedenza. Nella classe verranno dichiarati i membri e i metodi per operare sui giardini genitore e figlio. Un giardino temporaneo serve per far funzionare il metodo di ordinamento, perché dobbiamo ordinare sia il giardino figlio che quello genitore. Dichiariamo un array delle migliori coordinate della soluzione nel suo complesso e del miglior valore di fitness, oltre a variabili costanti per memorizzare i parametri esterni dell'algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

Nel metodo di inizializzazione Init (), si alloca la memoria per gli array e si assegnano i valori ai parametri costanti. Poiché il parametro seedlingsReplacementP è impostato in frazioni della dimensione del giardino (da 0,0 a 1,0), che è responsabile del numero di piantine figlio da piantare nel giardino genitore, deve essere convertito in una rappresentazione intera della dimensione del giardino. Azzeriamo il flag iniziale della piantina da giardino e inizializziamo la variabile decisionale globale con il valore double più piccolo possibile.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo pubblico chiamato a ogni iterazione, Sowing(), è la semina. Alla prima iterazione, quando l'algoritmo è appena in funzione, spargiamo le piantine nel giardino (spazio di ricerca) in modo casuale con una distribuzione uniforme. Qui vediamo che le coordinate sono generate in modo casuale nell'intervallo consentito tra il minimo e il massimo dei parametri ottimizzati, controlliamo che non ci sia un'uscita dall'intervallo consentito, quindi portiamo i valori delle coordinate in accordo con la fase di ottimizzazione.

In questa fase, l'adattabilità delle piantine è minima. Impostiamo il vettore vec[]. Ci servirà per scalare gli incrementi dei rami nell'operatore di ramificazione ed anche per calcolare la massima distanza euclidea possibile r nello spazio di ricerca. Sarà utile nell'operatore di incrocio per determinare la probabilità che dipende dalla distanza tra coppie di alberi.

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

Poi, nel metodo Sowing(), gli operatori di incrocio, ramificazione e vaccinazione vengono eseguiti alla seconda iterazione e alle successive. Gli operatori vengono eseguiti in sequenza nel ciclo principale:

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

Quando si eseguono gli operatori, i concetti di "figlio" e "genitore" sono molto arbitrari. In realtà, sono solo fonti di informazioni di base per la creazione di una nuova piantina. La nuova piantina copia tutti i rami (come ricorderete, i rami sono i parametri da ottimizzare) dall'albero figlio e ne riceve di nuovi dal genitore.

Per ogni nuova piantina, vengono selezionati individualmente due alberi dal giardino, uno figlio e uno genitore, in modo casuale, con uguale probabilità per tutti gli alberi del giardino. In altre parole, tutti gli alberi possono partecipare alla creazione di una nuova piantina con uguale probabilità e indipendentemente dalla loro fitness. Pertanto, 'figlio' e 'genitore' sono semplicemente gli indici dei due alberi originali nell'array del giardino dei genitori.

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

Il primo operatore è l'incrocio (crossing), o coniugazione (accoppiamento). Per eseguire l'operatore di incrocio su una piantina con indice t, è necessario calcolare lo spazio euclideo tra l'albero figlio e quello genitore con gli indici 'child' e 'parent':

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

La distanza euclidea è coinvolta nell'equazione per il calcolo della probabilità di incrocio attraverso la normalizzazione della distanza massima euclidea possibile r nello spazio di ricerca:

eM = 1.0 - (ed / r);

Generare un numero casuale nell'intervallo [0,0;1,0]. Se il numero risultante rientra nella probabilità calcolata eM, si esegue l'incrocio - copiando i rami dall'albero genitore con la probabilità probabMatingOperator per ogni ramo. Se la probabilità eM non è soddisfatta, la piantina procederà all'esecuzione dell'istruzione successiva con tutti i rami originali dell'albero figlio.

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Successivamente, viene eseguito l'operatore di ramificazione. La ramificazione prevede una variazione dei rami - allungamento e accorciamento. Questo è l'operatore principale che crea rami di una nuova lunghezza. Gli operatori rimanenti svolgono solo un ruolo combinatorio e non creano nuovi rami unici. Per ogni ramo, generiamo un numero casuale nell'intervallo [0,0;1,0] e se la probabilità di probabBranchOperator è soddisfatta, allora eseguiamo la ramificazione cambiando la lunghezza del ramo secondo la legge di distribuzione dei voli di Levy considerata qui.

Come si può notare, non tutti i rami degli alberelli saranno modificati. Saranno modificati indipendentemente dal fatto che il ramo sia stato copiato dall'albero genitore nell'istruzione precedente o che sia il ramo figlio originale. Dopo aver modificato il ramo, controlliamo che non ci siano valori fuori intervallo e lo allineiamo alla fase di ottimizzazione.

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Il terzo operatore è la vaccinazione. L'operatore di vaccinazione è stato concepito dagli autori, apparentemente, come un operatore combinatorio e dovrebbe essere eseguito per copiare i rami dall'albero genitore nel caso in cui i rami dell'albero figlio e dell'albero genitore differiscano di più della differenza media tra tutti i rami della coppia. Suona molto complicato, ma l'uso di questo operatore è di scarsa utilità pertanto viene commentato nei file sorgenti. In questo caso, non posso agire come un esperto e quindi ammetto che potrei non aver compreso correttamente questo operatore.

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

È arrivato il momento dell'ultima, ma non meno importante, operazione dell'algoritmo - la germinazione. Eseguiamo il secondo metodo pubblico Germination () che è obbligatorio eseguire ad ogni iterazione.

Se la prima iterazione sta volgendo al termine (lo sapremo sicuramente dal flag "sowing"), allora significa che il giardino del genitore è vuoto. Piantiamo tutti gli alberelli del giardino figlio in quello genitore semplicemente copiando tutti i giovani alberi uno per uno. Successivamente, ordiniamo il giardino genitore in base al valore di fitness utilizzando il metodo Sorting(). Se gli alberi sono ordinati, l'albero all'indice 0 avrà la migliore fitness e potremo aggiornare la soluzione globale migliore se non è già la migliore.

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

Più avanti nel codice, arriveremo solo alla seconda e alle successive iterazioni dell'algoritmo, poiché il flag "sowing" è stato prudentemente impostato su "true". Alla seconda iterazione e a quelle successive, il giardino figlio deve essere ordinato prima che le piantine vengano trasferite nel giardino genitore e gli alberi peggiori vengano sostituiti. Controlliamo se la soluzione globale è migliorata e copiamo le migliori n piantine alla fine del giardino dei genitori.

In conclusione, rimane solo da ordinare il giardino dei genitori. I nuovi membri della società dei giardini saranno in grado di sostituire gli alberi delle vecchie generazioni per compiacerci con i fiori risultato della soluzione dei problemi di ottimizzazione.

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);

3. Risultati del test

Risultati del banco di prova SSG:

2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    5 Rastrigin's; Func cicli 10000 risultato: 80.7052793572295
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.99998
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    25 Rastrigin's; Func cicli 10000 risultato: 77.3972262608643
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.95900
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    500 Rastrigin's; Func cicli 10000 risultato: 52.24518909141432
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.64735
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    5 Forest's; Func cicli 10000 risultato: 1.331178589711503
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.75298
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    25 Forest's; Func cicli 10000 risultato: 1.019329018074209
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.57658
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    500 Forest's; Func cicli 10000 risultato: 0.25410121872226443
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.14373
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    5 Megacity's; Func cicli 10000 risultato: 6,4
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.53333
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    25 Megacity's; Func cicli 10000 risultato: 4.504
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    Punteggio: 0.37533
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    500 Megacity's; Func cicli 10000 risultato: 1.2336
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Punteggio 0.10280
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Tutti i punteggi 5.09109

SSG non ha troppi parametri, sebbene sia una conseguenza della modifica dell'algoritmo (SSG originale ha ancora meno parametri). Tuttavia, tutti i parametri meritano un'attenzione eccezionale. Nei test sono stati utilizzati i seguenti parametri. Come ricorderete, in ogni articolo fornisco i migliori parametri dell'algoritmo che producono il massimo risultato possibile nei test.

C_AO_SSG:50;0.3;0.5;0.4;0.1

input int NumberTrees_P = 50; - numero di alberi nel giardino. Non ho fatto esperimenti con questo parametro lasciando il valore predefinito (il predefinito nei miei esperimenti). Nel caso del valore 100, l'algoritmo produce risultati aggregati ancora migliori, ma la capacità di scalare diminuisce a causa della diminuzione del numero di iterazioni ammissibili per giardino, data la dimensione del giardino stesso. Un giardino con un gran numero di rami non ha il tempo di evolversi.

input double SeedlingsReplacement_P = 0,3; - proporzione di piantine del giardino figlio da trasferire a quello genitore.
input double ProbabMatingOperator_P = 0,5; - probabilità di incrociare (copiare rami dall'albero genitore) se la probabilità che tiene conto della distanza tra una coppia di alberi è soddisfatta.
input double ProbabBranchOperator_P = 0,4; - probabilità di ramificazione (crescita/riduzione dei rami). Si tratta di un parametro importante che influisce in modo significativo sulle prestazioni dell'algoritmo (in generale, tutti i parametri sono importanti).
input double PowerBranchOperator_P = 0,1; - forza di ramificazione. Si tratta di un fattore di scalatura nella dimensione dei parametri da ottimizzare, 1,0 o più significherà la crescita dei rami fino ai confini del giardino, 0,0 - nessuna crescita dei rami, vale a dire che le nuove dimensioni dei rami non aumenteranno e l'algoritmo degenera in un semplice strumento combinatorio (che è probabilmente una grande idea per l'utilizzo di SSG, tuttavia sono necessarie ulteriori ricerche in merito).

Se si presta attenzione all'animazione dell'algoritmo SSG sulle funzioni di prova, si noterà l'assenza di pattern di movimento degli alberi nel giardino, si notano solo alcuni "raggruppamenti" negli estremi locali. Tuttavia, l'elevata qualità della convergenza è immediatamente percepibile se confrontata con gli algoritmi considerati in precedenza. Anche la stabile riproducibilità dei risultati è degna di nota.

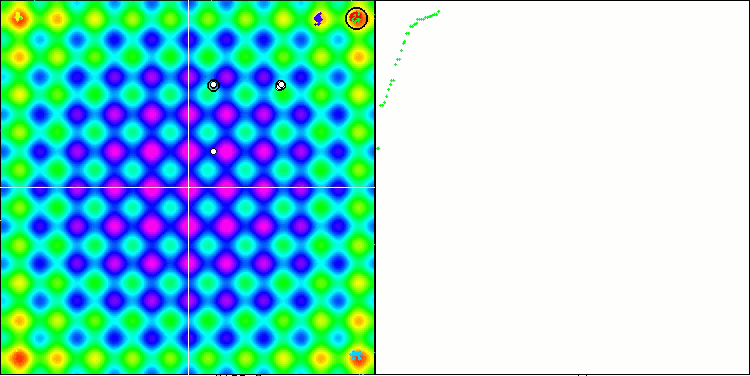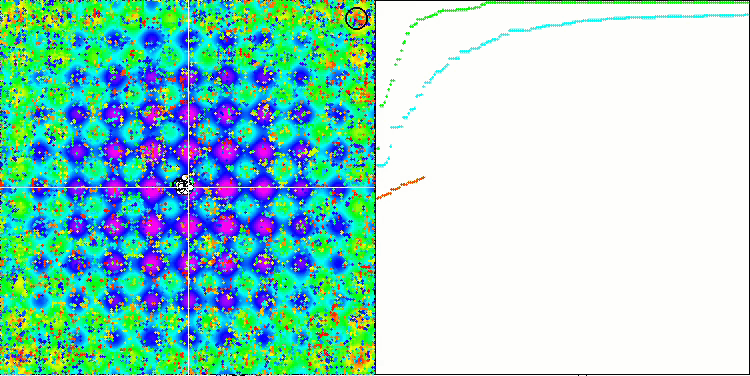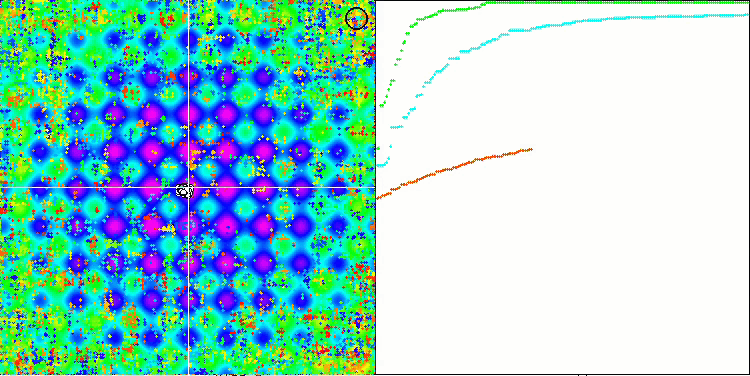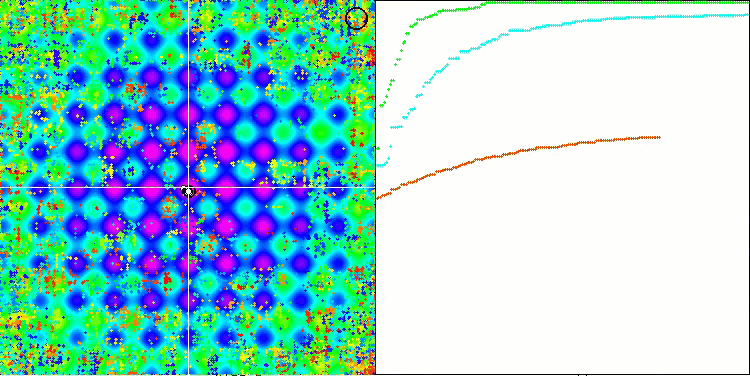
  SSG sulla funzione test Rastrigin.

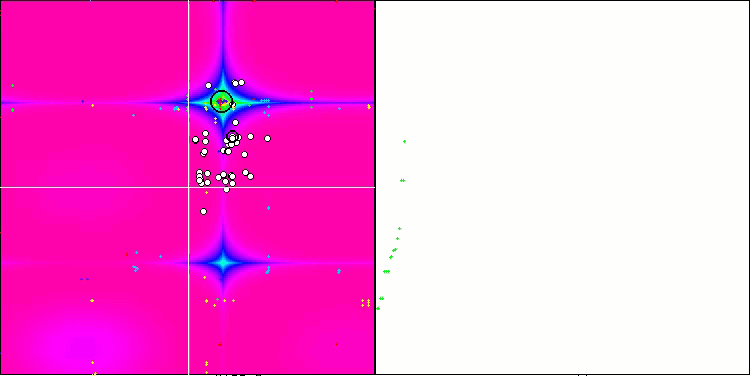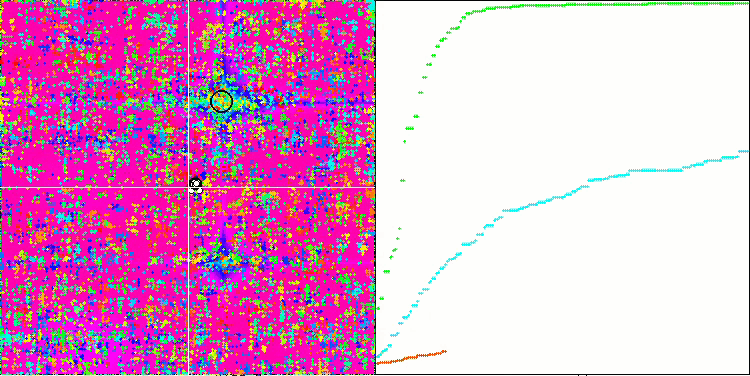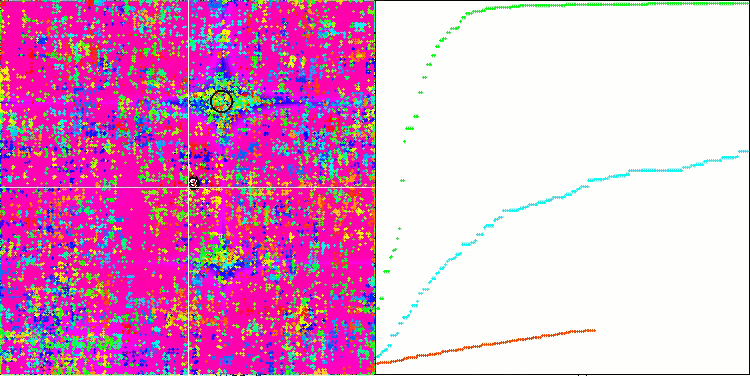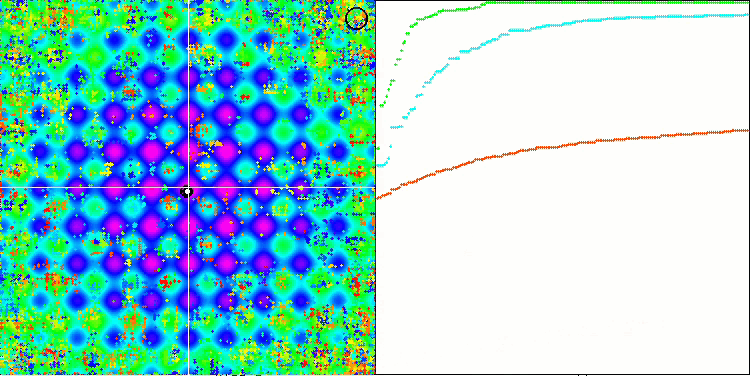
  SSG sulla funzione di test forest.

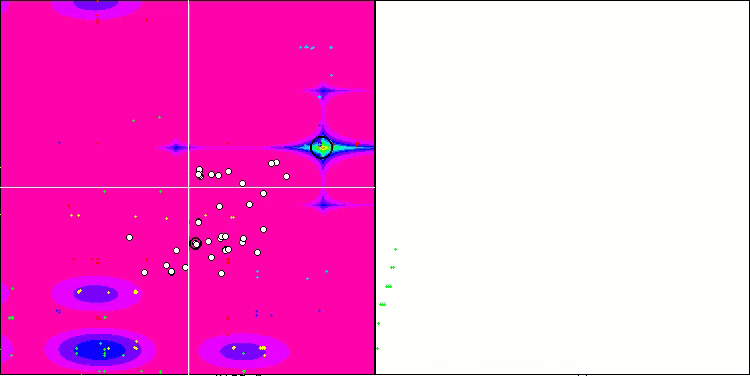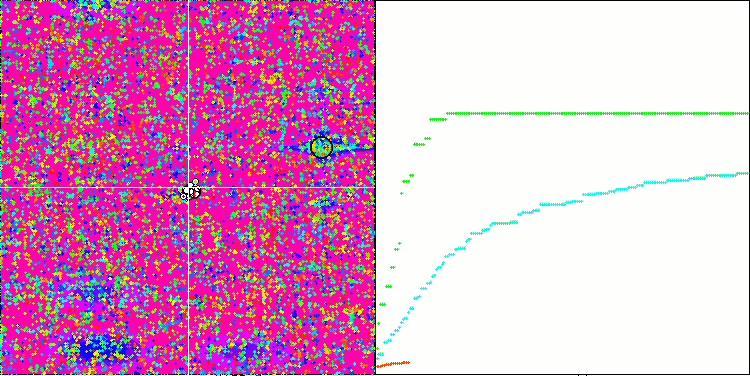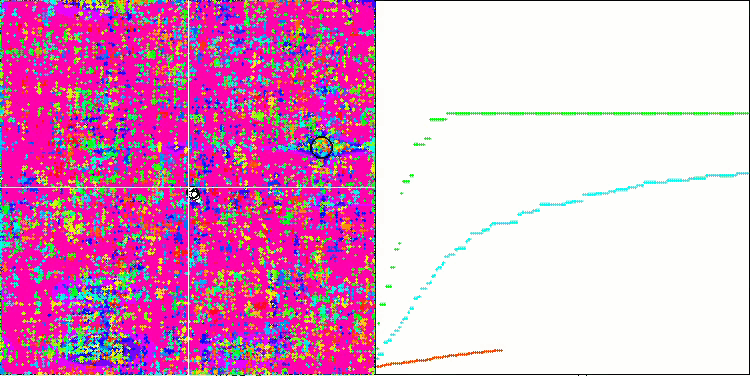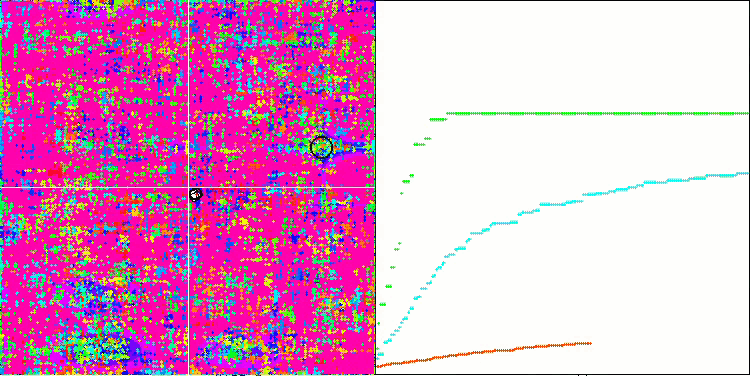
  SSG sulla funzione di test Megacity.

Passiamo a discutere i risultati dell'algoritmo SSG. C'è sicuramente qualcosa da dire. L'algoritmo ha trionfalmente fatto irruzione al primo posto della classifica lasciandosi alle spalle i rivali! L'algoritmo non utilizza direttamente la conoscenza del fitness per modificare gli alberi decisionali. La fitness è necessaria solo per ordinare il giardino figlio e il giardino genitore, quindi è ancora più sorprendente che l'algoritmo sia stato in grado di mostrare risultati così notevoli nei test.

È come se la squadra dei ciechi battesse quella dei vedenti in orientamento. L'algoritmo ha superato i partecipanti della tabella in quattro test su sei, mentre non è rimasto indietro nei test in cui non era leader. SSG ha mostrato il vantaggio più impressionante sui rivali nella funzione discreta Megacity, superando il concorrente più vicino HS di quasi il 60%! Questo dimostra l'eccellente scalabilità dell'algoritmo. Il miglior risultato di scalabilità è stato osservato anche sulla funzione di test “sharp” Forest. SSG ha superato il miglior concorrente in questo test (ACOm) di quasi il 30%.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
SSG	semina e crescita degli alberelli	1.00000	1.00000	0.65914	2.65914	0.70823	0.94522	1.00000	2.65345	0.71532	0.85412	1.00000	2.56944	100.000
HS	Ricerca dell'armonia	0.99676	0.95282	0.57048	2.52006	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	93.370
ACOm	Ottimizzazione della colonia di formiche M	0.34611	0.17985	0.20182	0.72778	0.85966	1.00000	0.77362	2.63327	1.00000	0.88484	0.05606	1.94090	66.407
IWO	Ottimizzazione delle piante infestanti	0.95828	0.67083	0.35295	1.98207	0.68718	0.46349	0.31773	1.46840	0.75912	0.39732	0.33289	1.48933	61.691
COAm	Algoritmo di ottimizzazione del cuculo M	0.92400	0.46794	0.30792	1.69987	0.55451	0.34034	0.16526	1.06012	0.67153	0.30326	0.17083	1.14561	48.226
FAm	Algoritmo della lucciola M	0.59825	0.33980	0.20290	1.14095	0.47632	0.42299	0.49790	1.39721	0.21167	0.25143	0.35258	0.81568	41.042
ABC	Colonia di api artificiali	0.78170	0.32715	0.24656	1.35541	0.50591	0.21455	0.13344	0.85390	0.47444	0.23609	0.13926	0.84979	37.204
BA	Algoritmo del pipistrello	0.40526	0.63761	1.00000	2.04287	0.15275	0.17477	0.25989	0.58741	0.15329	0.06334	0.17371	0.39034	36.703
GSA	Algoritmo di ricerca gravitazionale	0.70167	0.45217	0.00000	1.15384	0.26854	0.36416	0.33204	0.96475	0.51095	0.32436	0.00000	0.83531	35.834
BFO	Ottimizzazione del foraggiamento batterico	0.67203	0.30963	0.13988	1.12154	0.35462	0.26623	0.20652	0.82736	0.42336	0.30519	0.18932	0.91786	34.700
MA	Algoritmo della scimmia	0.33192	0.33451	0.17340	0.83983	0.03684	0.07891	0.08932	0.20508	0.05838	0.00383	0.10720	0.16941	13.185
FSS	Ricerca del banco di pesci	0.46812	0.25337	0.13383	0.85532	0.06711	0.05013	0.06516	0.18240	0.00000	0.00959	0.08283	0.09242	12.089
PSO	Ottimizzazione dello sciame di particelle	0.20449	0.08200	0.08478	0.37127	0.13192	0.10486	0.21738	0.45415	0.08028	0.02110	0.01957	0.12095	9.696
RND	Casuale	0.16826	0.09743	0.09495	0.36065	0.07413	0.04810	0.04715	0.16938	0.00000	0.00000	0.04922	0.04922	4.916
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.02557	0.25179	1.000

Riepilogo

Caratteristiche di SSG: nessun requisito di differenziabilità e continuità della funzione ottimizzata, nessuna restrizione sul tipo di rappresentazione e codifica applicata. L'algoritmo non utilizza le informazioni di fitness dei singoli agenti e la soluzione migliore nel suo complesso. Grazie a queste caratteristiche, SSG può essere facilmente applicata a vari problemi di ottimizzazione, anche molto complessi. SSG può essere sicuramente raccomandata per l'uso nei problemi dei trader e nell'apprendimento automatico. Al momento in cui scriviamo, l'algoritmo Semina e Crescita degli Alberelli è il leader indiscusso per qualità di convergenza, stabilità dei risultati e scalabilità.

La Fig. 2 mostra i risultati dei test dell'algoritmo.

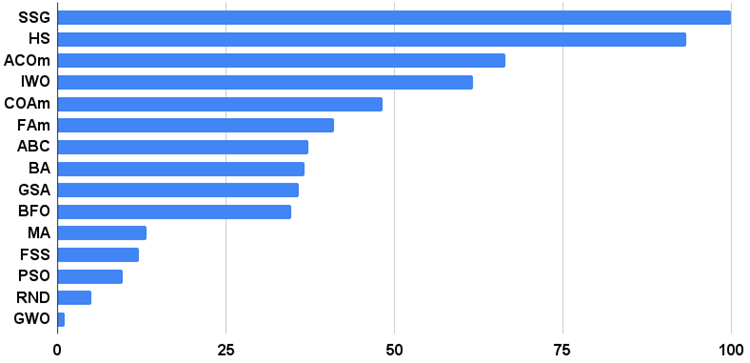
Figure 2. Istogramma dei risultati dei test degli algoritmi

Pro e contro dell’algoritmo SSG:

Pro:
1. Facile implementazione.
2. Eccellente convergenza su tutti i tipi di funzioni, senza eccezioni.
3. Scalabilità impressionante.

Contro:
1. Molte opzioni di personalizzazione, sebbene siano intuitivamente chiare.

Ogni articolo presenta un archivio che contiene le versioni aggiornate dei codici degli algoritmi per tutti gli articoli precedenti. L'articolo si basa sull'esperienza accumulata dall'autore e rappresenta la sua opinione personale. Le conclusioni e i giudizi si basano sugli esperimenti.