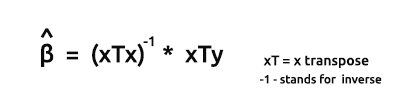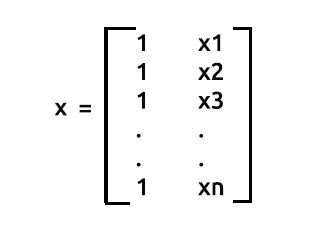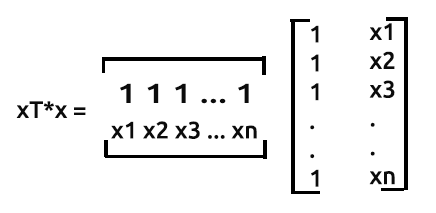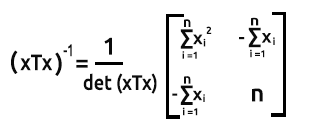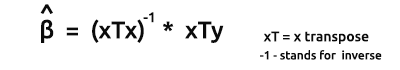데이터 과학 및 머신 러닝(파트 03): 행렬 회귀(Matrix Regressions)
오랜 시행착오 끝에 마침내 다중 동적 회귀의 수수께끼가 풀렸습니다...계속 읽어 보세요.
앞의 두 기사를 보시면 제가 가진 가장 큰 문제는 더 많은 독립 변수를 처리할 수 있는 프로그래밍 모델이라는 것을 알아 채셨을 것입니다. 즉 전략을 만들 때 우리는 수백 가지의 데이터를 처리해야 하기 때문에 우리의 모델이 더 많은 입력을 동적으로 처리할 수 있어야 한다는 의미입니다. 따라서 우리의 모델이 이러한 요구에 대처할 수 있는지 확인하여야 합니다.
회귀 모델 의 행렬
행렬
수학 수업을 건너뛴 사람들을 위해, 행렬은 수학적 객체 또는 그러한 객체의 속성을 나타내는 데 사용되는 행과 열로 배열된 직사각형의 배열 또는 숫자 또는 기타 수학적 객체의 표입니다.
예를 들어:
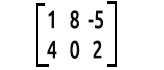
방안의 코끼리.
행렬을 읽는 방법은 행 x열입니다. 위의 행렬은 2행3열을 의미하는 2x3 행렬입니다.
행렬이 현대 컴퓨터에서 정보를 처리하고 커다란 수를 계산하는 방식에 큰 역할을 한다는 것은 의심의 여지가 없습니다. 이러한 일을 할 수 있는 주된 이유는 행렬의 데이터가 컴퓨터가 읽고 조작할 수 있는 배열의 형태로 저장되기 때문입니다. 이제 머신 러닝에서 행렬을 사용하는 것에 대해 살펴보겠습니다.
선형 회귀
행렬은 선형 대수학에서 계산에 사용될 수 있습니다. 행렬은 선형 대수학의 큰 부분입니다. 우리는 행렬을 사용하여 선형 회귀 모델을 만들 수 있습니다.
우리 모두가 알다시피 직선의 방정식은
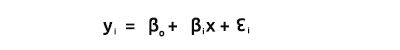
여기서 ∈은 오차항, Bo 및 Bi는 각각 계수 y절편 및 기울기 계수 입니다.
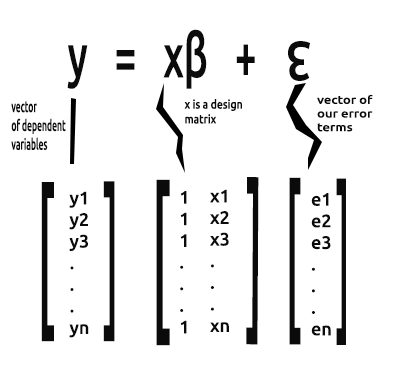
이 일련의 기사에서 우리가 관심을 갖는 것은 방정식의 벡터 형태입니다. 다음과 같습니다
이것은 행렬 형태의 단순 선형 회귀의 공식입니다.
단순 선형 모델(및 기타 회귀 모델)의 경우 우리는 일반적으로 slope coefficients/ ordinary least square estimators를 찾는 데 노력합니다.
벡터 베타는 베타를 포함하는 벡터입니다.
Bo 및 B1, 방정식에서 설명한 대로
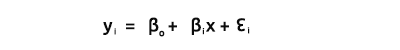
계수는 모델을 구축하는 데 매우 중요하기 때문에 우리는 계수를 찾는 데 관심이 있습니다.
벡터 형식 모델의 추정량 공식은 다음과 같습니다.
이것들은 기억해야 할 매우 중요한 공식입니다. 뒤에서 공식에서 요소를 찾는 방법에 대해 논의할 것입니다.
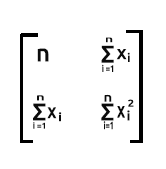
xTx 의 곱은xT의 열 수가x 의 행 수와 같기 때문에 대칭 행렬을 만듭니다. 이것은 나중에 실제로 보게 될 것입니다.
앞서 말했듯이 x는 디자인 행렬이라고도 하며 행렬의 모양은 다음과 같습니다.
디자인 행렬
맨 처음 열에서 볼 수 있듯이 행렬 배열의 행 끝까지 값 1만 넣었습니다. 이것은 행렬 회귀를 위해 데이터를 준비하는 첫 번째 단계입니다. 계산에 대해 더 자세히 알아보면 작업을 이렇게 수행하는 이점을 알게 될 것입니다.
라이브러리의 Init() 함수에서 이 프로세스를 처리합니다.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
여기까지 디자인 행렬 값을 인쇄할 때 출력되는 결과입니다. 1이 채워진 값이 x 값이 시작하는 행에서 끝나는 것을 볼 수 있습니다.
[ 0]1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[693]1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[714]1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[756]4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449]4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470]4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
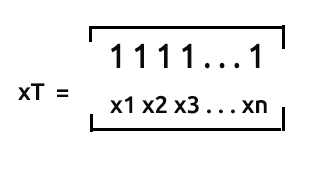
xT 또는 x 전치는 행렬에서 행을 열로 바꾸는 프로세스입니다.
즉 이 두 행렬을 곱하면
데이터를 수집하는 방식이 이미 전치된 형식이었으므로 여기서는 행렬 전치의 과정을 건너뛸 것입니다. 반면에 이미 전치된 x 행렬과 곱할 수 있도록 x 값을 전치 해제해야 합니다.
간단히 말해, 전치된 배열이 아닌 행렬 nx2 는 다음과 같습니다. [1 x1 1 x2 1 ... 1 xn]. 실제로 해 봅시다.
X Matrix 전치 해제
csv 파일에서 얻은 전치된 형식의 매트릭스는 프린트 하면 다음과 같습니다.
전치 행렬
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
이것을 전치 해제 하는 과정은 행을 열로 바꾸면 됩니다. 행렬 전치와 반대 과정입니다.
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
여기서 일이 까다로워집니다.
행렬의 전치 해제
행이 필요한 위치에 전치된 행렬의 열을 배치하고 열이 필요한 곳에 행을 배치합니다. 이 코드 스니펫을 실행할 때의 출력은 다음과 같습니다:
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT는2xn행렬이고x는nx2입니다. 그 결과 행렬은2x2행렬이 됩니다.
이들 곱셈의 결과가 어떻게 보이는지 알아보도록 하겠습니다.
주의: 행렬의 곱셈이 가능하려면 첫 번째 행렬의 열 수가 두 번째 행렬의 행 수와 같아야 합니다.
이 링크 https://en.wikipedia.org/wiki/Matrix_multiplication에서 행렬 곱셈의 규칙을 참조하세요.
이 행렬에서 곱셈이 수행되는 방식은 다음과 같습니다:
- 1행 1열
- 1행 2열
- 2행 1열
- 2행 2열
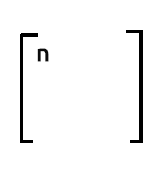
행렬 행 1 시간 열 1에서 출력은1이란 값을 포함하는 1행의 곱과 1이란 값을 포함하는 1열의 곱의 합이 됩니다. 이것은 값을 1씩 증가시키는 것을 반복하는 것과 마찬가지입니다.
메모:
데이터 세트의 관측값 수를 알고 싶다면 xTx출력에서 첫 번째 행의 첫 번째 열에 있는 숫자에 의해 가능합니다.
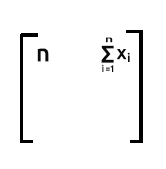
1행 곱하기 2열. 1행(값 1) 과 2열 (값 x)의 곱을 합산할 때 1행에는 1의 값이 포함되어 있으므로 출력은 x 항목의 합이 됩니다. 하나는 곱셈에 영향을 주지 않기 때문입니다.
2행 곱하기 1열. 2행의 값을 1열에 있는 x 값에 곱할 때 미치는 영향이 없으므로 출력은 x의 합이 됩니다.
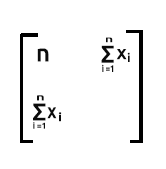
마지막 부분은 제곱될 때 x 값의 합입니다.
x 값을 포함하는 2행과 x 값도 포함하는 2열의 곱의 합이기 때문에
보시다시피, 이 경우 행렬의 출력은2x2행렬입니다.
선형 회귀https://www.mql5.com/ko/articles/10459와 관련한 첫 번째 기사에서 가져온 데이터 세트를 사용하여 이것이 실제 세계에서 어떻게 작동하는지를 살펴봅시다. 데이터를 추출하고 독립 변수는 x, 종속 변수는 y를 배열에 넣습니다.
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
첫 번째 기사에서 만든 CsimpleLinearRegression 라이브러리를 가져왔습니다.
CSimpleLinearRegression lr;
여기에는 데이터를 배열로 가져오는 것과 같은 특정 함수가 있기 때문입니다.
xTx를 찾아봅시다
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? the output of the matrix will be the row1 and col2 marked in red
배열 xT[]를 주의 깊게 살펴보면 x 값을 복사하여 이xT[]배열에 저장했음을 알 수 있습니다. 앞서 말했듯이 csv 파일에서 배열로 데이터를 수집하는 GetDataToArray() 함수를 사용하는 것이고 이를 통해 이미 전치된 데이터를 얻을 수 있습니다.
그런 다음 배열 xT[]에 현재 전치되지 않은 m_xvalues[] 를 곱했습니다. m_xvalues는 이 라이브러리의 x 값에 대해 전역적으로 정의된 배열입니다. 이것은 MatrixMultiply()함수의 내부입니다.
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
솔직히 말해 이 곱셈은 특히 다음과 같은 경우에 혼란스럽고 추하게 보입니다.
k + (i*row2); j + (k*col2);
이미 사용된 것. 걱정 마세요! 이러한 인덱스를 조작한 방법은 특정 행과 열에 인덱스를 제공할 수 있도록 하는 것입니다. 이 경우Matrix[i][k]가 되는Matrix[rows][columns]와 같은 2차원 배열을 사용했다면 쉽게 이해했을 것입니다. 그러나 다차원 배열에는 제한이 있으므로 사용하지 않았습니다. 그러므로 무언가 다른 방법을 찾아야 했습니다. 기사 끝에 링크된 간단한C++코드가 있습니다. 이 코드는 이 작업을 수행한 방법을 이해하는 데 도움이 될 것입니다. 또는 https://www.programiz.com/cpp-programming/examples/matrix-multiplication 에서 보다 자세한 내용을 이해할 수 있을 것입니다.
MatrixPrint() 함수를 사용하여 성공적으로xTx 함수를 수행한 결과는 다음과 같습니다.
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
xTx배열의 첫 번째 요소에는 데이터 세트의 각 데이터에 대한 관측값 수가 있으므로 이것이 바로 첫 번째 열에서 처음에 1의 값으로 디자인 행렬을 채우는 것이 매우 중요한 이유입니다.
이제 xTx 행렬의 역행렬을 구해 보겠습니다.
xTx 행렬의 역
2x2 행렬의 역행렬을 찾기 위해 먼저 대각선의 첫 번째 요소와 마지막 요소를 바꾼 다음 다른 두 값에 음수 기호를 추가합니다.
공식은 아래 이미지와 같습니다:
행렬의 행렬식을 찾으려면 det(xTx)=첫 번째 대각선의 곱 - 두 번째 대각선의 곱입니다.
다음은 mql5 코드에서 역함수를 찾는 방법입니다.
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
이 코드 블록을 실행한 결과는 다음과 같습니다.
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 행렬의 역행렬을 프린트하여 어떻게 보이는지 살펴보겠습니다.
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
출력은 반드시
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
이제 xTx 역이 있습니다. 계속 진행하겠습니다.
xTy 찾기
여기에서 xT[]와 y[]값을 곱합니다.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
출력은 반드시
xTy
[
10550016.7000000 46241904488.2699585
]
공식 참조
이제 xTx inverse와 xTy 가 있습니다. 이상입니다.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
함수를 호출한 방법에 대한 자세한 내용.
이 코드 조각의 출력은 다음과 같습니다.
계수
[
-5524.40278 4.49996
]
짱 !!! 이것은 이 기사 시리즈의 Part 01에서 스칼라 형식의 모델로 얻을 수 있었던 계수에서와 동일한 결과입니다.
Array Betas의 첫 번째 인덱스에 있는 숫자는 항상 상수/Y 절편입니다. 처음부터 이를 얻을 수 있었던 이유는 디자인 매트릭스를 1에서 첫 번째 열의 값으로 채웠기 때문입니다. 이는 이 프로세스가 얼마나 중요한지를 다시 한 번 보여줍니다. y 절편이 해당 열에 머물 수 있는 공간을 남깁니다.
이제 우리는 단순 선형 회귀 분석을 완료했습니다. 다중 회귀가 어떻게 생겼는지 봅시다. 다소 까다롭고 복잡하고 시간이 걸릴 수 있으므로 세심한 주의를 기울이십시오.
다중 동적 회귀 퍼즐 해결
매트릭스를 기반으로 모델을 만들 때 좋은 점은 모델을 빌드할 때 코드를 많이 변경하지 않고도 쉽게 확장할 수 있다는 것입니다. 다중 회귀에서 알아야할 중요한 변화는 행렬의 역행렬을 찾는 방법입니다. 왜냐하면 이것이 제가 오랫동안 알아내려고 노력해 온 가장 어려운 부분이기 때문입니다. 나중에 해당 섹션에 도달하면 자세히 설명하겠지만 지금은 MultipleMatrixRegression라이브러리에 필요할 수 있는 것들을 코딩해 봅시다.
함수 인수를 입력하도록 하여 단순 회귀와 다중 회귀를 모두 처리할 수 있는 라이브러리를 하나만 가질 수 있지만 좀더 명확하게 하기 위해 다른 파일을 만들기로 결정했습니다. 왜냐하면 제가 방금 설명한 단순 선형 회귀 섹션에서 수행한 계산을 이해했다면 그 과정은 거의 비슷하기 때문입니다.
먼저 라이브러리에 필요한 기본 사항을 코딩해 보겠습니다.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
이것은 Init() 함수 내부에서 일어나는 일입니다.
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
수행한 작업에 대한 자세한 내용
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
여기서 우리는 TestScript에서 Init 함수를 호출할 때 선택한 x 열(독립 변수)을 얻은 다음 해당 열을 전역 배열 m_XColsArray에 저장합니다. 열을 배열로 갖는 것은 이들을 곧 읽고 모든 x 값(독립 변수 Matrix)/설계 행렬의 배열에 적절한 순서로 저장하는데 도움이 되기 때문입니다.
데이터 세트의 모든 행이 동일한지도 확인해야 합니다. 한 행이나 열에만 차이가 있으면 모든 계산이 실패하기 때문입니다.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
그런 다음 모든 x 열 데이터를 모든 독립 변수에 대한 하나의 Matrix / Design Matrix / Array로 가져옵니다(이 이름들 중에서 하나라고 부를 수도 있습니다).
GetAllDataToArray(m_allxvalues);
또한 모든 종속 변수를 해당 행렬에 저장할 수도 있습니다.
GetColumnDatatoArray(y_column,m_yvalues);
이것은 계산을 위해 디자인 매트릭스를 준비하는 중요한 단계입니다. 앞에서 말했듯이 x 값 행렬의 첫 번째 열에 1의 값을 더합니다.
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} 이번에는 라이브러리를 초기화할 때 전치되지 않은 행렬을 프린트합니다.
이것이 지금 Init 함수에 필요한 전부입니다. multipleMatRegTestScript.mq5(기사 끝에 링크 됨)에서 호출해 보겠습니다.
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
스크립트가 성공적으로 실행되면 출력은다음과 같습니다(개요일 뿐입니다):
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
xTx 찾기
단순 회귀에서 수행한 것과 마찬가지로 여기에서도 동일한 프로세스를 따릅니다. csv 파일에서 원시 데이터인 xT 값을 가져온 다음 전치되지 않은 행렬과 곱합니다.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
xTx Matrix가 프린트 될 때의 결과는 다음과 같습니다.
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
예상대로 작동합니다.
xTx 역
이것은 다중 회귀의 가장 중요한 부분입니다. 수학에 대해 더 깊이 들어가면서 상황은 더 복잡해 지기 때문에 세심한 주의를 기울여야합니다.
이전 부분에서 xTx의 역수를 찾을 때 우리는 2x2 행렬의 역수를 찾았습니다. 그러나 지금은 4x4 행렬의 역행렬을 찾고 있는 것입니다. 왜냐하면 우리는 독립변수로 3개의 열을 선택했기 때문입니다. 우리가 역을 찾으며 한 열의 값을 추가할 때 4x4 행렬로 이어지는 4개의 열을 갖게 됩니다.
이번에는 역함수를 찾기 위해 이전에 사용했던 방법을 더 이상 사용할 수 없습니다. 왜 일까요?
행렬의 역행렬 찾기를 참조하십시오. 이전에 사용한 행렬식 방법은 행렬이 거대할 때 작동하지 않습니다. 3x3 행렬의 역행렬조차 찾을 수 없습니다.
여러 수학자들이 행렬의 역행렬을 찾은 후 여러 방법을 발명했습니다. 그 중 하나는 고전적인 Adjoint 방법이지만 저의 연구에 따르면 이러한 방법의 대부분은 코딩하기 어렵고 혼란스럽기도 합니다. 이에 대한 자세한 내용과 코딩 방법에 대한 내용을 보려면 이 블로그 게시물을 참조하세요. https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/.
저는 Gauss-Jordan 제거를 선택하였는데 모든 방법 중에서 가장 신뢰할 수 있고 코딩하기 쉽고 쉽게 확장할 수 있다는 이유 때문이었습니다. 여기 이에 대한 훌륭한 비디오가 있습니다.https://www.youtube.com/watch?v=YcP_KOB6KpQ 가우스 조던에 대해 잘 설명하고 있으니 개념 파악에 도움이 되었으면 합니다.
자, 이제 Gauss-Jordan을 코딩해 보겠습니다. 이해하기 어려운 코드를 발견했다면 C++ 코드가 있고 아래에 링크된 저의 GitHub에도 사용하면 작업이 어떻게 수행되었는지 이해하는 데 도움이 될 수 있습니다.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
좋습니다. 함수를 호출하고 행렬의 역을 출력해 보겠습니다.
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
출력은 반드시,
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
행렬의 역행렬을 찾는 것은 정방 행렬이어야 하므로 함수 인수에 행의 수와 열의 수가 같은 mat_order 인수가 있다는 점을 기억하십시오.
xTy 찾기
이제 x 전치와 Y의 행렬을 찾아봅시다.이전과 동일한 과정입니다.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
결과가 출력되면 다음과 같이 보입니다.
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
예상대로 1x4 행렬입니다.
공식을 참조하십시오,
행렬 형태의 의 계수 공식
계수를 찾는 데 필요한 모든 것이 준비되었습니다.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); 결과는 다음과 같습니다(다시 기억하십시오. 계수/베타 행렬의 첫 번째 요소는 상수 또는 다른 말로 y절편):
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
좋습니다! 이제 제가 틀렸다는 것을 증명할 파이썬을 찾아 주세요.
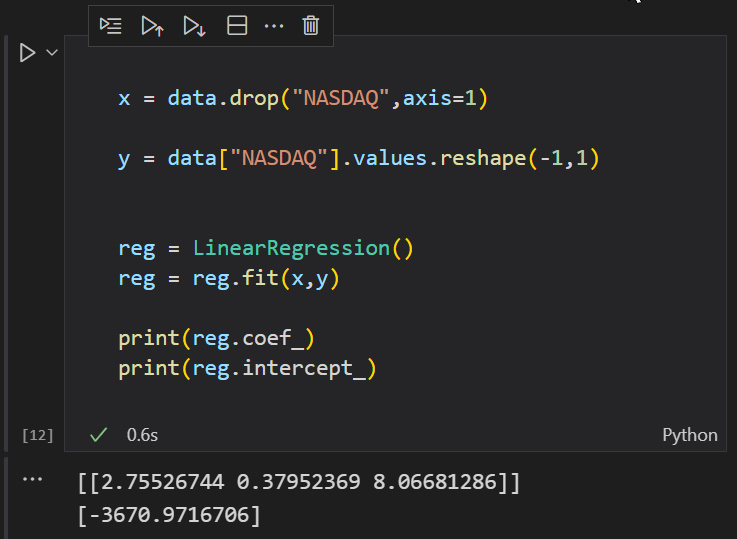
이번엔 더블 짱 ! ! !
이제 mql5에서 여러 다중 회귀 모델이 마침내 가능해졌습니다. 이제 이 모든 것이 어디에서 시작되었는지 살펴보겠습니다.
모든 것은 여기에서 시작되었습니다
matreg.Init(2,"1,3,4",filename);
아이디어는 무제한의 독립 변수를 넣는 데 도움이 되는 문자열 입력을 갖는 것이었고 mql5에서는 python과 같은 언어에서 많은 인수를 입력하게 할 수 있게 하는 *args나 *kwargs를 가질 수 있는 방법이 없는 것처럼 보입니다. 따라서 이를 수행하는 유일한 방법은 문자열을 사용한 다음 단일 배열에 모든 데이터가 포함되도록 배열을 조작할 수 있는 방법을 찾은 다음 나중에 조작하는 방법을 찾는 것입니다. 자세한 내용은https://www.mql5.com/ko/code/38894 저의 첫 번째 실패한 시도를 참조하십시오. 제가 이 모든 것을 말하는 이유는 누군가가 이 프로젝트나 다른 곳에서 저와 같은 길을 갈지도 모르기 때문입니다. 저는 저에게 효과가 있었던 것과 그렇지 않은 것을 설명한 것입니다.
마침말
여러분이 원하는 만큼 많은 독립 변수를 가질 수 있다는 것이 멋있게 들리겠지만 너무 많은 독립 변수를 갖는 것에는 한계가 있거나 너무 긴 데이터 세트 열은 방금 본 것처럼 컴퓨터의 계산 한계로 이어질 수 있음을 기억하십시오. 행렬 계산은 계산 중에 많은 숫자들이 나올 수 있습니다.
다중 선형 회귀 모델에 독립 변수를 추가하면 일반적으로 r-제곱으로 표현되는 종속 변수의 분산의 양이 항상 증가하므로 이론적으로 정당성 없이 너무 많은 독립 변수를 추가할 경우 모델이 과적합 될 수 있습니다.
예를 들어 이 시리즈의 첫 번째 기사에서 했던 것처럼 모델을 구축했다면 두 개의 변수 중 NASDAQ이 종속 변수가 되고 S&P500이 독립 변수가 되면 정확도는 95% 이상일 수 있지만 이제 3개의 독립 변수가 있으므로 이 변수에서는 그렇지 않을 수 있습니다.
모델을 구축한 후에는 항상 모델의 정확성을 확인하는 것이 좋습니다. 또한 모델을 구축하기 전에 각 독립 변수와 대상 간에 상관 관계가 있는지를 확인해야 합니다.
언제나 대상 변수와 강력한 선형 관계가 있는 것으로 입증된 데이터를 기반으로 모델을 작성하십시오.
읽어 주셔서 감사합니다! 저의 GitHub 저장소는 여기입니다. https://github.com/MegaJoctan/MatrixRegressionMQL5.git.
MetaQuotes 소프트웨어 사를 통해 영어가 번역됨
원본 기고글: https://www.mql5.com/en/articles/10928
 Expert Advisor 개발(파트 7): 가격에 볼륨 추가 (I)
Expert Advisor 개발(파트 7): 가격에 볼륨 추가 (I)
 ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
 ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
ADX 기반의 트레이딩 시스템을 설계하는 방법 알아보기
 이동 평균으로 할 수 있는 것
이동 평균으로 할 수 있는 것