Scienza dei Dati e Apprendimento Automatico (Parte 01): Regressione Lineare
Introduzione
La tentazione di formulare teorie premature su dati insufficienti è la rovina della nostra professione.
"Sherlock Holmes"
Scienza dei Dati
È un campo interdisciplinare che utilizza metodi scientifici, processi, algoritmi, e sistemi per estrarre conoscenze e informazioni da dati rumorosi, strutturati e non strutturati e applicare tali conoscenze e informazioni fruibili dai dati in un'ampia gamma di ambiti applicativi.
Uno studioso di dati è qualcuno che crea codice di programmazione e lo combina con la conoscenza statistica per creare informazioni dai dati.
Cosa aspettarsi da queste serie di articoli?
- Teoria (Come nelle equazioni matematiche): La teoria è molto importante nella scienza dei dati. È necessario conoscere gli algoritmi in modo approfondito e come un modello si comporta e perché si comporta in un certo modo, comprendendo che è molto più difficile che codificare l'algoritmo stesso.
- Esempi pratici in MQL5 e python.
Regressione Lineare
È un modello predittivo utilizzato per trovare la relazione lineare tra una variabile dipendente e una o più variabili indipendenti.
La regressione lineare è uno degli algoritmi principali utilizzato da molti algoritmi come:
- Regressione logistica che è un modello basato sulla regressione lineare
- Support Vector Machine, questo famoso algoritmo nella scienza dei dati è un modello lineare
Cos'è un modello
Un modello non è altro che un suffisso.
Teoria
Ogni linea retta che passa per il grafico ha un'equazione
Da dove prendiamo questa equazione?
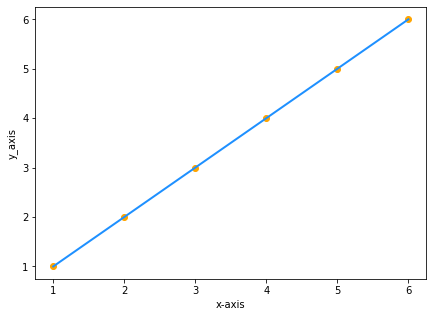
Supponiamo di avere due set di dati con gli stessi valori di x and y:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
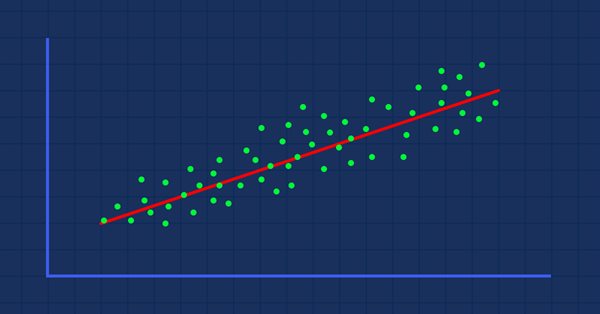
Tracciando i valori sul grafico sarà:
Poiché y è uguale a x, l'equazione della nostra linea sarà y=x giusto? SBAGLIATO
Considerato,
y = x è matematicamente la stessa cosa di y = 1x, questo è abbastanza diverso nella scienza dei dati, la formula per la linea sarà y=1x, dove 1 è l'angolo formato tra la linea e l' asse x nota anche come pendenza della linea
ma,
pendenza = variazione di y / variazione di x = m(indicato come m)
La nostra formula ora sarà y = mx.
Infine, dobbiamo aggiungere una costante alla nostra equazione, ovvero un valore di y quando x era zero in altre parole il valore di y quando la linea ha attraversato l'asse y.
Alla fine,
la nostra equazione sarà y = mx + c (Questo non è altro che un modello nella scienza dei dati)
dove c è l'intercetta y
Regressione Lineare Semplice
La regressione lineare semplice ha una variabile dipendente e una variabile indipendente. Qui stiamo cercando di capire la relazione tra due variabili, ad esempio, come cambia il prezzo di un'azione con il cambio di una media mobile semplice.
Dati Complessi
Supponiamo di avere valori casuali su un grafico di dispersione di un indicatore, confrontati con il prezzo delle azioni (qualcosa che accade nella vita reale).
In questo caso, il nostro Indicatore/variabile indipendente potrebbe non essere buono a predire il nostro prezzo delle azioni/variabile dipendente.
Il primo filtro che devi applicare nei tuoi set di dati è eliminare tutte le colonne che non sono fortemente correlate al tuo obiettivo poiché non costruirai il tuo modello lineare con quelle.
Costruire un modello lineare con dati correlati non lineari è un enorme errore fondamentale; stai attento!
La relazione può essere positiva o negativa, ma deve essere forte e poiché stiamo cercando relazioni lineari, è quello che vuoi trovare.
Quindi, come misuriamo la forza tra la variabile indipendente e il target? Utilizziamo una metrica conosciuta come coefficiente di correlazione.
Coefficente di Correlazione
Codifichiamo uno script per creare un set di dati da utilizzare come esempio principale per questo articolo. Troviamo i Predittori del NASDAQ.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Nello script abbiamo raccolto il prezzo di chiusura del NASDAQ, i valori di RSI a 13 periodi, l'S&P 500 e la Media Mobile a 50 periodi. Dopo aver raccolto con successo i dati in un file CSV, visualizziamo i dati in python sul notebook Jupyter di anaconda, per coloro che non hanno anaconda installato sulla propria macchina puoi eseguire il tuo codice python di data science utilizzato in questo articolo su google colab.
Prima di poter aprire un file CSV creato dal nostro script di test, devi convertirlo nella codifica UTF-8 in modo che possa essere letto da python. Apri il file CSV con blocco note quindi salvalo codificandolo come UTF-8. Sarà una buona cosa copiare il file nella directory esterna in modo che venga letto separatamente da Python quando ti colleghi a quella directory, usando pandas leggiamo il file CSV e memorizziamolo nella variabile dati.
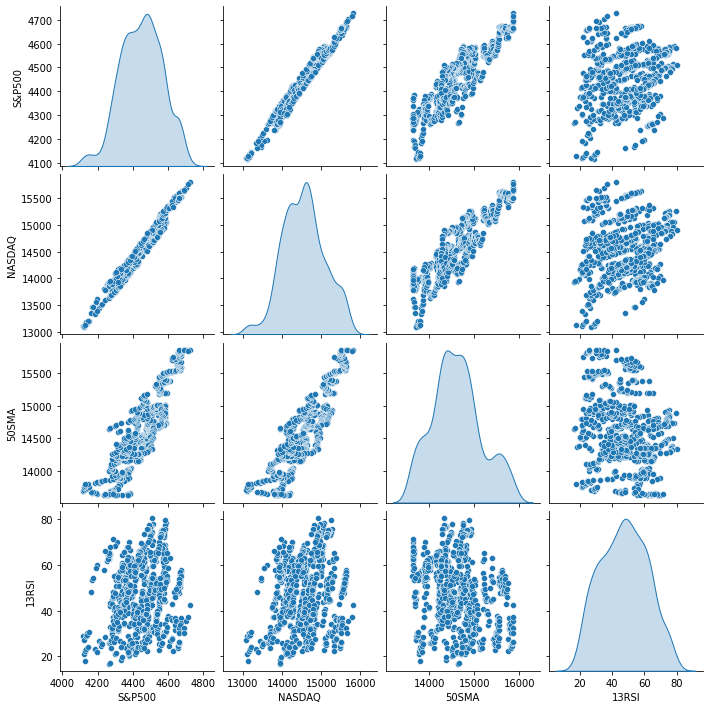
In uscita è come segue:
Dalla presentazione visiva dei dati, possiamo già vedere che c'è una relazione molto forte tra NASDAQ e S&P 500 e che esiste una forte relazione tra NASDAQ e la sua Media Mobile a 50 periodi. Come detto in precedenza, ogni volta che i dati sono sul grafico di dispersione, la variabile indipendente potrebbe non essere un buon predittore dell'obiettivo quando si tratta di trovare relazioni lineari, ma vediamo di cosa parlano i numeri sulla loro correlazione e traiamo una conclusione sui numeri piuttosto che dai nostri occhi, per scoprire come le variabili sono correlate tra loro utilizzeremo la metrica nota come coefficiente di correlazione.
Coefficente di Correlazione
Viene utilizzato per misurare la forza tra la variabile indipendente e il target.
Esistono diversi tipi di coefficienti di correlazione, ma useremo quello più popolare per la regressione lineare, noto anche come Coefficiente di correlazione di Pearson( R ) che varia tra -1 e +1.
La correlazione di possibili valori estremi di -1 e +1 indica una perfetta relazione lineare negativa e lineare positiva rispettivamente tra x e y mentre una correlazione di 0(zero) indica l'assenza di correlazione lineare.
La formula del coefficente di correlazione/coefficente di Pearson(R).
Ho creato la linearRegressionLib.mqh, all'interno della nostra libreria principale, codifichiamo la funzione corrcoef().
Iniziamo con la funzione media per i valori, media è la somma di tutti i dati poi divisa per il numero totale di elementi.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }Ora andiamo a codificare la Pearson's r
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
stampiamo il risultato nel nostro TestSript.mq5
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
In uscita sarà
Correlation Coefficient NASDAQ vs S&P 500 = 0.9807093773142763
Correlation Coefficient NASDAQ vs 50SMA = 0.8746579124626006
Correlation Coefficient NASDAQ Vs rsi = 0.24245225451004537
Come puoi vedere NASDAQ e S&P500 hanno una correlazione molto forte tra tutte le altre colonne di dati (perché il suo coefficiente di correlazione è molto vicino a 1), quindi dobbiamo eliminare le altre colonne deboli quando procediamo con la costruzione del nostro modello di regressione lineare semplice.
Ora abbiamo due colonne di dati su cui costruiremo il nostro modello, procediamo con la sua creazione.
Il Coefficente di X
Il coefficiente di x, noto anche come pendenza(m), è per definizione il rapporto tra la variazione di Y e la variazione di X o, in altre parole, la pendenza della linea.
Formula:
pendenza = Variazione di Y / Variazione di X
Ricorda dall' Algebra, che la pendenza è la m nella formula
Y = M X + C
Per trovare la pendenza della Regressione Lineare m la formula è
Ora che abbiamo visto la formula codifichiamo la pendenza del nostro modello.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Presta attenzione agli array y_values e x_values, questi sono array che sono stati inizializzati e copiati all'interno della funzione Init() all'interno della classe CSmpleLinearRegression.
Qui c'è la funzione CSimpleLinearRegression::Init()
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Abbiamo finito di codificare il Coefficiente di X, ora passiamo alla parte successiva.
L'intercetta Y
Come detto in precedenza, l'intercetta Y, è il valore di y quando il valore di x è zero, o il valore di y quando la linea taglia l'asse y.

Trovare l'intercetta y
Tramite l'equazione
Y = M X + C
Prendendo MX sul lato sinistro dell'equazione e capovolgendo l'equazione dal lato sinistro a destra, l'equazione finale per l'intercetta x sarà:
C = Y - M X
dove,
Y = media di tutti i valori y
x = media di tutti i valori x
Ora, codifichiamo la funzione per trovare l'intercetta y.
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Fatto con l'intercetta y, costruiamo il nostro modello di regressione lineare stampandolo nella nostra funzione Main LinearRegressionMain() .
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
Utilizziamo il nostro modello anche per ottenere i valori previsti di y, che saranno utili, a volte in futuro, per continuare a costruire il nostro modello e analizzarne l'accuratezza.
Chiamiamo la funzione, nella funzione Onstart() all'interno del nostro TestScript.mq5.
lr.LinearRegressionMain(y_nasdaq_predicted);
In uscita sarà
2022.03.03 10:41:35.888 TestScript (#SP500,H1) The Linear Regression Model is Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
All'interno della Funzione voidfileopen()
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
Ora all'interno del nostro TestScript la prima cosa che dobbiamo fare è dichiarare due array
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
La prossima cosa che dobbiamo fare è passare quegli array per ottenere il loro riferimento dalla nostra funzione void GetData ToArray()
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Presta attenzione ai numeri della colonna poiché i nostri argomenti di funzione appaiono così nella sezione pubblica della nostra classe
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Assicurati di fare riferimento al numero di colonna corretto. Come puoi vedere ecco come sono disposte le colonne nel nostro file CSV
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
Dopo aver chiamato la funzione GetDataToArray(), è il momento di chiamare la funzione Init(), poiché non ha senso inizializzare la libreria senza che i dati siano correttamente raccolti e memorizzati nei loro array. La chiamata della funzione nell'ordine corretto è simile a questa,
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
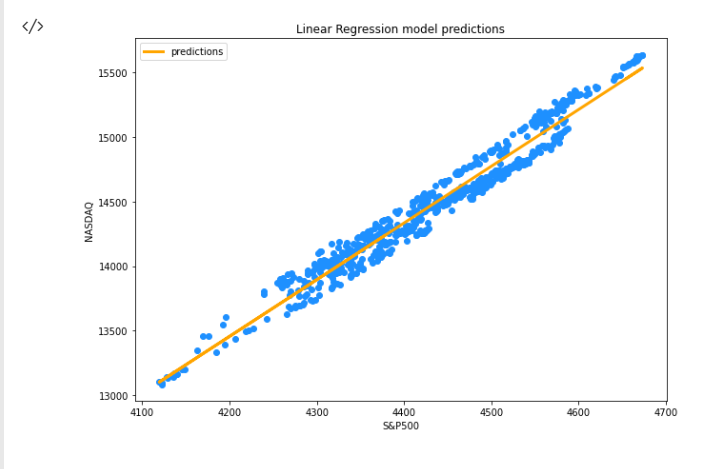
Ora che abbiamo i valori previsti memorizzati nell'array y_nasdaq_predicted visualizziamo la variabile Dipendente (NASDAQ), la variabile Indipendente (S&P500) e le predizioni sulla stessa curva.
Esegui il codice seguente sul tuo notebook Jupyter
Il riferimento completo del codice Python è allegato alla fine dell'articolo.
Dopo aver eseguito correttamente il frammento di codice sopra, vedrai il grafico seguente
Ora, abbiamo il nostro modello e altre cose in corso nella nostra libreria che dire dell'Accuratezza del nostro modello? Il nostro modello è abbastanza buono da significare qualcosa o da essere utilizzato in qualcosa?
Per capire quanto è bravo il nostro modello nel prevedere la variabile Target, utilizziamo una Metrica nota come coefficiente del determinante denominato R-quadro.
R-Quadro
Questa è la proposizione della varianza totale di y che è stata spiegata dal modello.
Per trovare l' r-quadro dobbiamo capire l'errore nella previsione. L'errore nella previsione è la differenza tra il valore effettivo/reale di y e il valore previsto di y.
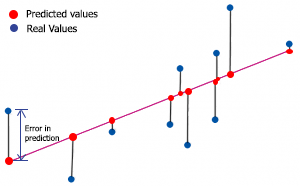
matematicamente,
Errore = Y attuale - Y previsto
La formula R-quadro è
Rsquared = 1 - (Somma totale degli errori al quadrato / Somma totale dei residui al quadrato)
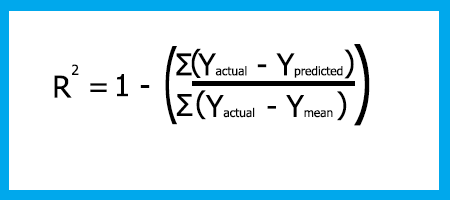
Perchè errori al quadrato?
- Gli errori possono essere positivi o negativi (sopra o sotto la linea) li eleviamo al quadrato per mantenerli positivi
- Valori negativi potrebbero ridurre l'errore
- Eleviamo al quadrato gli errori anche per penalizzare gli errori di grandi dimensioni in modo da poter ottenere il miglior adattamento possibile
Zero significa che il modello non è in grado di spiegare alcuna variazione di y indicando che il modello è il peggiore possibile, Uno indica che il modello è in grado di spiegare tutta la variazione di y nel tuo set di dati (questo modello non esiste).
Puoi fare riferimento all'output r-quadro come percentuale di quanto è genuino il tuo modello, zero significa, zero percentuale di accuratezza e uno significa che il tuo modello è accurato al cento percento.
Ora codifichiamo l' R quadro.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
Ricorda che, all'interno del nostro LinearRegressionMain in cui abbiamo archiviato i valori previsti nell'array predicted_y[] passato per riferimento, dobbiamo copiare quell'array in una variabile array globale che è stata dichiarata nella sezione privata del nostro classe.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
alla fine del nostro LinearRegressionMain ho aggiunto la riga per copiare quell'array in una variabile array globale m_ypredicted[].
//Alla fine della funzione LinearRegressionMain(double &predict_y[]) ho aggiunto la seguente riga,// Copia i valori previsti in m_ypredicted[], per accedervi all'interno della libreria ArrayCopy(m_ypredicted,predict_y);
Ora stampiamo il valore R-quadro all'interno del nostro TestScript
Print(" R_SQUARED = ",lr.r_squared());
L'output sarà:
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
Questo è tutto per la Regressione lineare semplice, ora vediamo come sarebbe una regressione lineare multipla.
Regressione Lineare Multipla
La Regressione lineare multipla ha una variabile indipendente e più di una variabile dipendente.
La formula per il modello di Regressione lineare multipla è il seguente
Ecco come appare la nostra libreria dopo aver codificato a fondo le sezioni private e pubbliche della nostra classe.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Poiché avremo a che fare con più valori, questa è la parte in cui giocheremo con molti array passati per riferimento agli Argomenti delle funzioni, non sono riuscito a trovare una scorciatoia da implementare.
Per creare il modello di Regressione lineare per due variabili dipendenti utilizzeremo questa funzione.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
L'intercetta-Y per questa istanza sarà basata sul numero di colonne di dati che abbiamo deciso di utilizzare. Dopo aver derivato la formula dalla regressione lineare multipla, la formula finale sarà:
C = Y - M1 X1 - M2 X2
Ecco come appare dopo averla codificata
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
Nel caso di tre variabili si trattava solo di codificare nuovamente la funzione e aggiungere un'altra variabile.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
La Costante/Intercetta Y per la nostra regressione lineare multipla, come detto in precedenza, sarà.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Ipotesi della Regressione Lineare
Il modello di regressione lineare si basa su una serie di ipotesi, se il set di dati sottostante non soddisfa queste ipotesi, potrebbe essere necessario trasformare i dati o un modello lineare potrebbe non essere adatto.
- L'ipotesi di linearità, presuppone una relazione lineare tra la variabile dipendente/obiettivo e le variabili indipendenti/predittive
- Ipotesi di normalità della distribuzione degli errori
- Gli errori dovrebbero essere normalmente distribuiti insieme al modello
- Un grafico sparso tra i valori effettivi e quelli previsti dovrebbe mostrare i dati distribuiti equamente nel modello
Vantaggi di un modello di regressione lineare
Semplice da implementare e di facile interpretazione degli output e dei coefficienti.
Svantaggi
- Ipotizza una relazione lineare tra variabili dipendenti e indipendenti, ovvero presuppone che esista una relazione lineare tra di esse
- I valori anomali hanno un enorme effetto sulla regressione
- La regressione lineare presuppone l'indipendenza tra gli attributi
- La Regressione Lineare esamina la relazione tra la media della variabile dipendente e la variabile indipendente
- Proprio come la media non è una descrizione completa di una singola variabile, la regressione lineare non è una descrizione completa delle relazioni tra variabili
- I confini sono lineari
Un'ultima riflessione
Penso che gli algoritmi di regressione lineare possano essere molto utili quando si creano strategie di trading basate sulla correlazione tra coppie e altre cose come gli indicatori, anche se la nostra libreria non è affatto vicina a una libreria finita non ho incluso la formazione e il test del nostro modello e ulteriori miglioramenti dei risultati , quella parte sarà nel prossimo articolo, resta sintonizzato ho un codice python collegato al mio repository Github qui ogni contributo alla libreria sarà apprezzato, sentiti anche libero di condividere il tuo pensiero nella sezione discussione dell'articolo.
A presto
Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/10459
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.
Questo articolo è stato scritto da un utente del sito e riflette le sue opinioni personali. MetaQuotes Ltd non è responsabile dell'accuratezza delle informazioni presentate, né di eventuali conseguenze derivanti dall'utilizzo delle soluzioni, strategie o raccomandazioni descritte.
 Scienza dei Dati e Apprendimento Automatico (Parte 02): Regressione Logistica
Scienza dei Dati e Apprendimento Automatico (Parte 02): Regressione Logistica
 Cosa è possibile fare con le Medie Mobili
Cosa è possibile fare con le Medie Mobili
 Impara a progettare un sistema di trading tramite ADX
Impara a progettare un sistema di trading tramite ADX
 Impara come progettare un sistema di trading con lo Stocastico
Impara come progettare un sistema di trading con lo Stocastico
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso

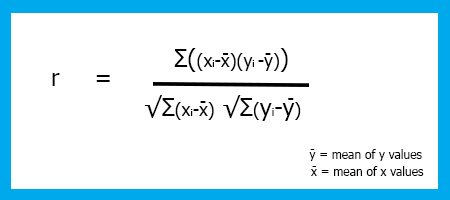
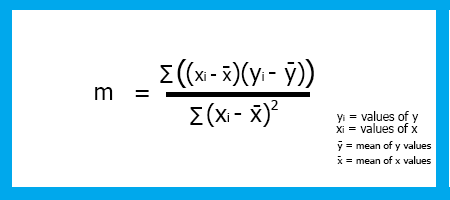
What is a Model
Un modello non è altro che un suffisso.
Un suffisso? Non capisco cosa significhi.
Prima di poter aprire un file CSV creato dal nostro script di test, è necessario convertirlo in codifica UTF-8 in modo che possa essere letto da python.
Perché? Basta creare un file di dati UTF-8 direttamente da MQL.
L'ellisse rossa è stata aggiunta da me. È sbagliato, questo punto non è una "intercetta y" e le sue coordinate non sono (0,-5).
Un suffisso? Non capisco cosa significhi.
Perché? Basta creare un file di dati UTF-8 direttamente da MQL.
Ellisse rossa aggiunta da me. È sbagliato, questo punto non è una "intercetta y" e le sue coordinate non sono (0,-5).
Con il termine suffisso intendo una notazione matematica, come y=mx+c, questo è un modello.
Sì, ho capito, ho fatto un errore nell'immagine: l'altro punto doveva essere (-5,0) e non è una "intercetta y".
Salve, grazie per l'articolo conciso sulla regressione lineare e le sue potenzialità.
La formula del coefficiente di Peasson ha dei difetti nel denominatore.
ciao, forse c'è, solo che non l'ho trovato, ma dove si trova il file NASDAQ.csv usato nell'articolo?