Algoritmi di ottimizzazione della popolazione: Ricerca dell'Armonia (Harmony Search HS)

Contenuti:

1. Introduzione
2. Algoritmo
3. Risultati del test

1. Introduzione

La composizione musicale è costituita da diversi componenti: ritmo, melodia e armonia. Mentre il ritmo e la melodia formano un unico insieme di un'opera musicale, l'armonia è ciò che la decora. Un suono o una canzone senza armonia è come un quadro non colorato nei libri per bambini - è disegnato, ma non c'è colore, né luminosità, né espressività. Un'armonia opportunamente selezionata accarezza le orecchie, nobilita il suono permettendoci di godere pienamente delle meravigliose sonorità del pianoforte, della chitarra o di qualsiasi altro strumento musicale. Una melodia può essere cantata, mentre un'armonia può essere solo suonata. L'armonia musicale è un insieme di accordi, senza i quali nessuna canzone o nessun pezzo di musica sarà completo e pieno di suono.

L'armonia appare esattamente nel momento in cui si collegano due suoni, uno dopo l'altro o in flusso simultaneo. Un sinonimo più capiente sarebbe "combinazione". Dopo aver collegato un suono con un altro, otteniamo una combinazione, in cui la gerarchia sta già cercando di allinearsi a modo suo. Nelle scuole di musica, nei college e nei conservatori esiste una disciplina speciale, l'armonia, dove gli studenti studiano tutti gli accordi esistenti nella teoria musicale, imparano ad applicarli nella pratica e persino a risolvere problemi di armonia.

Durante un'improvvisazione musicale, i musicisti cercano di accordare l'intonazione dei loro strumenti per ottenere un'armonia piacevole (condizione migliore). In natura, l'armonia è determinata da una relazione speciale tra diverse onde sonore che hanno frequenze differenti. La qualità dell'armonia improvvisata è determinata dalla valutazione estetica. Per migliorare l'apprezzamento estetico e trovare la migliore armonia, i musicisti si sottopongono a esercitazioni su esercitazioni. Esiste una similitudine tra l'improvvisazione e l'ottimizzazione.

Il metodo Harmony Search (HS) è un algoritmo di ottimizzazione meta-euristico emergente che è stato utilizzato per risolvere numerosi problemi complessi negli ultimi dieci anni. L'algoritmo Harmony Search (HS) è stato proposto per la prima volta nel 2001 da Z. W. Geem. Il metodo HS si ispira ai principi fondamentali dell'improvvisazione musicale e alla ricerca dell'armonia musicale. Le combinazioni di perfetta armonia dei suoni sono abbinate all'estremo globale nel problema di ottimizzazione multidimensionale, mentre il processo di improvvisazione musicale è abbinato alla ricerca dell'estremo.

Durante l'improvvisazione, ogni musicista riproduce un suono in qualsiasi misura di un brano musicale (nei limiti delle capacità del proprio strumento musicale), in modo che i suoni di tutti i musicisti dell'orchestra in quella misura formino un unico vettore armonico. Le combinazioni di suoni che formano armonie "buone" vengono memorizzate da ciascun musicista e possono essere utilizzate per formare armonie ancora migliori nelle misure successive del brano musicale.

Di norma, durante l'improvvisazione, il musicista soddisfa uno dei tre requisiti seguenti: formare un suono assolutamente casuale dalla gamma di suoni disponibili; suonare un suono qualsiasi dalla memoria delle armonie; suonare un vettore armonico adiacente dalla stessa memoria. Le caratteristiche principali dell'algoritmo HS sono la possibilità di utilizzarlo per risolvere problemi di ottimizzazione sia continui che discreti.

Le caratteristiche distintive di HS sono la semplicità dell'algoritmo e l'efficienza della ricerca. Per questo motivo, l'algoritmo attira una notevole attenzione da parte dei ricercatori e si sta sviluppando rapidamente sia in termini teorici che pratici. HS è una tecnica meta-euristica che fornisce un'elevata stabilità tra le fasi di esplorazione e di utilizzo nel processo di ricerca. HS si ispira alla creatività umana e il metodo per trovare la soluzione perfetta a un determinato problema è simile a quello utilizzato da un musicista per trovare un'armonia piacevole. Il metodo utilizzato per ottenere il valore della funzione di fitness è simile al metodo per ottenere un riferimento utilizzando la tonalità di ogni strumento musicale.

2. L’Algoritmo

Il lavoro della logica HS è simile a quello di un musicista nel creare un'armonia perfetta. Il musicista cerca di cambiare le varie tonalità fino a trovare l'armonia perfetta. Successivamente, l'insieme delle armonie trovate vengono memorizzate. In un problema di ottimizzazione, le armonie subiscono varie modifiche; se i risultati della modifica sono favorevoli, allora la memoria viene rinnovata aggiungendo armonie e rimuovendo gli elementi indesiderati... Tutto questo può sembrare piuttosto confuso. Che cos'è l'armonia? Cosa sono le tonalità? Cerchiamo di capire l'algoritmo usando i nostri termini.

Che cos'è un brano musicale? Naturalmente non sono un musicista (ed è un peccato), ma un programmatore. Ma ai fini del rilevamento dell'algoritmo, sarà sufficiente applicare il concetto di "nota". Un brano musicale è composto da note (accordi). La Figura 1 mostra schematicamente il "meccanismo" di costruzione di un brano musicale. La selezione delle note corrisponde a un brano musicale, facilmente determinabile anche senza un orecchio per la musica o una formazione musicale. Chi vuole indovinare può lasciare un commento qui sotto.

L'ottimizzazione dell'algoritmo HS consiste nel muovere le barre verdi con le note attraverso la barra blu del brano stesso. L'intervallo della barra verde è un'ottava, che è costituita da singole note. Il prodotto (barra blu) corrisponde a una delle soluzioni di ottimizzazione. Le note sulla barra verde sono i corrispondenti parametri di ottimizzazione del problema. La memoria del musicista memorizza diverse versioni del brano (diverse varianti di barre blu), questa è la popolazione dell'algoritmo.

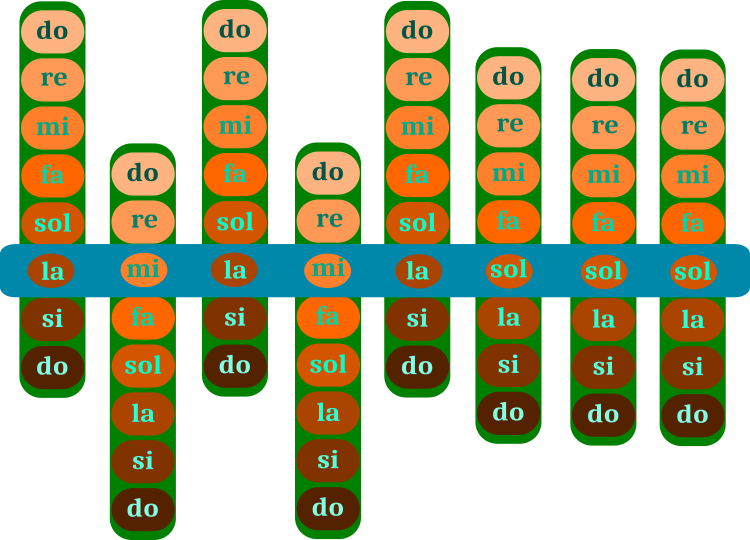
Figura 1. Selezione delle note in un pezzo musicale (ricerca dell'armonia). La barra blu è un pezzo. Le barre verdi sono un insieme di note

L'esempio della Figura 1 corrisponde alla soluzione di un problema discreto, in cui ci sono otto fasi nel parametro. L'esempio è fornito per facilitare la comprensione del funzionamento dell'algoritmo. Tuttavia, in un compito arbitrario, può esserci qualsiasi passo dei parametri ottimizzati e ci sono anche note intermedie - semitoni. I parametri corretti per risolvere il problema corrispondono alle note corrette del brano.

Quindi, il processo di creazione di un brano musicale inizia con un insieme casuale di suoni di uno strumento musicale che si trovano nella gamma di frequenze riproducibili dello strumento. È necessario creare diverse varianti di un brano per poter combinare le singole sezioni delle note della variante. La fase successiva consiste nel cambiare le note in queste varianti. Possiamo farlo in tre modi possibili:

1. Cambiare a caso una delle note del brano che si trova nella gamma dello strumento musicale.
2. Possiamo prendere una nota con il numero di serie corrispondente da altre versioni del brano.
3. Possiamo prendere una nota da un'altra versione del brano e cambiarla leggermente rendendola più alta o più bassa in chiave.

Avendo così ottenuto un nuovo insieme di varianti di un'opera musicale, valutiamo ciascuna delle varianti in termini di armonia sonora e memorizziamo le varianti nella loro posizione originale, a condizione che la nuova versione sia migliore della precedente. La caratteristica unica dell'algoritmo è che non è necessario ordinare la popolazione, nel nostro caso l'insieme dei prodotti. Ogni nuova opzione migliore sostituirà la vecchia opzione peggiore nello stesso posto. Questo processo è un po' come il lavoro degli algoritmi genetici che imitano l'evoluzione quando gli individui più idonei sopravvivono. Inoltre, si osservano somiglianze anche con la combinazione di geni nel cromosoma.

Sulla base di quanto sopra, possiamo comporre in via preliminare lo pseudocodice dell'algoritmo HS:

1. Generazione di armonie casuali.
2. Misura della qualità delle armonie (calcolo della funzione di fitness).
3. Utilizzare la selezione di accordi di un'armonia scelta a caso con la probabilità di Eh.
  3.1 Cambiare l'accordo secondo l'equazione se l'accordo è selezionato da qualche armonia con la probabilità di Ep.
    3.1.1 Lasciare invariato l'accordo selezionato.
  3.2 Nuovo accordo secondo l'equazione.
4. Misura della qualità delle armonie (calcolo della funzione di fitness).
5. Ripetere da p. 3 fino a quando non viene soddisfatto il criterio di arresto.

Passiamo quindi a descrivere i parametri di input dell'algoritmo, che sono pochi e intuitivi.

input int    Population_P = 50;    //Dimensione della popolazione
input double Eh_P         = 0.9;   //frequenza di selezione casuale
input double Ep_P         = 0.1;   //frequenza di regolazione passo-passo
input double Range_P      = 0.2;   //intervallo

• Population_P - il numero di varianti di un brano nella memoria del musicista (dimensione della popolazione);
• Eh_P - la frequenza con cui una variante di un brano viene selezionata dalla memoria influisce sulla frequenza con cui faremo riferimento ad un'altra variante per prendere in prestito una nota. Un valore più alto significa proprietà combinatorie più elevate dell'algoritmo;
• Ep_P - la frequenza con cui è necessario modificare leggermente la nota, con un tono più alto o più basso, se la nota è stata selezionata da un'altra versione del brano;
• Range_P - l'intervallo della nota nella versione modificata del brano, se non è stata presa da un'altra versione. Ad esempio, 0.2 significa il 20% della gamma di note di uno strumento musicale.
• 
  

L'algoritmo HS opera con le armonie (composizioni musicali), che possono essere descritte dalla struttura S_Harmony. L'armonia è costituita da note (accordi), questo è un array che rappresenta i parametri c[] da ottimizzare. I migliori accordi del brano saranno memorizzati nell'array cB[]. È in questo array che verrà inviata la composizione di successo, ed è con queste composizioni (armonie) che eseguiremo permutazioni combinatorie prendendo in prestito le note da esse. La qualità dell'armonia è memorizzata nella variabile h e l'armonia migliore è memorizzata nella variabile hB.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

L'array di strutture Harmony viene utilizzato nella classe C_AO_HS. Le dichiarazioni del metodo e della classe membro sono compatte, perché l'algoritmo è estremamente conciso ed ha bassi requisiti computazionali. Non vedremo l'ordinamento utilizzato in molti altri algoritmi di ottimizzazione. Avremo bisogno di array per impostare il massimo, il minimo e il passo dei parametri da ottimizzare (svolgono il ruolo di intervallo e passo degli accordi) e di variabili costanti per trasferirvi i parametri esterni dell'algoritmo. Passiamo alla descrizione dei metodi che contengono la logica principale di HS.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Il metodo pubblico Init () inizializza l'algoritmo. Qui impostiamo la dimensione degli array. Inizializziamo l'indicatore di qualità della migliore armonia trovata con il valore "double" minimo possibile. Faremo lo stesso con le variabili corrispondenti dell'array delle strutture harmony.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo pubblico Moving(), che deve essere eseguito a ogni iterazione, ha l’input 'iter', l'iterazione corrente. Alla prima iterazione, quando il flag "revision" è "false", è necessario inizializzare le armonie con valori casuali nella gamma degli strumenti musicali, il che equivale a far suonare a caso gli accordi da un musicista. Per ridurre le operazioni ripetitive, memorizziamo la gamma di frequenze sonore degli accordi corrispondenti (parametri ottimizzati) nell'array frequency[].

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

Nella seconda iterazione e in quelle successive, ha luogo l'improvvisazione, cioè il cambio sequenziale degli accordi e delle loro combinazioni. Ci sono diverse armonie in memoria, che cambieremo e combineremo. Per ogni nuova armonia, ordineremo in sequenza gli accordi. Per ogni accordo, c'è una probabilità di essere scelto casualmente dalla memoria dell'armonia, cioè l'armonia sarà scelta casualmente (in modo equiprobabile per tutte le armonie). Se l'accordo viene preso dalla memoria delle armonie, anche la probabilità di un suo cambiamento viene verificata dall'equazione:

h [har].c [c] = h [har].c [c] + r * B * frequency [c];

dove:

r - numero casuale compreso tra -1 e 1
frequency - gamma della frequenza dello strumento
B - coefficiente calcolato tramite la formula:

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

dove:

maxIterations - numero massimo di iterazioni
iter - iterazione corrente
maxB - limite massimo del coefficiente
minB - limite minimo del coefficiente

La Figura 2 mostra la dipendenza del coefficiente B dai parametri di regolazione dell'algoritmo e dall'iterazione corrente.

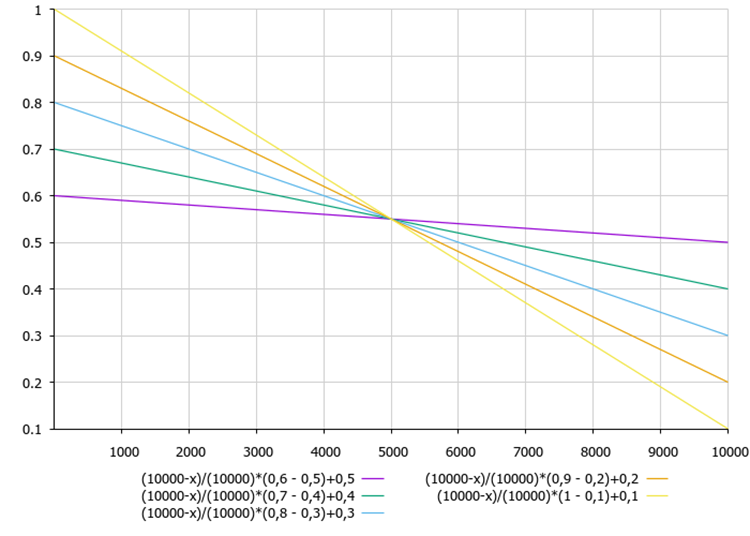
Figure 2. Dipendenza del coefficiente B dai parametri di regolazione dell'algoritmo maxB, minB e dall'iterazione corrente

L'equazione di calcolo del coefficiente B mostra che il coefficiente B diminuisce ad ogni iterazione. In questo modo, gli estremi trovati vengono perfezionati alla fine dell'ottimizzazione.
Se un accordo non è stato selezionato dalla memoria delle armonie, quello che esiste già al momento verrà cambiato. La differenza di un cambio di accordo rispetto al cambio precedente è la gamma fissa dei valori delle onde sonore.

Una volta completato il processo di modifica dell'accordo, controlliamo che l'accordo risultante non vada oltre i valori consentiti dello strumento musicale.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision () è il secondo metodo pubblico chiamato ad ogni iterazione dopo il calcolo della funzione di fitness. Il suo scopo è aggiornare la soluzione globale trovata. Se l'armonia è migliore della sua versione migliore h > hB, allora si aggiorna la versione migliore di questa armonia.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Dopo aver studiato attentamente il codice, vediamo che non ci sono idee fondamentalmente nuove nell'algoritmo di ricerca dell'armonia. L'algoritmo Harmony Search prende in prestito idee già utilizzate in precedenza negli algoritmi evolutivi, tra cui la ricombinazione uniforme globale, la mutazione uniforme, la mutazione gaussiana e la sostituzione dell'individuo peggiore a ogni generazione. Alcune fonti indicano la necessità di sostituire l’armonia peggiore in memoria con una nuova. Nel nostro algoritmo, l'armonia può sostituire solo la sua soluzione migliore. Si tratta di una versione leggermente diversa da quella classica, perché i miei studi indicano che questa implementazione dell'algoritmo sarà più produttiva.

Il contributo dell'algoritmo di ricerca delle armonie risiede in due aree: la combinazione di queste idee in questo algoritmo è nuova; la motivazione musicale dell'algoritmo di ricerca delle armonie è nuova. Pochissime pubblicazioni sulla ricerca delle armonie trattano di motivi musicali o di estensioni dell'algoritmo di ricerca delle armonie. La maggior parte delle pubblicazioni sono dedicate all'ibridazione dell'algoritmo di ricerca armonica con altri algoritmi evolutivi, alla regolazione dei parametri di ricerca armonica o all'applicazione dell'algoritmo di ricerca armonica a problemi specifici. Se si potessero applicare all'algoritmo HS estensioni più condizionate musicalmente, ciò contribuirebbe a distinguerlo come un algoritmo evolutivo separato. Tale ricerca richiederebbe lo studio della teoria musicale, lo studio del processo di composizione e arrangiamento musicale, lo studio delle teorie educative della musica e l'applicazione inventiva di queste teorie all'algoritmo di ricerca dell'armonia.

3. Risultati del test

I risultati del banco di prova HS sono i seguenti:

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's; Func cicli 10000 risultato: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Punteggio: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin's; Func cicli 10000 risultato: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Punteggio: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's; Func cicli 10000 risultato: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Punteggio: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's; Func cicli 10000 risultato: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Punteggio: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's; Func cicli 10000 risultato: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Punteggio: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's; Func cicli 10000 risultato: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Punteggio: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's; Func cicli 10000 risultato: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Punteggio: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's; Func cicli 10000 risultato: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Punteggio: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's; Func cicli 10000 risultato: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Punteggio: 0.05410

I valori elevati delle funzioni del test sono sorprendenti e fanno sperare che i risultati del punteggio complessivo del test saranno eccezionali. Una caratteristica dell'HS sulla visualizzazione è che non si vedono formazioni strutturali sotto forma di gruppi di coordinate, come nel caso di alcuni degli algoritmi precedenti. Visivamente non ci sono schemi nel movimento degli agenti nello spazio di ricerca. Questo è simile al comportamento dell'algoritmo di ottimizzazione RND, anche se i grafici di convergenza si comportano in modo molto sicuro, avvicinandosi progressivamente alla soluzione del problema di ottimizzazione. Il blocco negli estremi locali non è tipico di questo algoritmo.

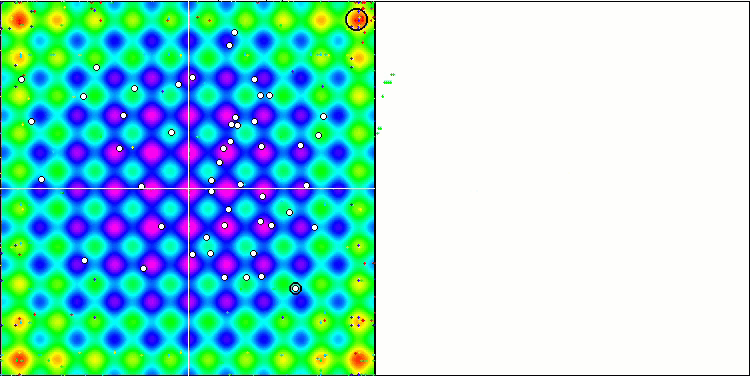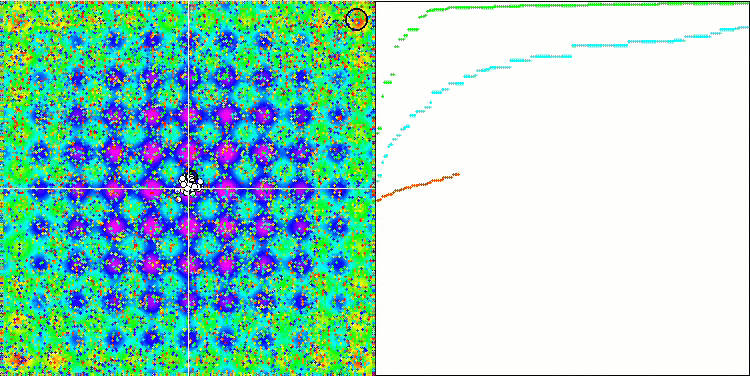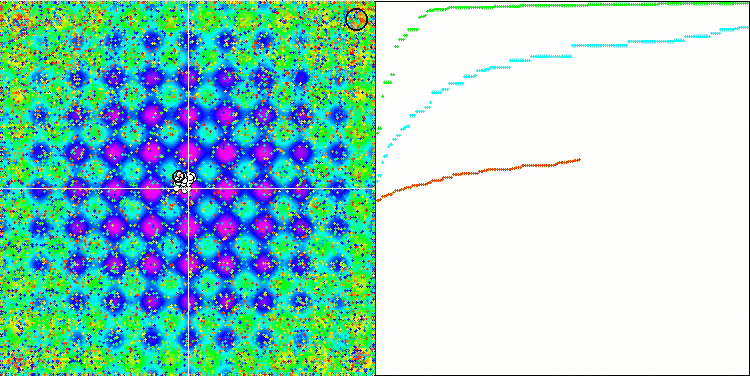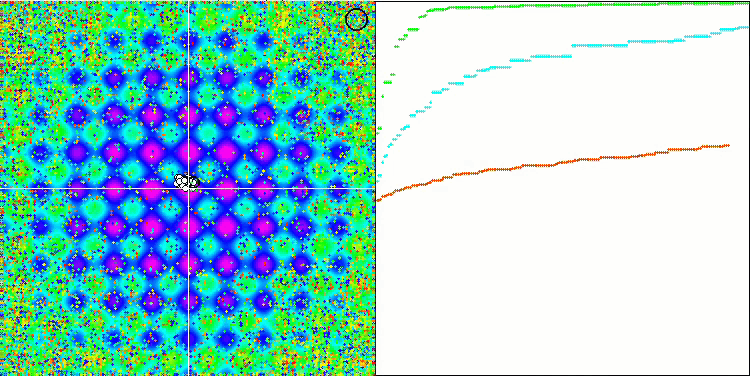
  HS sulla funzione di test Rastrigin

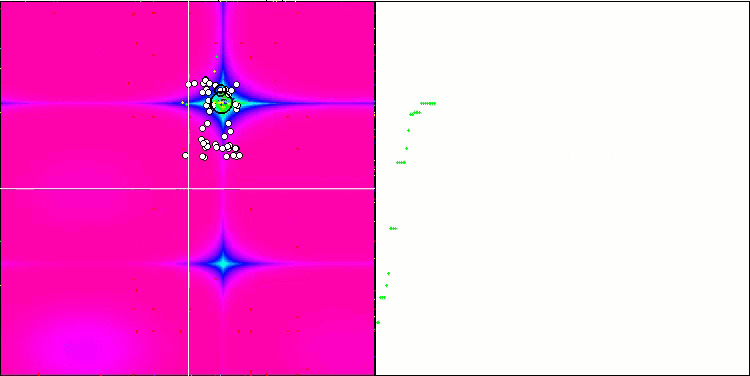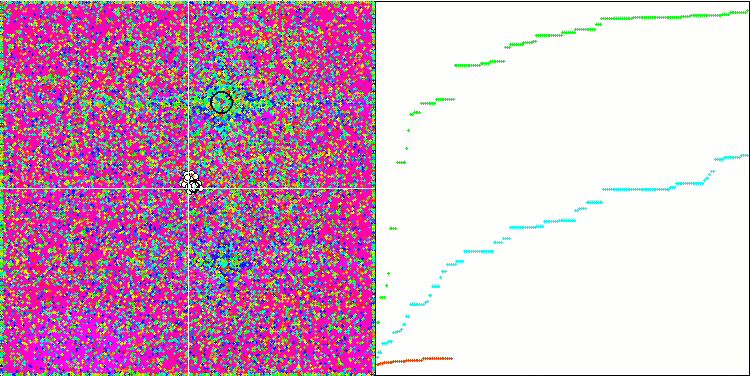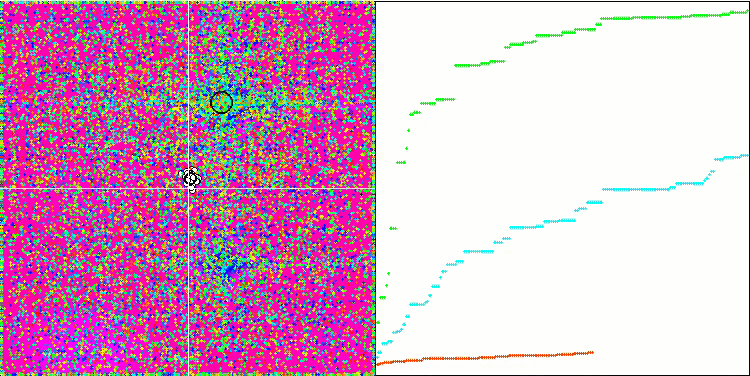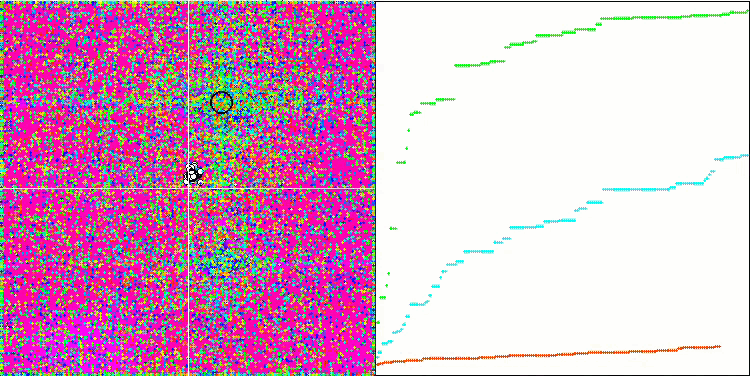
  HS sulla funzione di test Forest

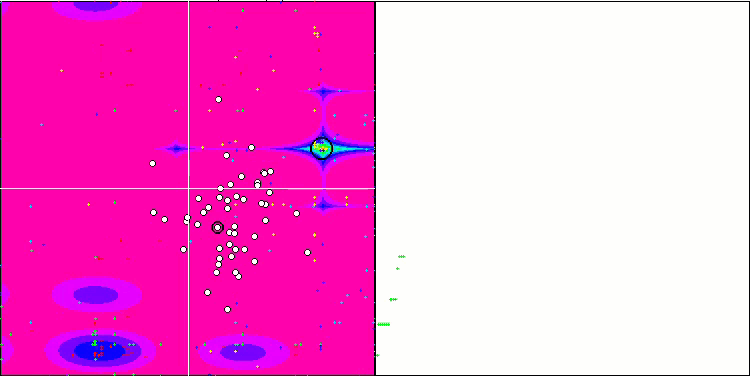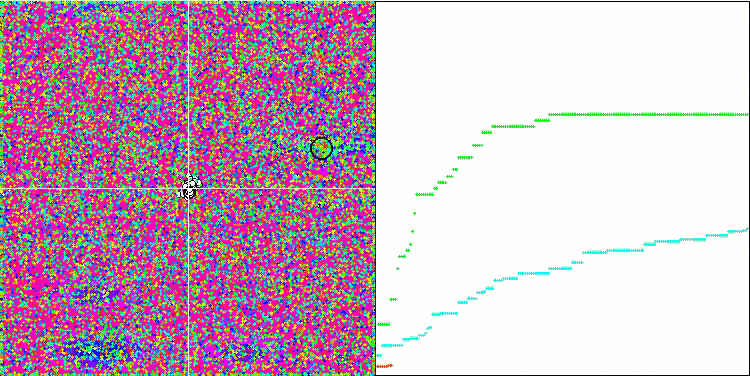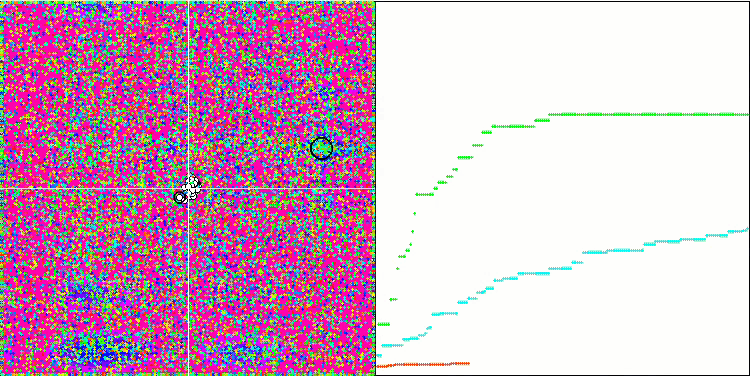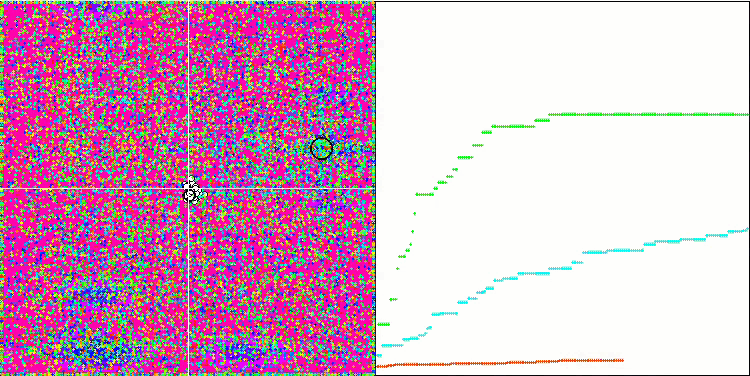
  HS sulla funzione di test Megacity

È il momento di analizzare i risultati della tabella e rispondere alla domanda posta nel titolo dell'articolo. Negli articoli precedenti, ho espresso il dubbio che si possa vedere un algoritmo in grado di scavalcare il leader nella tabella di valutazione su una funzione discreta. L'algoritmo, che visivamente sembra un algoritmo casuale, è stato in grado di diventare leader non solo su una funzione discreta (il migliore nei tre test), ma anche su altre funzioni di test, diventando alla fine il migliore in 6 test su 9.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
HS	ricerca dell'armonia	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.00000
ACOm	Ottimizzazione della colonia di formiche M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	Ottimizzazione delle piante infestanti	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	Algoritmo di ottimizzazione a cucù M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	Algoritmo della lucciola M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	Algoritmo del pipistrello	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	Colonia di api artificiali	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	Ottimizzazione del foraggiamento batterico	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	Algoritmo di ricerca gravitazionale	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
FSS	Ricerca del banco di pesci	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	Ottimizzazione dello sciame di particelle	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	Casuale	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Riassumiamo. Al momento della scrittura, l'algoritmo HS occupa una posizione di primo piano nell'istogramma dei risultati dei test con un enorme vantaggio rispetto ad altri algoritmi di ottimizzazione, il che indica la forza e la potenza dell'algoritmo e il suo potenziale nel campo dell'ottimizzazione dei processi di risoluzione di problemi di varia complessità.

A mio parere, un fattore molto importante che permette di dimostrare risultati impressionanti su vari tipi di funzioni di test, anche molto complessi, è l'ereditarietà di alcuni metodi (tecniche) presenti in altri algoritmi di ottimizzazione: HS non ha un pool di soluzioni, ogni soluzione aggiorna solo la sua decisione locale - questo è tipico dell'algoritmo di ottimizzazione della ricerca del cuculo, dove un nuovo percorso per lo sviluppo di un ramo decisionale avviene solo se l'uovo è migliore di quello nel nido. Inoltre, i metodi HS sono simili a quelli utilizzati negli algoritmi genetici - combinatoria di elementi di soluzione.

Il potente algoritmo di ottimizzazione HS, che ha prestazioni eccezionalmente elevate, può essere tranquillamente raccomandato per la risoluzione di un'ampia varietà di problemi complessi con molte variabili, sia per funzioni scalari lisce che per complessi problemi combinatori discreti. L'algoritmo HS è già stato applicato con successo in molti settori dell'ingegneria (ottimizzazione della topologia delle strutture e della forma ottimale dei pezzi), dell'elettronica e della logistica.

La facilità di implementazione dell'algoritmo HS lascia spazio alla ricerca, consentendo di aggiungere e combinare varie strategie di ottimizzazione. Ciò suggerisce che le capacità dell'algoritmo sono ben lontane dall'essere pienamente realizzate.

Di seguito è riportato l'istogramma dei risultati del test dell'algoritmo.

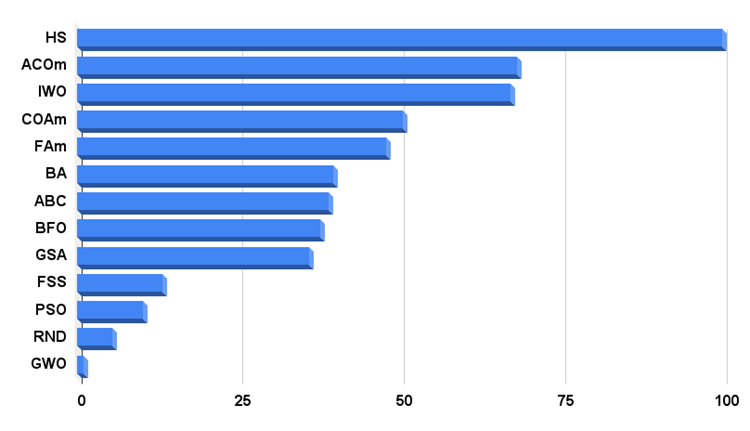
Figura 3. Istogramma dei risultati dei test degli algoritmi

Pro e contro dell'algoritmo di ricerca armonica HS:

Pro:
1. Facile implementazione.
2. Eccellente convergenza su tutti i tipi di funzioni, senza eccezioni.
3. Scalabilità impressionante.
4. Molto veloce.
5. Numero ridotto di parametri esterni.

Contro:
Non trovati.

Ogni articolo presenta un archivio che contiene le versioni aggiornate dei codici degli algoritmi per tutti gli articoli precedenti. L'articolo si basa sull'esperienza accumulata dall'autore e rappresenta la sua opinione personale. Le conclusioni e i giudizi si basano sugli esperimenti.