Algoritmi di ottimizzazione della popolazione: Algoritmo come-l’Elettromagnetismo (ЕМ)

Contenuti:

1. Introduzione
2. L’Algoritmo
3. Risultati del test

1. Introduzione

Negli ultimi decenni, i ricercatori di tutto il mondo hanno ideato molti metodi di ricerca meta-euristici per risolvere complessi problemi di ottimizzazione globale e modi per migliorarli.

L'algoritmo come-l’Elettromagnetismo (ЕМ) è un algoritmo di ricerca meta-euristico relativamente nuovo (https://www.sciencedirect.com/science/article/pii/S0304397516302328#br0040) basato sulla simulazione del comportamento delle particelle elettromagnetiche nello spazio fisico, introdotto per la prima volta da I. Birbil e S.С. Fang nel 2003. È descritto come un algoritmo evolutivo con rumore casuale e una popolazione basata sulla forza elettromagnetica dell'interazione tra particelle cariche.

Questo algoritmo si ispira al meccanismo di attrazione e repulsione delle cariche nella teoria dell'elettromagnetismo per risolvere problemi di ottimizzazioni non lineari senza restrizioni in un dominio continuo. Grazie alla sua capacità di risolvere problemi di ottimizzazione globale complessi, EM è ampiamente utilizzato come strumento di ottimizzazione in molti settori.

Fatti interessanti sull'elettromagnetismo e sulle cariche elettriche:

• Esistono due tipi di cariche elettriche: positive e negative. Tutte le cariche sono positive o negative.
• Il campo elettromagnetico può essere utilizzato per trasmettere informazioni sotto forma di onde radio. Utilizziamo questa funzione ogni giorno quando ascoltiamo la radio o guardiamo la TV.
• Abbiamo il campo magnetico terrestre, che ci protegge dal vento solare e dai raggi cosmici.
• Esistono diversi materiali che possono essere magnetizzati e questo rende possibile la creazione di elettromagneti. Gli elettromagneti vengono utilizzati in varie applicazioni, come i generatori di corrente.
• Esistono molte applicazioni basate sull'elettromagnetismo. Ad esempio, computer, telefoni cellulari e altri dispositivi utilizzano la tecnologia elettromagnetica.
• Tutti gli oggetti luminosi (ad esempio, le lampadine e i fari delle auto) emettono radiazioni elettromagnetiche.
• L'elettromagnetismo svolge un ruolo importante anche in medicina. I dispositivi medici come la Risonanza Magnetica e la TAC utilizzano un campo elettromagnetico per creare immagini all'interno del corpo.
• Alcuni animali, come gli squali e le anguille elettriche, possono usare l'elettromagnetismo per navigare in acqua.
• L'elettromagnetismo è una delle quattro forze fondamentali della natura, insieme alle forze gravitazionali, deboli e forti.

2. L’Algoritmo

Guidato dalla teoria dell'elettromagnetismo, EM simula il meccanismo di attrazione-repulsione delle cariche per ottenere una soluzione ottimale globale utilizzando variabili limitate. Nell'algoritmo, tutte le soluzioni sono considerate come particelle cariche nello spazio di ricerca e la carica di ogni particella è associata al valore della funzione target. Le particelle con un output obiettivo migliore applicheranno forze attrattive, mentre le particelle con valori obiettivi peggiori applicheranno forze repulsive alle altre particelle. Quanto migliore è il valore della funzione obiettivo, tanto maggiore sarà la quantità di attrazione o repulsione tra le particelle.

Il principio dell'algoritmo è che nella fase iniziale si forma una popolazione di soluzioni casuali e ogni soluzione è rappresentata da un vettore di coordinate corrispondenti alle cariche delle particelle elettromagnetiche. Inoltre, ad ogni iterazione dell'algoritmo, viene simulato il moto di queste cariche nello spazio sotto l'azione di forze elettromagnetiche. Durante il movimento, ogni carica interagisce con altre cariche, modificando la direzione del movimento e la velocità. Di conseguenza, c’è una graduale convergenza delle soluzioni verso il valore ottimale della funzione obiettivo.

I componenti principali dell'algoritmo EM sono:

1. Formazione della popolazione iniziale delle soluzioni (cariche), dove ogni carica è rappresentata da un vettore di coordinate che corrisponde a una determinata soluzione del problema di ottimizzazione.
2. Calcolo della forza elettromagnetica di interazione tra cariche. Il calcolo viene eseguito ad ogni iterazione dell'algoritmo e dipende dalla distanza tra le cariche (soluzioni).
3. Movimento delle cariche nello spazio sotto l'influenza di forze elettromagnetiche di interazione.
4. Aggiornare la popolazione delle soluzioni ad ogni iterazione tramite la funzione obiettivo (la funzione obiettivo può essere, ad esempio, la funzione di perdita nei problemi di apprendimento automatico).
5. Determinare la condizione per l'arresto dell'algoritmo, ad esempio il raggiungimento di un determinato valore della funzione obiettivo.

Le particelle interagiscono tra loro, attraendosi o respingendosi a seconda della carica e della distanza tra di loro. L'algoritmo viene eseguito in diverse iterazioni, in ognuna delle quali vengono aggiornate le coordinate e le cariche delle particelle e vengono calcolati i nuovi valori della funzione di fitness.

L'unità logica dell'algoritmo di ottimizzazione EM è una particella. Può essere descritto dalla struttura S_Particle, che è un agente nello spazio di ricerca. Ogni particella ha coordinate c [], che determinano la sua posizione nello spazio di ricerca, e la carica C, che influenza l'interazione con le altre particelle. Per ogni particella, viene calcolato il valore della funzione di fitness f, che valuta la qualità della soluzione corrispondente alla coordinata data. Inoltre, per ogni particella vengono calcolate le distanze R dalle altre particelle e i vettori forza F, che determinano la direzione del movimento delle particelle nello spazio di ricerca.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

La classe C_AO_EM è un'implementazione dell'algoritmo di ottimizzazione elettromagnetica. Si usa per trovare i valori ottimali di una funzione data su un insieme di numeri reali. L'algoritmo si basa sulla simulazione dei processi di interazione tra particelle magnetiche ed elettriche in un sistema fisico.

La classe contiene i seguenti campi:

• S_Particle p[] - array di particelle che rappresentano le potenziali soluzioni al problema di ottimizzazione.
• double rangeMax[] - array di valori massimi dell'intervallo di ricerca per ogni coordinata.
• double rangeMin[] - array di valori minimi dell'intervallo di ricerca per ogni coordinata.
• double rangeStep[] - array dei passi di ricerca per ogni coordinata.
• double cB[] - array di coordinate della soluzione migliore.
• double fB - valore della funzione della soluzione migliore.

La classe contiene i seguenti metodi:

• void Init() inizializza l'algoritmo, impostando il numero di coordinate, il numero di particelle, la costante ambientale e il passo del movimento.
• void Moving(int iter) itera l'algoritmo muovendo le particelle secondo le regole dell'interazione dei campi magnetici ed elettrici.
• void Revision() esegue una revisione delle particelle controllando che non vadano oltre l'intervallo di ricerca e regolando la loro posizione se necessario.

La classe contiene anche campi privati:

• int coordinatesNumber - numero di coordinate.
• int particlesNumber - numero di particelle.
• double envConstant - costante dell'ambiente.
• double movConstant - passo del movimento.
• double exponent - esponente della distanza.
• double vect[] - array di vettori.
• bool revision - flag che indica la necessità di una revisione della particella.

La classe contiene metodi privati:

• double SeInDiSp(double In, double InMin, double InMax, double Step) distribuisce i punti su una griglia uniforme.
• double RNDfromCI(double min, double max) genera un numero casuale nell'intervallo indicato.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Il metodo di inizializzazione dell'algoritmo di ottimizzazione "algoritmo elettromagnetico" inizia con l'azzeramento del generatore di numeri casuali e l'impostazione dei valori iniziali di alcune variabili. Il metodo prende in input diversi parametri: il numero di coordinate, il numero di particelle, il valore dell'ambiente e il passo del movimento. Successivamente, il metodo crea diversi array delle dimensioni richieste e li riempie con i valori iniziali.

Gli array memorizzano i valori massimi e minimi dell'intervallo per ogni coordinata, il passo di modifica della coordinata, il vettore e la posizione corrente di ciascuna particella. Il metodo crea quindi un array di particelle e per ogni particella, crea array per memorizzare le sue coordinate, la matrice delle distanze dalle altre particelle, il vettore forza e il valore migliore corrente della funzione. Alla fine, il metodo crea un array per memorizzare le coordinate migliori di tutte le particelle. In questo modo, il metodo inizializza tutte le variabili e gli array necessari per il funzionamento dell'algoritmo di ottimizzazione "algoritmo elettromagnetico".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Il metodo Moving() è il primo che deve essere eseguito ad ogni iterazione. È responsabile del movimento delle particelle nello spazio di ricerca della soluzione. Innanzitutto, il metodo controlla se le particelle sono già state inizializzate. In caso contrario, ogni particella riceve coordinate casuali entro i limiti indicati e azzera la stima e la carica corrente. Viene inoltre calcolato il vettore delle differenze vect [] tra i valori massimi e minimi in ciascuna dimensione dello spazio di ricerca.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

Se l'inizializzazione è già stata effettuata, il metodo calcola la carica di ogni particella in base alla sua deviazione dal massimo globale normalizzata alla somma delle deviazioni dal massimo globale di tutte le particelle. Calcolare la somma delle differenze come segue:

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

La carica delle particelle viene calcolata con l'equazione:

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));

Come si può notare, il valore della carica nell'equazione è positivo. Il segno della carica verrà preso in considerazione più avanti nell'algoritmo. Se la somma delle differenze delle deviazioni dal massimo globale è pari a zero, si assume che la carica della particella sia pari a zero. La carica calcolata della particella determina l'ampiezza della forza che agisce dalla particella su altre particelle rilevanti durante la fase del calcolo della forza. Il codice per calcolare la carica di una particella sarà simile a questo:

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

Prima di iniziare a calcolare le distanze tra le particelle, è necessario resettare la matrice delle distanze tra la particella e le altre particelle e reimpostare anche il vettore delle forze che agiscono sulla particella:

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

Quindi si calcolano le distanze tra tutte le coppie di particelle e le forze che agiscono tra loro. Utilizza una formula basata sulla legge di Coulomb, che descrive l'interazione tra particelle cariche. Le forze che agiscono su ogni particella sono calcolate come somma vettoriale di tutte le forze che agiscono su di essa dalle altre particelle.

Secondo la teoria elettromagnetica, la forza d'azione di una particella su un'altra è inversamente proporzionale alla distanza tra le due particelle e direttamente proporzionale al prodotto delle loro cariche. Una particella con un valore target inferiore applica una forza repulsiva a una particella con un valore target relativamente più alto. Allo stesso modo, allontana una particella buona da una regione con un valore target non buono. D'altra parte, una particella con un valore target più alto esercita attrazione su particelle con valori relativamente più bassi.

Tenendo conto di tutte le forze pertinenti generate da tutte le altre particelle, si calcola il vettore forza totale per la particella. Questo vettore di forza combinato determina la direzione in cui la particella si muoverà durante la fase di movimento. Gli autori dell'algoritmo raccomandano di normalizzare il vettore forza della particella al vettore delle forze tra tutte le particelle. I miei esperimenti hanno dimostrato che senza normalizzazione i risultati sono migliori e il codice viene presentato senza normalizzazione.

A seconda di quale particella ha il valore maggiore della funzione obiettivo, impostiamo la direzione della forza (imitando il segno della carica).

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

Infine, per ogni particella vengono calcolate nuove coordinate in base alla sua posizione attuale e alla forza che agisce su di essa. Le particelle non hanno massa, il che significa che non c'è accelerazione. A differenza dell'algoritmo di ricerca gravitazionale GSA, le particelle si spostano in una nuova posizione istantaneamente. Le coordinate di movimento sono limitate dal raggio di ricerca e dal passo di variazione.

Il codice commentato restituisce la particella sul lato opposto dell'intervallo a una distanza dalla coordinata corrispondente, nel caso in cui la particella sia fuori dall'intervallo.

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Il metodo Revision(), il secondo che deve essere eseguito ad ogni iterazione, nell'algoritmo di ottimizzazione EM, è responsabile del controllo della migliore posizione della particella all'iterazione corrente. All'interno del metodo, vengono eseguiti dei cicli su tutte le particelle e confrontato il valore della loro funzione di fitness con il miglior valore attuale di fB. Se il valore della funzione di fitness della particella corrente è maggiore di fB, si aggiorna fB e la posizione della particella viene copiata nell'array cB.

Pertanto, il metodo Revision() consente di tracciare la posizione migliore della particella a ogni iterazione dell'algoritmo e di memorizzarla nell'array cB. Ciò consente di ottimizzare il processo di ricerca della soluzione ottimale e di aumentare l'efficienza dell'algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il metodo SeInDiSp() dell'algoritmo di ottimizzazione "algoritmo elettromagnetico" viene utilizzato per limitare i valori della variabile In entro un determinato intervallo [InMin, InMax] con un Passo (Step). Se In è minore o uguale a InMin, il metodo restituisce InMin. Se In è maggiore o uguale a InMax, il metodo restituisce InMax. Se il passo è zero, il metodo restituisce il valore In originale. Altrimenti, il metodo calcola un nuovo valore di In utilizzando l'equazione: InMin + Step * (In - InMin) / Step, dove MathRound() è il metodo per arrotondare un numero al numero intero più vicino.

Pertanto, il metodo SeInDiSp() consente di controllare la variazione del valore della variabile In entro i limiti e con un passo specificati, il che aiuta a ottimizzare la funzione in modo più efficiente e rapido.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————

3. Risultati del test

Risultati del banco di prova dell'algoritmo ME:

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigin's; Func cicli 10000 risultato: 59.939529106561224
2023.03.26 18:27:43.215    Punteggio: 0.74268
2023.03.26 18:27:52.960    25 Rastrigin's; Func cicli 10000 risultato: 59.780143424645416
2023.03.26 18:27:52.960    Punteggio: 0.74071
2023.03.26 18:29:22.856    500 Rastrigin's; Func cicli 10000 risultato: 63.94951378068386
2023.03.26 18:29:22.856    Punteggio: 0.79237
2023.03.26 18:29:22.856 =============================
2023.03.26 18:29:28.901    5 Forest's; Func cicli 10000 risultato: 0.28698617113254693
2023.03.26 18:29:28.901    Punteggio: 0.16233
2023.03.26 18:29:38.103    25 Forest's; Func cicli 10000 risultato: 0.1571444033424823
2023.03.26 18:29:38.103    Punteggio: 0.08889
2023.03.26 18:30:53.341    500 Forest's; Func cicli 10000 risultato: 0.11734383105881332
2023.03.26 18:30:53.341    Punteggio: 0.06638
2023.03.26 18:30:53.341 =============================
2023.03.26 18:30:58.108    5 Megacity's; Func cicli 10000 risultato: 1.3599999999999999
2023.03.26 18:30:58.108    Punteggio: 0.11333
2023.03.26 18:31:08.897    25 Megacity's; Func cicli 10000 risultato: 0.776
2023.03.26 18:31:08.897    Punteggio: 0.06467
2023.03.26 18:32:23.199    500 Megacity's; Func cicli 10000 risultato: 0.34320000000000006
2023.03.26 18:32:23.199    Punteggio: 0.02860
2023.03.26 18:32:23.199 =============================
2023.03.26 18:32:23.199    Punteggio totale: 2.79996

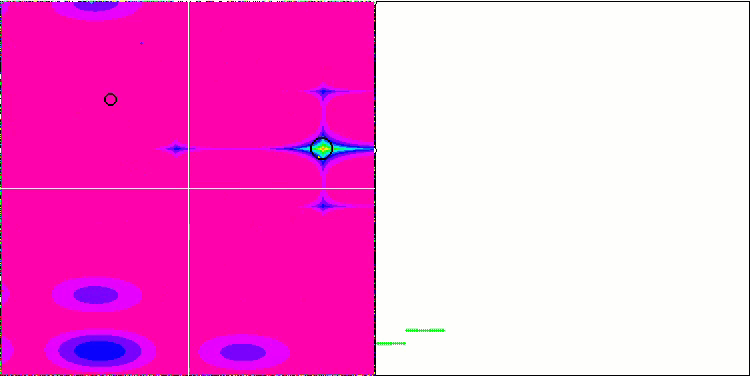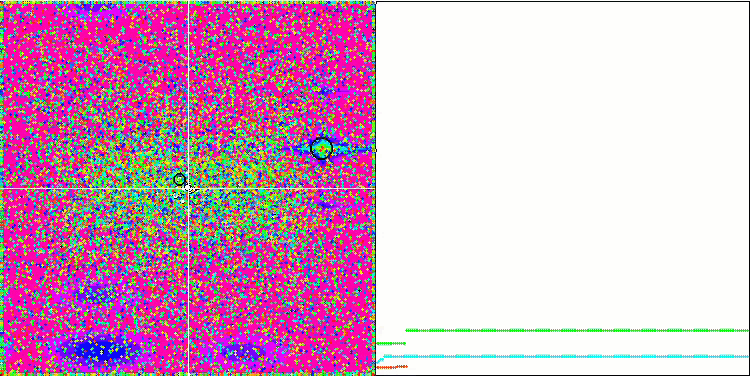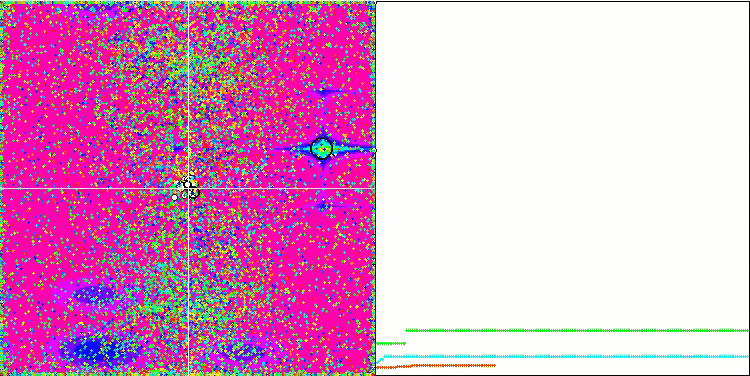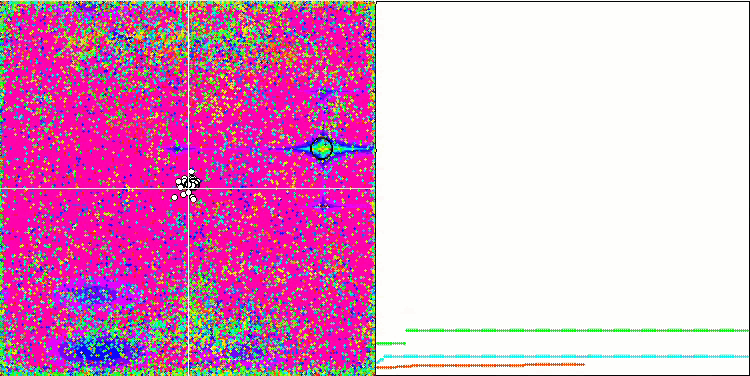
Prestando attenzione all'animazione dell'algoritmo ME sulle funzioni test, possiamo immaginare una sorta di "elettrificazione" del campo dello spazio di ricerca. Le particelle formano gruppi di cariche elevate seguendo le caratteristiche della superficie della funzione di test. Purtroppo la qualità della convergenza è notevolmente bassa, ma l'immagine è innegabilmente bella.

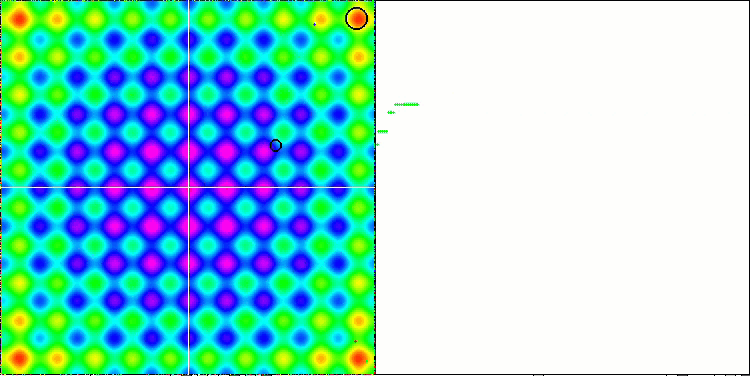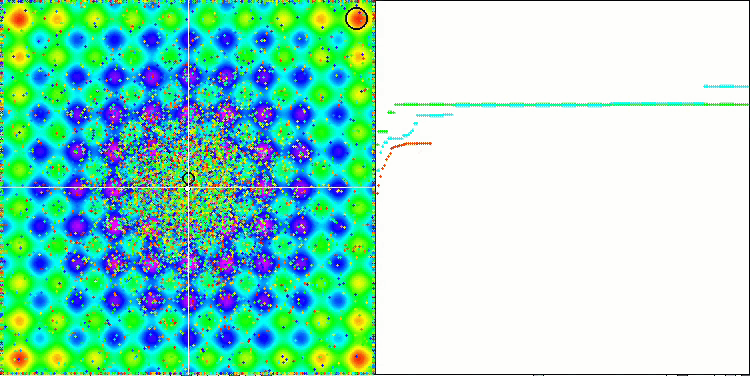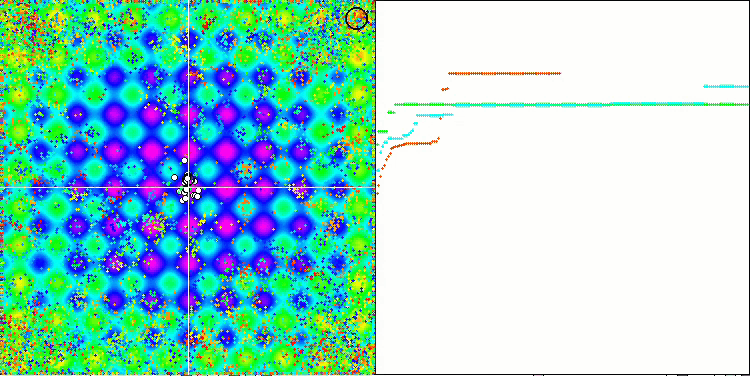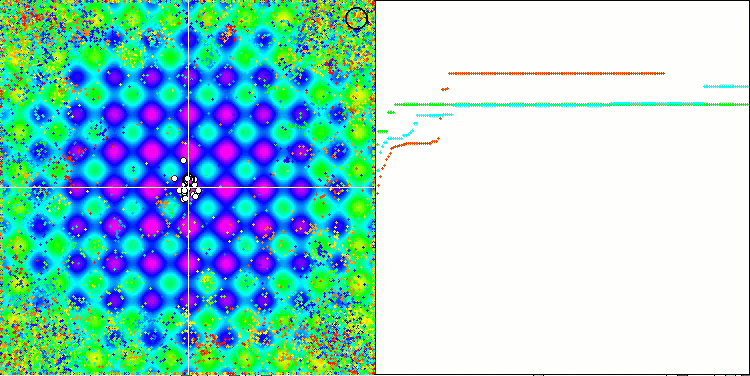
  EM sulla funzione test Rastrigin.

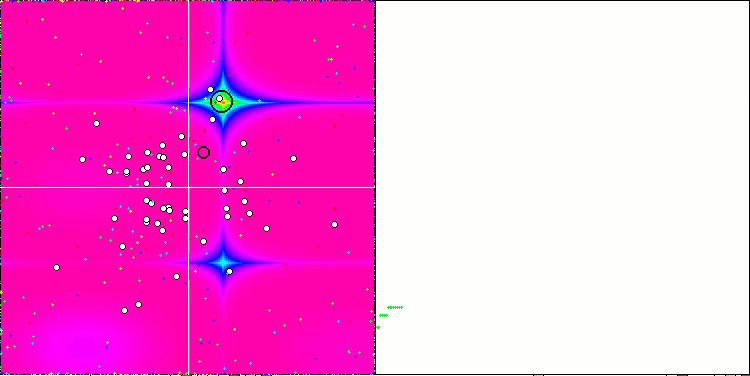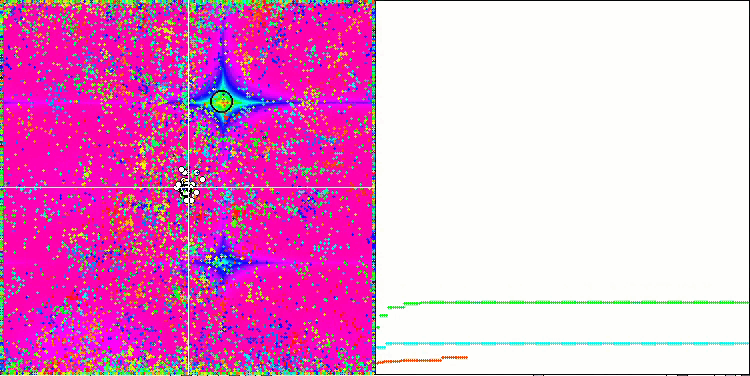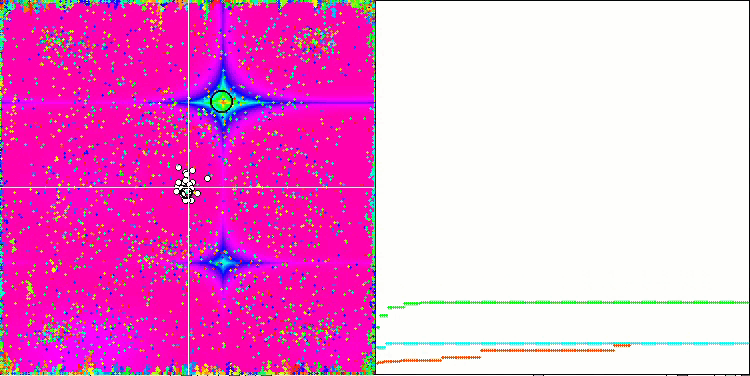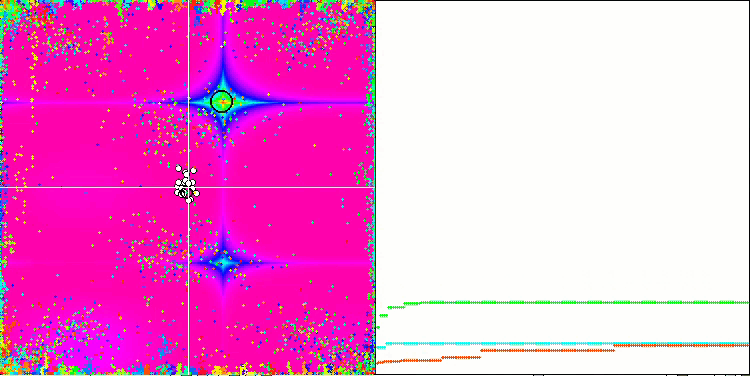
  EM sulla funzione test Forest.

  EM sulla funzione test Megacity.

Passiamo ai risultati dei test dell'algoritmo di ottimizzazione EM. EM ha ottenuto risultati inferiori alla media con un punteggio finale di 22. L'algoritmo ha ottenuto scarsi risultati in quasi tutti i test. L'eccezione è rappresentata dal test della funzione Rastrigin con 1000 parametri, in cui EM si è rivelato migliore di algoritmi potenti come SSG e BA. Inoltre, i valori assoluti della funzione con 1000 parametri sono risultati più elevati rispetto ai test con 10 e 50 parametri!

È la prima volta che i risultati della ricerca migliorano con l'aumento del numero dei parametri ottimizzati. Molto probabilmente, questo fenomeno è associato alle peculiarità della strategia di ricerca dell’EM stesso. È necessario notare la sensibilità dell'EM alla presenza di un gradiente e alla differenziabilità sull'intera area di definizione della funzione studiata.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
SSG	Semina e crescita degli alberelli	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	Ricerca dell'armonia	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	Ottimizzazione della colonia di formiche M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	Ottimizzazione delle piante infestanti	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	Algoritmo di ottimizzazione del cuculo M	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	Algoritmo della lucciola M	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	Colonia di api artificiali	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	Algoritmo di ricerca gravitazionale	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	Algoritmo del pipistrello	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	Ottimizzazione del foraggiamento batterico	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
EM	Algoritmo come l'elettromagnetismo	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
MA	Algoritmo della scimmia	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	Ricerca del banco di pesci	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	Ottimizzazione dello sciame di particelle	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	Casuale	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

Riepilogo

1. L'algoritmo EM è un metodo di ottimizzazione efficiente in grado di risolvere diversi problemi di ottimizzazione, in particolare quelli associati all'elaborazione di grandi quantità di dati e ad un'elevata dimensionalità su funzioni regolari.
2. L'algoritmo si basa sulla simulazione del comportamento delle particelle elettromagnetiche nello spazio fisico, il che consente di ottenere un'elevata precisione del risultato quando si lavora con funzioni multidimensionali complesse.
3. L'algoritmo EM non richiede il calcolo del gradiente, il che lo rende più versatile e più facile da applicare a vari problemi, ma è sensibile alla presenza di un gradiente nella funzione da ottimizzare.
4. L'algoritmo può essere modificato e personalizzato in base al problema di ottimizzazione specifico, il che lo rende uno strumento flessibile per l'ottimizzazione di varie funzioni.
5. Esistono diverse modifiche dell'algoritmo EM che possono essere migliorate rispetto alla versione di base e adattate a problemi di ottimizzazione specifici.
6. L'algoritmo EM può essere utilizzato in vari campi come l'apprendimento automatico, l'intelligenza artificiale, l'ottimizzazione dei mercati finanziari e altri.

Il vantaggio principale dell'algoritmo elettromagnetico è la capacità di risolvere problemi di ottimizzazione in spazi multidimensionali e di grandi dimensioni, pur mantenendo un'elevata precisione del risultato.

Pertanto, l'algoritmo EM è uno strumento efficace per l'ottimizzazione di varie funzioni e può essere utilizzato in un'ampia gamma di problemi di ottimizzazione, soprattutto quando si elaborano una grande quantità di dati e/o un'elevata dimensionalità.

Questa valutazione può essere utile per scegliere l'algoritmo più adatto a risolvere un particolare problema di ottimizzazione. Tuttavia, l'efficienza dell'algoritmo dipende da molti fattori, come la dimensione del problema, il tipo di funzione, il numero di variabili, ecc. Perciò, la scelta di un algoritmo dovrebbe basarsi su un'analisi approfondita di un particolare problema.

La Figura 1 mostra i risultati dei test degli algoritmi.

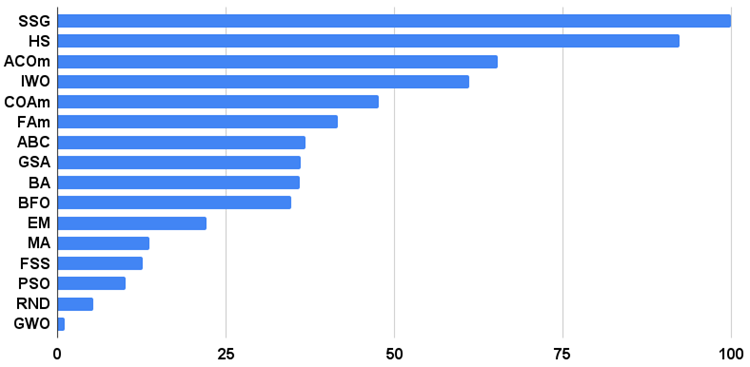
Figura 1. Istogramma dei risultati dei test degli algoritmi

Pro e contro dell'algoritmo elettromagnetico (EM):

Pro:
1. Facile implementazione.
2. Scalabilità impressionante sulle funzioni regolari.
3. Numero ridotto di parametri esterni.

Contro:
1. Elevata complessità computazionale.
2. Scarsi risultati sulle funzioni discrete.
3. Si blocca sulle funzioni con "piattaforme" orizzontali piatte.

Ogni articolo presenta un archivio che contiene le versioni aggiornate dei codici degli algoritmi per tutti gli articoli precedenti. L'articolo si basa sull'esperienza accumulata dall'autore e rappresenta la sua opinione personale. Le conclusioni e i giudizi si basano sugli esperimenti.